データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング(MMM)です。
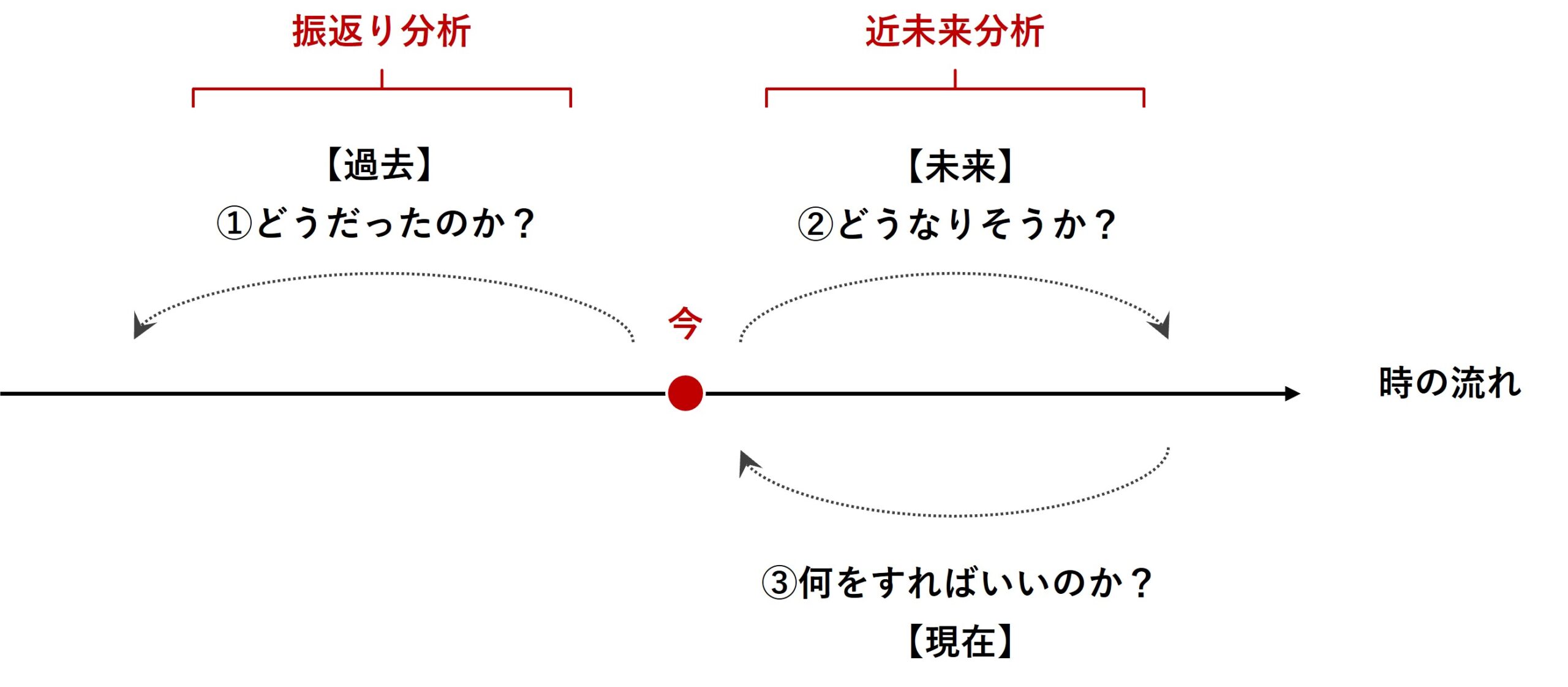
マーケティングミックスモデリング(MMM)は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。
通常のMMMは、アドストック(Ad Stock)が考慮されます。ここで言うアドストック(Ad Stock)とは、キャリーオーバー効果や飽和効果のことです。
MMMにアドストック(Ad Stock)を組み込むには、パイプラインを構築するといいでしょう。このようなパイプラインを、ここではMMMパイプラインと表現することにします。
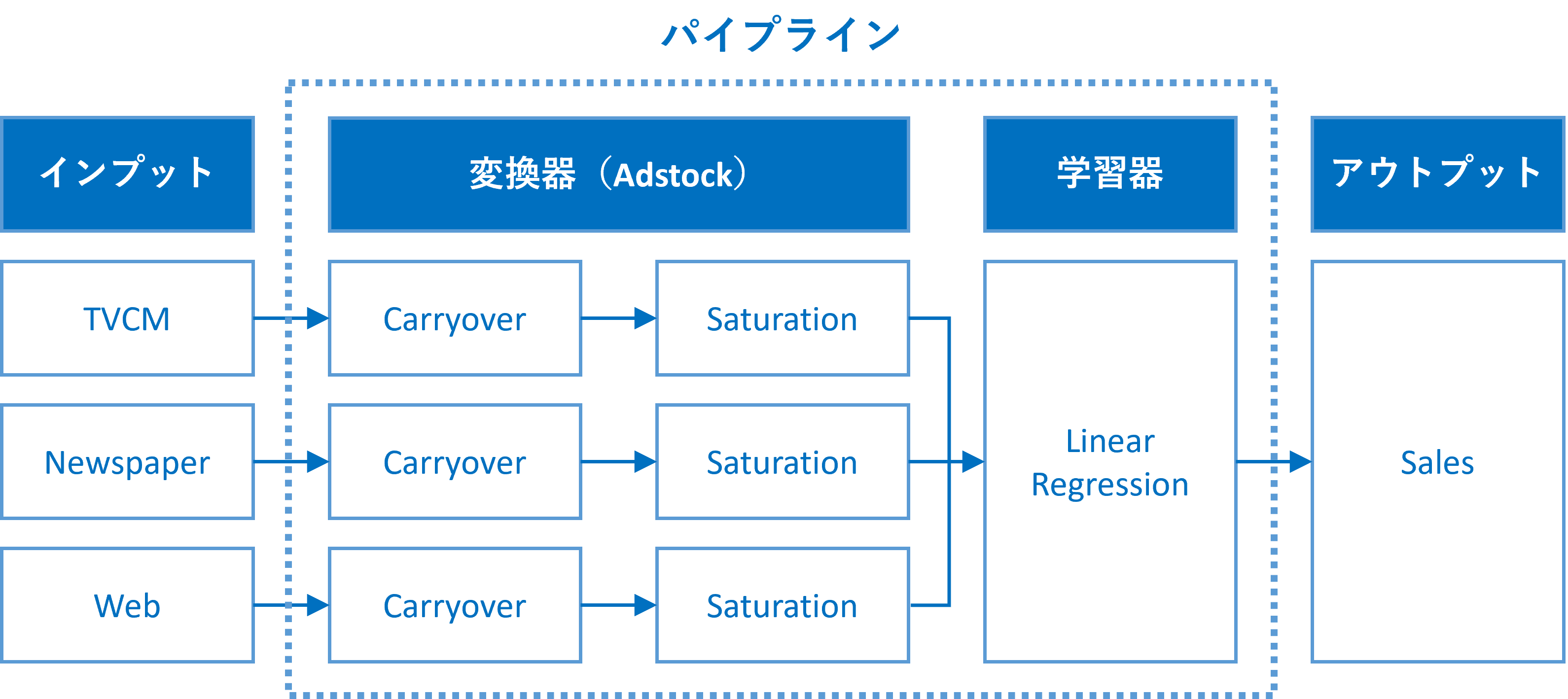
このMMMパイプラインは、少なくとも2つの変換器と1つの推定器が必要になります。
- 変換器
- キャリーオーバー効果関数(Carryover)
- 飽和関数(Saturation)
- 推定器
- 線形回帰系のモデル(Linear Regression):今回はRidge回帰を利用
前回は、アドストックの飽和関数を自動選択し構築するMMMというお話しをしました。
PythonによるMMM(マーケティングミックスモデリング)とビジネス活用- 振返り分析・線形回帰系モデル編(その5)-アドストック線形回帰系MMM(推定器自動選択)
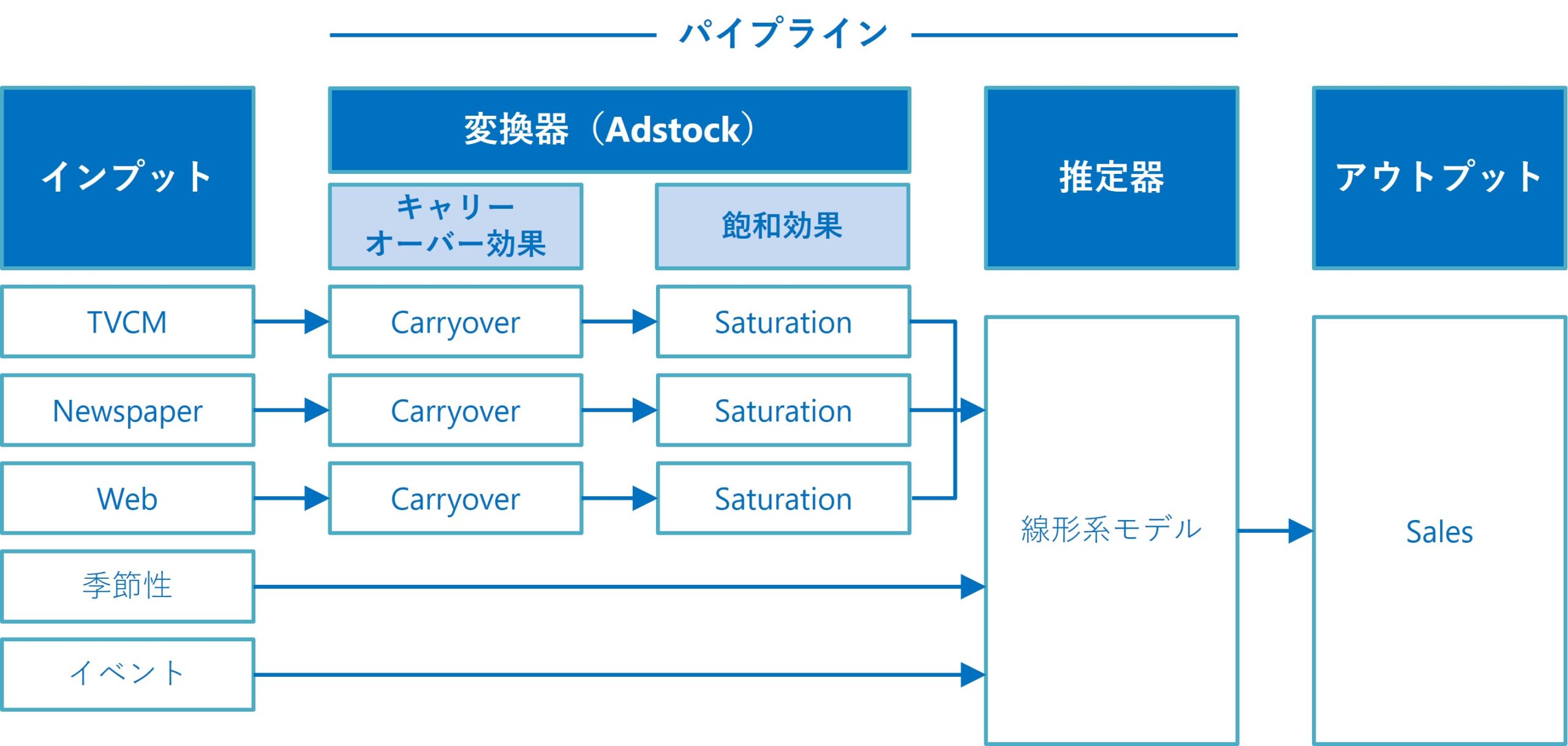
前回までは、すべての特徴量(説明変数)が、すべてアドストックを考慮すべき変数として扱っていました。
現実のMMMでは、すべての特徴量(説明変数)がアドストックを考慮すべき変数とは限りません。考慮すべきでない変数もあります。
例えば、メディア関連とは関係のないカレンダー情報を元にした特徴量(例:クリスマス変数、初売り初日変数などの○○の日)や、季節性を表現する三角関数特徴量(SinとCosで表現)などは、アドストックを考慮すべきでない変数かもしれません。
要するに、各特徴量(説明変数)の特性に応じて、MMMを構築するときに「アドストックを考慮すべき or アドストックを考慮すべきでない」を選べるといいでしょう。
ということで、今回は「アドストックを考慮すべき特徴量を指定し構築する線形回帰系MMM」というお話しをします。
MMMパイプラインの中で、各特徴量(説明変数)に対し「アドストックを考慮すべき or アドストックを考慮すべきでない」で分岐する感じになります。
前回までとコードがほぼ同じなので、コード説明は極力省略します。気になる方は、前回までの記事を参考にしてください。
Contents
- 利用するデータセット
- 今回構築する3つのMMM
- 準備
- モジュールの読み込み
- MMM推定器(およびパイプライン)のリスト
- データセットの読み込み
- アドストック系の関数とクラス、そのグラフ化関数の定義
- キャリオーバー効果関数
- 飽和関数
- アドストック視覚化(グラフ)関数
- アドストックを考慮する特徴量のリスト
- 手動MMM構築(人がハイパラ付与)
- ハイパーパラメータの設定
- MMM構築
- 後処理(結果の出力)
- 自動MMM構築(ハイパラ自動調整)
- ハイパーパラメータ自動調整
- MMM構築
- 後処理(結果の出力)
- 自動MMM構築(ハイパラ&推定器を自動選択&調整)
- ハイパーパラメータ自動調整
- MMM構築
- 後処理(結果の出力)
- まとめ
利用するデータセット
以下のデータセットを利用します。
- 目的変数:売上金額(Sales)
- 説明変数:
- メディア:TVCM、Newspaper、Webのコスト
- イベント:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
今回利用するデータセットは、以下からダウンロードできます。
MMM_xmas.csv
https://www.salesanalytics.co.jp/dcbd
今回は、以下のように設定しました。
- アドストックを考慮する:TVCM、Newspaper、Webのコスト
- アドストックを考慮しない:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
やり方は非常に簡単で、scikit-learn(sklearn)のColumnTransformerを使って特定の列(変数)にのみ変換を適用するようにします。ColumnTransformerは、変数に応じて処理を変えるときなどに利用します。
今回構築する3つのMMM
今回は、以下の3つのMMMを構築します。
- 手動MMM構築(人がハイパラ付与)
- 自動MMM構築(ハイパラ自動調整)
- 自動MMM構築(ハイパラ&推定器を自動選択&調整)
ハイパラとは、変換器(アドストック)のハイパーパラメータや推定器のハイパーパラメータのことです。ハイパーパラメータの調整には、Optunaを利用します。
要するに、前回までに構築していたMMMに対し、MMMパイプラインの中で、各特徴量(説明変数)に対し「アドストックを考慮すべき or アドストックを考慮すべきでない」で分岐する感じになります。
準備
モジュールの読み込み
以下、コードです。
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import TimeSeriesSplit
from sklearn.model_selection import cross_val_score
from functools import partial
import warnings
warnings.simplefilter('ignore')
import optuna
optuna.logging.set_verbosity(optuna.logging.WARNING)
optuna.logging.disable_default_handler()
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 7] #グラフサイズ
plt.rcParams['font.size'] = 9 #フォントサイズ
from mmm_functions import *
mmm_functionsは、以前作った以下の関数群です。
- MMM構築
train_and_evaluate_model:MMMの構築plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
- 後処理(結果の出力)
calculate_and_plot_contribution:売上貢献度の算出(時系列推移)summarize_and_plot_contribution:売上貢献度構成比の算出calculate_marketing_roi:マーケティングROIの算出
興味のある方、詳細を知りたい方は、以下を参照ください。
以下からダウンロードできます。
mmm_functions.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/oi17
mmm_functions.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
以下のコードで呼び出しています。
from mmm_functions import *
上手くいかないときは、mmm_functions.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。
MMM推定器(およびパイプライン)のリスト
自動MMM構築(ハイパラ&推定器を自動選択&調整)の自動選択対象のMMMモデル(もしくはMMMパイプライン)をリスト化します。
以下、コードです。
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import BayesianRidge
from sklearn.cross_decomposition import PLSRegression
estimators = [
("LR", LinearRegression()),
("Ridge", Ridge()),
("BayesianRidge", BayesianRidge()),
("PLS", Pipeline([('scaler', StandardScaler()),
("Reg", PLSRegression())
])),
("PCR", Pipeline([('scaler', StandardScaler()),
("PCA", PCA()),
("Reg", LinearRegression())
]))
]
これは、scikit-learn(sklearn)の5つの線形系のモデルのリストです。
LinearRegression:一般的な線形回帰モデルRidge:L2正則化を加えた線形回帰(リッジ回帰)BayesianRidge:ベイズ統計に基づいたリッジ回帰PLSRegression:部分的最小2乗回帰(Partial Least Squares Regression)- 主成分回帰:
PCAとLinearRegressionの組み合わせ
MMMのハイパーパラメータチューニングでは、この5つの推定器を選択し、さらに選択した推定器のハイパーパラメータ調整を含みます。
データセットの読み込み
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/dcbd'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
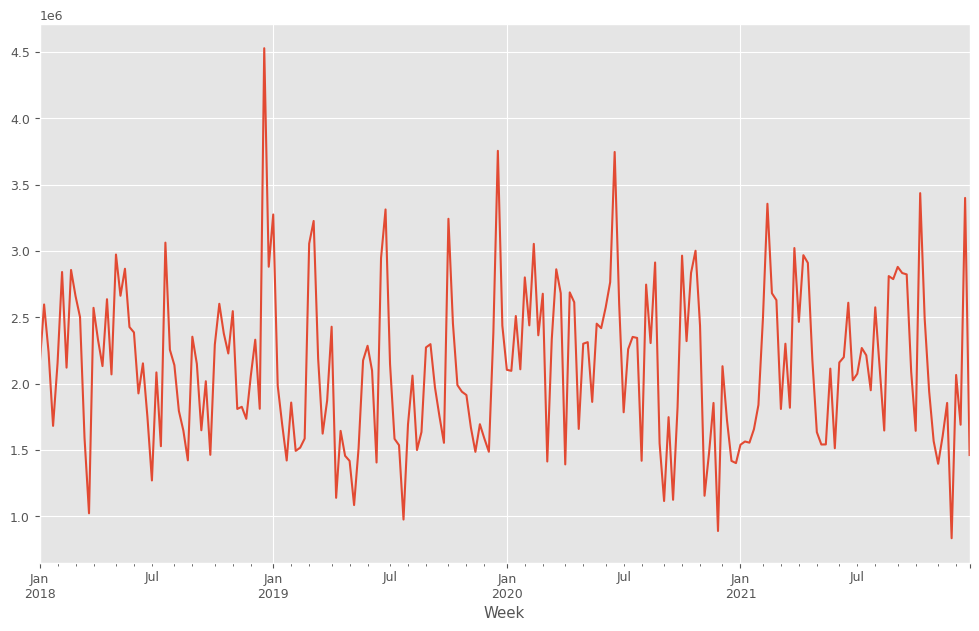
目的変数y(売上)をプロットします。
以下、コードです。
y.plot() plt.show()
以下、実行結果です。

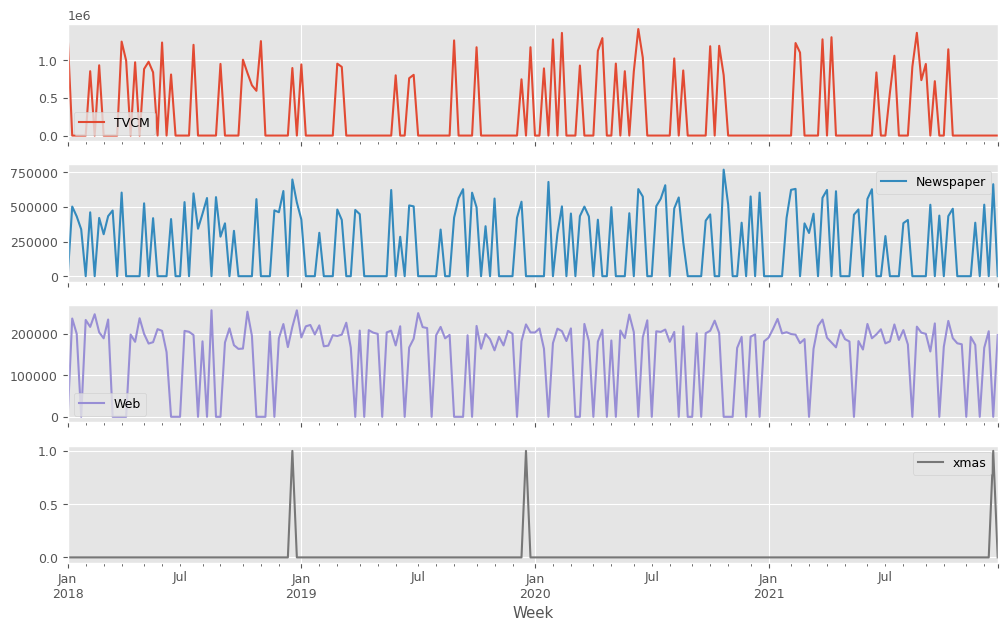
説明変数X(各メディアのコスト)をまとめてプロットします。
以下、コードです。
X.plot(subplots=True) plt.show()
以下、実行結果です。XMas変数は0-1変数(12月25日に1、その他の日は0)で、他の変数はコストデータです。

アドストック系の関数とクラス、そのグラフ化関数の定義
アドストック系の関数である、シンプルなキャリーオーバー効果関数とそのクラス、シンプルな飽和関数とそのクラス、そしてそれらを視覚化(グラフ)する関数を作っていきます。
キャリオーバー効果関数
先ずは、キャリーオーバー効果関数とそのクラスを作ります。
以下、コードです。
# キャリオーバー効果関数
def carryover_advanced(X: np.ndarray, length, peak, rate1, rate2, c1, c2):
X = np.append(np.zeros(length-1), X)
Ws = np.zeros(length)
for l in range(length):
if l<peak-1:
W = rate1**(abs(l-peak+1)**c1)
else:
W = rate2**(abs(l-peak+1)**c2)
Ws[length-1-l] = W
carryover_X = []
for i in range(length-1, len(X)):
X_array = X[i-length+1:i+1]
Xi = sum(X_array * Ws)/sum(Ws)
carryover_X.append(Xi)
return np.array(carryover_X)
# キャリオーバー効果を適用するカスタム変換器クラス
class CustomCarryOverTransformer(BaseEstimator, TransformerMixin):
def __init__(self, carryover_params=None):
self.carryover_params = carryover_params if carryover_params is not None else []
def fit(self, X, y=None):
return self
def transform(self, X):
if isinstance(X, pd.DataFrame):
X = X.to_numpy()
transformed_X = np.copy(X)
for i, params in enumerate(self.carryover_params):
transformed_X[:, i] = carryover_advanced(X[:, i], **params)
return transformed_X
飽和関数
次に、2つの飽和関数とそのクラスを作ります。
以下、コードです。
# 飽和関数(指数型)
def exponential_function(x, d):
result = 1 - np.exp(-d * x)
return result
# 飽和関数(ロジスティック曲線)
def logistic_function(x, L, k, x0):
result = L / (1+ np.exp(-k*(x-x0)))
return result
# 飽和関数を適用するカスタム変換器クラス
class CustomSaturationTransformer(BaseEstimator, TransformerMixin):
def __init__(self, curve_params=None):
self.curve_params = curve_params if curve_params is not None else []
def fit(self, X, y=None):
return self
def transform(self, X):
if isinstance(X, pd.DataFrame):
X = X.to_numpy()
transformed_X = np.copy(X)
for i, params in enumerate(self.curve_params):
saturation_function = params.pop('saturation_function')
if saturation_function == 'logistic':
transformed_X[:, i] = logistic_function(X[:, i], **params)
elif saturation_function == 'exponential':
transformed_X[:, i] = exponential_function(X[:, i], **params)
params['saturation_function'] = saturation_function # Returning the saturation_function back to params
return transformed_X
アドストック視覚化(グラフ)関数
どのようなアドストックになっているのかを視覚的に理解するために、視覚化(グラフ)する関数を作ります。
以下、コードです。
def plot_carryover_effect(params, feature_name, fig, axes, i):
max_length = max(10, params['length'])
x = np.concatenate(([1], np.zeros(max_length - 1)))
y = carryover_advanced(x, **params)
y = y / max(y) # Fixed line: y normalization moved here
axes[2*i].bar(np.arange(1, max_length + 1), y)
axes[2*i].set_title(f'Carryover Effect for {feature_name}')
axes[2*i].text(0, 1.1, params, ha='left',va='top')
axes[2*i].set_xlabel('Time Lag')
axes[2*i].set_ylabel('Effect')
axes[2*i].set_xticks(range(len(y)))
axes[2*i].set_ylim(0, 1.1)
def plot_saturation_curve(params, feature_name, fig, axes, i):
x = np.linspace(-1, 3, 400)
saturation_function = params.pop('saturation_function')
if saturation_function == 'logistic':
y = logistic_function(x, **params)
elif saturation_function == 'exponential':
y = exponential_function(x, **params)
axes[2*i+1].plot(x, y, label=feature_name)
axes[2*i+1].set_title(f'Saturation Curve for {feature_name}')
params['saturation_function'] = saturation_function
axes[2*i+1].text(-1, max(y)* 1.1, params, ha='left',va='top')
axes[2*i+1].set_xlabel('X')
axes[2*i+1].set_ylabel('Transformation')
axes[2*i+1].set_ylim(0, max(y) * 1.1)
axes[2*i+1].set_xlim(-1, 3)
def plot_effects(carryover_params, curve_params, feature_names):
fig, axes = plt.subplots(len(feature_names) * 2, 1, figsize=(12, 10*len(feature_names)))
for i, params in enumerate(carryover_params):
plot_carryover_effect(params, feature_names[i], fig, axes, i)
for i, params in enumerate(curve_params):
plot_saturation_curve(params, feature_names[i], fig, axes, i)
plt.tight_layout()
plt.show()
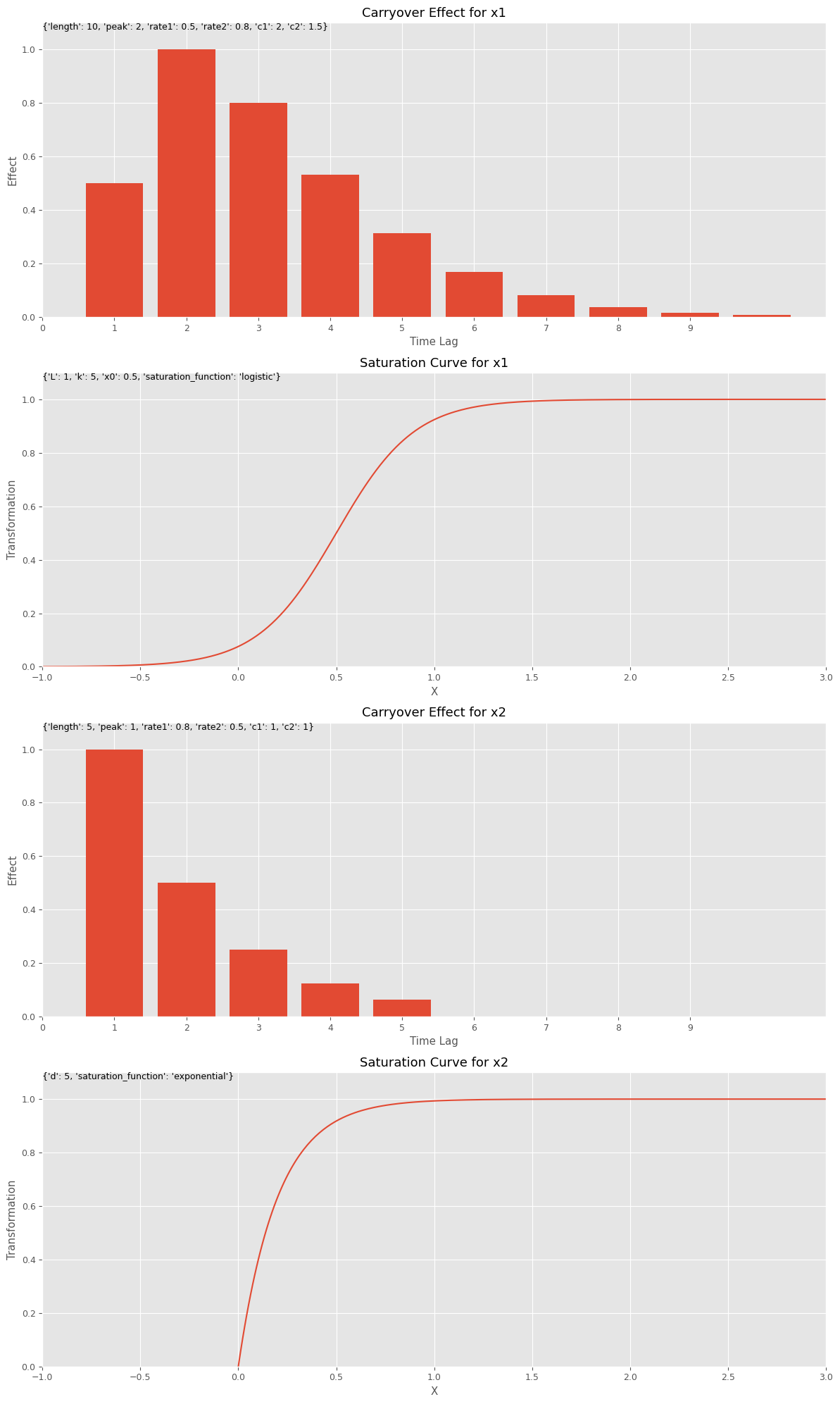
この関数を利用してみます。
先ず、キャリーオーバー効果関数と飽和関数のハイパーパラメータを設定します。このハイパーパラメータを、今作った視覚化(グラフ)する関数にインプットしグラフを描きます。特徴量名は何を設定しても問題ございません。
以下、コードです。
# キャリーオーバー効果関数のハイパーパラメータの設定
carryover_params = [
{'length': 10, 'peak': 2, 'rate1': 0.5, 'rate2': 0.8, 'c1': 2, 'c2': 1.5},
{'length': 5, 'peak': 1, 'rate1': 0.8, 'rate2': 0.5, 'c1': 1, 'c2': 1}
]
# 飽和関数のハイパーパラメータの設定
curve_params = [
{'saturation_function': 'logistic', 'L': 1, 'k': 5, 'x0': 0.5},
{'saturation_function': 'exponential', 'd': 5}
]
# 特徴量名の設定
feature_names = ['x1', 'x2']
# グラフで確認
plot_effects(carryover_params, curve_params, feature_names)
以下、実行結果です。
アドストックを考慮する特徴量のリスト
アドストックを考慮する特徴量のリストと、そうでない特徴量のリスト、インデックスのリストを生成します。
以下、コードです。
# アドストックを考慮する特徴量のリストを作成 apply_effects_features = ['TVCM', 'Newspaper', 'Web'] # アドストックを考慮する特徴量 no_effects_features = X.columns.drop(apply_effects_features) # アドストックを考慮しない特徴量 # 列名リストからインデックスのリストを作成 apply_effects_indices = [X.columns.get_loc(column) for column in apply_effects_features] no_effects_indices = [X.columns.get_loc(column) for column in no_effects_features]
このコードは、最初のアドストックを考慮する特徴量のリストを作成するだけで、残りの3つの残りを生成できるようにしてあります。
特徴量の変数名を使う処理と、特徴量のインデックス(列番号)を使った処理の2パターンがあるため、2つのインデックスのリストも生成してます。
基本的には、特徴量の変数名を使う処理を実施しますが、特徴量のインデックス(列番号)を使った方が楽なケースがありますので、そのときは特徴量のインデックス(列番号)を使った処理を実施します。
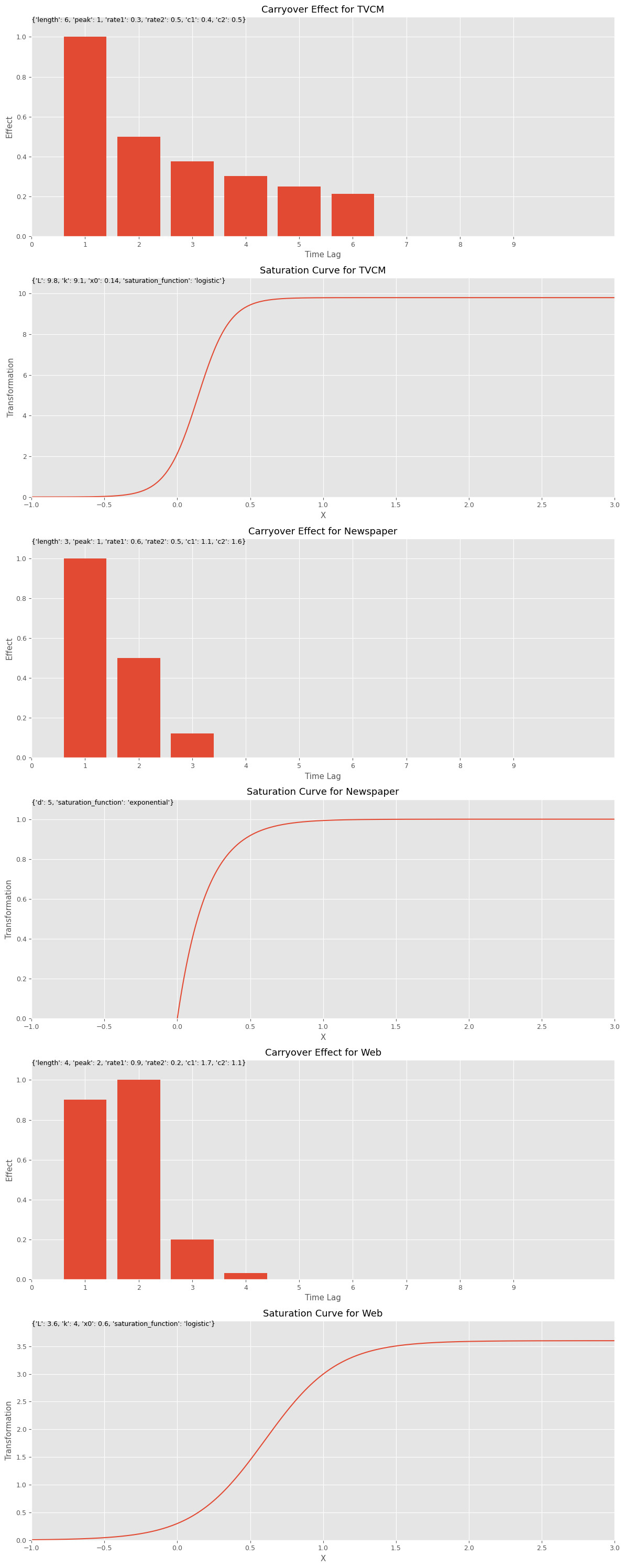
手動MMM構築(人がハイパラ付与)
ハイパーパラメータの設定
ハイパーパラメータを設定し、グラフで視覚的に確認します。
以下、コードです。
# 各特徴量に対するキャリーオーバー効果のパラメータ設定
carryover_params = [
{'length': 6,'peak': 1,'rate1': 0.3,'rate2': 0.5,'c1': 0.4,'c2': 0.5},
{'length': 3,'peak': 1,'rate1': 0.6,'rate2': 0.5,'c1': 1.1,'c2':1.6},
{'length': 4,'peak': 2,'rate1': 0.9,'rate2': 0.2,'c1': 1.7,'c2': 1.1}
]
# 各特徴量に対する飽和関数のパラメータ設定
curve_params = [
{'saturation_function': 'logistic','L': 9.8,'k': 9.1,'x0': 0.14},
{'saturation_function': 'exponential', 'd': 5},
{'saturation_function': 'logistic','L': 3.6,'k': 4,'x0': 0.6}
]
# 特徴量名の設定
feature_names = apply_effects_features
# グラフで確認
plot_effects(carryover_params, curve_params, feature_names)
以下、実行結果です。
MMM構築
MMMパイプラインを構築します。
ColumnTransformerを使って特定の列(変数)にのみアドストックの変換(キャリーオーバー効果関数と飽和関数)を適用するためのパイプライン変換器(トランスフォーマー)であるpreprocessor を定義します。
このpreprocessor をMMMパイプラインの中に組み込みます。
以下、コードです。
# ColumnTransformerを使って特定の列にのみ変換を適用する
preprocessor = ColumnTransformer(
transformers=[
('effects', Pipeline([
('carryover_transformer', CustomCarryOverTransformer(carryover_params=carryover_params)),
('saturation_transformer', CustomSaturationTransformer(curve_params=curve_params))
]), apply_effects_indices),
('no_effects', 'passthrough', no_effects_indices)
],
remainder='drop'
)
# パイプラインの構築
MMM_pipeline = Pipeline([
('scaler', MinMaxScaler()),
('preprocessor', preprocessor),
('ridge', Ridge(alpha=1))
])
# パイプラインの表示
MMM_pipeline
以下、実行結果(構築したMMMパイプライン)です。MinMaxScalerの次の処理で変数の処理が分岐していることが分かるかと思います。

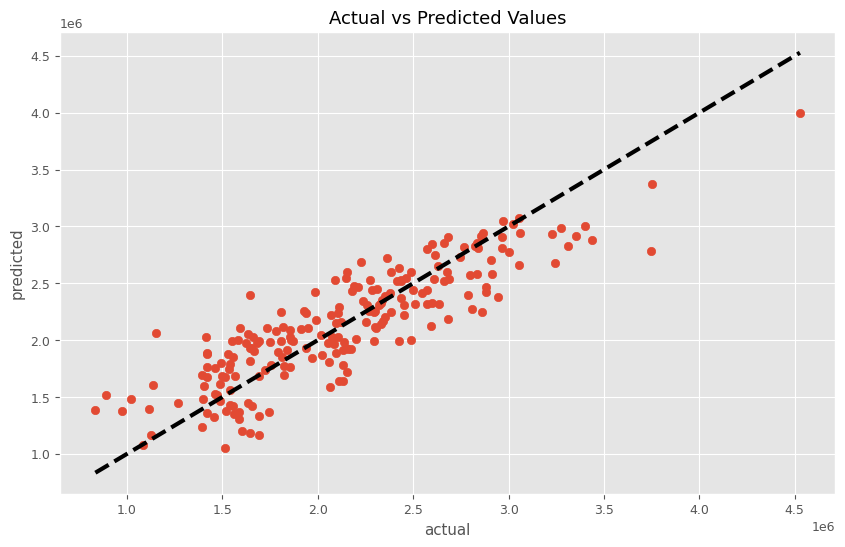
MMMパイプラインを学習し、その結果を散布図(横軸:実測値、縦軸:予測値)をプロットします。
以下、コードです。
# パイプラインを使って学習
trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)
# 予測結果の表示
plt.figure(figsize=(10, 6))
plt.scatter(y, pred)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=3)
plt.xlabel('actual')
plt.ylabel('predicted')
plt.title('Actual vs Predicted Values')
plt.show()
以下、実行結果です。
RMSE: 296340.3031890805 MAE: 238849.91174925564 MAPE: 0.12512848085904074 R2: 0.7546773035954673
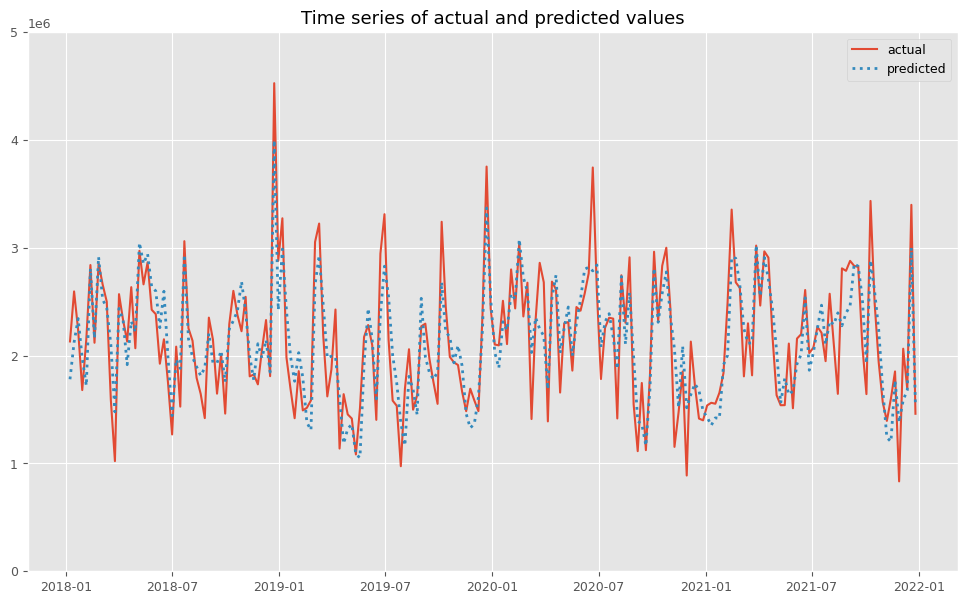
予測値と実測値の時系列推移を見てみます。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 5e6))
以下、実行結果です。
後処理(結果の出力)
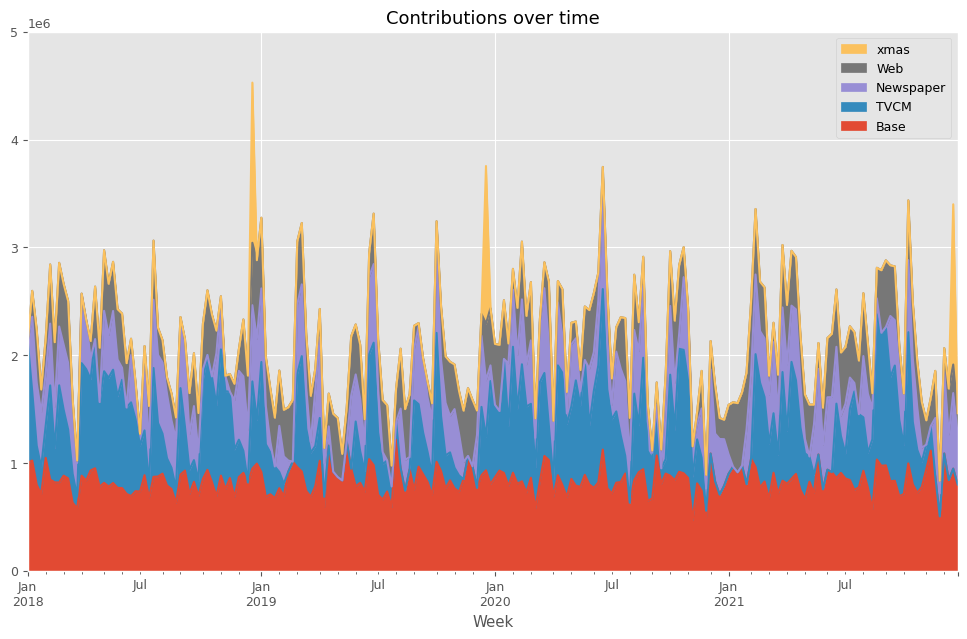
MMMを構築したら、貢献度やマーケティングROIなどを計算していきます。
先ずは、貢献度を計算します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 5e6))
以下、実行結果です。
Base TVCM Newspaper Web \
Week
2018-01-07 1.000697e+06 1.131303e+06 0.000000 0.000000
2018-01-14 1.022413e+06 6.407488e+05 693227.728751 239710.358369
2018-01-21 7.975337e+05 3.631155e+05 583636.510512 491914.299864
2018-01-28 7.111474e+05 2.515021e+05 509220.782804 209029.693254
2018-02-04 1.046806e+06 2.990721e+05 482464.229379 327057.885593
... ... ... ... ...
2021-11-28 5.042975e+05 0.000000e+00 212530.277864 117072.212187
2021-12-05 1.087274e+06 0.000000e+00 761830.249135 215595.459216
2021-12-12 8.406574e+05 0.000000e+00 424028.209569 424814.410744
2021-12-19 9.472107e+05 0.000000e+00 700945.247936 264697.671783
2021-12-26 7.992093e+05 0.000000e+00 460049.827620 201840.887008
xmas
Week
2018-01-07 0.000000e+00
2018-01-14 0.000000e+00
2018-01-21 0.000000e+00
2018-01-28 0.000000e+00
2018-02-04 0.000000e+00
... ...
2021-11-28 0.000000e+00
2021-12-05 0.000000e+00
2021-12-12 0.000000e+00
2021-12-19 1.486346e+06
2021-12-26 0.000000e+00
[208 rows x 5 columns]
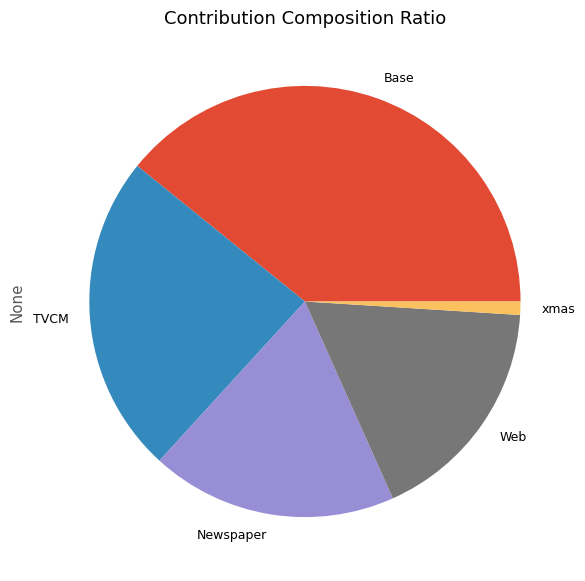
次に、貢献度の割合を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 1.740112e+08 0.391744 TVCM 1.067782e+08 0.240385 Newspaper 8.206516e+07 0.184750 Web 7.690863e+07 0.173141 xmas 4.433500e+06 0.009981
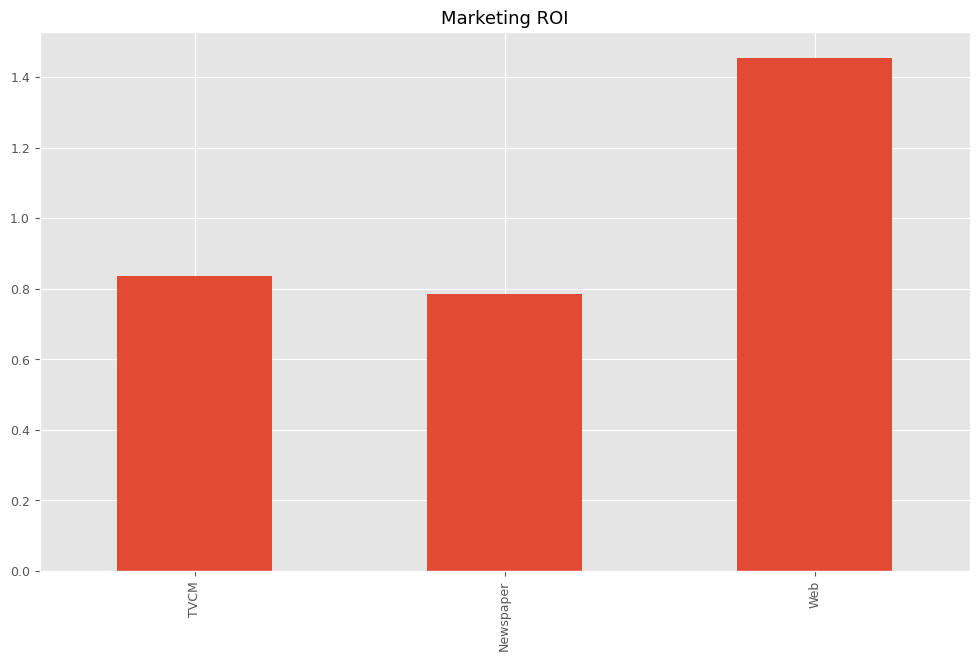
最後に、各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出
ROI = calculate_marketing_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
以下、実行結果です。
TVCM 0.836334 Newspaper 0.784561 Web 1.454847 dtype: float64
自動MMM構築(ハイパラ自動調整)
ハイパーパラメータ自動調整
ハイパーパラメータを自動チューニングするため、Optunaの目的関数を定義します。
以下、コードです。
def objective(trial, X, y):
carryover_params = []
curve_params = []
for feature in apply_effects_features:
carryover_length = trial.suggest_int(f'carryover_length_{feature}', 1, 10)
carryover_peak = trial.suggest_int(f'carryover_peak_{feature}', 1, carryover_length)
carryover_rate1 = trial.suggest_float(f'carryover_rate1_{feature}', 0, 1)
carryover_rate2 = trial.suggest_float(f'carryover_rate2_{feature}', 0, 1)
carryover_c1 = trial.suggest_float(f'carryover_c1_{feature}', 0, 2)
carryover_c2 = trial.suggest_float(f'carryover_c2_{feature}', 0, 2)
carryover_params.append({
'length': carryover_length,
'peak': carryover_peak,
'rate1': carryover_rate1,
'rate2': carryover_rate2,
'c1': carryover_c1,
'c2': carryover_c2,
})
saturation_function = trial.suggest_categorical(f'saturation_function_{feature}', ['logistic', 'exponential'])
if saturation_function == 'logistic':
curve_param_L = trial.suggest_float(f'curve_param_L_{feature}', 0, 10)
curve_param_k = trial.suggest_float(f'curve_param_k_{feature}', 0, 10)
curve_param_x0 = trial.suggest_float(f'curve_param_x0_{feature}', 0, 2)
curve_params.append({
'saturation_function': saturation_function,
'L': curve_param_L,
'k': curve_param_k,
'x0': curve_param_x0,
})
elif saturation_function == 'exponential':
curve_param_d = trial.suggest_float(f'curve_param_d_{feature}', 0, 10)
curve_params.append({
'saturation_function': saturation_function,
'd': curve_param_d,
})
alpha = trial.suggest_float('alpha', 1e-3, 1e+3)
preprocessor = ColumnTransformer(
transformers=[
('effects', Pipeline([
('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
('saturation', CustomSaturationTransformer(curve_params=curve_params))
]), apply_effects_indices),
('no_effects', 'passthrough', no_effects_indices)
],
remainder='drop'
)
pipeline = Pipeline(steps=[
('scaler', MinMaxScaler()),
('preprocessor', preprocessor),
('ridge', Ridge(alpha=alpha))
])
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(pipeline, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
return rmse
目的関数を最適化し、最適なハイパーパラメータを探索します。
以下、コードです。
# Optunaのスタディの作成と最適化の実行
study = optuna.create_study(direction='minimize')
objective_with_data = partial(objective, X=X, y=y)
study.optimize(objective_with_data, n_trials=10000, show_progress_bar=True)
print("Best trial:")
trial = study.best_trial
print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
print(f"{key}: {value}")
以下、実行結果です。
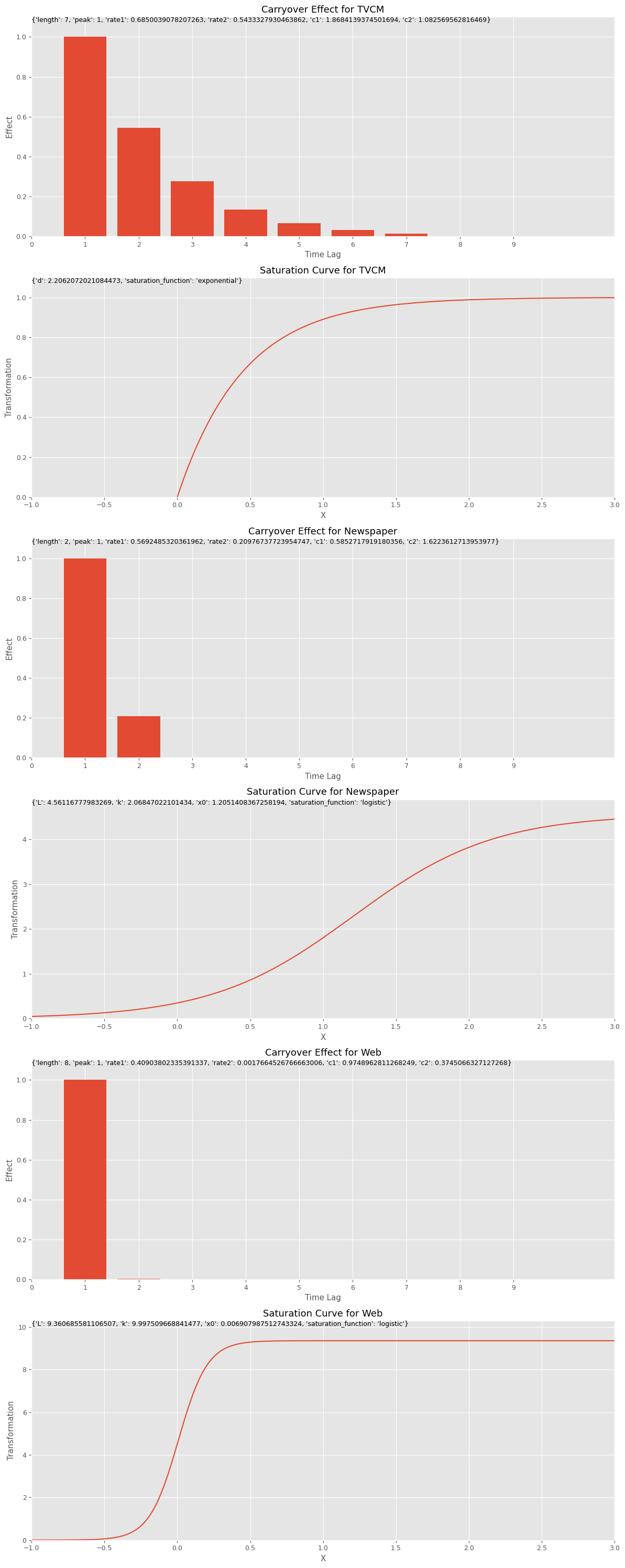
Best trial: 9973. Best value: 207865: 100%|██████████| 10000/10000 [2:42:33<00:00, 1.03it/s]Best trial: Value: 207865.35029227482 Params: carryover_length_TVCM: 7 carryover_peak_TVCM: 1 carryover_rate1_TVCM: 0.6850039078207263 carryover_rate2_TVCM: 0.5433327930463862 carryover_c1_TVCM: 1.8684139374501694 carryover_c2_TVCM: 1.082569562816469 saturation_function_TVCM: exponential curve_param_d_TVCM: 2.2062072021084473 carryover_length_Newspaper: 2 carryover_peak_Newspaper: 1 carryover_rate1_Newspaper: 0.5692485320361962 carryover_rate2_Newspaper: 0.20976737723954747 carryover_c1_Newspaper: 0.5852717919180356 carryover_c2_Newspaper: 1.6223612713953977 saturation_function_Newspaper: logistic curve_param_L_Newspaper: 4.56116777983269 curve_param_k_Newspaper: 2.06847022101434 curve_param_x0_Newspaper: 1.2051408367258194 carryover_length_Web: 8 carryover_peak_Web: 1 carryover_rate1_Web: 0.40903802335391337 carryover_rate2_Web: 0.0017664526766663006 carryover_c1_Web: 0.9748962811268249 carryover_c2_Web: 0.3745066327127268 saturation_function_Web: logistic curve_param_L_Web: 9.360685581106507 curve_param_k_Web: 9.997509668841477 curve_param_x0_Web: 0.006907987512743324 alpha: 0.007682286853647326
最適なハイパーパラメータを抽出します。
先ずは、そのための関数を定義します。
以下、コードです。
# 関数で最適ハイパーパラメータを取得してリストを返す
def get_optimal_hyperparameters(trial):
carryover_keys = ['length', 'peak', 'rate1', 'rate2', 'c1', 'c2']
curve_keys_logistic = ['L', 'k', 'x0']
curve_keys_exponential = ['d']
n_features = len(apply_effects_features)
indices = apply_effects_features
# ハイパーパラメータを抽出しキーと値の辞書を作成
def fetch_params(prefix, feature_name, params, trial_params):
return {key: trial_params[f'{prefix}_{key}_{feature_name}'] for key in params}
# キャリーオーバー効果関数ハイパーパラメータを抽出
carryover_params = [fetch_params('carryover', feature_name, carryover_keys, trial.params) for feature_name in indices]
# 飽和関数ハイパーパラメータを抽出
curve_params = []
for feature_name in indices:
saturation_function = trial.params[f'saturation_function_{feature_name}']
curve_param = {'saturation_function': saturation_function}
if saturation_function == 'logistic':
curve_param.update(fetch_params('curve_param', feature_name, curve_keys_logistic, trial.params))
elif saturation_function == 'exponential':
curve_param.update(fetch_params('curve_param', feature_name, curve_keys_exponential, trial.params))
curve_params.append(curve_param)
# 推定器ハイパーパラメータを抽出
alpha = trial.params['alpha']
return carryover_params, curve_params, alpha
この関数を使い、最適なハイパーパラメータを抽出します。
以下、コードです。
# ハイパーパーパラメータ抽出 best_carryover_params, best_curve_params, best_alpha = get_optimal_hyperparameters(study.best_trial)
グラフで視覚的に確認します。
以下、コードです。
# グラフで確認 plot_effects(best_carryover_params, best_curve_params, apply_effects_features)
以下、実行結果です。
MMM構築
最適なハイパーパラメータを使いMMMを構築します。
以下、コードです。
# ColumnTransformerを使って特定の列にのみ変換を適用する
preprocessor = ColumnTransformer(
transformers=[
('effects', Pipeline([
('carryover_transformer', CustomCarryOverTransformer(best_carryover_params)),
('saturation_transformer', CustomSaturationTransformer(best_curve_params))
]), apply_effects_indices),
('no_effects', 'passthrough', no_effects_indices)
],
remainder='drop'
)
# 新しいパイプラインの構築
MMM_pipeline = Pipeline([
('scaler', MinMaxScaler()),
('preprocessor', preprocessor),
('ridge', Ridge(alpha=1))
])
MMMパイプラインを学習し、その結果を散布図(横軸:実測値、縦軸:予測値)をプロットします。
以下、コードです。
# パイプラインを使って学習
trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)
# 予測結果の表示
plt.figure(figsize=(10, 6))
plt.scatter(y, pred)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=3)
plt.xlabel('actual')
plt.ylabel('predicted')
plt.title('Actual vs Predicted Values')
plt.show()
以下、実行結果です。
RMSE: 181967.90937937467 MAE: 145175.07226988877 MAPE: 0.07235033054184194 R2: 0.9074991126757249
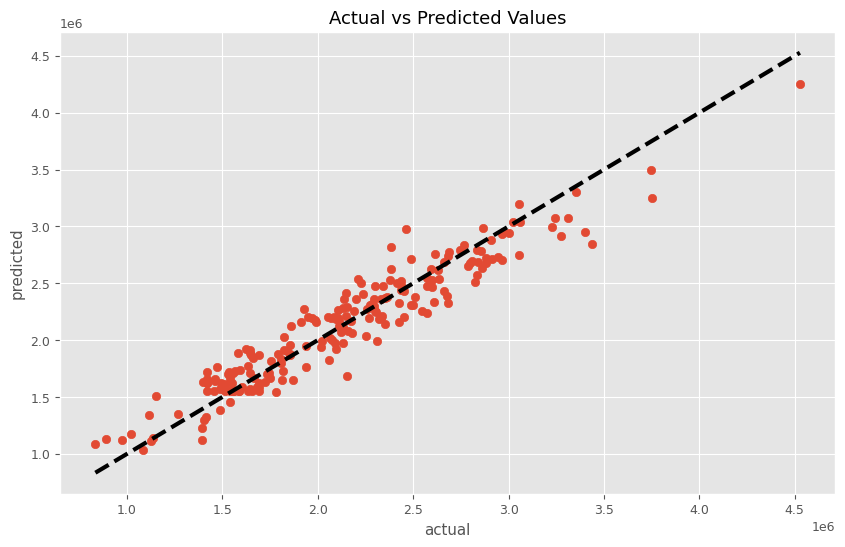
予測値と実測値の時系列推移を見てみます。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 5e6))
以下、実行結果です。
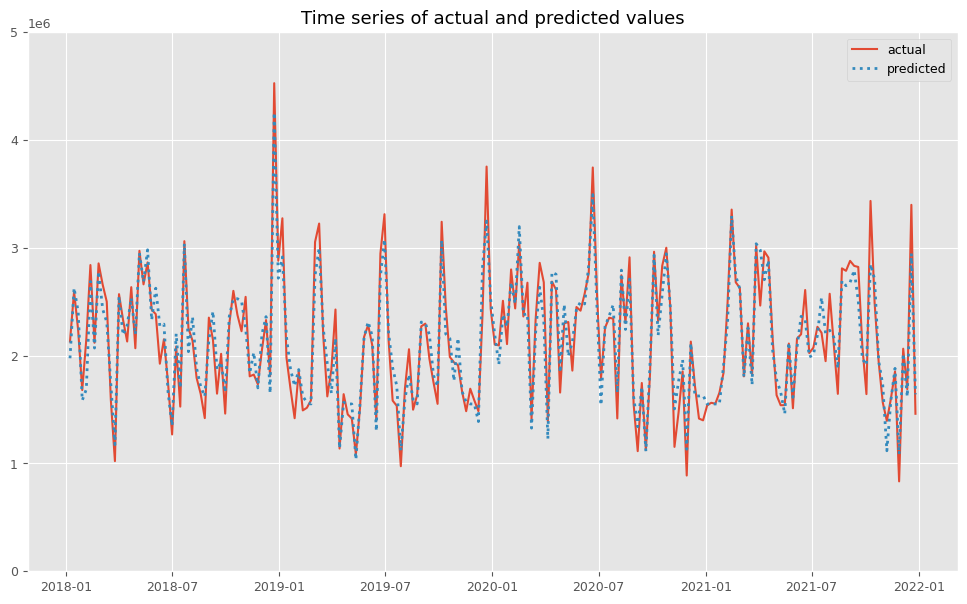
後処理(結果の出力)
MMMを構築したら、貢献度やマーケティングROIなどを計算していきます。
先ずは、貢献度を計算します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 5e6))
以下、実行結果です。
Base TVCM Newspaper Web \
Week
2018-01-07 1.113852e+06 1.018148e+06 0.000000 0.000000
2018-01-14 1.019528e+06 6.174509e+05 445651.435006 513469.488221
2018-01-21 9.591025e+05 3.326732e+05 461699.908459 482724.426115
2018-01-28 1.094730e+06 1.992811e+05 382571.244157 4318.189671
2018-02-04 1.317746e+06 1.193643e+05 54646.008674 663643.321643
... ... ... ... ...
2021-11-28 7.932539e+05 0.000000e+00 37909.894858 2736.189402
2021-12-05 1.055244e+06 0.000000e+00 479595.350151 529860.491253
2021-12-12 1.076807e+06 0.000000e+00 70632.809992 542060.671279
2021-12-19 1.190498e+06 0.000000e+00 785966.436278 4671.191386
2021-12-26 9.188668e+05 0.000000e+00 79814.672767 462418.559057
xmas
Week
2018-01-07 0.000000e+00
2018-01-14 0.000000e+00
2018-01-21 0.000000e+00
2018-01-28 0.000000e+00
2018-02-04 0.000000e+00
... ...
2021-11-28 0.000000e+00
2021-12-05 0.000000e+00
2021-12-12 0.000000e+00
2021-12-19 1.418065e+06
2021-12-26 0.000000e+00
[208 rows x 5 columns]
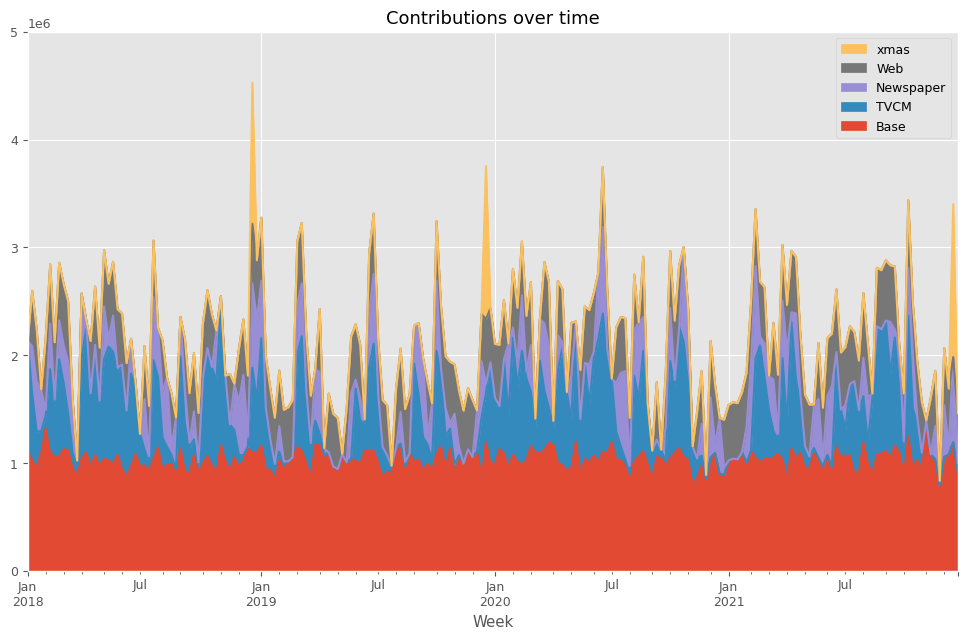
次に、貢献度の割合を計算します。
以下、コードです。
貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.138458e+08 0.481421 TVCM 9.425843e+07 0.212200 Newspaper 5.056515e+07 0.113835 Web 8.137948e+07 0.183206 xmas 4.147825e+06 0.009338
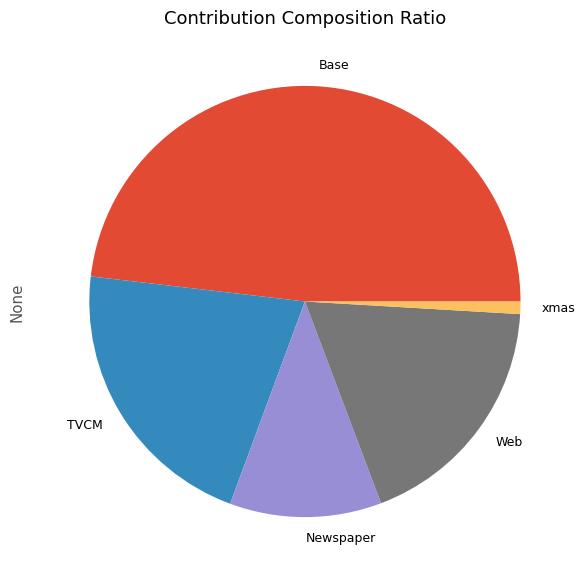
最後に、各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出
ROI = calculate_marketing_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
以下、実行結果です。
TVCM 0.621023 Newspaper 0.099572 Web 1.597552 dtype: float64
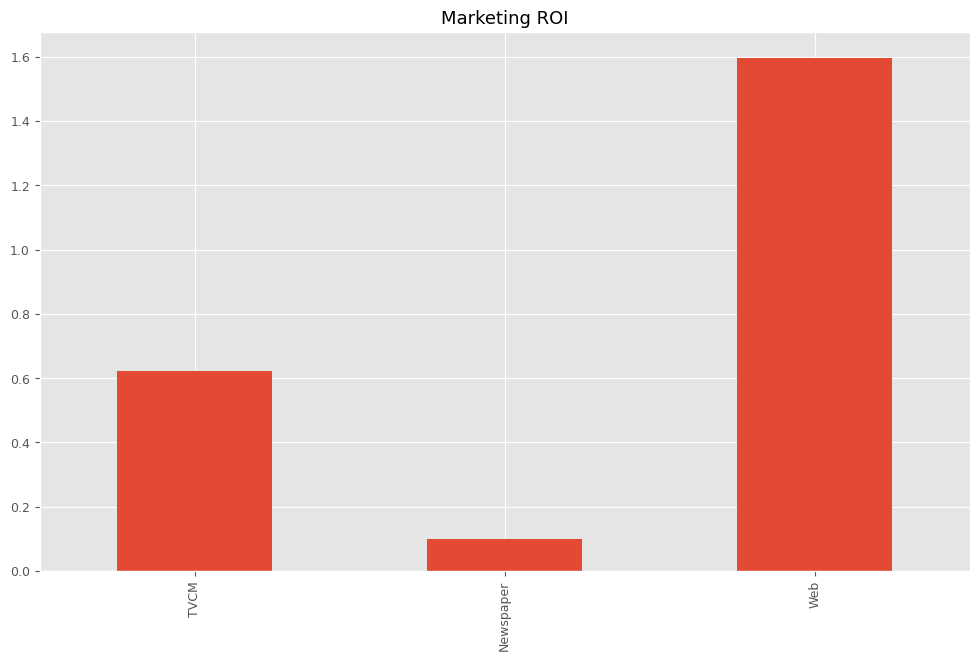
自動MMM構築(ハイパラ&推定器を自動選択&調整)
ハイパーパラメータ自動調整
ハイパーパラメータを自動チューニングするため、Optunaの目的関数を定義します。
以下、コードです。
def objective(trial, X, y):
carryover_params = []
curve_params = []
# アドストックを考慮する特徴量と考慮しない特徴量の処理
apply_effects_indices = [X.columns.get_loc(column) for column in apply_effects_features]
no_effects_indices = [X.columns.get_loc(column) for column in no_effects_features]
# 推定器(もしくはパイプライン)の選択
estimator_name = trial.suggest_categorical("estimator", [name for name, _ in estimators])
estimator = next((est for name, est in estimators if name == estimator_name), None)
if estimator_name == "LR":
pass
if estimator_name == "Ridge":
alpha = trial.suggest_float("alpha_" + estimator_name, 0.01, 10)
estimator.set_params(alpha=alpha)
if estimator_name == "BayesianRidge":
alpha_1 = trial.suggest_float("alpha_1_" + estimator_name, 1e-6, 1e-3)
alpha_2 = trial.suggest_float("alpha_2_" + estimator_name, 1e-6, 1e-3)
lambda_1 = trial.suggest_float("lambda_1_" + estimator_name, 1e-6, 1e-3)
lambda_2 = trial.suggest_float("lambda_2_" + estimator_name, 1e-6, 1e-3)
estimator.set_params(
alpha_1=alpha_1, alpha_2=alpha_2, lambda_1=lambda_1, lambda_2=lambda_2)
if estimator_name == "PLS":
n_comp = trial.suggest_int("n_comp_" + estimator_name, 1, X.shape[1])
estimator.set_params(Reg__n_components=n_comp)
if estimator_name == "PCR":
n_comp = trial.suggest_int("n_comp_" + estimator_name, 1, X.shape[1])
estimator.set_params(PCA__n_components=n_comp)
# アドストック(キャリーオーバー効果関数・飽和関数)の選択
for feature in apply_effects_features:
carryover_length = trial.suggest_int(f'carryover_length_{feature}', 1, 10)
carryover_peak = trial.suggest_int(f'carryover_peak_{feature}', 1, carryover_length)
carryover_rate1 = trial.suggest_float(f'carryover_rate1_{feature}', 0, 1)
carryover_rate2 = trial.suggest_float(f'carryover_rate2_{feature}', 0, 1)
carryover_c1 = trial.suggest_float(f'carryover_c1_{feature}', 0, 2)
carryover_c2 = trial.suggest_float(f'carryover_c2_{feature}', 0, 2)
carryover_params.append({
'length': carryover_length,
'peak': carryover_peak,
'rate1': carryover_rate1,
'rate2': carryover_rate2,
'c1': carryover_c1,
'c2': carryover_c2,
})
saturation_function = trial.suggest_categorical(f'saturation_function_{feature}', ['logistic', 'exponential'])
if saturation_function == 'logistic':
curve_param_L = trial.suggest_float(f'curve_param_L_{feature}', 0, 10)
curve_param_k = trial.suggest_float(f'curve_param_k_{feature}', 0, 10)
curve_param_x0 = trial.suggest_float(f'curve_param_x0_{feature}', 0, 2)
curve_params.append({
'saturation_function': saturation_function,
'L': curve_param_L,
'k': curve_param_k,
'x0': curve_param_x0,
})
elif saturation_function == 'exponential':
curve_param_d = trial.suggest_float(f'curve_param_d_{feature}', 0, 10)
curve_params.append({
'saturation_function': saturation_function,
'd': curve_param_d,
})
pipeline = Pipeline(steps=[
('scaler', MinMaxScaler()),
('preprocessor', ColumnTransformer(
transformers=[
('effects', Pipeline([
('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
('saturation', CustomSaturationTransformer(curve_params=curve_params))
]), apply_effects_indices),
('no_effects', 'passthrough', no_effects_indices)
],
remainder='drop' # 効果適用外の特徴量は処理しない
)),
('estimator', estimator)
])
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(pipeline, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
return rmse
目的関数を最適化し、最適なハイパーパラメータを探索します。
以下、コードです。
# Optunaのスタディの作成と最適化の実行
study = optuna.create_study(direction='minimize')
objective_with_data = partial(objective, X=X, y=y)
study.optimize(objective_with_data, n_trials=10000, show_progress_bar=True)
print("Best trial:")
trial = study.best_trial
print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
print(f"{key}: {value}")
以下、実行結果です。
Best trial: Value: 197541.00633135185 Params: estimator: PLS n_comp_PLS: 2 carryover_length_TVCM: 5 carryover_peak_TVCM: 1 carryover_rate1_TVCM: 0.833309635688961 carryover_rate2_TVCM: 0.43391303587182917 carryover_c1_TVCM: 1.9604667795910393 carryover_c2_TVCM: 0.8640667372215822 saturation_function_TVCM: exponential curve_param_d_TVCM: 1.601468975465903 carryover_length_Newspaper: 7 carryover_peak_Newspaper: 1 carryover_rate1_Newspaper: 0.26136300892474174 carryover_rate2_Newspaper: 0.23825796157884188 carryover_c1_Newspaper: 1.961925920046449 carryover_c2_Newspaper: 1.933819060881763 saturation_function_Newspaper: exponential curve_param_d_Newspaper: 0.0024718846932345073 carryover_length_Web: 1 carryover_peak_Web: 1 carryover_rate1_Web: 0.8425938663471378 carryover_rate2_Web: 0.5089648947777047 carryover_c1_Web: 0.589876251049012 carryover_c2_Web: 1.64809517217672 saturation_function_Web: logistic curve_param_L_Web: 4.751470679050619 curve_param_k_Web: 2.8797379020546328 curve_param_x0_Web: 0.24478733204525605
MMM構築
最適なハイパーパラメータを使いMMMを構築します。
先ず、そのための関数を定義します。
以下、コードです。
def create_model_from_trial(trial, estimators):
carryover_params = []
curve_params = []
n_features = len(apply_effects_features)
carryover_keys = ['length', 'peak', 'rate1', 'rate2', 'c1', 'c2']
curve_keys_logistic = ['L', 'k', 'x0']
curve_keys_exponential = ['d']
indices = apply_effects_features
# ハイパーパラメータを抽出しキーと値の辞書を作成
def fetch_params(prefix, feature_name, params, trial_params):
return {key: trial_params[f'{prefix}_{key}_{feature_name}'] for key in params}
# キャリーオーバー関数ハイパーパラメーターを取得
carryover_params = [fetch_params('carryover', feature_name, carryover_keys, trial.params) for feature_name in indices]
# 飽和関数ハイパーパラメーターを取得
for feature_name in indices:
saturation_function = trial.params[f'saturation_function_{feature_name}']
curve_param = {'saturation_function': saturation_function}
if saturation_function == 'logistic':
curve_param.update(fetch_params('curve_param', feature_name, curve_keys_logistic, trial.params))
elif saturation_function == 'exponential':
curve_param.update(fetch_params('curve_param', feature_name, curve_keys_exponential, trial.params))
curve_params.append(curve_param)
# 推定器ハイパーパラメーターを取得
best_estimator_name = trial.params['estimator']
best_estimator = next((est for name, est in estimators if name == best_estimator_name), None)
if best_estimator_name == "Ridge":
alpha = trial.params.get('alpha_Ridge', 1.0)
best_estimator.set_params(alpha=alpha)
elif best_estimator_name == "BayesianRidge":
best_estimator.set_params(
alpha_1=trial.params['alpha_1_BayesianRidge'],
alpha_2=trial.params['alpha_2_BayesianRidge'],
lambda_1=trial.params['lambda_1_BayesianRidge'],
lambda_2=trial.params['lambda_2_BayesianRidge']
)
elif best_estimator_name == "PLS":
n_comp = trial.params['n_comp_PLS']
best_estimator.set_params(Reg__n_components=n_comp)
elif best_estimator_name == "PCR":
n_comp = trial.params['n_comp_PCR']
best_estimator.set_params(PCA__n_components=n_comp)
# パイプラインを作成
MMM_pipeline = Pipeline(steps=[
('scaler', MinMaxScaler()),
('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
('saturation', CustomSaturationTransformer(curve_params=curve_params)),
('estimator', best_estimator)
])
return MMM_pipeline,carryover_params,curve_params
では、この関数を実行します。
以下、コードです。
MMM_pipeline,best_carryover_params,best_curve_params = create_model_from_trial(study.best_trial, estimators)
この関数から以下が出力されます。
- 最適なハイパーパラメータで設定したMMMパイプライン
MMM_pipeline - キャリオーバー効果に関連するハイパーパラメータのリスト
carryover_params - 飽和関数に関連するハイパーパラメータのリスト
curve_params
アドストック(キャリーオーバー効果関数と飽和関数)になったのかをグラフで確認してみます。
以下、コードです。
# グラフで確認 plot_effects(best_carryover_params, best_curve_params, apply_effects_features)
以下、実行結果です。
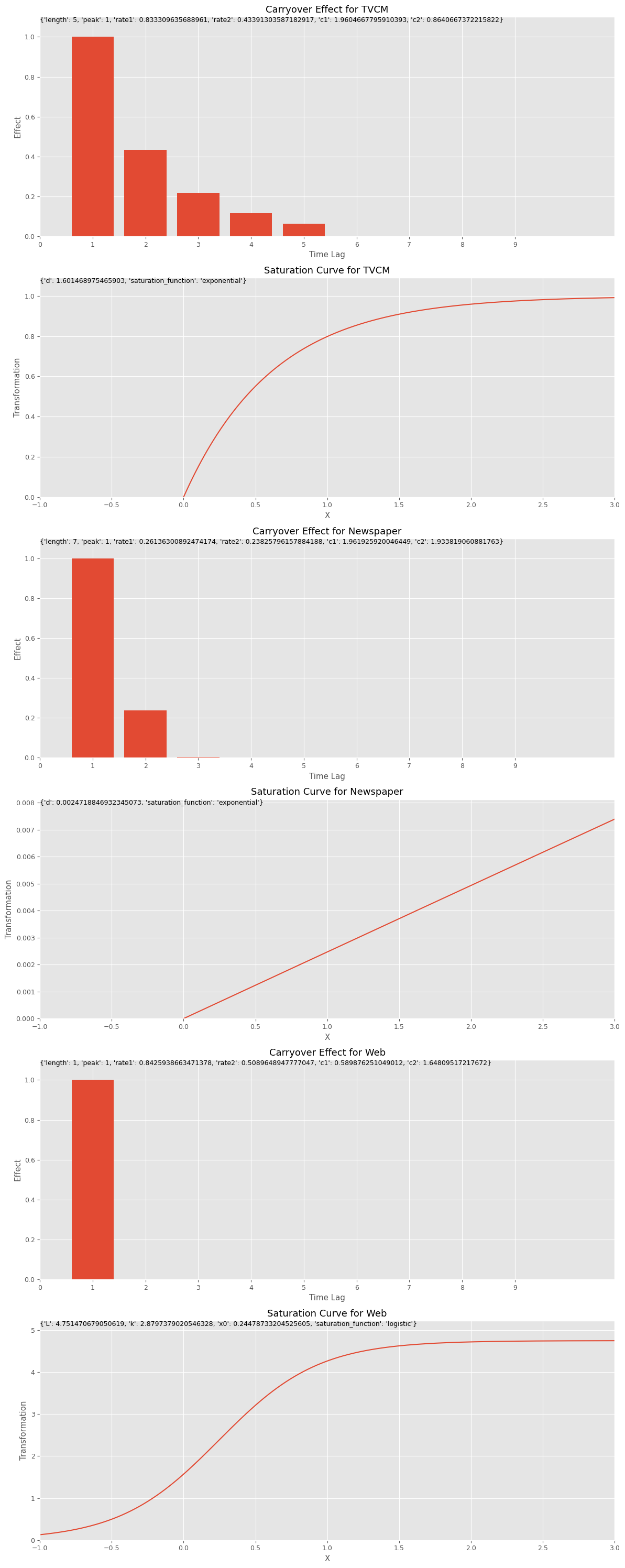
MMMパイプラインを学習し、その結果を散布図(横軸:実測値、縦軸:予測値)をプロットします。
以下、コードです。
# パイプラインを使って学習
trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)
# 予測結果の表示
plt.figure(figsize=(10, 6))
plt.scatter(y, pred)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=3)
plt.xlabel('actual')
plt.ylabel('predicted')
plt.title('Actual vs Predicted Values')
plt.show()
以下、実行結果です。
RMSE: 161446.30199006773 MAE: 132278.27217304983 MAPE: 0.06634709343418346 R2: 0.927186402092658
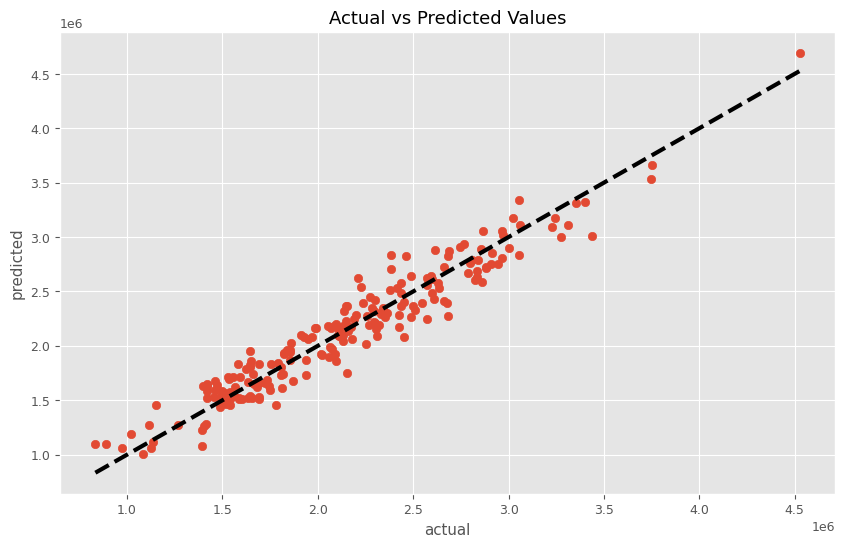
予測値と実測値の時系列推移を見てみます。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 5e6))
以下、実行結果です。
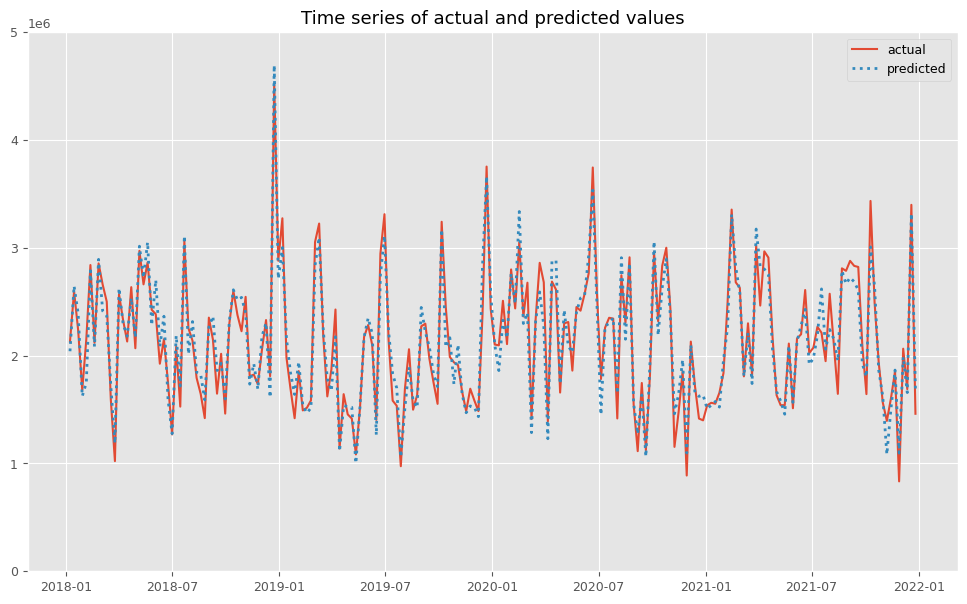
後処理(結果の出力)
MMMを構築したら、貢献度やマーケティングROIなどを計算していきます。
先ずは、貢献度を計算します。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 5e6))
以下、実行結果です。
Base TVCM Newspaper Web \
Week
2018-01-07 1.046789e+06 1.085211e+06 0.000000 0.000000
2018-01-14 9.830728e+05 5.444645e+05 505313.328633 563249.383200
2018-01-21 9.373145e+05 2.845754e+05 528721.948146 485588.117826
2018-01-28 1.037290e+06 1.734246e+05 470185.283451 0.000000
2018-02-04 1.234672e+06 1.147025e+05 104080.455985 701944.556225
... ... ... ... ...
2021-11-28 7.621629e+05 0.000000e+00 71737.123533 0.000000
2021-12-05 1.041300e+06 0.000000e+00 551633.284296 471766.262750
2021-12-12 1.021463e+06 0.000000e+00 128594.820115 539442.135624
2021-12-19 1.026504e+06 0.000000e+00 699297.942424 0.000000
2021-12-26 8.724178e+05 0.000000e+00 141241.531600 447440.681093
xmas
Week
2018-01-07 0.000000e+00
2018-01-14 0.000000e+00
2018-01-21 0.000000e+00
2018-01-28 0.000000e+00
2018-02-04 0.000000e+00
... ...
2021-11-28 0.000000e+00
2021-12-05 0.000000e+00
2021-12-12 0.000000e+00
2021-12-19 1.673398e+06
2021-12-26 0.000000e+00
[208 rows x 5 columns]
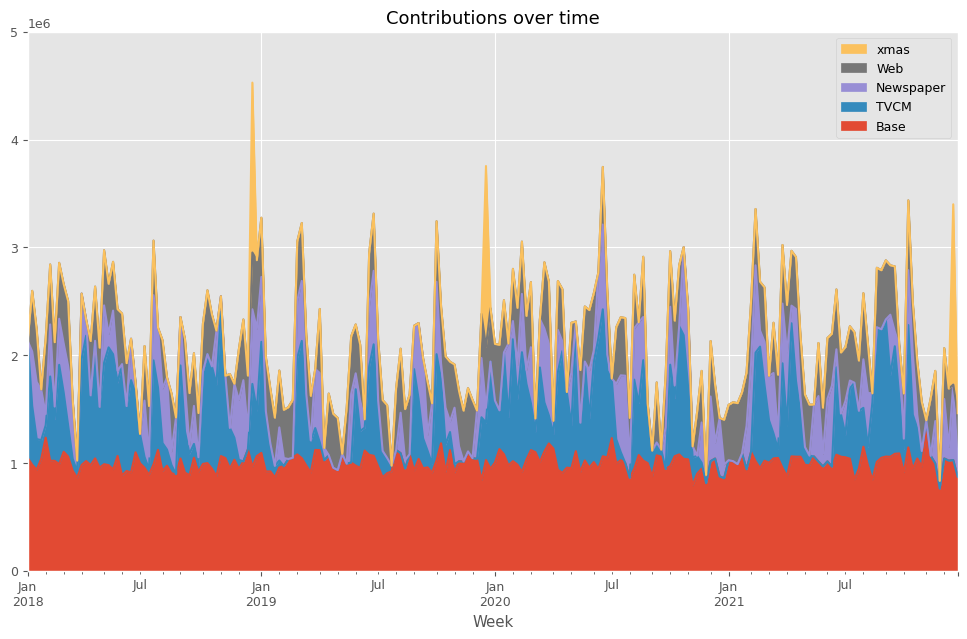
次に、貢献度の割合を計算します。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
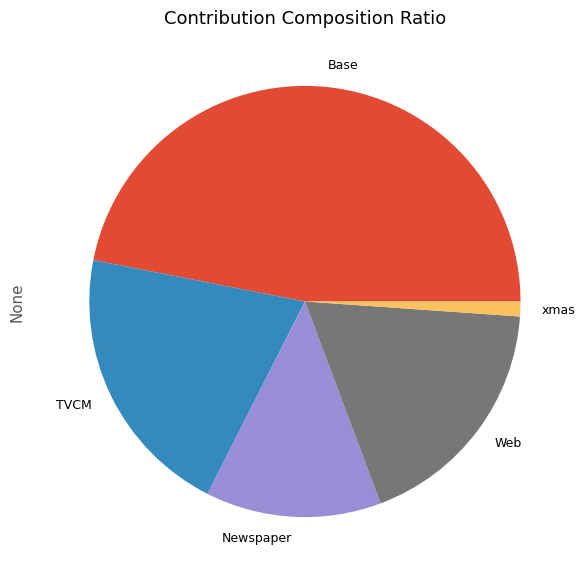
contribution ratio Base 2.084320e+08 0.469234 TVCM 9.156894e+07 0.206145 Newspaper 5.850798e+07 0.131716 Web 8.076419e+07 0.181821 xmas 4.923618e+06 0.011084
最後に、各メディアのマーケティングROIを計算します。
以下、コードです。
# マーケティングROIの算出
ROI = calculate_marketing_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
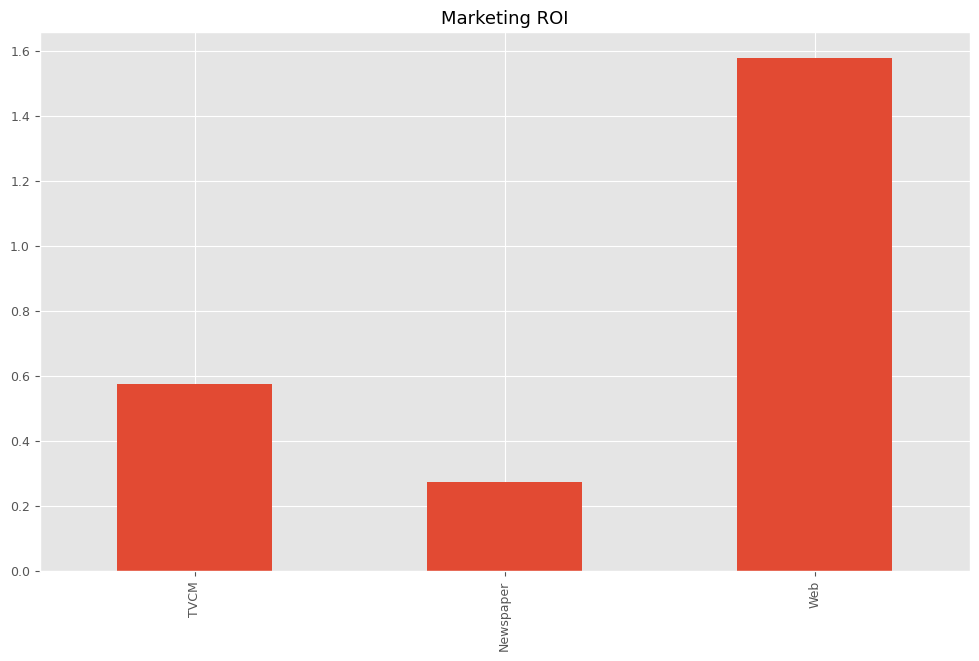
以下、実行結果です。
TVCM 0.574770 Newspaper 0.272294 Web 1.577912 dtype: float64
まとめ
今回は、「アドストックを考慮すべき特徴量を指定し構築する線形回帰系MMM」というお話しをしました。
各特徴量(説明変数)の特性に応じて、MMMを構築するときに「アドストックを考慮すべき or アドストックを考慮すべきでない」を選び構築するということです。
今回までのお話しから、MMMモデルから売上貢献度やマーケティングROIなどが算定されることが分かったかと思います。
これらの結果をもとに、売上を最大化する広告・販促の投資配分をどうすべきかという議論をすることができます。
議論をしながら投資配分を決めるというのもいいですが、その議論の前にデータサイエンス技術の助けを借りるのもいいです。
例えば、ある非線形計画問題を解くことで、データから最適投資配分を算出する方法があります。
そこで次回は、非線形計画問題を解くことで最適な投資配分を算出する方法について簡単に説明します。
数理計画法の深い話しは避けます。
PythonによるMMM(マーケティングミックスモデリング)とビジネス活用- 振返り分析・最適投資配分編(その1)-線形回帰系MMMの最適投資配分

