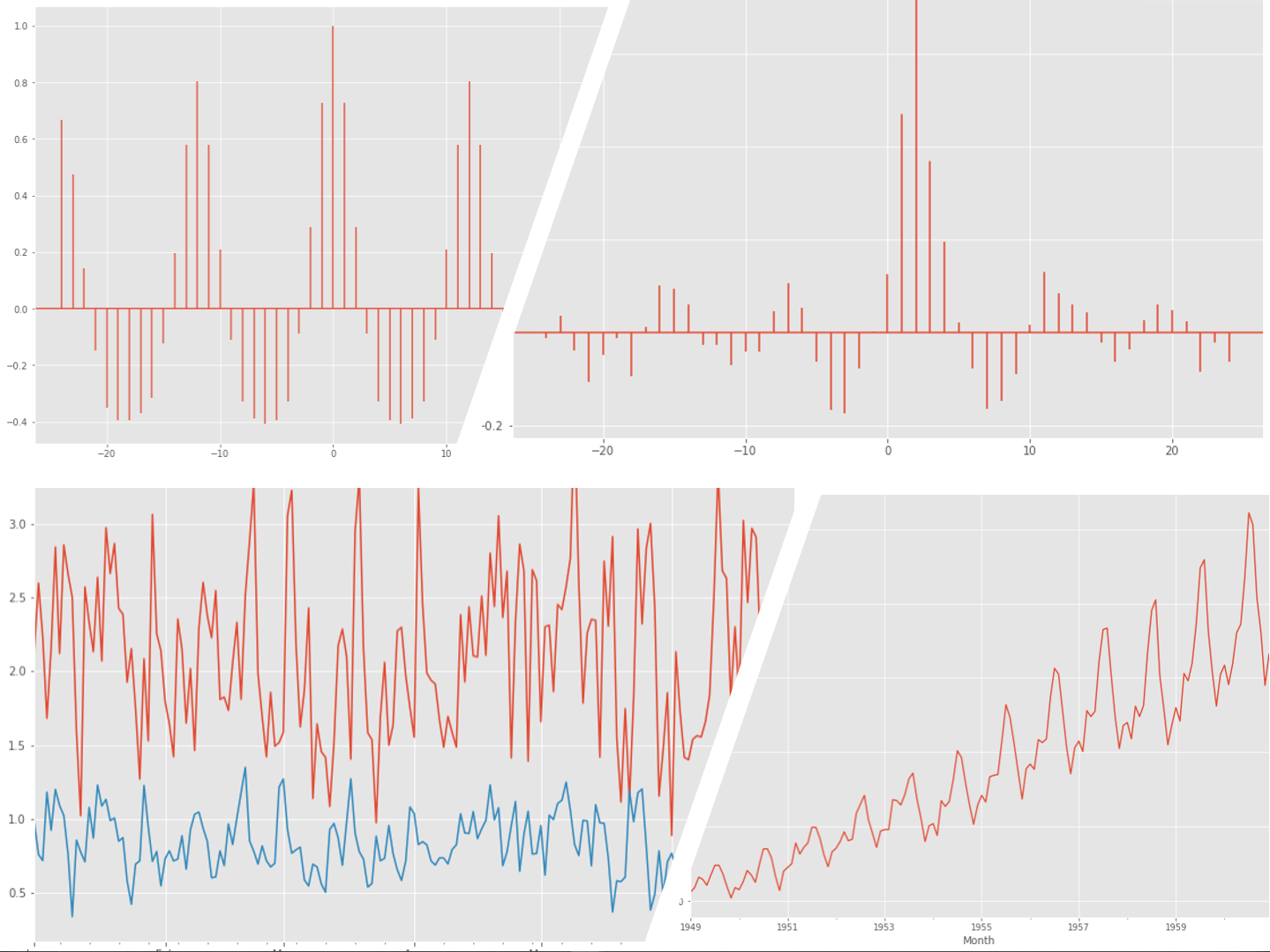
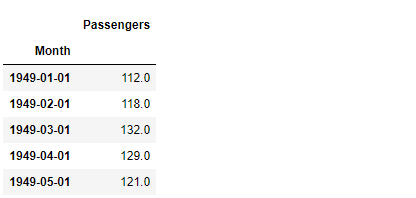時系列データを分析するとき、時系列データの性質を知るために自己相関と相互相関を求めたりします。
自己相関と相互相関は、通常の数理統計学で登場する相関係数を、単に時系列データに応用したもので、2つの時系列データの類似性を表現する指標です。
過去の自分との類似性を見るのが「自己相関」、他の時系列データとの類似性を見るのが「相互相関」です。
ポイントは、時間をずらして相関係数を求めるところです。
1期ずれ、2期ずれ、3期ずれ、……のように一方の時系列データをずらして相関係数を求めます。
このずれをラグという表現で表したりします。例えば、1期ずれのことをラグ1、2期ずれのことをラグ2、3期ずれのことをラグ3、……などなど。
このような相関係数を求めることで、時系列データの季節性や因果関係などを検討する材料にします。
ということで今回は、「時系列データの自己相関と相互相関をPythonで求めてみよう」というお話しをします。
Contents
自己相関と季節性
今、次のような7日周期の時系列データがあったとします。
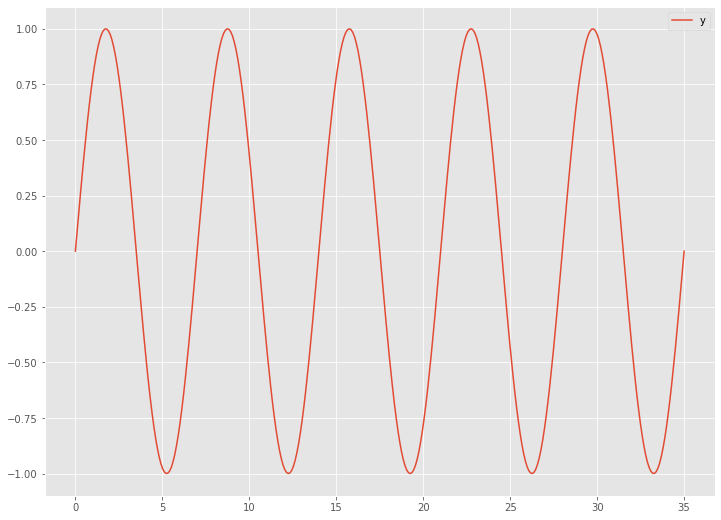
この時系列データを7日間ずらした時系列データ(ラグ7の時系列データ)は、以下のようになります。
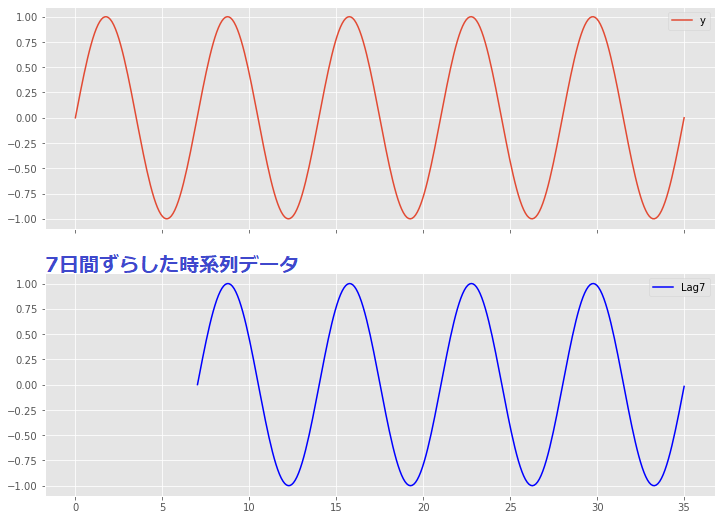
7日周期の時系列データは、7日間ずらした時系列データ(ラグ7の時系列データ)との類似性は非常に高くなります。
過去の自分との類似性を見る「自己相関」を利用することで、どのような周期がありそうか見えてきます。
相互相関と因果推論
因果は推論できても特定できない
データから因果を特定することは、恐らく無理でしょう。因果は特定できませんが、データから因果を推論することができます。
あくまでも推論ですから、その結果をどう解釈するのかは、人に委ねられています。
時系列データを活用した因果推論は、時系列データ同士の類似性を見ることで考えていきます。
一致系列
例えば、次のような売上と広告に関する時系列データがあったとします。
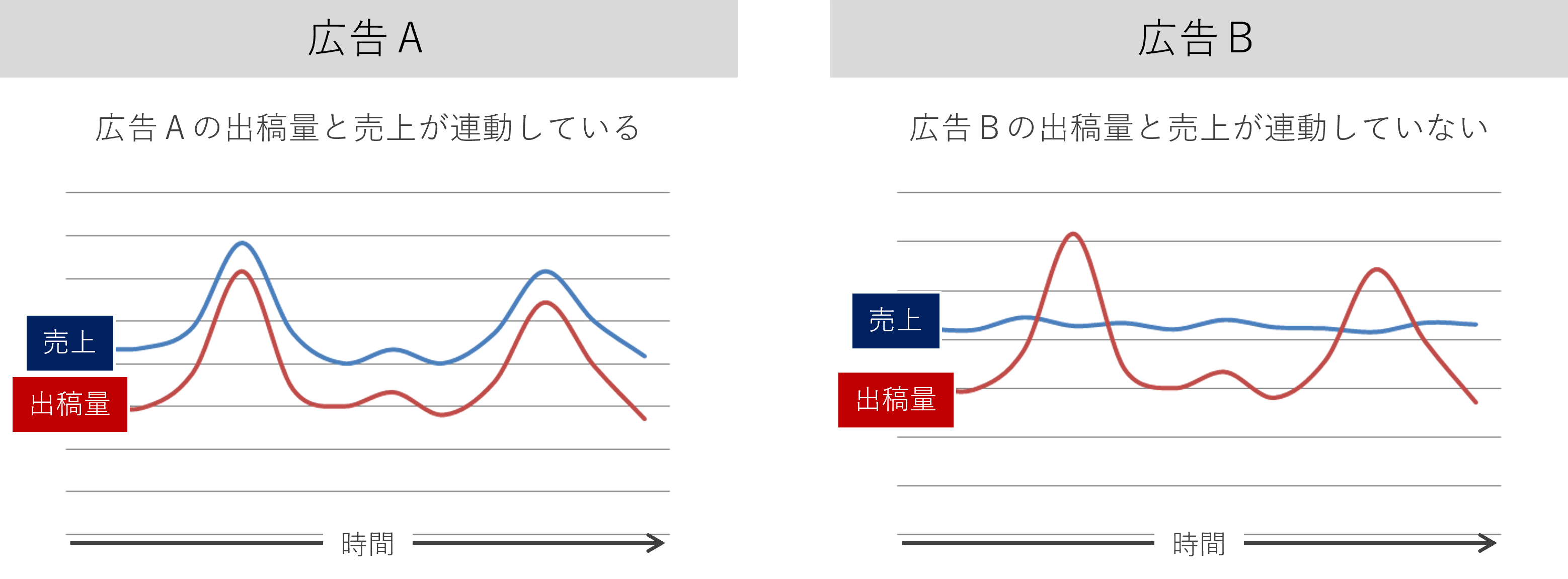
広告Aの出稿量は、売上と連動しているように見えます。一方、広告Bの出稿量は、売上と連動しているように見えません。
共に変動する時系列データを一致系列といいます。この例では、広告Aの出稿量は売上の一致系列です。
表現を変えます。
広告Aの出稿量と売上の時系列データの推移は類似しているように見えます。一方、広告Bの出稿量と売上の時系列データの推移は類似しているように見えません。
広告と売上の間に因果関係があるのであれば、少なくとも連動して動くかと思います。そういう意味で、広告Bは売上を左右する要因とは考えらない、となります。
広告Aはどうでしょうか。広告Aの出稿量と売上は連動しているように見えますが、広告Aが売上を左右する要因であると断定できるわけではありません。可能性がある、ということに過ぎません。
先行系列
因果は、時間の概念で考えると「因」が先にあり「果」が後にあります。時系列データで考えると、「因」である時系列データが先に変動し、「果」である時系列データが後に変動します。
例えば、次のような売上と広告に関する時系列データがあったとします。
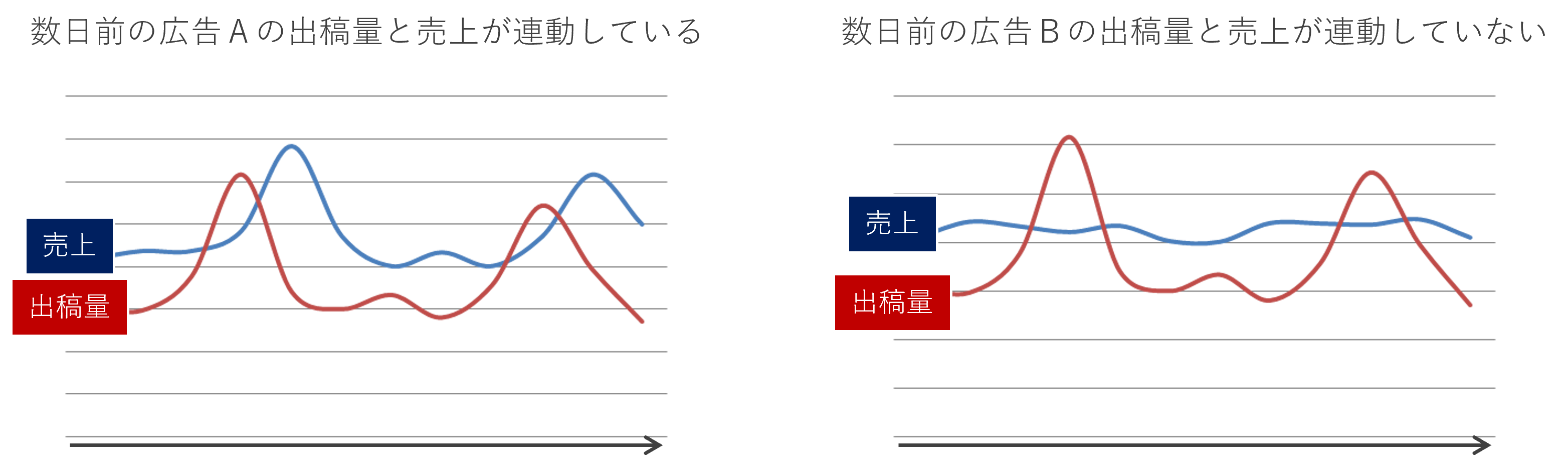
広告Aの出稿量の変動が先にきて、その後に売上が連動しているように見えます。
先に変動する時系列データを先行系列といいます。この例では、広告Aの出稿量は売上の先行系列です。
表現を変えます。
広告Aの出稿量のラグと売上の時系列データの推移は類似しているように見えます。
他の時系列データとの類似性を見る「相互相関」を利用することで、一致系列や先行系列となる時系列データを検討することができます。
Python Matplotlibで自己相関と相互相関を求めてみよう
では、自己相関と相互相関をPythonで求めてみましょう。
グラフ描写のパッケージであるMatplotlibでどうにかなります。Matplotlibをインストールされていない方は、インストールしておいてください。
Matplotlibを使い、自己相関と相互相関を棒グラフで表現したコレログラムを作ることができます。以下の2つの関数です。
- 自己相関:acorr()
- 相互相関:xcorr()
先ずは、必要なライブラリーを読み込みます。
以下、コードです。
import pandas as pd
import numpy as np
from scipy import signal
from scipy import stats
from matplotlib import mlab
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定
自己相関:acorr()
今回利用する時系列データのデータセットは、Airline Passengers(飛行機乗客数)は、Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。
弊社のHPからもダウンロードできます。
弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/591h
では、データセットを読み込みます。
以下、コードです。
# データセットの読み込み
url='https://www.salesanalytics.co.jp/591h' #データセットのあるURL
df=pd.read_csv(url, #読み込むデータのURL
dtype = {'Passengers':'float'},
index_col='Month', #変数「Month」をインデックスに設定
parse_dates=True) #インデックスを日付型に設定
df.head() #確認
以下、実行結果です。
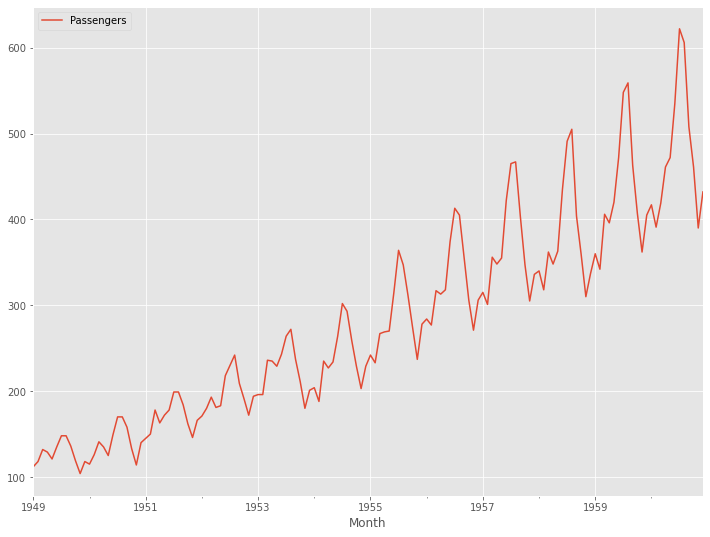
グラフ化してます。
以下、コードです。
# グラフ化 df.plot()
以下、実行結果です。
時系列データを標準化(平均0、分散1)します。
以下、コードです。
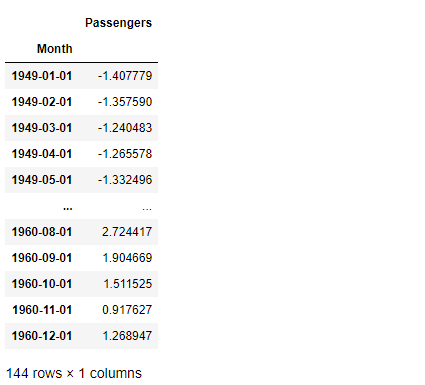
# 標準化(平均0、分散1) df_std = stats.zscore(df) df_std #確認
以下、実行結果です。
自己相関のコレログラムを作成します。
以下、コードです。
# 自己相関コレログラム(原系列)
acor_value = plt.acorr(df_std['Passengers'],
detrend=mlab.detrend_none,
maxlags=24)
plt.show()
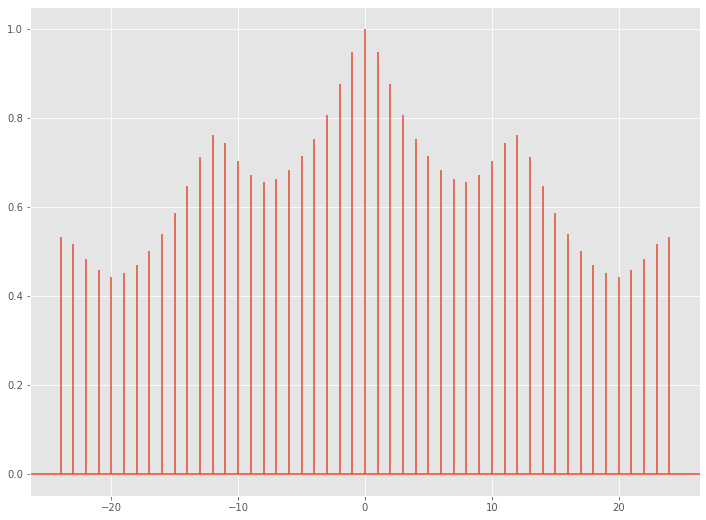
以下、実行結果です。
横軸がラグで、縦軸が相関係数です。ラグ0の相関係数は1です。自分自身との相関なので、当たり前といえば当たり前です。
自己相関係数は「acor_value」に格納されています。
必要な情報を抽出しデータフレームに変換し直し見てみます。
以下、コードです。
# 自己相関の値 acor_pd = pd.DataFrame(acor_value[1],acor_value[0]) acor_pd.index.name = 'lag' acor_pd.columns = ['acor'] acor_pd #確認
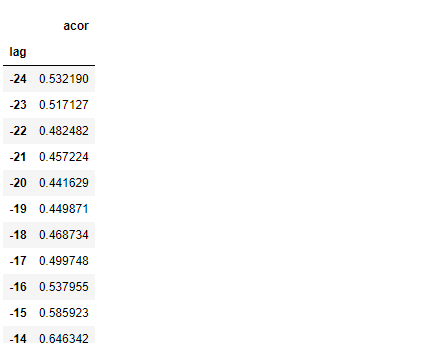
以下、実行結果です。
この時系列データには、上昇傾向のトレンドがあります。トレンドがある時系列データの場合、トレンドを除去した時系列データで自己相関を計算する必要があります。
トレンドを除去した時系列データの自己相関を求める方法が、幾つか紹介します。「detrend」に以下のいずれかを設定するだけです。
- mlab.detrend_linear
- signal.detrend
- np.diff
mlab.detrend_linearは、Matplotlibに最初から備わっているもので、線形トレンドを除去する場合に設定します。
signal.detrendは、SciPyのトレンド除去関数です。それを、設定します。
np.diffは、NumPyの階差を求める関数です。当期と前期の差分を階差といいます。階差はトレンドが除去された時系列データになります。
それぞれ簡単に、トレンド除去後の自己相関を見てみます。
以下、mlab.detrend_linearによるトレンド除去後の自己相関を求めるコードです。
# 自己相関コレログラム(線形トレンド除去)
acor_value = plt.acorr(df_std['Passengers'],
detrend=mlab.detrend_linear,
maxlags=24)
plt.show()
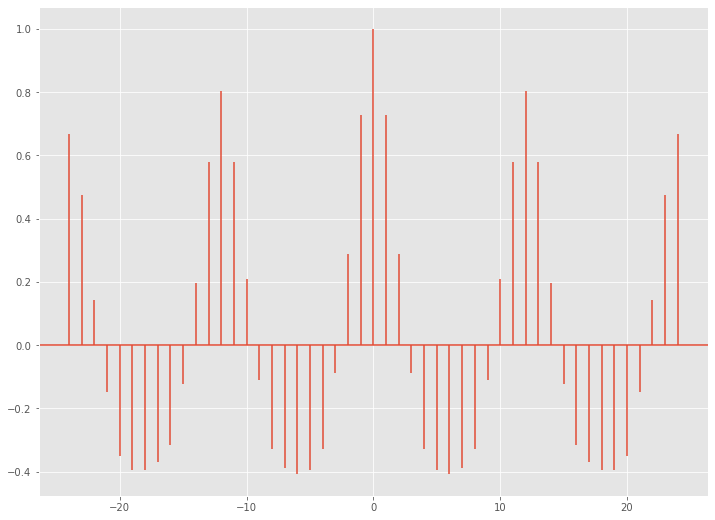
以下、実行結果です。
ラグ12やラグ24、もしくは、ラグ-12やラグ-24の相関係数が高くなっています。12ヶ月周期があることがわかります。
以下、signal.detrendによるトレンド除去後の自己相関を求めるコードです。
# 自己相関コレログラム(線形トレンド除去)
acor_value = plt.acorr(df_std['Passengers'],
detrend=signal.detrend,
maxlags=24)
plt.show()
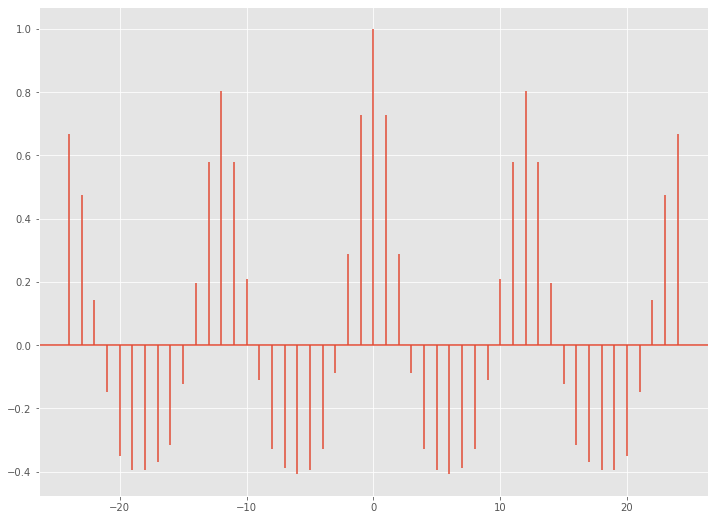
以下、実行結果です。
以下、np.diffによるトレンド除去後の自己相関を求めるコードです。
# 自己相関コレログラム(階差系列)
acor_value = plt.acorr(df_std['Passengers'],
detrend=np.diff,
maxlags=24)
plt.show()
以下、実行結果です。
相互相関:xcorr()
今回利用する時系列データのデータセットは、売上(Sales)と広告(AD)の時系列データです。
弊社のHPからもダウンロードできます。
弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/glrg
では、データセットを読み込みます。
以下、コードです。
# データセット読み込み
url = 'https://www.salesanalytics.co.jp/glrg'
df = pd.read_csv(url,
parse_dates=True,
index_col='day'
)
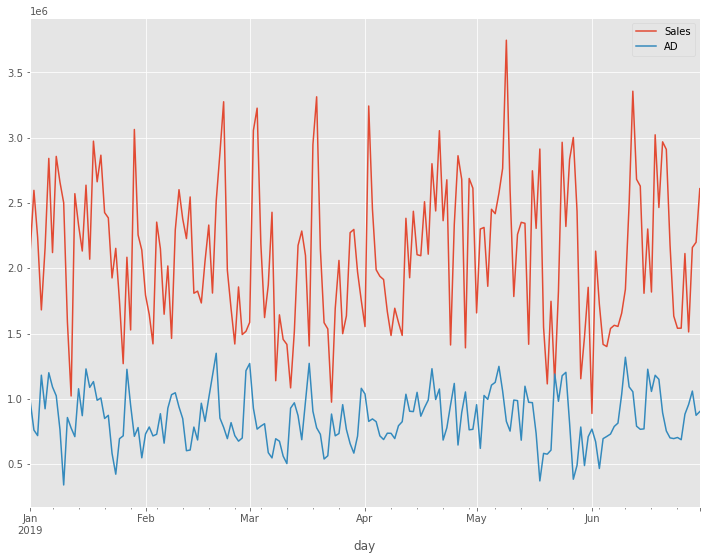
# グラフ化
df.plot()
以下、実行結果です。
先ず、相互相関を求める関数を使わずに、ラグ変数などを作り相互相関を計算してみます。
ADのラグ変数を幾つか作り、Sales変数と一緒にしたデータセットを作ります。このデータセットの変数間の相関係数を計算します。これで相互相関を求めることができます。
以下は、データセットを作るコードです。
# ADラグ+Salesのデータセットの生成
df_AD = pd.concat([df['AD'],
df['AD'].shift(1),
df['AD'].shift(2),
df['AD'].shift(3),
df['AD'].shift(4),
df['AD'].shift(5),
],
axis=1)
df_AD.columns = ['AD_lag0',
'AD_lag1',
'AD_lag2',
'AD_lag3',
'AD_lag4',
'AD_lag5'
]
df_AD['Sales']=df['Sales']
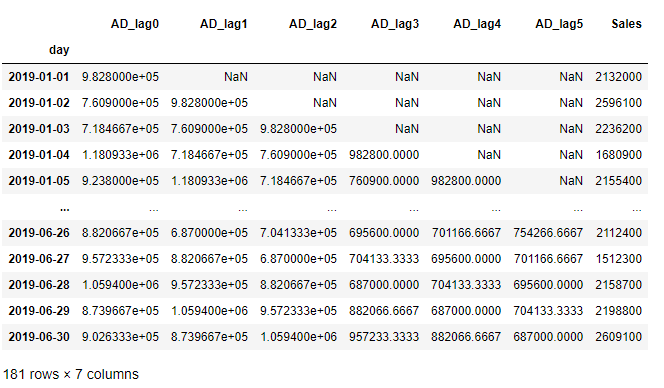
df_AD #確認
以下、実行結果です。
以下、データセットのSales変数と他の変数(ADのラグ変数)との相関係数を計算するコードです。
# Salesとの相関係数 df_AD.corr()['Sales']
以下、実行結果です。
SalesとADのラグ2の相関係数が、約0.9と最大です。
次に、相互相関を求める関数を使い、サクッと相互相関のコレログラムを作ってみます。
時系列データを標準化(平均0、分散1)します。
以下、コードです。
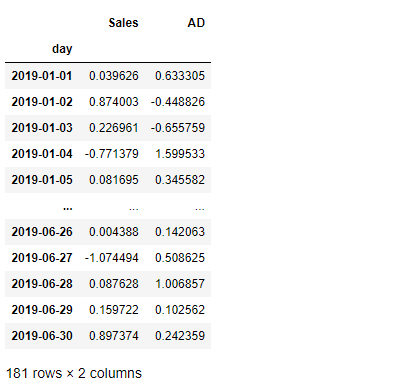
# 標準化(平均0、分散1) df_std = stats.zscore(df) df_std #確認
以下、実行結果です。
相互相関のコレログラムを作成します。
以下、コードです。
# 相互相関コレログラム(原系列)
xcor_value = plt.xcorr(df_std['Sales'],
df_std['AD'],
detrend=mlab.detrend_none,
maxlags=24)
plt.show()
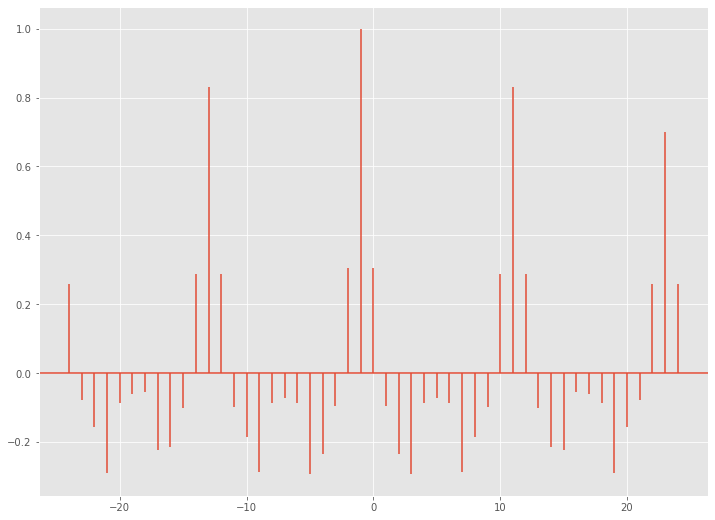
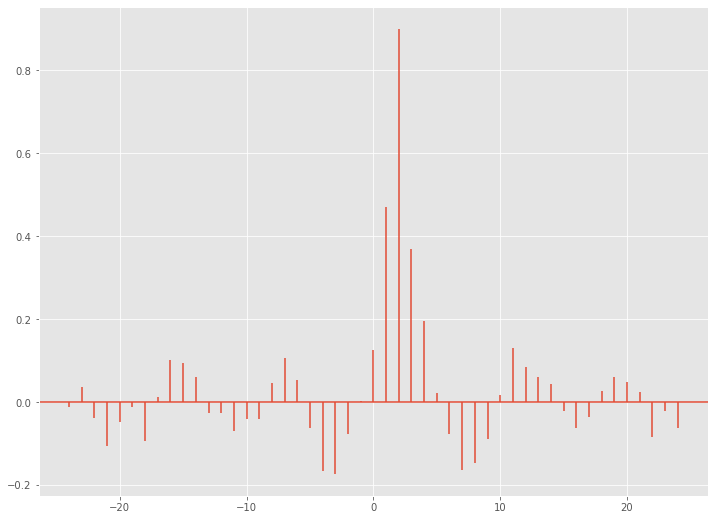
以下、実行結果です。
横軸がラグで、縦軸がSalesとの相関係数です。
ラグ2が約0.9と最大になっています。
AD(広告)効果が最大になるのが2日後、かもしれません。少なくともデータ上はそう見える、ということです。
相互相関係数は「xcor_value」に格納されています。
必要な情報を抽出しデータフレームに変換し直し見てみます。
以下、コードです。
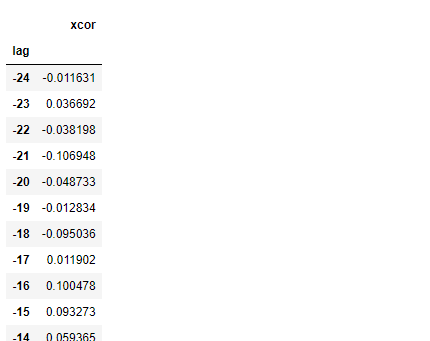
# 相互相関の値 xcor_pd = pd.DataFrame(xcor_value[1],xcor_value[0]) xcor_pd.index.name = 'lag' xcor_pd.columns = ['xcor'] xcor_pd #確認
以下、実行結果です。
念のため、トレンド除去して相互相関を見てみます。
以下、コードです。
# 相互相関コレログラム(線形トレンド除去)
xcor_value = plt.xcorr(df_std['Sales'],
df_std['AD'],
detrend=mlab.detrend_linear,
maxlags=24)
plt.show()
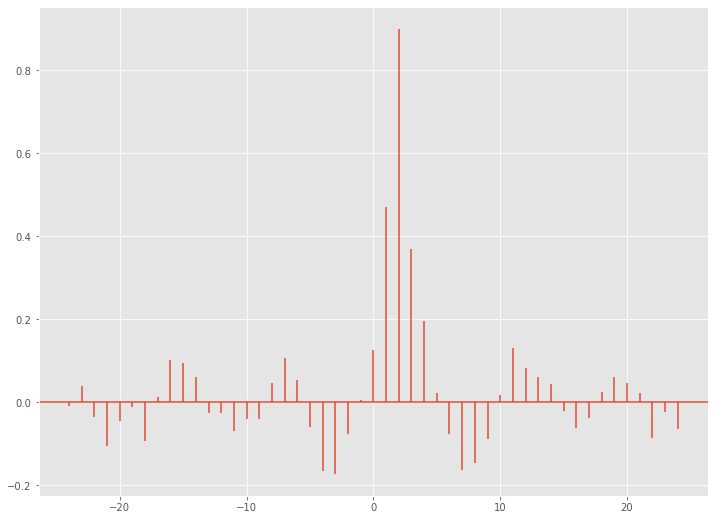
以下、実行結果です。
トレンド除去する前の原系列の相互相関のコレログラムと、大差ないことがわかります。
まとめ
今回は、「時系列データの自己相関と相互相関をPythonで求めてみよう」というお話しをしました。
相関係数を求めることは、時系列データを使った因果推論や要因探索の第1歩です。
もちろん、本当の因果を特定するものではありませんし、データからは永遠に因果かどうかの判別は不可能でしょう。ただただ推論するだけです。