ここまでの3回で、PCAの仕組みを一から学んできました。
— 第1回 —
なぜ「次元を減らす」のか? 情報の海で溺れないために
https://www.salesanalytics.co.jp/datascience/datascience286/
— 第2回 —
PCAのしくみを分散・共分散・固有値分解で理解する
https://www.salesanalytics.co.jp/datascience/datascience288/
— 第3回 —
次元はいくつ残す? 寄与率とスクリープロットの読み方
https://www.salesanalytics.co.jp/datascience/datascience289/
NumPyで手計算した経験があるからこそ、ライブラリが「裏で何をしているか」がわかります。
今回は、scikit-learnライブラリを使って、PCAを効率的に実行する方法を学びましょう。
Contents
準備
ライブラリの準備
必要なライブラリなどを読み込みます。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import japanize_matplotlib # scikit-learn from sklearn.datasets import load_iris from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA
データの準備
今回もIrisデータセットを使います。
# Irisデータセットを読み込み
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
# 標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print(f"データの形状: {X_scaled.shape}")
print(f"特徴量: {feature_names}")
以下、実行結果です。
データの形状: (150, 4) 特徴量: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Irisデータを標準化しています。
scikit-learnでPCAを実行する
scikit-learnは、機械学習でよく使われるライブラリです。シンプルなAPIで、数行でPCAを実行できます。
基本的な使い方
scikit-learnのPCAは、fitでモデルを学習し、transformでデータを変換します。fit_transformを使えば、一度に両方を行えます。
# PCAのインスタンスを作成 # n_componentsで主成分の次元数を指定 pca_sklearn = PCA(n_components=2) # fit_transformで主成分分析を実行 # 主成分得点をZ_sklearnに格納 Z_sklearn = pca_sklearn.fit_transform(X_scaled) # 主成分得点を表示(先頭5行のみ表示) print(Z_sklearn[:5])
以下、実行結果です。
[[-2.26470281 0.4800266 ] [-2.08096115 -0.67413356] [-2.36422905 -0.34190802] [-2.29938422 -0.59739451] [-2.38984217 0.64683538]]
4次元のデータが2次元に変換されます。
たった2行で、前回までにNumPyで行った固有値分解などが完了しました。
寄与率を確認する
PCAオブジェクトpca_sklearnには、寄与率の情報は属性explained_variance_ratio_に、固有値の情報は属性explained_variance_に保存されています。
# 各主成分の寄与率と固有値を出力
print("=== 寄与率と固有値 ===")
for i, (ratio, eigenvalue) in enumerate(
zip(
pca_sklearn.explained_variance_ratio_, # 寄与率
pca_sklearn.explained_variance_ # 固有値
)
):
print(
f"PC{i+1}: "
f"寄与率 = {ratio*100:.2f}%, "
f"固有値 = {eigenvalue:.4f}"
)
# 累積寄与率
cumsum = np.cumsum(pca_sklearn.explained_variance_ratio_)
print(f"\n累積寄与率: {cumsum[-1]*100:.2f}%")
以下、実行結果です。
=== 寄与率と固有値 === PC1: 寄与率 = 72.96%, 固有値 = 2.9381 PC2: 寄与率 = 22.85%, 固有値 = 0.9202 累積寄与率: 95.81%
第1主成分と第2主成分の寄与率と累積寄与率が表示されます。
主成分の方向(固有ベクトル)を確認する
components_属性には、各主成分の方向(固有ベクトル)が格納されています。
# 主成分の方向(各行が1つの主成分)
print("=== 主成分の方向(components_) ===")
components_df = pd.DataFrame(
pca_sklearn.components_,
index=['PC1', 'PC2'],
columns=feature_names
)
print(components_df.round(3))
以下、実行結果です。
=== 主成分の方向(components_) === sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) PC1 0.521 -0.269 0.580 0.565 PC2 0.377 0.923 0.024 0.067
各主成分がどの特徴量から構成されているかがわかります。
主成分負荷量は別途計算する必要があります。
# 主成分負荷量を計算
loadings = (
components_df.T *
np.sqrt(pca_sklearn.explained_variance_)
)
# データフレームに変換
loadings_df = pd.DataFrame(
loadings,
columns=['PC1', 'PC2']
)
print(loadings_df.round(3))
以下、実行結果です。
PC1 PC2 sepal length (cm) 0.893 0.362 sepal width (cm) -0.462 0.886 petal length (cm) 0.995 0.023 petal width (cm) 0.968 0.064
主成分を列方向にしています。
散布図で可視化する
主成分得点で散布図を作ります。
plt.figure(figsize=(10, 8))
# 各品種に対応する色を設定
colors = ['#E74C3C', '#2ECC71', '#3498DB']
# 散布図を描画
for i, (name, color) in enumerate(zip(target_names, colors)):
mask = y == i
plt.scatter(
Z_sklearn[mask, 0], Z_sklearn[mask, 1],
c=color, label=name, s=80, alpha=0.7
)
plt.xlabel(f'PC1 ({pca_sklearn.explained_variance_ratio_[0]*100:.1f}%)')
plt.ylabel(f'PC2 ({pca_sklearn.explained_variance_ratio_[1]*100:.1f}%)')
plt.title('scikit-learn PCA: Irisデータセット')
plt.legend(title='品種')
plt.grid(True, alpha=0.3)
plt.axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
plt.axvline(x=0, color='gray', linestyle='-', linewidth=0.5)
plt.show()
以下、実行結果です。
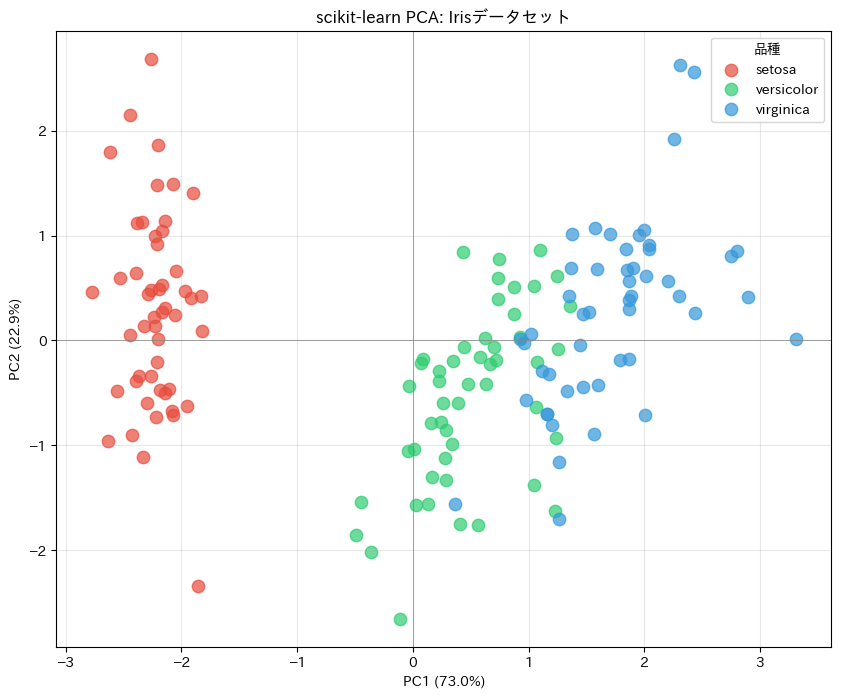
このグラフから、3品種がきれいに分離されていることが確認できます。前回の手計算と同じ結果が、より簡潔なコードで得られました。
スクリープロットを作成
特定の主成分数を指定せずに、すべての主成分を抽出することもできます。
すべての主成分を抽出しスクリープロットを作成します。
# すべての主成分を抽出
pca_full = PCA() # n_componentsを指定しない
pca_full.fit(X_scaled)
# スクリープロットを作成
fig, axes = plt.subplots(2, 1, figsize=(10, 10))
# 上: 固有値
ax = axes[0]
x = np.arange(1, len(pca_full.explained_variance_) + 1)
ax.bar(x, pca_full.explained_variance_)
ax.set_xlabel('主成分')
ax.set_ylabel('固有値(分散)')
ax.set_title('スクリープロット')
ax.set_xticks(x)
# 下: 累積寄与率
ax = axes[1]
cumsum = np.cumsum(pca_full.explained_variance_ratio_) * 100
ax.bar(
x, pca_full.explained_variance_ratio_ * 100,
label='寄与率'
)
ax.plot(
x, cumsum,
'ro-', markersize=10, linewidth=2,
label='累積寄与率'
)
ax.axhline(y=80, color='green', linestyle='--', label='80%ライン')
ax.set_xlabel('主成分')
ax.set_ylabel('寄与率 (%)')
ax.set_title('寄与率と累積寄与率')
ax.set_xticks(x)
ax.legend(loc='center right')
plt.tight_layout()
plt.show()
以下、実行結果です。
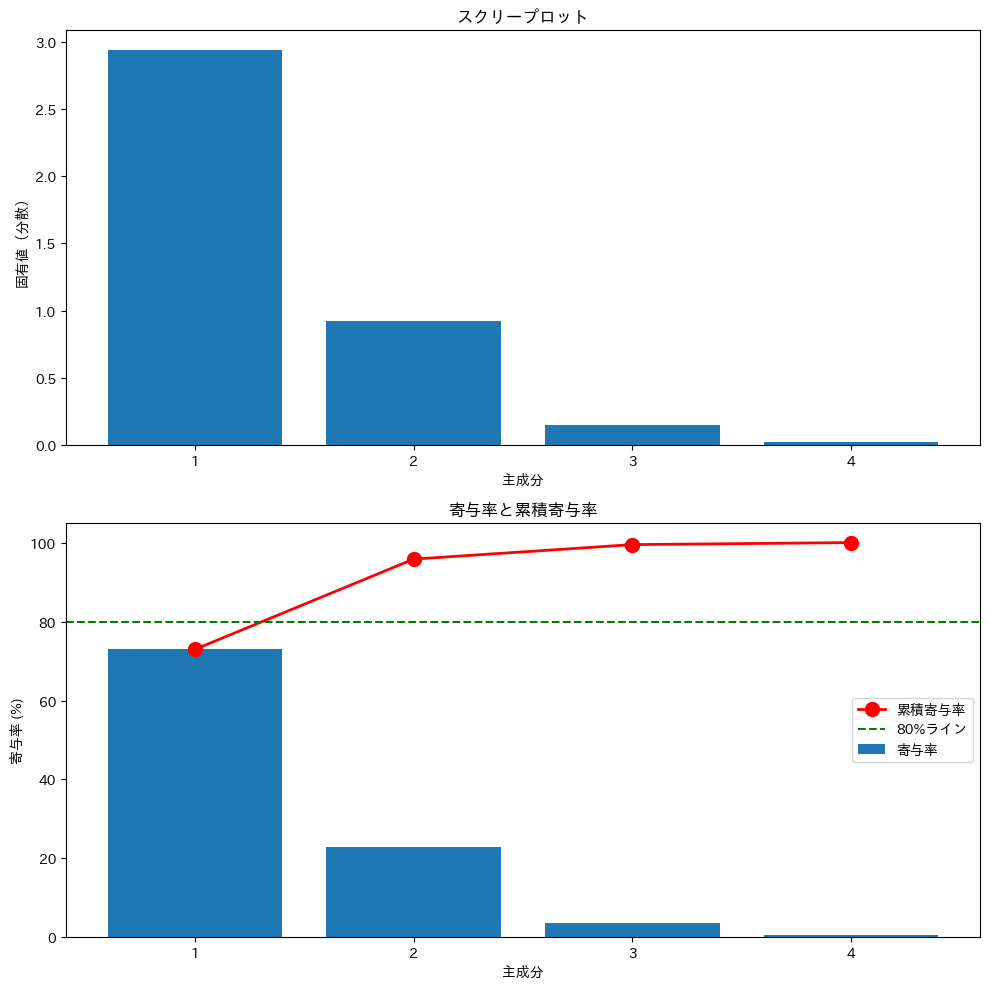
このグラフを使って、適切な主成分数を判断できます。
まとめ
scikit-learnを使ってPCAを実行する方法を学びました。
PCA(n_components=2)でインスタンス作成fit_transform(X)で学習しデータを変換explained_varianceで固有値を取得explained_variance_ratio_で寄与率を取得components_で固有ベクトルを取得
第1〜3回で学んだ「中身」を理解しているからこそ、ライブラリの出力が何を意味するかがわかります。
ブラックボックスとして使うのではなく、必要に応じて手計算と照らし合わせることで、より深い分析ができるようになります。
次回は、PCAと似ているようで異なる「因子分析」を取り上げます。
両者の違いを理解することで、分析目的に応じた手法選択ができるようになります。

