あなたは今日、無意識のうちに何回「似たものをまとめる」という行動をしたでしょうか。
朝起きてクローゼットを開ければ、シャツはシャツ、パンツはパンツでまとまっています。
本棚を見れば、小説、技術書、漫画がそれぞれのエリアに収まっているかもしれません。
スマートフォンのアプリも、「SNS」「ゲーム」「仕事」といったフォルダで整理している人は多いでしょう。
これらはすべてクラスタリング(グループ分け)という行為です。
私たちは「似ているもの」を直感的に見分け、自然とグループにまとめています。
では、コンピュータに同じことをさせるにはどうすればいいでしょうか。
コンピュータには「直感」がありません。「このTシャツとあのTシャツは似ている」と判断させるには、「似ている」を数値で表現する必要があります。
今回は、クラスター分析の土台となる「距離」という概念を、Pythonを使いながら一緒に学んでいきましょう。
Contents
「似ている」とは「距離が近い」こと
「似ている」という感覚を数値化する最もシンプルな方法は、距離を使うことです。
日常生活でも、「東京と横浜は近い」「東京とニューヨークは遠い」と言いますよね。地理的に近い都市は、気候や文化も似ていることが多いです。
この「近さ」の考え方をデータに応用するのです。
- 距離が小さい → 似ている
- 距離が大きい → 似ていない
シンプルですが、これがクラスター分析の根幹をなす考え方です。
まずはPythonの準備をしよう
これから実際にPythonでコードを動かしていきます。まずは必要なライブラリをインポートしましょう。
# 数値計算のためのライブラリ import numpy as np # データ操作のためのライブラリ import pandas as pd # 可視化のためのライブラリ import matplotlib.pyplot as plt import japanize_matplotlib
エラーが出た場合は、pip install numpy pandas matplotlib japanize_matplotlib でインストールしてください。
2つの主な距離
ユークリッド距離:最も直感的な「距離」
最も基本的な距離の測り方がユークリッド距離です。これは中学校で習った「2点間の直線距離」そのものです。
たとえば、ある飲食店の顧客データを考えてみましょう。
顧客Aは「月間購買金額10万円、来店頻度5回」、顧客Bは「月間購買金額8万円、来店頻度3回」だとします。
この2人の「距離」を計算してみましょう。
# 顧客データを定義
customer_A = np.array([10, 5]) # [購買金額(万円), 来店頻度(回)]
customer_B = np.array([8, 3])
# 要素ごとに差を計算
diff = customer_A - customer_B
print(f"差: 購買金額 {diff[0]}万円, 来店頻度 {diff[1]}回")
以下、実行結果です。
差: 購買金額 2万円, 来店頻度 2回
購買金額の差は2万円、来店頻度の差は2回であることがわかります。これらの差を使って距離を計算していきます。
ユークリッド距離は、中学校で習ったピタゴラスの定理(三平方の定理)の応用です。
$$
d = \sqrt{(差_1)^2 + (差_2)^2}
$$
直角三角形の斜辺を求める公式と同じですね。実際に計算してみましょう。
# ユークリッド距離を手計算
euclidean_manual = np.sqrt(diff[0]**2 + diff[1]**2)
print(f"ユークリッド距離: {euclidean_manual:.2f}")
# NumPyの関数を使った計算
euclidean_numpy = np.linalg.norm(diff)
print(f"ユークリッド距離(NumPyのlinalg関数): {euclidean_numpy:.2f}")
以下、実行結果です。
ユークリッド距離: 2.83 ユークリッド距離(NumPyのlinalg関数): 2.83
どちらも同じ結果(2.83)が得られます。
NumPyの np.linalg.norm() を使えば、簡単にユークリッド距離を計算できます。
2次元だけでなく、何次元のデータでも同じ考え方で距離を計算できます。
p個の特徴量を持つ2つのデータ点 \mathbf{a} = (a_1, a_2, \ldots, a_p) と \mathbf{b} = (b_1, b_2, \ldots, b_p) のユークリッド距離は次のように定義されます。$$
d(\mathbf{a}, \mathbf{b}) = \sqrt{\sum_{i=1}^{p}(a_i – b_i)^2}
$$
「すべての次元で差を取り、2乗して、足し合わせて、ルートを取る」という操作です。次元が増えても、やっていることは同じです。
マンハッタン距離:碁盤の目を歩くように
ユークリッド距離は「直線距離」でしたが、現実世界では直線で移動できないこともあります。
たとえば、碁盤の目のような街路を持つ都市(京都やニューヨーク)を想像してください。AからBへ行くには、まっすぐ飛んでいくことはできません。東西と南北の道を使って移動する必要があります。
このような移動距離を測るのがマンハッタン距離(市街地距離とも呼ばれます)です。
$$
d(\mathbf{a}, \mathbf{b}) = \sum_{i=1}^{p}|a_i – b_i|
$$
各次元の差の絶対値を単純に足し合わせるだけです。
# マンハッタン距離の計算
manhattan = np.sum(np.abs(diff))
print(f"マンハッタン距離: {manhattan}")
以下、実行結果です。
マンハッタン距離: 4
マンハッタン距離は4、ユークリッド距離は約2.83となります。
マンハッタン距離の方が大きいですね。これは「迂回して進む」ため、直線距離より長くなるからです。
ユークリッド距離 vs マンハッタン距離
2つの距離には、それぞれ特徴があります。
ユークリッド距離は最も一般的で、ほとんどの場面で使われます。ただし、外れ値(極端に大きい・小さい値)の影響を受けやすいという弱点があります。差を2乗するため、大きな差がさらに強調されてしまうのです。
マンハッタン距離は外れ値の影響を受けにくいという利点があります。差をそのまま足すだけなので、極端な値があっても影響が限定的です。
最初はユークリッド距離を使い、外れ値が問題になるようならマンハッタン距離を試してみる、というのが実践的なアプローチです。
複数データ間の距離を計算してみよう
ここからは、もう少し実践的なデータで距離を計算してみましょう。5人の顧客データを用意します。
# 5人の顧客データを作成
customers = pd.DataFrame({
'顧客ID': ['A', 'B', 'C', 'D', 'E'],
'月間購買金額': [10, 8, 12, 3, 4], # 万円
'来店頻度': [5, 3, 6, 8, 7] # 回/月
})
print(customers)
以下、実行結果です。
顧客ID 月間購買金額 来店頻度 0 A 10 5 1 B 8 3 2 C 12 6 3 D 3 8 4 E 4 7
このデータフレームを見ると、顧客A・B・Cは購買金額が高めで来店頻度は中程度、顧客D・Eは購買金額が低いが来店頻度は高い、という傾向が見えてきます。
では、すべての顧客ペア間の距離を計算してみましょう。
from scipy.spatial.distance import (
pdist, # 全ペア間の距離を計算
squareform, # 距離行列を作成
)
# 数値データだけを抽出
X = customers[['月間購買金額', '来店頻度']].values
# 全ペア間のユークリッド距離を計算
distances = pdist(X, metric='euclidean')
# 見やすい行列形式に変換
dist_matrix = squareform(distances)
dist_df = pd.DataFrame(
dist_matrix,
index=customers['顧客ID'],
columns=customers['顧客ID']
)
print(dist_df.round(2))
以下、実行結果です。
顧客ID A B C D E 顧客ID A 0.00 2.83 2.24 7.62 6.32 B 2.83 0.00 5.00 7.07 5.66 C 2.24 5.00 0.00 9.22 8.06 D 7.62 7.07 9.22 0.00 1.41 E 6.32 5.66 8.06 1.41 0.00
この「距離行列」を見ると、どの顧客同士が「近い(似ている)」かが一目でわかります。
たとえば、AとBの距離、DとEの距離が比較的小さいはずです。これがクラスター分析で「同じグループにまとめられる」根拠になるのです。
マンハッタン距離でも計算してみましょう。
# 全ペア間のマンハッタン距離を計算
distances_manhattan = pdist(X, metric='cityblock')
# 見やすい行列形式に変換
dist_matrix_manhattan = squareform(distances_manhattan)
dist_df_manhattan = pd.DataFrame(
dist_matrix_manhattan,
index=customers['顧客ID'],
columns=customers['顧客ID']
)
print(dist_df_manhattan.round(2))
以下、実行結果です。
顧客ID A B C D E 顧客ID A 0.0 4.0 3.0 10.0 8.0 B 4.0 0.0 7.0 10.0 8.0 C 3.0 7.0 0.0 11.0 9.0 D 10.0 10.0 11.0 0.0 2.0 E 8.0 8.0 9.0 2.0 0.0
落とし穴①:スケールの違いに要注意!
この落とし穴を体験してみよう
ここまでの例では、「購買金額」と「来店頻度」はどちらも1桁〜10程度の数値でした。しかし、実際のデータではこんなにきれいにいかないことがほとんどです。
たとえば、「年収(単位:万円)」と「年齢(単位:歳)」を使ってクラスタリングしたいとしましょう。
# スケールの異なるデータ
people = pd.DataFrame({
'名前': ['田中', '鈴木', '佐藤', '山田'],
'年収': [500, 570, 490, 780], # 万円
'年齢': [25, 27, 65, 42 ], # 歳
})
print(people)
以下、実行結果です。
名前 年収 年齢 0 田中 500 25 1 鈴木 570 27 2 佐藤 490 65 3 山田 780 42
年収は500〜800の範囲、年齢は25〜45の範囲です。この差が問題を引き起こします。
# そのまま距離を計算
X_raw = people[['年収', '年齢']].values
raw_distances = squareform(pdist(X_raw))
raw_dist_df = pd.DataFrame(
raw_distances,
index=people['名前'],
columns=people['名前']
)
print("標準化なしの距離行列:")
print(raw_dist_df.round(1))
以下、実行結果です。
標準化なしの距離行列: 名前 田中 鈴木 佐藤 山田 名前 田中 0.0 70.0 41.2 280.5 鈴木 70.0 0.0 88.6 210.5 佐藤 41.2 88.6 0.0 290.9 山田 280.5 210.5 290.9 0.0
「田中-鈴木」と「田中-佐藤」の距離を比較してください。田中と佐藤は年齢も近いのに対し、田中と鈴木は年齢が大きく異なります。しかし、距離の計算結果は年収の差に圧倒的に引きずられてしまいます。
解決策:標準化
この問題を解決するのが標準化(Standardization)です。各変数を「平均0、標準偏差1」に変換することで、すべての変数を同じ土俵に乗せます。
$$
z = \frac{x – \bar{x}}{s}
$$
ここで、\bar{x}は平均、sは標準偏差です。
from sklearn.preprocessing import StandardScaler
# 標準化を実行
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_raw)
# 標準化後のデータを確認
scaled_df = pd.DataFrame(
X_scaled,
columns=['年収(標準化)', '年齢(標準化)']
)
print("標準化後のデータ:")
print(scaled_df.round(2))
以下、実行結果です。
標準化後のデータ: 年収(標準化) 年齢(標準化) 0 -0.73 -0.92 1 -0.13 -0.80 2 -0.81 1.58 3 1.67 0.14
標準化後は、両方の変数が同じくらいの範囲(だいたい-2〜+2程度)に収まっています。これで公平に距離を計算できます。
# 標準化後の距離を計算
scaled_distances = squareform(pdist(X_scaled))
scaled_dist_df = pd.DataFrame(
scaled_distances,
index=people['名前'],
columns=people['名前']
)
print("標準化後の距離行列:")
print(scaled_dist_df.round(2))
以下、実行結果です。
標準化後の距離行列: 名前 田中 鈴木 佐藤 山田 名前 田中 0.00 0.61 2.50 2.62 鈴木 0.61 0.00 2.47 2.03 佐藤 2.50 2.47 0.00 2.87 山田 2.62 2.03 2.87 0.00
今度は「田中-鈴木」の距離が「田中-佐藤」より小さくなっているはずです。
標準化の重要性を可視化する
言葉だけではピンとこないかもしれないので、グラフで確認してみましょう。
fig, axes = plt.subplots(2, 1, figsize=(6, 10))
# 標準化前
axes[0].scatter(X_raw[:, 0], X_raw[:, 1], s=100)
for i, name in enumerate(people['名前']):
axes[0].annotate(name, (X_raw[i, 0], X_raw[i, 1]))
axes[0].set_xlabel('Annual Income (10K JPY)')
axes[0].set_ylabel('Age')
axes[0].set_title('Before Standardization')
axes[0].set_aspect('equal')
# 標準化後
axes[1].scatter(X_scaled[:, 0], X_scaled[:, 1], s=100)
for i, name in enumerate(people['名前']):
axes[1].annotate(name, (X_scaled[i, 0], X_scaled[i, 1]))
axes[1].set_xlabel('Annual Income (standardized)')
axes[1].set_ylabel('Age (standardized)')
axes[1].set_title('After Standardization')
axes[1].set_aspect('equal')
plt.tight_layout()
plt.show()
以下、実行結果です。
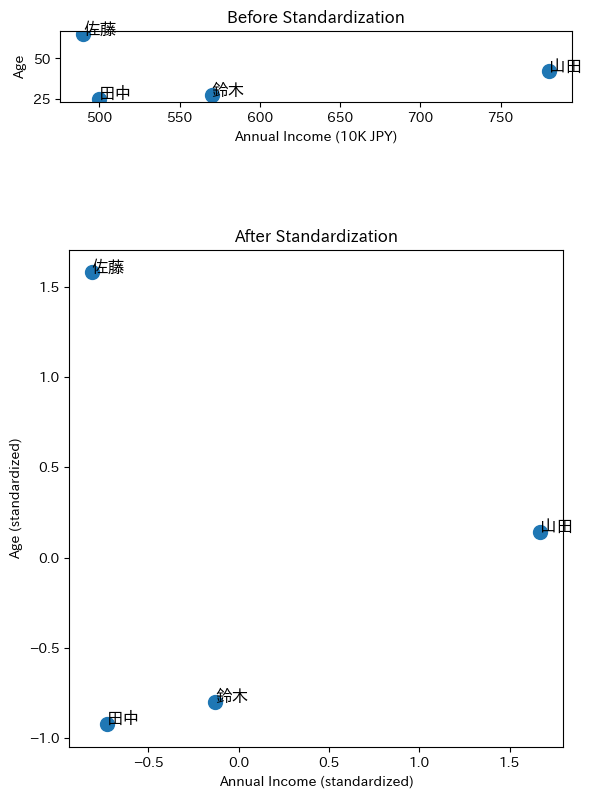
上のグラフ(標準化前)では、年収の軸が圧倒的に長く、年齢の差がほとんど見えないように見えます。
下のグラフ(標準化後)では、両方の軸が同じスケールになり、田中と鈴木が近いことが視覚的にもわかるようになりました。
落とし穴②:数値とカテゴリが混在するデータ
現実のデータは複雑
ここまで紹介したユークリッド距離やマンハッタン距離は、すべての変数が数値であることを前提としています。
しかし、実務で扱うデータには「性別」「居住地域」「会員ランク」といったカテゴリ変数が含まれていることがほとんどです。
たとえば、こんな顧客データを考えてみましょう。
# 数値とカテゴリが混在するデータ
mixed_data = pd.DataFrame({
'顧客ID': ['A', 'B', 'C', 'D'],
'年齢': [25, 45, 28, 42],
'購買金額': [50000, 120000, 55000, 115000],
'性別': ['男性', '女性', '男性', '女性'],
'会員ランク': ['ゴールド', 'シルバー', 'ゴールド', 'ブロンズ']
})
print(mixed_data)
以下、実行結果です。
顧客ID 年齢 購買金額 性別 会員ランク 0 A 25 50000 男性 ゴールド 1 B 45 120000 女性 シルバー 2 C 28 55000 男性 ゴールド 3 D 42 115000 女性 ブロンズ
「年齢25歳の男性」と「年齢45歳の女性」の距離をどう測ればいいでしょうか。
「男性」と「女性」の差を数値で表現できないため、ユークリッド距離は使えません。
Gower距離:万能な距離指標
この問題を解決するのがGower距離(ガワー距離)です。
Gower距離は、変数の種類に応じて異なる方法で類似度を計算し、それらを統合するという柔軟なアプローチを取ります。
Gower距離の基本的な考え方は次の通りです。
$$
d_{ij} = 1 – S_{ij} = 1 – \frac{\displaystyle \sum_{k=1}^{p} w_{ijk} \cdot s_{ijk}}{\displaystyle \sum_{k=1}^{p} w_{ijk}}
$$
ここで、S_{ij}は2つのデータ点iとjの間の類似度(0〜1の値)、s_{ijk}は変数kにおける類似度、w_{ijk}は重みです。
難しそうに見えますが、要するに「各変数ごとに類似度を計算して、平均を取る」ということです。
変数タイプ別の類似度計算
Gower距離のポイントは、変数のタイプによって類似度の計算方法を変えることです。
数値変数(量的変数)の場合
$$
s_{ijk} = 1 – \frac{|x_{ik} – x_{jk}|}{R_k}
$$
ここでR_kは変数kの範囲(最大値 – 最小値)です。差が小さいほど類似度が高くなります。
範囲で割ることで、自動的に0〜1の範囲に正規化されるのがポイントです。
カテゴリ変数(質的変数)の場合
$$
s_{ijk} = \begin{cases} 1 & (\text{同じカテゴリの場合}) \\ 0 & (\text{異なるカテゴリの場合}) \end{cases}
$$
シンプルに、同じカテゴリなら類似度1、違えば類似度0です。
PythonでGower距離を計算する
Gower距離を計算するには `gower` ライブラリを使います。まずインストールしましょう。
# インストール(初回のみ) pip install gower
では、先ほどの混在データでGower距離を計算してみます。
import gower
# 分析に使う列を選択(顧客IDは除外)
X_mixed = mixed_data[['年齢', '購買金額', '性別', '会員ランク']]
# Gower距離行列を計算
gower_dist = gower.gower_matrix(X_mixed)
# 見やすく表示
gower_df = pd.DataFrame(
gower_dist,
index=mixed_data['顧客ID'],
columns=mixed_data['顧客ID']
)
print("Gower距離行列:")
print(gower_df.round(3))
以下、実行結果です。
Gower距離行列: 顧客ID A B C D 顧客ID A 0.000 1.000 0.055 0.945 B 1.000 0.000 0.945 0.305 C 0.055 0.945 0.000 0.889 D 0.945 0.305 0.889 0.000
この距離行列を見ると、数値変数(年齢・購買金額)とカテゴリ変数(性別・会員ランク)の両方を考慮した距離が計算されています。
顧客AとCは年齢が近く、性別も同じ、会員ランクも同じなので、距離が小さくなっています。
まとめ
クラスター分析では、データ間の「似ている度合い」を距離という数値で測ります。距離が小さいほど似ている、という考え方です。
- ユークリッド距離:直線距離。最も一般的で、まずはこれを使う
- マンハッタン距離:各軸方向の差の合計。外れ値に強い
- Gower距離:数値とカテゴリの混合データに対応。実務で重宝する
変数のスケールが異なると、大きな値を持つ変数に距離が引きずられてしまいます。ユークリッド距離やマンハッタン距離を使う場合は、必ず標準化を行いましょう。Gower距離は自動的に正規化されるので標準化不要です。
距離の概念を理解したところで、次回はいよいよ階層的クラスタリングについて説明します。

