前回学んだ階層的クラスタリングは、データの階層構造を美しく可視化できる素晴らしい手法でした。

Pythonで学ぶ クラスター分析入門— 第2回 —樹形図で見える化 ― 階層的クラスタリング

しかし、「データが大きいと計算に時間がかかる」という弱点がありましたね。

今回は、大規模データにも対応できるk-means法を学びます。

クラスター分析の中で最もポピュラーな手法で、実務でも頻繁に使われています。

k-means法のアルゴリズム

　3ステップで理解する

K-means法のアルゴリズムは、驚くほどシンプルです。

• ステップ1【初期化】：K個の「中心点（セントロイド）」をランダムに配置する
  
• ステップ2【割り当て】：各データ点を、最も近い中心点のクラスタに割り当てる
  
• ステップ3【更新】：各クラスタの重心（平均）を計算し、中心点をその位置に移動する
  
• ステップ2と3を、中心点が動かなくなるまで繰り返す

たったこれだけです。「割り当て」と「更新」を繰り返すことで、中心点が徐々に最適な位置に収束していきます。

 

　数式で表現すると

少し数学的に表現してみましょう。

n 個のデータ点 \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n を K 個のクラスタに分割するとき、k-means 法は以下の クラスタ内誤差平方和（Within-Cluster Sum of Squares, WCSS）を最小化することを目的とします。
$$
J = \sum_{k=1}^{K} \sum_{\mathbf{x}_i \in C_k} \|\mathbf{x}_i – \boldsymbol{\mu}_k\|^2
$$
ここで、C_k はクラスタ k に属するデータ点の集合、\boldsymbol{\mu}_k はクラスタ k の中心（重心）を表します。

この式は、「各データ点と、それが属するクラスタの中心とのユークリッド距離の二乗を、すべてのデータ点について合計したもの」を意味しています。

つまり、各クラスタ内のデータ点ができるだけ中心に近く集まるようにし、クラスタ内のばらつきを最小化することが K-means 法の目標です。

 

Pythonで動きを確認しよう

　準備

まずは必要なライブラリをインポートします。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib

from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_blobs

# 乱数シードを固定（再現性のため）
np.random.seed(42)

 

sklearn.cluster.KMeans がk-means法を実行するクラスです。

 

　サンプルデータを生成する

まずは、k-means法の動きを確認しやすい「きれいなデータ」を作ってみましょう。

make_blobs関数を使うと、指定した数のクラスタを持つサンプルデータを生成できます。

# 3つのクラスタを持つサンプルデータを生成
X, y_true = make_blobs(
    n_samples=300,      # データ点の数
    centers=3,          # クラスタの数
    cluster_std=0.8,    # クラスタ内の標準偏差
    random_state=42
)

# データの形状を確認
print(f"データの形状: {X.shape}")
print(f"最初の5件:\n{X[:5]}")

 

以下、実行結果です。

データの形状: (300, 2)
最初の5件:
[[-7.24711591 -7.55998509]
[-7.56795788 -7.18775403]
[-1.85116169 8.03761121]
[ 4.46573387 2.85219117]
[-8.51012682 -7.68657864]]

 

300個のデータ点が生成され、それぞれが2次元の座標（x, y）を持っています。

y_trueには「本当のクラスタラベル」が入っていますが、これはk-means法には渡しません。

 

　データを可視化する

生成したデータを散布図で確認してみましょう。

plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], s=50, alpha=0.6)
plt.title('Sample Data (Before Clustering)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True, alpha=0.3)
plt.show()

 

以下、実行結果です。

 

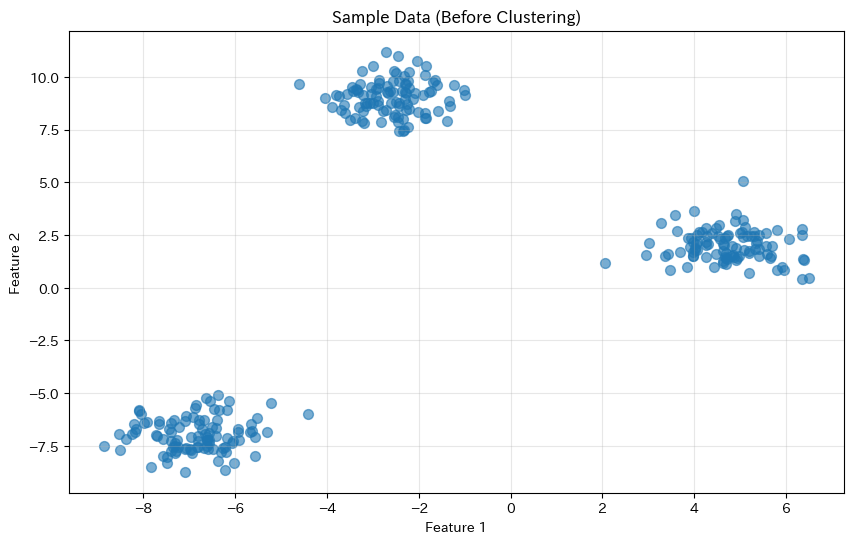
3つのグループがなんとなく見えるでしょうか？

k-means法でこの構造を自動的に発見できるか試してみましょう。

 

　k-means法を実行する

いよいよk-means法を実行します。scikit-learnでは非常に簡単です。

# k-means法を実行（K=3）
kmeans = KMeans(
    n_clusters=3,     # クラスタ数
    random_state=42,  # 乱数シード
    init='k-means++', # 初期値の選び方
    n_init=10,        # 初期値の試行回数
    max_iter=300,     # 最大反復回数
)
kmeans.fit(X)

# クラスタラベルを取得
labels = kmeans.labels_

# クラスタの中心点を取得
centers = kmeans.cluster_centers_

# クラスタ内誤差平方和を取得
inertia = kmeans.inertia_

print(f"各データのクラスタラベル（最初の10件）: {labels[:10]}")
print(f"\nクラスタの中心点:\n{centers}")
print(f"\nクラスタ内誤差平方和: {inertia}")

 

以下、実行結果です。

各データのクラスタラベル（最初の10件）: [1 1 0 2 1 2 0 2 0 0]

クラスタの中心点:
[[-2.60842567 9.03771305]
[-6.88302287 -6.96320924]
[ 4.72565847 2.00310936]]

クラスタ内誤差平方和: 362.7901127196244

 

KMeansクラスのインスタンスを作成し、fit()メソッドでクラスタリングを実行します。

結果として、各データ点がどのクラスタに属するか（labels_）と、各クラスタの中心点（cluster_centers_）が得られます。

 

　クラスタリング結果を可視化する

結果を散布図で確認してみましょう。各クラスタを異なる色で表示し、中心点も一緒にプロットします。

plt.figure(figsize=(10, 6))

# データ点をクラスタごとに色分けしてプロット
scatter = plt.scatter(
    X[:, 0], X[:, 1], c=labels, 
    cmap='viridis', s=50, alpha=0.6
)
# クラスタの中心点をプロット
plt.scatter(
    centers[:, 0], centers[:, 1], 
    c='red', marker='X', s=100, 
    edgecolors='white', linewidths=1, 
    label='Centroids'
)

plt.title('k-means Clustering Result (K=3)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.colorbar(scatter, label='Cluster')
plt.grid(True, alpha=0.3)
plt.show()

 

以下、実行結果です。

 

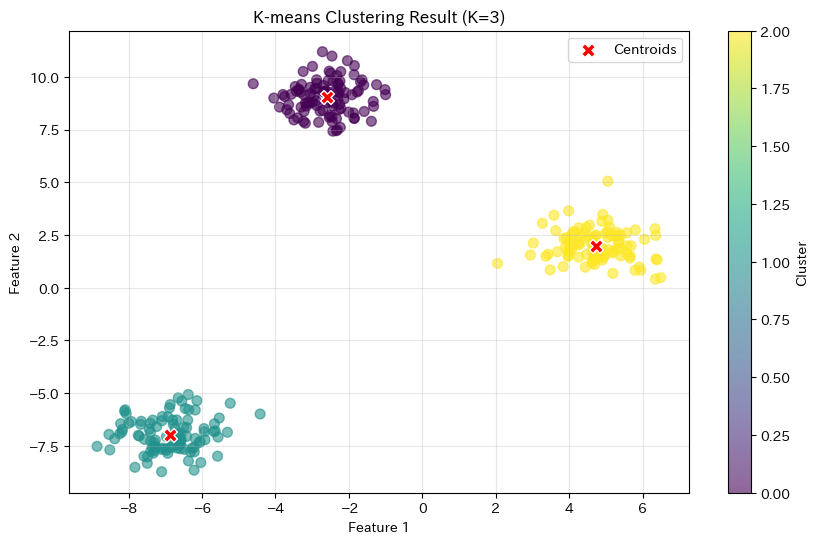
データ点が3色に分かれ、各クラスタの中心に赤い×マーク（セントロイド）が配置されていることがわかります。

k-means法が正しく3つのグループを発見できました。

 

初期値問題とk-means++

　初期値によって結果が変わる？

k-means法には1つ大きな弱点があります。

初期中心点の選び方によって、結果が変わることがあるのです。

運が悪いと、最適でない位置に中心点が収束してしまうことがあります。

 

　k-means++：賢い初期値の選び方

この問題を解決するために開発されたのがk-means++というアルゴリズムです。

k-means++の考え方はシンプルです。

• Step 1：最初の中心点をランダムに1つ選ぶ
• Step 2：2つ目以降の中心点は、既存の中心点から遠いデータ点を優先的に選ぶ
• Step 2 をK個の中心点が選ばれるまで繰り返す

これにより、初期中心点が互いに離れた位置に配置され、局所最適解にはまりにくくなります。

scikit-learnでは、init='k-means++'がデフォルト設定になっています。また、n_init=10は「10回異なる初期値で実行し、最も良い結果を採用する」という設定です。

これらの工夫により、安定した結果が得られます。

 

実践：顧客セグメンテーション

　顧客データを用意する

ここからは、より実践的な例として顧客セグメンテーションに挑戦しましょう。小売店の顧客データを使って、顧客をいくつかのグループに分類します。

# 顧客データを作成（100人分）
np.random.seed(42)

n_customers = 100

customers = pd.DataFrame({
    '顧客ID': [f'C{i:03d}' for i in range(1, n_customers + 1)],
    '年間購買金額': np.concatenate([
        np.random.normal(50000, 10000, 30),   # ライトユーザー
        np.random.normal(150000, 20000, 40),  # ミドルユーザー
        np.random.normal(300000, 30000, 30)   # ヘビーユーザー
    ]),
    '来店頻度': np.concatenate([
        np.random.normal(3, 1, 30),    # 月3回程度
        np.random.normal(8, 2, 40),    # 月8回程度
        np.random.normal(15, 3, 30)    # 月15回程度
    ]),
    '平均購入点数': np.concatenate([
        np.random.normal(2, 0.5, 30),   # 2点程度
        np.random.normal(5, 1, 40),     # 5点程度
        np.random.normal(10, 2, 30)     # 10点程度
    ])
})

# 負の値を補正
customers['来店頻度'] = customers['来店頻度'].clip(lower=1)
customers['平均購入点数'] = customers['平均購入点数'].clip(lower=1)

print(customers.head(10))
print(f"\n基本統計量:\n{customers.describe()}")

 

以下、実行結果です。

顧客ID 年間購買金額 来店頻度 平均購入点数
0 C001 54967.141530 1.584629 2.178894
1 C002 48617.356988 2.579355 2.280392
2 C003 56476.885381 2.657285 2.541526
3 C004 65230.298564 2.197723 2.526901
4 C005 47658.466253 2.838714 1.311165
5 C006 47658.630431 3.404051 1.531087
6 C007 65792.128155 4.886186 2.257518
7 C008 57674.347292 3.174578 2.256893
8 C009 45305.256141 3.257550 2.257524
9 C010 55425.600436 2.925554 3.926366

基本統計量:
年間購買金額 来店頻度 平均購入点数
count 100.000000 100.000000 100.000000
mean 163392.030256 8.622932 5.659207
std 100418.155468 5.045681 3.450417
min 30867.197553 1.081229 1.066367
25% 56214.064145 4.054875 2.514426
50% 148123.415960 8.482747 4.816348
75% 280230.603860 12.335699 8.649286
max 346939.309674 23.160507 14.266067

 

この顧客データには「年間購買金額」「来店頻度」「平均購入点数」の3つの特徴量があります。

 

　データの標準化

スケールの異なる変数を扱う場合は標準化が重要です。年間購買金額は数万〜数十万円、来店頻度は数回〜十数回とスケールが全く異なります。

# 分析に使う列を選択
features = ['年間購買金額', '来店頻度', '平均購入点数']
X_customers = customers[features].values

# 標準化
scaler = StandardScaler()
X_customers_scaled = scaler.fit_transform(X_customers)

print("標準化後のデータ（最初の5件）:")
print(
    pd.DataFrame(
        X_customers_scaled, 
        columns=features
    ).head()
)

 

以下、実行結果です。

標準化後のデータ（最初の5件）:
年間購買金額 来店頻度 平均購入点数
0 -1.085173 -1.401944 -1.013746
1 -1.148725 -1.203806 -0.984181
2 -1.070063 -1.188284 -0.908118
3 -0.982454 -1.279823 -0.912378
4 -1.158322 -1.152145 -1.266498

 

標準化により、すべての変数が平均0、標準偏差1の範囲に変換されました。

 

　k-means法でセグメンテーション

それでは、顧客を3つのセグメントに分類してみましょう。

# k-means法を実行（K=3）
kmeans_customers = KMeans(
    n_clusters=3, 
    random_state=42, 
    n_init=10
)
kmeans_customers.fit(X_customers_scaled)

# クラスタラベルを元のデータに追加
customers['セグメント'] = kmeans_customers.labels_

print("クラスタリング結果:")
print(customers.sample(10))

 

以下、実行結果です。

クラスタリング結果:
顧客ID 年間購買金額 来店頻度 平均購入点数 セグメント
77 C078 291029.779486 19.360602 8.799566 1
71 C072 346141.096994 12.552569 7.128276 1
92 C093 278938.407184 15.642281 8.821270 1
91 C092 329059.349716 17.569196 9.013998 1
20 C021 64656.487689 3.791032 3.157329 2
83 C084 284451.893452 16.447417 7.524369 1
55 C056 168625.602382 6.571297 4.515766 0
93 C094 290170.135602 11.262784 11.699204 1
32 C033 149730.055505 5.875393 5.045572 0
79 C080 240372.932562 23.160507 9.229373 1

 

各顧客に「セグメント」というラベル（0, 1, 2）が付与されました。

このラベルが何を意味するのか、分析してみましょう。

 

　セグメントの特徴を分析する

各セグメントの平均値を計算して、特徴を把握します。

# セグメントごとの平均値を計算
segment_profile = customers.groupby('セグメント')[features].mean()
segment_profile['顧客数'] = customers.groupby('セグメント').size()

print("=== セグメント別プロファイル ===\n")
print(segment_profile.round(1))

 

以下、実行結果です。

=== セグメント別プロファイル ===
年間購買金額 来店頻度 平均購入点数 顧客数
セグメント
0 148107.3 8.1 4.9 40
1 299045.2 14.9 10.2 30
2 48118.5 3.1 2.1 30

 

この結果を見ると、各セグメントの特徴が明確になります。

たとえば、購買金額と来店頻度がともに高いセグメントは「ヘビーユーザー」、低いセグメントは「ライトユーザー」と解釈できます。

 

　セグメントを可視化する

2つの変数を選んで散布図を描き、セグメンテーションの結果を視覚的に確認しましょう。

fig, axes = plt.subplots(2, 1, figsize=(10, 10))

# 年間購買金額 vs 来店頻度
colors = ['#3498db', '#e74c3c', '#2ecc71']
for seg in range(3):
    mask = customers['セグメント'] == seg
    axes[0].scatter(
        customers.loc[mask, '年間購買金額'],
        customers.loc[mask, '来店頻度'],
        c=colors[seg], label=f'Segment {seg}', s=60, alpha=0.7
    )
axes[0].set_xlabel('Annual Purchase Amount (JPY)')
axes[0].set_ylabel('Visit Frequency (per month)')
axes[0].set_title('Customer Segmentation: Purchase vs Frequency')
axes[0].legend()
axes[0].grid(True, alpha=0.3)

# 来店頻度 vs 平均購入点数
for seg in range(3):
    mask = customers['セグメント'] == seg
    axes[1].scatter(
        customers.loc[mask, '来店頻度'],
        customers.loc[mask, '平均購入点数'],
        c=colors[seg], label=f'Segment {seg}', s=60, alpha=0.7
    )
axes[1].set_xlabel('Visit Frequency (per month)')
axes[1].set_ylabel('Average Items per Visit')
axes[1].set_title('Customer Segmentation: Frequency vs Items')
axes[1].legend()
axes[1].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

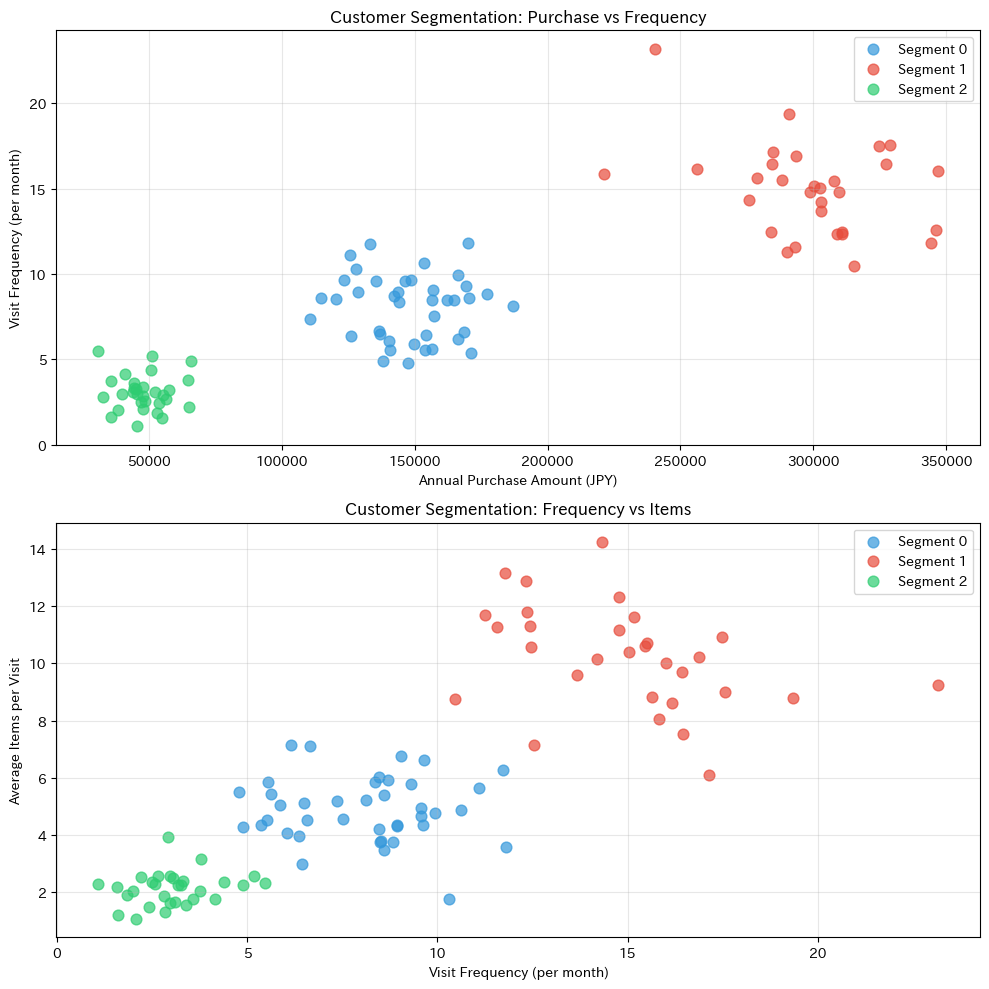
散布図を見ると、3つのセグメントがきれいに分かれていることがわかります。

k-means法が購買行動の異なる顧客グループを正しく識別できています。

 

階層的クラスタリングとk-means法の比較

ここまでで2つのクラスタリング手法を学びました。それぞれの特徴を比較してみましょう。

項目	階層的クラスタリング	k-means法
クラスタ数	事後に決定可能	事前に指定が必要
計算速度	遅い（O(n²)〜O(n³)）	速い（O(nKt)）
データサイズ	小〜中規模（〜数千件）	大規模（数万件〜）
結果の再現性	完全に再現可能	初期値依存（k-means++で軽減）
可視化	デンドログラム	散布図
適した場面	階層構造の発見、探索的分析	大規模データ、明確なクラスタ数がある場合

• データが数百〜数千件で、階層構造を探りたい → 階層的クラスタリング
• データが大規模で、クラスタ数の目安がある → k-means法
• 両方試して、解釈しやすい方を採用 → 実務ではよくあるアプローチ

 

まとめ

今回は、k-means法の基本についてお話ししました。

k-means法は、「K個の中心点を配置し、各データを最も近い中心に割り当てる」というシンプルなアルゴリズム。「割り当て」と「更新」を繰り返して収束させます。

しかし、初期中心点の選び方によって結果が変わることがある。k-means++を使うことで、安定した結果が得られます（scikit-learnのデフォルト）。

以下、実施するときのポイントです。

• 標準化を忘れずに
• n_initで複数回実行して最良の結果を採用
• inertia_で結果の良さを評価

顧客セグメンテーションなど、ビジネスで広く活用されています。結果に意味のある名前をつけることで、施策につなげやすくなります。

今回は「K=3」と決め打ちでクラスタ数を指定しましたが、「本当に3が最適なの？」と思いませんでしたか？

次回は、クラスタ数の決め方を学びます。エルボー法やシルエット分析といった手法を使って、データに適したクラスタ数を見極める方法を解説します。