こんにちは！「Pythonで始める分類モデル入門」の第4回です。

前回は決定木を学びました。

https://www.salesanalytics.co.jp/datascience/datascience303/

直感的で解釈しやすい反面、「過学習しやすい」「データが少し変わると木の構造が大きく変わる」という弱点がありました。

今回は、この弱点を克服するために生まれたランダムフォレスト（Random Forest）を学びます。

名前の通り、たくさんの決定木を「森」のように束ねることで、1本の木では得られない安定性と精度を実現します。

「三人寄れば文殊の知恵」

日本には「三人寄れば文殊の知恵」ということわざがあります。

一人で考えるよりも、複数人で知恵を出し合った方が良いアイデアが生まれるという意味です。

実は、機械学習の世界にも同じ発想があります。

それがアンサンブル学習（Ensemble Learning）です。

クイズ番組を思い出してください。

難しい問題で「オーディエンス（会場の観客）に聞く」というライフラインがあることがあります。

一人の専門家に聞くよりも、100人の一般人の多数決の方が正解率が高いことが多いのです。

これは「群衆の知恵（Wisdom of Crowds）」と呼ばれる現象です。

ランダムフォレストは、まさにこの考え方を機械学習に応用したものです。

1本の決定木は「不安定で過学習しやすい」けれど、100本の決定木の多数決を取れば、安定した予測ができるようになります。

 

必要なライブラリを読み込もう

今回使うライブラリを読み込みます。ランダムフォレストはsklearn.ensembleモジュールに含まれています。

以下、コードです。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib

# 決定木モデル
from sklearn.tree import DecisionTreeClassifier
# ランダムフォレストモデル
from sklearn.ensemble import RandomForestClassifier
# データ分割
from sklearn.model_selection import train_test_split
# 評価関数：正解率
from sklearn.metrics import accuracy_score

# 乱数のシードを固定
np.random.seed(42)

 

今回は決定木とランダムフォレストを比較するので、両方をインポートしています。

 

顧客離脱データを作ってみよう

今回は「通信会社の顧客が解約するかどうかを予測する」問題に取り組みます。

これはチャーン予測（Churn Prediction）と呼ばれ、実務で非常によく使われる分析の一つです。

そのサンプルデータを生成します。

以下、コードです。

# 1000人分の顧客データを生成
n_customers = 1000

# 特徴量を生成
contract_months = np.random.randint(1, 72, n_customers)      # 契約月数（1〜72ヶ月）
monthly_charge = np.random.randint(3000, 15000, n_customers) # 月額料金（3000〜15000円）
support_calls = np.random.poisson(2, n_customers)            # サポート問合せ回数
data_usage = np.random.exponential(5, n_customers)           # データ使用量（GB）

# 離脱確率を計算（契約が短く、問合せが多く、料金が高いと離脱しやすい）
churn_score = (-0.05 * contract_months 
               + 0.0003 * monthly_charge 
               + 0.3 * support_calls 
               - 0.1 * data_usage)
churn_prob = 1 / (1 + np.exp(-churn_score))
churn = np.random.binomial(1, churn_prob)

# DataFrameにまとめる
df = pd.DataFrame({
    'contract_months': contract_months,
    'monthly_charge': monthly_charge,
    'support_calls': support_calls,
    'data_usage': data_usage,
    'churn': churn
})

print(f"データ数: {len(df)}人")
print(f"離脱者数: {churn.sum()}人 ({churn.mean()*100:.1f}%)")
print(df.head())

 

以下、実行結果です。

データ数: 1000人
離脱者数: 662人 (66.2%)
   contract_months  monthly_charge  support_calls  data_usage  churn
0               52           14383              2    5.181267      1
1               15            5538              2    6.836671      1
2               61            7547              3    1.321291      1
3               21            8619              0    2.598704      1
4               24           11356              2    1.567814      1

 

4つの特徴量から顧客の離脱（解約）を予測するシナリオです。

契約期間（contract_months）が短い、月額料金（monthly_charge）が高い、サポートへの問い合わせ（support_calls）が多いほど離脱しやすい設定になっています。

 

バギング：データをブートストラップする

ランダムフォレストの基盤となる技術がバギング（Bagging）です。

Baggingは「Bootstrap Aggregating」の略で、2つのステップからなります。

• ステップ1：ブートストラップサンプリング
• ステップ2：複数モデルの集約

 

　ステップ1：ブートストラップサンプリング

元のデータから復元抽出（同じデータを複数回選んでもよい）でサンプルを作成します。

たとえば、1000人のデータから1000人分をランダムに選びますが、同じ人が2回以上選ばれることもあれば、1回も選ばれない人もいます。

このようにして作った「ブートストラップサンプル」は、元のデータと似ているけれど少し違うデータセットになります。

以下、コードです。

# ブートストラップサンプリングの例
original_data = np.array([1, 2, 3, 4, 5])

print("【ブートストラップサンプリングの例】")
print(f"元のデータ: {original_data}")
print()

for i in range(3):
    # 復元抽出でサンプルを作成
    bootstrap_sample = np.random.choice(
        original_data,           # 元のデータ
        size=len(original_data), # サンプルサイズ
        replace=True             # 復元抽出
    )
    print(f"ブートストラップサンプル{i+1}: {bootstrap_sample}")

 

以下、実行結果です。

【ブートストラップサンプリングの例】
元のデータ: [1 2 3 4 5]

ブートストラップサンプル1: [2 3 4 4 4]
ブートストラップサンプル2: [3 3 2 1 5]
ブートストラップサンプル3: [5 1 2 1 1]

 

同じ要素が複数回出現したり、出現しない要素があることがわかります。

 

　ステップ2：複数モデルの集約

各ブートストラップサンプルで別々の決定木を学習し、予測時には全ての木の予測を多数決（分類の場合）または平均（回帰の場合）で集約します。

この仕組みにより、個々の決定木が持つ「癖」や「ノイズへの過適合」が打ち消し合い、より安定した予測が可能になります。

 

ランダムフォレスト：さらにランダム性を加える

バギングだけでも効果はありますが、ランダムフォレストはさらに一工夫を加えています。

各決定木を学習する際に、使用する特徴量もランダムに選択するのです。

通常の決定木は、各ノードで「すべての特徴量」の中から最も良い分岐を探します。

一方、ランダムフォレストでは、「ランダムに選んだ一部の特徴量」の中から最も良い分岐を探します。

これにより、決定木同士がより「多様」になります。

もし全ての木が同じような構造になってしまったら、多数決を取っても意味がありませんよね。

ランダムフォレストは、意図的に「バラバラな木」を作ることで、アンサンブルの効果を最大化しています。

 

ランダムフォレストを実装しよう

それでは実際にランダムフォレストを実装してみましょう。

まずはデータを訓練用とテスト用に分割します。

以下、コードです。

# 特徴量（説明変数）とラベル（目的変数）を準備
X = df[[
    'contract_months', 
    'monthly_charge', 
    'support_calls', 
    'data_usage'
]].values
y = df['churn'].values

# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42)

print(f"訓練データ: {len(X_train)}人")
print(f"テストデータ: {len(X_test)}人")

 

以下、実行結果です。

訓練データ: 700人
テストデータ: 300人

 

データが7:3の割合で分割されました。

訓練データでモデルを学習し、テストデータで性能を評価します。

 

決定木とランダムフォレストを比較しよう

単一の決定木とランダムフォレストの性能を比較してみましょう。

以下、コードです。

# 単一の決定木
tree_model = DecisionTreeClassifier(random_state=42)
tree_model.fit(X_train, y_train)

# ランダムフォレスト（100本の木）
rf_model = RandomForestClassifier(
    n_estimators=100, # 木の数 
    random_state=42
)
rf_model.fit(X_train, y_train)

# 精度を比較
print("【決定木 vs ランダムフォレスト】")
print()
print("決定木（単一）:")
print(
    f"  訓練データ正解率: "
    f"{accuracy_score(y_train, tree_model.predict(X_train))*100:.1f}%"
)
print(
    f"  テストデータ正解率: "
    f"{accuracy_score(y_test, tree_model.predict(X_test))*100:.1f}%"
)
print()
print("ランダムフォレスト（100本）:")
print(
    f"  訓練データ正解率: "
    f"{accuracy_score(y_train, rf_model.predict(X_train))*100:.1f}%"
)
print(
    f"  テストデータ正解率: "
    f"{accuracy_score(y_test, rf_model.predict(X_test))*100:.1f}%"
)

 

以下、実行結果です。

【決定木 vs ランダムフォレスト】

決定木（単一）:
  訓練データ正解率: 100.0%
  テストデータ正解率: 68.0%

ランダムフォレスト（100本）:
  訓練データ正解率: 100.0%
  テストデータ正解率: 74.7%

 

結果を見ると、ランダムフォレストはテストデータでは決定木より正解率が高く、高い性能を発揮しています。

これは過学習が抑制されている証拠です。

 

なぜランダムフォレストは過学習に強いのか

ランダムフォレストが過学習に強い理由を、数学的な観点から理解しましょう。

予測の誤差は、大きくバイアス（偏り）とバリアンス（分散）の2つに分解できます。

$$
\text{予測誤差} = \text{バイアス}^2 + \text{バリアンス} + \text{ノイズ}
$$

バイアスは、モデルが単純すぎてデータのパターンを捉えられない誤差です。

バリアンスは、モデルがデータの小さな変動に敏感すぎて、訓練データが変わると予測も大きく変わってしまう誤差です。

決定木（深い木）は、バイアスは低いですがバリアンスが高い傾向があります。つまり、訓練データにはよく適合するけれど、データが少し変わると予測がガラッと変わってしまいます。

ランダムフォレストは、多数の木の予測を平均（または多数決）することで、このバリアンスを大幅に削減します。個々の木の「ブレ」が打ち消し合うのです。

n本の独立した木の予測を平均すると、バリアンスは理論的に 1/n に減少します。

ただし、実際には木同士に相関があるため、完全に 1/n にはなりませんが、それでも大幅な削減効果があります。

 

木の本数と精度の関係

木の本数（n_estimators）を変えると、精度がどう変化するか確認してみましょう。

以下、コードです。

# 木の本数を変えて精度を計算
n_trees_list = [1, 5, 10, 20, 50, 100, 200]
train_scores = []
test_scores = []

for n_trees in n_trees_list:
    rf = RandomForestClassifier(
        n_estimators=n_trees, 
        random_state=42
    )
    rf.fit(X_train, y_train)
    train_scores.append(
        accuracy_score(y_train, rf.predict(X_train)))
    test_scores.append(
        accuracy_score(y_test, rf.predict(X_test)))

# グラフで可視化
plt.figure(figsize=(10, 6))
plt.plot(n_trees_list, train_scores, 'b-o', label='Training')
plt.plot(n_trees_list, test_scores, 'r-s', label='Test')
plt.xlabel('Number of Trees')
plt.ylabel('Accuracy')
plt.title('Accuracy vs Number of Trees')
plt.legend()
plt.grid(True, alpha=0.3)
plt.xscale('log')
plt.show()

 

以下、実行結果です。

 

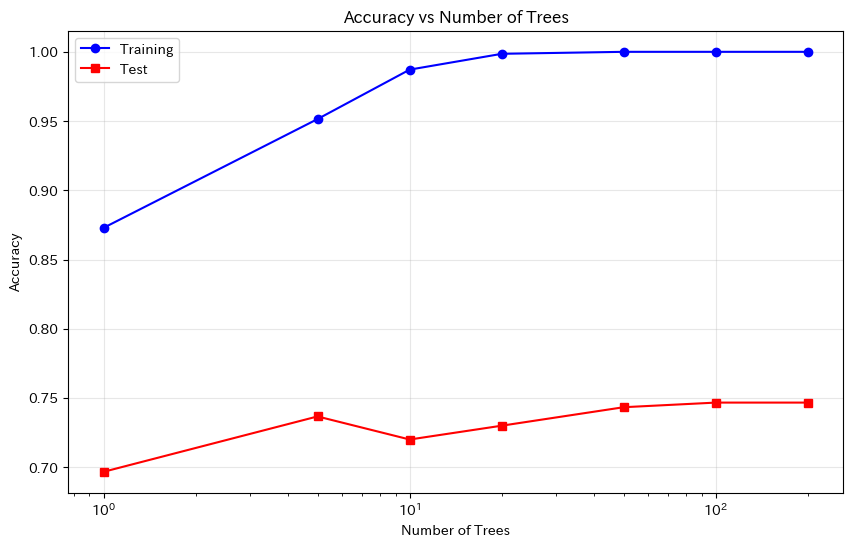
木の本数が増えるにつれて、テスト精度が安定していくことがわかります。

特に最初の数十本で大きく改善し、その後は緩やかに収束（頭打ち）します。

一般的に、100〜500本あれば十分な性能が得られることが多いです。

重要なポイントは、木の本数を増やしても過学習しないことです。

決定木の深さを増やすと過学習しましたが、ランダムフォレストで木の本数を増やしても過学習は起きません。

これがランダムフォレストの大きな利点です。

 

特徴量重要度：何が予測に効いているか

ランダムフォレストの大きな魅力の一つが、特徴量重要度（Feature Importance）を計算できることです。

これにより、「どの変数が予測に重要なのか」を定量的に把握できます。

特徴量重要度は、各特徴量を使った分岐が「どれだけ不純度を減少させたか」を、全ての木にわたって平均したものです。

数式で書くと、次のようになります。
$$
\text{重要度}_j = \frac{1}{T} \sum_{t=1}^{T} \sum_{v \in \text{ノード}_j^{(t)}} \frac{n_v}{n} \cdot \Delta \text{Gini}_v
$$

ここで、Tは木の本数、n_vはノードvのサンプル数、\Delta \text{Gini}_vはそのノードでの分岐によるジニ不純度の減少量です。

実際に計算してみましょう。

以下、コードです。

# 特徴量の名前をリストに格納
feature_names = [
    'contract_months', 
    'monthly_charge', 
    'support_calls', 
    'data_usage'
]

# 特徴量重要度を取得
importances = rf_model.feature_importances_

# DataFrameにまとめてソート
importance_df = pd.DataFrame({
    'Feature': feature_names,
    'Importance': importances
}).sort_values('Importance', ascending=False)

print("【特徴量重要度】")
print(importance_df.to_string(index=False))

 

以下、実行結果です。

【特徴量重要度】
        Feature  Importance
 monthly_charge    0.352217
contract_months    0.316263
     data_usage    0.246900
  support_calls    0.084620

 

各特徴量が離脱予測にどれだけ貢献しているかがわかります。

この情報は、ビジネス上の意思決定に非常に有用です。

 

特徴量重要度を可視化しよう

棒グラフで特徴量重要度を可視化してみましょう。

plt.figure(figsize=(10, 6))

# 棒グラフを作成
plt.barh(
    importance_df['Feature'], # 特徴量の名前
    importance_df['Importance'], # 特徴量重要度
    color='#2E86AB'
)

plt.xlabel('Importance')
plt.ylabel('Feature')
plt.title('Feature Importance in Random Forest')
plt.gca().invert_yaxis()  # 重要度が高い順に上から表示
plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

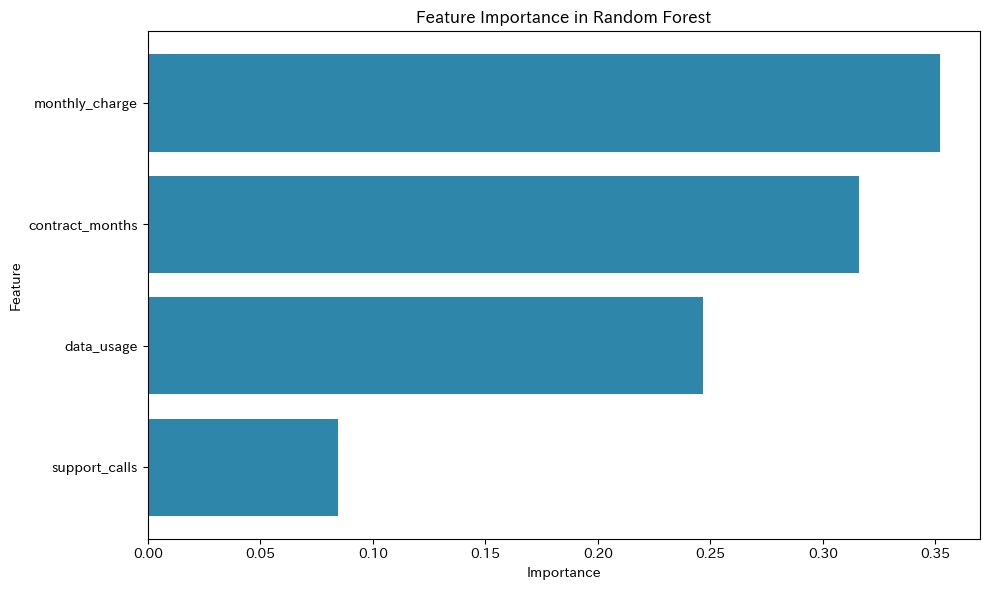
このグラフから、どの特徴量が離脱予測に最も影響しているかが一目でわかります。

ブラックボックスになりがちな機械学習モデルの中で、ランダムフォレストは比較的解釈しやすい手法と言えます。

 

決定境界を比較しよう

2つの特徴量を使って、決定木とランダムフォレストの決定境界を比較してみましょう。

以下、コードです。

# 2つの特徴量だけを使用（可視化のため）
X_2d = df[['contract_months', 'support_calls']].values
y_2d = df['churn'].values

X_train_2d, X_test_2d, y_train_2d, y_test_2d = train_test_split(
    X_2d, y_2d, test_size=0.3, random_state=42)

# モデルを訓練
# 決定木
tree_2d = DecisionTreeClassifier(
    max_depth=5,
    random_state=42
)
tree_2d.fit(X_train_2d, y_train_2d)
# ランダムフォレスト
rf_2d = RandomForestClassifier(
    max_depth=5,
    n_estimators=100, 
    random_state=42
)
rf_2d.fit(X_train_2d, y_train_2d)

# メッシュグリッドを作成
h = 0.5
x_min, x_max = X_2d[:, 0].min() - 5, X_2d[:, 0].max() + 5
y_min, y_max = X_2d[:, 1].min() - 1, X_2d[:, 1].max() + 1
xx, yy = np.meshgrid(
    np.arange(x_min, x_max, h),
    np.arange(y_min, y_max, h)
)

# 決定境界を描画（上下に表示）
fig, axes = plt.subplots(2, 1, figsize=(10, 12))

for ax, model, title in [
    (axes[0], tree_2d, 'Decision Tree'),
    (axes[1], rf_2d, 'Random Forest (100 trees)')
]:
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # 決定境界を描画
    ax.contourf(xx, yy, Z, alpha=0.3, cmap='RdBu')
    # 継続者（Stay）のデータ点を描画
    ax.scatter(
        X_test_2d[y_test_2d==0, 0], 
        X_test_2d[y_test_2d==0, 1],
        c='#E94F37', s=50, alpha=0.7, 
        label='Stay'
    )
    # 離反者（Churn）のデータ点を描画
    ax.scatter(
        X_test_2d[y_test_2d==1, 0], 
        X_test_2d[y_test_2d==1, 1],
        c='#2E86AB', s=50, alpha=0.7, 
        label='Churn'
    )
    ax.set_xlabel('Contract Months')
    ax.set_ylabel('Support Calls')
    ax.set_title(title)
    ax.legend()

plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

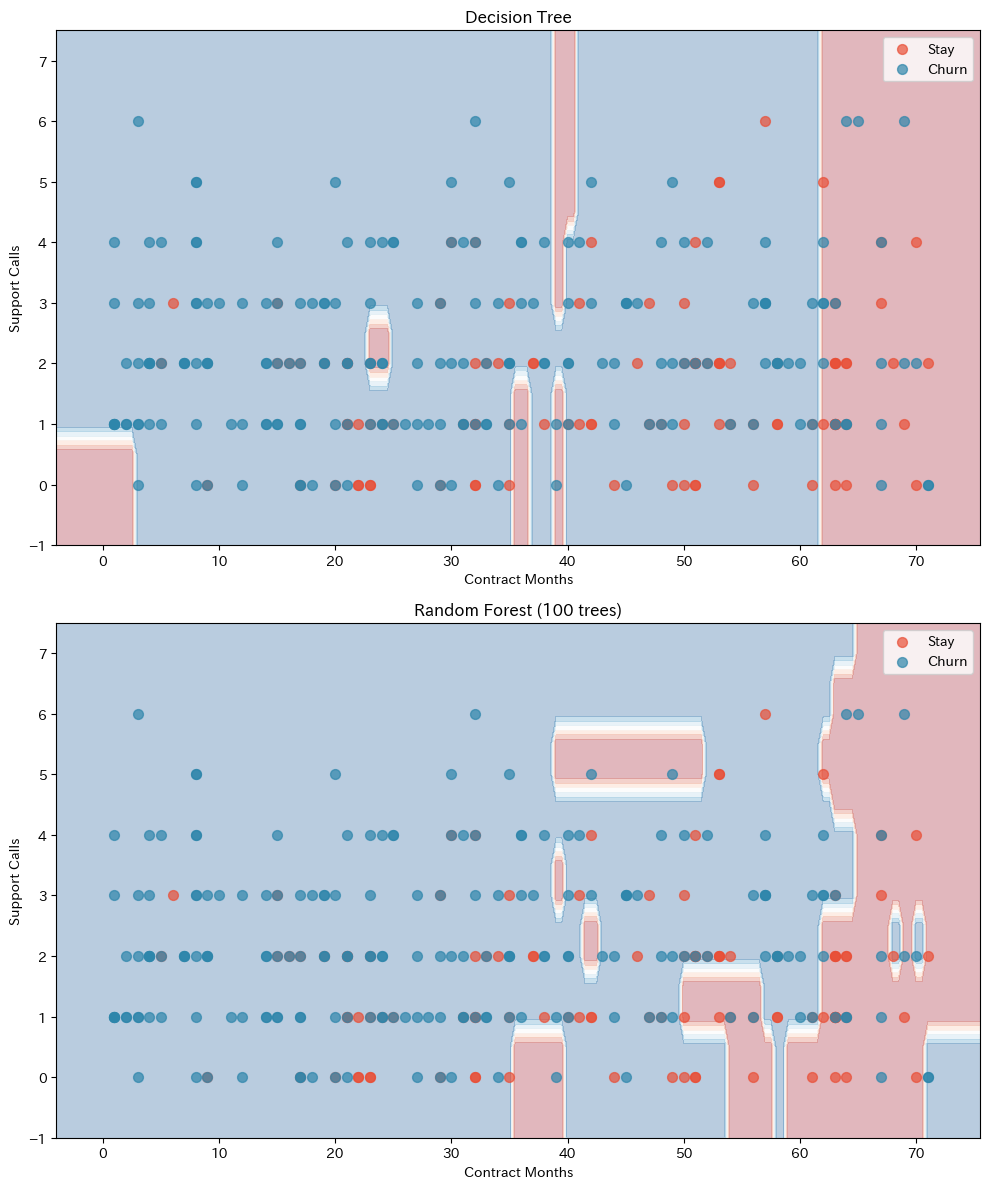
決定木の境界は「角ばった」感じになっているのに対し、ランダムフォレストの境界はより「滑らか」になっています。

これは、多数の木の予測を平均することで、個々の木の極端な分岐が緩和されるためです。

 

ランダムフォレストの主要パラメータ

ランダムフォレストを使う際に調整する主なパラメータを紹介します。

パラメータ名	意味	役割・調整の考え方
n_estimators（木の本数）	ランダムフォレストを構成する決定木の本数	本数を増やすほど予測は安定するが、計算時間も増加する。実務では 100〜500本程度 がよく使われる。
max_depth（最大深さ）	各決定木がどこまで分岐を繰り返すかを制御	None にすると制限なしで成長する。深くなりすぎると過学習しやすいため、必要に応じて上限を設定する。
max_features（分岐時に使う特徴量数）	各ノードの分岐で、候補としてランダムに選ばれる特徴量の数	分類問題ではデフォルトの 'sqrt'（全特徴量数の平方根）がよく使われる。決定木同士のばらつきを生み、汎化性能の向上につながる。
min_samples_split（分割に必要な最小サンプル数）	ノードをさらに分割するために必要な最小サンプル数	値を大きくすると、データの少ないノードでの分割が抑えられ、モデルが単純になり過学習を防ぎやすくなる。
min_samples_leaf（葉に含まれる最小サンプル数）	葉ノードに必ず含まれていなければならない最小サンプル数	葉が極端に小さくなるのを防ぐパラメータ。予測のばらつきを抑え、安定した推定につながる。

 

パラメータを調整してみましょう。

以下、コードです。

# パラメータを調整したランダムフォレスト
rf_tuned = RandomForestClassifier(
    n_estimators=200,     # 木の本数
    max_depth=10,         # 最大深さ
    min_samples_split=10, # 分割に必要な最小サンプル数
    min_samples_leaf=5,   # 葉に含まれる最小サンプル数
    max_features='sqrt',  # 分岐時に使う特徴量数
    random_state=42
)
rf_tuned.fit(X_train, y_train)

print("【パラメータ調整後のランダムフォレスト】")
print(
    f"訓練データ正解率: "
    f"{accuracy_score(y_train, rf_tuned.predict(X_train))*100:.1f}%"
)
print(
    f"テストデータ正解率: "
    f"{accuracy_score(y_test, rf_tuned.predict(X_test))*100:.1f}%"
)

 

以下、実行結果です。

【パラメータ調整後のランダムフォレスト】
訓練データ正解率: 85.9%
テストデータ正解率: 77.0%

 

パラメータを調整することで、さらに性能が向上することがあります。

ただし、ランダムフォレストは比較的頑健で、デフォルト設定でも良い結果が得られることが多いです。

 

予測確率を活用しよう

ランダムフォレストは、単純な分類だけでなく予測確率も出力できます。

これは、各決定木が出力したクラスごとの予測確率を平均することで計算されます。

以下、コードです。

# 予測確率を取得
y_prob = rf_model.predict_proba(X_test)

# 最初の10人の予測確率を表示
print("【テストデータの予測確率（最初の10人）】")
print("-" * 60)
print(f"{'継続確率':>9} {'離脱確率':>9} {'予測':>6} {'実際':>6}")
print("-" * 60)

for i in range(10):
    prob_stay = y_prob[i, 0]
    prob_churn = y_prob[i, 1]
    pred = "Churn" if prob_churn > 0.5 else "Stay"
    actual = "Churn" if y_test[i] == 1 else "Stay"
    print(
        f"{prob_stay:>12.1%} {prob_churn:>12.1%} "
        f"{pred:>8} {actual:>8}"
    )

 

以下、実行結果です。

【テストデータの予測確率（最初の10人）】
------------------------------------------------------------
     継続確率      離脱確率     予測     実際
------------------------------------------------------------
       60.0%        40.0%     Stay    Churn
        1.0%        99.0%    Churn    Churn
       48.0%        52.0%    Churn    Churn
       14.0%        86.0%    Churn    Churn
        8.0%        92.0%    Churn    Churn
       73.0%        27.0%     Stay     Stay
       74.0%        26.0%     Stay     Stay
       42.0%        58.0%    Churn     Stay
       28.0%        72.0%    Churn     Stay
       44.0%        56.0%    Churn     Stay

 

予測確率を使うと、「離脱リスクが高い顧客」を特定してターゲティングキャンペーンを行うなど、より細かな施策が可能になります。

たとえば「離脱確率70%以上の顧客」にだけ特別な割引を提供する、といった使い方ができます。

 

Out-of-Bag（OOB）スコア

ランダムフォレストには OOBスコア という便利な機能があります。

ブートストラップサンプリングでは、各決定木の学習に使われなかったデータ（Out-of-Bag データ）が自然に発生します。

この OOB データを使って、その木が学習していないデータに対する予測を行い、それらを集約することでモデルの性能を評価できます。

これが OOB（Out-of-Bag）評価です。

OOBスコアを使えば、テストデータを別途用意しなくても、ランダムフォレストの汎化性能を推定できます。

では、実際に実施してみます。

以下、コードです。

# OOBスコアを計算
rf_oob = RandomForestClassifier(
    n_estimators=100, # 木の数
    oob_score=True,   # OOBスコアを計算する
    random_state=42
)
rf_oob.fit(X_train, y_train)

print("【OOBスコア】")
print(f"OOBスコア: {rf_oob.oob_score_*100:.1f}%")
print(
    f"テストデータ正解率: "
    f"{accuracy_score(y_test, rf_oob.predict(X_test))*100:.1f}%"
)

 

以下、実行結果です。

【OOBスコア】
OOBスコア: 75.3%
テストデータ正解率: 74.7%

 

OOBスコアとテストデータの正解率がほぼ一致していることがわかります。

OOBスコアは、クロスバリデーションの代わりとして使うこともできます。

 

決定木からランダムフォレストへの進化

ここまでの内容を整理して、決定木からランダムフォレストへの進化を確認しましょう。

以下、コードです。

# 各モデルの性能比較
models = {
    'Decision Tree (no limit)': DecisionTreeClassifier(
        random_state=42
    ),
    'Decision Tree (max_depth=10)': DecisionTreeClassifier(
        max_depth=10, 
        random_state=42
    ),
    'Random Forest (10 trees)': RandomForestClassifier(
        max_depth=10, 
        n_estimators=10,
        random_state=42
    ),
    'Random Forest (100 trees)': RandomForestClassifier(
        max_depth=10, 
        n_estimators=100,
        random_state=42
    ),
}

print("【モデル性能比較】")
print("-" * 65)
print(f"{'モデル':<30} {'訓練精度':>8} {'テスト精度':>8}")
print("-" * 65)

for name, model in models.items():
    model.fit(X_train, y_train)
    train_acc = accuracy_score(y_train, model.predict(X_train))
    test_acc = accuracy_score(y_test, model.predict(X_test))
    print(f"{name:<30} {train_acc:>12.1%} {test_acc:>12.1%}")

 

以下、実行結果です。

【モデル性能比較】
-----------------------------------------------------------------
モデル                                訓練精度    テスト精度
-----------------------------------------------------------------
Decision Tree (no limit)             100.0%        68.0%
Decision Tree (max_depth=10)          96.3%        70.0%
Random Forest (10 trees)              96.3%        72.7%
Random Forest (100 trees)             98.4%        75.0%

 

この結果から、以下のことがわかります。

深さ制限なしの決定木は訓練精度が非常に高いですが、テスト精度との差が大きく、過学習しています。

深さを制限した決定木は過学習が軽減されていますが、訓練精度も下がっています。

ランダムフォレストは訓練精度とテスト精度の差が小さく、バランスの取れた学習ができています。

 

実務でのランダムフォレスト活用

最後に、実務でランダムフォレストを使う際のポイントをまとめます。

強みとして、過学習に強いため、パラメータ調整が比較的容易です。

特徴量重要度が計算でき、ビジネスインサイトが得られます。欠損値やカテゴリ変数にも比較的頑健です。並列計算が可能で、大規模データにも対応できます。

弱みとして、個々の木の解釈が難しく、「なぜその予測になったか」の説明が複雑になります。

決定木に比べて計算コストが高くなります。非常に高次元なデータでは、他の手法（勾配ブースティングなど）に劣ることがあります。

使いどころとしては、特徴量の数が多い分類・回帰問題、特徴量重要度を知りたい場合、まずベースラインとして試したい場合に適しています。

 

まとめ

今回学んだことを振り返りましょう。

アンサンブル学習は、複数のモデルを組み合わせて、より強力なモデルを作る手法です。「三人寄れば文殊の知恵」の機械学習版と言えます。

バギングは、ブートストラップサンプリングで複数のデータセットを作り、それぞれで学習したモデルの予測を集約する手法です。これにより、バリアンス（予測のブレ）を削減できます。

ランダムフォレストは、バギングに加えて、各分岐で使用する特徴量もランダムに選択することで、木の多様性をさらに高めた手法です。100本以上の決定木を「森」として束ねることで、1本の木では得られない安定性と精度を実現します。

特徴量重要度は、ランダムフォレストの大きな魅力です。各特徴量が予測にどれだけ貢献しているかを定量的に評価でき、ビジネス上の意思決定に活用できます。

次回は最終回「混同行列と評価指標の使い分け」です。

ここまで「正解率」でモデルの性能を評価してきましたが、実は正解率だけでは不十分な場合があります。「スパム検出」「病気の診断」「不正取引検知」など、問題の性質によって重視すべき指標が異なります。

混同行列、適合率、再現率、F1スコア、ROC曲線、AUCといった評価指標を学び、「本当に良いモデルとは何か」を考えましょう。