これまでの2回では、1つの変数について「代表値」や「ばらつき」を分析してきました。
しかし、現実のデータ分析では「2つの変数の関係」を知りたい場面がたくさんあります。
たとえば、こんな疑問を持ったことはありませんか?
- 勉強時間を増やせば、テストの点数は上がるのか?
- 気温が上がると、アイスクリームの売上は伸びるのか?
- 広告費を増やせば、売上は増えるのか?
- 睡眠時間と集中力には関係があるのか?
これらはすべて「2つの変数の関係」についての問いです。
今回学ぶ相関係数を使えば、この「つながりの強さ」を-1から+1の数値で表現できるようになります。
Contents
- まずは散布図で「目で見る」
- 2つの変数の関係を可視化する
- さまざまな相関のパターン
- 共分散:2つの変数が「一緒に動く」度合い
- 共分散の考え方
- 共分散の数式
- 共分散の問題点:単位に依存する
- 相関係数:-1から+1に標準化する
- 相関係数の定義
- 相関係数の解釈
- さまざまな相関係数を体験する
- 相関係数と散布図の対応
- 複数の変数間の相関を調べる
- 相関行列とヒートマップ
- 相関係数の落とし穴
- 落とし穴①:外れ値の影響
- 落とし穴②:非線形な関係は検出できない
- 落とし穴③:相関と因果は違う
- 相関係数を正しく使うためのチェックリスト
- ステップ1:まず散布図で関係を確認する
- ステップ2:相関係数を計算してよいかを判断する
- ステップ3:相関係数を計算し、数値を解釈する
- 最後に必ず添える注意点
- まとめ
まずは散布図で「目で見る」
2つの変数の関係を可視化する
2つの変数の関係を調べるとき、最初にやるべきことは散布図を描くことです。
散布図は、一方の変数を横軸、もう一方を縦軸にとり、各データを点としてプロットしたグラフです。
10人の学生について「勉強時間」と「テストの点数」のデータを作成し、散布図で可視化します。
以下、コードです。
import numpy as np
import matplotlib.pyplot as plt
# 勉強時間(時間)とテストの点数
study_hours = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
test_scores = np.array([35, 45, 50, 55, 65, 70, 75, 82, 88, 95])
# 散布図を描く
plt.figure(figsize=(8, 6))
plt.scatter(study_hours, test_scores, s=100)
plt.xlabel('勉強時間(時間)')
plt.ylabel('テストの点数')
plt.title('勉強時間とテストの点数の関係')
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
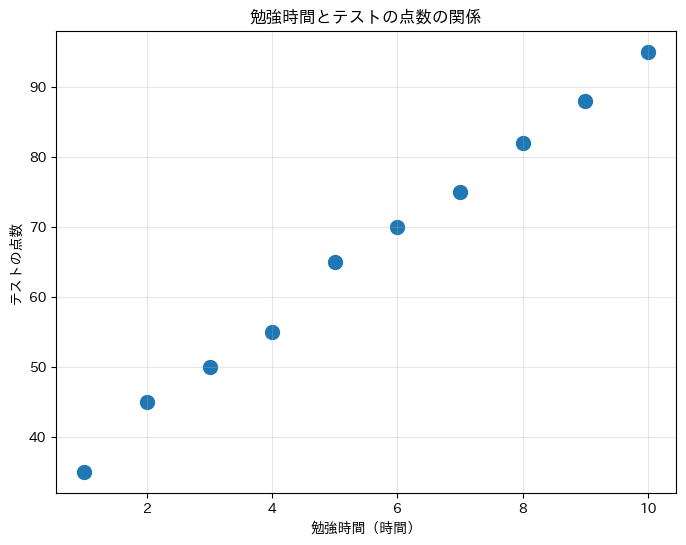
点が左下から右上に向かって並んでいることがわかります。
これは「勉強時間が増えると、テストの点数も増える傾向がある」ことを示しています。
このような関係を正の相関と呼びます。
さまざまな相関のパターン
正の相関、負の相関、相関なしの3パターンを並べて比較します。
以下、コードです。
np.random.seed(42)
fig, axes = plt.subplots(3, 1, figsize=(8, 16))
# 正の相関
x1 = np.random.randn(50)
y1 = x1 + np.random.randn(50) * 0.3
axes[0].scatter(x1, y1)
axes[0].set_title('正の相関\n(一方が増えると他方も増える)')
# 負の相関
x2 = np.random.randn(50)
y2 = -x2 + np.random.randn(50) * 0.3
axes[1].scatter(x2, y2)
axes[1].set_title('負の相関\n(一方が増えると他方は減る)')
# 相関なし
x3 = np.random.randn(50)
y3 = np.random.randn(50)
axes[2].scatter(x3, y3)
axes[2].set_title('相関なし\n(関係が見られない)')
plt.tight_layout()
plt.show()
以下、実行結果です。
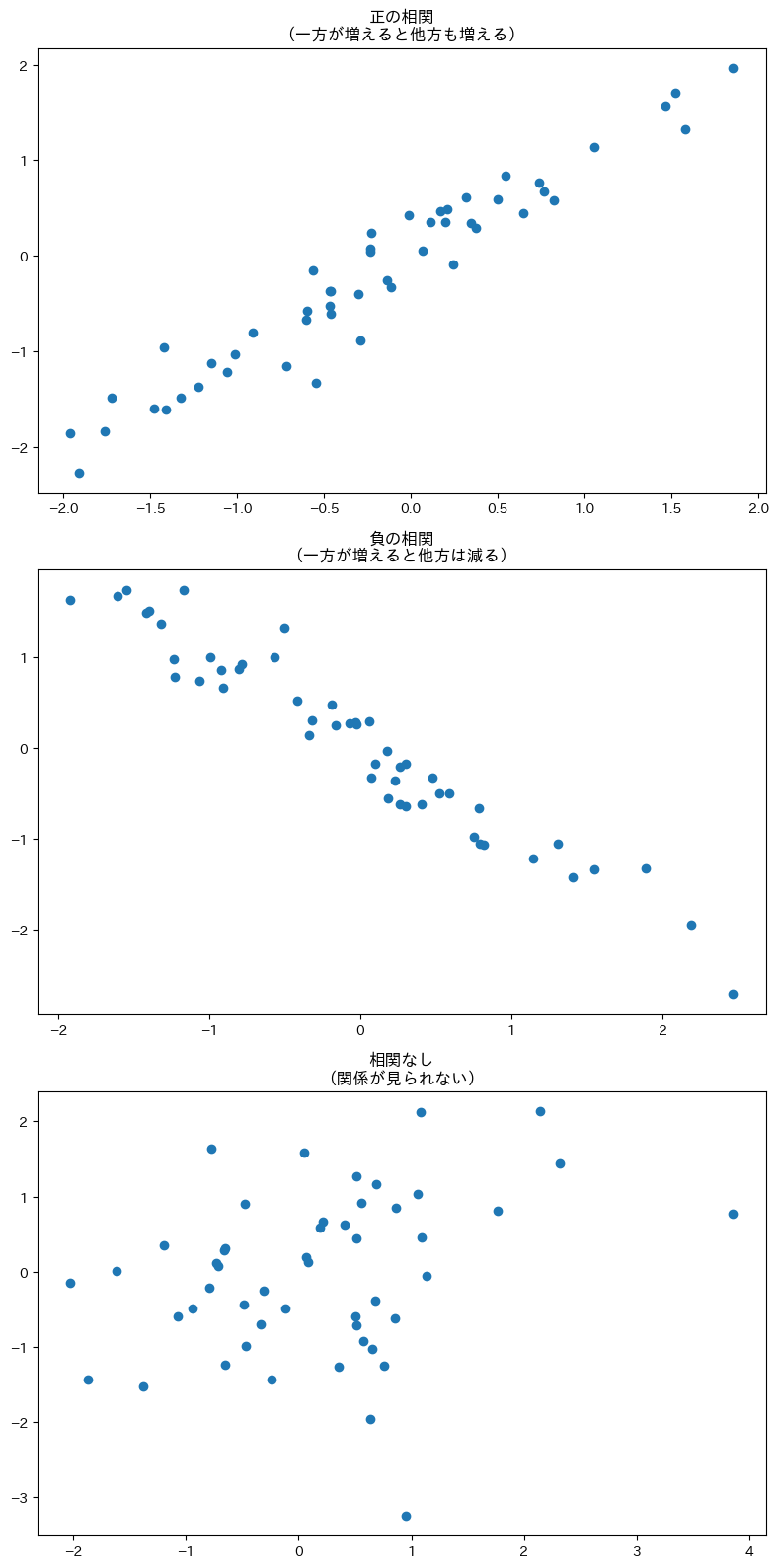
一番上のグラフは右上がり(正の相関)、中央は右下がり(負の相関)、一番下は点がバラバラに散らばっています(相関なし)。
散布図を見れば、2つの変数の関係を直感的に把握できます。
共分散:2つの変数が「一緒に動く」度合い
共分散の考え方
散布図で見た「関係」を数値化するために、まず共分散という概念を導入します。
前回学んだ分散は「1つの変数が平均からどれだけばらついているか」を測りました。
共分散は「2つの変数が一緒にどう動くか」を測ります。
具体的には、以下の手順で計算します。
- STEP 1:各変数について、平均からの偏差を求める
- STEP 2:2つの偏差を掛け合わせる
- STEP 3:その平均を取る
勉強時間とテストの点数の共分散を、手計算の手順で求めます。
以下、コードです。
# データの確認
print("勉強時間:", study_hours)
print("テストの点数:", test_scores)
# 各変数の平均
mean_hours = np.mean(study_hours)
mean_scores = np.mean(test_scores)
print(f"\n勉強時間の平均: {mean_hours}時間")
print(f"テストの点数の平均: {mean_scores}点")
以下、実行結果です。
勉強時間: [ 1 2 3 4 5 6 7 8 9 10] テストの点数: [35 45 50 55 65 70 75 82 88 95] 勉強時間の平均: 5.5時間 テストの点数の平均: 66.0点
勉強時間の平均は5.5時間、テストの点数の平均は66点です。
ここから各データの偏差を計算していきます。
各データについて偏差を計算し、偏差同士を掛け合わせます。
以下、コードです。
# 各変数の偏差
dev_hours = study_hours - mean_hours
dev_scores = test_scores - mean_scores
print("勉強時間の偏差:", dev_hours)
print("テスト点数の偏差:", dev_scores)
# 偏差の積
product = dev_hours * dev_scores
print("\n偏差の積:", product)
以下、実行結果です。
勉強時間の偏差: [-4.5 -3.5 -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 4.5] テスト点数の偏差: [-31. -21. -16. -11. -1. 4. 9. 16. 22. 29.] 偏差の積: [139.5 73.5 40. 16.5 0.5 2. 13.5 40. 77. 130.5]
偏差の積を見てください。ほとんどの値がプラスになっています。
これは「勉強時間が平均より多い人は、点数も平均より高い」傾向があることを示しています。
両方の偏差が同じ符号(両方プラス、または両方マイナス)なら、積はプラスになります。
偏差の積の平均を取って、共分散を求めます。
以下、コードです。NumPyの共分散を求める関数covでも求めています。
# 共分散 = 偏差の積の平均
covariance = np.mean(product)
print(f"共分散: {covariance}")
# NumPyで確認
cov_numpy = np.cov(
study_hours, # 勉強時間のデータ
test_scores, # テスト点数のデータ
ddof=0 # 偏差の分母をN(標本数)にする
)[0, 1] # 共分散行列の(0, 1)成分を取り出す
print(f"NumPyで計算した共分散: {cov_numpy}")
以下、実行結果です。
共分散: 53.3 NumPyで計算した共分散: 53.300000000000004
共分散は49.5と計算されました。この値がプラスなので、「勉強時間とテストの点数には正の関係がある」ことがわかります。
共分散の数式
n 個のデータ (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) の共分散 \text{Cov}(X, Y) は次の式で計算されます。$$
\text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})
$$
この式は「xの偏差とyの偏差を掛け合わせて、その平均を取る」という先ほどの手順をそのまま表しています。
共分散の問題点:単位に依存する
共分散には大きな問題があります。変数の単位やスケールによって値が変わってしまうのです。
勉強時間を「分」単位に変換して、共分散がどう変わるか確認します。
以下、コードです。
# 時間単位での共分散
cov_hours = np.cov(
study_hours, test_scores, ddof=0
)[0, 1]
# 勉強時間を分単位に変換(1時間 = 60分)
study_minutes = study_hours * 60
# 分単位に変換した場合の共分散
cov_minutes = np.cov(
study_minutes, test_scores, ddof=0
)[0, 1]
print(f"勉強時間(時間)との共分散: {cov_hours}")
print(f"勉強時間(分)との共分散: {cov_minutes}")
以下、実行結果です。
勉強時間(時間)との共分散: 53.300000000000004 勉強時間(分)との共分散: 3198.0
同じデータなのに、単位を変えただけで共分散が60倍になってしまいました。
これでは「共分散が53.3」と言われても、関係が強いのか弱いのか判断できません。
この問題を解決するのが、次に学ぶ相関係数です。
相関係数:-1から+1に標準化する
相関係数の定義
相関係数(ピアソンの積率相関係数)は、共分散を各変数の標準偏差で割って標準化したものです。これにより、必ず-1から+1の範囲に収まるようになります。
$$
r = \frac{\text{Cov}(X, Y)}{\sigma_X \cdot \sigma_Y}
$$
ここで、\sigma_X と \sigma_Y はそれぞれ X と Y の標準偏差です。
相関係数を手計算の手順で求めます。
以下、コードです。
# 各変数の標準偏差
std_hours = np.std(study_hours)
std_scores = np.std(test_scores)
print(f"勉強時間の標準偏差: {std_hours:.2f}")
print(f"テストの点数の標準偏差: {std_scores:.2f}")
# 相関係数 = 共分散 / (標準偏差の積)
correlation = covariance / (std_hours * std_scores)
print(f"\n相関係数: {correlation:.4f}")
以下、実行結果です。
勉強時間の標準偏差: 2.87 テストの点数の標準偏差: 18.60 相関係数: 0.9979
相関係数は1に非常に近い値で、勉強時間とテストの点数には「非常に強い正の相関」があることがわかります。
単位を変えても相関係数は変わらないことを確認します。
以下、コードです。NumPyの相関係数を求めるcorrcoef関数を使います。
# NumPyの corrcoef を使う
corr_hours = np.corrcoef(study_hours, test_scores)[0, 1]
corr_minutes = np.corrcoef(study_minutes, test_scores)[0, 1]
print(f"勉強時間(時間)との相関係数: {corr_hours:.4f}")
print(f"勉強時間(分)との相関係数: {corr_minutes:.4f}")
以下、実行結果です。
勉強時間(時間)との相関係数: 0.9979 勉強時間(分)との相関係数: 0.9979
時間でも分でも、相関係数は同じ0.9945です。
標準化によって単位の影響が消え、純粋に「関係の強さ」だけを比較できるようになりました。
相関係数の解釈
相関係数 r の値は以下のように解釈します。
| r の値 | 解釈 |
|---|---|
| r = 1 | 完全な正の相関(完全に右上がりの直線上に並ぶ) |
| 0.7 \leq r < 1 | 強い正の相関 |
| 0.4 \leq r < 0.7 | 中程度の正の相関 |
| 0.2 \leq r < 0.4 | 弱い正の相関 |
| -0.2 < r < 0.2 | ほとんど相関なし |
| -0.4 < r \leq -0.2 | 弱い負の相関 |
| -0.7 < r \leq -0.4 | 中程度の負の相関 |
| -1 < r \leq -0.7 | 強い負の相関 |
| r = -1 | 完全な負の相関(完全に右下がりの直線上に並ぶ) |
ただし、この基準は分野によって異なります。
文脈によっては0.5で「強い」とされることもあれば、0.9でも「まだ弱い」とされることもあります。
文脈に応じて判断しましょう。
さまざまな相関係数を体験する
相関係数と散布図の対応
相関係数の値ごとに散布図がどう見えるか、複数のパターンを並べて確認します。
以下、コードです。
np.random.seed(42)
# 相関係数 r を指定して、相関のあるデータを生成する関数
def generate_correlated_data(r, n=100):
x = np.random.randn(n)
y = (
r * x +
np.sqrt(1 - r**2) *
np.random.randn(n)
)
return x, y
# 相関係数 r を変えて、散布図を描く
fig, axes = plt.subplots(4, 2, figsize=(10, 15))
cs = [1.0, 0.8, 0.5, 0.2, -0.2, -0.5, -0.8, -1.0]
for ax, r in zip(axes.flatten(), cs):
x, y = generate_correlated_data(r)
ax.scatter(x, y, alpha=0.6)
ax.set_title(f'r = {r}')
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
plt.tight_layout()
plt.show()
以下、実行結果です。
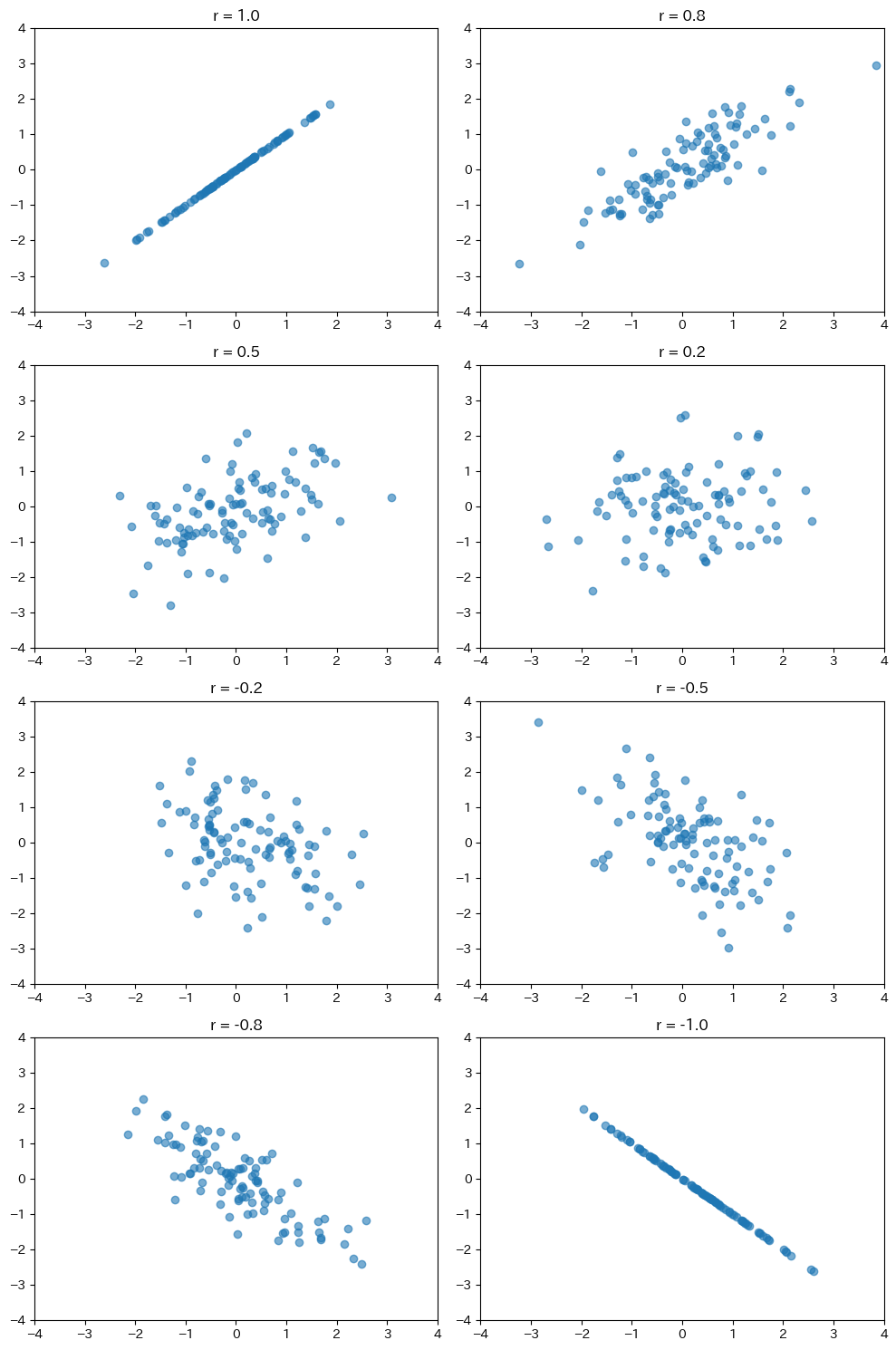
相関係数が1や-1に近いほど、点が直線状にきれいに並びます。
0に近づくにつれて点が散らばり、関係性が見えにくくなります。
この図を頭に入れておくと、相関係数の値から散布図のイメージが浮かぶようになります。
複数の変数間の相関を調べる
相関行列とヒートマップ
実際のデータ分析では、3つ以上の変数を同時に扱うことがほとんどです。
そのとき便利なのが相関行列です。すべての変数のペアについて相関係数を計算し、表の形にまとめたものです。
学生の「勉強時間」「睡眠時間」「テストの点数」「ゲーム時間」の4変数について、相関行列を計算します。
以下、コードです。
import pandas as pd
import numpy as np
np.random.seed(42)
# サンプルデータを作成
n = 50
study = np.random.uniform(1, 10, n)
sleep = np.random.uniform(5, 9, n)
game = np.random.uniform(0, 6, n)
score = (
40 + 5 * study +
3 * sleep - 2 * game +
np.random.randn(n) * 5
)
# DataFrameにまとめる(列名を英数字に変更)
df = pd.DataFrame({
'study_hours': study, # 勉強時間
'sleep_hours': sleep, # 睡眠時間
'game_hours': game, # テストの点数
'test_score': score # ゲーム時間
})
print(df.head(10))
以下、実行結果です。
study_hours sleep_hours game_hours test_score 0 4.370861 8.878339 0.188575 87.150366 1 9.556429 8.100531 3.818462 105.954549 2 7.587945 8.757996 1.886136 100.267884 3 6.387926 8.579309 3.051424 85.731322 4 2.404168 7.391600 5.445399 69.018955 5 2.403951 8.687497 1.495753 78.850403 6 1.522753 5.353970 2.462298 62.706237 7 8.795585 5.783931 4.533307 87.716170 8 6.410035 5.180909 1.372789 91.861297 9 7.372653 6.301321 0.461879 87.834216
4つの変数を持つデータフレームが作成されました。
これらの変数間の関係を相関行列で調べていきます。
pandasの corr() メソッドで相関行列を計算します。
以下、コードです。
# 相関行列を計算
correlation_matrix = df.corr()
print("【相関行列】")
print(correlation_matrix.round(3))
以下、実行結果です。
【相関行列】
study_hours sleep_hours game_hours test_score
study_hours 1.000 0.062 -0.122 0.880
sleep_hours 0.062 1.000 -0.111 0.314
game_hours -0.122 -0.111 1.000 -0.370
test_score 0.880 0.314 -0.370 1.000
対角線上は自分自身との相関なので必ず1.0です。
表の他の部分を見ると、「勉強時間(study_hours)とテスト点数(test_score)」の相関が0.9程度で強い正の相関、「ゲーム時間(game_hours)とテスト点数(test_score)」は負の相関(ゲームが多いと点数が下がる傾向)があることがわかります。
相関行列をヒートマップで可視化します。色の濃淡で相関の強さが一目でわかります。
以下、コードです。
import seaborn as sns
plt.figure(figsize=(8, 6))
sns.heatmap(
correlation_matrix, # 相関行列のデータ
annot=True, # セル内に値を表示
cmap='coolwarm', # カラーマップを指定
center=0, # カラーマップの中心を0に設定
vmin=-1, vmax=1, # カラーマップの範囲を[-1, 1]に設定
fmt='.2f', # セル内の値の表示形式を指定
square=True # セルを正方形にする
)
plt.title('相関行列のヒートマップ')
plt.tight_layout()
plt.show()
以下、実行結果です。
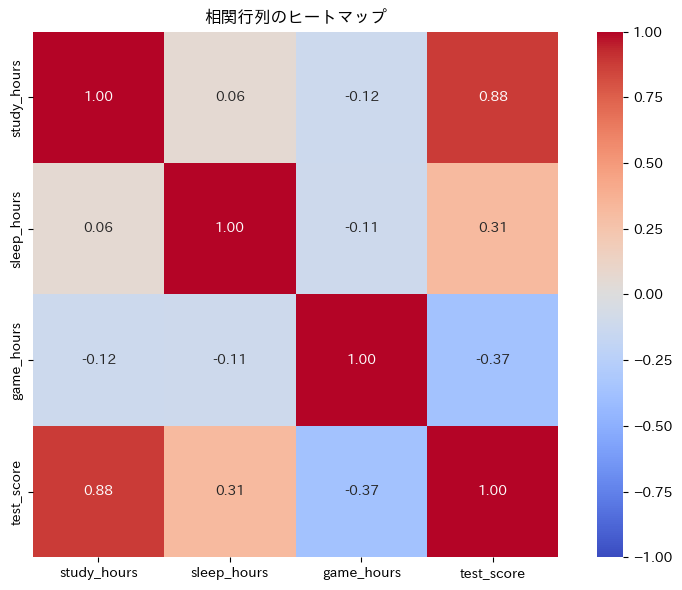
赤色が正の相関、青色が負の相関を示しています。
色が濃いほど相関が強いことを意味します。
このヒートマップを見れば、どの変数とどの変数が強く関係しているかを瞬時に把握できます。
すべての変数ペアの散布図を一度に描画する「ペアプロット」も便利です。
以下、コードです。
sns.pairplot(df)
plt.suptitle('変数間の散布図行列', y=1.02)
plt.show()
以下、実行結果です。
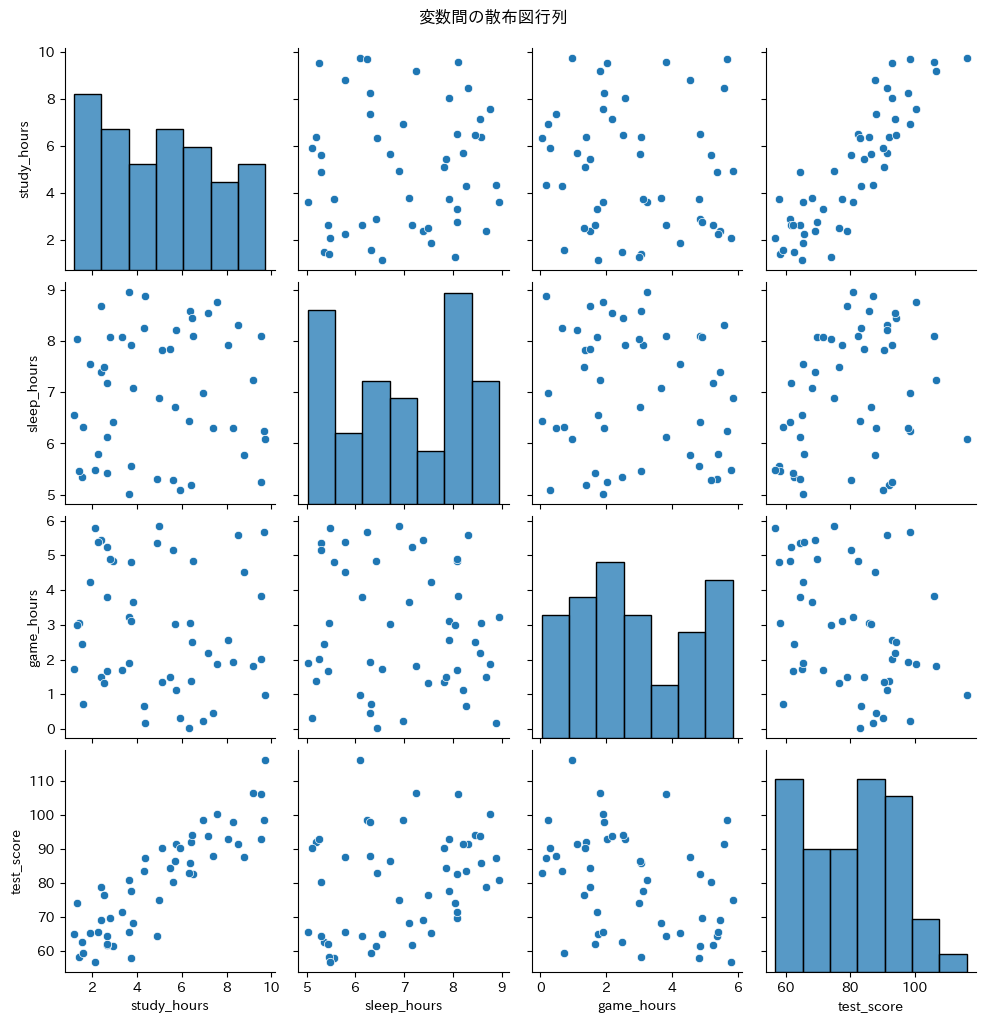
対角線にはヒストグラム(各変数の分布)、それ以外には散布図が表示されます。
「勉強時間(study_hours)とテスト点数(test_score)」の散布図を見ると、右上がりの傾向がはっきり見えます。
相関行列の数値と合わせて見ることで、データの全体像を把握できます。
相関係数の落とし穴
落とし穴①:外れ値の影響
相関係数は平均と同様に、外れ値の影響を強く受けます。
1つの外れ値が相関係数をどれだけ変えてしまうか確認します。
以下、コードです。
# 相関がないデータ
np.random.seed(42)
x = np.random.randn(20)
y = np.random.randn(20)
# 外れ値を1つ追加
x_outlier = np.append(x, 5)
y_outlier = np.append(y, 5)
fig, axes = plt.subplots(2, 1, figsize=(8, 12))
# 外れ値なし
axes[0].scatter(x, y)
axes[0].set_title(
f'外れ値なし: '
f'r = {np.corrcoef(x, y)[0,1]:.3f}'
)
axes[0].set_xlim(-3, 6)
axes[0].set_ylim(-3, 6)
# 外れ値あり
axes[1].scatter(x_outlier, y_outlier)
axes[1].scatter(
5, 5,
color='red', s=200, marker='x',
label='外れ値'
)
axes[1].set_title(
f'外れ値あり: '
f'r = {np.corrcoef(x_outlier, y_outlier)[0,1]:.3f}'
)
axes[1].set_xlim(-3, 6)
axes[1].set_ylim(-3, 6)
axes[1].legend()
plt.tight_layout()
plt.show()
以下、実行結果です。
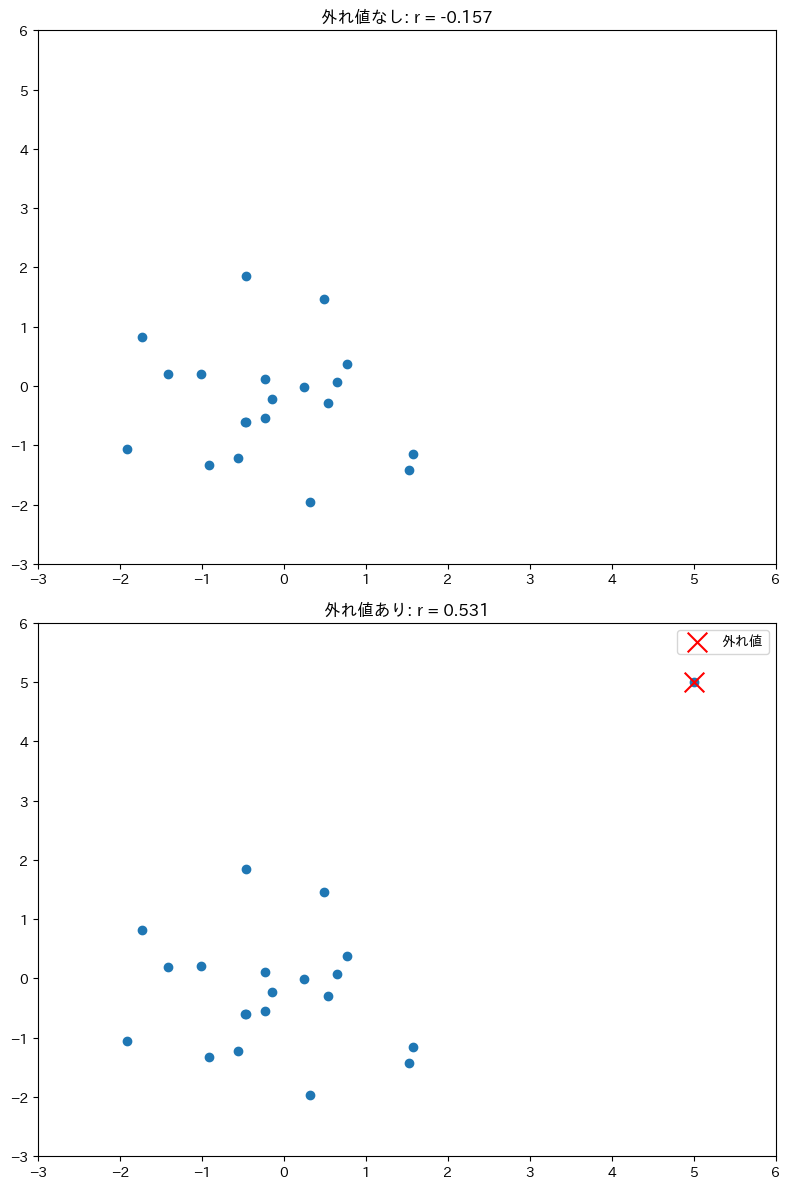
元のデータでは相関係数がほぼ0(相関なし)でしたが、右上に外れ値を1つ追加しただけで、相関係数が0.5程度に跳ね上がりました。
相関係数を報告する前に、必ず散布図で外れ値の有無を確認しましょう。
落とし穴②:非線形な関係は検出できない
ピアソンの相関係数は直線的な関係しか捉えられません。
曲線的な関係がある場合、相関係数は低くなってしまいます。
完全な二次関数の関係があるのに、相関係数が0になる例を見てみます。
以下、コードです。
# 完全な二次関数の関係
x = np.linspace(-3, 3, 100)
y = x ** 2 # y = x^2
plt.figure(figsize=(8, 5))
plt.scatter(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title(
f'y = x² の関係\n相関係数 '
f'r = {np.corrcoef(x, y)[0,1]:.3f}'
)
plt.show()
以下、実行結果です。
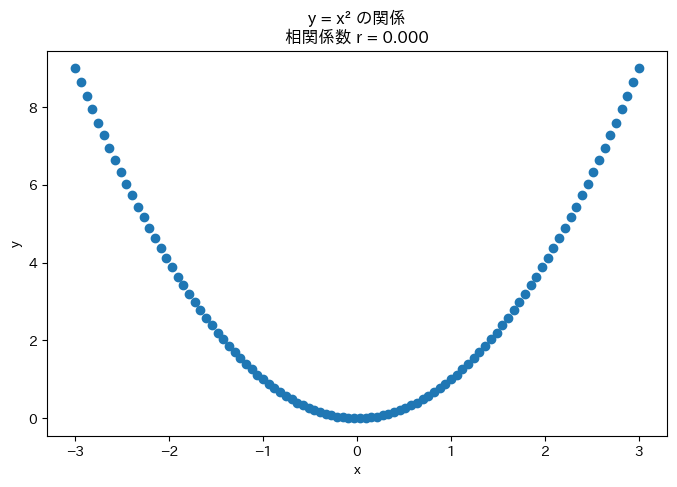
y = x^2 という完璧な関係があるにもかかわらず、相関係数はほぼ0です。
これは相関係数が「直線的な関係」しか測れないためです。
散布図を見れば明らかに関係があるのに、相関係数だけを見ると見落としてしまいます。必ず散布図とセットで確認することが大切です。
落とし穴③:相関と因果は違う
これは最も重要な注意点です。相関があっても、因果関係があるとは限りません。
たとえば、「アイスクリームの売上」と「水難事故の件数」には強い正の相関があります。
しかし、アイスを食べると溺れるわけではありません。
両方とも「気温」という第三の変数に影響されているだけです。このような変数を交絡変数(こうらくへんすう)と呼びます。
見せかけの相関(疑似相関)の例を作成します。
以下、コードです。
np.random.seed(42)
# 真の原因:気温
temperature = np.random.uniform(15, 35, 30)
# 気温に影響される2つの変数
ice_cream_sales = (
100 + 10 * temperature +
np.random.randn(30) * 20
)
drowning_accidents = (
-5 + 0.5 * temperature +
np.random.randn(30) * 2
)
# 見せかけの相関
r = np.corrcoef(ice_cream_sales, drowning_accidents)[0, 1]
plt.figure(figsize=(8, 5))
plt.scatter(ice_cream_sales, drowning_accidents)
plt.xlabel('アイスクリームの売上')
plt.ylabel('水難事故の件数')
plt.title(
f'アイスの売上と水難事故\n相関係数 '
f'r = {r:.3f}\n(両方とも気温に影響されている)'
)
plt.show()
以下、実行結果です。
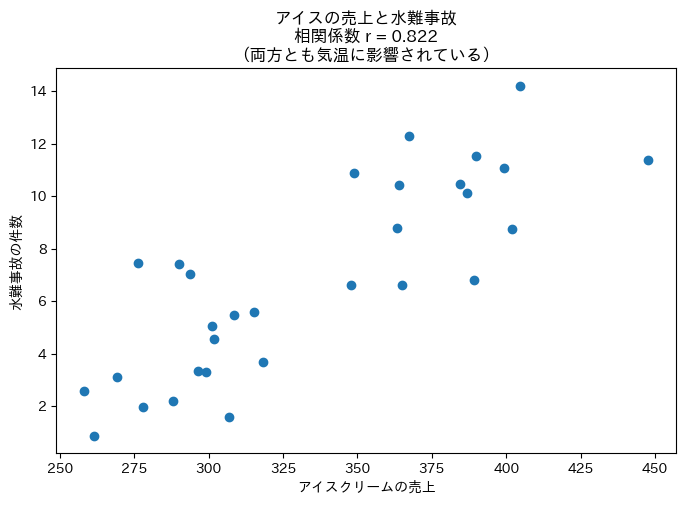
相関係数は0.8程度と高いですが、これは因果関係ではありません。
「アイスの販売を禁止すれば水難事故が減る」という結論は明らかに誤りです。
相関関係から因果関係を主張するには、実験や追加の分析が必要です。
相関係数を正しく使うためのチェックリスト
相関係数を計算・解釈する際には、いきなり数値を見るのではなく、必ず事前の確認を行うことが重要です。
以下は、良い分析の基本的な流れです。
ステップ1:まず散布図で関係を確認する
最初に、2つの変数の関係を散布図で確認します。
この例では、横軸に X、縦軸に Y をとった散布図を描くと、点は全体として右上がりに並んでいます。
この段階で、次の点を目で確認します。
- 極端に離れた点(外れ値)が存在しないか
- 点の並び方が、おおよそ直線的に見えるか
- 曲線的な関係や、グループ分かれが起きていないか
ステップ2:相関係数を計算してよいかを判断する
散布図を確認した結果……
- 明らかな外れ値は見当たらない
- 変数同士の関係は直線的に見える
……と判断できた場合にのみ、相関係数を計算します。
この確認を行わずに、数値だけで相関の強さを判断するのは危険です。
相関係数は「直線的な関係の強さ」を測る指標であり、前提条件を満たしていない場合、誤解を招く結果になることがあります。
ステップ3:相関係数を計算し、数値を解釈する
上記の確認を踏まえたうえで相関係数を計算すると、このデータでは 約 0.998 という値が得られます。
これは……
- 0 に近い → ほとんど関係がない
- ±1 に近い → 非常に強い関係がある
……という相関係数の性質から見て、非常に強い正の相関があると解釈できます。
最後に必ず添える注意点
ただし、どれほど相関係数が高くても、それだけで因果関係を結論づけることはできません。
- 相関があること
- 片方が原因で、もう片方が結果であること
この2つは別の話です。
相関係数を使う際には、必ず「これは相関であり、因果関係を示すものではない」という一文を添えるようにしましょう。
まとめ
今回は、2つの変数の関係を数値化する「相関係数」について学びました。
相関係数を理解するために、まず共分散という概念を導入しました。
共分散は「2つの変数が一緒にどう動くか」を測る指標で、各変数の偏差を掛け合わせた平均として計算されます。しかし、共分散は変数の単位やスケールに依存してしまうため、そのままでは関係の強さを比較できません。
そこで登場するのが相関係数(ピアソンの積率相関係数)です。
共分散を各変数の標準偏差で割って標準化することで、必ず-1から+1の範囲に収まるようになります。+1に近いほど強い正の相関(一方が増えると他方も増える)、-1に近いほど強い負の相関(一方が増えると他方は減る)、0に近いほど相関がないことを意味します。
ただし、相関係数にはいくつかの落とし穴があります。
外れ値があると値が大きく歪むこと、直線的でない関係は検出できないこと、そして何より相関があっても因果関係があるとは限らないことです。
アイスクリームの売上と水難事故の例のように、第三の変数(交絡変数)が両方に影響している場合、見せかけの相関が生じます。相関係数を報告する際は、必ず散布図で確認し、因果関係との違いを意識しましょう。

