Pythonで動かして身につける 統計学はじめの一歩
— 第5回 —
「差がある」と言えるのか — t検定とp値の正しい読み方

43
Pythonで動かして身につける 統計学はじめの一歩— 第5回 —「差がある」と言えるのか — t検定とp値の正しい読み方

ある学習塾で、新しい教材Bを試験的に導入しました。

1ヶ月後、従来の教材Aを使ったクラスと、新教材Bを使ったクラスのテスト結果を比較したところ、次のような結果が得られました。

  • 教材Aクラス（25人）：平均68点
  • 教材Bクラス（28人）：平均73点

教材Bクラスの方が5点高いですね。

これを見た塾長は「新教材の効果があった！全クラスに導入しよう！」と言います。

しかし、ちょっと待ってください。この5点の差は、本当に教材の効果なのでしょうか？

それとも、たまたまこのクラスに成績の良い生徒が多かっただけかもしれません。

このような「観測された差が本物かどうか」を判断する方法が、今回学ぶ仮説検定です。

仮説検定の中でも最も基本的なt検定を使い、「差がある」と言えるための統計的な根拠を学んでいきます。

仮説検定の考え方：「差がない」を否定する

　背理法的なアプローチ

仮説検定の考え方は、数学の背理法に似ています。

「差がある」ことを直接証明するのではなく、「差がない」と仮定して、その仮定のもとで観測されたデータがどれくらい珍しいかを調べます。

もし非常に珍しければ、「差がない」という仮定を棄却し、「差がある」と結論づけます。

具体的な手順は次の通りです。

  • STEP 1：「差がない」という仮説を立てる（帰無仮説）
  • STEP 2：その仮説のもとで、観測されたデータが起きる確率を計算する（p値）
  • STEP 3：p値が十分に小さければ、帰無仮説を棄却する
  • STEP 4：「差がある」と結論づける（対立仮説を採用）

 

　帰無仮説と対立仮説

帰無仮説（null hypothesis, H_0）とは、「効果がない」「差がない」という仮説。検定で棄却することを目指す仮説です。

対立仮説（alternative hypothesis, H_1）とは、「効果がある」「差がある」という仮説。帰無仮説が棄却されたときに採用される仮説です。

先ほどの教材の例では、次のように設定します。

  • H_0：教材Aと教材Bで平均点に差はない（\mu_A = \mu_B）
  • H_1：教材Aと教材Bで平均点に差がある（\mu_A \neq \mu_B）

 

サンプルデータの作成

教材AクラスとBクラスのテスト結果データを作成し、基本統計量を確認します。

以下、コードです。

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import japanize_matplotlib

np.random.seed(42)

# 教材Aクラス（従来）：平均65点、標準偏差10点
class_A = np.random.normal(
    loc=65, 
    scale=10,
    size=25
)
# 教材Bクラス（新教材）：平均72点、標準偏差10点
class_B = np.random.normal(
    loc=72, 
    scale=10, 
    size=28
)
print("【2つのクラスの成績データ】")
print(
    f"教材Aクラス: n={len(class_A)}, "
    f"平均={np.mean(class_A):.1f}点, "
    f"標準偏差={np.std(class_A, ddof=1):.1f}"
)
print(
    f"教材Bクラス: n={len(class_B)}, "
    f"平均={np.mean(class_B):.1f}点, "
    f"標準偏差={np.std(class_B, ddof=1):.1f}"
)
print(
    "\n平均の差: "
    f"{np.mean(class_B) - np.mean(class_A):.1f}点"
)

 

以下、実行結果です。

【2つのクラスの成績データ】
教材Aクラス: n=25, 平均=63.4点, 標準偏差=9.6
教材Bクラス: n=28, 平均=69.2点, 標準偏差=8.8

平均の差: 5.8点

 

教材Bクラスの平均が数点高いことがわかります。

しかし、この差が「偶然」なのか「本当の差」なのかは、数字を見ただけでは判断できません。

2つのクラスの分布をヒストグラムで可視化します。

以下、コードです。

plt.figure(figsize=(10, 5))

# 教材Aのヒストグラムを描画
plt.hist(
    class_A, bins=10, 
    alpha=0.7, edgecolor='white',
    label=f'教材A (平均{np.mean(class_A):.1f}点)', 
)
# 教材Bのヒストグラムを描画
plt.hist(
    class_B, bins=10, 
    alpha=0.7, edgecolor='white',
    label=f'教材B (平均{np.mean(class_B):.1f}点)'
)
# 教材Aの平均を垂直線で表示
plt.axvline(
    np.mean(class_A), 
    color='blue', linestyle='--', linewidth=2
)
# 教材Bの平均を垂直線で表示
plt.axvline(
    np.mean(class_B), 
    color='orange', linestyle='--', linewidth=2
)
plt.xlabel('点数')
plt.ylabel('人数')
plt.title('2つのクラスのテスト結果分布')
plt.legend()
plt.show()

 

以下、実行結果です。

 

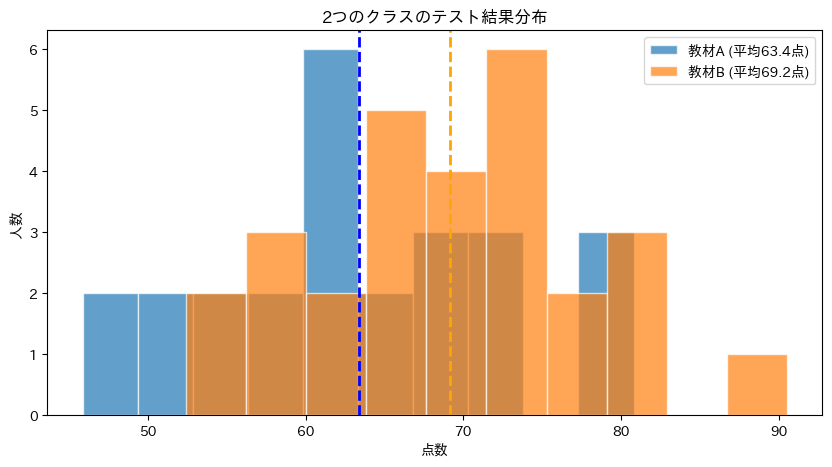
2つの分布はある程度重なっていますが、教材Bクラス（オレンジ）の方が全体的に右寄り（高得点側）にあるように見えます。

この「見た目の差」が統計的に意味のある差かどうかを、t検定で判断します。

 

t検定の実行：2つの平均を比較する

　独立2標本t検定

2つの独立したグループの平均を比較するには、独立2標本t検定を使います。

Pythonでは scipy.stats.ttest_ind() で簡単に実行できます。

t検定を実行し、結果を確認します。

以下、コードです。

# 独立2標本t検定の実行
t_statistic, p_value = stats.ttest_ind(
    class_A, # 教材Aの点数データ
    class_B  # 教材Bの点数データ
)

print("【t検定の結果】")
print(f"t統計量: {t_statistic:.4f}")
print(f"p値: {p_value:.4f}")

 

以下、実行結果です。

【t検定の結果】
t統計量: -2.2960
p値: 0.0258

 

2つの値が出力されました。

t統計量は「差の大きさ」を標準化した値で、絶対値が大きいほど差が大きいことを意味します。

p値が最も重要で、これが「帰無仮説のもとで、このようなデータが得られる確率」を表します。

 

　p値による判断

一般的に、p値が0.05未満であれば「統計的に有意」と判断します（この0.05を有意水準と呼びます）。

今回の場合、p値は0.0258です。

p値が0.05より小さいため、「差がない」という帰無仮説を棄却し、「差がある」と結論づけます。

これが仮説検定の基本的な流れです。

 

p値の正しい理解：「確率」の意味

　p値とは何か

p値は、仮説検定で最も誤解されやすい概念です。定義は次の通りです。

p値とは、帰無仮説が正しいと仮定したとき、観測されたデータと同じかそれ以上に極端なデータが得られる確率

重要なのは、p値は「帰無仮説が正しい確率」ではないということです。

p値が0.03だからといって、「差がない確率が3%」という意味ではありません。

 

　シミュレーションでp値を理解する

「本当は差がない」状況（帰無仮説が正しい状況）でt検定を繰り返し、p値の分布を確認します。

以下、コードです。

np.random.seed(42)

# 帰無仮説が正しい状況：両グループとも同じ母平均
p_values_null = []

for _ in range(1000):
    # 同じ母平均（70点）から2つのグループを抽出
    group1 = np.random.normal(
        loc=70, scale=10, size=25
    )
    group2 = np.random.normal(
        loc=70, scale=10, size=25
    )
    _, p = stats.ttest_ind(group1, group2)
    p_values_null.append(p)

print("【帰無仮説が正しいときのp値の分布】")
print(
    "p < 0.05 となった割合: "
    f"{np.mean(np.array(p_values_null) < 0.05) * 100:.1f}%"
)
print(
    "p < 0.01 となった割合: "
    f"{np.mean(np.array(p_values_null) < 0.01) * 100:.1f}%"
)

 

以下、実行結果です。

【帰無仮説が正しいときのp値の分布】
p < 0.05 となった割合: 5.1%
p < 0.01 となった割合: 1.0%

 

帰無仮説が正しい（本当は差がない）のに、約5%の確率で「p < 0.05」となり、「有意差あり」と誤判定してしまいます。

これが有意水準5%の意味であり、第1種の過誤の確率です。

p値の分布をヒストグラムで可視化します。

以下、コードです。

plt.figure(figsize=(10, 5))

# ヒストグラムを描く
plt.hist(
    p_values_null, bins=20, 
    edgecolor='white', alpha=0.7
)
# α = 0.05 の線を引く
plt.axvline(
    0.05, 
    color='red', linestyle='--', linewidth=2, 
    label='α = 0.05'
)
plt.xlabel('p値')
plt.ylabel('頻度')
plt.title('帰無仮説が正しいときのp値の分布')
plt.legend()
plt.show()

 

以下、実行結果です。

 

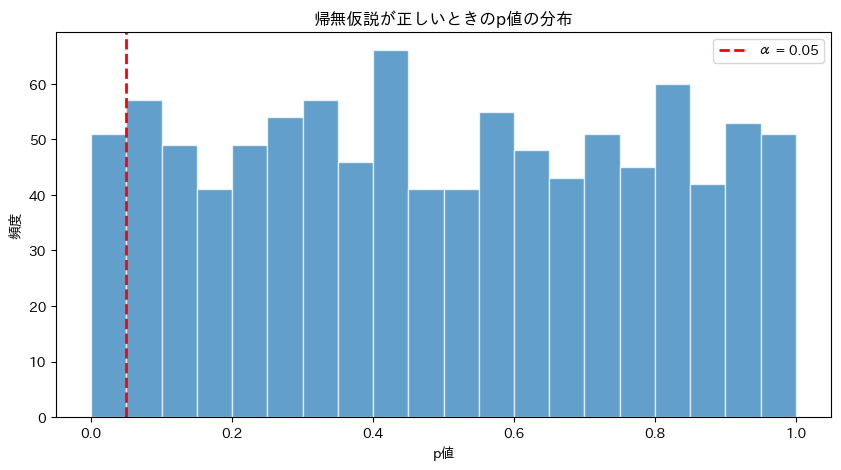
帰無仮説が正しいとき、p値は0から1まで一様に分布します。

そのうち5%（赤い線より左）が偶然「有意」と判定されてしまうのです。

 

第1種の過誤と第2種の過誤

仮説検定では、2種類の間違いを犯す可能性があります。

第1種の過誤（Type I Error）：帰無仮説が正しいのに、誤って棄却してしまう。

  • 本当は効果がないのに、効果があると判断してしまう
  • この確率は有意水準 α（通常0.05）で管理される

第2種の過誤（Type II Error）：帰無仮説が誤りなのに、棄却できない。

  • 本当は効果があるのに、効果があるとは言えないと判断してしまう
  • この確率は β で表され、1 – β を検出力（power）と呼ぶ
帰無仮説が真 帰無仮説が偽
棄却する 第1種の過誤 (α) 正しい判断（検出力 1-β）
棄却しない 正しい判断 第2種の過誤 (β)

 

「本当は差がある」状況で、どのくらいの確率で差を検出できるか（検出力）を調べます。

以下、コードです。

np.random.seed(42)

# 対立仮説が正しい状況：母平均に差がある
p_values_alt = []

for _ in range(1000):
    # 異なる母平均（65点 vs 72点）から2つのグループを抽出
    group1 = np.random.normal(
        loc=65, scale=10, size=25
    )
    group2 = np.random.normal(
        loc=72, scale=10, size=25
    )
    _, p = stats.ttest_ind(group1, group2)
    p_values_alt.append(p)

power = np.mean(np.array(p_values_alt) < 0.05)

print("【対立仮説が正しいときの検出力】")
print(
    "p < 0.05 で差を検出できた割合: "
    f"{power * 100:.1f}%"
)
print(
    "差を見逃した割合（第2種の過誤）: "
    f"{(1-power) * 100:.1f}%"
)

 

以下、実行結果です。

【対立仮説が正しいときの検出力】
p < 0.05 で差を検出できた割合: 67.1%
差を見逃した割合（第2種の過誤）: 32.9%

 

本当に差がある場合でも、100%検出できるわけではありません。

約70〜80%程度の確率で検出でき、20〜30%は「差があるとは言えない」と見逃してしまいます。

検出力はサンプルサイズや効果の大きさに依存します。

 

効果量：p値だけでは不十分

　なぜ効果量が必要か

p値は「差が偶然かどうか」を教えてくれますが、「差がどのくらい大きいか」は教えてくれません。

サンプルサイズが非常に大きければ、実質的に意味のない小さな差でも「統計的に有意」になってしまいます。

サンプルサイズを大きくすると、わずかな差でも有意になることを確認します。

以下、コードです。

np.random.seed(42)

# わずかな差（70点 vs 70.5点）
small_diff_sizes = [30, 100, 500, 2000, 10000]

print("【サンプルサイズとp値の関係】")
print("（母平均の差はわずか0.5点）")
print(f"{'n':>6} | {'平均差':>6} | {'p値':>9} | 有意？")
print("-" * 45)

for n in small_diff_sizes:
    group1 = np.random.normal(
        loc=70.0, scale=10, size=n
    )
    group2 = np.random.normal(
        loc=70.5, scale=10, size=n
    )
    _, p = stats.ttest_ind(group1, group2)
    diff = np.mean(group2) - np.mean(group1)
    sig = "Yes" if p < 0.05 else "No" print( f"{n:>6} | "
        f"{diff:>8.2f} | "
        f"{p:>10.4f} | "
        f"{sig}"
    )

 

以下、実行結果です。

【サンプルサイズとp値の関係】
（母平均の差はわずか0.5点）
     n |    平均差 |        p値 | 有意？
---------------------------------------------
    30 |     1.17 |     0.6226 | No
   100 |     1.93 |     0.1688 | No
   500 |     2.04 |     0.0012 | Yes
  2000 |     0.11 |     0.7386 | No
 10000 |     0.48 |     0.0007 | Yes

 

たった0.5点の差でも、サンプルサイズが数千になると「統計的に有意」になります。

しかし、テストで0.5点の差に実用的な意味があるでしょうか？

p値だけを見ていると、このような「意味のない有意差」に振り回されてしまいます。

 

　Cohen’s d：効果の大きさを標準化する

効果量（effect size）は、差の「大きさ」を標準化して表す指標です。

最もよく使われるのがCohen’s dで、2群の平均差を標準偏差で割った値です。
$$
d = \frac{\bar{x}_1 – \bar{x}_2}{s_p}
$$

ここで s_p はプールされた標準偏差です。

Cohen’s d を計算する関数を作成し、先ほどの教材データに適用します。

以下、コードです。

# Cohen's dの計算をする関数
def cohens_d(group1, group2):
    # 標本サイズ
    n1 = len(group1)
    n2 = len(group2)
    # 標本分散
    var1 = np.var(group1, ddof=1)
    var2 = np.var(group2, ddof=1)
    # プールされた標準偏差
    pooled_std = np.sqrt(
        ((n1-1)*var1 + (n2-1)*var2)
         / (n1+n2-2)
    )
    # Cohen's d
    d = (
        (np.mean(group1) - np.mean(group2))
         / pooled_std
    )
    return d

# 教材A vs 教材B
d = cohens_d(class_A, class_B)

print("【効果量（Cohen's d）】")
print(f"Cohen's d = {d:.3f}")
print(f"絶対値 |d| = {abs(d):.3f}")

 

以下、実行結果です。

【効果量（Cohen's d）】
Cohen's d = -0.632
絶対値 |d| = 0.632

 

Cohen’s d は「標準偏差何個分の差があるか」を表します。

符号はどちらが大きいかを示し、絶対値が効果の大きさです。

 

　効果量の解釈の目安

Cohen’s d の絶対値には、以下のような解釈の目安があります（Cohen, 1988）。

|d| の範囲 解釈
0.2 未満 効果は非常に小さい（ほぼなし）
0.2 〜 0.5 効果は小さい
0.5 〜 0.8 効果は中程度
0.8 以上 効果は大きい

p値が有意でも、効果量が小さければ実用的な意味は限られます。

p値と効果量の両方を報告することが推奨されています。

 

統計的有意 ≠ 実用的に意味がある

　よくある誤解

「p < 0.05 で有意だから効果がある」という言い方は、誤解を生みやすい表現です。

p値が示しているのは、ざっくり言えば……

効果が「ゼロ」だと仮定したとき、
いま観測された差（あるいはそれ以上の差）が「たまたま」出る確率

……であり、効果の大きさ（どれくらい役に立つか）を直接示しているわけではありません。

そのため、統計的に有意でも実用的に意味が薄い場合もあれば、逆に 有意でなくても検討の価値がある場合もあります。

 

　比較例で理解する2つの典型パターン

ここでは、教育評価（テスト得点）を例にして比較します。

　　ケース1：大規模調査では「ごく小さな差」でも有意になりうる

  • 対象者が非常に多い（例：各群 5,000 人規模）
  • 平均点の差は 0.5 点しかない

このような状況では、データのばらつきが平均化されるため、差が極めて小さくても p値が 0.05 未満になりやすいことがあります。

しかし、実務の意思決定では次の問いが重要です。

  • 0.5点の改善に、現場で意味があるのか？
  • その改善のために、費用や工数をかける価値があるのか？

つまり、「有意」＝「意思決定すべき」ではないのです。

このケースは「統計的に有意だが、実用的にはほぼ意味がない」典型例です。

 

　　ケース2：小規模調査では「大きな差」があっても有意にならないことがある

  • 対象者が少ない（例：各群 15 人程度）
  • 平均点の差は 8 点と大きい

この場合、差は十分大きく見えますが、人数が少ないため推定の不確かさが大きく、p値が 0.05 を下回らないことがあります。

このときに「有意じゃないから効果なし」と切り捨てるのは早計です。

むしろ実務としては……

  • 8点差は教育的に重要かもしれない
  • 追加データを集めれば有意になる可能性がある
  • 現場試験（パイロット導入）として検討する価値がある

……と判断することもあります。

 

　では何を見るべきか（効果量と信頼区間）

実用的な判断のためには、p値だけでなく次の2つが重要です。

  • 効果量（例：Cohen’s d） → 差が「どれくらい大きいか」を、ばらつきと比較して定量化する指標
  • 信頼区間（例：平均との差の95%信頼区間） → 効果の推定範囲。「最悪でもどれくらい」「最大でどれくらい」かが見える

特に信頼区間を見ると、たとえば次の判断ができます。

  • 信頼区間がほぼ 0 付近に集中している → 実用的な改善は期待しにくい
  • 信頼区間が広いが、改善方向に大きく偏っている → 不確かだが、可能性が大きい（追加調査の価値あり）

 

　検定結果の報告方法

検定結果を報告するときに、p値だけを書くと読者は判断できません。

最低限、次の情報をセットで示すのがいいでしょう。

  • 検定の種類（例：独立2標本t検定）
  • t統計量と自由度（例：t(28) = …）
  • p値（例：p = …）
  • 効果量（例：Cohen’s d = …）
  • 95%信頼区間（例：平均との差の95%CI [下限, 上限]）

 

　報告文のテンプレ例

教材A群（n = ○○, 平均 = ○○, 標準偏差 = ○○）と教材B群（n = ○○, 平均 = ○○, 標準偏差 = ○○）を比較した。
– 独立2標本t検定の結果、両群の平均に（有意な差が認められた／有意な差は認められなかった）：t(自由度) = ○○, p = ○○。
– 平均差は ○○ 点で、95%信頼区間は [○○, ○○] であった。
– 効果量は Cohen’s d = ○○（小／中／大）であった。

この形で書けば、読者は少なくとも……

  • 有意かどうか（p値）
  • 差の大きさ（効果量）
  • 推定の確かさ（信頼区間）

……を同時に見て、結果の妥当性と実用的意味を評価できます。

 

まとめ

今回は、仮説検定の基本的な考え方とt検定の実践方法を学びました。

仮説検定は「差がない」という帰無仮説を立て、観測されたデータがその仮説のもとでどれくらい珍しいかをp値で評価する手法です。p値が有意水準（通常0.05）より小さければ帰無仮説を棄却し、「差がある」と結論づけます。

ただし、p値には注意すべき点がいくつかあります。

p値は「帰無仮説が正しい確率」ではなく、「帰無仮説が正しいと仮定したときに、このようなデータが得られる確率」です。また、仮説検定では第1種の過誤（本当は差がないのに「ある」と判断）と第2種の過誤（本当は差があるのに「ない」と判断）の2種類の間違いを犯す可能性があり、有意水準αは第1種の過誤の確率を制御しています。

さらに重要なのは、「統計的に有意」と「実用的に意味がある」は別物だということです。

サンプルサイズが非常に大きければ、実質的に意味のない小さな差でも「有意」になりえます。そこで効果量（Cohen’s d など）を併用し、差の「大きさ」を評価することが推奨されます。

検定結果を報告する際は、p値だけでなく、効果量や信頼区間も含めることで、読者が結果の実用的な意味を判断できるようになります。

全5回のシリーズを通じて、統計学の基礎を学んできました。

第1回では、平均・中央値・最頻値という代表値を学び、データを一つの数字で要約することの意味と限界を理解しました。

第2回では、分散と標準偏差を通じて、データの「ばらつき」を数値化する方法を学びました。なぜ偏差を二乗するのか、なぜn-1で割るのかという「なぜ？」にも答えました。

第3回では、相関係数を使って2つの変数の関係を定量化し、「相関と因果は違う」という重要な注意点を学びました。

第4回では、標本から母集団を推測するという推測統計の考え方を学び、標準誤差・中心極限定理・信頼区間の意味を理解しました。

そして第5回の今回、仮説検定の考え方とt検定の実践を学び、p値や効果量の正しい解釈方法を身につけました。

これらの知識は、データサイエンス・研究・ビジネスなど、あらゆる分野でデータに基づいた意思決定を行うための基盤となります。

統計学は奥が深い分野ですが、この5回で学んだ内容を土台にして、回帰分析・分散分析・機械学習などへとステップアップしていってください。

Pythonで手を動かしながら学ぶことで、数式だけでは見えなかった統計学の「感覚」が身についたはずです。ぜひ実際のデータで試してみてください。

お疲れさまでした！