データ分析の世界には、一見すると驚くような相関関係が存在します。
アイスクリームの売上が増えると、プールでの事故も増える。
この事実だけを見ると、「アイスクリームを食べるとプールで溺れやすくなる」と考えてしまうかもしれません。
しかし、これは典型的な「見せかけの関係」なのです。
今回は、このような罠に陥らないための考え方と、因果関係を正しく理解するための実践的な方法をご紹介します。
Contents
相関と因果の違い
アイスクリーム売上とプール事故の不思議な関係
アイスクリームの売上とプール事故の関係を考えてみましょう。
実際のデータを見ると、確かに両者には強い相関があります。
夏になるとアイスクリームの売上は急増し、同時にプールでの事故件数も増加します。冬になると両方とも減少します。
しかし、ここで立ち止まって考えてみてください。
アイスクリームを食べることが、本当にプール事故の原因なのでしょうか。
もちろん違います。実は、両者に共通して影響を与えている「気温」という要因があるのです。
相関が意味するもの、意味しないもの
相関は「一緒に動く」ことを示すだけで、「一方が他方を引き起こす」ことを証明するものではありません。
気温が上がれば、人々はアイスクリームを食べたくなり、同時にプールで泳ぐ人も増えます。
泳ぐ人が増えれば、確率的に事故も増えるというわけです。
このような見せかけの関係を見抜くことが、正しいデータ分析の第一歩なのです。
交絡因子という見えない第三者
交絡因子とは何か
アイスクリームの例で登場した「気温」のような要因を、統計学では「交絡因子」と呼びます。
交絡因子は、調べたい二つの要因の両方に影響を与えることで、あたかも二つの要因の間に関係があるように見せかけてしまう、いわば「見えない第三者」です。
DAG(有向非巡回グラフ)で表現すると、次のようになります。
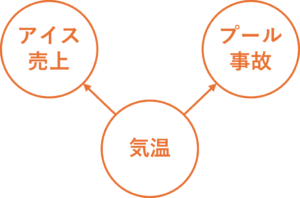
この図を見れば、アイス売上とプール事故の間に直接の矢印(因果関係)がないことが一目瞭然です。
朝食と成績の本当の関係
もう一つ、身近な例を見てみましょう。
「朝食を食べる子どもは成績が良い」というデータがあったとします。
これをDAGで表現すると、次のようになります。
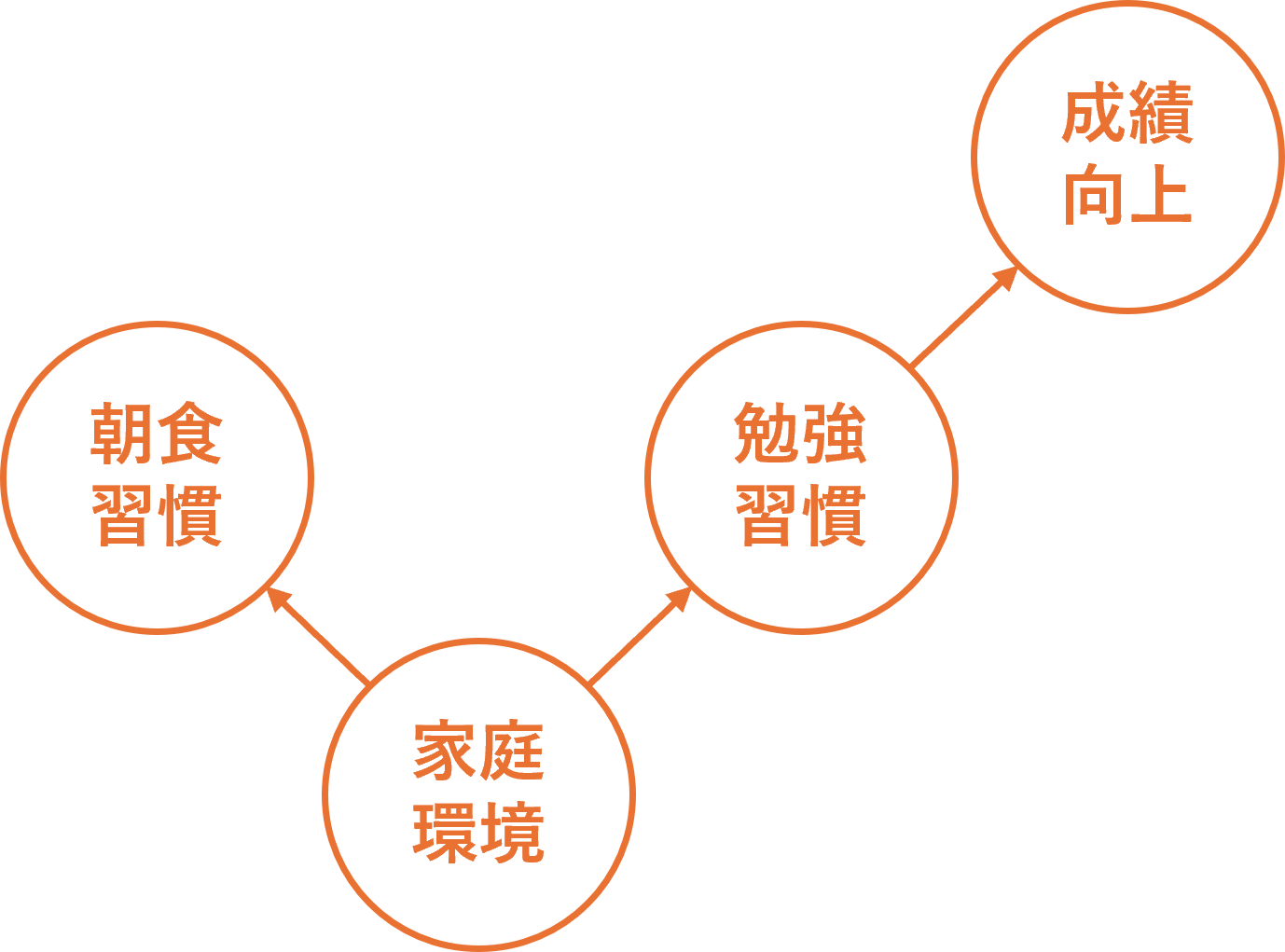
朝食を毎日きちんと用意する家庭は、規則正しい生活習慣を大切にしており、宿題を見てあげる時間もあり、教育への関心も高いかもしれません。
つまり、「規則正しい家庭環境」という交絡因子が、朝食習慣と成績の両方に影響している可能性があるのです。
因果関係を可視化するDAGの基本
DAGの3つの基本ルール
DAG(有向非巡回グラフ)は「原因と結果を矢印でつないだ図」のことです。
描くときには、次の3つのルールを守ります。
| ルール | 説明 |
|---|---|
| 矢印は一方向のみ | 時間は過去から未来にしか流れないので、原因から結果への向きで矢印を描きます。 |
| 循環しない | 矢印をたどっても元の場所に戻ってこないようにします。 |
| シンプルな表記 | 要因を点や箱で、影響を矢印で表現します。 |
よくある因果構造の3パターン
DAGには、覚えておくべき3つの基本パターンがあります。
フォーク(共通原因)
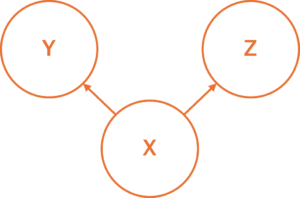
XがYとZの両方に影響する構造です。
アイスクリームの例がこれに当たります。
チェーン(連鎖)

XがYを通じてZに影響する構造です。
例えば、「勉強時間→知識量→試験成績」のような場合です。
コライダー(合流点)
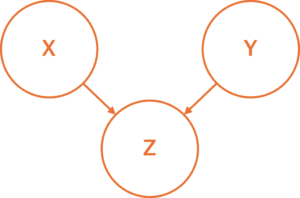
XとYが共にZに影響する構造です。
例えば、「料理の腕と人脈が、有名シェフになることに影響する」のような場合です。
実践:コーヒーと仕事効率の分析
ステップ1:単純な関係から始める
「コーヒーを飲むと仕事の効率が上がるか」という問題を、DAGを使って分析してみましょう。
まず最も単純に、次のようなDAGを作成します。

ステップ2:経路を詳細化する
しかし、これだけでは不十分です。
コーヒーの効果には複数の経路があります。
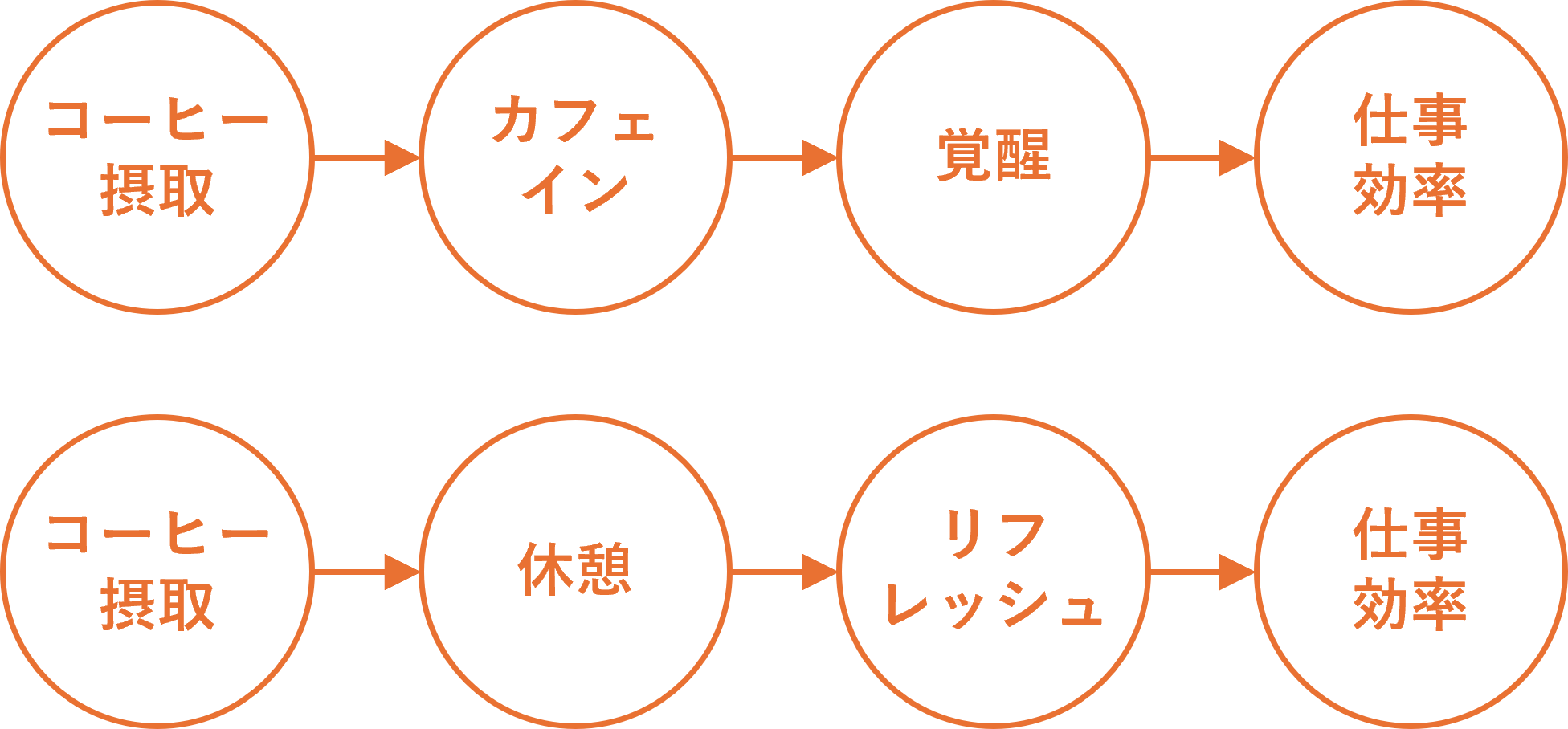
ステップ3:交絡因子を追加する
さらに重要なのは、交絡因子の存在です。
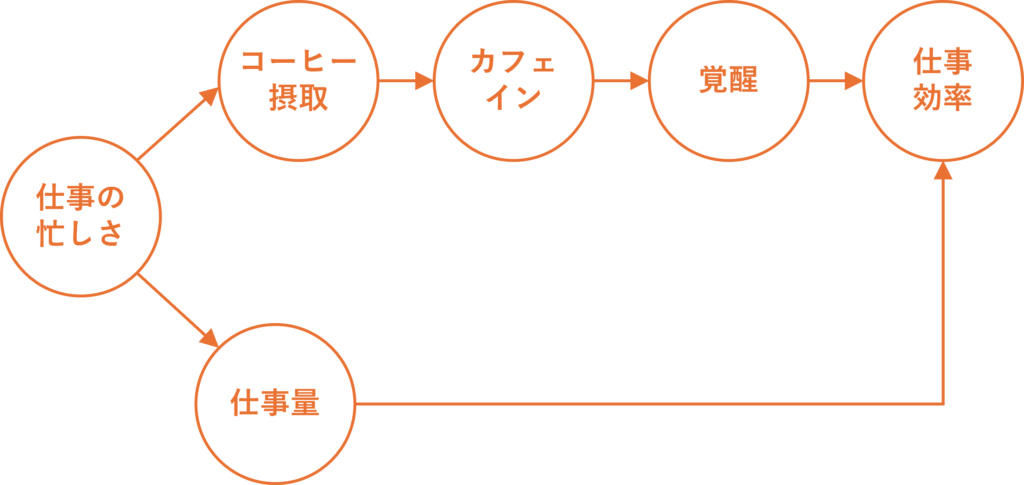
忙しい人ほどコーヒーを飲む傾向があり、かつ仕事量が多いので見かけ上「効率的」に見える可能性があります。
このDAGから、コーヒーの真の効果を知るには、「仕事の忙しさ」を統計的に調整する必要があることが分かります。
今回のまとめ
今回は、「なぜアイスクリームの売上とプール事故は相関するのか? 見せかけの関係を見抜く方法」というお話しをしました。
データ分析において最も重要なのは、見かけの相関に惑わされず、真の因果関係を見極めることです。
そのためには、交絡因子の存在を常に意識し、DAGのような図を使って関係性を整理することが有効です。
完璧な分析は存在しません。
ただ、「他に影響している要因はないか」「逆の因果関係は考えられないか」といった批判的な視点を持つことで、より真実に近い結論にたどり着けるはずです。
次回データを見るときは、まず簡単なDAGを描いてみてください。
アイスクリームとプール事故の例のように、隠れた交絡因子が見つかるかもしれません。
データの向こう側にある真実を見つけるために、今日学んだ視点を活用していただければ幸いです。

