前回(第6回)で、個別の不良品に対してSHAPとBreak Downを使って原因を究明し、具体的な改善アクションを立案しました。
DALEXで実践する説明可能AI超入門— 第6回 —製造業でのXAI実践(その2)- 個別不良品の原因究明と改善アクション
品質管理におけるXAIの活用により、「なぜこの製品が不良なのか」を明確に説明できるようになりました。
今回は、製造現場の「設備予知保全」にXAIを適用します。
設備の故障は、品質不良以上に大きな損失をもたらす可能性があります。
突発的な設備停止は、生産計画の大幅な変更、納期遅延、そして多額の機会損失につながるからです。
振動データを使った故障予測モデルを構築し、PDPやSHAPを使って「なぜこの設備が危険なのか」を明確に説明するケースを扱います。
さらに、品質管理と予知保全を統合することで得られる相乗効果と、これらの技術を実際の製造現場に実装するための考え方の一つも紹介します。
Contents
- 熟練者の耳を数値化する
- 予知保全データの準備と故障パターンの設定
- データセットの全体像
- 時間領域特徴量の理解
- 周波数領域特徴量の理解
- 残存寿命と特徴量の関係
- まとめと推奨アクション
- 残存寿命予測モデルの構築と評価
- データの準備とモデルの訓練
- モデルの評価と選択
- 安全性の観点からの評価
- PDPで故障進行パターンを理解する
- PDPによる全体傾向の把握
- ICEによる個体差の分析
- SHAPで緊急メンテナンスの判断根拠を説明
- SHAP分析による要因分解
- SHAP値の解釈と対策立案
- 品質管理と予知保全の統合
- なぜ統合管理が必要なのか
- データ統合で見えてきた真実
- 統合ダッシュボードの設計
- アラートの最適化
- 現場への実装とベストプラクティス
- 段階的導入による成功パターン
- 現場の巻き込み方
- データリテラシーの向上
- 継続的改善のサイクル
- 投資効果の測定
- まとめ
熟練者の耳を数値化する
製造現場の保全担当の高橋さん(仮名)は毎朝6時に出社します。
彼の最初の仕事は、工場内の回転機械の音を聞いて回ることです。
「この軸受の音がいつもと違う」「このモーターは振動が大きくなってきた」
30年の経験が培った彼の耳は、機械の異常を敏感に察知します。
しかし、若手への技術伝承は困難を極めていました。「音が違う」と言っても、何がどう違うのか、言葉では説明できないのです。
予知保全におけるAIの役割は、まさにこの「熟練者の感覚」を数値化し、説明可能にすることです。
振動データには、人間の耳では聞き取れない微細な変化が記録されています。
これらのパターンを学習したAIは、故障の兆候を数週間前から検知できます。
予知保全データの準備と故障パターンの設定
データセットの全体像
以下のデータセット(vibration_data.csv)を使います。これは主に機械の振動データで構成されています。
このデータセットには、9つの特徴量と、目的変数である残存寿命(RUL)、そして故障タイプのラベルが含まれています。
まず、このデータセットを読み込みます。
# CSVファイルからデータを読み込む
vibration_df = pd.read_csv('vibration_data.csv')
# データフレームの内容を表示する
print(vibration_df)
以下、実行結果です。
RMS Peak Crest_Factor Kurtosis Skewness 1X_Amplitude \
0 0.367449 0.756542 2.058906 1.717507 -0.001791 5.383227
1 0.370038 0.784419 2.119835 1.693268 0.004646 16.574714
2 0.362522 0.763038 2.104805 1.718465 -0.042212 48.493093
3 0.373453 0.738931 1.978646 1.692860 0.026596 15.002546
4 0.363325 0.781913 2.152104 1.703755 0.017600 26.773940
.. ... ... ... ... ... ...
989 0.601842 1.843311 3.062783 2.496660 0.059412 20.459750
990 0.621054 1.711213 2.755338 2.424775 0.054242 43.315993
991 0.674651 2.053610 3.043960 2.481649 0.078789 54.206158
992 0.638048 1.962351 3.075555 2.477355 0.080800 42.651307
993 0.619565 1.820200 2.937868 2.501591 0.072281 200.475499
2X_Amplitude 3X_Amplitude High_Freq_Energy RUL Fault_Type \
0 1.623129 2.045123 2909.233627 111.319135 normal
1 2.400214 1.624020 3059.193009 108.379762 normal
2 2.142850 1.206559 3004.441450 99.959181 normal
3 1.190856 1.940184 3183.756623 84.468104 normal
4 1.712279 1.027207 2946.783509 93.831027 normal
.. ... ... ... ... ...
989 1.587575 2.110160 9771.479235 20.046143 bearing
990 1.151773 3.495697 104906.285278 12.430693 bearing
991 4.121968 4.505806 134742.894315 11.349258 bearing
992 3.582332 2.261407 115725.296503 16.814475 bearing
993 3.066533 8.380884 100531.905188 19.841720 bearing
Severity Label
0 0.0 正常
1 0.0 正常
2 0.0 正常
3 0.0 正常
4 0.0 正常
.. ... ...
989 0.7 重度ベアリング劣化
990 0.7 重度ベアリング劣化
991 0.7 重度ベアリング劣化
992 0.7 重度ベアリング劣化
993 0.7 重度ベアリング劣化
[994 rows x 13 columns]
このデータがどのような構造を持っているか確認しましょう。
# 特徴量のリストを作成する
feature_columns = [
'RMS', # 振動の二乗平均平方根
'Peak', # 振動のピーク値
'Crest_Factor', # ピーク値とRMSの比率
'Kurtosis', # 振動信号の尖度
'Skewness', # 振動信号の歪度
'1X_Amplitude', # 基本周波数成分の振幅
'2X_Amplitude', # 2倍周波数成分の振幅
'3X_Amplitude', # 3倍周波数成分の振幅
'High_Freq_Energy', # 高周波成分のエネルギー
]
# データセットの基本情報を表示する
print("データセットの基本情報:")
print("="*50)
print(f"- 総データ数: {len(vibration_df)}")
print(f"- 特徴量の数: {len(feature_columns)}")
print(f"- 故障タイプ: {vibration_df['Fault_Type'].nunique()}種類")
print(f"- 重症度レベル: {vibration_df['Severity'].nunique()}段階")
# 各故障タイプのデータ数と残存寿命の分布を表示する
print("\n各故障タイプのデータ数:")
print("="*50)
print(vibration_df['Label'].value_counts())
# 残存寿命の分布を表示する
print("\n残存寿命の分布:")
print("="*50)
print(f"- 平均: {vibration_df['RUL'].mean():.1f}日")
print(f"- 最小: {vibration_df['RUL'].min():.1f}日")
print(f"- 最大: {vibration_df['RUL'].max():.1f}日")
以下、実行結果です。
データセットの基本情報: ================================================== - 総データ数: 994 - 特徴量の数: 9 - 故障タイプ: 4種類 - 重症度レベル: 3段階 各故障タイプのデータ数: ================================================== Label 正常 142 軽度アンバランス 142 重度アンバランス 142 軽度ミスアライメント 142 重度ミスアライメント 142 軽度ベアリング劣化 142 重度ベアリング劣化 142 Name: count, dtype: int64 残存寿命の分布: ================================================== - 平均: 35.8日 - 最小: 1.5日 - 最大: 127.5日
時間領域特徴量の理解
時間領域の特徴量は、振動信号を時間軸で直接分析した結果です。
- RMS(実効値)は振動の全体的なエネルギーを表します。電力で言えば、実効電力に相当する概念です。RMSが増加することは、設備全体に加わる力が増大していることを意味し、アンバランスや全体的な劣化を示唆します。
- Peak(ピーク値)は振動の最大振幅です。瞬間的に大きな力が加わっていることを示し、衝撃的な振動の有無を検出できます。ベアリングの剥離や歯車の欠損などが原因で発生します。
- Crest Factor(波高率)はPeakをRMSで割った値です。この値が大きいほど、振動に衝撃成分が多く含まれていることを意味します。正常な回転機械では通常2.5〜3.0の範囲にありますが、4.0を超えると局所的な損傷が疑われます。
- Kurtosis(尖度)は振動分布の尖り具合を表します。正規分布では3.0になりますが、衝撃振動が含まれると値が大きくなります。ベアリング損傷の初期段階で敏感に反応する指標です。
- Skewness(歪度)は振動分布の非対称性を示します。正の値は上方向への振動が強く、負の値は下方向への振動が強いことを意味します。軸の偏心や片当たりなどを検出できます。
故障タイプごとに、それぞれの特徴量の基本統計量を見てみます。
# 時間領域の特徴量をリストとして定義
time_features = [
'RMS', # 振動の二乗平均平方根
'Peak', # 振動のピーク値
'Crest_Factor', # ピーク値とRMSの比率
'Kurtosis', # 振動信号の尖度
'Skewness' # 振動信号の歪度
]
# 各特徴量について、ラベルごとの統計情報を計算して表示
for feature in time_features:
print(f"\n{feature}の統計:") # 現在処理中の特徴量名を表示
print("="*50)
print(
vibration_df.groupby('Label') # データをラベルごとにグループ化
[feature].describe() # 各特徴量の統計情報を計算
[['mean', 'std', 'min', 'max']]
)
以下、実行結果です。
RMSの統計:
==================================================
mean std min max
Label
正常 0.367508 0.003495 0.357115 0.377709
軽度アンバランス 0.795244 0.134115 0.489620 1.106986
軽度ベアリング劣化 0.430162 0.036328 0.365947 0.556397
軽度ミスアライメント 0.504676 0.077332 0.375170 0.734865
重度アンバランス 1.336046 0.148758 0.880508 1.703888
重度ベアリング劣化 0.617000 0.056755 0.476843 0.796396
重度ミスアライメント 0.850667 0.099034 0.580467 1.071229
Peakの統計:
==================================================
mean std min max
Label
正常 0.775544 0.037644 0.684504 0.937923
軽度アンバランス 1.387463 0.194279 0.955974 1.810306
軽度ベアリング劣化 1.130658 0.182633 0.715284 1.745543
軽度ミスアライメント 1.156633 0.190038 0.760305 1.644861
重度アンバランス 2.141394 0.220049 1.462124 2.669961
重度ベアリング劣化 1.789442 0.222472 1.111390 2.458923
重度ミスアライメント 1.865382 0.191234 1.362066 2.349370
Crest_Factorの統計:
==================================================
mean std min max
Label
正常 2.110445 0.104058 1.877146 2.572031
軽度アンバランス 1.754604 0.083598 1.602361 2.083049
軽度ベアリング劣化 2.614042 0.231942 1.935758 3.176356
軽度ミスアライメント 2.288630 0.090436 1.979117 2.530768
重度アンバランス 1.604674 0.035324 1.529666 1.708829
重度ベアリング劣化 2.898296 0.219154 2.071086 3.284375
重度ミスアライメント 2.197114 0.062316 2.028474 2.380334
Kurtosisの統計:
==================================================
mean std min max
Label
正常 1.714041 0.023670 1.655677 1.775640
軽度アンバランス 1.553330 0.020877 1.519615 1.634749
軽度ベアリング劣化 2.154692 0.180961 1.697966 2.539382
軽度ミスアライメント 2.482204 0.277428 1.712399 2.788342
重度アンバランス 1.517940 0.006510 1.503581 1.545412
重度ベアリング劣化 2.453573 0.085191 1.969118 2.589082
重度ミスアライメント 2.621351 0.069036 2.455047 2.766893
Skewnessの統計:
==================================================
mean std min max
Label
正常 -0.012992 0.021182 -0.063688 0.057887
軽度アンバランス -0.012235 0.011766 -0.053105 0.022181
軽度ベアリング劣化 0.000523 0.028315 -0.073732 0.087614
軽度ミスアライメント -0.007349 0.025237 -0.070948 0.053881
重度アンバランス -0.012032 0.009180 -0.033587 0.009143
重度ベアリング劣化 0.040422 0.059746 -0.249468 0.115825
重度ミスアライメント -0.001702 0.014463 -0.040006 0.033593
正常状態では、RMS値は平均0.37程度で安定しており、Peak値も0.77程度と低く、Crest_Factorは約2.11で比較的均一です。Kurtosisは1.71で尖度が低く、Skewnessはほぼ0に近い値を示しており、振動信号が対称的で安定していることを示しています。
軽度アンバランスでは、RMS値が0.79と上昇し、Peak値も1.39と増加していますが、Crest_Factorは1.75と低下しています。Kurtosisは1.55で尖度がさらに低く、Skewnessもほぼ0に近い値を保っています。
軽度ベアリング劣化では、RMS値は0.43と正常よりやや高く、Peak値は1.13と増加しています。Crest_Factorは2.61と高く、Kurtosisも2.15と尖度が増加しており、Skewnessは0.00付近で対称性を保っています。
軽度ミスアライメントでは、RMS値が0.50、Peak値が1.16と増加し、Crest_Factorは2.29とやや高めです。Kurtosisは2.48と尖度が増加し、Skewnessは-0.01付近でほぼ対称的です。
重度アンバランスでは、RMS値が1.33と大幅に上昇し、Peak値も2.14と高くなっていますが、Crest_Factorは1.60と低下しています。Kurtosisは1.52で尖度が低く、Skewnessは-0.01付近で対称性を保っています。
重度ベアリング劣化では、RMS値が0.62、Peak値が1.79と増加し、Crest_Factorは2.90と非常に高くなっています。Kurtosisは2.45と尖度が増加し、Skewnessは0.04とやや非対称性を示しています。
重度ミスアライメントでは、RMS値が0.85、Peak値が1.86と高く、Crest_Factorは2.20とやや高めです。Kurtosisは2.62と尖度が増加し、Skewnessは-0.00付近でほぼ対称的です。
これらの結果から、故障の種類や重症度に応じて振動信号の特徴量が変化することがわかります。特に、RMS値やPeak値、Crest_Factor、Kurtosisは故障の検出や分類に有用な指標となる可能性があります。
| 状態 | RMS | Peak | CrestFactor | Kurtosis | Skewness | 傾向・特徴 |
|---|---|---|---|---|---|---|
| 正常 | 0.37 | 0.78 | 2.11 | 1.71 | -0.01 | 振動は低く安定的。波形は対称。 |
| 軽度アンバランス | 0.80 | 1.39 | 1.75 | 1.55 | -0.01 | RMS・Peakが増加。CF・Kurtosisは低下。 |
| 重度アンバランス | 1.34 | 2.14 | 1.60 | 1.52 | -0.01 | RMS・Peakが大幅に上昇。CFは低いまま。 |
| 軽度ベアリング劣化 | 0.43 | 1.13 | 2.61 | 2.15 | 0.00 | RMSは微増だが、CFが高くなる。 |
| 重度ベアリング劣化 | 0.62 | 1.79 | 2.90 | 2.45 | 0.04 | CFが非常に高い。やや非対称(Skewness増)。 |
| 軽度ミスアライメント | 0.50 | 1.16 | 2.29 | 2.48 | -0.01 | RMS微増。Kurtosis(尖度)が高くなる。 |
| 重度ミスアライメント | 0.85 | 1.87 | 2.20 | 2.62 | 0.00 | Kurtosisが高い。RMS・Peakも増加傾向。 |
周波数領域特徴量の理解
周波数領域の特徴量は、FFT(高速フーリエ変換)により振動を周波数成分に分解した結果です。
- 1X_Amplitude(回転周波数成分)は、回転体が1回転する際に1回発生する振動成分です。アンバランスが主な原因で、質量の偏りや回転体の変形により発生します。データを見ると、アンバランス故障で特に大きな値を示していることが分かります。
- 2X_Amplitude(2倍周波数成分)は、1回転に2回発生する振動です。ミスアライメント(軸の芯ずれ)が主な原因です。カップリングの不良や軸受の取り付け不良でも発生します。
- 3X_Amplitude(3倍周波数成分)は、機械的なゆるみや、ベルト駆動の問題などで発生します。複数の故障が重なった場合にも増加する傾向があります。
- High_Freq_Energy(高周波エネルギー)は、100Hz以上の高周波成分の総和です。ベアリング損傷の初期段階で増加し、人間の耳では聞き取りにくい「キーン」という高音として現れます。潤滑不良や異物混入が原因となることが多いです。
特定の周波数成分の強度から、故障モードを特定できます。
では、この周波数領域の特徴量が、故障の種類(Label)によってどのように異なる分布を示しているかを視覚的に確認します。
# 周波数領域の特徴量をリストとして定義
freq_features = [
'1X_Amplitude', # 基本周波数成分の振幅
'2X_Amplitude', # 2倍周波数成分の振幅
'3X_Amplitude', # 3倍周波数成分の振幅
'High_Freq_Energy' # 高周波成分のエネルギー
]
# 2行2列のサブプロットを作成
fig, axes = plt.subplots(2, 2, figsize=(10, 10))
axes = axes.flatten() # サブプロットを1次元配列に変換
# 各周波数領域の特徴量について、箱ひげ図を作成
for idx, feature in enumerate(freq_features):
vibration_df.boxplot(
column=feature, # 箱ひげ図を作成する特徴量
by='Label', # ラベルごとにデータを分割
ax=axes[idx] # 対応するサブプロットに描画
)
axes[idx].set_title(f'{feature}の分布') # サブプロットのタイトルを設定
axes[idx].set_xlabel('故障タイプ') # x軸のラベルを設定
axes[idx].set_ylabel(feature) # y軸のラベルを設定
axes[idx].tick_params(axis='x', rotation=90) # x軸のラベルを90度回転
# レイアウトを調整してプロットを表示
plt.tight_layout()
plt.show()
以下、実行結果です。
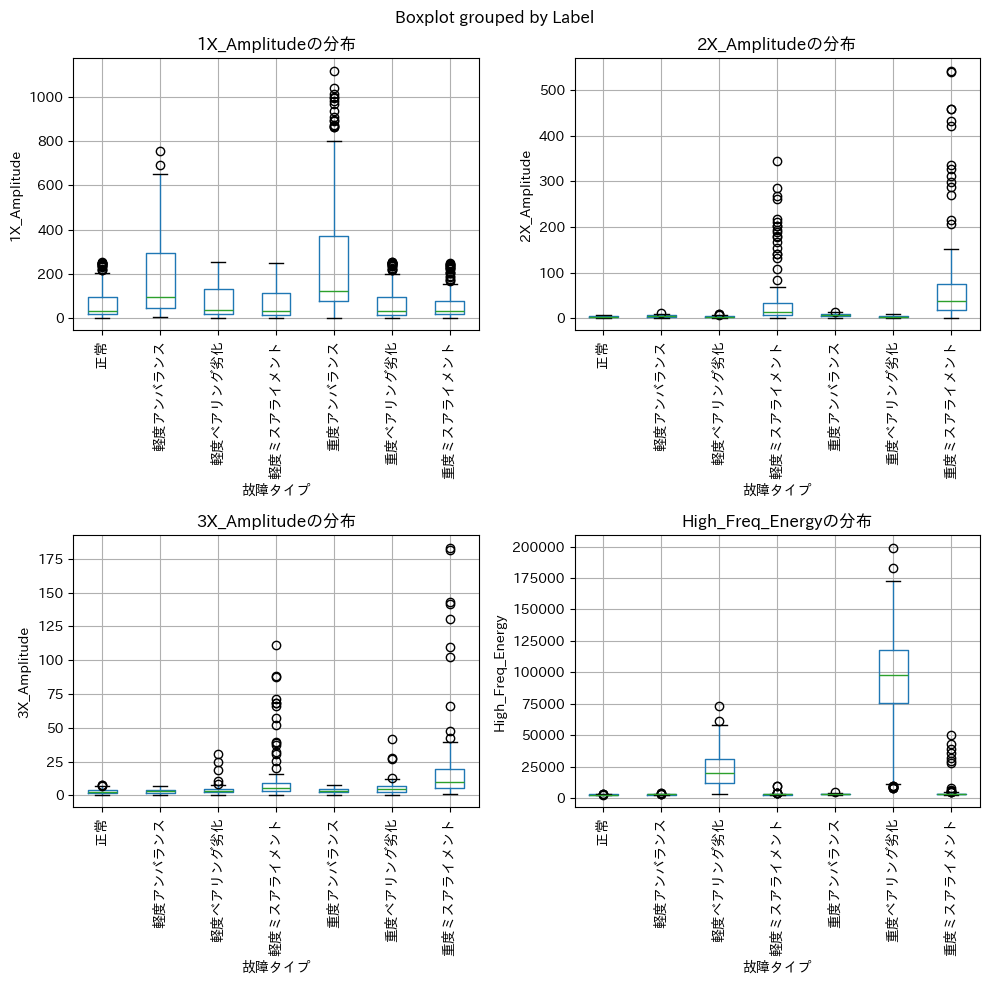
この箱ひげ図(Boxplot)から、故障の種類ごとに「どの周波数成分が反応しているか」が非常に明確に表れています。
| 特徴量 | 主に検出できる故障 | 判別のポイント |
|---|---|---|
| 1X_Amplitude | アンバランス | 1Xだけが突出して高ければアンバランス。 |
| 2X / 3X_Amplitude | ミスアライメント | 1Xだけでなく、2X/3Xも高ければミスアライメント。 |
| High_Freq_Energy | ベアリング劣化 | 高周波成分が出ていれば、ほぼ間違いなくベアリング異常。 |
まず、アンバランス(不釣合い)の状態については、回転の基本周波数成分である「1X_Amplitude」が最も顕著な指標となっています。グラフを見ると、重度のアンバランスにおいてこの値が突出して高く、軽度の場合でも他の故障に比べて明確な上昇が見られます。一方で、他の故障タイプではこの1X成分は低く抑えられています。物理的にもアンバランスは回転周期に同期した振動を生むため、この成分の増大はアンバランス特有の現象であると言えます。
次に、ミスアライメント(軸芯ずれ)については、基本周波数の倍音成分である「2X_Amplitude」および「3X_Amplitude」に顕著な特徴が現れています。特に重度のミスアライメントでは、これらの倍音成分が大きく跳ね上がっており、これはアンバランスのグラフには見られない挙動です。つまり、1X成分だけでなく、2倍・3倍の周波数成分が強く検出された場合は、ミスアライメントが発生している可能性が高いと解釈できます。
最後に、ベアリング劣化については、「High_Freq_Energy(高周波成分のエネルギー)」が決定的な識別材料となっています。このグラフだけ縦軸の桁が異なることからも分かる通り、重度のベアリング劣化では高周波エネルギーが桁違いに増大しています。軽度であっても、他の故障タイプ(アンバランスやミスアライメント)がほぼゼロに近い値であるのに対し、ベアリング劣化だけは明確に高い値を示しています。これは、ベアリングの傷による衝撃が金属特有の高周波振動を生み出すためであり、低周波が主体の他の機械的故障とは明確に区別が可能です。
以上のことから、これら4つの特徴量を用いれば、「1Xが高ければアンバランス」「2X・3Xが高ければミスアライメント」「高周波が出ていればベアリング劣化」というように、非常に高い精度で故障原因を特定できることがデータから読み取れます。
残存寿命と特徴量の関係
各特徴量が残存寿命とどのような関係にあるのか、相関分析により確認します。
# vibration_dfから必要な列を抽出
target_df = vibration_df[feature_columns + ['RUL']]
# 数値列だけに絞る
numeric_df = target_df.select_dtypes(include='number')
# 相関行列を取得
corr_matrix = numeric_df.corr()
# RULとの相関のみ取り出し降順にソート
correlations = corr_matrix.loc[:, 'RUL'].drop('RUL').sort_values()
# 各特徴量とRULの相関係数を表示し、相関の強さを分類
print("残存寿命(RUL)との相関係数:")
print("="*50)
for feature, corr_value in correlations.items():
print(f"{feature:20s}: {corr_value:+.3f}")
if abs(corr_value) > 0.5:
print(f" → 強い相関あり({'負' if corr_value < 0 else '正'}の相関)")
elif abs(corr_value) > 0.3:
print(f" → 中程度の相関あり")
else:
print(f" → 弱い相関")
以下、実行結果です。
残存寿命(RUL)との相関係数: ================================================== Peak : -0.752 → 強い相関あり(負の相関) RMS : -0.556 → 強い相関あり(負の相関) Kurtosis : -0.347 → 中程度の相関あり High_Freq_Energy : -0.280 → 弱い相関 Skewness : -0.194 → 弱い相関 2X_Amplitude : -0.164 → 弱い相関 3X_Amplitude : -0.157 → 弱い相関 1X_Amplitude : -0.124 → 弱い相関 Crest_Factor : -0.089 → 弱い相関
すべての項目で「負の相関」が示されています。これは、「特徴量の値が大きくなるほど、残存寿命が短くなる」ことを意味します。
これは、機械が劣化して振動が激しくなるほど、故障までの残り時間が減るという物理的な直感と完全に一致しています。
この中で、Peak値(-0.752)とRMS(-0.556)が、RULに対して非常に強い相関を持っています。
- Peak値 (-0.752): 最も相関が高い指標です。劣化が進行すると、機械部品(特にベアリングやギア)の損傷箇所がぶつかる際の衝撃が大きくなり、波形の「最大振幅」が直線的に増加していくためと考えられます。「あとどれくらい持つか?」を予測する上で、最も信頼できる指標です。
- RMS (-0.556): 振動の全体的なエネルギー量を表すRMSも強い相関を示しています。故障が進行するにつれて振動エネルギー全体が底上げされるため、劣化の進行度合い(=寿命の減少)を素直に反映しています。
Kurtosisは相関係数が -0.347 と、PeakやRMSに比べるとやや低くなっています。
これは、Kurtosisが「劣化の初期段階」では鋭いピークが発生して急上昇するものの、劣化が進行して振動全体が激しくなると(波形がノイズだらけになり)、逆に値が下がったり安定したりする性質があるためです。 寿命の「全期間」を通して見ると、直線的な関係になりにくいため、相関係数が少し低めに出ていると解釈できます。
先ほどの箱ひげ図では「故障の種類の特定(分類)」に非常に役立っていた周波数特徴量(1X, 2X, High_Freq_Energyなど)ですが、「寿命の予測(回帰)」においては相関が弱いという興味深い結果になっています。
これらは「特定の故障タイプ」には強く反応しますが、故障の種類に関わらず共通して増大し続ける指標ではないためと考えられます。
たとえば、アンバランスなら1Xは増えますが高周波は増えません。ベアリング劣化ならその逆です。RUL予測モデルが「あらゆる故障を含む全体的な寿命」を予測しようとしている場合、特定の周波数成分だけを見ても全体像がつかめず、相関が低くなってしまいます。
まとめと推奨アクション
整理すると次のようになります。
- RUL予測(いつ壊れるか): Peak値とRMSをメインの特徴量として採用するのがベストです。これらは故障の種類を問わず、劣化の深刻度を素直に表してくれます。
- 故障診断(どこが壊れたか): 先ほどの分析通り、周波数成分(1X, 2X, High_Freq_Energy)を使用します。
この2つの結果を合わせると、「PeakやRMSで寿命の深刻度を監視しつつ、異常検知されたら周波数成分を見て原因を特定する」というハイブリッドな運用が、データ分析の観点から最適解であると言えます。
残存寿命予測モデルの構築と評価
データの準備とモデルの訓練
残存寿命(RUL)を予測するモデルを構築します。まず、特徴量と目的変数を分離し、訓練データとテストデータに分割します。
# 特徴量データ (X) とターゲット変数 (y) を設定
X = vibration_df[feature_columns]
y = vibration_df['RUL']
# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=42
)
# 分割後のデータ数を表示
print(f"訓練データ数: {len(X_train)}") # 訓練データのサンプル数
print(f"テストデータ数: {len(X_test)}") # テストデータのサンプル数
以下、実行結果です。
訓練データ数: 745 テストデータ数: 249
RandomForestモデルとXGBoostモデルを構築し、性能を比較します。
# ランダムフォレストモデルのインスタンスを作成
rf_model = RandomForestRegressor(
n_estimators=100, # 決定木の数
max_depth=10, # 決定木の最大深さ
min_samples_split=10, # ノードを分割するために必要な最小サンプル数
random_state=42 # 再現性のための乱数シード
)
# ランダムフォレストモデルを訓練データで学習
rf_model.fit(X_train, y_train)
# テストデータを用いて予測を実行
y_pred_rf = rf_model.predict(X_test)
# XGBoostモデルのインスタンスを作成
xgb_model = XGBRegressor(
n_estimators=100, # 決定木の数
max_depth=6, # 決定木の最大深さ
learning_rate=0.1, # 学習率
random_state=42 # 再現性のための乱数シード
)
# XGBoostモデルを訓練データで学習
xgb_model.fit(X_train, y_train)
# テストデータを用いて予測を実行
y_pred_xgb = xgb_model.predict(X_test)
モデルの評価と選択
両モデルの性能を評価し、より良いモデルを選択します。
from sklearn.metrics import mean_absolute_error, r2_score
# ランダムフォレストモデルの平均絶対誤差(MAE)と決定係数(R2)を計算
mae_rf = mean_absolute_error(y_test, y_pred_rf)
r2_rf = r2_score(y_test, y_pred_rf)
# XGBoostモデルの平均絶対誤差(MAE)と決定係数(R2)を計算
mae_xgb = mean_absolute_error(y_test, y_pred_xgb)
r2_xgb = r2_score(y_test, y_pred_xgb)
# モデル性能を比較して出力
print("モデル性能比較:")
print("="*50)
print(f"RandomForest - MAE: {mae_rf:.2f}日, R2: {r2_rf:.3f}")
print(f"XGBoost - MAE: {mae_xgb:.2f}日, R2: {r2_xgb:.3f}")
# MAEが小さい方のモデルを選択
if mae_rf < mae_xgb:
selected_model = rf_model # ランダムフォレストモデルを選択
model_name = "RandomForest"
y_pred = y_pred_rf
else:
selected_model = xgb_model # XGBoostモデルを選択
model_name = "XGBoost"
y_pred = y_pred_xgb
# 選択されたモデル名を出力
print(f"\n選択されたモデル: {model_name}")
以下、実行結果です。
モデル性能比較: ================================================== RandomForest - MAE: 5.21日, R2: 0.935 XGBoost - MAE: 5.24日, R2: 0.929 選択されたモデル: RandomForest
安全性の観点からの評価
予知保全では、特に危険な見逃し(実際の寿命が短いのに長いと予測)を避ける必要があります。
- 危険な見逃しは、突発停止につながる最も避けるべきエラー
- 過剰な早期警告は、不要なメンテナンスコストを発生
この観点からモデルを評価します。
# RUL(残存寿命)が10日未満であるにもかかわらず、
# 予測値が10日以上の場合をカウント(危険な見逃し)
critical_miss = np.sum((y_test < 10) & (y_pred >= 10))
# RUL(残存寿命)が30日以上であるにもかかわらず、
# 予測値が10日未満の場合をカウント(過剰警告)
false_alarm = np.sum((y_test >= 30) & (y_pred < 10))
# 安全性評価の結果を出力
print("安全性評価:")
print("="*50)
print(f"危険な見逃し(RUL<10日を見逃し): {critical_miss}件")
print(f"過剰警告(RUL≥30日を危険と判定): {false_alarm}件")
# 危険な見逃しの件数に応じた評価を出力
if critical_miss == 0:
print("\n→ 優秀:危険な見逃しがありません")
elif critical_miss < 3:
print("\n→ 良好:危険な見逃しが少ない")
else:
print("\n→ 要改善:危険な見逃しが多い")
以下、実行結果です。
安全性評価: ================================================== 危険な見逃し(RUL<10日を見逃し): 15件 過剰警告(RUL≥30日を危険と判定): 0件 → 要改善:危険な見逃しが多い
予知保全の最大の目的は「ドカ停(突発的なライン停止)」を防ぐことです。
そのため「危険な見逃し:15件」は深刻な問題になります。
- 現場で起きること: RUL(残存寿命)が10日を切っている(=今すぐ部品交換の準備が必要)にもかかわらず、AIは「まだ10日以上持つ」と判断しました。
- 結果: メンテナンス担当者はAIを信じて部品発注や修理計画を先送りにし、結果として機械が稼働中に突然故障します。
- 15件という数字: テストデータの中で15回もこの判断ミスが起きているため、このまま現場導入すると「AIを入れたのに機械が止まる」という事態が頻発し、現場の信頼を完全に失います。
では、「過剰警告:0件」はどうでしょうか。
一見「無駄な交換提案がなくて良いこと」に見えますが、「見逃し15件」とセットで考えると、これは「モデルが楽観的すぎるバイアス」を持っていることを示しています。
要するに、このモデルは、迷ったときに「まだ寿命はある(安全側)」と予測する傾向が強すぎます。
予知保全のモデルとしては、「多少の空振り(過剰警告)をしてでも、見逃しは絶対に防ぐ」という、いわゆる「心配性なモデル」の方が安全です。現在のモデルは「自信満々なモデル」になってしまっています。
この問題を解決するためには、モデルに「寿命を長く見積もることへのペナルティ」を与えるなどの工夫が必要になります。
まずは、「見逃しゼロ(あるいは限りなくゼロ)」を目指してモデルのチューニングを行うのが、次の最優先事項です。
PDPで故障進行パターンを理解する
PDPによる全体傾向の把握
PDP(Partial Dependence Plot)を使って、各特徴量と残存寿命の関係を可視化します。
PDPは、ある特徴量が変化したときに、モデルの予測がどう変化するかを示す強力なツールです。
各特徴量のPDPを可視化します。
# Explainerの作成
explainer_maintenance = dx.Explainer(
selected_model,
X_test,
y_test,
label=f"{model_name}予知保全モデル"
)
# PDPの作成
pdp = explainer_maintenance.model_profile(
type='pdp', # PDP(部分依存プロット)を指定
variables=feature_columns # 特徴量を指定
)
# PDPのプロット
pdp.plot()
以下、実行結果です。
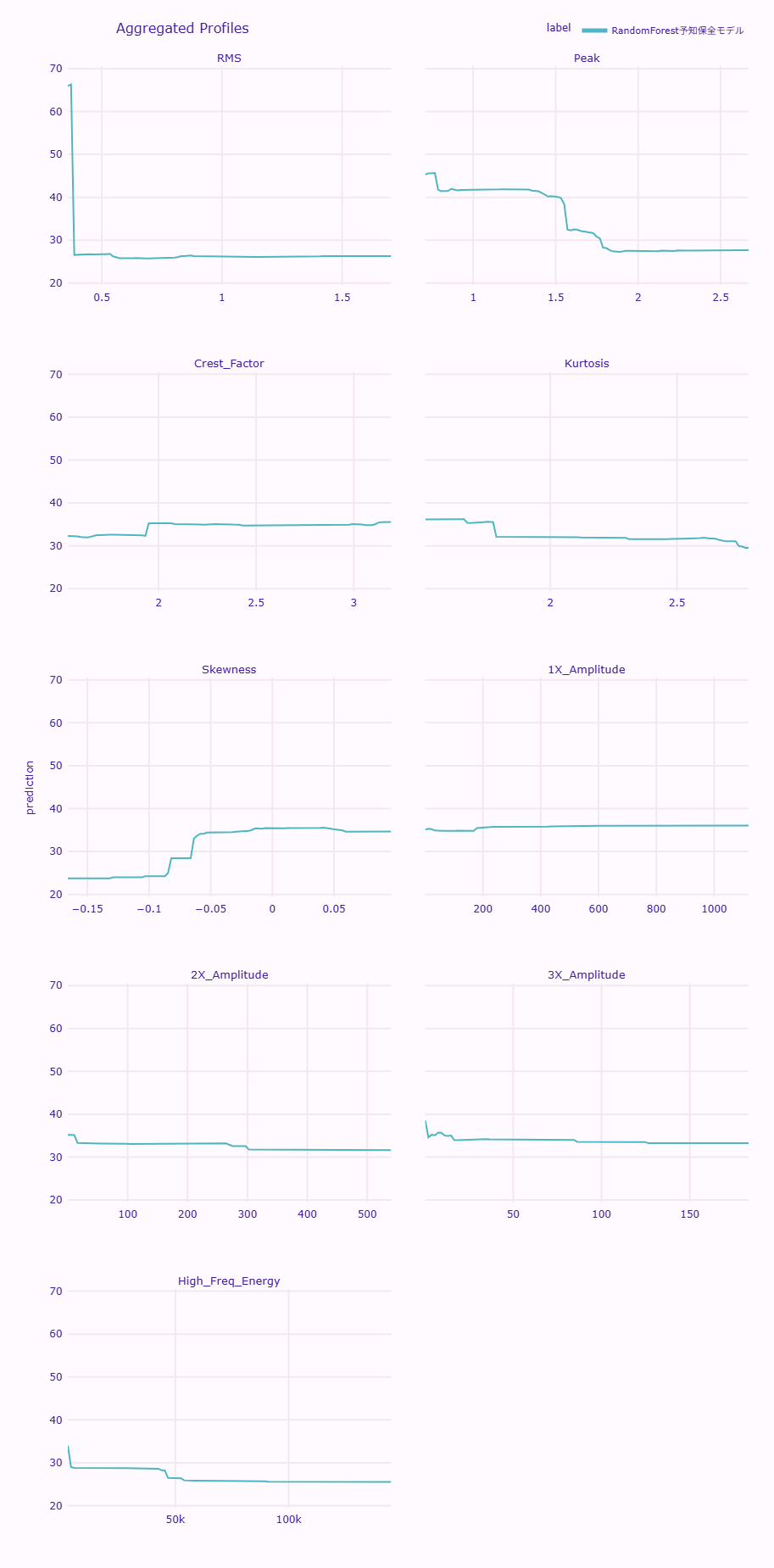
RMS値による管理基準 RMS値のPDPを見ると、RMS値が約0.4までは残存寿命の予測値が高く維持されていますが、0.4を超えると急激に減少し、その後は約28日程度の低い水準で横ばいとなります。
これを基に、RMS値0.5を重要な管理閾値として設定することが妥当と考えられます。
- 正常範囲(RMS < 0.4付近): 残存寿命は長く保たれている状態。
- 要注意範囲(RMS ≥ 0.4付近): 残存寿命が大幅に短縮している可能性が高く、詳細な点検や対応の検討が必要な状態。
ICEによる個体差の分析
PDPは全体的な傾向を示しますが、実際の設備には個体差があります。
ICE(Individual Conditional Expectation)を使って、この個体差を分析します。
# サンプルサイズを設定
sample_size = 30
# テストデータからランダムにサンプルを選択
sample_indices = np.random.choice(
X_test.index,
size=sample_size,
replace=False
)
sample_data = X_test.loc[sample_indices]
# ICE(個別効果)プロファイルを生成
# RMS特徴量に対する個別の予測効果を計算
ice_rms = explainer_maintenance.predict_profile(
sample_data, # サンプルデータ
variables=['RMS'] # 対象の特徴量
)
# ICEプロファイルをプロット
ice_rms.plot()
以下、実行結果です。
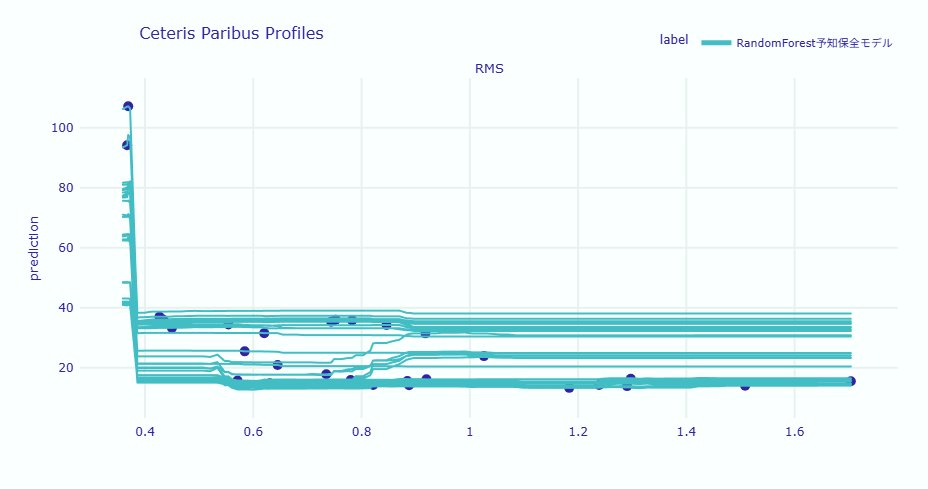
ICEプロットを見ると、ほぼ全てのサンプルでRMS値が0.4付近を超えた段階で急激に予測値が低下する共通の傾向が見られます。しかし、低下して安定した後の残存寿命の水準(縦軸の高さ)には、約15日から40日程度までの大きな開きがあります。
これは、RMS値が同じ「異常域」にあったとしても、その他の複合的な要因(使用環境、負荷パターン、メンテナンス履歴など)によって、実際の残存寿命予測が大きく異なることを示しています。
したがって、現場での運用においては、RMS値による「異常検知(トリガー)」は共通化しつつも、そこから交換までの猶予期間(残存寿命)については、設備ごとの個体差や使用環境(コンテキスト)を加味して判断することが重要です。
SHAPで緊急メンテナンスの判断根拠を説明
SHAP分析による要因分解
SHAP分析を振動データに適用し、なぜ特定の設備が緊急メンテナンスを必要とするのかを見ていきます。
# RUL(残存寿命)が15日未満の設備を抽出
urgent_mask = (y_test < 15)
urgent_indices = y_test[urgent_mask].index
# 緊急対応が必要な設備の数を出力
print(f"緊急対応が必要な設備数: {len(urgent_indices)}台")
# 緊急対応が必要な設備が存在する場合の処理
if len(urgent_indices) > 0:
# 最も緊急性の高い設備(RULが最小)のインデックスを取得
most_urgent_idx = y_test.idxmin()
# 最も緊急性の高い設備の特徴量データを取得
urgent_equipment = X_test.loc[[most_urgent_idx]]
# 実際のRUL(残存寿命)を取得
actual_rul = y_test.loc[most_urgent_idx]
# モデルによる予測RULを計算
predicted_rul = selected_model.predict(urgent_equipment)[0]
# 最も緊急性の高い設備の情報を出力
print(f"\n最も緊急性の高い設備(ID: {most_urgent_idx}):")
print(f" 実際のRUL: {actual_rul:.1f}日") # 実際のRULを小数点1桁で表示
print(f" 予測RUL: {predicted_rul:.1f}日") # 予測RULを小数点1桁で表示
以下、実行結果です。
緊急対応が必要な設備数: 51台 最も緊急性の高い設備(ID: 664): 実際のRUL: 5.8日 予測RUL: 14.3日
SHAP分析を実行し、各特徴量の寄与度を計算します。
# predict_partsメソッドを使用して、緊急設備のSHAP値を計算
shap_analysis = explainer_maintenance.predict_parts(
urgent_equipment, # 緊急設備の特徴量データ
type='shap', # SHAP値を計算する指定
B=100, # モンテカルロシミュレーションのサンプル数
)
# SHAP値の計算結果を取得
shap_result = shap_analysis.result
# 各特徴量の平均的なSHAP値を計算
shap_values = shap_result.groupby(
'variable_name' # 特徴量名でグループ化
)[
'contribution' # SHAP値の平均を計算する列を指定
].mean().sort_values() # 平均SHAP値でソート
# ベースライン(平均的な設備のRUL)を計算
baseline = y_train.mean()
# ベースラインを出力
print(f"ベースライン(平均的な設備のRUL): {baseline:.1f}日")
# SHAP値をプロット
shap_analysis.plot(show=True)
以下、実行結果です。
ベースライン(平均的な設備のRUL): 35.9日
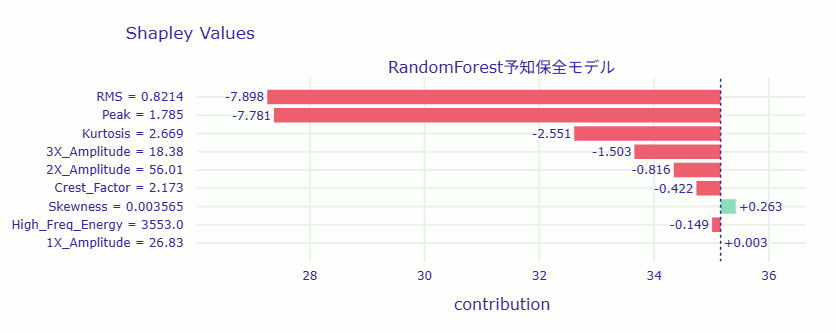
SHAP値の解釈と対策立案
どの要因が残存寿命を短くしているかを明確にし、各特徴量のSHAP値(寄与度)がマイナス(寿命を縮めている)の場合には、次のような対策案を考えました。
| 特徴量 | 振動の「癖」 | 物理的な現象 | 推奨される対策 |
|---|---|---|---|
| RMS | 全体的に揺れる | エネルギー過多・ガタつき | ボルト増し締め、基礎点検 |
| Peak / Kurtosis | ガツンと叩く衝撃 | 衝突・欠損 | ギア点検、異物確認 |
| Crest Factor | チリチリした鋭い衝撃 | 点接触の異常(初期) | ベアリング精密診断 |
| 1X | ブンブン回る揺れ | 重心ズレ(遠心力) | バランシング(バランス取り) |
| 2X / 3X | 軸がこじれる揺れ | 軸芯のズレ・拘束 | 芯出し(アライメント) |
| High Freq | キーキー擦れる音 | 摩擦・油切れ | グリスアップ・給油 |
この表をもとに、劣化要因分析と推奨アクションを提示します。
# 劣化要因の分析
print("=== 劣化要因分析と推奨アクション ===")
for feature in shap_values.index:
contribution = shap_values[feature]
feature_value = urgent_equipment[feature].values[0]
# 寄与度がマイナス(寿命を縮めている)の場合のみ詳細表示
# しきい値を少し調整(画像ではKurtosisが-2.5なので、ここも拾えるように-2.0などにするのも手です)
if contribution < -2.0:
print(f"\n[{feature}]")
print(f" 現在値: {feature_value:.3f}")
print(f" 寄与度: {contribution:+.1f}日")
# 深刻度判定
if contribution < -5.0:
print(" ★判定: 重大な劣化要因 (Critical)")
else:
print(" ☆判定: 注意が必要な要因 (Warning)")
# 具体的な対策ロジック
if feature == 'RMS':
print(" → 対策: 設備全体の締結確認、基礎ボルトの緩み点検")
elif feature == 'Peak':
print(" → 対策: 衝撃振動が発生中。ギア欠損や異物噛み込みの点検")
elif feature == 'Crest_Factor':
print(" → 対策: ベアリングの初期損傷(剥離・圧痕)の精密診断")
elif feature == 'Kurtosis': # 画像で3番目に高い要因
print(" → 対策: 振動波形の衝撃性増大。ベアリング・接触状態の確認")
elif feature == 'High_Freq_Energy':
print(" → 対策: 潤滑不足の確認、グリスアップ、異物混入の調査")
elif feature == '1X_Amplitude':
print(" → 対策: 回転体のアンバランス修正(バランシング)")
elif feature in ['2X_Amplitude', '3X_Amplitude']:
print(" → 対策: カップリングの芯出し調整(ミスアライメント修正)")
以下、実行結果です。
=== 劣化要因分析と推奨アクション === [RMS] 現在値: 0.821 寄与度: -7.9日 ★判定: 重大な劣化要因 (Critical) → 対策: 設備全体の締結確認、基礎ボルトの緩み点検 [Peak] 現在値: 1.785 寄与度: -7.8日 ★判定: 重大な劣化要因 (Critical) → 対策: 衝撃振動が発生中。ギア欠損や異物噛み込みの点検 [Kurtosis] 現在値: 2.669 寄与度: -2.6日 ☆判定: 注意が必要な要因 (Warning) → 対策: 振動波形の衝撃性増大。ベアリング・接触状態の確認
この結果から、単なる部品の摩耗ではなく、設備が「激しいガタつき」と「衝突」を併発している危険な状態にあることが分かります。
- RMSとPeakが致命的: 振動エネルギー(RMS)と衝撃の最大値(Peak)が共に寿命を約8日ずつ縮めており、これが劣化の主原因です。
- 構造的な緩みが疑われる: この2つが同時に高い場合、ベアリング単体の損傷というより、基礎ボルトの緩みや剛性不足による「機械全体のガタつき」が疑われます。
分析結果に基づく推奨対策として、最優先で基礎ボルトやケーシング固定ボルトの増し締めが挙げられます。現状のデータ傾向は外部的なガタつきを強く示唆しており、締結部の緩みを解消することで状態が改善する可能性が高いためです。
なお、増し締めを実施しても振動レベルの改善が見られない場合は、ギア欠損やカップリング破損といった物理的な内部損傷が進行している懸念があるため、速やかな開放点検への移行が必要と判断されます。
このようにSHAP分析により、単に「危険」と判定するだけでなく、なぜ危険なのか、どの要因が最も影響しているのかを定量的に説明できます。これにより、的確な対策を立案できます。
品質管理と予知保全の統合
なぜ統合管理が必要なのか
前回取り上げた品質管理と、今回の予知保全は、実は密接に関連しています。
この企業内での調査によると、品質不良の約65%は設備の劣化や異常が根本原因となっていました。
しかし、多くの工場では品質部門と保全部門が独立して活動しており、この関連性を見逃していることが多いです。
データ統合で見えてきた真実
品質データと振動データを統合して時系列で分析したところ、興味深いパターンが発見されました。
月曜日の朝、週末明けの生産立ち上げ時に金型交換を行うのですが、作業者が急いで作業を行うため、わずかなミスアライメント(芯ずれ)が生じていました。
このミスアライメント自体は微細で、月曜日の品質には影響しません。
しかし、累積した振動により、火曜日の午後になると金型の位置がさらにずれ、寸法不良を引き起こしていたのです。
振動データ単独では「正常範囲内」、品質データ単独では「原因不明」でしたが、統合することで真の原因が明らかになりました。
対策は簡単でした。
月曜朝の金型交換時に、レーザー測定器で芯出しを確認するステップを追加したのです。
これにより、火曜日問題は完全に解決し、週間の不良率が40%減少しました。
統合ダッシュボードの設計
データを統合しても、現場で活用されなければ意味がありません。
使いやすく、アクションにつながるダッシュボードの設計が重要です。
効果的なダッシュボードは3階層構造を持ちます。
第1階層の「健康診断画面」では、全設備と全製品の状態を信号機形式(緑・黄・赤)で一覧表示します。異常があれば一目で分かり、優先順位も明確です。
第2階層の「診断画面」では、選択した設備や製品の詳細情報を表示します。振動トレンド、品質トレンド、相関グラフなどを確認でき、問題の原因を探ることができます。
第3階層の「処方箋画面」では、XAIが分析した結果を基に、具体的な対策を提示します。「振動が原因で3日後に品質異常が発生する可能性80%。推奨対策:軸受点検(作業時間2時間、必要部品は在庫あり)」といった形で、実行可能なアクションを提案します。
アラートの最適化
統合管理の大きなメリットは、アラートの精度向上です。
従来は振動と品質を別々に監視していたため、誤報が多く発生していました。
たとえば、振動が0.8mmを超えただけでアラートを出すと、月に50回以上の誤報が発生します。
しかし、「振動が0.8mmを超え、かつ品質スコアが低下傾向にある」という複合条件にすることで、誤報を90%削減しながら、真の異常を確実に検出できるようになりました。
また、アラートには必ず具体的なアクションを付けることが重要です。
「異常発生」という警告だけでなく、「振動増加により2日後に品質異常の可能性あり。軸受点検を推奨(予想作業時間:2時間、必要工具:振動計、聴診棒)」という形で、次の行動を明確に示します。
現場への実装とベストプラクティス
段階的導入による成功パターン
XAIシステムの導入で最も重要なのは、段階的なアプローチです。
いきなり全設備に適用するのではなく、「痛みの大きい場所」から始めることが成功の鍵となります。
実際の成功事例を紹介しましょう。
ある大手自動車部品メーカーでは、まず最も品質要求が厳しく、生産額が大きいエンジン部品ラインの20台の設備から開始しました。
6ヶ月のパイロット期間で、品質不良率を3.2%から1.1%に削減し、緊急停止を月3回から0.5回に削減しました。
この成功により経営層の信頼を獲得し、全社展開への道が開けました。
段階的導入のもう一つのメリットは、既存インフラを最大限活用できることです。
多くの工場では、PLC(Programmable Logic Controller)やDCS(Distributed Control System)に大量のデータが蓄積されていますが、活用されていません。
まずはこれらのデータから始めることで、初期投資を最小限に抑えられます。
現場の巻き込み方
技術的に優れたシステムでも、現場に受け入れられなければ失敗します。
成功のポイントは、現場作業者を「共同開発者」として位置づけることです。
ベテラン保全員の経験則をシステムに組み込むことから始めましょう。
「この音がしたら軸受交換時期」という暗黙知を、振動パターンとして定義し、AIに学習させます。
AIが出した結果をベテランに確認してもらい、「確かにこのパターンの時に異常が起きる」という納得感を得ることが重要です。
若手作業者には「AIの先生」という役割を与えます。
AIが誤診断した際、なぜ間違えたのかを分析し、正しい判断を教える役割です。
これにより、AIへの理解が深まると同時に、設備診断スキルも向上します。
実際、この方法により、従来3年かかっていた技能習得期間を1年に短縮できた事例もあります。
データリテラシーの向上
全員をデータサイエンティストにする必要はありませんが、基本的なデータリテラシーは必要です。
重要なのは、現場の言葉で教育することです。
たとえば、標準偏差を説明する際は「ばらつきの大きさ」、相関係数は「2つの値がどれだけ一緒に動くか」というように、専門用語を避けて説明します。
また、自分たちのデータを使った実例で学ぶことで、理解が深まります。
定期的な改善事例発表会も効果的です。
XAIを活用して問題を解決した事例を共有し、成功体験を組織全体に広げます。失敗事例も隠さず共有することで、組織全体の学習を促進します。
継続的改善のサイクル
XAIシステムは導入して終わりではありません。
継続的な改善により、精度と価値を高め続ける必要があります。
モデルの性能は時間とともに劣化します。
これは「コンセプトドリフト」と呼ばれる現象で、製造条件の変更、材料の変更、季節変動などが原因です。
月次でモデルの性能を評価し、精度が5%以上低下した場合は再学習を実施します。
特に重要なのは、「レアイベント」(めったに起こらない珍しい出来事)の扱いです。
年に1回しか起きない重大故障のデータは、通常運転データの1万倍の価値があります。
こうした貴重なデータを確実に蓄積し、モデルに反映させる仕組みが必要です。
フィードバックループも重要です。
XAIの予測と実際の結果を比較し、誤差の大きかったケースを分析します。
なぜ予測が外れたのか、どのような特徴を見逃していたのかを理解し、モデルや特徴量を改善します。
投資効果の測定
経営層への報告では、定量的な効果測定が重要です。
一般的に、適切に導入されたXAIシステムは6〜12ヶ月で投資を回収できます。
たとえば、測定すべき指標は以下の通りです。
- 品質改善:不良率の削減率、品質コストの削減額
- 設備効率:緊急停止回数の削減、設備稼働率の向上
- 保全効率:メンテナンスコストの削減、部品在庫の最適化
- 人材育成:技能習得期間の短縮、ベテラン技能の形式知化率
これらを月次でモニタリングし、改善効果を可視化することで、組織全体のモチベーション向上にもつながります。
まとめ
第5回(製造業でのXAI実践 その1)から今回の第7回(製造業でのXAI実践 その3)まで、とある製造業のXAI事例を取り上げました。
XAIの真の価値は、単に高精度な予測をすることではありません。
「なぜその予測をしたのか」を説明できることで、人間の理解と信頼を獲得し、適切な行動につながることに価値があります。
ベテランの経験とAIの分析力を融合させることで、これまで不可能だった高度な製造管理が可能になります。
今後、製造業におけるXAIはさらに進化していくでしょう。
しかし、技術がどれだけ進化しても、最終的に価値を生み出すのは人間です。
XAIを「魔法の箱」ではなく「優秀な相棒」として活用し、人間の創造性と判断力を増幅させることが、製造業の未来を切り開く鍵となります。

