私たちは日々、膨大な情報に囲まれて生活しています。

スマートフォンには何百ものアプリがあり、ニュースサイトには無数の記事があふれ、SNSでは毎秒新しい投稿が生まれています。

この情報の洪水の中で、私たちは無意識のうちに「本当に大切な情報は何か」を選別しながら生活しています。

データ分析の世界でも、同じような課題に直面します。

たとえば、ある企業の顧客データベースには、顧客一人ひとりについて年齢、性別、居住地、年収、職業、購買履歴、サイト訪問回数、滞在時間、クリック数、お気に入り登録数……と、数十から数百もの項目（変数）が記録されているかもしれません。

「こんなにたくさんの変数、どうやって分析すればいいの？」

そんな疑問に答えてくれるのが、今回から学ぶ次元削減という技術です。

身近な例で考える「次元削減」

　5教科の成績を1つの数字にまとめる

次元削減の考え方を、身近な例で理解してみましょう。

あなたが高校の先生で、生徒たちの学力を把握したいとします。

国語、数学、英語、理科、社会の5教科のテスト結果があります。

5教科すべての点数を見れば詳細な情報が得られますが、「この生徒は全体的にどのくらいできるのか」を一言で表現したいとき、私たちは自然と「5教科の合計点」や「平均点」を使います。

これこそが、5次元のデータを1次元に要約する次元削減の一例なのです。

 

　単純な合計では失われる情報もある

しかし、単純な合計や平均では失われてしまう情報もあります。

たとえば、「文系科目が得意で理系科目が苦手」といった傾向は、合計点だけでは分かりません。

同じ合計300点でも、こんな2人の生徒がいたとしましょう。

• 生徒A：国語80、数学40、英語80、理科40、社会60
• 生徒B：国語60、数学60、英語60、理科60、社会60

合計点は同じでも、2人の「強み・弱み」のパターンはまったく異なりますよね。

主成分分析は、このような「データの中に隠れた構造」を発見しながら、効率的に次元を削減する方法を提供してくれます。

 

Pythonで実際にデータを見てみよう

それでは、実際にPythonを使いながらPCAの考え方を体感していきましょう。

 

　ライブラリの準備

以下のコードでは、データ分析と可視化に必要なライブラリを読み込みます。

NumPyは数値計算、pandasはデータ操作、matplotlibとseabornはグラフ描画に使います。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib

# 乱数のシードを固定して再現性を確保
np.random.seed(42)  

 

このコードを実行すると、以降のすべてのコードを動かす準備が整います。

np.random.seed(42)を設定することで、何度実行しても同じ結果が得られるようになります。

 

シンプルな2次元データで直感をつかむ

いきなり5次元のデータを扱うのは大変なので、まずは2次元のデータを使ってPCAの基本的な考え方を理解しましょう。

 

　サンプルデータの作成

ある店舗の従業員について、「接客スキル」と「商品知識」の2つの評価スコアがあるとします。

この2つのスキルには相関がある（片方が高い人はもう片方も高い傾向がある）と仮定してデータを作成します。

# 従業員50人分の評価データを生成
n_employees = 50

# 基礎能力（両方のスキルに影響する共通の要因）
base_ability = np.random.normal(0, 1, n_employees)

# 接客スキルと商品知識（基礎能力 + 個別のばらつき）
接客スキル = (
    base_ability * 3 + 
    np.random.normal(0, 1, n_employees) + 
    50
)
商品知識 = (
    base_ability * 2 + 
    np.random.normal(0, 1.5, n_employees) + 
    50
)

# DataFrameにまとめる
df = pd.DataFrame({
    '接客スキル': 接客スキル,
    '商品知識': 商品知識
})

print("従業員評価データ（最初の10人）:")
print(df.head(10).round(1))
print(f"\nデータ数: {len(df)}人")

 

以下、実行結果です。

従業員評価データ（最初の10人）:
   接客スキル  商品知識
0   51.1  48.6
1   51.6  52.1
2   49.0  51.8
3   51.8  52.0
4   49.5  48.3
5   46.9  47.8
6   56.1  55.6
7   51.9  49.9
8   46.9  48.3
9   55.8  52.5

データ数: 50人

 

このコードを実行すると、50人分の従業員評価データが生成されます。

両方のスキルが50点を中心に分布しており、「基礎能力が高い人は両方のスキルが高くなる」という構造を持っています。

この「隠れた構造」をPCAで発見できるかどうかがポイントになります。

 

　散布図でデータの形を確認する

次に、このデータを散布図で可視化してみましょう。

データがどのような「形」をしているかを目で見ることは、分析の第一歩として非常に重要です。

# グラフのサイズを指定
plt.figure(figsize=(8, 8))

# 散布図を描く
plt.scatter(
    df['接客スキル'], 
    df['商品知識'], 
    alpha=0.6, 
    s=100

)
plt.xlabel('接客スキル')
plt.ylabel('商品知識')
plt.title('従業員の評価スコア分布')
plt.axis('equal')  # 縦横の比率を揃える
plt.grid(True, alpha=0.3)
plt.show()

 

以下、実行結果です。

 

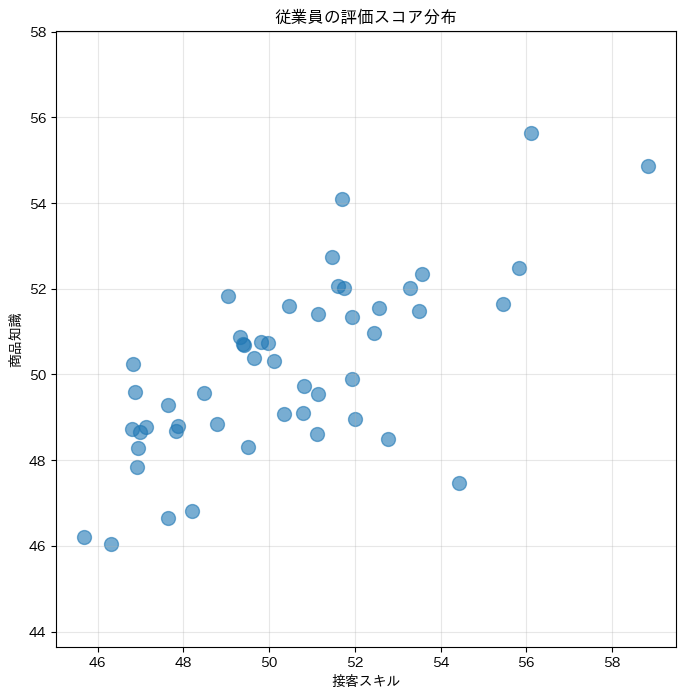
50人の従業員が2次元平面上にプロットされた散布図です。

データが右上がりの楕円形に分布していることが見て取れるはずです。

これは、接客スキルが高い人は商品知識も高い傾向があることを示しています。

 

相関を数字で確認する

散布図で視覚的に確認した「右上がりの傾向」を、数字でも確認してみましょう。

2つの変数の関係の強さを表す指標が相関係数です。

# 相関係数を計算
cor = df['接客スキル'].corr(df['商品知識'])
print(f"接客スキルと商品知識の相関係数: {cor:.3f}")

 

以下、実行結果です。

接客スキルと商品知識の相関係数: 0.693

 

相関係数は-1から1の間の値を取り、1に近いほど強い正の相関（一方が増えると他方も増える）、-1に近いほど強い負の相関を示します。

 

「データが広がる方向」を見つける（PCAの核心）

ここからが、PCAの核心部分です。

散布図をもう一度見てください。データは楕円形に分布していますね。

この楕円には、長い軸と短い軸があります。

PCAの基本的なアイデアは、この「データが最も広がっている方向」を見つけることです。

 

　なぜ「広がっている方向」が大事なのか？

データが広がっている方向には、そのデータを特徴づける重要な情報が含まれています。

逆に、データがあまり広がっていない方向には、あまり重要でない情報（またはノイズ）が含まれていることが多いのです。

先ほどの従業員データで考えてみましょう。

• 最も広がっている方向：「総合的な能力の高低」を表している（両方のスキルが高い人と低い人の違い）
• あまり広がっていない方向：「接客重視か商品知識重視か」という個人差を表している

 

　平均を中心にデータを見る

PCAを行う前に、データを中心化（平均を0にする）します。

これにより、「データがどの方向に広がっているか」を原点を基準に考えやすくなります。

# データを中心化（平均を引く）
X_centered = df.values - df.values.mean(axis=0)

print("中心化前の平均:")
print(f"  接客スキル: {df['接客スキル'].mean():.2f}")
print(f"  商品知識: {df['商品知識'].mean():.2f}")

print("\n中心化後の平均:")
print(f"  接客スキル: {X_centered[:, 0].mean():.6f}")
print(f"  商品知識: {X_centered[:, 1].mean():.6f}")

 

このコードを実行すると、中心化によって両方の変数の平均が0（ほぼ0）になったことが確認できます。これで、原点を中心にデータの「広がり」を分析できるようになりました。

 

　中心化したデータを可視化する

中心化したデータを散布図で確認してみましょう。

plt.figure(figsize=(8, 8))
plt.scatter(X_centered[:, 0], X_centered[:, 1], 
            alpha=0.6, s=100, c='#2E86AB')
plt.axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
plt.axvline(x=0, color='gray', linestyle='-', linewidth=0.5)
plt.xlabel('接客スキル（中心化後）', fontsize=12)
plt.ylabel('商品知識（中心化後）', fontsize=12)
plt.title('中心化後のデータ分布', fontsize=14, fontweight='bold')
plt.axis('equal')
plt.grid(True, alpha=0.3)
plt.show()

 

以下、実行結果です。

中心化前の平均:
  接客スキル: 50.40
  商品知識: 50.14

中心化後の平均:
  接客スキル: -0.000000
  商品知識: -0.000000

 

データを中心化しても、データそのものの「形」は変わっていませんが、中心が原点に移動したことで、これからの分析がしやすくなります。

 

様々な方向への「射影」を試してみる

PCAでは、データを様々な方向に「射影」（投影）して、その方向でのばらつき（分散）を調べます。

射影とは、データ点から直線に垂線を下ろす操作のことです。

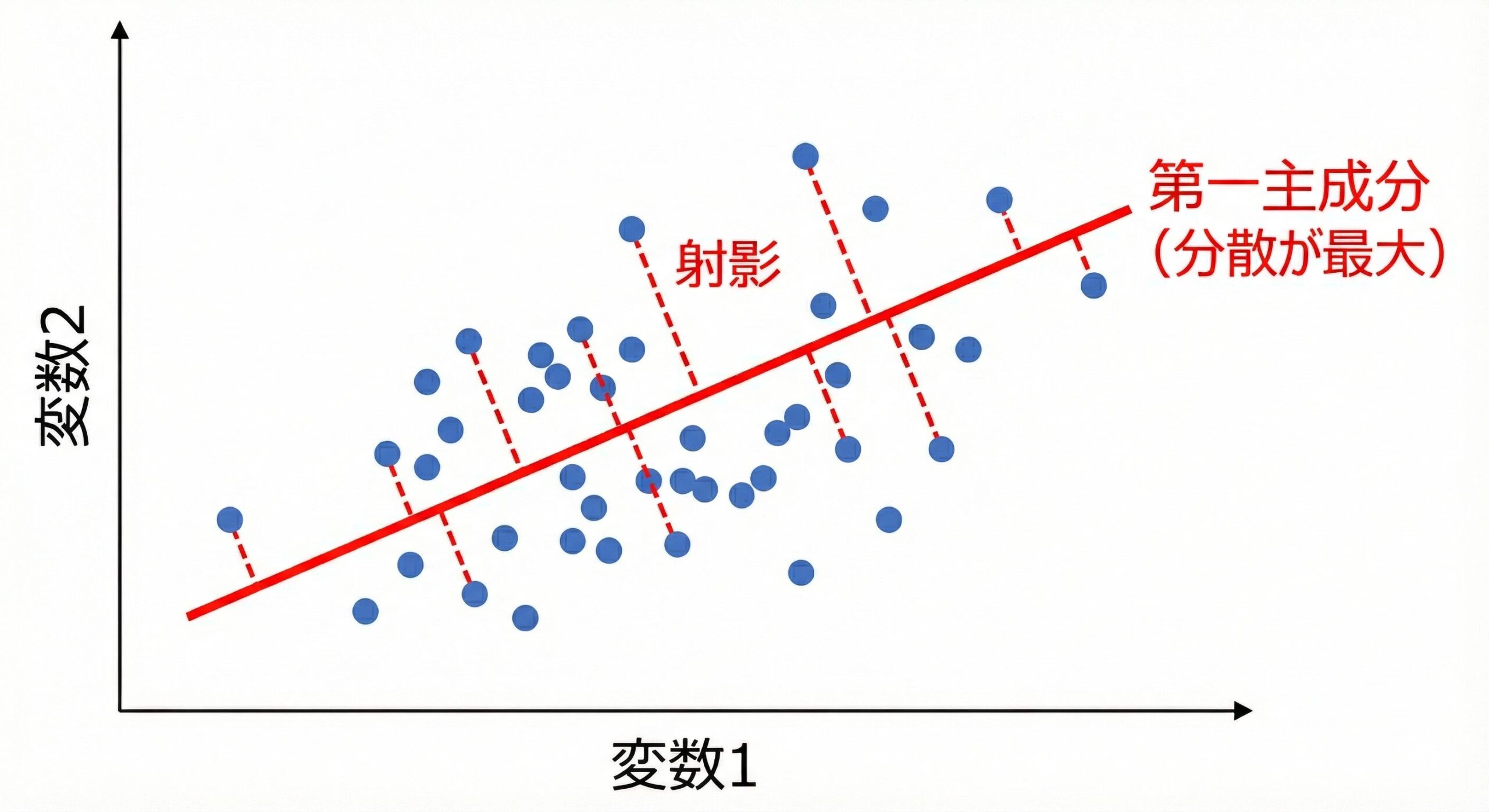
ここでは、様々な角度の直線にデータを射影したとき、どの方向で分散が最大になるかを探してみましょう。

# 様々な角度での射影分散を計算
angles = np.linspace(0, 180, 181)
variances = []

for angle in angles:
    # 角度をラジアンに変換
    rad = np.radians(angle)
    # 方向ベクトル（長さ1）
    w = np.array([np.cos(rad), np.sin(rad)])
    # 各データ点を方向wに射影
    projections = X_centered @ w
    # 射影後の分散を計算
    var = np.var(projections, ddof=1)
    variances.append(var)

# 最大分散となる角度を見つける
max_idx = np.argmax(variances)
best_angle = angles[max_idx]

print(f"分散が最大となる角度: {best_angle:.1f}度")
print(f"そのときの分散: {variances[max_idx]:.2f}")

 

以下、実行結果です。

分散が最大となる角度: 32.0度
そのときの分散: 10.81

 

最大分散となる角度の方向こそが、第1主成分の方向なのです。

 

　結果をグラフで確認する

角度と分散の関係をグラフで可視化してみましょう。

# グラフのサイズを設定
plt.figure(figsize=(10, 5))

# 分散の変化をプロット
plt.plot(angles, variances, 'b-', linewidth=2)

# 最大分散となる角度を赤い破線で示す
plt.axvline(
    x=best_angle, 
    color='red', 
    linestyle='--', 
    label=f'最大分散: {best_angle:.0f}度'
)
plt.xlabel('角度（度）')
plt.ylabel('射影後の分散')
plt.title('方向による射影後の分散の変化')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

 

以下、実行結果です。

 

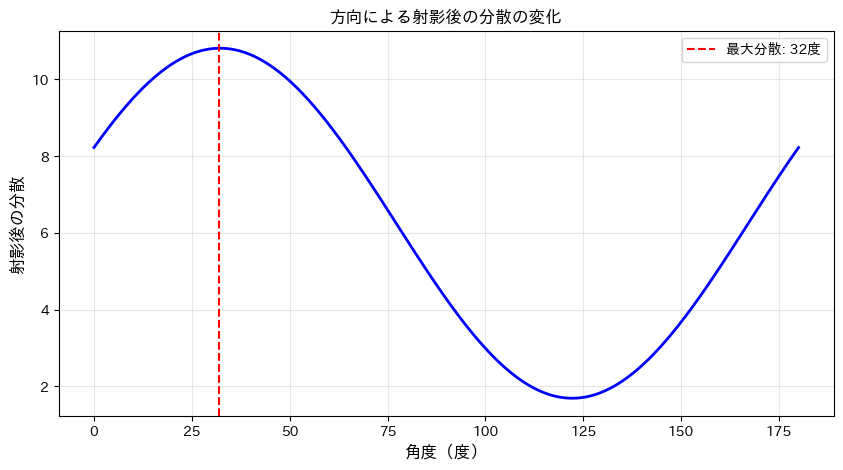
このグラフを見ると、角度によって分散が大きく変化することがわかります。

分散が最大になる角度（赤い点線）が、データが最も広がっている方向です。

 

最大分散の方向を散布図に重ねる

見つけた「最大分散の方向」を、元の散布図に矢印として重ねて表示してみましょう。

# グラフのサイズを設定
plt.figure(figsize=(8, 8))

# データ点をプロット
plt.scatter(
    X_centered[:, 0], X_centered[:, 1], 
    alpha=0.4, s=60, label='データ点'
)

# 最大分散の方向（第1主成分）を矢印で表示
rad = np.radians(best_angle)
w1 = np.array([np.cos(rad), np.sin(rad)])
arrow_length = 8
plt.arrow(
    0, 0, w1[0]*arrow_length, w1[1]*arrow_length, 
    head_width=0.4, head_length=0.3, 
    fc='red', ec='red', linewidth=2
)
plt.text(
    w1[0]*arrow_length - 0.4, w1[1]*arrow_length + 0.6, 
    '第1主成分の方向\n（最大分散）', 
    fontsize=10, color='red'
)

# 直交する方向（第2主成分）も表示
w2 = np.array([-np.sin(rad), np.cos(rad)])
plt.arrow(
    0, 0, w2[0]*4, w2[1]*4, 
    head_width=0.3, head_length=0.2, 
    fc='green', ec='green', linewidth=2
)
plt.text(
    w2[0]*4 - 1, w2[1]*4 + 0.5, 
    '第2主成分の方向', 
    fontsize=10, color='green'
)

plt.axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
plt.axvline(x=0, color='gray', linestyle='-', linewidth=0.5)
plt.xlabel('接客スキル（中心化後）')
plt.ylabel('商品知識（中心化後）')
plt.title('データの主成分方向')
plt.axis('equal')
plt.grid(True, alpha=0.3)
plt.legend(loc='lower right')
plt.show()

 

以下、実行結果です。

 

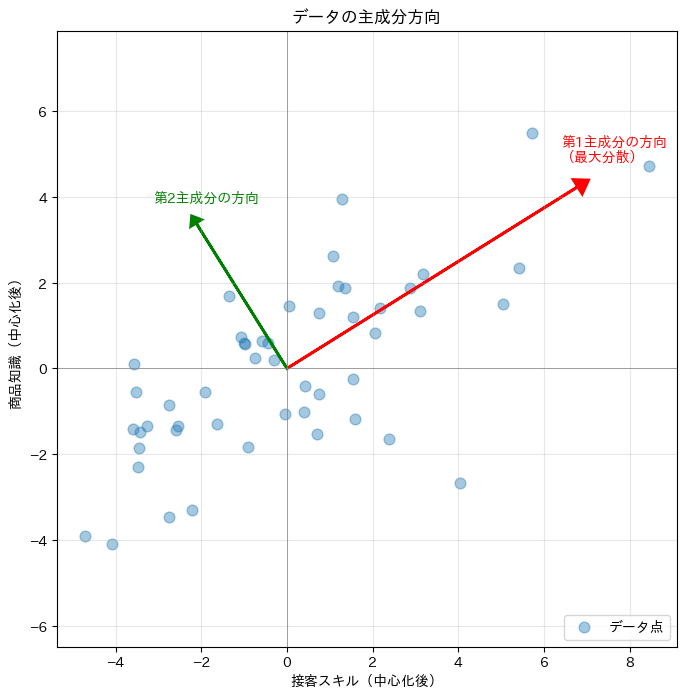
データの「広がり」の方向が赤い矢印で、それに直交する方向が緑の矢印で表示されます。

赤い矢印（第1主成分）の方向にデータが大きく広がっていることが視覚的に確認できます。

 

まとめ

この第1回では、次元削減とPCAの基本的な考え方をお話ししました。

次元削減とは、多数の変数を持つデータから、本質的な情報をできるだけ保ちながら、より少数の変数に要約する技術です。

たとえば、5教科の成績を合計点にまとめるのも、次元削減の一例と言えます。

PCAの基本的なアイデアは、「データが最も広がっている方向」を見つけることです。

この方向には、データを特徴づける重要な情報が含まれています。

今回は2次元のデータで、様々な角度に射影して分散を比較することで、この「最大分散の方向」を探しました。

次回は、共分散行列と固有値分解という数学的な道具を使って、この方向（主成分）を見つけていく方法についてお話しいたします。

Pythonで体感する次元削減入門 – PCAと因子分析の基礎のキソ— 第2回 —PCAのしくみを分散・共分散・固有値分解で理解する