このシリーズでは、機械学習の中でも特に実用的な「分類モデル」について、Pythonを使いながら一緒に学んでいきます。
第1回となる今回は、ロジスティック回帰という手法を使って「模試の点数から大学入試の合否を予測する」モデルを作ります。
数式が出てきても怖がらなくて大丈夫。数式を飛ばしても分かるようにしています。
身近な例えを交えながら、一歩ずつ進んでいきましょう。
Contents
私たちは毎日「分類」をしている
実は、私たちは日常生活の中で無意識に「分類」を行っています。
- 朝起きて天気予報を見て「今日は傘が必要か、不要か」を判断する
- メールを開いて「これは重要なメールか、迷惑メールか」を見分ける
- 友達からLINEが来て「これは冗談か、本気か」を読み取る
これらはすべて、いくつかの情報をもとに「どちらのグループに属するか」を判定する作業です。
機械学習の世界では、このような問題を分類問題と呼びます。
回帰と分類の違い
今まで「回帰分析」を学んだ方もいるかもしれません。
回帰と分類は似ているようで、実は予測するものが違います。
回帰分析は「売上は何円になるか」「気温は何度か」のような連続的な数値を予測します。
一方、分類は「合格か不合格か」「購入するかしないか」のようなカテゴリ(グループ)を予測します。
今回取り組む「模試の点数から合否を予測する」問題は、まさに分類問題の典型例です。
準備
必要なライブラリを読み込もう
まずは、今回使うPythonライブラリを読み込みます。
データ分析でおなじみのNumPy、Pandas、そして機械学習ライブラリのscikit-learnを使います。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import japanize_matplotlib from sklearn.linear_model import LogisticRegression from sklearn.linear_model import LinearRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # 乱数のシードを固定(結果を再現可能にするため) np.random.seed(42)
np.random.seed(42)は、乱数の結果を毎回同じにするためのおまじないです。
サンプルデータを作ってみよう
実際のデータを使う前に、まずは自分でデータを作ってみましょう。
100人の学生の「模試の点数」と「合否」のデータを生成します。
# 100人分のデータを生成
n_students = 100
# 模試の点数(20点〜100点の範囲でランダムに生成)
mock_scores = np.random.uniform(20, 100, n_students)
# 合格確率は点数に依存する(点数が高いほど合格しやすい)
pass_probability = 1 / (1 + np.exp(-0.1 * (mock_scores - 60)))
# 確率に基づいて合否を決定(1=合格、0=不合格)
pass_fail = np.random.binomial(1, pass_probability)
# DataFrameにまとめる
exam_df = pd.DataFrame({
'mock_scores': mock_scores,
'pass_fail': pass_fail
})
print(f"データ数: {len(exam_df)}人")
print()
print(f"合格者数: {pass_fail.sum()}人 / {n_students}人")
print()
print(exam_df.head(10))
このコードでは、模試の点数(mock_scores)が高いほど合格しやすくなるようにデータを作っています。
以下、実行結果です。
データ数: 100人 合格者数: 45人 / 100人 mock_scores pass_fail 0 49.963210 0 1 96.057145 1 2 78.559515 1 3 67.892679 1 4 32.481491 0 5 32.479562 0 6 24.646689 0 7 89.294092 1 8 68.089201 1 9 76.645806 1
pass_fail(合否)の列は、1が「合格」、0が「不合格」を表します。実際のデータでもこのように0と1で表現することが多いです。
データを可視化してみよう
数字だけ見てもピンとこないので、グラフで可視化してみましょう。
横軸に模試点数、縦軸に合否(0か1)をプロットします。
# グラフのサイズを設定
plt.figure(figsize=(10, 6))
# 不合格者のデータを散布図にプロット
plt.scatter(
exam_df['mock_scores'][exam_df['pass_fail']==0], # x軸に模試点数を設定
exam_df['pass_fail'][exam_df['pass_fail']==0], # y軸に合否を設定
c='#E94F37', # 色を設定
s=80, # サイズを設定
alpha=0.7, # 透明度を設定
label='Fail (0)' # 凡例のラベルを設定
)
# 合格者のデータを散布図にプロット
plt.scatter(
exam_df['mock_scores'][exam_df['pass_fail']==1], # x軸に模試点数を設定
exam_df['pass_fail'][exam_df['pass_fail']==1], # y軸に合否を設定
c='#2E86AB', # 色を設定
s=80, # サイズを設定
alpha=0.7, # 透明度を設定
label='Pass (1)' # 凡例のラベルを設定
)
# x軸のラベルを設定
plt.xlabel('Mock Exam Score', fontsize=12)
# y軸のラベルを設定
plt.ylabel('Result (0=Fail, 1=Pass)', fontsize=12)
# グラフのタイトルを設定
plt.title('Mock Exam Score vs Pass/Fail', fontsize=14)
# 凡例を表示
plt.legend()
# グリッドを表示
plt.grid(True, alpha=0.3)
# グラフを表示
plt.show()
以下、実行結果です。
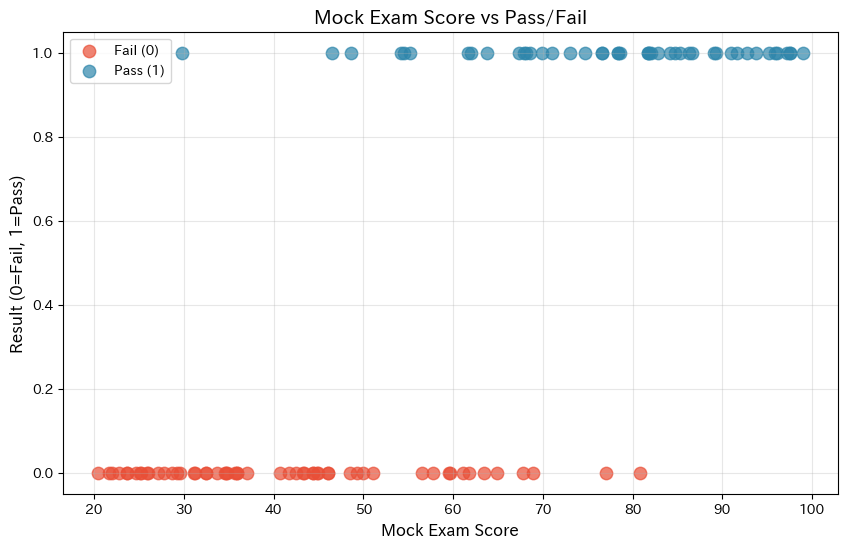
グラフを見ると、点数が低い領域(左側)には不合格者が多く、点数が高い領域(右側)には合格者が多いことがわかります。
なぜ線形回帰では分類に使えないのか?
「分類も予測の一種なら、普通の回帰分析を使えばいいのでは?」と思うかもしれません。
実際に試してみましょう。
# 線形回帰モデルを作成
model_linear = LinearRegression()
model_linear.fit(
exam_df[['mock_scores']], # 説明変数
exam_df['pass_fail'] # 目的変数
)
# 0点と100点での予測値を確認
print("【線形回帰で合否を予測】")
print(
f" 0点の学生の予測値:"
f"{model_linear.predict(pd.DataFrame([[0]], columns=['mock_scores']))[0]:.3f}"
)
print(
f" 50点の学生の予測値: "
f"{model_linear.predict(pd.DataFrame([[50]], columns=['mock_scores']))[0]:.3f}"
)
print(
f"100点の学生の予測値: "
f"{model_linear.predict(pd.DataFrame([[100]], columns=['mock_scores']))[0]:.3f}"
)
print(
f"150点の学生の予測値: "
f"{model_linear.predict(pd.DataFrame([[150]], columns=['mock_scores']))[0]:.3f}"
)
以下、実行結果です。
【線形回帰で合否を予測】 0点の学生の予測値:-0.470 50点の学生の予測値: 0.328 100点の学生の予測値: 1.127 150点の学生の予測値: 1.925
おかしなことが起きました。予測値が0〜1の範囲を超えてしまっています。合格確率が-47%や192.5%というのは意味をなしません。
これが線形回帰を分類問題に使えない理由です。
線形回帰は直線で予測するため、どこまでも値が伸びてしまいます。私たちが欲しいのは「0〜1の範囲に収まる確率」なのです。
救世主登場:シグモイド関数
この問題を解決するのがシグモイド関数(ロジスティック関数とも呼ばれます)です。
この関数は、どんな入力値も0から1の間に変換してくれる魔法のような関数です。
数式で書くと、次にようになります。
$$
\sigma(z) = \frac{1}{1 + e^{-z}}
$$
難しそうに見えますが、大切なのは「S字型のカーブを描いて、出力が必ず0〜1に収まる」ということです。
実際にグラフで見てみましょう。
# シグモイド関数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# -8から8までの値を用意
z = np.linspace(-8, 8, 200)
# シグモイド関数をプロット
plt.figure(figsize=(10, 6))
plt.plot(z, sigmoid(z), 'b-', linewidth=3)
# シグモイド関数の特徴を示すための線を引く
plt.axhline(
y=0.5,
color='red', linestyle='--', alpha=0.7,
label='Threshold = 0.5'
)
plt.axhline(
y=0,
color='gray', linestyle='-', alpha=0.3
)
plt.axhline(
y=1, color='gray', linestyle='-', alpha=0.3
)
plt.xlabel('z (Input)', fontsize=12)
plt.ylabel('σ(z) (Output: Probability)', fontsize=12)
plt.title('Sigmoid Function', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
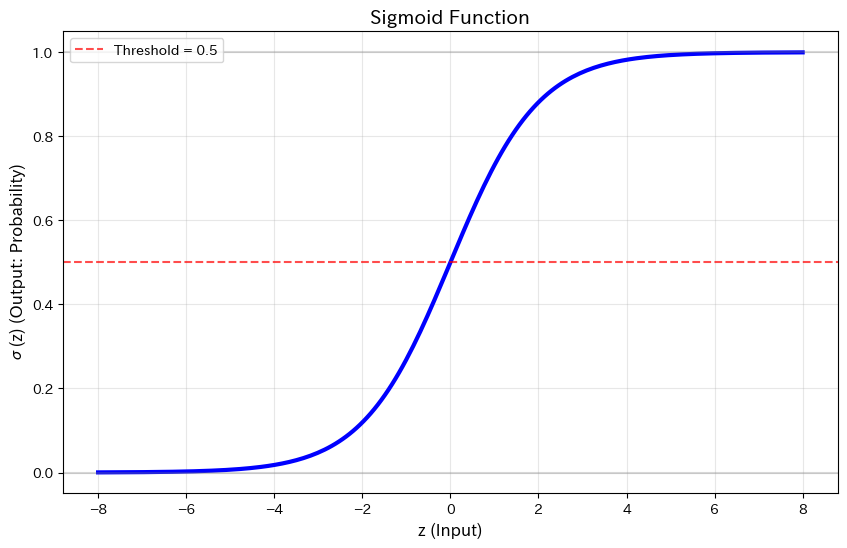
美しいS字カーブが描かれました。
重要なポイントをまとめると、入力zがどんな値でも、出力は必ず0から1の間に収まります。
z=0のとき、出力はちょうど0.5になります。zが大きくなると1に近づき、小さくなると0に近づきます。この性質のおかげで、出力を「確率」として解釈できるのです。
ロジスティック回帰のしくみ
ロジスティック回帰は、シグモイド関数を使って分類を行います。
模試点数 x から合格確率 P を求める式は次のようになります。
$$
P(\text{合格}|x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x)}}
$$
ここで、\beta_0 は切片、\beta_1 は模試点数の係数です。
シグモイド関数の中身 (\beta_0 + \beta_1 x) は線形回帰と同じ形をしていますが、それをシグモイド関数に通すことで、出力が0〜1に収まるようになります。
scikit-learnでロジスティック回帰を実装しよう
理論はここまでにして、実際にモデルを作ってみましょう。scikit-learnを使えば、たった数行で実装できます。
# ロジスティック回帰モデルを作成
model_logistic = LogisticRegression(random_state=42)
# データを整形してモデルを訓練
X = exam_df[['mock_scores']] # 説明変数
y = exam_df['pass_fail'] # 目的変数
model_logistic.fit(X, y)
print("【ロジスティック回帰の結果】")
print(f"切片 (β0): {model_logistic.intercept_[0]:.4f}")
print(f"係数 (β1): {model_logistic.coef_[0][0]:.4f}")
以下、実行結果です。
【ロジスティック回帰の結果】 切片 (β0): -7.1594 係数 (β1): 0.1168
係数が正の値であれば、模試点数が高いほど合格確率が上がることを意味します。
予測結果を可視化しよう
訓練したモデルがどのような予測をするか、グラフで確認してみましょう。
# 予測用のデータを作成(0点から100点まで)
x_plot = np.linspace(0, 100, 200)
# x_plotにカラム名を追加してDataFrameに変換
x_plot_df = pd.DataFrame(x_plot, columns=['mock_scores'])
# 合格確率を予測
y_prob = model_logistic.predict_proba(x_plot_df)[:, 1]
# グラフを描画
plt.figure(figsize=(10, 6))
plt.scatter(
exam_df['mock_scores'][exam_df['pass_fail']==0],
exam_df['pass_fail'][exam_df['pass_fail']==0],
c='#E94F37', s=80, alpha=0.7, label='Fail'
)
plt.scatter(
exam_df['mock_scores'][exam_df['pass_fail']==1],
exam_df['pass_fail'][exam_df['pass_fail']==1],
c='#2E86AB', s=80, alpha=0.7, label='Pass'
)
plt.plot(
x_plot, y_prob, 'g-', linewidth=3,
label='Predicted Probability'
)
plt.axhline(
y=0.5,
color='orange', linestyle='--', alpha=0.7,
label='Decision Boundary (0.5)'
)
plt.xlabel('Mock Exam Score')
plt.ylabel('Pass Probability')
plt.title('Logistic Regression: Pass/Fail Prediction')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
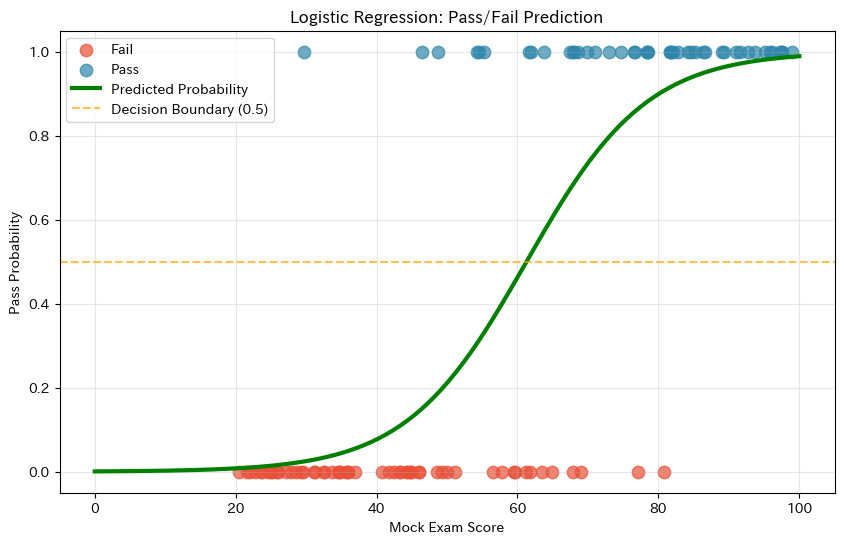
緑色のS字カーブが予測確率を表しています。
曲線が0.5を横切る点が決定境界で、この点数を境に「合格」「不合格」の予測が切り替わります。
線形回帰と違って、予測値がきちんと0〜1の範囲に収まっていますね。
具体的な点数で合格確率を計算してみよう
特定の点数での合格確率を計算してみましょう。
ロジスティック回帰の強みは、「合格か不合格か」だけでなく「合格確率は何%か」という情報も得られることです。
print("【点数別の合格確率】")
print("-" * 35)
test_scores = [40, 50, 60, 70, 80]
for score in test_scores:
score_df = pd.DataFrame([[score]], columns=['mock_scores'])
prob = model_logistic.predict_proba(score_df)[0, 1]
prediction = "合格" if prob >= 0.5 else "不合格"
print(
f"{score}点"
f" → 合格確率 {prob*100:5.1f}%"
f" → 予測: {prediction}"
)
以下、実行結果です。
【点数別の合格確率】 ----------------------------------- 40点 → 合格確率 7.7% → 予測: 不合格 50点 → 合格確率 21.1% → 予測: 不合格 60点 → 合格確率 46.3% → 予測: 不合格 70点 → 合格確率 73.5% → 予測: 合格 80点 → 合格確率 89.9% → 予測: 合格
オッズ比で係数を解釈しよう
ロジスティック回帰の係数は、オッズとオッズ比を使うことで直感的に解釈できます。まずはこの 2 つを押さえましょう。
オッズ(odds)とは?
成功(例:合格)する確率をp = P(\text{成功})とすると、オッズ(odds)は次の式で定義されます。
$$
\text{odds} = \frac{p}{1 – p}
$$
たとえば、合格確率 p = 0.8の場合、次のようになります。
$$
\text{odds} = \frac{0.8}{0.2} = 4
$$
これは、「不合格の4倍だけ合格しやすい」という意味です。
オッズ比(Odds Ratio)とは?
2つの条件 A と B があるとします。それぞれの成功確率を p_A, p_B とすると、オッズ比(OR)は次にようになります。
$$
\text{OR}=\frac{\displaystyle \frac{p_B}{1-p_B}}{\displaystyle \frac{p_A}{1-p_A}}
$$
これは「条件 B は条件 A に比べて、成功しやすさが何倍か」を表す指標です。
- OR = 1:効果なし
- OR > 1:成功する確率を高める
- OR < 1:成功する確率を下げる
ロジスティック回帰とオッズの関係
ロジスティック回帰は確率そのものではなく、オッズの対数(log-odds)を線形で説明するモデルです。
$$
\log\left(\frac{p}{1-p}\right)=\beta_0+\beta_1 x
$$
係数 β₁ とオッズ比の関係
x のときのオッズは、以下です。
$$
\exp(\beta_0 + \beta_1 x)
$$
x+1 のときのオッズは、以下です。
$$
\exp(\beta_0 + \beta_1 (x+1))
$$
この比(オッズ比)を取ると次のようになります。
$$
\frac{\exp(\beta_0 + \beta_1 (x+1))}{\exp(\beta_0 + \beta_1 x)} = \exp(\beta_1) = e^{\beta_1}
$$
これは、説明変数が 1 増えたときのオッズの変化(オッズ比)は次のように β₁ から直接求められことを意味します。
$$
\text{オッズ比} = e^{\beta_1}
$$
つまり、係数 \beta_1 の指数関数 e^{\beta_1} は、「説明変数が1単位増えたときにオッズが何倍になるか」を表します。
# 係数の取得
beta_1 = model_logistic.coef_[0][0]
# オッズ比の計算
odds_ratio = np.exp(beta_1)
print("【係数のオッズ比による解釈】")
print(f"係数 β1 = {beta_1:.4f}")
print(f"オッズ比 = exp(β1) = {odds_ratio:.4f}")
print()
print(f"→ 模試点数が1点上がると、合格のオッズが {odds_ratio:.3f}倍になる")
print(f"→ 模試点数が10点上がると、合格のオッズが {odds_ratio**10:.2f}倍になる")
以下、実行結果です。
【係数のオッズ比による解釈】 係数 β1 = 0.1168 オッズ比 = exp(β1) = 1.1239 → 模試点数が1点上がると、合格のオッズが 1.124倍になる → 模試点数が10点上がると、合格のオッズが 3.22倍になる
オッズ比が1より大きければ正の効果(点数が上がると合格しやすい)、1より小さければ負の効果を意味します。
モデルの精度を確認しよう
最後に、モデルがどれくらい正確に予測できているか確認しましょう。
# 予測を実行
y_pred = model_logistic.predict(X)
# 正解率を計算
accuracy = accuracy_score(y, y_pred)
print("【モデルの精度】")
print(f"正解率: {accuracy*100:.1f}%")
print(f"正解数: {sum(y == y_pred)}人 / {len(y)}人")
以下、実行結果です。
【モデルの精度】 正解率: 87.0% 正解数: 87人 / 100人
この正解率は、モデルが全データのうち何割を正しく予測できたかを示しています。
ただし、正解率だけでモデルの良し悪しを判断するのは危険です。
まとめ
今回学んだことを振り返りましょう。
分類問題は、データがどのカテゴリに属するかを予測する問題です。「合格/不合格」「スパム/通常メール」のような二択の問題がその典型です。
線形回帰は分類に使えません。予測値が0〜1の範囲を超えてしまい、確率として解釈できないからです。
シグモイド関数は、どんな入力も0〜1に変換するS字型の関数です。これにより、出力を確率として扱えるようになります。
ロジスティック回帰は、シグモイド関数を使って分類を行う手法です。「合格か不合格か」だけでなく「合格確率は何%か」も分かるのが強みです。
オッズ比を使えば、「点数が1点上がると合格のしやすさが何倍になるか」のように、係数を直感的に解釈できます。
次回は「線形判別分析(LDA)」を学びます。LDAは、ロジスティック回帰とは異なるアプローチで分類を行う手法で、データの「分布」に注目するのが特徴です。

