ECサイトやアプリケーションでクーポンを配布したところ、売上が20%向上したという報告を受けたとします。
一見すると施策は成功のように思えますが、ここで重要な疑問が生じます。「そのお客様は、クーポンがなくても購入していたのではないか」という疑問です。
従来の効果測定では、施策を実施したグループの購入率を単純に計測することが一般的でした。しかし、この方法では施策の「純粋な効果」を把握することができません。
今回は、この課題を解決する「アップリフト分析」について、基本的な考え方から実装方法まで順を追って説明します。
Contents
アップリフト分析の基本概念
アップリフト分析とは、マーケティング施策が顧客の行動に与える「増分効果」を測定する手法です。
単に施策後の結果を見るのではなく、「施策を実施した場合」と「実施しなかった場合」の差分を分析することで、施策の真の効果を明らかにします。
数式で理解するアップリフト効果
アップリフト効果を数学的に定式化すると、個人レベルのアップリフト効果 \tau_i は以下のように表現されます。
$$\tau_i = P(Y_i = 1 | T_i = 1, X_i) – P(Y_i = 1 | T_i = 0, X_i)$$
- Y_i は顧客 i の購入行動を表す二値変数(1=購入、0=非購入)
- T_i は施策の実施有無を表す二値変数(1=施策あり、0=施策なし)
- X_i は顧客 i の特徴量ベクトル(年齢、購入履歴など)
この式は、同一の顧客iに対して「施策を実施した場合の購入確率」と「施策を実施しなかった場合の購入確率」の差を計算しています。
しかし、現実には同一顧客に対して施策ありとなしの両方を同時に観測することはできません。これは因果推論における根本問題(Fundamental Problem of Causal Inference)と呼ばれます。
そこで、条件付き平均処置効果(Conditional Average Treatment Effect: CATE)を推定します。
$$\tau(x) = E[Y | T = 1, X = x] – E[Y | T = 0, X = x]$$
この式は、特徴量 X が x である顧客群における平均的なアップリフト効果を表しています。E[·] は期待値を表す記号で、特定の条件下での平均値を意味します。
具体例として数値を当てはめると、年齢が30歳で購入履歴が5回の顧客群において、クーポンありの場合の平均購入率が0.35(35%)、クーポンなしの場合の平均購入率が0.20(20%)であれば、この顧客群のアップリフト効果は0.15(15%)となります。
4タイプの顧客セグメント
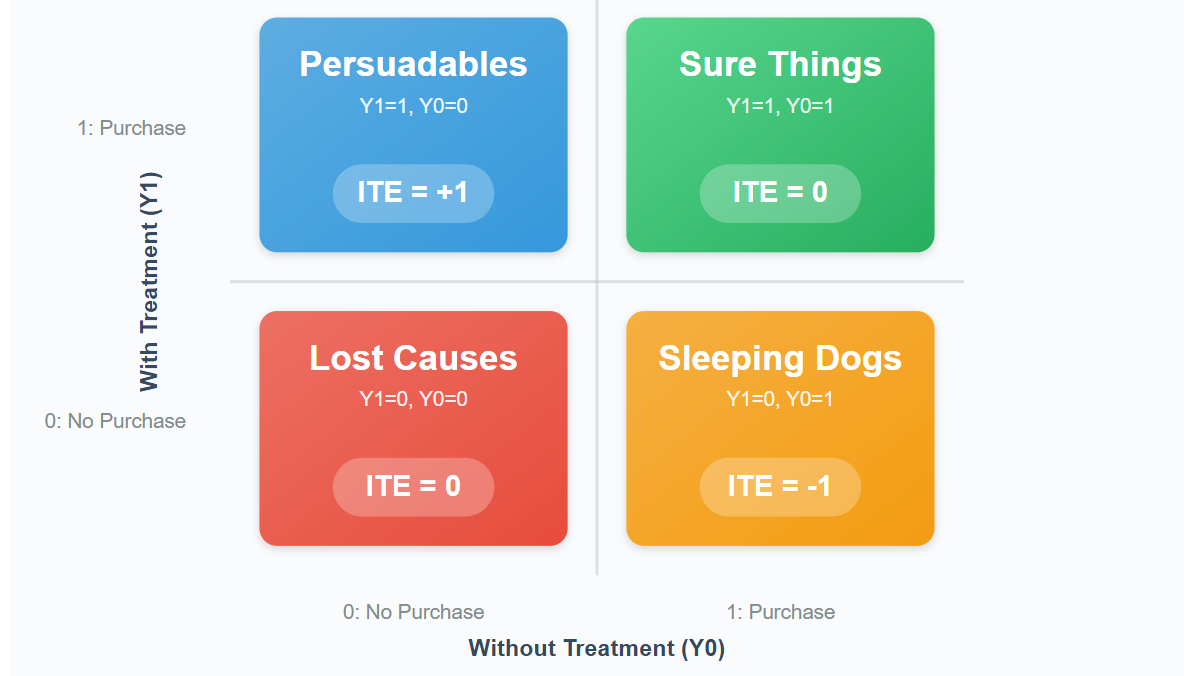
アップリフト分析では、顧客を施策への反応に基づいて4つのタイプに分類します。
これらの分類は、個人レベルの処置効果 \tau_i = Y_i^{(1)} - Y_i^{(0)} と、潜在的結果 Y_i^{(1)} および Y_i^{(0)} の値によって数学的に定義されます。
実際のデータ分析においては、これらの潜在的結果を直接観測することはできないため、条件付き平均処置効果 \tau(x) = E[Y^{(1)} - Y^{(0)} | X = x] を推定し、その値に基づいて顧客を分類することになります。
Two-Model法の仕組み
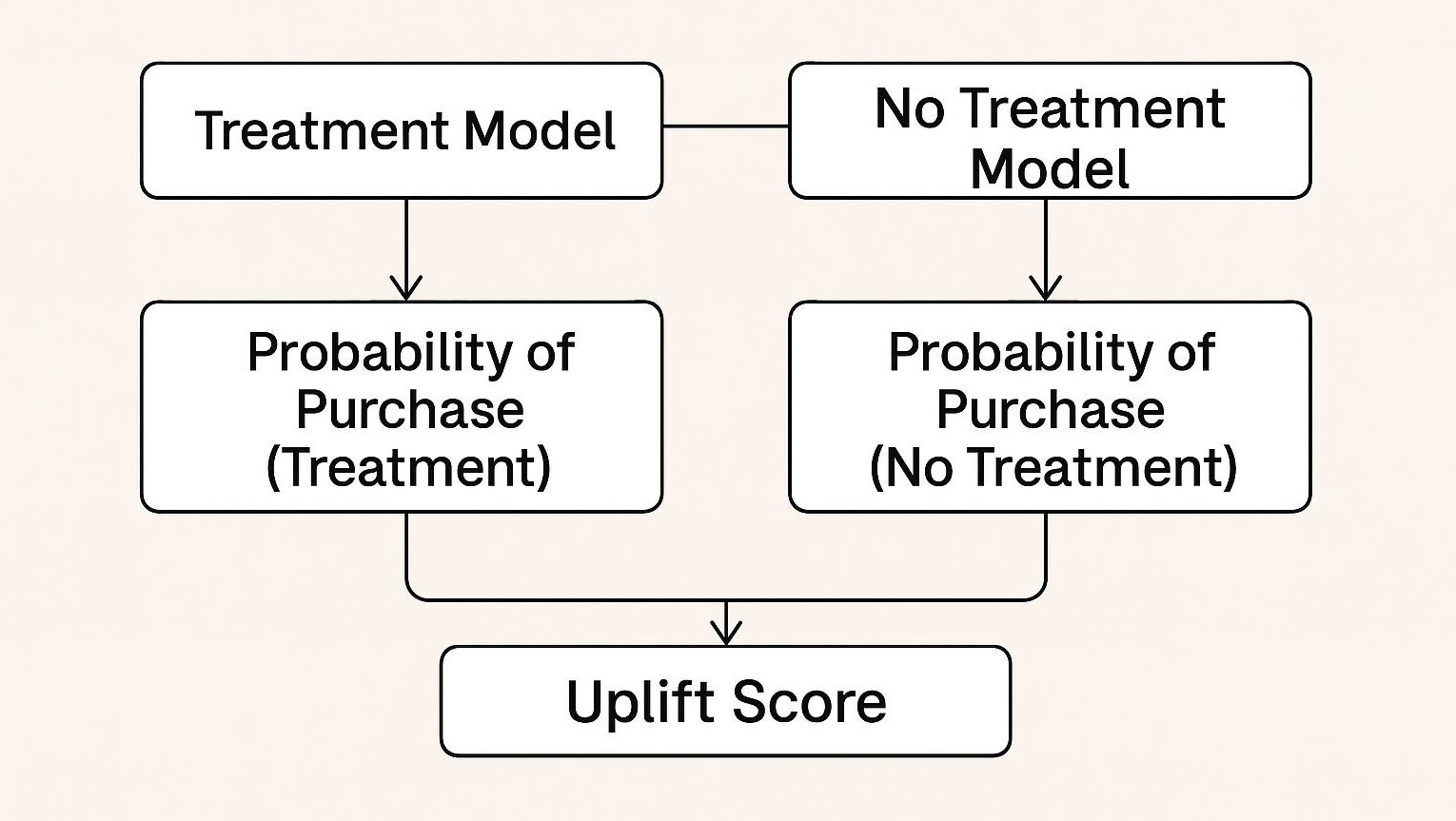
Two-Model法は、アップリフト効果を推定する最も直感的な手法の一つです。この手法の数学的な定式化を以下に示します。
観測データを \mathcal{D} = {(X_i, T_i, Y_i)}, i=1,\dots,n とします。ここで、X_i \in \mathbb{R}^d は d 次元の特徴量ベクトル、T_i \in {0, 1} は処置変数、Y_i \in {0, 1} は結果変数です。
Two-Model法では、2つの独立したモデルを構築します。
最終的なアップリフト推定値は、これら2つのモデルの予測値の差として計算されます。
$$\hat{\tau}(x) = \hat{\mu}_1(x) – \hat{\mu}_0(x)$$
ここで、\hat{\mu}_1(x) と \hat{\mu}_0(x) は、それぞれのモデルによる予測値を表します。
この手法が有効である理論的根拠は、ランダム化比較試験(RCT)や条件付き独立性の仮定の下で、以下の等式が成立することにあります。
$$E[Y | T = 1, X = x] – E[Y | T = 0, X = x] = E[Y^{(1)} – Y^{(0)} | X = x]$$
ここで、Y^{(1)} と Y^{(0)} は、それぞれ処置を受けた場合と受けなかった場合の潜在的結果(potential outcomes)を表します。
Pythonによる実装
それでは、実際にPythonでTwo-Model法を実装してみましょう。
必要なライブラリは、pandas、numpy、scikit-learnの3つだけです。
以下、コードです。
import pandas as pd import numpy as np from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestClassifier import matplotlib.pyplot as plt # 乱数のシードを固定(結果の再現性のため) np.random.seed(42)
サンプルデータの作成
実際の分析を始める前に、以下のような方法で、ECサイトの顧客データを模したサンプルデータを作成します。
顧客 i の購入確率 p_i は、基本購入確率 p_{base,i} とクーポン効果 \tau_i \cdot T_i の和として定義します。
$$p_i = p_{base,i} + \tau_i \cdot T_i$$
ここで、基本購入確率 p_{base,i} は過去の購入履歴に依存し作成します。
$$p_{base,i} = 0.1 + 0.02 \times \text{purchase_history}_i$$
クーポン効果(処置効果) \tau_i は、顧客の年齢と購入履歴に基づいて異質性を持たせています。
$$\tau_i = 0.2 \times \mathbb{1}(\text{age}_i < 40) + 0.15 \times \mathbb{1}(\text{purchase_history}_i > 3)$$
ここで、\mathbb{1}(\cdot) は指示関数であり、条件が真の場合に1、偽の場合に0を返します。
以下、コードです。
# 5000人の顧客データを生成
n_customers = 5000
# 顧客の特徴量を作成
data = pd.DataFrame({
'age': np.random.normal(35, 10, n_customers), # 年齢(平均35歳、標準偏差10)
'purchase_history': np.random.poisson(5, n_customers), # 過去の購入回数
'last_purchase_days': np.random.exponential(30, n_customers), # 最終購入からの日数
'email_open_rate': np.random.beta(2, 5, n_customers), # メール開封率
})
# クーポンをランダムに配布(50%の確率)
data['coupon'] = np.random.binomial(1, 0.5, n_customers)
# 購入確率を計算(現実的なシミュレーション)
base_prob = 0.1 + 0.02 * data['purchase_history'] # 基本購入確率
coupon_effect = 0.2 * (data['age'] < 40) + 0.15 * (data['purchase_history'] > 3)
purchase_prob = base_prob + coupon_effect * data['coupon']
purchase_prob = np.clip(purchase_prob, 0, 1) # 確率を0-1の範囲に制限
# 実際の購入フラグを生成
data['purchased'] = np.random.binomial(1, purchase_prob)
print("生成されたデータの一部", "="*20)
print(data.head())
print("\nデータの基本統計量", "="*20)
print(f"- データサイズ: {len(data)}行")
print(f"- クーポン配布率: {data['coupon'].mean():.1%}")
print(f"- 全体の購入率: {data['purchased'].mean():.1%}")
以下、実行結果です。
生成されたデータの一部 ====================
age purchase_history last_purchase_days email_open_rate coupon \
0 40.118679 3 1.483941 0.061822 1
1 28.043810 3 1.667866 0.237897 0
2 25.597469 5 0.809217 0.162868 1
3 32.979213 2 45.621347 0.414113 1
4 25.059354 4 33.838538 0.326091 0
purchased
0 0
1 0
2 1
3 1
4 0
データの基本統計量 ====================
- データサイズ: 5000行
- クーポン配布率: 50.1%
- 全体の購入率: 32.8%
Two-Model法の実装
次に、Two-Model法を実装するクラスを作成します。
以下、コードです。
"""
Two-Model法によるアップリフト予測クラス
"""
class TwoModelUplift:
def __init__(self, base_model=RandomForestClassifier):
"""
初期化
base_model: 使用する機械学習モデル(デフォルトはランダムフォレスト)
"""
self.model_treatment = base_model(n_estimators=100, random_state=42)
self.model_control = base_model(n_estimators=100, random_state=42)
def fit(self, X, treatment, y):
"""
モデルの学習
X: 特徴量
treatment: 施策実施フラグ(1=実施、0=非実施)
y: 目的変数(購入フラグ)
"""
# 処置群(クーポンあり)のデータ
treatment_mask = treatment == 1
X_treatment = X[treatment_mask]
y_treatment = y[treatment_mask]
# 対照群(クーポンなし)のデータ
control_mask = treatment == 0
X_control = X[control_mask]
y_control = y[control_mask]
# それぞれのモデルを学習
self.model_treatment.fit(X_treatment, y_treatment)
self.model_control.fit(X_control, y_control)
print(f"処置群のサンプル数: {len(X_treatment)}")
print(f"対照群のサンプル数: {len(X_control)}")
def predict_uplift(self, X):
"""
アップリフトスコアの予測
X: 予測対象の特徴量
"""
# 施策ありの場合の購入確率
prob_treatment = self.model_treatment.predict_proba(X)[:, 1]
# 施策なしの場合の購入確率
prob_control = self.model_control.predict_proba(X)[:, 1]
# アップリフトスコア = 施策ありの確率 - 施策なしの確率
uplift_score = prob_treatment - prob_control
return uplift_score
このTwoModelUpliftクラスは、Two-Model法の核となる実装を提供しています。重要な点は、処置群と対照群それぞれに対して独立した予測モデルを保持することです。
- 初期化メソッド(__init__)では、デフォルトでランダムフォレストを使用していますが、任意の分類器を指定することも可能です。
- 学習メソッド(fit)では、入力データを処置の有無に基づいて2つのサブセットに分割し、それぞれのモデルを独立して訓練します。この分離により、各グループ固有のパターンを適切に捉えることが可能となります。
- 予測メソッド(predict_uplift)では、新しい顧客データに対して両モデルで購入確率を算出し、その差分をアップリフトスコアとして返します。このスコアが正の値であれば施策が効果的であることを示し、値が大きいほど効果が高いことを意味します。
モデルの学習と予測
作成したクラスを使用して、実際にモデルを学習させてみましょう。
以下、コードです。
# 特徴量の列を定義
feature_columns = [
'age',
'purchase_history',
'last_purchase_days',
'email_open_rate',
]
# データを特徴量Xと処置変数treatment、目的変数yに分割
X = data[feature_columns]
treatment = data['coupon']
y = data['purchased']
# データを訓練用とテスト用に分割
X_train, X_test, treatment_train, treatment_test, y_train, y_test = train_test_split(
X, treatment, y, test_size=0.3, random_state=42
)
# モデルの学習
model = TwoModelUplift()
model.fit(X_train, treatment_train, y_train)
# テストデータでアップリフトスコアを予測
uplift_scores = model.predict_uplift(X_test)
print(f"\nアップリフトスコアの統計情報:")
print(f"平均値: {uplift_scores.mean():.3f}")
print(f"標準偏差: {uplift_scores.std():.3f}")
print(f"最小値: {uplift_scores.min():.3f}")
print(f"最大値: {uplift_scores.max():.3f}")
以下、実行結果です。
処置群のサンプル数: 1784 対照群のサンプル数: 1716 アップリフトスコアの統計情報: 平均値: 0.247 標準偏差: 0.221 最小値: -0.400 最大値: 0.840
- 処置群のサンプル数: 1784
- 処置群とは、クーポンを配布された顧客のグループを指します。
- このグループには1784人の顧客が含まれています。
- 対照群のサンプル数: 1716
- 対照群とは、クーポンを配布されなかった顧客のグループを指します。
- このグループには1716人の顧客が含まれています。
- アップリフトスコアの統計情報
- 平均値 0.247:アップリフトスコアの平均値は0.247であり、全体的にクーポン配布が購入確率を約24.7%向上させる効果があることを示唆しています。
- 標準偏差 0.221:標準偏差は0.221であり、アップリフトスコアのばらつきが比較的小さいことを示しています。
- 最小値 -0.400:最小値が負の値であることから、一部の顧客においてはクーポン配布が逆効果(購入確率の低下)となる可能性があることが分かります。
- 最大値 0.840:最大値は0.840であり、クーポン配布が購入確率を大幅に向上させる顧客も存在することを示しています。
平均アップリフトスコアが正の値であることから、クーポン配布は全体的に購入確率を向上させる効果があることが確認できました。
ただし、一部の顧客には逆効果が出る可能性もあるため、ターゲティング戦略の一部として活用することが考えられます。
結果の可視化と解釈
予測結果を可視化して、どのような顧客にクーポンが効果的かを確認しましょう。
以下、コードです。
# アップリフトスコアの分布を可視化
plt.figure(figsize=(10, 6))
# ヒストグラムの作成
plt.hist(
uplift_scores,
bins=50,
alpha=0.7,
color='skyblue',
edgecolor='black',
)
# 平均値と0のラインを追加
plt.axvline(
0,
color='red',
linestyle='--',
linewidth=2,
label='No Effect',
)
# 平均値のラインを追加
plt.axvline(
uplift_scores.mean(),
color='green',
linestyle='--',
linewidth=2,
label=f'Mean ({uplift_scores.mean():.3f})',
)
# グラフの設定
plt.xlabel('Uplift Score')
plt.ylabel('Number of Customers')
plt.title('Distribution of Uplift Scores')
plt.legend()
plt.grid(True, alpha=0.3)
# グラフの表示
plt.show()
# スコア上位の顧客の特徴を確認
top_10_percent_threshold = np.percentile(uplift_scores, 90)
top_customers_mask = uplift_scores >= top_10_percent_threshold
print(f"\n上位10%の顧客(アップリフトスコア >= {top_10_percent_threshold:.3f})の特徴:")
print(f"平均年齢: {X_test[top_customers_mask]['age'].mean():.1f}歳")
print(f"平均購入履歴: {X_test[top_customers_mask]['purchase_history'].mean():.1f}回")
print(f"最終購入からの平均日数: {X_test[top_customers_mask]['last_purchase_days'].mean():.1f}日")
以下、実行結果です。
上位10%の顧客(アップリフトスコア >= 0.530)の特徴: 平均年齢: 28.2歳 平均購入履歴: 5.2回 最終購入からの平均日数: 28.1日
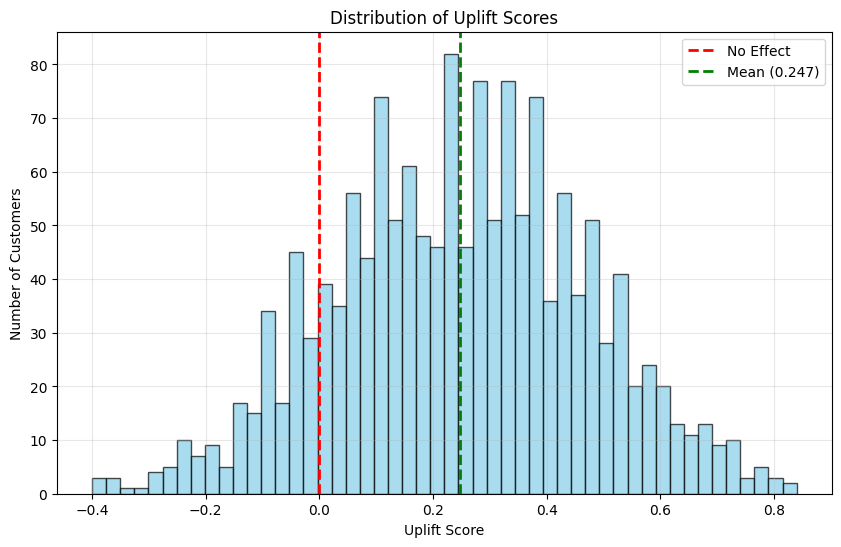
アップリフトスコアの分布を可視化した結果、スコアの範囲は-0.400から0.840まで広がっています。
この分布は、クーポンの効果が顧客ごとに異なることを示しています。
- スコアが正の値である顧客は、クーポンを配布することで購入確率が高まる可能性がある
- 逆にスコアが負の値である顧客は、クーポンが逆効果になる可能性がある
アップリフトスコアが上位10%に該当する顧客の特徴を分析した結果、以下のような傾向が見られました。
- 平均年齢 28.2歳 : 若年層の顧客が多いことがわかります。
- 平均購入履歴 5.2回 : 過去の購入回数が比較的多い顧客が含まれています。
- 最終購入からの平均日数 28.1日 : 最終購入からの経過日数が短い顧客が多いことが示されています。
今回のこの分析では、Two-Model法を用いてアップリフトスコアを算出し、クーポン配布の効果が高い顧客層を特定しました。
特に、若年層で過去の購入履歴が多く、最終購入からの経過日数が短い顧客が、クーポン配布による購入促進効果が高いことが示唆されました。
この結果を基に、ターゲットを絞ったマーケティング施策を実施することで、より高いROI(投資対効果)が期待できるでしょう。
アップリストスコアの保存
今求めたアップリフトスコアを、データフレーム化しCSVファイルとして保存します。
以下、コードです。
# アップリフト分析の結果を含むデータフレームを作成
uplift_results = X_test.copy()
uplift_results['uplift_score'] = uplift_scores
uplift_results['treatment'] = treatment_test.values
uplift_results['actual_purchase'] = y_test.values
# CSVに出力
uplift_results.to_csv('uplift_analysis_results.csv', index=False)
このCSVファイルを使い、次回はアップリフトモデルの性能を定量的に評価していきます。
アップリストモデル(Two-Model法)の保存
アップリフトスコアを予測する、Two-Model法によるアップリストモデルを保存します。
以下、コードです。
import joblib # モデルを保存 joblib.dump(model, 'uplift_model.pkl')
このモデルを読み込む(ロード)するときのコードは、以下です。
import joblib
# モデルをロード
loaded_model = joblib.load('uplift_model.pkl')
実務運用時には、このモデルをロードしバッチ処理やリアルタイム処理などを実施することでしょう。
実務での活用に向けて
実装したモデルから得られるアップリフトスコア \hat{\tau}(x) は、マーケティング施策の費用対効果を最適化する上で極めて重要な指標となります。
推定されたアップリフトスコアに基づく顧客セグメンテーションにより、限られたマーケティング予算を最も効果的に配分することが可能となります。
具体的には、アップリフトスコアが高い顧客群は、施策によって購入確率が大きく向上する「Persuadables」セグメントに属する可能性が高く、これらの顧客を優先的にターゲティングすることで、ROI(投資収益率)の最大化が期待できます。
実務における適用例として、アップリフトスコアの上位パーセンタイルに基づく施策対象の選定が挙げられます。
仮に全顧客の上位30%(アップリフトスコア上位30%)のみを施策対象とした場合、以下の期待効果が得られます。
$$\text{ROI向上率} = \frac{\text{選択的施策のROI} – \text{全体施策のROI}}{\text{全体施策のROI}}$$
この式を計算するためには、まず各施策のROIを個別に算出する必要があります。ROIは一般的に「(利益-投資額)/ 投資額」で計算されます。
この最適化により、マーケティングコストを70%削減しながら、売上効果の大部分(経験的には80-90%)を維持することが可能となります。
さらに、否定的な効果を持つ「Sleeping Dogs」セグメントを施策対象から除外することで、顧客満足度の向上という副次的効果も期待できます。
まとめ
今回は、マーケティング施策の真の効果を測定するアップリフト分析について、その基本概念から実装方法まで簡単に解説しました。
今回実装したモデルにより、顧客を4つのセグメントに分類し、施策が真に効果的な「Persuadables」層を特定できるようになります。
これにより、マーケティング予算を最適配分し、ROIの向上と顧客満足度の両立を実現する道筋が明確になります。
次回は、このアップリフトモデルの性能を定量的に評価するための手法について解説します。
これらの技術により、マネジメント層への報告や施策の意思決定がより科学的かつ説得力のあるものとなることでしょう。

