第3回では、グローバル解釈の手法(Permutation Importance、PDP、ICE)を通じて、AIモデル全体の振る舞いを俯瞰的に理解する方法をお話ししました。
DALEXで実践する説明可能AI超入門— 第3回 —グローバル解釈で全体像を把握するPFI・PDP・ALE・Surrogate Model
グローバル解釈で、「どの特徴量が重要か」「特徴量の変化が予測にどう影響するか」という全体的な傾向を把握できるようになりますが、実際のビジネスシーンでは、もっと具体的な質問に答える必要があります。
たとえば……
- 「なぜこの顧客は融資を断られたのか?」
- 「この製品が不良品と判定された具体的な理由は?」
- 「この患者さんの診断結果の根拠を教えてください」
- 「もし年収がもう少し高かったら、審査は通っていましたか?」
こうした個別の予測に対する詳細な説明や、条件を変えた場合のシミュレーションを提供するのが、今回取り上げる「ローカル解釈」です。
今回は、以下の3つの強力な手法を紹介します。
- SHAP(シャープ):ゲーム理論に基づき、各特徴量の貢献度を公平に算出する
- Break Down(ブレイクダウン):特徴量を順番に追加しながら、予測値の変化を段階的に分解する
- Ceteris Paribus(ケテリス・パリブス):「もし〜だったら」という仮定のもと、特徴量を変化させたときの予測の変化を可視化する
まるで探偵が事件を解決するように、一つ一つの手がかりから、AIがなぜその結論に至ったのか、そしてどうすれば結果が変わるのかを明らかにしていきます。
Contents
- なぜローカル解釈が必要なのか
- 全体傾向だけでは説明できない個別ケース
- 信頼関係を築くための透明性
- シャープレイ値の直感的理解
- 機械学習におけるSHAP
- DALEXでSHAPを実践する
- ステップ1:環境準備とデータ読み込み
- ステップ2:データの前処理
- ステップ3:モデルの構築と評価
- ステップ4:Explainerの作成
- ステップ5:分析対象の乗客を選択
- ステップ6:SHAPによる要因分解
- ステップ7:複数の乗客でSHAPを比較
- Break Down法:段階的に予測を分解する
- Break Downの仕組みと特徴
- Break Downの実践
- 複雑なケースでのBreak Down分析
- SHAPとBreak Downの使い分け
- 両手法の基本的な違い
- SHAPの考え方:公平な成果配分
- Break Downの考え方:段階的な積み上げ
- 医療診断での簡易例
- Ceteris Paribus:「もし〜だったら」を検証する
- Ceteris Paribusとは何か
- タイタニック乗客のWhat-if分析
- 性別の影響を詳しく見る
- 年齢の影響を連続的に見る
- 具体的な値を指定したWhat-if分析
- 複数の条件を同時に変更する
- 複数の乗客を比較する
- Ceteris Paribusの実務での活用
- SHAPとCeteris Paribusの使い分け
- 製造業での異常検知の例
- 製造データの準備
- 品質予測モデルの構築
- 不良品の要因分析
- AIがこの「不良パターン」を知らなかった
- AIが「見ていない」場所が原因だった
- まとめ
なぜローカル解釈が必要なのか
全体傾向だけでは説明できない個別ケース
簡単な仮ストーリーで、ローカル解釈の必要性を説明します。
山田さんは地方銀行の融資担当者です。
AIによる融資審査システムを導入してから、審査時間は大幅に短縮されました。
グローバル解釈により、システムが「年収」「勤続年数」「既存借入額」を重視していることも分かっています。
ある日、長年の顧客である田中さんが住宅ローンの申請に来ました。
田中さんは年収600万円、勤続15年、既存借入なし。
一見すると優良顧客です。
しかし、AIは「融資不可」と判定しました。
田中さんは困惑し、山田さんに詰め寄ります。
「なぜダメなんですか?私の何が問題なんですか?」
山田さんは答えに窮しました。
グローバル解釈で「年収が重要」と分かっていても、田中さん個人の申請がなぜ却下されたのかは説明できません。
ここで必要なのが、個別の予測を詳細に説明する「ローカル解釈」なのです。
信頼関係を築くための透明性
個別の説明ができることは、人と人、企業と顧客の信頼関係の基盤となります。
「あなたの申請が却下された理由は、転職歴が多いことによる安定性への懸念(-30ポイント)と、申請額が年収に対して高すぎること(-25ポイント)が主な要因です。もし申請額を4,000万円から3,500万円に減額すれば、承認の可能性が高まります」
このような具体的な説明ができれば、顧客は納得し、改善策を検討できます。
これがローカル解釈の真の価値です。
シャープレイ値の直感的理解
ローカル解釈の主要な手法であるSHAPを簡単に説明します。
3人の友人(Aさん、Bさん、Cさん)が協力してケーキ屋を経営し、月100万円の利益を上げたとします。
- この利益を3人でどう分配すべきでしょうか?
- 単純に3等分?
- それとも働いた時間で按分?
SHAPの基となる「シャープレイ値」は、この問題に数学的に公平な答えを出します。
全ての可能な組み合わせを考慮し、各人がいる場合といない場合の差分から貢献度を計算するのです。
例えば、Aさんの貢献度を計算するには……
- Aさんだけの場合:20万円の利益
- AさんとBさんの場合:60万円(Aさんの追加貢献は40万円)
- AさんとCさんの場合:50万円(Aさんの追加貢献は30万円)
- 3人全員の場合:100万円(Aさんの追加貢献は50万円)
これらすべての組み合わせを考慮して、Aさんの平均的な貢献度を算出します。
これがシャープレイ値の考え方です。
機械学習におけるSHAP
同じ考え方を機械学習に適用したのがSHAPです。
各特徴量を「プレイヤー」、予測値を「利益」と考えて、各特徴量の貢献度を計算します。
タイタニック号の生存予測で考えてみましょう。
ある乗客の生存確率が70%と予測されたとき、その70%に対して「性別(女性)」が+40%、「客室クラス(1等)」が+20%、「年齢(若い)」が+10%貢献した、といった具合に分解できるのです。
DALEXでSHAPを実践する
それでは実際にコードを書いて、SHAPによる要因分解を体験しましょう。
ステップ1:環境準備とデータ読み込み
まず最初に、必要なライブラリをインポートし、分析の準備を整えましょう。
# 必要なライブラリをインポート
import pandas as pd # データフレーム操作用
import numpy as np # 数値計算用
import dalex as dx # XAI(説明可能AI)のメインライブラリ
from sklearn.model_selection import train_test_split # データ分割用
from sklearn.ensemble import RandomForestClassifier # ランダムフォレストモデル用
from sklearn.preprocessing import LabelEncoder # カテゴリ変数の数値化用
import warnings
warnings.filterwarnings('ignore') # 不要な警告を非表示
次に、タイタニックのデータセットを読み込んで、データの基本的な構造を確認しましょう。
# タイタニックデータセットを読み込む
titanic = dx.datasets.load_titanic()
# データの形状を確認
print("データの形状:", titanic.shape)
print(f" 行数(乗客数): {titanic.shape[0]}")
print(f" 列数(特徴量数): {titanic.shape[1]}")
以下、実行結果です。
データの形状: (2207, 8) 行数(乗客数): 2207 列数(特徴量数): 8
2,207名の乗客データと8つの特徴量があることが確認できました。データの中身を詳しく見てみましょう。
# データの最初の3行を確認
print("最初の3行のデータ:")
print(titanic.head(3))
# 各カラムの意味を確認
print("\n各カラムの説明:")
print("- survived: 生存したか(1=生存、0=死亡)")
print("- gender: 性別")
print("- age: 年齢")
print("- class: 客室クラス")
print("- embarked: 乗船港")
print("- fare: 運賃")
print("- sibsp: 同乗した兄弟・配偶者の数")
print("- parch: 同乗した親・子供の数")
以下、実行結果です。
最初の3行のデータ: gender age class embarked fare sibsp parch survived 0 male 42.0 3rd Southampton 7.11 0 0 0 1 male 13.0 3rd Southampton 20.05 0 2 0 2 male 16.0 3rd Southampton 20.05 1 1 0 各カラムの説明: - survived: 生存したか(1=生存、0=死亡) - gender: 性別 - age: 年齢 - class: 客室クラス - embarked: 乗船港 - fare: 運賃 - sibsp: 同乗した兄弟・配偶者の数 - parch: 同乗した親・子供の数
データの構造が理解できたところで、各変数のデータ型を確認しておきましょう。
# データ型の確認
print("各変数のデータ型:")
print(titanic.dtypes)
# 文字列型の変数を特定
categorical_columns = titanic.select_dtypes(include=['object']).columns
print(f"\nカテゴリ変数: {list(categorical_columns)}")
以下、実行結果です。
各変数のデータ型: gender object age float64 class object embarked object fare float64 sibsp int64 parch int64 survived int64 dtype: object カテゴリ変数: ['gender', 'class', 'embarked']
gender、class、embarkedが文字列型(カテゴリ変数)であることが分かりました。これらは後で数値に変換する必要があります。
ステップ2:データの前処理
機械学習モデルは数値データしか扱えないため、文字データを数値に変換する必要があります。
まず、目的変数(予測したいもの)と特徴量(予測に使う情報)を分離しましょう。
# 目的変数(生存フラグ)と特徴量を分離
X = titanic.drop(columns=['survived']) # survivedを除いたすべての列を特徴量として使用
y = titanic['survived'] # survivedを目的変数として使用
print("特徴量の形状:", X.shape)
print("目的変数の形状:", y.shape)
以下、実行結果です。
特徴量の形状: (2207, 7) 目的変数の形状: (2207,)
次に、生存率を確認しましょう。これは後でモデルの予測値を評価する際の基準になります。
# 生存率の確認
survival_rate = y.mean()
print(f"\n全体の生存率: {survival_rate:.2%}")
print(f"生存者数: {y.sum()}名")
print(f"死亡者数: {len(y) - y.sum()}名")
以下、実行結果です。
全体の生存率: 32.22% 生存者数: 711名 死亡者数: 1496名
約32%の乗客が生存したことが分かりました。
次に、カテゴリ変数を数値に変換していきます。まず性別から変換しましょう。
# 性別の変換
print("性別(gender)の変換:")
print(f"変換前のユニーク値: {X['gender'].unique()}")
# LabelEncoderを使って変換
le_gender = LabelEncoder()
X['gender'] = le_gender.fit_transform(X['gender'])
print("\n変換ルール:")
for i, gender_name in enumerate(le_gender.classes_):
print(f" {gender_name} → {i}")
print(f"\n変換後の分布:")
print(X['gender'].value_counts().sort_index())
以下、実行結果です。
性別(gender)の変換: 変換前のユニーク値: ['male' 'female'] 変換ルール: female → 0 male → 1 変換後の分布: gender 0 489 1 1718 Name: count, dtype: int64
同様に、客室クラスも変換します。
# 客室クラスの変換
print("客室クラス(class)の変換:")
print(f"変換前のユニーク値: {X['class'].unique()}...")
le_class = LabelEncoder()
X['class'] = le_class.fit_transform(X['class'])
print("\n変換ルール:")
for i, class_name in enumerate(le_class.classes_):
print(f" {class_name} → {i}")
print(f"\n変換後の分布:")
print(X['class'].value_counts().sort_index())
以下、実行結果です。
客室クラス(class)の変換: 変換前のユニーク値: ['3rd' '2nd' '1st' 'engineering crew' 'victualling crew' 'restaurant staff' 'deck crew']... 変換ルール: 1st → 0 2nd → 1 3rd → 2 deck crew → 3 engineering crew → 4 restaurant staff → 5 victualling crew → 6 変換後の分布: class 0 324 1 284 2 709 3 66 4 324 5 69 6 431 Name: count, dtype: int64
最後に乗船港を変換します。
# 乗船港の変換
print("乗船港(embarked)の変換:")
print(f"変換前のユニーク値: {X['embarked'].unique()}")
le_embarked = LabelEncoder()
X['embarked'] = le_embarked.fit_transform(X['embarked'])
print("\n変換ルール:")
for i, embarked_name in enumerate(le_embarked.classes_):
print(f" {embarked_name} → {i}")
print(f"\n変換後の分布:")
print(X['embarked'].value_counts().sort_index())
以下、実行結果です。
乗船港(embarked)の変換: 変換前のユニーク値: ['Southampton' 'Cherbourg' 'Belfast' 'Queenstown'] 変換ルール: Belfast → 0 Cherbourg → 1 Queenstown → 2 Southampton → 3 変換後の分布: embarked 0 197 1 271 2 123 3 1616 Name: count, dtype: int64
データの前処理が完了しました。次に、データを訓練用とテスト用に分割します。
# データを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.25, # 25%をテストデータに
random_state=42, # 再現性のために乱数シードを固定
stratify=y # 生存率の比率を保つ(層化抽出)
)
print("データ分割:")
print(f" 訓練データ: {len(X_train)}件")
print(f" テストデータ: {len(X_test)}件")
以下、実行結果です。
データ分割: 訓練データ: 1655件 テストデータ: 552件
層化抽出により、訓練データとテストデータの生存率が同じになっているか確認しましょう。
# 分割後の生存率を確認
train_survival_rate = y_train.mean()
test_survival_rate = y_test.mean()
print(f"生存率の確認:")
print(f" 訓練データ: {train_survival_rate:.2%}")
print(f" テストデータ: {test_survival_rate:.2%}")
print(f" 差: {abs(train_survival_rate - test_survival_rate):.2%}")
以下、実行結果です。
生存率の確認: 訓練データ: 32.21% テストデータ: 32.25% 差: 0.04%
差が非常に小さく、適切に分割されていることが確認できました。
ステップ3:モデルの構築と評価
データの準備ができたので、ランダムフォレストモデルを構築しましょう。ランダムフォレストは、多数の決定木を組み合わせることで、高い予測精度と安定性を実現するアルゴリズムです。
# ランダムフォレストモデルのパラメータ設定
rf_model = RandomForestClassifier(
n_estimators=100, # 100本の決定木を使用
max_depth=5, # 各決定木の最大深さを5に制限(過学習防止)
min_samples_split=20, # ノード分割に必要な最小サンプル数
random_state=42 # 再現性のため乱数シードを固定
)
モデルを訓練します。
# モデルの訓練 rf_model.fit(X_train, y_train)
訓練が完了したら、モデルの精度を評価しましょう。
# 訓練データでの精度
train_accuracy = rf_model.score(X_train, y_train)
print(f"訓練データでの精度: {train_accuracy:.2%}")
# テストデータでの精度
test_accuracy = rf_model.score(X_test, y_test)
print(f"テストデータでの精度: {test_accuracy:.2%}")
以下、実行結果です。
訓練データでの精度: 81.99% テストデータでの精度: 79.53%
精度差が小さく、モデルが適切に学習されていることが確認できました。
ステップ4:Explainerの作成
DALEXの核心となるExplainerオブジェクトを作成します。これにより、ブラックボックスなモデルに説明機能を追加できます。
# DALEXのExplainerオブジェクトを作成
explainer = dx.Explainer(
rf_model, # 解釈対象のモデル
X_test, # テストデータ(特徴量)
y_test, # テストデータ(正解ラベル)
label="Random Forest" # モデルの名前(グラフ表示用)
)
以下、実行結果です。
Preparation of a new explainer is initiated -> data : 552 rows 7 cols -> target variable : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray. -> target variable : 552 values -> model_class : sklearn.ensemble._forest.RandomForestClassifier (default) -> label : Random Forest -> predict function : <function yhat_proba_default at 0x7f3c2c5e3010> will be used (default) -> predict function : Accepts pandas.DataFrame and numpy.ndarray. -> predicted values : min = 0.0731, mean = 0.31, max = 0.936 -> model type : classification will be used (default) -> residual function : difference between y and yhat (default) -> residuals : min = -0.879, mean = 0.0122, max = 0.861 -> model_info : package sklearn A new explainer has been created!
ステップ5:分析対象の乗客を選択
個別予測を分析するために、興味深いケースを選びましょう。まず、生存した乗客の中から選んでみます。
# 生存した乗客を抽出
survived_passengers = X_test[y_test == 1]
print(f"テストデータ中の生存者数: {len(survived_passengers)}名")
# インデックスを確認
survived_indices = survived_passengers.index[:5]
print(f"最初の5名のID: {list(survived_indices)}")
以下、実行結果です。
テストデータ中の生存者数: 178名 最初の5名のID: [594, 533, 1858, 844, 1828]
これらの乗客の予測確率を確認してみましょう。
# 生存者の予測確率を確認
print("生存者の予測確率(最初の5名):")
for i, idx in enumerate(survived_indices):
# 一人分のデータを取得
passenger = X_test.loc[[idx]]
# 予測確率を計算([0]で死亡確率、[1]で生存確率)
pred_proba = rf_model.predict_proba(passenger)[0][1]
print(f" 乗客ID {idx}: 生存確率 {pred_proba:.2%}")
以下、実行結果です。
生存者の予測確率(最初の5名): 乗客ID 594: 生存確率 19.10% 乗客ID 533: 生存確率 49.91% 乗客ID 1858: 生存確率 16.60% 乗客ID 844: 生存確率 55.63% 乗客ID 1828: 生存確率 21.99%
最初の乗客を詳細分析の対象として選択し、選択した乗客の詳細情報を確認します。
# 分析対象の乗客を選択
passenger_idx = survived_indices[0]
passenger_data = X_test.loc[[passenger_idx]]
print(f"分析対象: 乗客ID {passenger_idx}")
print("データ形状:", passenger_data.shape)
# 乗客の特徴を詳しく確認
passenger_features = passenger_data.iloc[0]
print("-" * 40)
# 性別の表示
gender_value = passenger_features['gender']
gender_label = "女性" if gender_value == 0 else "男性"
print(f"性別: {gender_label} (値: {gender_value})")
# 年齢の表示
age_value = passenger_features['age']
print(f"年齢: {age_value:.0f}歳")
# 客室クラスの表示
class_value = passenger_features['class']
print(f"客室クラス: {class_value} (値が小さいほど上級)")
以下、実行結果です。
分析対象: 乗客ID 594 データ形状: (1, 7) ---------------------------------------- 性別: 男性 (値: 1.0) 年齢: 30歳 客室クラス: 2.0 (値が小さいほど上級)
その他の特徴も確認しましょう。
# その他の特徴を確認
print(f"乗船港: {passenger_features['embarked']}")
print(f"運賃: {passenger_features['fare']:.2f}")
print(f"同乗の兄弟・配偶者数: {passenger_features['sibsp']}")
print(f"同乗の親・子供数: {passenger_features['parch']}")
以下、実行結果です。
乗船港: 1.0 運賃: 7.17 同乗の兄弟・配偶者数: 0.0 同乗の親・子供数: 0.0
この乗客の予測結果と実際の結果を比較しましょう。
# 予測と実際の結果を確認
pred_proba = rf_model.predict_proba(passenger_data)[0][1]
actual_result = y_test.loc[passenger_idx]
print(f"AIの予測生存確率: {pred_proba:.2%}")
print(f"実際の結果: {'生存' if actual_result == 1 else '死亡'}")
以下、実行結果です。
AIの予測生存確率: 19.10% 実際の結果: 生存
ステップ6:SHAPによる要因分解
いよいよSHAPを使って、なぜAIがその予測をしたのかを分析します。
まず、SHAP分析を実行しましょう。
# SHAP分析を実行
shap_explanation = explainer.predict_parts(
passenger_data, # 分析対象のデータ
type='shap', # SHAP法を指定
B=25 # サンプリング回数(精度と計算時間のバランス)
)
SHAP分析の結果を取得して、整理しましょう。
# 結果を取得
shap_result = shap_explanation.result
# 結果の構造を確認
print(f"結果の行数: \n{len(shap_result)}")
print("\nSHAP結果のカラム:")
print(shap_result.columns.tolist())
以下、実行結果です。
結果の行数: 182 SHAP結果のカラム: ['variable', 'contribution', 'variable_name', 'variable_value', 'sign', 'label', 'B']
各特徴量の寄与度を計算して、分かりやすく表示しましょう。
サンプリング回数だけ推定結果がありますので、平均や標準偏差などを計算します。
# SHAP値の結果を集計
agg = shap_result.groupby("variable_name").agg(
mean_change=("contribution", "mean"),
mean_abs_change=("contribution", lambda x: x.abs().mean()),
std_change=("contribution", "std"),
n_paths=("contribution", "count")
).reset_index()
寄与度の大きさでソートして、最も影響力のある要因を特定しましょう。
# 影響度の大きい順(絶対値平均)で並べ替え
agg_sorted = agg.sort_values("mean_abs_change", ascending=False)
# 表示
print("各特徴量の寄与度(SHAP値の平均):")
for _, row in agg_sorted.iterrows():
var = str(row["variable_name"])
m = float(row["mean_change"])
sd = float(row["std_change"]) if row["std_change"] == row["std_change"] else 0.0
n = int(row["n_paths"])
direction = "↑ 生存に有利" if m > 0 else ("↓ 生存に不利" if m < 0 else "→ 影響なし")
print(f"{var:25s}: {m:+.4f} (|mean|={abs(m):.4f}, sd={sd:.4f}, n={n}) {direction}")
# TOP3(影響度:絶対値平均の大きい順)
print("\n影響力の大きい要因 TOP3(絶対値平均ベース):")
for i, (_, r) in enumerate(agg_sorted.head(3).iterrows(), 1):
print(f"{i}位: {r['variable_name']} (mean={r['mean_change']:+.3f}, |mean|={abs(r['mean_change']):.3f})")
以下、実行結果です。
各特徴量の寄与度(SHAP値の平均): gender : -0.0732 (|mean|=0.0732, sd=0.0085, n=26) ↓ 生存に不利 fare : -0.0417 (|mean|=0.0417, sd=0.0085, n=26) ↓ 生存に不利 class : -0.0210 (|mean|=0.0210, sd=0.0108, n=26) ↓ 生存に不利 embarked : +0.0214 (|mean|=0.0214, sd=0.0041, n=26) ↑ 生存に有利 parch : -0.0056 (|mean|=0.0056, sd=0.0046, n=26) ↓ 生存に不利 sibsp : +0.0041 (|mean|=0.0041, sd=0.0038, n=26) ↑ 生存に有利 age : -0.0033 (|mean|=0.0033, sd=0.0047, n=26) ↓ 生存に不利 影響力の大きい要因 TOP3(絶対値平均ベース): 1位: gender (mean=-0.073, |mean|=0.073) 2位: fare (mean=-0.042, |mean|=0.042) 3位: class (mean=-0.021, |mean|=0.021)
SHAP値の可視化も行いましょう。
# SHAP値を可視化 shap_explanation.plot(show=True)
以下、実行結果です。
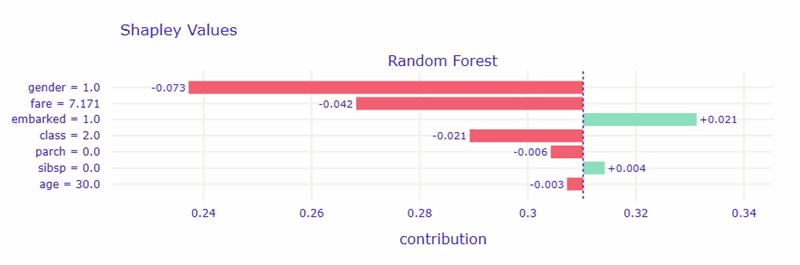
このグラフは、AI(ランダムフォレスト)が「なぜこの乗客を生存しにくい」と判断したかを示したものです。
横軸は「生存確率への影響」を表しており、右(緑)は生存に有利、左(赤)は生存に不利な要因です。
この乗客では、「男性であること」が最も強く生存確率を下げる方向に働いています。次に、「運賃が安い(=低いクラスの客室)」ことも不利に作用しています。 一方で、「乗船した港(embarked)」がわずかに生存確率を高める要因になっています。
つまり、この人の生存率が平均より低く予測された主な理由は、男性であり、比較的安いチケットで乗船していたからです。
| 特徴量 | 値 | SHAP寄与 | 解釈 |
|---|---|---|---|
| gender = 1.0 | 男性 | -0.073 | 最も大きく「生存確率を下げる」要因。男性であることが、生存確率を低くする方向に強く働いている。 |
| fare = 7.171 | 運賃が低い | -0.042 | 安いチケットの乗客は、救命ボートへのアクセスや客室階層が低く、生存率が下がる傾向。 |
| embarked = 1.0 | 港コード 1(例:Cherbourgなど) | +0.021 | この乗船港の乗客は平均よりやや生存率が高い。社会階層や乗船デッキの違いを反映している可能性。 |
| class = 2.0 | 2等船室 | -0.021 | 1等に比べてやや不利。3等よりは良いが、1等に比べ救出確率は低め。 |
| parch = 0.0 | 家族なし | -0.006 | 家族同行者がいないことが、わずかに生存確率を下げている。助け合い効果の欠如か。 |
| sibsp = 0.0 | 同乗兄弟・配偶者なし | +0.004 | ごく僅かに有利。家族がいないことで、単独行動できた可能性も。 |
| age = 30.0 | 中年層 | -0.003 | 年齢による影響は小さいが、若年層ほどではない。 |
ステップ7:複数の乗客でSHAPを比較
異なる特徴を持つ乗客を比較することで、モデルの判断パターンをより深く理解しましょう。まず、対照的な特徴を持つ乗客を探します。
# 上級クラスの女性を探す
high_survival_mask = (
(y_test == 1) & # 生存
(X_test['gender'] == 0) & # 女性
(X_test['class'] <= 1) # 上級クラス
)
high_survival_candidates = X_test[high_survival_mask]
print(f"該当する乗客数: {len(high_survival_candidates)}名")
if len(high_survival_candidates) > 0:
high_survival_idx = high_survival_candidates.index[0]
print(f"選択: 乗客ID {high_survival_idx}")
以下、実行結果です。
該当する乗客数: 47名 選択: 乗客ID 283
同様に、下級クラスの男性を探します。
# 下級クラスの男性を探す
low_survival_mask = (
(y_test == 0) & # 死亡
(X_test['gender'] == 1) & # 男性
(X_test['class'] >= 2) # 下級クラス
)
low_survival_candidates = X_test[low_survival_mask]
print(f"該当する乗客数: {len(low_survival_candidates)}名")
if len(low_survival_candidates) > 0:
low_survival_idx = low_survival_candidates.index[0]
print(f"選択: 乗客ID {low_survival_idx}")
以下、実行結果です。
該当する乗客数: 283名 選択: 乗客ID 1873
選択した2人の乗客を比較分析しましょう。
まず、乗客A(上級女性客)から分析します。
# 乗客A(上級女性客)の分析
print("【乗客A:上級女性客】")
print("=" * 50)
# データを取得
passenger_a = X_test.loc[[high_survival_idx]]
# 基本情報を表示
print("基本情報:")
print(f" 性別: 女性")
print(f" 年齢: {passenger_a.iloc[0]['age']:.0f}歳")
print(f" 客室クラス: {passenger_a.iloc[0]['class']}")
# 予測結果
pred_a = rf_model.predict_proba(passenger_a)[0][1]
actual_a = y_test.loc[high_survival_idx]
print(f"\n予測結果:")
print(f" 生存確率: {pred_a:.2%}")
print(f" 実際: {'生存' if actual_a == 1 else '死亡'}")
以下、実行結果です。
【乗客A:上級女性客】 ================================================== 基本情報: 性別: 女性 年齢: 39歳 客室クラス: 0.0 予測結果: 生存確率: 84.86% 実際: 生存
乗客A(上級女性客)のSHAP分析を実行します。
# 乗客A(上級女性客)のSHAP分析
shap_a = explainer.predict_parts(
passenger_a,
type='shap',
B=100
)
shap_a_result = shap_a.result
# 各変数の寄与度を集計
agg_a = shap_a_result.groupby(
"variable_name",
as_index=False).agg(
mean_contribution=(
"contribution",
"mean"
)
)
# 絶対値で寄与度の大きい順に並べ替え
agg_a_sorted_abs = agg_a.reindex(
agg_a.mean_contribution.abs(
).sort_values(ascending=False).index
)
# ランキングを表示
print("各特徴量の寄与度(絶対値での平均):")
for _, row in agg_a_sorted_abs.iterrows():
print(f" {row['variable_name']:8s}: {row['mean_contribution']:+.3f}")
以下、実行結果です。
各特徴量の寄与度(絶対値での平均): gender : +0.318 class : +0.172 parch : +0.031 fare : +0.027 age : -0.016 sibsp : +0.007 embarked: -0.000
次に、乗客B(下級男性客)を分析します。
# 乗客B(下級男性客)の分析
print("【乗客B:下級男性客】")
print("=" * 50)
# データを取得
passenger_b = X_test.loc[[low_survival_idx]]
# 基本情報を表示
print("基本情報:")
print(f" 性別: 男性")
print(f" 年齢: {passenger_b.iloc[0]['age']:.0f}歳")
print(f" 客室クラス: {passenger_b.iloc[0]['class']}")
# 予測結果
pred_b = rf_model.predict_proba(passenger_b)[0][1]
actual_b = y_test.loc[low_survival_idx]
print(f"\n予測結果:")
print(f" 生存確率: {pred_b:.2%}")
print(f" 実際: {'生存' if actual_b == 1 else '死亡'}")
以下、実行結果です。
【乗客B:下級男性客】 ================================================== 基本情報: 性別: 男性 年齢: 30歳 客室クラス: 4.0 予測結果: 生存確率: 22.03% 実際: 死亡
乗客B(下級男性客)のSHAP分析も実行します。
# 乗客B(下級男性客)のSHAP分析
shap_b = explainer.predict_parts(
passenger_b,
type='shap',
B=100
)
shap_b_result = shap_b.result
# 各変数の寄与度を集計
agg_b = shap_b_result.groupby(
"variable_name",
as_index=False).agg(
mean_contribution=(
"contribution",
"mean"
)
)
# 絶対値で寄与度の大きい順に並べ替え
agg_b_sorted_abs = agg_b.reindex(
agg_b.mean_contribution.abs(
).sort_values(ascending=False).index
)
# ランキングを表示
print("各特徴量の寄与度(絶対値での平均):")
for _, row in agg_b_sorted_abs.iterrows():
print(f" {row['variable_name']:8s}: {row['mean_contribution']:+.3f}")
以下、実行結果です。
各特徴量の寄与度(絶対値での平均): gender : -0.078 class : -0.018 fare : +0.010 sibsp : +0.006 parch : -0.004 embarked: -0.004 age : -0.001
2人の比較から見えてくることをまとめます。
# 比較結果のまとめ
print("【比較結果のまとめ】")
print("=" * 50)
print(f"乗客A(上級女性): 生存確率 {pred_a:.2%}")
print(f"乗客B(下級男性): 生存確率 {pred_b:.2%}")
print(f"差: {abs(pred_a - pred_b):.2%}")
以下、実行結果です。
【比較結果のまとめ】 ================================================== 乗客A(上級女性): 生存確率 84.86% 乗客B(下級男性): 生存確率 22.03% 差: 62.83%
この比較から、タイタニック号では「女性と子供を優先」「上級客室を優先」という避難方針が実際に守られていたことが、データから明確に読み取れます。
Break Down法:段階的に予測を分解する
Break Downの仕組みと特徴
Break Down法は、SHAPとは異なるアプローチで予測を分解します。
料理のレシピのように、一つずつ材料(特徴量)を加えていき、最終的な味(予測値)がどのように作られるかを段階的に示します。
Break Downの特徴は、特徴量を重要度順に並べ、順番に寄与度を計算することです。
Break Downの実践
最初に分析した乗客と同じデータを使って、Break Down法による分析を行います。
# Break Down法による分析を実行
print("Break Down法による段階的分解")
print("=" * 60)
# 最初に分析した乗客のデータを再利用
print(f"対象: 乗客ID {passenger_idx}")
# Break Down分析を実行
bd_explanation = explainer.predict_parts(
passenger_data, # 分析対象のデータ
type='break_down' # Break Down法を指定
)
以下、実行結果です。
Break Down法による段階的分解 ============================================================ 対象: 乗客ID 594
Break Downの結果を取得して確認しましょう。
# 結果を取得
bd_result = bd_explanation.result
print(f"結果の行数: {len(bd_result)}")
print(f"含まれる変数: {bd_result['variable_name'].tolist()}")
以下、実行結果です。
結果の行数: 9 含まれる変数: ['intercept', 'embarked', 'sibsp', 'age', 'parch', 'class', 'fare', 'gender', '']
段階的な予測値の変化を追跡していきます。
# 段階的な変化を追跡
print("予測値の段階的構築:")
print("-" * 50)
# 各ステップを処理
for idx, row in bd_result.iterrows():
var_name = row['variable_name']
contribution = row['contribution']
cumulative = row['cumulative']
if var_name == 'intercept':
# ステップ1: 開始点
print(f"ステップ0: ベースライン")
print(f" 値: {contribution:.3f}")
print(f" (これが開始点です)")
prev_cumulative = contribution
elif var_name == 'prediction':
# 最終結果
print(f"\n最終予測値: {contribution:.3f}")
else:
# 各特徴量の追加
change = cumulative - prev_cumulative
print(f"\nステップ{idx}: {var_name}を追加")
print(f" 変化: {change:+.3f}")
print(f" 累積値: {cumulative:.3f}")
prev_cumulative = cumulative
以下、実行結果です。
予測値の段階的構築: -------------------------------------------------- ステップ0: ベースライン 値: 0.310 (これが開始点です) ステップ1: embarkedを追加 変化: +0.019 累積値: 0.329 ステップ2: sibspを追加 変化: +0.005 累積値: 0.335 ステップ3: ageを追加 変化: +0.003 累積値: 0.337 ステップ4: parchを追加 変化: -0.006 累積値: 0.331 ステップ5: classを追加 変化: -0.016 累積値: 0.315 ステップ6: fareを追加 変化: -0.050 累積値: 0.265 ステップ7: genderを追加 変化: -0.074 累積値: 0.191 ステップ8: を追加 変化: +0.000 累積値: 0.191
Break Downの結果を可視化します。
# Break Downプロットを表示 bd_explanation.plot(show=True)
以下、実行結果です。
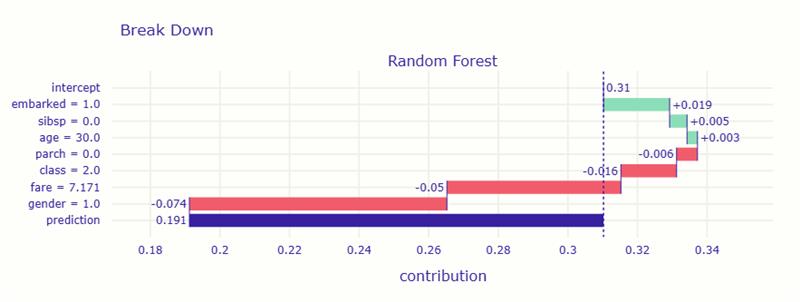
グラフでは、ベースラインから始まって、各特徴量が順番に加わることで予測値がどのように変化していくかが段階的に表示されます。
まず、平均的な生存確率は 約0.31(31%) でしたが、特徴量の影響によって 最終的な予測は約0.19(19%) まで下がりました。
主な理由は、男性であること と 運賃が安いこと です。これらが大きく生存確率を下げました。
一方で、乗船した港(embarked) がやや生存に有利に働き、わずかに確率を押し上げています。
つまり、この人は「男性で、安いチケットで乗船したため、生存しにくいと判断された」という結果です。
| 要因 | 値 | 寄与方向 | 内容 |
|---|---|---|---|
| gender = 1.0(男性) | -0.074 | 生存に強く不利 | 最も大きく生存確率を下げた要因。男性であることがマイナス方向に働いた。 |
| fare = 7.171(運賃が低い) | -0.05 | 生存に不利 | 安いチケットの乗客は低階層の船室の傾向があり、生存確率が下がる。 |
| class = 2.0(2等船室) | -0.016 | やや不利 | 1等よりは不利だが、3等ほどではない。 |
| parch = 0.0(家族なし) | -0.006 | わずかに不利 | 家族がいないことで助け合いが難しい可能性。 |
| age = 30.0 | +0.003 | わずかに有利 | 若すぎず高齢でもない、中間的な年齢。ほぼ影響なし。 |
| sibsp = 0.0(兄弟・配偶者なし) | +0.005 | わずかに有利 | 一人行動できた可能性。影響はごく小さい。 |
| embarked = 1.0(特定の乗船港) | +0.019 | やや有利 | この港の乗客は比較的生存率が高い傾向。 |
複雑なケースでのBreak Down分析
予測が難しい境界線上のケース(生存確率が50%前後)を見つけて分析してみましょう。
# 予測確率が50%前後の乗客を探す
all_predictions = rf_model.predict_proba(X_test)[:, 1]
# 40%~60%の範囲を境界線上と定義
borderline_mask = (all_predictions > 0.4) & (all_predictions < 0.6)
borderline_indices = X_test[borderline_mask].index
print(f"境界線上の乗客数: {len(borderline_indices)}名")
以下、実行結果です。
境界線上の乗客数: 66名
境界線上の乗客が見つかったら、詳しく分析しましょう。
# 最初の境界線上の乗客を選択
borderline_idx = borderline_indices[0]
borderline_data = X_test.loc[[borderline_idx]]
print(f"選択した境界線上の乗客: ID {borderline_idx}")
# 基本情報を表示
borderline_features = borderline_data.iloc[0]
print("\n基本情報:")
print(f" 性別: {'女性' if borderline_features['gender'] == 0 else '男性'}")
print(f" 年齢: {borderline_features['age']:.0f}歳")
print(f" 客室クラス: {borderline_features['class']}")
# 予測結果
borderline_pred = rf_model.predict_proba(borderline_data)[0][1]
borderline_actual = y_test.loc[borderline_idx]
print(f"\n予測結果:")
print(f" 生存確率: {borderline_pred:.2%}")
print(f" 実際: {'生存' if borderline_actual == 1 else '死亡'}")
以下、実行結果です。
選択した境界線上の乗客: ID 533 基本情報: 性別: 女性 年齢: 22歳 客室クラス: 2.0 予測結果: 生存確率: 49.91% 実際: 生存
境界線上のケースのBreak Down分析を実行します。
# Break Down分析を実行
bd_explanation = explainer.predict_parts(
borderline_data, # 分析対象のデータ
type='break_down' # Break Down法を指定
)
# Break Downプロットを表示
bd_explanation.plot(show=True)
以下、実行結果です。
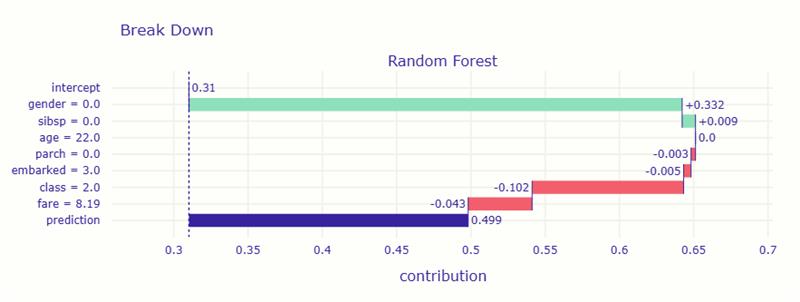
境界線上のケースでは、プラスとマイナスの要因が綱引きをしている様子が明確に分かります。
全体の平均的な生存確率は 約0.31(31%) ですが、女性であること が大きく生存確率を上げ、運賃が安いこと や 2等船室だったこと が少し不利に働きました。これが予測を難しくしている原因です。
結果として、プラスとマイナスの要因がほぼ釣り合い、 AIは「生き残る可能性は約50%」と判断しています。
| 要因 | 値 | 影響 | 解釈 |
|---|---|---|---|
| gender = 0.0(女性) | +0.332 | 生存に非常に有利 | 女性であることが大きく生存確率を押し上げた。 |
| fare = 8.19(運賃がやや安い) | -0.043 | やや不利 | 低価格チケットのため、客室や救助機会が限られた可能性。 |
| class = 2.0(2等船室) | -0.102 | 不利 | 1等よりは劣るが、3等よりはやや良い。中間的な不利要因。 |
| embarked = 3.0(乗船港) | -0.005 | ほぼ影響なし | この港からの乗客は特に有利でも不利でもない。 |
| sibsp = 0.0, parch = 0.0, age = 22.0 | ±0.01未満 | 影響小 | 若く単身の乗客だが、明確な影響はほとんどない。 |
SHAPとBreak Downの使い分け
両手法の基本的な違い
SHAPとBreak Downは、同じ「個別予測の要因分解」という目的を持ちながら、異なるアプローチをとっています。
まず、SHAPとBreak Downの違いを整理しました。
| 比較項目 | SHAP | Break Down |
|---|---|---|
| 核心的な考え方 | すべての可能性を考慮した公平な配分 | 情報を順番に追加する段階的な説明 |
| 例えると | 全員の意見を聞いて決める民主的な方法 | 重要な人から順に意見を聞く階層的な方法 |
| 理論的基盤 | 協力ゲーム理論(シャープレイ値) | 条件付き期待値の逐次計算 |
| 結果の性質 | 理論的に唯一の答え | 順序により複数の答えが存在 |
| 計算時間 | 遅い(指数関数的に増加) | 速い(線形時間で計算) |
| 説明のスタイル | 「総合的に見て〇〇の影響」 | 「まずこれ、次にこれを考慮すると…」 |
| 実装の難易度 | 複雑(近似アルゴリズムが必要) | シンプル(直接計算可能) |
| 結果の安定性 | 高い(わずかな変動のみ) | 低い(順序に大きく依存) |
| 異なるケースの比較 | 比較可能(同じ基準) | 比較困難(順序が異なると不可) |
| 特徴量の相関への対応 | 適切に処理される | 順序により影響が変わる |
簡単に言うと、SHAPが「数学的な厳密性と公平性」を追求するのに対し、Break Downは「計算の効率性と説明の分かりやすさ」を重視しています。
厳密性のSHAPとスピードのBreak Downということです。
このことを、具体的な実務に当てはめると、より使い分け方が分かりやすいかもしれません。以下は、あくまでも一例です。
| 使用場面 | 推奨手法 | 選択理由 | 具体例 |
|---|---|---|---|
| 金融機関の融資審査 | SHAP | 法的説明責任、公平性の保証 | 「なぜAさんは融資可でBさんは不可なのか」を説明 |
| 医療診断の根拠提示 | SHAP | 生命に関わる判断の厳密性 | 「がんリスク70%」の根拠を医師に提示 |
| 保険料の算定 | SHAP | 規制要件、顧客間の公平性 | 保険料差額の正当性を証明 |
| ECサイトのレコメンド | Break Down | リアルタイム性、理解しやすさ | 「この商品がおすすめの理由」を即座に表示 |
| 営業スコアリング | Break Down | 営業担当者への即座の説明 | 「この顧客を訪問すべき理由」を簡潔に説明 |
| 品質検査の異常検知 | Break Down | 現場での迅速な対応 | 「不良品と判定した理由」を作業者に提示 |
| モデルの改善分析 | SHAP | 真の重要度の把握 | どの特徴量を改良すべきか判断 |
| A/Bテストの分析 | SHAP | 群間の公平な比較 | 施策効果を正確に測定 |
| 顧客クレーム対応 | Break Down | 納得感のある説明 | 段階的な説明で顧客を納得させる |
| リアルタイムチャット | Break Down | 応答速度の優先 | ユーザーの質問に即座に回答 |
どちらの手法を活用するのかは、各業界・場面で求められる「説明の質」に依存します。
規制産業や人命に関わる判断では「数学的な正当性」が不可欠ですが、日常的な業務や顧客対応では「素早さと分かりやすさ」が優先されます。
また、同じ金融業界でも、監査対応ではSHAP、店頭での顧客説明ではBreak Downというように、同一組織内でも使い分けることが効果的かなと思います。
| 手法 | 計算量 | 特徴量10個 | 特徴量20個 |
|---|---|---|---|
| SHAP(厳密) | 1,024通り | 約100万通り | |
| SHAP(近似) | 実用的 | 実用的 | |
| Break Down | 10ステップ | 20ステップ |
両手法の理論的背景を理解することで、適切な場面で適切な手法を選択し、AIの説明可能性を最大限に活用できるようになります。
重要なのは、どちらか一方に固執するのではなく、目的と制約に応じて柔軟に使い分けることです。
SHAPの考え方:公平な成果配分
あるレストランで、シェフ、ソムリエ、ウェイターの3人が働いており、今月100万円の利益が出ました。
この利益を公平に配分するにはどうすればよいでしょうか?
ここで、すべての組み合わせでの貢献(売上)を考えてみます。
- シェフだけの場合:料理だけで30万円の売上
- ソムリエだけの場合:ワインだけで20万円の売上
- ウェイターだけの場合:サービスだけで10万円の売上
- シェフ+ソムリエの場合:料理とワインで60万円の売上
- シェフ+ウェイターの場合:料理とサービスで50万円の売上
- ソムリエ+ウェイターの場合:ワインとサービスで35万円の売上
- 全員の場合:すべて揃って100万円の売上
SHAPは、各人が「いる場合」と「いない場合」の差をすべてのパターンで計算し、その平均を取ります。例えばシェフの貢献は次のようになります。
- 一人の時:30万円 – 0万円 = 30万円の貢献
- ソムリエと二人の時:60万円 – 20万円 = 40万円の貢献
- ウェイターと二人の時:50万円 – 10万円 = 40万円の貢献
- 全員の時:100万円 – 35万円 = 65万円の貢献
これらを適切に重み付けして平均すると、シェフの公平な配分額(貢献度)が決まります。
この方法が公平な理由は3つあります。
- 完全性:全員の配分額の合計が必ず100万円になる
- 対称性:同じ貢献をした人は同じ配分を受ける
- ゼロ貢献はゼロ配分:何も貢献しなかった人は配分を受けない
これらの条件を同時に満たすことが、数学的に証明されています。
Break Downの考え方:段階的な積み上げ
5000万円の家を建てる過程を考えてみましょう。
- 土地:まず2000万円の土地を購入(基礎価値2000万円)
- 基礎工事:土地に基礎を作る(+500万円、累計2500万円)
- 建物本体:家を建てる(+2000万円、累計4500万円)
- 内装:内装を整える(+500万円、累計5000万円)
Break Downはまさにこの考え方です。最も重要な要素から順番に追加し、各段階でどれだけ価値が増えるかを示します。
ただ、同じ家でも「説明の順序」を変えると各要素の貢献度が変わります。
順序1:土地→建物→基礎→内装
- 土地:0→2000万円(+2000万円)「まず土地がないと始まらない」
- 建物:2000→4000万円(+2000万円)「建物が主要な価値」
- 基礎:4000→4500万円(+500万円)「建物があるので基礎の追加価値は小さい」
- 内装:4500→5000万円(+500万円)「仕上げの価値」
順序2:建物→土地→内装→基礎
- 建物:0→0万円(+0万円)「土地がないと建物の価値はゼロ」
- 土地:0→4000万円(+4000万円)「土地があって初めて建物に価値が生まれる」
- 内装:4000→4500万円(+500万円)
- 基礎:4500→5000万円(+500万円)
このように、同じ要素でも評価する順序によって貢献度が大きく変わるのがBreak Downの特徴です。
医療診断での簡易例
患者の心臓病リスクを予測する場面で、両手法の違いを見てみましょう。
患者情報:
- 年齢:65歳
- 血圧:高い
- コレステロール:高い
- 喫煙:あり
- 運動:なし
SHAP的な説明:
あなたの心臓病リスク70%の内訳は、喫煙が+25%、高血圧が+20%、高コレステロールが+15%、運動不足が+10%です。これらはすべての要因の組み合わせを考慮した平均的な影響度です。
Break Down的な説明:
平均的なリスク30%から始めて、まず喫煙習慣でリスクが50%に上昇、次に高血圧で65%に、高コレステロールで68%に、最後に運動不足で70%になります。最も重要なのは禁煙です。
Ceteris Paribus:「もし〜だったら」を検証する
SHAPとBreak Downは、「なぜその予測になったのか」を説明する手法でした。
しかし実務では、もう一つ重要な問いがあります。
「もしこの値が違っていたら、予測はどう変わるのか?」
融資を断られた田中さんは、こう尋ねるかもしれません。
「もし年収がもう少し高かったら、通っていましたか?」 「借入希望額を下げたら、どうなりますか?」
こうした「What-if(もし〜だったら)」の問いに答えるのが、Ceteris Paribus(ケテリス・パリブス)です。
Ceteris Paribusとは何か
Ceteris Paribusはラテン語で「他の条件が同じならば」という意味です。
経済学でよく使われる概念で、「ある要因だけを変化させて、その影響を見る」という分析手法を指します。
機械学習の文脈では、特定のインスタンス(個別データ)について、ある特徴量だけを変化させたときに予測がどう変わるかを可視化する手法です。
第3回で紹介したICE(Individual Conditional Expectation)プロットと同じものです。
第3回ではICEがグローバル解釈の文脈で「複数のインスタンスを重ね合わせて傾向を見る」のに対し、今回はCeteris Paribusは特定の1人(1件)に焦点を当てた「個別のWhat-if分析」として使います。
タイタニック乗客のWhat-if分析
先ほど分析した乗客について、「もし条件が違っていたら」を検証してみましょう。
まず、分析対象の乗客の現在の状態を確認します。
# 分析対象の乗客を再確認
print(f"分析対象: 乗客ID {passenger_idx}")
print(f"現在の予測生存確率: {rf_model.predict_proba(passenger_data)[0][1]:.2%}")
print(f"実際の結果: {'生存' if y_test.loc[passenger_idx] == 1 else '死亡'}")
以下、実行結果です。
分析対象: 乗客ID 594 現在の予測生存確率: 19.10% 実際の結果: 生存
DALEXのpredict_profileメソッドでCeteris Paribusプロファイルを作成します。
# Ceteris Paribusを実行
cp_profile = explainer.predict_profile(
passenger_data,
variables=['gender', 'age', 'class', 'fare']
)
# 結果をプロット
cp_profile.plot(show=True)
以下、実行結果です。
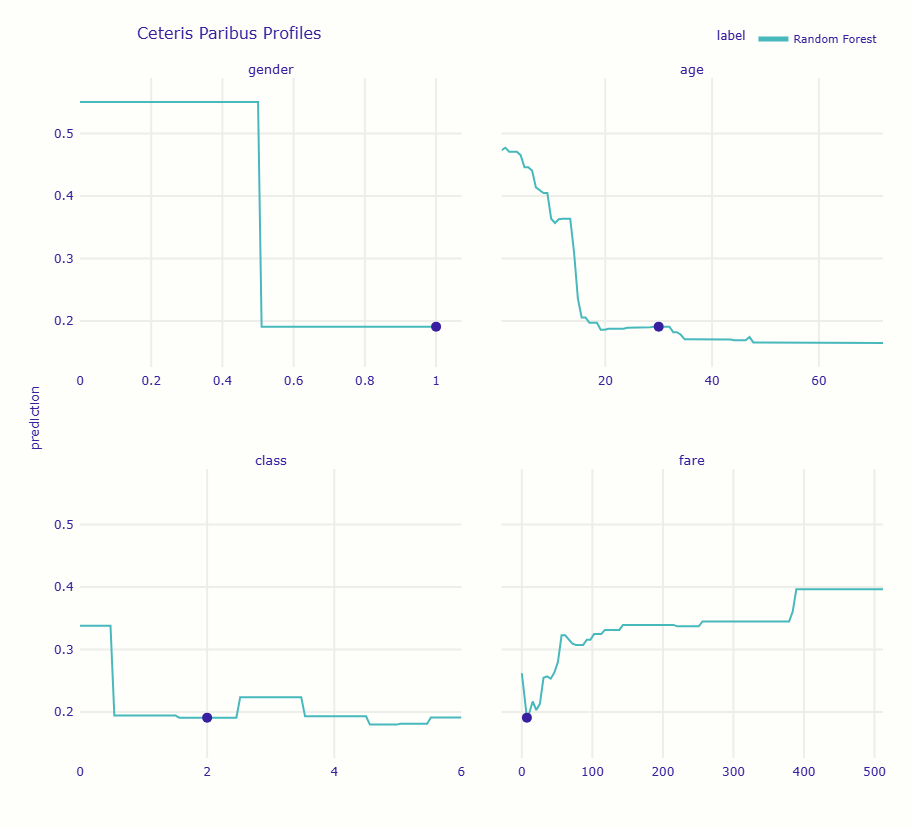
グラフには4つのパネルが表示されます。各パネルは、その特徴量だけを変化させたときに予測がどう変わるかを示しています。
横軸は特徴量の値、縦軸は予測される生存確率です。現在の値の位置に点がプロットされています。
性別の影響を詳しく見る
最も劇的な変化が見られるのは性別です。
# 性別(gender)のCeteris Paribus分析を実行
cp_gender = explainer.predict_profile(
passenger_data, # 分析対象のデータ
variables=['gender'] # 分析する変数
)
# 結果をプロット
cp_gender.plot(show=True)
# 結果を取得
cp_result = cp_gender.result
# 性別が0(女性)の場合の予測値
female_pred = cp_result[cp_result['gender'] == 0]['_yhat_'].values[0]
print(f" 女性 (gender=0): 予測値 = {female_pred:.6f}")
# 性別が1(男性)の場合の予測値
male_pred = cp_result[cp_result['gender'] == 1]['_yhat_'].values[0]
print(f" 男性 (gender=1): 予測値 = {male_pred:.6f}")
以下、実行結果です。
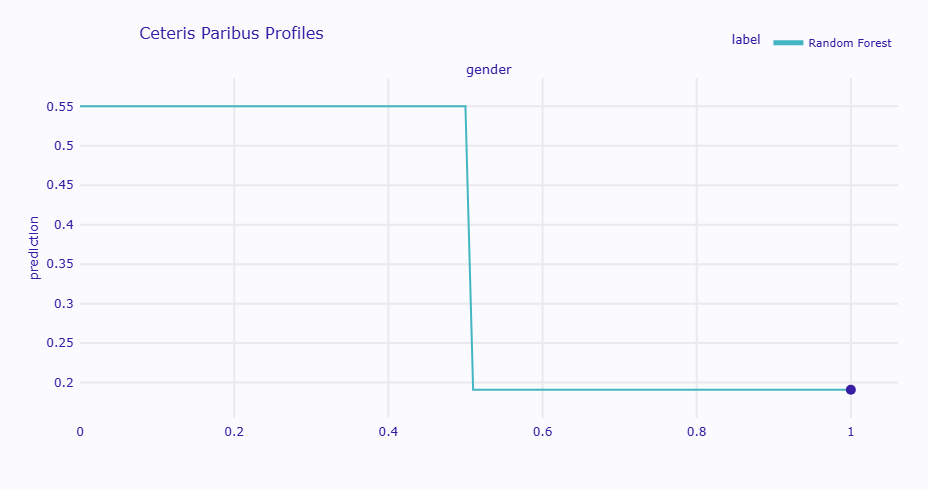
女性 (gender=0): 予測値 = 0.550034 男性 (gender=1): 予測値 = 0.190993
この乗客は男性(gender=1)で生存確率19.1%ですが、「もし女性(gender=0)だったら」生存確率は55.0%へと大幅に上昇します。
他のすべての条件(年齢30歳、3等客室、運賃7ドルなど)を固定したまま、性別だけを変えた場合の予測値です。
年齢の影響を連続的に見る
年齢は連続値なので、より細かい変化を追跡できます。
# 年齢(age)のCeteris Paribus分析を実行
cp_age = explainer.predict_profile(
passenger_data,
variables=['age']
)
# 結果をプロット
cp_age.plot(show=True)
以下、実行結果です。
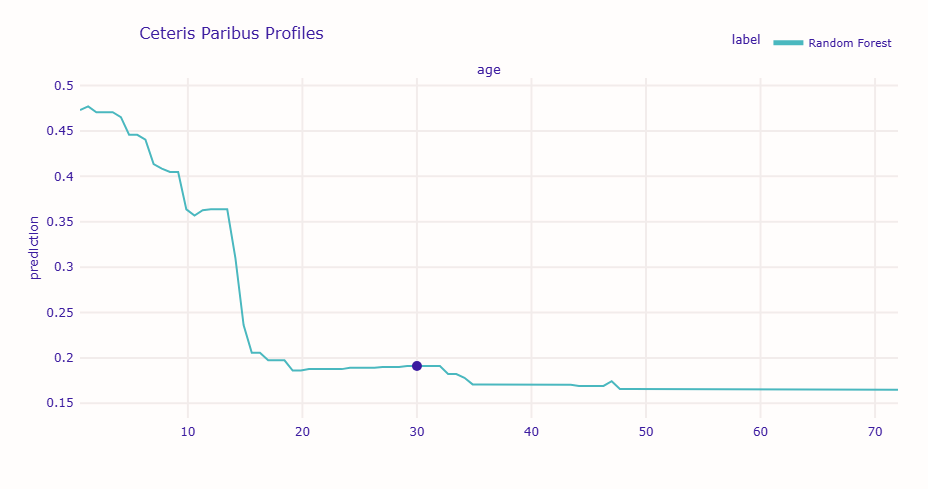
グラフを見ると、この乗客の場合、年齢が若くなるほど生存確率が上がる傾向が確認できます。
特に10歳未満では生存確率が顕著に上昇しています。これは「子供を優先」という避難方針を反映しています。
具体的な値を指定したWhat-if分析
プロファイル全体を可視化するだけでなく、「もし年齢が5歳だったら」「もし1等客室だったら」といった具体的なシナリオを検証したい場面も多いでしょう。
元のデータをコピーして特定の値を変更し、予測を比較することでこれを実現できます。
まず、現在の乗客の状態と予測を確認します。
# 分析対象の乗客データを表示 print(passenger_data) # 予測モデルによる生存確率を表示 print(rf_model.predict_proba(passenger_data)[0][1])
以下、実行結果です。
gender age class embarked fare sibsp parch 594 1 30.0 2 1 7.1711 0 0 0.19099344991597664
この乗客は30歳の男性、2等客室、生存確率は約19%です。
「もし女性だったら」を検証します。
# 性別を女性にした場合のデータを作成 what_if_female = passenger_data.copy() what_if_female['gender'] = 0 # 性別を女性にした場合の生存確率を表示 print(rf_model.predict_proba(what_if_female)[0][1])
以下、実行結果です。
0.5500337113375382
性別を女性に変えるだけで、生存確率は19%から55%に上昇しました。
次に、「もし5歳の子供だったら」を検証します。
# 年齢を5歳にした場合のデータを作成 what_if_child = passenger_data.copy() what_if_child['age'] = 5 # 年齢を5歳にした場合の生存確率を表示 print(rf_model.predict_proba(what_if_child)[0][1])
以下、実行結果です。
0.4458072001224707
年齢を5歳に変えると、生存確率は19%から45%に上昇しました。
「もし1等客室だったら」を検証します。
# クラスをFirstにした場合のデータを作成 what_if_first_class = passenger_data.copy() what_if_first_class['class'] = 0 # クラスをFirstにした場合の生存確率を表示 print(rf_model.predict_proba(what_if_first_class)[0][1])
以下、実行結果です。
0.33792132320752544
1等客室に変えると、生存確率は19%から34%に上昇しました。
複数の条件を同時に変更する
実務では「複数の条件を同時に変えたらどうなるか」を検証したいことも多いでしょう。
「もし女性で、かつ1等客室だったら」を検証します。
# 性別を女性、クラスをFirstにした場合のデータを作成 what_if_best = passenger_data.copy() what_if_best['gender'] = 0 what_if_best['class'] = 0 # 性別を女性、クラスをFirstにした場合の生存確率を表示 print(rf_model.predict_proba(what_if_best)[0][1])
以下、実行結果です。
0.7367758777323193
女性かつ1等客室という条件では、生存確率は73%まで上昇しました。
「もし5歳の女の子で、1等客室だったら」を検証します。
# 性別を女性、クラスをFirst、年齢を5歳にした場合のデータを作成 what_if_child_best = passenger_data.copy() what_if_child_best['gender'] = 0 what_if_child_best['class'] = 0 what_if_child_best['age'] = 5 # 性別を女性、クラスをFirst、年齢を5歳にした場合の生存確率を表示 print(rf_model.predict_proba(what_if_child_best)[0][1])
以下、実行結果です。
0.7775665474653712
5歳の女の子で1等客室なら、生存確率は78%に達します。
複数のシナリオをまとめて比較すると、どの条件がどれだけ影響するかが明確になります。
# シナリオごとの生存確率を格納するリスト
scenarios = []
# 現状の生存確率を計算し、シナリオに追加
base_prob = rf_model.predict_proba(passenger_data)[0][1]
scenarios.append(('現状(30歳男性、2等客室)', base_prob))
# 性別を女性に変更した場合の生存確率を計算し、シナリオに追加
what_if = passenger_data.copy()
what_if['gender'] = 0
scenarios.append(('女性に変更', rf_model.predict_proba(what_if)[0][1]))
# 年齢を5歳に変更した場合の生存確率を計算し、シナリオに追加
what_if = passenger_data.copy()
what_if['age'] = 5
scenarios.append(('5歳に変更', rf_model.predict_proba(what_if)[0][1]))
# 客室クラスを1等に変更した場合の生存確率を計算し、シナリオに追加
what_if = passenger_data.copy()
what_if['class'] = 0
scenarios.append(('1等客室に変更', rf_model.predict_proba(what_if)[0][1]))
# 性別を女性、客室クラスを1等に変更した場合の生存確率を計算し、シナリオに追加
what_if = passenger_data.copy()
what_if['gender'] = 0
what_if['class'] = 0
scenarios.append(('女性+1等客室', rf_model.predict_proba(what_if)[0][1]))
# 性別を女性、客室クラスを1等、年齢を5歳に変更した場合の生存確率を計算し、シナリオに追加
what_if = passenger_data.copy()
what_if['gender'] = 0
what_if['class'] = 0
what_if['age'] = 5
scenarios.append(('5歳女児+1等客室', rf_model.predict_proba(what_if)[0][1]))
# 各シナリオの結果を出力
for scenario, prob in scenarios:
print(f"{scenario}: {prob:.1%}")
以下、実行結果です。
現状(30歳男性、2等客室): 19.1% 女性に変更: 55.0% 5歳に変更: 44.6% 1等客室に変更: 33.8% 女性+1等客室: 73.7% 5歳女児+1等客室: 77.8%
この比較から、性別の変更が最も大きなインパクトを持ち、次いで年齢という順で影響度が高いことが確認できます。
また、複数の条件を組み合わせることで効果が累積し、最良の条件では生存確率が78%に達することも分かりました。
複数の乗客を比較する
異なる特徴を持つ乗客のCeteris Paribusプロファイルを重ね合わせることで、「同じ変化でも人によって影響が異なる」ことを可視化できます。
# 乗客A(上級女性客)のデータを取得 passenger_a_data = X_test.loc[[high_survival_idx]] # 乗客B(下級男性客)のデータを取得 passenger_b_data = X_test.loc[[low_survival_idx]] # 乗客Aの年齢に関するCeteris Paribusプロファイルを計算 cp_a = explainer.predict_profile(passenger_a_data, variables=['age']) # 乗客Bの年齢に関するCeteris Paribusプロファイルを計算 cp_b = explainer.predict_profile(passenger_b_data, variables=['age']) # 乗客Aと乗客BのCeteris Paribusプロファイルを比較プロット cp_a.plot(cp_b, show=True)
以下、実行結果です。
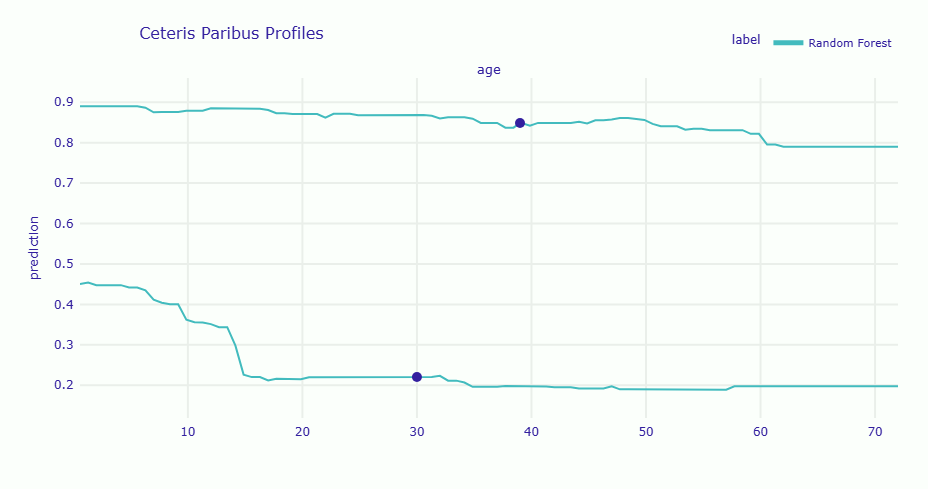
グラフには2本の線が表示されます。上級女性客(上の線)と下級男性客(下の線)では、年齢を変化させても生存確率の「レベル」が大きく異なることが分かります。
女性の場合は年齢が上がっても比較的高い生存確率を維持していますが、男性の場合は全体的に低い水準で推移しています。
これは、年齢の影響が性別や客室クラスによって「調整」されていることを示しています。
Ceteris Paribusの実務での活用
Ceteris Paribusは、以下のような場面で特に威力を発揮します。
顧客への改善提案
融資審査で却下された顧客に対して、「借入希望額を〇〇万円に下げれば承認の可能性があります」「年収が〇〇万円以上になれば状況が変わります」といった具体的なアドバイスができます。
感度分析
製造業では、「温度をあと5℃下げたら不良率はどう変わるか」「材料Aの濃度を2%上げたらどうなるか」といった調整の効果を事前にシミュレーションできます。
意思決定の境界の特定
「生存確率が50%を超えるのは、運賃がいくら以上の場合か」といった閾値を特定できます。これにより、予測が変わる「臨界点」を把握できます。
SHAPとCeteris Paribusの使い分け
両者は補完的な関係にあります。
| SHAP | Ceteris Paribus | |
|---|---|---|
| 答える問い | 「なぜこの予測になったか」 | 「もし〜だったらどうなるか」 |
| 出力形式 | 各特徴量の寄与度(数値) | 特徴量の変化に対する予測の変化(曲線) |
| 時制 | 過去(なぜそうなったか) | 未来(どうすれば変わるか) |
| 主な用途 | 説明責任、監査対応 | 改善提案、シミュレーション |
実務では、まずSHAPで「なぜその予測になったか」を説明し、次にCeteris Paribusで「どうすれば改善できるか」を提案する、という流れが効果的です。
製造業での異常検知の例
製造データの準備
製造現場での品質管理を想定した、製造データを生成します。
# 製造業の品質データを模擬的に作成
np.random.seed(42) # 再現性のため
n_products = 1000 # 1000個の製品データ
# 製造パラメータを生成
manufacturing_data = pd.DataFrame({
'温度': np.random.normal(150, 10, n_products), # 平均150℃、標準偏差10
'圧力': np.random.normal(100, 5, n_products), # 平均100kPa、標準偏差5
'速度': np.random.normal(50, 3, n_products), # 平均50m/min、標準偏差3
'湿度': np.random.normal(60, 8, n_products), # 平均60%、標準偏差8
'材料A濃度': np.random.normal(30, 2, n_products), # 平均30%、標準偏差2
'材料B濃度': np.random.normal(20, 1.5, n_products), # 平均20%、標準偏差1.5
})
不良品の発生条件を、以下のように設定します。
- 温度が135-165℃の範囲外: 不良率増加
- 圧力が92-108kPaの範囲外: 不良率増加
- 材料A濃度が26%未満: 不良率増加
# 不良確率を計算
defect_probability = (
0.1 + # 基本不良率10%
0.3 * ((manufacturing_data['温度'] > 165) | (manufacturing_data['温度'] < 135)) +
0.2 * ((manufacturing_data['圧力'] > 108) | (manufacturing_data['圧力'] < 92)) +
0.1 * (manufacturing_data['材料A濃度'] < 26)
)
# 不良品フラグを生成
manufacturing_data['不良品'] = np.random.random(n_products) < defect_probability
defect_count = manufacturing_data['不良品'].sum()
print(f"不良品数: {defect_count}個")
print(f"良品数: {n_products - defect_count}個")
print(f"不良率: {defect_count / n_products:.2%}")
以下、実行結果です。
不良品数: 166個 良品数: 834個 不良率: 16.60%
データのサンプルを確認します。
# データサンプルを表示
print("製造データのサンプル(最初の5件):")
print(manufacturing_data.head())
以下、実行結果です。
製造データのサンプル(最初の5件):
温度 圧力 速度 湿度 材料A濃度 材料B濃度 不良品
0 154.967142 106.996777 47.974465 44.737540 28.273013 19.364360 False
1 148.617357 104.623168 49.566444 53.116920 29.937593 19.319879 False
2 156.476885 100.298152 47.622740 56.691156 30.036034 17.306535 False
3 165.230299 96.765316 49.076115 75.101501 30.945261 19.504865 False
4 147.658466 103.491117 44.319156 64.452425 27.266283 21.099244 False
品質予測モデルの構築
品質を予測する機械学習モデルを構築します。
# データを特徴量と目的変数に分割
X_mfg = manufacturing_data.drop('不良品', axis=1)
y_mfg = manufacturing_data['不良品'].astype(int)
print(f"特徴量の数: {X_mfg.shape[1]}")
print(f"サンプル数: {X_mfg.shape[0]}")
以下、実行結果です。
特徴量の数: 6 サンプル数: 1000
データを訓練用とテスト用に分割します。
# 訓練データとテストデータに分割
X_train_mfg, X_test_mfg, y_train_mfg, y_test_mfg = train_test_split(
X_mfg, y_mfg,
test_size=0.2, # 20%をテストデータに
random_state=42
)
print(f"訓練データ: {len(X_train_mfg)}件")
print(f"テストデータ: {len(X_test_mfg)}件")
以下、実行結果です。
訓練データ: 800件 テストデータ: 200件
品質予測モデルを構築します。
# ランダムフォレストモデルを構築
rf_mfg = RandomForestClassifier(
n_estimators=50, # 決定木の数を50に
max_depth=4, # 各木の最大深さを4に
random_state=42
)
# モデルを訓練
rf_mfg.fit(X_train_mfg, y_train_mfg)
# 精度を評価
accuracy = rf_mfg.score(X_test_mfg, y_test_mfg)
print(f"モデルの予測精度: {accuracy:.2%}")
以下、実行結果です。
モデルの予測精度: 80.50%
不良品の要因分析
実際に不良品と判定された製品について、その原因を分析します。
AIモデル(rf_mfg)とテストデータ(X_test_mfg, y_test_mfg)を読み込み、「AIの予測根拠を説明するための準備」(Explainerの作成)をします。
# 品質管理用のExplainerを作成
explainer_mfg = dx.Explainer(
rf_mfg,
X_test_mfg,
y_test_mfg,
label="品質管理AI"
)
以下、実行結果です。
Preparation of a new explainer is initiated -> data : 200 rows 6 cols -> target variable : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray. -> target variable : 200 values -> model_class : sklearn.ensemble._forest.RandomForestClassifier (default) -> label : 品質管理AI -> predict function : <function yhat_proba_default at 0x7f3c2c5e3010> will be used (default) -> predict function : Accepts pandas.DataFrame and numpy.ndarray. -> predicted values : min = 0.1, mean = 0.158, max = 0.539 -> model type : classification will be used (default) -> residual function : difference between y and yhat (default) -> residuals : min = -0.538, mean = 0.0269, max = 0.897 -> model_info : package sklearn A new explainer has been created!
テストデータは200製品分、6つのパラメータで構成されており、AIが予測した「不良品である確率」は平均で15.8%であることがわかります。
不良品のサンプルを選んで分析します。
# テストデータから不良品を抽出
defect_products = X_test_mfg[y_test_mfg == 1]
print(f"テストデータ中の不良品: {len(defect_products)}個")
if len(defect_products) > 0:
# 最初の不良品を選択
defect_idx = defect_products.index[0]
defect_sample = defect_products.iloc[[0]]
print(f"\n分析対象: 製品ID {defect_idx}")
# 不良品確率を予測
defect_pred = rf_mfg.predict_proba(defect_sample)[0][1]
print(f"AIの不良品確率予測: {defect_pred:.2%}")
以下、実行結果です。
テストデータ中の不良品: 37個 分析対象: 製品ID 883 AIの不良品確率予測: 11.83%
テストデータ200個のうち、37個が実際の不良品です。今回はその中から「製品ID 883」をピックアップして詳細分析を行います。
AIモデルは、この「製品ID 883」が不良品である確率を 11.83% と予測しました。
これは、AIの視点では不良品である可能性は低い(むしろ良品寄り)と判断されていることを示しています。
選択した不良品の製造パラメータを詳しく確認します。
# 製造パラメータの詳細確認
print("製造パラメータの測定値:")
print("-" * 40)
defect_params = defect_sample.iloc[0]
# 各パラメータと基準値を比較
print(f"温度: {defect_params['温度']:.1f}℃")
if defect_params['温度'] > 165:
print(" → ⚠️ 基準値より高い(上限165℃)")
elif defect_params['温度'] < 135:
print(" → ⚠️ 基準値より低い(下限135℃)")
else:
print(" → ✓ 正常範囲内")
print(f"\n圧力: {defect_params['圧力']:.1f}kPa")
if defect_params['圧力'] > 108:
print(" → ⚠️ 基準値より高い(上限108kPa)")
elif defect_params['圧力'] < 92:
print(" → ⚠️ 基準値より低い(下限92kPa)")
else:
print(" → ✓ 正常範囲内")
print(f"\n材料A濃度: {defect_params['材料A濃度']:.1f}%")
if defect_params['材料A濃度'] < 26:
print(" → ⚠️ 基準値より低い(下限26%)")
else:
print(" → ✓ 正常範囲内")
以下、実行結果です。
製造パラメータの測定値: ---------------------------------------- 温度: 160.4℃ → ✓ 正常範囲内 圧力: 97.0kPa → ✓ 正常範囲内 材料A濃度: 31.0% → ✓ 正常範囲内
「製品ID 883」の各製造パラメータ(温度、圧力、材料A濃度)は、個別に設定された品質管理の基準値(閾値)をすべてクリアしています。
これは、従来の閾値管理(上限・下限チェック)では、この製品は「正常品」として扱われ、見逃されてしまうことを示しています。
しかし、実際にはこの製品は不良品です。
SHAPを使って不良の要因を詳細に分析します。
基準となるベースライン不良率(テストデータ全体の不良品確率の予測値の平均)は15.8%です。
# SHAP分析で不良要因を特定
print("SHAP分析による不良要因の特定:")
print("-" * 50)
# SHAP分析を実行
shap_defect = explainer_mfg.predict_parts(
defect_sample,
type='shap',
B=100
)
shap_defect_result = shap_defect.result
# 変数ごとに平均化
mean_contributions = shap_defect_result.groupby('variable_name')['contribution'].mean().reset_index()
# 影響度を計算してリスト化
impacts = []
for _, row in mean_contributions.iterrows():
param_name = row['variable_name']
impact = row['contribution']
impacts.append((param_name, impact))
# 影響度の大きい順にソート
impacts.sort(key=lambda x: abs(x[1]), reverse=True)
# 表示
for param_name, impact in impacts:
if impact > 0:
print(f" {param_name:10s}: {impact:+.4f} (不良リスク増大)")
else:
print(f" {param_name:10s}: {impact:+.4f} (品質向上効果)")
以下、実行結果です。
SHAP分析による不良要因の特定: -------------------------------------------------- 温度 : -0.0237 (品質向上効果) 速度 : -0.0062 (品質向上効果) 材料B濃度 : -0.0059 (品質向上効果) 材料A濃度 : -0.0032 (品質向上効果) 湿度 : -0.0010 (品質向上効果) 圧力 : +0.0002 (不良リスク増大)
ベースライン不良率(15.8%)に対し、AIはこの製品(ID 883)の不良品確率を 11.83% と予測しました。
これは、AIが「良品である可能性が高い」と判断したことを意味します。
SHAP分析の結果も、AIがなぜそう判断したかを示しています。
「温度」(-0.0237)や「速度」(-0.0062)など、AIの学習データに含まれるほとんどのパラメータが「品質向上効果」(不良率を下げる方向)に働くとAIは解釈しました。
しかし、この製品は実際には不良品でした。この事実は非常に重要です。
AIが「大丈夫(良品)」と判断したのに、実際は「ダメ(不良品)」だった。
この食い違いが起きた理由は、シンプルに言うと2つです。
AIがこの「不良パターン」を知らなかった
AIは過去のデータから「不良品とはこういうものだ」と学んでいます。
しかし、今回の不良品はAIがまだ勉強していない「新しい問題」でした。
AIが知っているどの不良パターンにも当てはまらなかったため、「良品だ」と間違って判断してしまいました。
AIが「見ていない」場所が原因だった
AIは「温度」や「圧力」など、決められた6つの項目しかチェックしていません。
もし不良の本当の原因が、AIが見ていない「材料を混ぜる時間」や「部品の微妙な違い」など別の場所にあったとしたら、AIには見つけようがありません。
結論として、この製品 883 は「従来の基準値管理でも、現在のAIモデルでも検知・説明が困難な、特殊な不良品」であると言えます。
このような「AIが予測を外した事例(False Negative)」を詳細に分析し、なぜAIが良品と判断したのか(SHAP)、なぜ実際は不良品だったのか(現場の知見)を突き合わせることこそが、AIモデルを改善し、真の不良原因を特定する鍵となります。
次のアクションとして、この製品 883 の製造ログや現物を確認し、「AIが学習していない要因」を探すべきです。
この分析により、製造現場の担当者は具体的にどのパラメータを改善すべきか、そしてその改善によってどの程度の効果が期待できるかを明確に理解できます。
まとめ
今回は、個別予測を詳細に説明するローカル解釈の手法として、SHAP、Break Down、Ceteris Paribusの3つを紹介しました。
SHAPは、ゲーム理論に基づいた公平な貢献度配分により、理論的に厳密な説明を提供します。計算コストは高いものの、金融や医療など規制が厳しい分野で威力を発揮します。
Break Downは、段階的で直感的な説明により、技術的な背景を持たない人にも分かりやすい形で予測根拠を示せます。計算も高速で、リアルタイムでの説明生成に適しています。
Ceteris Paribusは、「もしこの値が違っていたら」という問いに答えます。SHAPやBreak Downが「なぜそうなったか」を説明するのに対し、Ceteris Paribusは「どうすれば変わるか」を示し、顧客への改善提案や製造パラメータの調整シミュレーションに直結します。
実務では、厳密性が求められる場面ではSHAPを、分かりやすさ重視ならBreak Downを、改善提案にはCeteris Paribusを、と状況に応じた使い分けが重要です。
AIの判断根拠を説明できることは、もはや「あったら良い」機能ではなく、「なくてはならない」要件になりつつあります。今回学んだ手法を、ぜひ自分のプロジェクトでも活用してみてください。

