金属プレス加工を専門とする中堅メーカーのXAI事例です。
朝の品質会議で、品質管理課の鈴木さんが困った顔をしていました。
「昨日の夜勤で製造されたロット番号A-2457の製品が不良と判定されたんですが、見た目にも測定値にも問題がないように見えるんです。なぜAIが不良と判断したのか、説明できますか?」
これこそが、第4回で学んだSHAPとBreak Downの真の出番です。
今回は、実際の不良品を例に、AIの判断を徹底的に分解し、改善アクションまでつなげたお話しになります。
- SHAPによる不良要因の公平な配分
- Break Downによる段階的な原因追跡
- What-If分析による改善シミュレーション
- コスト効果を考慮した最適改善戦略
前回(第5回)構築した品質予測モデルを使って、個別の不良品を分析していきましょう。
Contents
不良品の要因分解
境界線上の不良品を特定する
まず、前回構築したモデルと利用したデータを使って、実際の不良品サンプルを選び出します。
このデータセットは、製造業におけるプレス加工ラインの製品に関するものです。
- プレス温度 (℃): プレス加工時の温度で、通常は150℃が最適です。温度の変動は製品の品質に影響を与える可能性があります。
- プレス圧力 (MPa): プレス加工時の圧力で、通常は200MPaが標準です。圧力が不適切だと、成形不良や亀裂の原因となることがあります。
- プレス速度 (mm/s): プレス加工の速度で、速すぎても遅すぎても問題が生じます。速すぎると材料に負荷がかかり、遅すぎると温度管理が困難になります。
- 材料厚 (mm): 材料の厚さで、ロットごとにわずかなバラツキがあります。材料メーカーの公差内でも、品質に影響する場合があります。
- 潤滑油温度 (℃): 潤滑油の温度で、温度管理が重要です。潤滑油の温度が不適切だと、摩擦係数が変化し品質に影響を与える可能性があります。
- 金型温度 (℃): プレス温度と相関があります。
- 環境湿度 (%): 季節変動があり、時間帯による湿度変化をあります(日中と夜間の差)。
- 品質スコア: 上記の製造パラメータ(プラス温度から環境湿度まで)から計算されるスコアで、低いスコアほど不良の可能性が高いです。
- 不良品: 不良品=1、良品=0。品質スコアが65未満の場合は不良品として分類されています。
サンプルデータ(manufacturing_data_qs.csv)を読み込みます。以下からダウンロードできます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
import dalex as dx
import warnings
warnings.filterwarnings('ignore')
import japanize_matplotlib # 日本語表示のため
# CSVファイルから製造データを読み込む
manufacturing_data_qs = pd.read_csv(
'manufacturing_data_qs.csv'
)
# データの最初の5行を表示
print(manufacturing_data_qs.head())
以下、実行結果です。
プレス温度 プレス圧力 プレス速度 材料厚 潤滑油温度 金型温度 \
0 153.973713 171.382887 44.429593 2.076540 45.874070 107.064483
1 148.893886 187.094225 46.845346 2.107341 30.605095 104.062440
2 155.181508 193.795917 45.289699 2.049869 38.361025 108.948530
3 162.184239 228.315315 47.260021 1.805750 39.791700 118.263275
4 148.126773 208.348297 48.929248 1.984458 40.079543 99.952655
環境湿度 品質スコア 不良品
0 61.609176 56.461251 1
1 58.681402 76.230623 0
2 68.456782 81.612110 0
3 64.119259 40.783415 1
4 72.408029 89.226620 0
前回同様、データを訓練用とテスト用に分割します。
# 特徴量と目的変数の分離
# 品質スコアは実際の運用では分からないので除外
X = manufacturing_data_qs.drop(['不良品', '品質スコア'], axis=1)
y = manufacturing_data_qs['不良品']
# データの基本情報を表示
print("モデル構築のためのデータ準備:")
print(f" 特徴量の数: {X.shape[1]}")
print(f" 特徴量: {list(X.columns)}")
# 訓練データとテストデータに分割(75:25)
# stratifyで良品と不良品の比率を保つ
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.25,
random_state=42,
stratify=y # 不良品の比率を保持
)
以下、実行結果です。
モデル構築のためのデータ準備: 特徴量の数: 7 特徴量: ['プレス温度', 'プレス圧力', 'プレス速度', '材料厚', '潤滑油温度', '金型温度', '環境湿度']
前回構築したものを同じRandomForestモデルを、訓練データで構築します。
# RandomForestモデルの構築
rf_model = RandomForestClassifier(
n_estimators=100, # 100本の決定木を使用
max_depth=10, # 各決定木の最大深さ
min_samples_split=20, # ノード分割の最小サンプル数
min_samples_leaf=10, # 葉ノードの最小サンプル数
random_state=42
)
# モデルの訓練
rf_model.fit(X_train, y_train)
テストデータから不良品を抽出し、それぞれの不良確率を計算します。10件を表示します。
# 不良品のインデックスを取得
defect_indices = X_test[y_test == 1].index
print(f"不良品数: {len(defect_indices)}")
# 各不良品の予測確率を計算(10件を表示)
defect_probabilities = []
for idx in defect_indices[:10]:
sample = X_test.loc[[idx]]
prob = rf_model.predict_proba(sample)[0, 1]
defect_probabilities.append((idx, prob))
print(f"ID {idx}: {prob:.2%}")
以下、実行結果です。
不良品数: 221 ID 1956: 40.74% ID 978: 43.01% ID 1382: 62.93% ID 1178: 68.88% ID 559: 23.51% ID 2762: 30.17% ID 1219: 83.77% ID 2528: 67.37% ID 522: 51.48% ID 1870: 69.88%
特に興味深いのは、「境界線上の不良品」(予測確率が0.5に近い製品)、つまりAIが迷いながら不良と判定したケースです。これらは品質管理の微妙なラインを理解する上で特に重要です。
0.5に近い順にソートし、0.5に近い上位5つを表示します。その中で最も0.5に近いものを分析対象とします。
# 境界線からの距離でソート(0.5に近い順)
defect_probabilities.sort(key=lambda x: abs(x[1] - 0.5))
# 上位5つを表示
for idx, prob in defect_probabilities[:5]:
print(f"ID {idx}: 不良確率 {prob:.2%} (境界から {abs(prob-0.5)*100:.1f}%)")
# 最も判定が微妙だった製品を選択
target_idx = defect_probabilities[0][0]
target_product = X_test.loc[[target_idx]]
print(f"\n分析対象: ID {target_idx}")
以下、実行結果です。
ID 522: 不良確率 51.48% (境界から 1.5%) ID 978: 不良確率 43.01% (境界から 7.0%) ID 1956: 不良確率 40.74% (境界から 9.3%) ID 1382: 不良確率 62.93% (境界から 12.9%) ID 2528: 不良確率 67.37% (境界から 17.4%) 分析対象: ID 522
選定した製品(ID 522)の製造条件を確認し、各パラメータが正常範囲からどの程度逸脱しているかを標準偏差(
# 製造条件の確認
for col in target_product.columns:
value = target_product.iloc[0][col]
mean_val = X_train[col].mean()
std_val = X_train[col].std()
deviation = (value - mean_val) / std_val
print(f"{col}: {value:.2f} (偏差: {deviation:+.1f}σ)")
以下、実行結果です。
プレス温度: 144.70 (偏差: -0.7σ) プレス圧力: 185.52 (偏差: -0.9σ) プレス速度: 48.16 (偏差: -0.4σ) 材料厚: 2.10 (偏差: +1.0σ) 潤滑油温度: 35.25 (偏差: -1.0σ) 金型温度: 89.88 (偏差: -2.1σ) 環境湿度: 44.62 (偏差: -1.7σ)
2 \sigmaを超える偏差は異常値、
金型温度は偏差が
他のパラメータは異常値や注意値には該当しませんが、プレス温度とプレス圧力は基準値からやや離れているため、今後の製造プロセスでの改善が望まれます。
これらの情報を基に、製造条件の見直しを行い、品質向上を図ることが重要です。
SHAPによる要因分解の実行
選定した製品(ID 522)を、DALEXのExplainerを使ってSHAP分析を実施します。
SHAPは、ゲーム理論のシャープレイ値という概念を使って、各特徴量が予測結果にどれだけ貢献したかを公平に配分します。
# Explainerの作成
explainer = dx.Explainer(
rf_model,
X_test,
y_test,
label="品質予測モデル"
)
# SHAP値の計算
shap_explanation = explainer.predict_parts(
target_product, # 選定した製品(ID 522)
type='shap', # SHAP値を計算
B=100 # 100回のブートストラップサンプリング
)
SHAP値は以下のように解釈されます。
- 正の値:不良率を上昇させる要因(品質悪化)
- 負の値:不良率を低下させる要因(品質改善)
- 値の大きさ:影響の強さ
選定した製品(ID 522)の分析結果を見てみます。
# 結果の集計
# SHAP値の結果を取得
shap_result = shap_explanation.result
# 変数ごとの平均寄与度を計算
shap_values = shap_result.groupby(
'variable_name' # 変数名でグループ化
)[
'contribution' # 寄与度を集計
].mean().sort_values() # 平均値を計算し、ソート
# ベースライン(平均不良率)の取得
baseline = y_train.mean()
print(f"ベースライン: {baseline:.4f}")
# 各パラメータの寄与度を整理
contributions = {}
for param, contribution in shap_values.items():
if param not in ['intercept', 'prediction']:
actual_value = target_product.iloc[0][param]
contributions[param] = contribution
print(f"{param}: {contribution:+.4f} (値: {actual_value:.2f})")
# 結果出力
total_contribution = sum(contributions.values())
predicted_prob = baseline + total_contribution
actual_prediction = rf_model.predict_proba(target_product)[0, 1]
print(f"計算値: {predicted_prob:.4f}, 実際: {actual_prediction:.4f}")
以下、実行結果です。
ベースライン: 0.2956 プレス速度: -0.0212 (値: 48.16) 材料厚: -0.0072 (値: 2.10) 潤滑油温度: -0.0044 (値: 35.25) 環境湿度: +0.0068 (値: 44.62) 金型温度: +0.0529 (値: 89.88) プレス温度: +0.0649 (値: 144.70) プレス圧力: +0.1242 (値: 185.52) 計算値: 0.5117, 実際: 0.5148
ベースラインの不良率は0.2956です。プレス速度、材料厚、潤滑油温度は不良率を減少させる要因です。
一方、環境湿度、金型温度、プレス温度、プレス圧力は不良率を増加させる要因です。
最終的な計算値は0.5117で、実際の不良率は0.5148です。
SHAP値の合計がベースラインに加算されて最終予測値となることが確認できます。これがSHAPの数学的な美しさです。
SHAP値をグラフで可視化します。
# SHAP値の可視化 shap_explanation.plot(show=True)
以下、実行結果です。
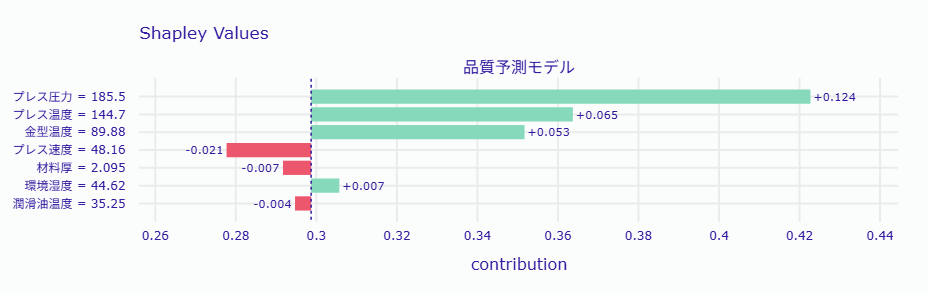
主要な不良要因の詳細分析
選定した製品(ID 522)の品質への影響度の大きい要因TOP3について、より詳しく分析します。
# 影響度の大きい順にソート
top_factors = sorted(
contributions.items(),
key=lambda x: abs(x[1]),
reverse=True
)[:3]
for rank, (factor, contribution) in enumerate(top_factors, 1):
factor_mean = X_train[factor].mean()
factor_std = X_train[factor].std()
actual_value = target_product.iloc[0][factor]
deviation = (actual_value - factor_mean) / factor_std
good_mean = X_train[y_train == 0][factor].mean()
defect_mean = X_train[y_train == 1][factor].mean()
print(f"\n第{rank}位: {factor}")
print(f" SHAP値: {contribution:+.4f}")
print(f" 測定値: {actual_value:.2f} ({deviation:+.1f}σ)")
print(f" 良品平均: {good_mean:.2f}")
print(f" 不良品平均: {defect_mean:.2f}")
以下、実行結果です。
第1位: プレス圧力 SHAP値: +0.1242 測定値: 185.52 (-0.9σ) 良品平均: 200.10 不良品平均: 198.30 第2位: プレス温度 SHAP値: +0.0649 測定値: 144.70 (-0.7σ) 良品平均: 150.01 不良品平均: 150.46 第3位: 金型温度 SHAP値: +0.0529 測定値: 89.88 (-2.1σ) 良品平均: 105.10 不良品平均: 105.69
各要因について、以下の観点から改善提案を導出します。
- SHAP値が正の場合:不良の主要原因なので改善が必要
- 測定値と良品平均の差:調整の目標値を設定
- 標準偏差での乖離:調整の難易度を評価
プレス圧力は不良の主要原因であり、良品平均の200.10に近づけることが目標です。測定値は185.52であり、標準偏差での乖離は-0.9σです。
プレス温度も不良の原因であり、良品平均の150.01に近づけることが目標です。測定値は144.70であり、標準偏差での乖離は-0.7σです。
金型温度は不良の原因であり、良品平均の105.10に近づけることが目標です。測定値は89.88であり、標準偏差での乖離は-2.1σです。
Break Downで段階的に原因を追跡
Break Downは、料理のレシピのように、一つずつ材料(特徴量)を加えていき、最終的な味(予測)がどのように作られるかを示す手法です。
SHAPとは異なり、最も重要な要因から順番に影響を積み上げていくため、現場の方にとって理解しやすいのが特徴です。
選定した製品(ID 522)について、Break Down分析を実行します。
# Break Down分析
bd_explanation = explainer.predict_parts(
target_product,
type='break_down'
)
# 結果の取得
bd_result = bd_explanation.result
Break Downの結果を段階的に追跡します。各ステップで、どのパラメータがどの程度不良率を変化させたかが明確になります。
# 段階的な分解
cumulative_value = 0
step_number = 0
for idx, row in bd_result.iterrows():
var_name = row['variable_name']
var_value = row['variable_value']
contribution = row['contribution']
cumulative = row['cumulative']
if var_name == 'intercept':
print(f"開始: {contribution:.4f}")
cumulative_value = contribution
elif var_name not in ['prediction', '']:
step_number += 1
change = cumulative - cumulative_value
print(f"Step {step_number} - {var_name}: {change:+.4f}")
print(f" 値: {var_value}, 累積: {cumulative:.4f}")
cumulative_value = cumulative
print(f"最終: {cumulative_value:.4f}")
以下、実行結果です。
開始: 0.2987 Step 1 - 金型温度: +0.0476 値: 89.88, 累積: 0.3463 Step 2 - プレス圧力: +0.0838 値: 185.5, 累積: 0.4301 Step 3 - プレス温度: +0.1086 値: 144.7, 累積: 0.5388 Step 4 - 環境湿度: +0.0065 値: 44.62, 累積: 0.5452 Step 5 - 材料厚: -0.0063 値: 2.095, 累積: 0.5389 Step 6 - 潤滑油温度: -0.0004 値: 35.25, 累積: 0.5385 Step 7 - プレス速度: -0.0237 値: 48.16, 累積: 0.5148 最終: 0.5148
各ステップは流れです。
- 開始点:全データに基づくモデルの平均予測値(基準値)
- 各ステップ:まだ反映していない変数を1つ追加したときに
その時点で 予測値が最も大きく変化した変数 を選んで表示したもの
(※寄与の大きさ順ではなく、“その時その瞬間に最も予測を動かした順番”) - 最終値:すべての変数を反映したときの最終的な予測値
可視化します。
# Break Downの可視化 bd_explanation.plot(show=True)
以下、実行結果です。
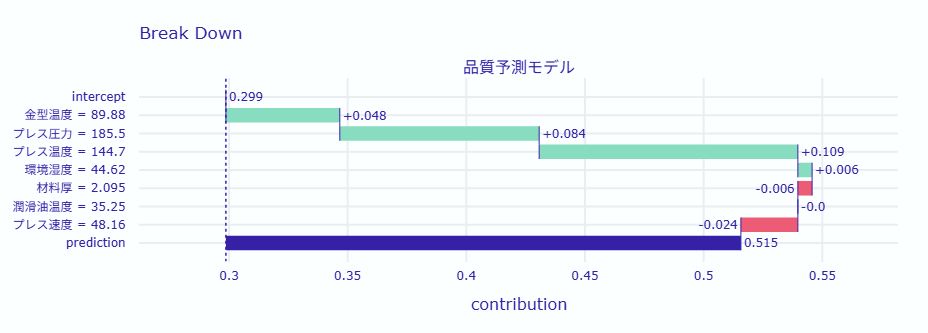
製品の不良率に最も影響を与えた要因は金型温度、プレス圧力、プレス温度です。
金型温度は不良率を増加させる要因であり、次にプレス圧力が続きます。プレス温度も不良率を増加させる要因として重要です。
これらの要因を改善することで、製品の品質向上が期待できます。
その他の要因として環境湿度、材料厚、潤滑油温度、プレス速度が挙げられますが、これらは不良率に対する影響が比較的小さいです。
製造プロセスの見直しにおいて、特に金型温度、プレス圧力、プレス温度の管理を強化することが重要です。
改善シミュレーション(What-If分析)
原因が特定できたら、次は「どう改善すれば良品になるか」を具体的にシミュレーションします。
What-If分析では、パラメータを仮想的に調整して、品質がどう変化するかを予測します。
段階的な改善シナリオの検証
選定した製品(ID 522)に対し、現状から段階的にパラメータを改善していき、どの時点で良品になるかを探ります。
# 現状の確認
simulation_conditions = target_product.copy()
current_defect_prob = rf_model.predict_proba(simulation_conditions)[0, 1]
print(f"現状: {current_defect_prob:.2%}")
以下、実行結果です。
現状: 51.48%
影響度(SHAP値を使用)の大きい順にソートします。
# 影響度(SHAP値を使用)の大きい順にソート
top_factors = sorted(
contributions.items(),
key=lambda x: abs(x[1]),
reverse=True
)
# データフレームに変換
df_top_factors = pd.DataFrame(
top_factors,
columns=['Factor', 'Contribution']
)
print("影響度の大きい順にソート(SHAP値を使用)")
print(df_top_factors)
以下、実行結果です。
影響度の大きい順にソート(SHAP値を使用) Factor Contribution 0 プレス圧力 0.124228 1 プレス温度 0.064929 2 金型温度 0.052935 3 プレス速度 -0.021181 4 材料厚 -0.007203 5 環境湿度 0.006769 6 潤滑油温度 -0.004367
シナリオ1:最重要要因のみ改善
最も影響の大きい要因(プレス圧力)だけを改善した場合の効果を検証します。
# 最重要要因の特定と改善
top_factor = df_top_factors['Factor'].iloc[0]
optimal_value = X_train[y_train == 0][top_factor].mean()
current_value = simulation_conditions.iloc[0][top_factor]
print(f"対象: {top_factor}")
print(f"現在値: {current_value:.2f}")
print(f"目標値: {optimal_value:.2f}")
# 条件を更新して予測
simulation_conditions[top_factor] = optimal_value
new_prob = rf_model.predict_proba(simulation_conditions)[0, 1]
improvement = (current_defect_prob - new_prob) / current_defect_prob * 100
print(f"新不良率: {new_prob:.2%}")
print(f"改善率: {improvement:.1f}%")
以下、実行結果です。
対象: プレス圧力 現在値: 185.52 目標値: 200.10 新不良率: 13.86% 改善率: 73.1%
シナリオ2:上位2要因を改善
最も影響の大きい要因(プレス圧力)に続き、次に影響の大きい要因(プレス温度)を改善した場合の効果を検証します。
# 2番目の要因も改善
second_factor = df_top_factors['Factor'].iloc[i]
optimal_value = X_train[y_train == 0][second_factor].mean()
current_value = simulation_conditions.iloc[0][second_factor]
print(f"対象: {second_factor}")
print(f"現在値: {current_value:.2f}")
print(f"目標値: {optimal_value:.2f}")
# 条件を更新して予測
simulation_conditions[second_factor] = optimal_value
new_prob = rf_model.predict_proba(simulation_conditions)[0, 1]
improvement = (current_defect_prob - new_prob) / current_defect_prob * 100
print(f"新不良率: {new_prob:.2%}")
print(f"改善率: {improvement:.1f}%")
以下、実行結果です。
対象: プレス温度 現在値: 144.70 目標値: 150.01 新不良率: 10.55% 改善率: 79.5%
シナリオ3:全パラメータ最適化
# 全パラメータを最適化したケース
optimal_conditions = target_product.copy()
# 全ての要因を最適化
for factor in df_top_factors['Factor']:
optimal_value = X_train[y_train == 0][factor].mean()
current_value = optimal_conditions.iloc[0][factor]
print(f"{factor}:\n - 現在値: {current_value:.2f}\n - 目標値: {optimal_value:.2f}")
# 条件を更新
optimal_conditions[factor] = optimal_value
# 最適化後の予測
new_prob = rf_model.predict_proba(optimal_conditions)[0, 1]
improvement = (current_defect_prob - new_prob) / current_defect_prob * 100
print(f"全パラメータ最適化後の新不良率: {new_prob:.2%}")
print(f"全パラメータ最適化後の改善率: {improvement:.1f}%")
以下、実行結果です。
プレス圧力: - 現在値: 185.52 - 目標値: 200.10 プレス温度: - 現在値: 144.70 - 目標値: 150.01 金型温度: - 現在値: 89.88 - 目標値: 105.10 プレス速度: - 現在値: 48.16 - 目標値: 50.04 材料厚: - 現在値: 2.10 - 目標値: 1.99 環境湿度: - 現在値: 44.62 - 目標値: 59.79 潤滑油温度: - 現在値: 35.25 - 目標値: 40.12 全パラメータ最適化後の新不良率: 1.64% 全パラメータ最適化後の改善率: 96.8%
感度分析
各パラメータを微調整した場合の品質への影響を分析する、感度分析を実施します。
具体的には、主要な3つのパラメータに対して、現在の値から±2標準偏差の範囲で調整を行い、それぞれの調整値に対する不良率を計算し、不良率が最小化する最適な調整値を特定します。
これにより、各パラメータの変化が不良率にどのように影響するかを理解することができます。
# 主要3パラメータの感度分析
sensitivity_results = {}
# 使用するモデルを指定
selected_model = rf_model
# 主要3パラメータの感度分析
for param in df_top_factors['Factor'][:3]:
# 現在の値と標準偏差を取得
current_value = target_product.iloc[0][param]
param_std = X_train[param].std()
# -2σから+2σまで変化させる
adjustments = np.linspace(-2*param_std, 2*param_std, 201)
# 不良率を格納するリスト
probabilities = []
# 各調整値に対する不良率を計算
for adj in adjustments:
temp_conditions = target_product.copy()
temp_conditions[param] = current_value + adj
prob = selected_model.predict_proba(temp_conditions)[0, 1]
probabilities.append(prob)
# 結果を保存
sensitivity_results[param] = (adjustments, probabilities)
# 最適値の特定
optimal_idx = np.argmin(probabilities)
optimal_adjustment = adjustments[optimal_idx]
optimal_prob = probabilities[optimal_idx]
print(f"{param}:")
print(f" 最適調整: {optimal_adjustment:+.2f}")
print(f" 最適値: {current_value + optimal_adjustment:.2f}")
print(f" 最適時不良率: {optimal_prob:.2%}")
以下、実行結果です。最適値のみ出力しています。
プレス圧力: 最適調整: +15.38 最適値: 200.90 最適時不良率: 13.51% プレス温度: 最適調整: +4.43 最適値: 149.12 最適時不良率: 24.48% 金型温度: 最適調整: +14.80 最適値: 104.68 最適時不良率: 45.14%
感度分析の結果を可視化します。
# 感度分析の可視化
fig, axes = plt.subplots(3, 1, figsize=(8, 10))
for idx, (param, (adjustments, probabilities)) in enumerate(sensitivity_results.items()):
# 現在の値を取得
current_value = target_product.iloc[0][param]
# 調整値の計算
actual_values = current_value + adjustments
# 感度分析の結果(調整値の不良率)のプロット
axes[idx].plot(
actual_values,
probabilities,
'b-',
linewidth=2,
label='不良率'
)
# 不良率の閾値(0.5)の水平線を追加
axes[idx].axhline(
y=0.5,
color='r',
linestyle='--',
label='不良率閾値 (0.5)'
)
# 現在の不良率の水平線を追加
axes[idx].axhline(
y=current_defect_prob,
color='black',
linestyle=':',
label='現在の不良率'
)
# 現在の値の垂直線を追加
axes[idx].axvline(
x=current_value,
color='orange',
label='現在の値'
)
# 最適値の垂直線を追加
optimal_adjustment = adjustments[np.argmin(probabilities)]
optimal_value = current_value + optimal_adjustment
axes[idx].axvline(
x=optimal_value,
color='green',
linestyle='--',
label='最適値'
)
# 不良率が0.5未満の領域を緑色で塗り分け
axes[idx].fill_between(
actual_values,
0,
probabilities,
where=(np.array(probabilities) < 0.5),
alpha=0.2,
color='green',
label='不良率 < 0.5'
)
# 不良率が0.5以上の領域を赤色で塗り分け
axes[idx].fill_between(
actual_values,
probabilities,
1,
where=(np.array(probabilities) >= 0.5),
alpha=0.2,
color='red',
label='不良率 >= 0.5'
)
# グラフの設定
axes[idx].set_xlabel(param)
axes[idx].set_ylabel('不良率')
axes[idx].set_title(f'{param}の感度分析')
axes[idx].grid(True, alpha=0.3)
axes[idx].legend(loc='upper left', bbox_to_anchor=(1, 1))
plt.tight_layout()
plt.show()
以下、実行結果です。
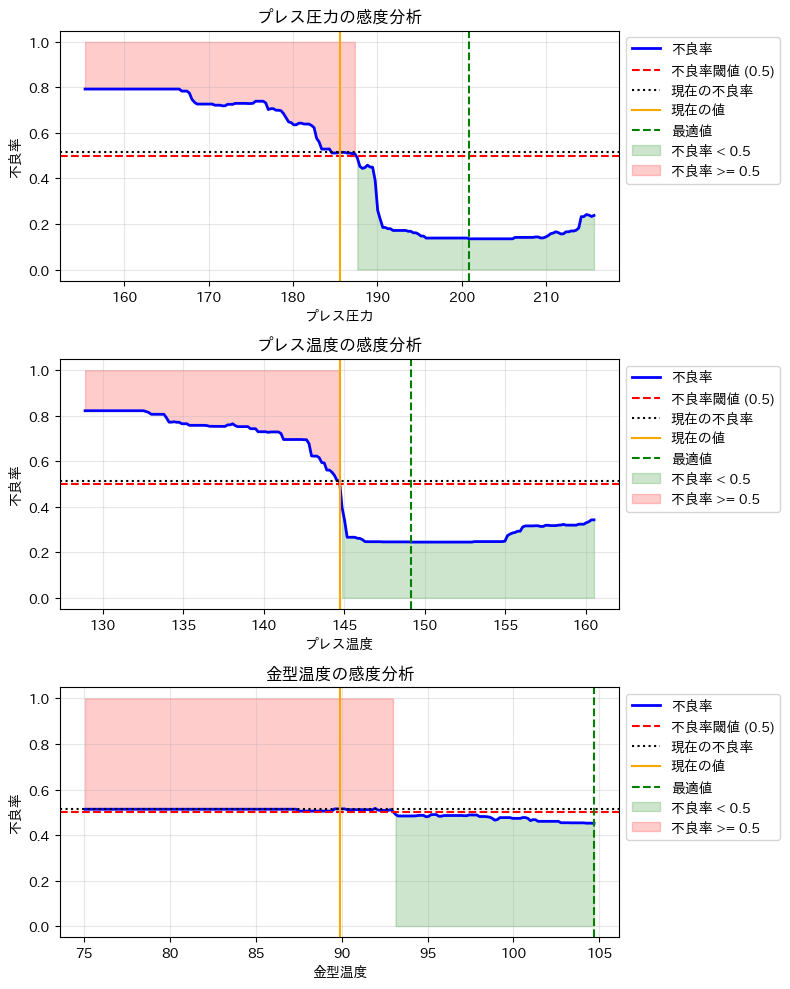
グラフの緑色の領域が「良品ゾーン」です。各パラメータをこの範囲内に調整することで、不良品を良品に改善できる可能性が高まります。
現場カイゼンへ(運用)
ここまで、特定の製品(ID 522)の分析結果だけ見てきました。この製品固有の問題のみ深掘りし、解決策を考えるだけでは不十分です。
重要なのは、この分析から得られた知見をどのように一般化し、未知の製品にも適用できる仕組みを作るかです。
たとえば、過去3ヶ月間に発生した不良品100件に対しSHAP分析を実施し、可能な限り一般化を試みます。
- 不良品の82%でプレス圧力が195MPa以下
- 不良品の65%で金型温度が100℃以下
- プレス圧力の低下と金型温度の低下が同時に発生した場合、不良率が通常の3倍に跳ね上がることが判明
SHAP分析結果を集計分析するだけで、このようなものが見えてきます。
さらに、SHAP分析結果に対し、統計学などの手法を活用し分析するのもいいでしょう。
これらの知見を基に、予防的な品質管理システムを構築することもできるかもしれません。
従来は不良品が発生してから原因を究明する事後対応でしたが、新しいシステムではパラメータの組み合わせから不良発生リスクをリアルタイムで評価し、問題が起きる前にアラートを発する仕組みです。
この企業の場合、毎朝のラインスタート時、オペレーターはXAIダッシュボードで各パラメータの健全性を確認するようになりました。
黄色信号が点灯したら、実際に不良品が出る前に設備調整を行います。
まとめ
今回は、実際の製造現場で発生した「AIが不良と判定したが理由が分からない製品」を題材に、XAIを使った原因究明から改善アクションまでの簡単な流れを説明しました。
まず、予測確率が50%に近い「境界線上の不良品」を選定し、SHAPとBreak Downという2つの手法で不良要因を分解します。
SHAPでは各要因の公平な寄与度を、Break Downでは段階的な影響の積み上げを可視化し、プレス圧力、プレス温度、金型温度が主要因であることを突き止めました。
続いて、What-If分析により「もしパラメータを調整したら」という仮想シナリオで改善効果を事前検証し、感度分析で各パラメータの最適な調整範囲を特定します。
最後に、個別製品の分析結果を蓄積してパターン化し、予防的な品質管理システムへと発展させるといいでしょう。
次回(第7回)では、振動データによる設備予知保全システムの構築に挑戦します。
時系列データの分析とXAIの組み合わせで、故障を事前に予測する実践的な手法を学びます。
製造現場でのAI活用は、「なぜ」を説明できることで、真の価値を発揮します。

