前回と前々回にベイズ推定について簡単に説明しました。

以下、前回の記事です。

以下、前々回の記事です。

通常の線形回帰モデルは、切片や係数、予測の値は1つです。

一方，ベイズ線形回帰モデルで得られるのは分布です。正確には、分布から得られるサンプルです。

今回は、PyMC3を使ってベイズ線形回帰モデルを構築する方法を紹介します。

通常の線形回帰モデルと比較します。

通常の線形回帰とベイズ線形回帰

簡単に数式で考えていきます。

通常の線形回帰モデルは、以下のように表現されます。yが目的変数で、xが説明変数です。

$\displaystyle y = a + b x + \epsilon , \epsilon \sim \mathcal{N}(0,\sigma^2)$

これは、$y$が平均$ax+b$と標準偏差$\sigma$で正規分布していることを意味します。

$\displaystyle y \sim \mathcal{N}(a + b x,\sigma^2)$

この$a$と$b$は、ある固定した値です。

一方、ベイズ統計学では$a$と$b$を固定したものとして扱うのではなく、変化するものとして扱います。

例えば、以下のような分布として扱います。

$\displaystyle a \sim \mathcal{N}(0,\sigma_a^2), b \sim \mathcal{N}(0,\sigma_b^2)$

これは、$a$は平均$0$と標準偏差$\sigma_a$で、$b$は平均$0$と標準偏差$\sigma_b$で正規分布していることを意味します。

線形回帰モデルには、$a$と$b$以外にもパラメータがあります。$y = a + b x + \epsilon , \epsilon \sim \mathcal{N}(0,\sigma^2)$の$\sigma^2$です。

この分散$\sigma^2$にも何かしら分布を仮定する必要があります。分散なので非負です。そのため、指数分布やガンマ分布、半正規分布など、非負の値を取る分布を仮定します。

分散の場合、指数分布と仮定するケースが多いです。

$\displaystyle \sigma^2 \sim EXP(\lambda)$

ベイズ線形回帰では、このようにパラメータに対し事前に何らかの分布を仮定します。データ量が少ないときには、事前に設定した分布からの影響が大きいですが、学習データが増えれば増えるほどその影響が小さくなります。

データセット

statsmodels経由で取得できるRの以下の、ボストン近郊の住宅価値のデータを利用します。

Housing Values in Suburbs of Boston
https://vincentarelbundock.github.io/Rdatasets/doc/MASS/Boston.html

14変数、506レコードのサンプルデータです。以下の2変数を利用します。1つが目的変数で、もう1つが説明変数です。

• 目的変数y：ｍedv（持ち家の価格の中央値、千円単位）
• 説明変数x：lstat（下位ステータスの人の占める割合）

要は、単回帰モデルを構築していきます。

準備

必要なライブラリーを読み込みます。

以下、コードです。

import numpy as np
import pandas as pd
import statsmodels.api as sm

import pymc3 as pm
import arviz as az

from matplotlib import pyplot as plt

# グラフのスタイルとサイズ
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 9]

必要なデータセットを読み込みます。

以下、コードです。

# データセットの読み込み
dataset = sm.datasets.get_rdataset("Boston", "MASS")

dataset.data #確認

以下、実行結果です。

必要なデータを抜き出し、目的変数yと説明変数xを設定します。

以下、コードです。

y = dataset.data.medv
x = dataset.data.lstat

通常の線形回帰モデル

通常の線形回帰モデルを構築します。

以下、コードです。

# 単回帰モデル
X = sm.add_constant(x) #切片追加

model = sm.OLS(y, X)   #モデルのインスタンス生成
results = model.fit()   #mモデルの学習

results.summary() #確認

以下、実行結果です。

以下の単回帰式が得られました。

$y = 34.5538 - 0.9500 \times x$

グラフ化し見てみます。

以下、コードです。

# 回帰係数と切片の推定値
a = results.params[0] #切片
b = results.params[1] #係数
 
# グラフ化
plt.plot(x, y,"o", label='data') #散布図
plt.plot(x, a + b * x, label='y = a + b * x') #直線
plt.legend()
plt.show()

以下、実行結果です。

ベイズ線形回帰モデル

PyMC3を使いベイズ線形回帰モデルを構築していきます。

　パラメータの事後分布

先ず、パラメータ$a$、$b$、$\sigma^2$の事後分布を求めてみます。

以下、コードです。

# 各パラメータの事後分布

with pm.Model() as model:
    
    # 事前分布
    a_ = pm.Normal('intercept', a, 10)
    b_ = pm.Normal('slope', b, 10)
    e_ = pm.Exponential('error', 1)
    
    # 予測
    y_ = pm.Normal('observation', a_ + b_ * x, e_, observed=y)
    
    # 事後分布からデータ生成（MCMC）
    trace = pm.sample(return_inferencedata=True)

事後分布のサマリーを見てみます。

以下、コードです。

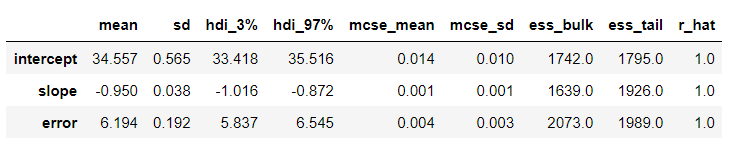
az.summary(trace)

以下、実行結果です。

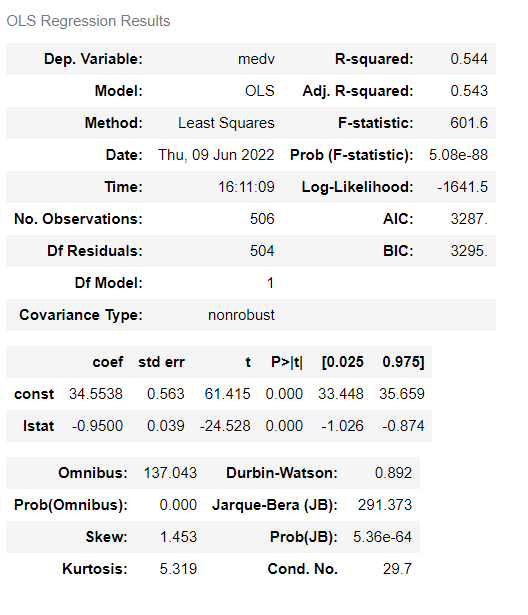
グラフで見てみます。

以下、コードです。

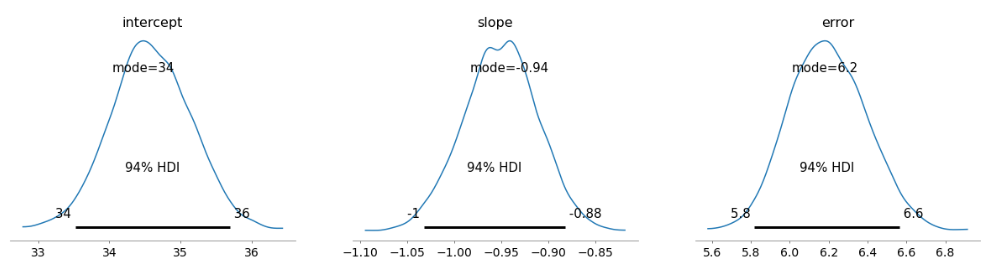
az.plot_posterior(trace, point_estimate='mode')

以下、実行結果です。

MCMCのサンプリング状況を見ることもできます。

以下、コードです。

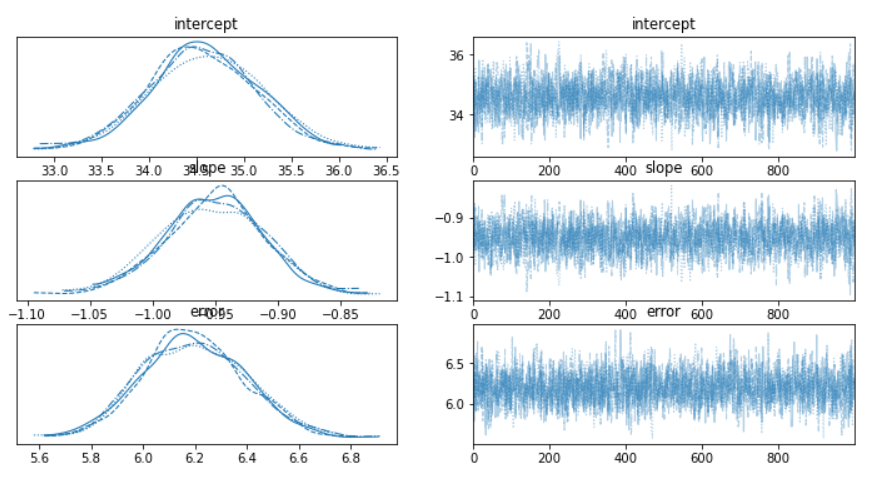
az.plot_trace(trace)

以下、実行結果です。

事後分布から目的変数yのサンプルを生成し、プロットしてみます。

以下、コードです。

# 事後分布から目的変数yのサンプル生成
y_ = pm.sample_posterior_predictive(trace, samples=1000, model=model)

予測値だけ抽出し、y_pred に格納します。

以下、コードです。

y_pred = y_['observation']

y_pred は2次元の配列です。どのような配列なのか見てみます。

以下、コードです。

y_pred.shape

以下、実行結果です。

1,000行×506列の配列です。各 x の予測値 y はどこを見ればいいのでしょうか。

各列が、各 x に該当します。行は、同じx に対する予測 y の値になります。要は、1つの x に対し1,000個の予測値 y があることになります。これが事後分布からのサンプルになります。

各x に対し1,000個の予測値 y の代表値（例：平均値や中央値、最頻値など）を予測値とします。さらに、信頼区間や標準偏差なども計算できます。

ある1つのxに対し、どのような分布になっているのかを見てみます。

ヒストグラムで見てみます。

以下、コードです。

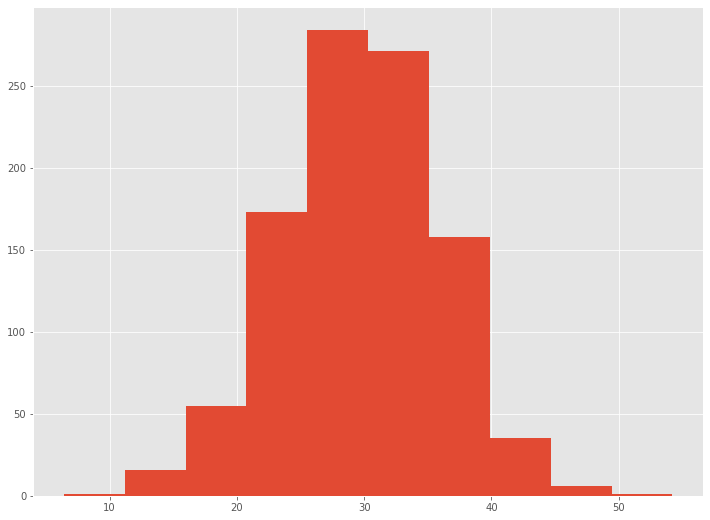
# ヒストグラム表示
plt.hist(y_pred[:,0])

以下、実行結果です。

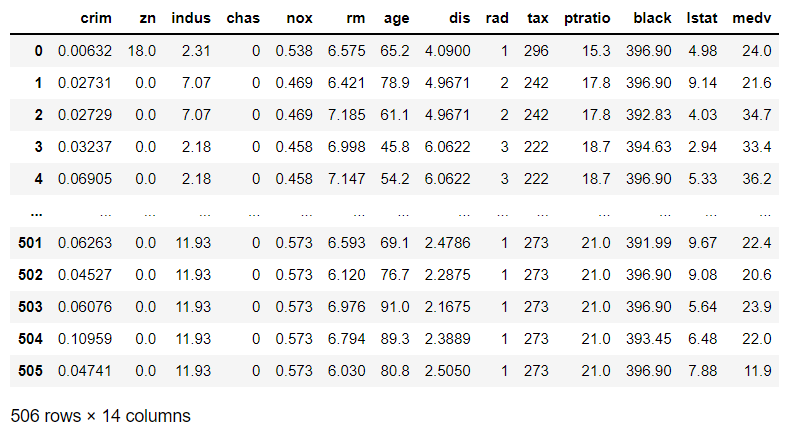
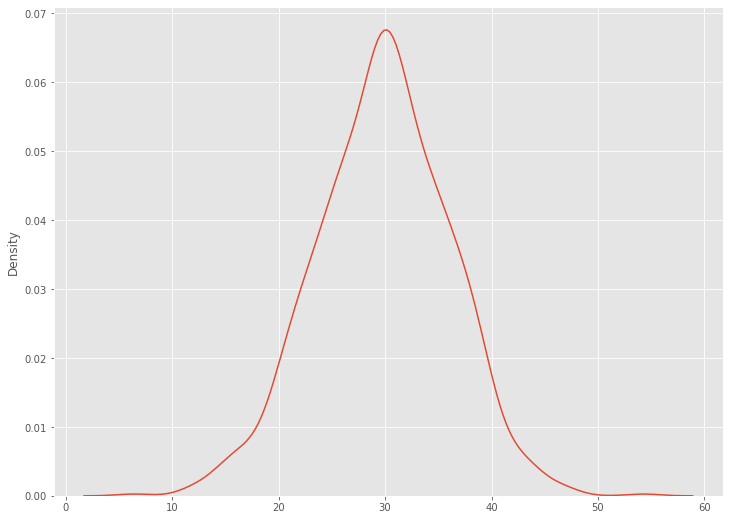
ついでに、seabornを使ってカーネル密度推定で見てみます。

以下、コードです。

# カーネル密度推定
import seaborn as sns
sns.kdeplot(data=y_pred[:,0])

以下、実行結果です。

1つ1つのxに対し、このように見ていくのは大変ですが、このように分布を出力することができます。

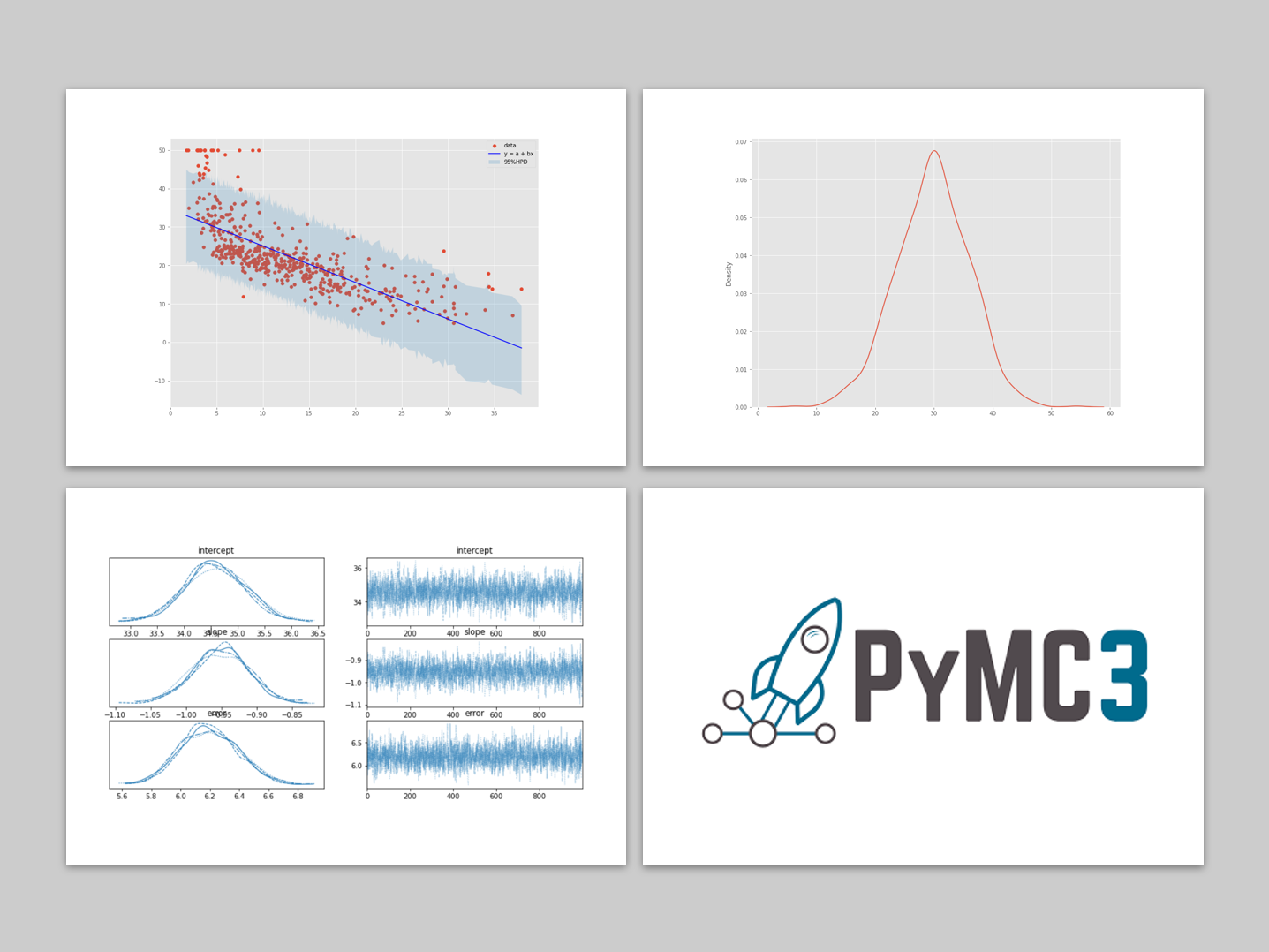
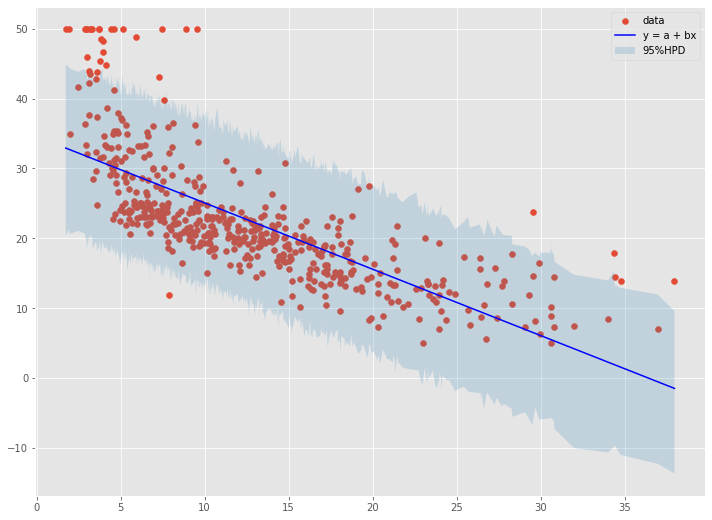
元のデータと、回帰直線、信頼区間をプロットしてみます。

以下、コードです。

# 回帰係数と切片の推定値
a_m = trace.posterior['intercept'].values.mean()
b_m = trace.posterior['slope'].values.mean()

# 信頼区間
x_id = np.argsort(x)
x_ = x[x_id]
ci_95 = az.hdi(y_['observation'], hdi_prob=0.95)[x_id]

# プロット
plt.scatter(x, 
            y, 
            label='data'
           )
plt.plot(x_, 
         a_m + b_m * x_, 
         color = 'b',
         label='y = a + bx'
        )
plt.fill_between(x_, 
                 ci_95[:,0], ci_95[:,1],
                 alpha=0.2, 
                 label='95%HPD'
                )
plt.legend()
plt.show()

以下、実行結果です。

パラメータ$a$と$b$の値と予測値yは、分布のサンプルから平均値を求め、その値を利用しています。信頼区間は、予測値yの分布のサンプルから計算しています。

　予測モデル

次に、予測で使えるベイズ線形回帰モデルを構築してみます。外部から与えられた説明変数xに対し予測値を出すモデルです。

以下、コードです。

# 予測モデル
with pm.Model() as predictive_model:
    
    # 事前分布
    a_ = pm.Normal('intercept', a, 10)
    b_ = pm.Normal('slope', b, 10)
    e_ = pm.Exponential('error', 1)
    
    #外部から入力するxのハコ
    x_ = pm.Data('features', x)
    
    # 予測
    y_ = pm.Normal('observation', a_ + b_ * x_, e_, observed=y)
    
    trace = pm.sample()

先ほどと異なり、外から説明変数$x$をインプットできるハコのようなものを設定しています（上のコードの中で背景色の異なる箇所）。

新しい説明変数 x の値を作成します。

以下、コードです。

# 予測で利用するx
x_new = np.linspace(0, 40, 400)

0～40の範囲から説明変数用のデータを等間隔で400個作成し、x_new に格納しています。

この x_new をインプットし y を予測してみます。

以下、コードです。

# x_newに対する予測
with predictive_model:
    pm.set_data({'features': x_new})
    posterior = pm.sample_posterior_predictive(trace)

予測値だけ抽出し、y_pred に格納します。

以下、コードです。

# 予測結果（予測値の分布からのサンプル）
y_pred = posterior['observation']

y_pred は2次元の配列です。どのような配列なのか見てみます。

以下、コードです。

# y_predの行×列
y_pred.shape

以下、実行結果です。

4,000行×400列の配列です。

各列が、各 x_new に該当します。行は、同じx_new に対する予測 y の値になります。要は、1つの x_new に対し4,000個の予測値 y があることになります。これが事後分布からのサンプルになります。

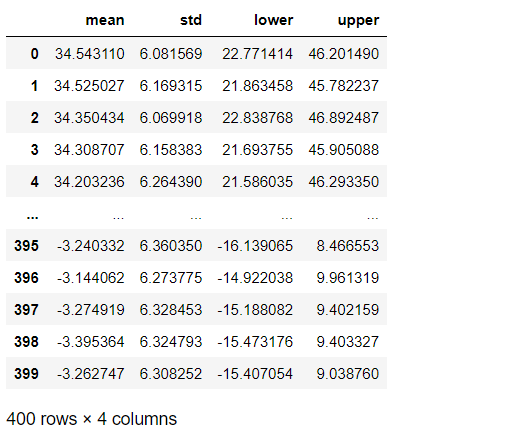
各x_new に対し平均値と標準偏差、95%信頼区間の下と上を計算し、データフレームとして整えます。

以下、コードです。

# 各予測の平均値と標準偏差、信頼区間
y_mean = y_pred.mean(axis=0)
y_std = y_pred.std(axis=0)
ci_95 = az.hdi(y_pred, hdi_prob=0.95)

# データフレーム化
pred_result = pd.DataFrame(np.vstack([y_mean,y_std,ci_95[:,0],ci_95[:,1]]).T)
pred_result.columns= ['mean','std','lower','upper']

pred_result #確認

以下、実行結果です。

まとめ

今回は、「ベイズ型線形回帰モデルを作ってみよう！」というお話しをしました。

通常の線形回帰モデルを構築するよりも手軽ではなく時間が掛かりますが、予測値が分布として得られるという特典があります。

興味のある方は、試してみてはいかがでしょうか。