前回、気温からアイスコーヒーの売上を予測する回帰モデルを作りました。
「気温が1℃上がると売上が約10杯増える」という結果が得られましたが、この数値はどの程度信頼できるのでしょうか?
たまたま得られた30日分のデータから計算した値が、偶然の産物ではなく、真の関係を反映していると言えるでしょうか?
また、明日の予測値が「150杯」だったとして、実際の売上はどの程度の範囲に収まると期待できるのでしょうか?
本記事では、回帰分析の結果に対する統計的推論(Statistical Inference)を学び、推定値の不確実性を定量化し、結果の信頼性を評価する方法を身につけていきます。
Contents
サンプルデータ生成
前回のデータと同じサンプルデータを生成します。
# 数値計算とデータ処理のためのライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from scipy import stats
# 再現性のための乱数シード固定
np.random.seed(42)
# データ生成のパラメータ設定
n = 30 # サンプル数(30日間の営業データ)
# 真のモデルのパラメータ
TRUE_BETA_0 = -150 # 真の切片
TRUE_BETA_1 = 10 # 真の傾き(気温1℃上昇で10杯増加)
SIGMA = 15 # 誤差の標準偏差
print("真のモデル設定:")
print(f" y = {TRUE_BETA_0} + {TRUE_BETA_1}x + ε")
print(f" 誤差の標準偏差 σ = {SIGMA}")
# 説明変数:気温データの生成
# 夏季(7月)の東京の気温分布を想定
mu_temp = 27.5 # 平均気温
sigma_temp = 3.5 # 気温の標準偏差
# 正規分布に従う乱数を生成
temp = np.random.normal(
mu_temp, # 平均
sigma_temp, # 標準偏差
n, # サンプル数
)
# 気温を現実的な範囲に制限
temp = np.clip(
temp, # 制限対象の配列
20, # 下限値
35 # 上限値
)
print(f"\n気温データ生成:")
print(f" 平均: {np.mean(temp):.1f}℃")
print(f" 標準偏差: {np.std(temp):.1f}℃")
print(f" 範囲: {np.min(temp):.1f}℃ ~ {np.max(temp):.1f}℃")
# 誤差項の生成(平均0、標準偏差SIGMAの正規分布に従う)
epsilon = np.random.normal(
0, # 平均
SIGMA, # 標準偏差
n # サンプル数
)
# 真の関係式による理論値
ice_coffee_sales_true = TRUE_BETA_0 + TRUE_BETA_1 * temp
# 観測値(理論値+ノイズ)
ice_coffee_sales = ice_coffee_sales_true + epsilon
print(f"\n売上データ生成:")
print(f" 理論値の平均: {np.mean(ice_coffee_sales_true):.1f}杯")
print(f" 観測値の平均: {np.mean(ice_coffee_sales):.1f}杯")
print(f" ノイズの影響: {np.mean(epsilon):.1f}杯(平均)")
# データフレームの作成
data = pd.DataFrame({
'日付': pd.date_range(
'2024-07-01', # 開始日
periods=n # 期間
),
'気温': temp,
'理論値': ice_coffee_sales_true,
'売上': ice_coffee_sales
})
# 最初の5行を表示
print("\n生成したデータ(最初の5日間):")
print(data.head())
以下、実行結果です。
真のモデル設定:
y = -150 + 10x + ε
誤差の標準偏差 σ = 15
気温データ生成:
平均: 26.8℃
標準偏差: 3.1℃
範囲: 20.8℃ ~ 33.0℃
売上データ生成:
理論値の平均: 118.4杯
観測値の平均: 116.6杯
ノイズの影響: -1.8杯(平均)
生成したデータ(最初の5日間):
日付 気温 理論値 売上
0 2024-07-01 29.238500 142.384995 133.359396
1 2024-07-02 27.016075 120.160749 147.944922
2 2024-07-03 29.766910 147.669099 147.466640
3 2024-07-04 32.830604 178.306045 162.440381
4 2024-07-05 26.680463 116.804632 129.142806
前回と同じ回帰分析(単回帰)を実行します。
# データの準備
x = data['気温'].values
y = data['売上'].values
n = len(x)
# 平均の計算
x_bar = np.mean(x)
y_bar = np.mean(y)
# 平均からの偏差の計算
x_dev = x - x_bar
y_dev = y - y_bar
# 偏差積和・偏差平方和の計算
S_xy = np.sum(x_dev * y_dev) # 偏差積和
S_xx = np.sum(x_dev**2) # xの偏差平方和
# 回帰係数の計算
beta_1_hat = S_xy / S_xx # 傾きの推定値
beta_0_hat = y_bar - beta_1_hat * x_bar # 切片の推定値
print(f"推定した回帰式: ŷ = {beta_0_hat:.2f} + {beta_1_hat:.2f}x")
以下、実行結果です。
推定した回帰式: ŷ = -163.58 + 10.44x
この推定値(切片と係数)の信頼性をこれから評価していきます。
回帰係数の統計的性質
推定量の確率分布
前回学んだ最小二乗推定量について、改めて考えてみましょう。
単回帰モデル y_i = \beta_0 + \beta_1 x_i + \varepsilon_i における、傾きの最小二乗推定量\hat{\beta}_1は次の式で与えられます。
$$
\hat{\beta}_1=\frac{\displaystyle \sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}
{\displaystyle \sum_{i=1}^{n} (x_i – \bar{x})^2}
$$
- x_i:i 番目の説明変数(例:気温)の観測値
- y_i:i 番目の目的変数(例:売上)の観測値
- \bar{x}:説明変数 (x) の標本平均
- \bar{y}:目的変数 (y) の標本平均
- n:観測データの個数(例:30日分なら (n=30))
この \hat{\beta}_1 は、与えられたデータ (x_1, y_1), \dots, (x_n, y_n) から計算される統計量です。
もし別の30日間のデータを収集すれば、観測値の組合せが変わるため、そこから計算される \hat{\beta}_1 も異なる値になります。
このように、\hat{\beta}_1 は データの取り方によって値が変わり得る量である確率変数として扱われます。
そのため、推定量 \hat{\beta}_1 がどのようなばらつきを持つのか、その確率分布を考えていく必要があります。
ガウス・マルコフの仮定
最小二乗推定量が望ましい性質を持つためには、次の条件(ガウス・マルコフの仮定)が成り立っている必要があります。
■ 線形性:モデルがパラメータ \beta_0, \beta_1 に関して線形であるとします。
$$
y_i = \beta_0 + \beta_1 x_i + \varepsilon_i
$$
■ 期待値ゼロ:誤差項 \varepsilon_i の平均は 0 であり、系統的なずれが存在しないことを意味します。
$$
E[\varepsilon_i] = 0
$$
■ 等分散性:すべての観測において、誤差の分散が一定であることを仮定します。
$$
\mathrm{Var}(\varepsilon_i) = \sigma^2
$$
■ 無相関性:異なる観測に対応する誤差同士は互いに無相関であるとします。
$$
\mathrm{Cov}(\varepsilon_i, \varepsilon_j) = 0 \quad (i \neq j)
$$
■ 完全共線性がない:(説明変数が複数ある重回帰)説明変数同士が完全な線形関係にないとします。
上記のガウス・マルコフの仮定を満たせば、最小二乗推定量がすべての線形推定量の中で最も分散が小さい(最も精度が高い)「BLUE」(Best Linear Unbiased Estimator)になります。
さらに、正規性の仮定が加われば、統計的仮説検定であるt検定やF検定などが正しく機能し、p値を用いた有意性の判断が可能になります。
■ 正規性:誤差項は、平均 0、分散 \sigma^2 の正規分布に従うと仮定します。
$$
\varepsilon_i \sim \mathcal{N}(0, \sigma^2)
$$
これらの仮定が成り立つとき、傾きの最小二乗推定量 \hat{\beta}_1 は、次の正規分布に従います。
$$
\hat{\beta}_1 \sim \mathcal{N}\!\left(
\beta_1,\;
\frac{\sigma^2}{S_{xx}}
\right)
$$
傾きの最小二乗推定量 \hat{\beta}_1 の分布の中心である期待値は真の回帰係数 \beta_1 に一致し、その分散は \sigma^2/S_{xx} となります。S_{xx} は以下の偏差平方和です。
$$
S_{xx} = \sum_{i=1}^{n} (x_i – \bar{x})^2
$$
この偏差平方和 S_{xx} が推定量 \hat{\beta}_1 の分散に入っていることから、S_{xx} が大きい(説明変数 x が広い範囲にばらついて観測されている)ほど、\hat{\beta}_1 の分散は小さくなり、結果として \hat{\beta}_1 の不確実性も小さくなります。
直感的には、x の値が狭い範囲にしか分布していない場合、回帰直線の傾きはわずかなデータの揺らぎに大きく左右されます。一方で、x が広い範囲に分布していれば、傾きはより安定して推定できるのです。
標準誤差の意味
前節で見たように、傾きの最小二乗推定量 \hat{\beta}_1 の分散は \sigma^2 / S_{xx} で与えられます。この分散の平方根、すなわち「推定量の標準偏差」を「標準誤差」(Standard Error, SE)と呼びます。
傾きの推定量 \hat{\beta}_1 の標準誤差は、次のように表されます。
$$
\mathrm{SE}(\hat{\beta}_1)
=
\sqrt{\mathrm{Var}(\hat{\beta}_1)}
=
\frac{\sigma}{\sqrt{S_{xx}}}
=
\frac{\sigma}{\displaystyle\sqrt{\sum_{i=1}^{n} (x_i – \bar{x})^2}}
$$
この式から分かるように、標準誤差は推定値のばらつきの大きさを直接的に表す指標です。
誤差項の標準偏差 \sigma が小さいほど、もしくは説明変数 x のばらつきを表す偏差平方和 S_{xx} が大きいほど、標準誤差は小さくなり、傾きの推定精度は高くなります。
さらに、サンプルサイズ n が大きくなると、通常は S_{xx} も大きくなるため、結果として標準誤差は小さくなる傾向があります。
切片の推定量の分布とばらつき
これまで、回帰直線の傾き \hat{\beta}_1 について、その分布や標準誤差を考えてきました。
しかし、単回帰モデル y_i = \beta_0 + \beta_1 x_i + \varepsilon_i には、傾き \beta_1 だけでなく、切片 \beta_0 も含まれています。最小二乗推定量は次の式のようになります。
$$
\hat{\beta}_0 = \bar{y} – \hat{\beta}_1 \bar{x}
$$
この式から分かるように、\hat{\beta}_0 は \hat{\beta}_1 と \bar{x} に依存しており、データが変われば推定量の値も変わります。したがって、\hat{\beta}_0 も \hat{\beta}_1 と同様に確率変数として扱われます。
ガウス・マルコフの仮定の下では、切片の推定量 \hat{\beta}_0 は次のような正規分布に従います。
$$
\hat{\beta}_0
\sim
\mathcal{N}
\!\left(
\beta_0,\;
\sigma^2
\left(
\frac{1}{n}
+
\frac{\bar{x}^2}{S_{xx}}
\right)
\right)
$$
この分散の形から、切片の推定精度はサンプルサイズ n だけでなく、説明変数の平均 \bar{x} やばらつき S_{xx} にも影響されることが分かります。特に、\bar{x} が 0 から離れている場合、切片の分散は大きくなりやすくなります。
この分散の平方根が、切片の推定量 \hat{\beta}_0 の 標準誤差に対応します。
$$
\mathrm{SE}(\hat{\beta}_0) = \sqrt{
\sigma^2
\left(
\frac{1}{n}
+
\frac{\bar{x}^2}{S_{xx}}
\right)
}
$$
この標準誤差は、切片がどの程度の不確実性を持って推定されているかを表す指標です。
標準誤差の推定
最小二乗推定量 \hat{\beta}_1 の標準誤差 \mathrm{SE}(\hat{\beta}_1) = \sigma/\sqrt{S_{xx}} には、誤差項の分散 \sigma^2 が含まれています。最小二乗推定量 \hat{\beta}_0 の標準誤差にも、誤差項の分散 \sigma^2 が含まれています。
そのため実際の分析では、未知である \sigma^2 をデータから推定する必要があります。
誤差分散 \sigma^2 は、残差平方和 SSE=\sum_{i=1}^{n} (y_i - \hat{y}_i)^2/(n - 2) を用いて推定されます。具体的には、次の量が \sigma^2 の不偏推定量 \hat{\sigma}^2 となります。
$$
\hat{\sigma}^2
=
\frac{\mathrm{SSE}}{n – 2}
=
\frac{\displaystyle \sum_{i=1}^{n} (y_i – \hat{y}_i)^2}{n – 2}
$$
- \hat{y}_i:i 番目の観測に対する回帰モデルの予測値
- n - 2:自由度
分母が n-2 となっているのは、切片 \beta_0 と傾き \beta_1 の 2つのパラメータをデータから推定しているためです。その分、データの自由度が n から 2 だけ減少します。
この調整を行うことで \hat{\sigma}^2 は 不偏推定量、すなわち平均的に真の誤差分散 \sigma^2 に一致する推定量になります。
この誤差分散の推定値 \hat{\sigma}^2 を用いることで、回帰係数や切片の標準誤差をデータから推定することができます。
具体的には、理論式に含まれていた未知の \sigma を、その推定値 \hat{\sigma} に置き換えます。
傾きの推定量 \hat{\beta}_1 の標準誤差は、次の式で与えられます。
$$
\widehat{\mathrm{SE}}(\hat{\beta}_1) = \frac{\hat{\sigma}}{\sqrt{S_{xx}}}
$$
一方、切片の推定量 \hat{\beta}_0 の標準誤差は、次の式で与えられます。
$$
\widehat{\mathrm{SE}}(\hat{\beta}_0)
=
\hat{\sigma}
\sqrt{
\frac{1}{n}
+
\frac{\bar{x}^2}{S_{xx}}
}
$$
これらの標準誤差は、回帰係数の推定精度を表す指標であり、後に学ぶ「t検定」や「信頼区間」の計算において中心的な役割を果たします。
回帰係数の標準誤差の計算
回帰係数の標準誤差を計算します。
# 残差標準誤差の計算
SSE = np.sum(residuals**2)
df_residual = n - 2 # 自由度
sigma_hat = np.sqrt(SSE / df_residual) # 残差標準誤差
# 回帰係数の標準誤差
SE_beta1 = sigma_hat / np.sqrt(S_xx)
SE_beta0 = sigma_hat * np.sqrt(1/n + x_bar**2/S_xx)
print(f"残差標準誤差: σ̂ = {sigma_hat:.2f}")
print(f"\n標準誤差:")
print(f" SE(β̂₁) = {SE_beta1:.4f}")
print(f" SE(β̂₀) = {SE_beta0:.2f}")
以下、実行結果です。
残差標準誤差: σ̂ = 14.14 標準誤差: SE(β̂₁) = 0.8338 SE(β̂₀) = 22.53
標準誤差は推定値のばらつきを表します。傾きの標準誤差 \widehat{\mathrm{SE}}(\hat{\beta}_1) が小さいことは、推定が比較的安定していることを示しています。
t検定による有意性の判定
帰無仮説と対立仮説
回帰係数が統計的に有意かどうかを判断するために、仮説検定を行います。
仮説検定とは、データから得られた結果が単なる偶然によるものなのか、それとも母集団における真の関係を反映しているのかを、確率的に評価する手法です。
ここでは、回帰直線の傾き \beta_1 について検定を行います。
帰無仮説 H_0 は、「気温が変化しても売上は変わらず、両者に線形な関係はない」という状況を表します。
$$
H_0:\ \beta_1 = 0
$$
これは検定の出発点となる仮説です。
これに対して対立仮説 H_1 は、「気温と売上の間に何らかの線形な関係がある」という仮説を表します。
$$
H_1:\ \beta_1 \neq 0
$$
仮説検定では、帰無仮説が正しいと仮定したときに、観測されたデータがどの程度起こりにくいかを評価し、その結果に基づいて帰無仮説を棄却するかどうかを判断します。
t 統計量
帰無仮説 H_0:\,\beta_1 = 0 のもとで、傾きの推定値がどの程度 0 から離れているかを評価するために、「t 統計量」を用います。
t 統計量は、推定値と帰無仮説で仮定された値との差を、その標準誤差 \widehat{\mathrm{SE}}(\hat{\beta}_1) で割った量として定義されます。
傾き \beta_1 の場合、次のようになります。
$$
t
=
\frac{\hat{\beta}_1 – 0}{\widehat{\mathrm{SE}}(\hat{\beta}_1)}
=
\frac{\hat{\beta}_1}{\widehat{\mathrm{SE}}(\hat{\beta}_1)}
$$
この値は、「推定された傾きが 0 から 何標準誤差分だけ離れているか」を表しています。
したがって、|t| が大きいほど、観測された結果は帰無仮説のもとでは起こりにくいと判断されます。
ガウス・マルコフの仮定と正規性の仮定が成り立つとき、この t統計量は 自由度 n-2 の t 分布に従います。
t分布は次のような特徴を持ちます。
- 正規分布に似た釣鐘型の分布である
- 正規分布より裾が厚く、極端な値が出やすい
- サンプルサイズが大きくなるにつれて、正規分布に近づく
- スチューデント(Student)によって導かれたことから、「Student の t 分布」とも呼ばれる
この t 統計量を用いて行うのが t 検定 です。
t 検定では、帰無仮説が正しいと仮定したときに、計算された t 統計量が 「t 分布のどの位置にあるか」を確認します。
具体的には、自由度 n-2 の t 分布において、観測された |t| 以上の値がどれくらい起こりやすいかを調べ、その確率(p値)をもとに帰無仮説を棄却するかどうかを、あらかじめ定めておいた有意水準をもとに判断(p値が有意水準より小さい場合に有意と判断)します。
このとき、分布の両側を考える検定は「両側 t 検定」と呼ばれ、回帰係数の有意性検定では通常こちらが用いられます。
t 検定を実行し、回帰係数の有意性を検定します。
# t統計量の計算
t_beta1 = beta_1_hat / SE_beta1
t_beta0 = beta_0_hat / SE_beta0
# p値の計算(両側検定)
p_value_beta1 = 2 * (1 - stats.t.cdf(abs(t_beta1), df_residual))
p_value_beta0 = 2 * (1 - stats.t.cdf(abs(t_beta0), df_residual))
# 有意水準
alpha = 0.05
print("【傾き β₁】")
print(f" 推定値: {beta_1_hat:.4f}")
print(f" 標準誤差: {SE_beta1:.4f}")
print(f" t統計量: {t_beta1:.3f}")
print(f" p値: {p_value_beta1:.4f}")
print(f" 判定: {'有意' if p_value_beta1 < alpha else '有意でない'} (α={alpha})")
print("【切片 β₀】")
print(f" 推定値: {beta_0_hat:.2f}")
print(f" 標準誤差: {SE_beta0:.2f}")
print(f" t統計量: {t_beta0:.3f}")
print(f" p値: {p_value_beta0:.4f}")
print(f" 判定: {'有意' if p_value_beta0 < alpha else '有意でない'} (α={alpha})")
以下、実行結果です。
【傾き β₁】 推定値: 10.4382 標準誤差: 0.8338 t統計量: 12.519 p値: 0.0000 判定: 有意 (α=0.05) 【切片 β₀】 推定値: -163.58 標準誤差: 22.53 t統計量: -7.261 p値: 0.0000 判定: 有意 (α=0.05)
p値が0.05(有意水準)より小さいため、傾きは統計的に有意です。
これは「気温と売上に関係がない」という帰無仮説を棄却し、両者に有意な関係があると結論できます。
p値の解釈
p値は、仮説検定において中心的な役割を果たす指標であるため、もう少し詳しく説明します。
p値とは「帰無仮説が正しいと仮定したもとで、観測された t 統計量の絶対値 |t| 以上の値が得られる確率」を表します。
もう少しかみ砕くと、「今回計算された t 統計量と同じか、それ以上に極端な値が、偶然によって得られる確率」という意味になります。
この p値が非常に小さい場合、帰無仮説が正しいとすると、そのような結果は偶然では起こりにくいと判断されます。そこで、帰無仮説は成り立ちにくいと考え、対立仮説を採択します。
この定義から分かるように、p値は「帰無仮説の正しさそのもの」を示すものではありません。そのため、次の点には特に注意が必要です。
- p値は「帰無仮説が正しい確率」ではない
- p値は「効果の大きさ」や「実務的な重要性」を直接表すものではない
- p値が小さくても、必ずしも意味のある効果が存在するとは限らない
仮説検定では、あらかじめ 有意水準 \alpha を定めます。
有意水準は、誤って帰無仮説を棄却してしまう確率(第1種の過誤)の上限を表し、通常は 0.05(5%)や 0.01(1%)が用いられます。
p値が有意水準 \alpha より小さい場合、観測された結果は帰無仮説のもとでは起こりにくいと判断し、帰無仮説を棄却します。
t統計量の関係を視覚化
t分布とt統計量の関係を視覚化します。
# t分布の可視化
fig, axes = plt.subplots(2, 1, figsize=(10, 8))
# t分布
x_t = np.linspace(-15, 15, 1000) # t値の範囲を設定
y_t = stats.t.pdf(x_t, df_residual) # t分布の確率密度関数を計算
#
# 上図:t分布と観測されたt統計量
#
# t分布を描画
axes[0].plot(
x_t, y_t, 'b-', linewidth=2, label=f't分布 (自由度={df_residual})'
)
# 観測されたt統計量を描画
axes[0].axvline(
t_beta1, color='red', linestyle='--', linewidth=2,
label=f'観測値 t={t_beta1:.2f}'
)
# 観測されたt統計量の負の値を描画
axes[0].axvline(
-t_beta1, color='red', linestyle='--', linewidth=2
)
# 棄却域の塗りつぶし
critical_value = stats.t.ppf(
1 - alpha/2, df_residual
) # 棄却域の臨界値を計算
# 棄却域の右側を設定
x_reject_right = x_t[x_t > critical_value]
# 棄却域の左側を設定
x_reject_left = x_t[x_t < -critical_value] # 棄却域の右側を塗りつぶし axes[0].fill_between( x_reject_right, 0, stats.t.pdf(x_reject_right, df_residual), alpha=0.3, color='red', label='棄却域' ) # 棄却域の左側を塗りつぶし axes[0].fill_between( x_reject_left, 0, stats.t.pdf(x_reject_left, df_residual), alpha=0.3, color='red' ) # x軸のラベルを設定 axes[0].set_xlabel('t値') # y軸のラベルを設定 axes[0].set_ylabel('確率密度') # グラフのタイトルを設定 axes[0].set_title('t分布と検定統計量') # 凡例を表示 axes[0].legend() # グリッドを表示 axes[0].grid(True, alpha=0.3) # # 下図:p値の視覚化 # # t分布を描画 axes[1].plot(x_t, y_t, 'b-', linewidth=2) # p値の右側を設定 x_extreme_right = x_t[x_t >= abs(t_beta1)]
# p値の左側を設定
x_extreme_left = x_t[x_t <= -abs(t_beta1)]
# p値を塗りつぶし
axes[1].fill_between(
x_extreme_right, 0,
stats.t.pdf(x_extreme_right, df_residual),
alpha=0.5, color='orange',
label=f'p値 = {p_value_beta1:.4f}'
)
# p値を塗りつぶし
axes[1].fill_between(
x_extreme_left, 0,
stats.t.pdf(x_extreme_left, df_residual),
alpha=0.5, color='orange'
)
# 観測されたt統計量を描画
axes[1].axvline(
t_beta1, color='red',
linestyle='--', linewidth=2,
label=f't = {t_beta1:.2f}'
)
# 観測されたt統計量の負の値を描画
axes[1].axvline(
-t_beta1, color='red',
linestyle='--', linewidth=2
)
# x軸のラベルを設定
axes[1].set_xlabel('t値')
# y軸のラベルを設定
axes[1].set_ylabel('確率密度')
# グラフのタイトルを設定
axes[1].set_title('p値の意味')
# 凡例を表示
axes[1].legend()
# グリッドを表示
axes[1].grid(True, alpha=0.3)
# レイアウトを調整
plt.tight_layout()
# グラフを表示
plt.show()
以下、実行結果です。
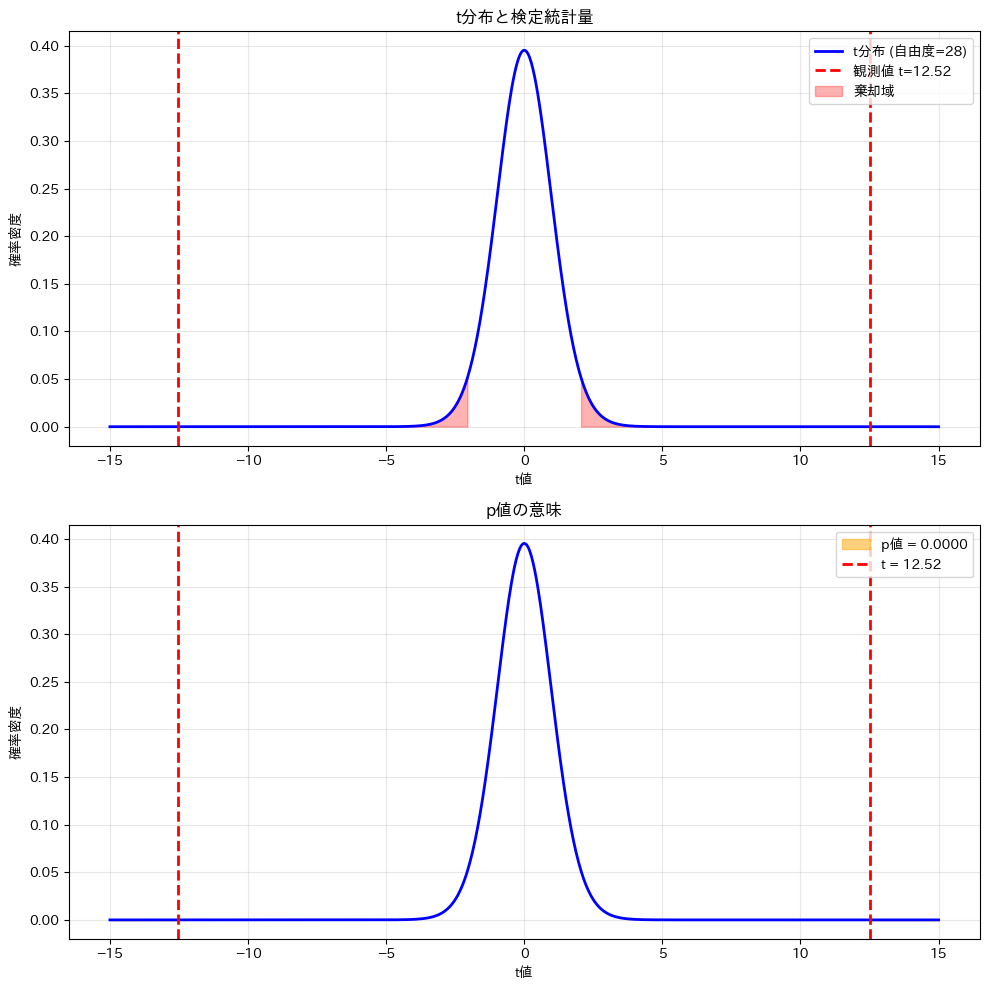
上図の赤い領域は棄却域で、下図のオレンジ色の面積がp値を表します。見え難いので拡大します。
# t分布の可視化
fig, axes = plt.subplots(2, 1, figsize=(10, 4))
# t分布
x_t = np.linspace(-15, 15, 1000) # t値の範囲を設定
y_t = stats.t.pdf(x_t, df_residual) # t分布の確率密度関数を計算
#
# 上図:t分布と観測されたt統計量
# - 縦のスケールを最大1e-12に設定
#
# t分布を描画
axes[0].plot(
x_t, y_t, 'b-', linewidth=2, label=f't分布 (自由度={df_residual})'
)
# 観測されたt統計量を描画
axes[0].axvline(
t_beta1, color='red', linestyle='--', linewidth=2,
label=f'観測値 t={t_beta1:.2f}'
)
# 観測されたt統計量の負の値を描画
axes[0].axvline(
-t_beta1, color='red', linestyle='--', linewidth=2
)
# 棄却域の塗りつぶし
critical_value = stats.t.ppf(
1 - alpha/2, df_residual
) # 棄却域の臨界値を計算
# 棄却域の右側を設定
x_reject_right = x_t[x_t > critical_value]
# 棄却域の左側を設定
x_reject_left = x_t[x_t < -critical_value] # 棄却域の右側を塗りつぶし axes[0].fill_between( x_reject_right, 0, stats.t.pdf(x_reject_right, df_residual), alpha=0.3, color='red', label='棄却域' ) # 棄却域の左側を塗りつぶし axes[0].fill_between( x_reject_left, 0, stats.t.pdf(x_reject_left, df_residual), alpha=0.3, color='red' ) # x軸のラベルを設定 axes[0].set_xlabel('t値') # y軸のラベルを設定 axes[0].set_ylabel('確率密度') # グラフのタイトルを設定 axes[0].set_title('t分布と検定統計量') # 凡例を表示 axes[0].legend() # グリッドを表示 axes[0].grid(True, alpha=0.3) # 縦のスケールを最大1e-12に設定 axes[0].set_ylim(0, 1e-12) # # 下図:p値の視覚化 # - 縦のスケールを最大1e-12に設定 # # t分布を描画 axes[1].plot(x_t, y_t, 'b-', linewidth=2) # p値の右側を設定 x_extreme_right = x_t[x_t >= abs(t_beta1)]
# p値の左側を設定
x_extreme_left = x_t[x_t <= -abs(t_beta1)]
# p値を塗りつぶし
axes[1].fill_between(
x_extreme_right, 0,
stats.t.pdf(x_extreme_right, df_residual),
alpha=0.5, color='orange',
label=f'p値 = {p_value_beta1:.4f}'
)
# p値を塗りつぶし
axes[1].fill_between(
x_extreme_left, 0,
stats.t.pdf(x_extreme_left, df_residual),
alpha=0.5, color='orange'
)
# 観測されたt統計量を描画
axes[1].axvline(
t_beta1, color='red',
linestyle='--', linewidth=2,
label=f't = {t_beta1:.2f}'
)
# 観測されたt統計量の負の値を描画
axes[1].axvline(
-t_beta1, color='red',
linestyle='--', linewidth=2
)
# x軸のラベルを設定
axes[1].set_xlabel('t値')
# y軸のラベルを設定
axes[1].set_ylabel('確率密度')
# グラフのタイトルを設定
axes[1].set_title('p値の意味')
# 凡例を表示
axes[1].legend()
# グリッドを表示
axes[1].grid(True, alpha=0.3)
# 縦のスケールを最大1e-12に設定
axes[1].set_ylim(0, 1e-12)
# レイアウトを調整
plt.tight_layout()
# グラフを表示
plt.show()
以下、実行結果です。
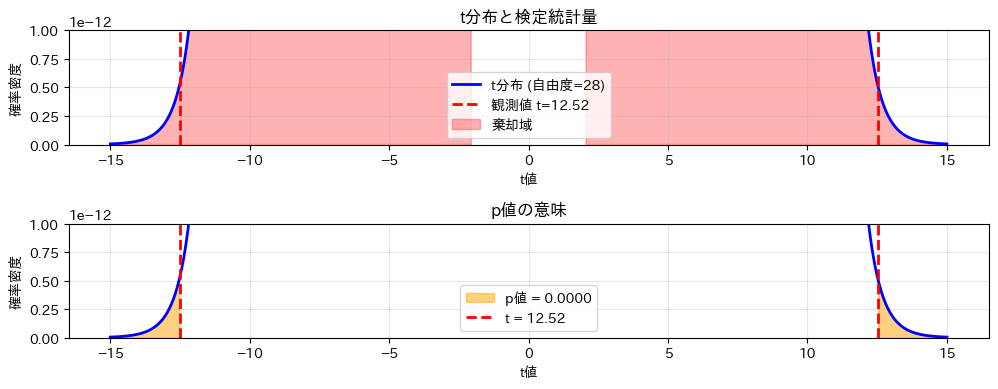
上図の赤い領域は棄却域で、観測されたt値がこの領域に入っているため帰無仮説を棄却します。下図のオレンジ色の面積がp値を表し、これが有意水準0.05より小さいことが視覚的に確認できます。
信頼区間の構成
信頼区間の理論
信頼区間(Confidence Interval, CI)は、推定したパラメータの不確実性を区間として表したものです。
直感的には、「真のパラメータ値が含まれていそうな範囲」を示します。
たとえば、 95%信頼区間とは「同じ手続きを用いて標本抽出と推定を繰り返したとき、そのうち約95%の区間が真の値を含む」という意味です。
ここで注意すべき点は、「この区間に真の値が入る確率が95%である」わけではないということです。真のパラメータ値は固定されており、データのばらつきによって変動するのは区間の方です。
回帰直線の傾き \beta_1 に対する信頼区間は、次の式で与えられます。
$$
\hat{\beta}_1
\;\pm\;
t_{\alpha/2,\;n-2}
\,
\widehat{\mathrm{SE}}(\hat{\beta}_1)
$$
- t_{\alpha/2,\;n-2}:自由度 n-2 の t 分布における上側 \alpha/2 点(両側信頼区間に対応する臨界値)
- \widehat{\mathrm{SE}}(\hat{\beta}_1):傾きの推定標準誤差
- \pm:推定値を中心として、上限と下限の区間を構成することを表す記号
この信頼区間は、推定値のばらつきと不確実性を可視化するものであり、t検定による有意性判断とも密接に関係しています。
回帰係数の信頼区間を計算します。
# 信頼水準
confidence_level = 0.95
alpha_ci = 1 - confidence_level
# t分布の臨界値
t_critical = stats.t.ppf(
1 - alpha_ci/2, # 上側の確率
df_residual # 自由度
)
# 信頼区間の計算
CI_beta1 = [
beta_1_hat - t_critical * SE_beta1,
beta_1_hat + t_critical * SE_beta1
]
CI_beta0 = [
beta_0_hat - t_critical * SE_beta0,
beta_0_hat + t_critical * SE_beta0
]
print(f"【傾き β₁】")
print(f" 点推定値: {beta_1_hat:.4f}")
print(f" 95%信頼区間: [{CI_beta1[0]:.4f}, {CI_beta1[1]:.4f}]")
print(f" 真の値 β₁={TRUE_BETA_1}")
print(f"【切片 β₀】")
print(f" 点推定値: {beta_0_hat:.2f}")
print(f" 95%信頼区間: [{CI_beta0[0]:.2f}, {CI_beta0[1]:.2f}]")
print(f" 真の値 β₀={TRUE_BETA_0}")
以下、実行結果です。
【傾き β₁】 点推定値: 10.4382 95%信頼区間: [8.7302, 12.1462] 真の値 β₁=10 【切片 β₀】 点推定値: -163.58 95%信頼区間: [-209.73, -117.43] 真の値 β₀=-150
95%信頼区間は真の値を含んでいます。これは期待通りの結果です。
信頼区間が0を含まない場合、その係数は統計的に有意と判断できます。
信頼区間の視覚化
信頼区間を視覚的に表示し、複数回のシミュレーションで信頼区間の性質を確認します。
# 信頼区間の可視化
fig, axes = plt.subplots(2, 1, figsize=(10, 10))
#
# 上図:傾きの信頼区間
#
axes[0].errorbar(
1, beta_1_hat, yerr=t_critical*SE_beta1,
fmt='o', markersize=10, capsize=5, capthick=2,
color='blue', label='推定値 ± 95%CI'
)
axes[0].axhline(
TRUE_BETA_1, color='red', linestyle='--',
linewidth=2, label=f'真の値 ({TRUE_BETA_1})'
)
axes[0].axhline(
0, color='gray', linestyle='-',
linewidth=1, alpha=0.5
)
axes[0].set_ylabel('傾き $β_1$')
axes[0].set_title('傾きの95%信頼区間')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
axes[0].set_xticks([1])
axes[0].set_xticklabels(['$β_1$'])
#
# 下図:複数のサンプリングをシミュレーション
#
n_simulations = 100
ci_contains_true = 0
for i in range(n_simulations):
# 新しいデータを生成
eps_sim = np.random.normal(0, SIGMA, n)
y_sim = TRUE_BETA_0 + TRUE_BETA_1 * temp + eps_sim
# 回帰分析
S_xy_sim = np.sum((temp - x_bar) * (y_sim - np.mean(y_sim)))
beta1_sim = S_xy_sim / S_xx
y_hat_sim = np.mean(y_sim) - beta1_sim * x_bar + beta1_sim * temp
SSE_sim = np.sum((y_sim - y_hat_sim)**2)
sigma_sim = np.sqrt(SSE_sim / df_residual)
SE_beta1_sim = sigma_sim / np.sqrt(S_xx)
# 信頼区間
ci_lower = beta1_sim - t_critical * SE_beta1_sim
ci_upper = beta1_sim + t_critical * SE_beta1_sim
# プロット
color = 'green' if ci_lower <= TRUE_BETA_1 <= ci_upper else 'red'
axes[1].plot([i, i], [ci_lower, ci_upper], color=color, alpha=0.5)
if ci_lower <= TRUE_BETA_1 <= ci_upper:
ci_contains_true += 1
axes[1].axhline(TRUE_BETA_1, color='blue', linestyle='-',
linewidth=2, label=f'真の値 ({TRUE_BETA_1})')
axes[1].set_xlabel('シミュレーション番号')
axes[1].set_ylabel('傾き$β_1$')
axes[1].set_title(f'100回のシミュレーション({ci_contains_true}%が真の値を含む)')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
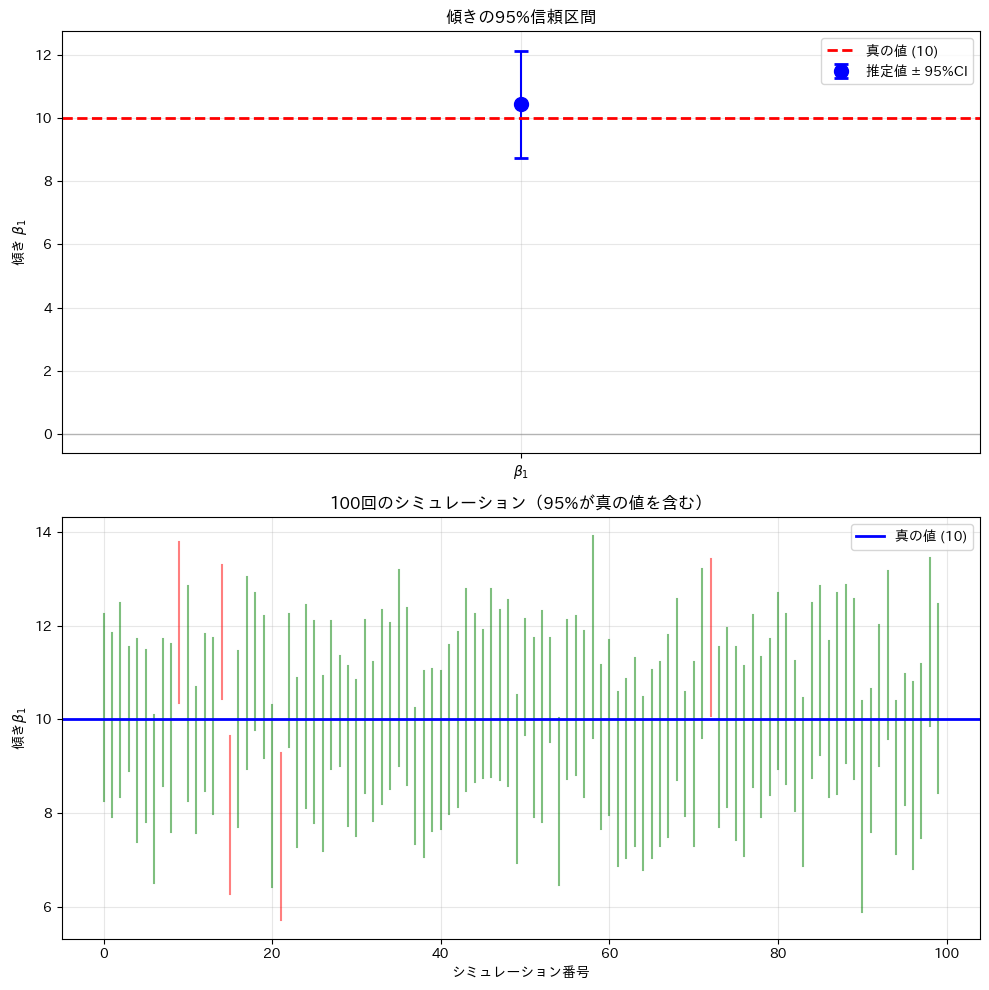
下の図は100回のシミュレーションを示しています。
緑の線は真の値を含む信頼区間、赤の線は含まない信頼区間です。約95%の信頼区間が真の値を含んでいることが確認できます。
信頼区間と予測区間
二つの区間の違い
回帰分析による予測では、目的に応じて二種類の区間を使い分けます。
信頼区間(Confidence Interval)は、「ある気温における平均的な売上」の不確実性を表す区間です。回帰直線そのものの位置がどの程度不確かかを示すため、区間は比較的狭くなります。
一方、予測区間(Prediction Interval)は、「ある気温のもとでの明日の実際の売上」の不確実性を表す区間です。平均的な傾向に加えて、日々のばらつき(個別の誤差)も含むため、信頼区間よりも必ず広くなります。
数学的定式化
新しい説明変数の値を x_0 とし、そのときの予測値 \hat{y}_0 を以下とします。
$$
\hat{y}_0 = \hat{\beta}_0 + \hat{\beta}_1 x_0
$$
このとき、売上の平均的な水準に対する信頼区間は、次のようになります。
$$
\hat{y}_0
\;\pm\;
t_{\alpha/2,\;n-2}
\,
\hat{\sigma}
\sqrt{
\frac{1}{n}
+
\frac{(x_0 – \bar{x})^2}{S_{xx}}
}
$$
一方、個別の将来観測値に対する予測区間は、次のようになります。
$$
\hat{y}_0
\;\pm\;
t_{\alpha/2,\;n-2}
\,
\hat{\sigma}
\sqrt{
1
+
\frac{1}{n}
+
\frac{(x_0 – \bar{x})^2}{S_{xx}}
}
$$
信頼区間に比べ予測区間の平方根の中に「1」が追加で含まれていることが分かります。これは、日ごとの売上が持つ自然なばらつきを表しています。
- 信頼区間:売上の「平均的な水準」の不確実性
- 予測区間:平均の不確実性 + 日々の売上のばらつき
そのため、予測区間は必ず信頼区間よりも広くなるのです。
区間の算出
特定の気温での予測と、両方の区間を計算します。
# 予測したい気温
x_new = np.array([25, 27, 30, 32])
# 予測値
y_pred = beta_0_hat + beta_1_hat * x_new
# 平均値の標準誤差
SE_mean = sigma_hat * np.sqrt(1/n + (x_new - x_bar)**2/S_xx)
# 信頼区間
CI_mean_lower = y_pred - t_critical * SE_mean
CI_mean_upper = y_pred + t_critical * SE_mean
# 予測値の標準誤差
SE_pred = sigma_hat * np.sqrt(1 + 1/n + (x_new - x_bar)**2/S_xx)
# 予測区間
PI_lower = y_pred - t_critical * SE_pred
PI_upper = y_pred + t_critical * SE_pred
print(f"{'気温':>6} {'予測値':>8} {'95%信頼区間':>12} {'95%予測区間':>16}")
print("-" * 70)
for i in range(len(x_new)):
print(f"{x_new[i]:>6.0f}℃ {y_pred[i]:>8.1f} "
f" [{CI_mean_lower[i]:>8.1f}, {CI_mean_upper[i]:>8.1f}] "
f" [{PI_lower[i]:>8.1f}, {PI_upper[i]:>8.1f}]")
以下、実行結果です。
気温 予測値 95%信頼区間 95%予測区間
----------------------------------------------------------------------
25℃ 97.4 [ 91.2, 103.5] [ 67.8, 127.0]
27℃ 118.3 [ 113.0, 123.5] [ 88.8, 147.7]
30℃ 149.6 [ 142.0, 157.1] [ 119.6, 179.5]
32℃ 170.4 [ 160.2, 180.7] [ 139.7, 201.2]
予測区間が信頼区間より広いことが確認できます。
信頼区間は「この気温での平均売上」の範囲、予測区間は「個別の日の売上」の範囲を示しています。
信頼帯と予測帯の視覚化
回帰直線の周りの信頼帯と予測帯を描画します。
# 予測範囲の設定
x_range = np.linspace(temp.min(), temp.max(), 100)
y_range_pred = beta_0_hat + beta_1_hat * x_range
# 各点での標準誤差
SE_mean_range = sigma_hat * np.sqrt(1/n + (x_range - x_bar)**2/S_xx)
SE_pred_range = sigma_hat * np.sqrt(1 + 1/n + (x_range - x_bar)**2/S_xx)
# 信頼帯(信頼区間の帯、confidence band)
CI_lower_range = y_range_pred - t_critical * SE_mean_range
CI_upper_range = y_range_pred + t_critical * SE_mean_range
# 予測帯(予測区間の帯、prediction band)
PI_lower_range = y_range_pred - t_critical * SE_pred_range
PI_upper_range = y_range_pred + t_critical * SE_pred_range
# グラフ作成
plt.figure(figsize=(10, 7))
# データ点をプロット
plt.scatter(
temp, y, alpha=0.6, s=50,
color='darkblue', label='観測データ'
)
# 回帰直線をプロット
plt.plot(
x_range, y_range_pred, 'r-',
linewidth=2, label='回帰直線'
)
# 信頼帯をプロット
plt.fill_between(
x_range, CI_lower_range, CI_upper_range,
alpha=0.3, color='red', label='95%信頼帯(平均)'
)
# 予測帯をプロット
plt.fill_between(
x_range, PI_lower_range, PI_upper_range,
alpha=0.2, color='blue', label='95%予測帯(個別)'
)
plt.xlabel('気温 [℃]', fontsize=12)
plt.ylabel('アイスコーヒー売上 [杯]', fontsize=12)
plt.title('信頼帯と予測帯', fontsize=14)
plt.legend(loc='upper left')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
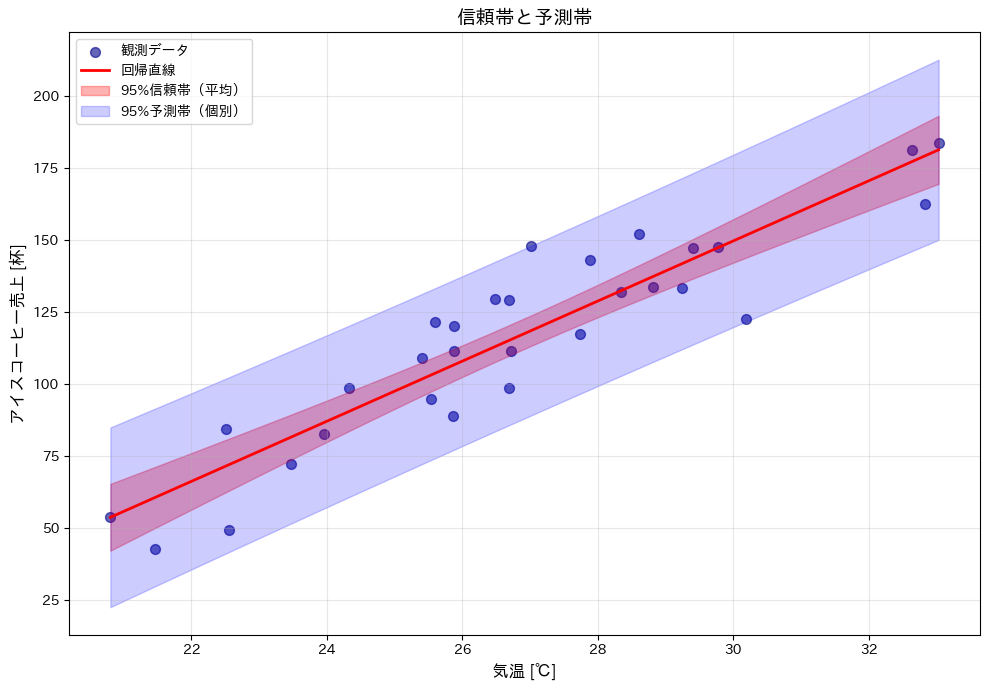
赤い帯(信頼帯)は平均的な売上の不確実性を、青い帯(予測帯)は個別の売上の不確実性を表しています。
データの中心(平均値付近)では区間が狭く、端に行くほど広くなることが分かります。
まとめ
本記事では、回帰分析の結果に対する統計的推論について学びました。
- 推定量の確率分布:回帰係数はデータのばらつきによって変動する確率変数であり、ガウス・マルコフの仮定のもとで正規分布に従う
- 標準誤差:推定値のばらつきを定量化する指標であり、サンプルサイズや説明変数のばらつきに依存する
- t検定:帰無仮説「傾き = 0」を検定し、回帰係数の統計的有意性を判断する
- p値:帰無仮説が正しいときに観測結果以上に極端な値が得られる確率
- 信頼区間:推定値の不確実性を区間として表現し、真のパラメータが含まれる範囲を示す
- 予測区間:個別の観測値の不確実性を表し、信頼区間より必ず広くなる
これらの概念を理解することで、「気温が1℃上がると売上が約10杯増える」という結果が統計的に信頼できるものかどうかを客観的に評価できるようになりました。
次回の第3回では、モデルの評価と診断について学びます。
- 決定係数とANOVAによるモデルの説明力の評価
- 残差分析による仮定の詳細な確認
- 外れ値と影響力のある点の検出(Cook’s Distance)
- モデル選択の基準(AIC、BICなど)
回帰モデルの良し悪しを総合的に判断する方法を身につけていきましょう。