ある大学で「学生の1日の平均勉強時間」を調べたいとします。
学生が1万人いるとしたら、全員にアンケートを取るのは現実的でしょうか?
時間もコストも膨大にかかりますし、全員から回答を得るのは事実上不可能です。
そこで私たちは「一部の学生だけに聞いて、全体を推測する」という方法を取ります。
たとえば100人にアンケートを取り、その平均が3.2時間だったら、「大学全体の平均も3時間くらいだろう」と推測するわけです。
この「一部から全体を推測する」という考え方が、今回学ぶ推測統計の核心です。
ただし、一部のデータから全体を推測するには、「どのくらい確かなのか」を知る必要があります。
それを教えてくれるのが信頼区間です。
Contents
- 母集団と標本:全体と一部
- 基本用語を押さえよう
- Pythonで母集団と標本を体験する
- 標本平均のばらつき:何度も抽出してみる
- 標準誤差:標本平均のばらつきの指標
- 標準誤差(SE)とは
- 標本サイズと標準誤差の関係
- 中心極限定理:統計学で最も重要な定理
- 中心極限定理とは
- 偏った分布でも中心極限定理は成り立つ
- 点推定と区間推定
- 点推定の限界
- 区間推定:幅を持って推定する
- 95%信頼区間の正しい解釈
- 実務での信頼区間の計算
- 母標準偏差がわからない場合
- 標本サイズと信頼区間の幅
- 信頼区間を使った意思決定
- 例:販促キャンペーンは本当に売上を伸ばしたのか?
- 差の95%信頼区間を見る
- 効果があるとは言い切れないケース
- 信頼区間が「意思決定向き」な理由
- まとめ
母集団と標本:全体と一部
基本用語を押さえよう
推測統計を学ぶ上で、まず2つの重要な用語を理解しましょう。
- 母集団(population):調査したい対象の全体。例:大学の全学生1万人
- 標本(sample):母集団から選び出した一部。例:アンケートに回答した100人
母集団の特性を表す値を母数(パラメータ)、標本から計算した値を統計量と呼びます。
| 対象 | 平均 | |
|---|---|---|
| 母集団 | 母平均 \mu | 母分散 \sigma^2 |
| 標本 | 標本平均 \bar{x} | 標本分散 s^2 |
私たちの目標は、標本から計算した統計量を使って、未知の母数を推測することです。
Pythonで母集団と標本を体験する
仮想的な母集団(1万人の学生の勉強時間)を作成し、そこから標本を抽出してみます。
以下、コードです。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
np.random.seed(42)
# 母集団:1万人の学生の勉強時間(平均3時間、標準偏差1時間)
population = np.random.normal(
loc=3.0, # 母平均
scale=1.0, # 母標準偏差
size=10000 # 母集団のサイズ
)
# 母集団の真の値(普通は知ることができない)
true_mean = np.mean(population)
true_std = np.std(population)
print("【母集団の情報】(実際には知ることができない)")
print(f" 母集団のサイズ: {len(population)}人")
print(f" 母平均 μ: {true_mean:.3f}時間")
print(f" 母標準偏差 σ: {true_std:.3f}時間")
以下、実行結果です。
【母集団の情報】(実際には知ることができない) 母集団のサイズ: 10000人 母平均 μ: 2.998時間 母標準偏差 σ: 1.003時間
母平均は約3時間、母標準偏差は約1時間です。
ただし、これは「神の視点」で見た値であり、現実の調査では母集団全体を調べることはできないため、この値は未知のままです。
母集団から100人を無作為に抽出して、標本を作成します。
以下、コードです。
# 標本:100人を無作為に抽出
sample_size = 100
sample = np.random.choice(
population, # 母集団
size=sample_size, # 標本サイズ
replace=False # 重複抽出なし
)
# 標本から計算した統計量
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1)
print("【標本の情報】")
print(f" 標本サイズ n: {sample_size}人")
print(f" 標本平均: {sample_mean:.3f}時間")
print(f" 標本標準偏差: {sample_std:.3f}時間")
以下、実行結果です。
【標本の情報】 標本サイズ n: 100人 標本平均: 3.012時間 標本標準偏差: 0.914時間
標本平均は母平均と完全には一致しません。少しズレがあります。
これは「たまたまこの100人を選んだから」生じる誤差で、標本誤差と呼ばれます。
別の100人を選べば、また違う値になるでしょう。
標本平均のばらつき:何度も抽出してみる
同じ母集団から標本を抽出しても、選ばれる人が違えば標本平均も変わります。
この「標本平均のばらつき」を理解することが、推測統計の鍵です。
標本抽出を1000回繰り返し、毎回の標本平均を記録します。
以下、コードです。
# 標本抽出を1000回繰り返す
n_simulations = 1000
sample_size = 100
sample_means = []
for _ in range(n_simulations):
sample = np.random.choice(population, size=sample_size, replace=False)
sample_means.append(np.mean(sample))
sample_means = np.array(sample_means)
print(f"【{n_simulations}回の標本抽出の結果】")
print(f" 標本平均の最小値: {np.min(sample_means):.3f}時間")
print(f" 標本平均の最大値: {np.max(sample_means):.3f}時間")
print(f" 標本平均の平均: {np.mean(sample_means):.3f}時間")
print(f" 標本平均の標準偏差: {np.std(sample_means):.3f}時間")
以下、実行結果です。
【1000回の標本抽出の結果】 標本平均の最小値: 2.682時間 標本平均の最大値: 3.369時間 標本平均の平均: 2.998時間 標本平均の標準偏差: 0.097時間
1000回の標本抽出で、標本平均は約2.7〜約3.4時間程度の範囲でばらついています。
しかし、その平均は母平均(約3時間)にほぼ一致しています。
つまり、標本平均は母平均の周りにばらつきながらも、平均すれば正しい値に近くなるのです。
標本平均の分布をヒストグラムで可視化します。
以下、コードです。
plt.figure(figsize=(10, 5))
# 標本平均のヒストグラムを描く
plt.hist(
sample_means, # ヒストグラムを描くデータ
bins=30, # ビンの数
edgecolor='white', alpha=0.7, density=True
)
# 母平均を赤い破線で描く
plt.axvline(
true_mean,
color='red', linestyle='--', linewidth=2,
label=f'母平均 μ = {true_mean:.3f}'
)
# 標本平均の平均を青い実線で描く
plt.axvline(
np.mean(sample_means),
color='blue', linestyle='-', linewidth=2,
label=f'標本平均の平均 = {np.mean(sample_means):.3f}'
)
plt.xlabel('標本平均(時間)')
plt.ylabel('密度')
plt.title('標本平均の分布(n=100, 1000回抽出)')
plt.legend()
plt.show()
以下、実行結果です。
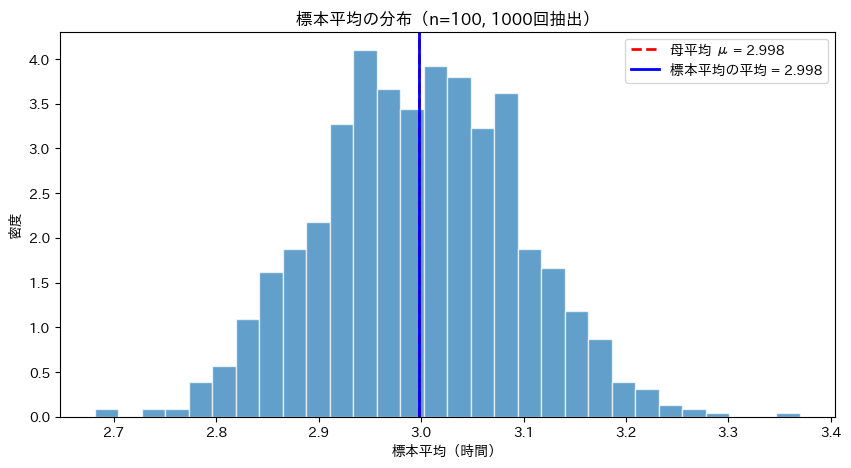
標本平均の分布は、母平均を中心としたきれいな釣鐘型(正規分布)になっています。
この分布を標本分布と呼びます。
標本分布を理解することで、「標本平均がどのくらいの範囲に収まりやすいか」がわかるようになります。
標準誤差:標本平均のばらつきの指標
標準誤差(SE)とは
標本平均のばらつき(標準偏差)には、標準誤差(Standard Error, SE)という特別な名前がついています。
標準誤差は次の式で計算できます。
$$
SE = \frac{\sigma}{\sqrt{n}}
$$
ここで、\sigma は母標準偏差、n は標本サイズです。
理論値と実際のシミュレーション結果を比較します。
以下、コードです。
# 理論的な標準誤差
th_SE = true_std / np.sqrt(sample_size)
# シミュレーションで得られた標本平均の標準偏差
si_SE = np.std(sample_means)
print("【標準誤差の比較】")
print(f" 理論値(σ/√n): {th_SE:.4f}時間")
print(f" シミュレーション結果: {si_SE:.4f}時間")
以下、実行結果です。
【標準誤差の比較】 理論値(σ/√n): 0.1003時間 シミュレーション結果: 0.0966時間
理論値とシミュレーション結果がほぼ一致しています。
この式 SE = \sigma/\sqrt{n} が正しいことが実験的に確認できました。
標本サイズと標準誤差の関係
標準誤差の式を見ると、\sqrt{n} が分母にあります。
つまり、標本サイズが大きくなるほど、標準誤差は小さくなります。
標本サイズを変えて、標準誤差がどう変化するか確認します。
以下、コードです。
sample_sizes = [10, 25, 50, 100, 200, 400]
print("【標本サイズと標準誤差の関係】")
print(f"{'標本サイズ n':>8} | {'理論的SE':>8} | {'実測SE':>8}")
print("-" * 40)
for n in sample_sizes:
# 理論値
th = true_std / np.sqrt(n)
# シミュレーション
means = [
np.mean(np.random.choice(
population,
n,
replace=False))
for _ in range(500)
]
si = np.std(means)
print(f"{n:>12} | {th:>10.4f} | {si:>10.4f}")
以下、実行結果です。
【標本サイズと標準誤差の関係】
標本サイズ n | 理論的SE | 実測SE
----------------------------------------
10 | 0.3173 | 0.3311
25 | 0.2007 | 0.1965
50 | 0.1419 | 0.1426
100 | 0.1003 | 0.0983
200 | 0.0710 | 0.0702
400 | 0.0502 | 0.0468
標本サイズが10のときSEは0.3ぐらいですが、100になると0.1ぐらい、400になると0.05ぐらいまで下がります。
標本サイズを4倍にすると、標準誤差は半分(\sqrt{4}=2 で割る)になることがわかります。
この関係をグラフで視覚化します。
以下、コードです。
n_values = np.arange(10, 501, 10)
se_values = true_std / np.sqrt(n_values)
plt.figure(figsize=(10, 5))
plt.plot(n_values, se_values, linewidth=2)
plt.xlabel('標本サイズ n')
plt.ylabel('標準誤差 SE')
plt.title('標本サイズと標準誤差の関係(SE = σ/√n)')
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
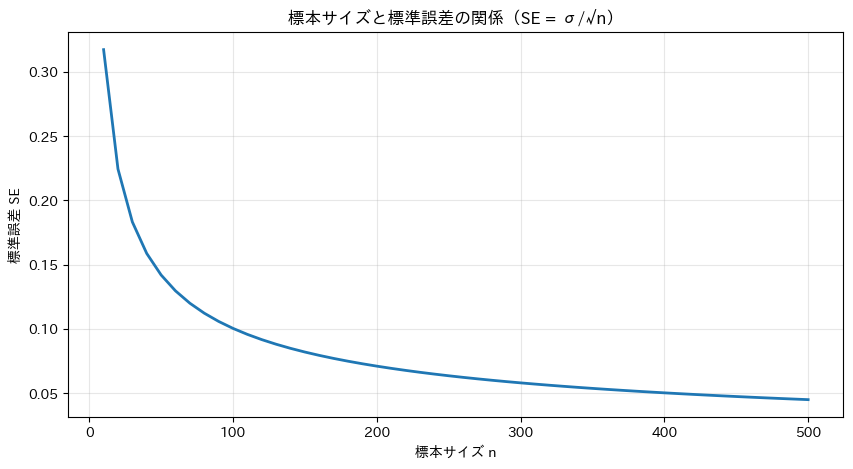
標本サイズが増えるにつれて標準誤差は急速に減少しますが、ある程度以上になると減り方が緩やかになります。
たとえばn=100からn=400に増やしても、SEは0.1から0.05になるだけです。
調査コストとのバランスを考えると、むやみに標本サイズを増やせばよいわけではありません。
中心極限定理:統計学で最も重要な定理
中心極限定理とは
ここまでのシミュレーションで、標本平均の分布が正規分布に近い形になることを見てきました。
これは偶然ではなく、中心極限定理(Central Limit Theorem, CLT)という数学的な定理によって保証されています。
中心極限定理の主張は次の通りです。
標本サイズ n が十分に大きければ、
標本平均の分布は正規分布に近づく
これは驚くべき結果です。元のデータが正規分布でなくても、歪んだ分布でも、平均を取ると正規分布になるのです。
偏った分布でも中心極限定理は成り立つ
正規分布ではない「指数分布」から標本を抽出し、中心極限定理を確認します。
指数分布は右に長く裾を引く、非対称な分布です。
以下、コードです。
# 指数分布の母集団(右に歪んだ分布)
pop_exp = np.random.exponential(
scale=2.0, # 平均値
size=10000 # 母集団のサイズ
)
plt.figure(figsize=(10, 5))
plt.hist(
pop_exp, bins=50,
edgecolor='black', alpha=0.7,
density=True
)
plt.xlabel('値')
plt.ylabel('密度')
plt.title('母集団の分布(指数分布:右に歪んでいる)')
plt.show()
print(f"母集団の平均: {np.mean(pop_exp):.3f}")
print(f"母集団の標準偏差: {np.std(pop_exp):.3f}")
以下、実行結果です。
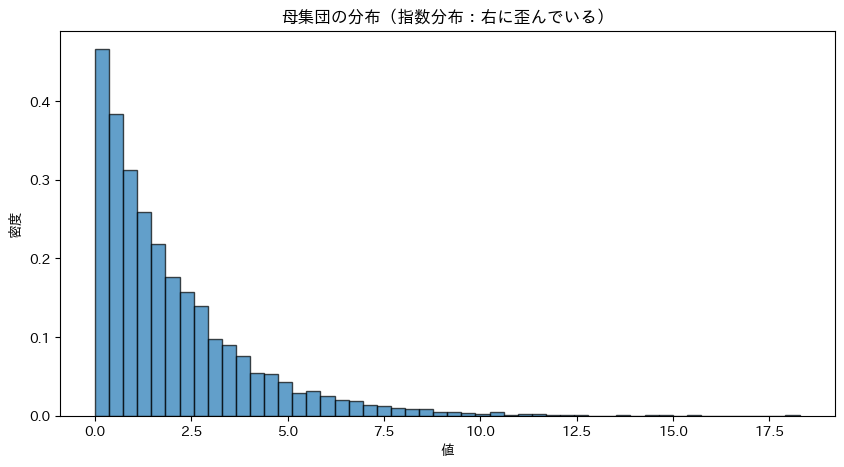
母集団の平均: 1.991 母集団の標準偏差: 2.001
指数分布は0付近に集中し、右に長い裾を持つ非対称な分布です。これは正規分布とは全く異なる形をしています。
この偏った分布から標本平均を繰り返し計算し、その分布を確認します。
以下、コードです。
fig, axes = plt.subplots(3, 1, figsize=(10, 10))
sample_sizes = [5, 30, 100]
for ax, n in zip(axes, sample_sizes):
means = [
np.mean(
np.random.choice(pop_exp, n, replace=False)
)
for _ in range(1000)
]
ax.hist(
means, bins=30,
edgecolor='white', alpha=0.7,
density=True
)
ax.axvline(
np.mean(pop_exp),
color='red', linestyle='--', linewidth=2
)
ax.set_xlabel('標本平均')
ax.set_ylabel('密度')
ax.set_title(f'n = {n}')
plt.suptitle('中心極限定理:歪んだ分布でも標本平均は正規分布に近づく')
plt.tight_layout()
plt.show()
以下、実行結果です。
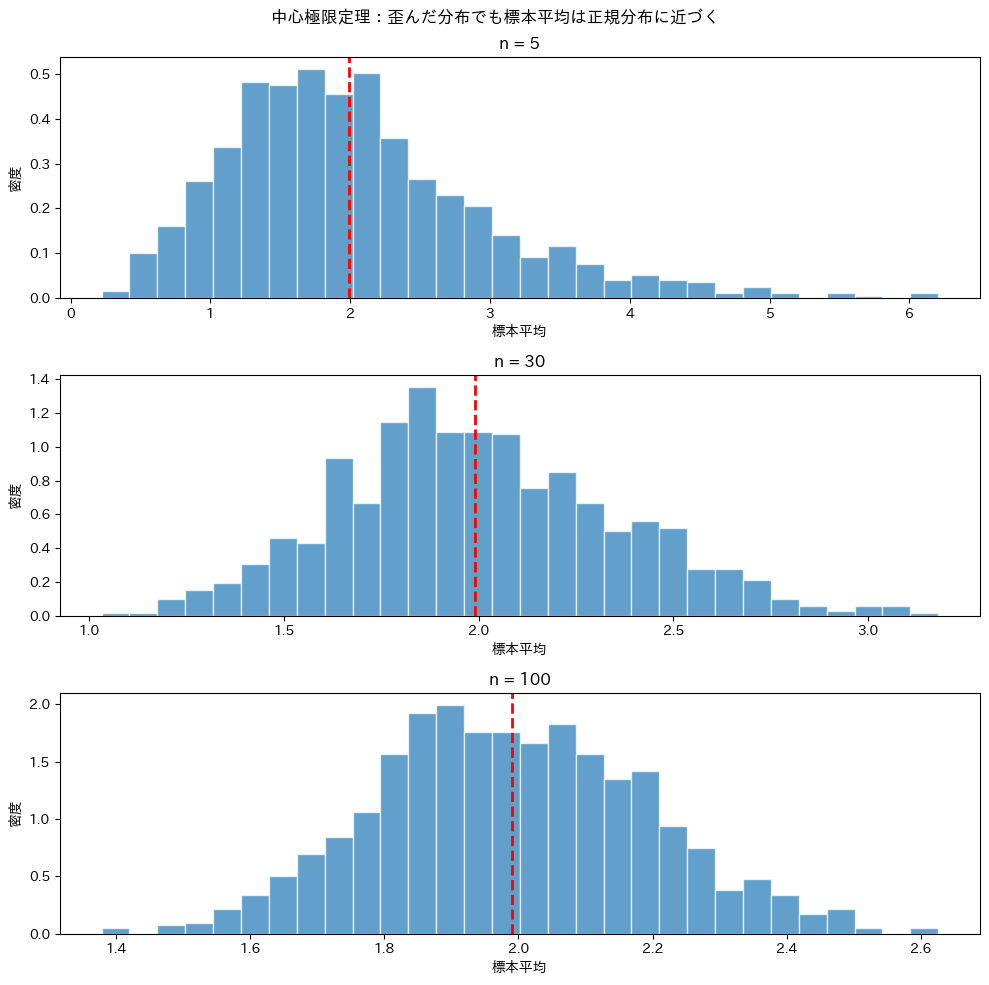
n=5では分布がまだ歪んでいますが、n=30ではかなり正規分布に近づき、n=100ではほぼ正規分布になっています。
元の母集団が正規分布でなくても、標本サイズが大きくなれば標本平均は正規分布に従う。これが中心極限定理の威力です。
点推定と区間推定
点推定の限界
標本平均 \bar{x} を使って母平均 \mu を推定することを点推定と呼びます。
しかし、点推定には「どのくらい確かなのか」という情報がありません。
同じ母集団から3回標本を抽出し、点推定の不確かさを確認します。
以下、コードです。
np.random.seed(None) # 毎回異なる結果を得るため
print("【3回の標本抽出と点推定】")
print(f"母平均(真の値): {true_mean:.3f}時間\n")
for i in range(3):
sample = np.random.choice(
population,
size=100,
replace=False
)
print(
f" {i+1}回目: "
f"標本平均 = {np.mean(sample):.3f}時間"
)
以下、実行結果です。
【3回の標本抽出と点推定】 母平均(真の値): 2.998時間 1回目: 標本平均 = 3.210時間 2回目: 標本平均 = 3.109時間 3回目: 標本平均 = 2.821時間
3回の抽出で、3つの異なる推定値が得られました。
どれも「母平均の推定値」として正当ですが、どれがより正確かはわかりません。
点推定だけでは不十分なのです。
区間推定:幅を持って推定する
点推定の限界を補うのが区間推定です。
「母平均は○○から××の間にあるだろう」という形で、幅を持って推定します。
この区間を信頼区間と呼びます。
最もよく使われるのは95%信頼区間です。これは次のように計算されます。
$$
\bar{x} \pm 1.96 \times SE = \bar{x} \pm 1.96 \times \frac{\sigma}{\sqrt{n}}
$$
1.96という数字は、正規分布において中央の95%をカバーする範囲に対応しています。
95%信頼区間を計算し、母平均が含まれるかどうか確認します。
以下、コードです。
np.random.seed(42)
# 標本を抽出
sample = np.random.choice(
population,
size=100,
replace=False
)
sample_mean = np.mean(sample)
# 標準誤差(母標準偏差がわかっている場合)
SE = true_std / np.sqrt(len(sample))
# 95%信頼区間
ci_lower = sample_mean - 1.96 * SE
ci_upper = sample_mean + 1.96 * SE
print("【95%信頼区間の計算】")
print(f" 標本平均: {sample_mean:.3f}時間")
print(f" 標準誤差: {SE:.3f}時間")
print(
" 95%信頼区間: "
f"[{ci_lower:.3f}, {ci_upper:.3f}]"
)
以下、実行結果です。
【95%信頼区間の計算】 標本平均: 3.080時間 標準誤差: 0.100時間 95%信頼区間: [2.883, 3.277]
95%信頼区間が計算され、母平均がその区間内に含まれていることが確認できました。
ただし、これは「この区間に95%の確率で母平均がある」という意味ではありません。
95%信頼区間の正しい解釈
95%信頼区間の解釈は、多くの人が誤解しているポイントです。正しい解釈は次の通りです。
95%の回で真の母平均が区間内に含まれる
これを実験で確認してみましょう。
信頼区間の計算を1000回繰り返し、何回母平均を含むか数えます。
以下、コードです。
np.random.seed(42)
n_exp = 1000
sample_size = 50
cts_true_mean = 0
results = []
for i in range(n_exp):
sample = np.random.choice(
population,
size=sample_size,
replace=False
)
sample_mean = np.mean(sample)
SE = true_std / np.sqrt(sample_size)
ci_lower = sample_mean - 1.96 * SE
ci_upper = sample_mean + 1.96 * SE
cts = ci_lower <= true_mean <= ci_upper
if cts:
cts_true_mean += 1
results.append((ci_lower, ci_upper, cts))
print(f"【100回の実験結果】")
print(f" 母平均を含んだ回数: {cts_true_mean}回")
percentage = cts_true_mean / n_exp * 100
print(f" 割合: {percentage:.2f}%")
以下、実行結果です。
【100回の実験結果】 母平均を含んだ回数: 954回 割合: 95.40%
100回の実験のうち、約95回で母平均が信頼区間内に含まれています。
これが「95%信頼区間」の意味です。
個々の区間について「95%の確率で母平均が含まれる」のではなく、「このような区間を作る手続きは、95%の確率で正しい」ということです。
実務での信頼区間の計算
母標準偏差がわからない場合
ここまで母標準偏差 \sigma がわかっている前提で計算してきましたが、現実の調査では \sigma は未知です。
その場合は、標本標準偏差 s で代用し、正規分布の代わりにt分布を使います。
scipyを使って信頼区間を計算します。
以下、コードです。
from scipy import stats
np.random.seed(42)
# 標本を抽出
sample = np.random.choice(
population,
size=30,
replace=False
)
# 信頼区間を計算(母標準偏差が未知の場合)
confidence_level = 0.95
ci = stats.t.interval(
confidence_level, # 信頼係数
df=len(sample)-1, # 自由度
loc=np.mean(sample), # 標本平均
scale=stats.sem(sample) # 標準誤差
)
print("【実務的な95%信頼区間の計算】")
print(f" 標本サイズ: {len(sample)}")
print(f" 標本平均: {np.mean(sample):.3f}時間")
print(f" 標準誤差(推定): {stats.sem(sample):.3f}時間")
print(f" 95%信頼区間: [{ci[0]:.3f}, {ci[1]:.3f}]")
以下、実行結果です。
【実務的な95%信頼区間の計算】 標本サイズ: 30 標本平均: 3.230時間 標準誤差(推定): 0.172時間 95%信頼区間: [2.878, 3.582]
scipy.stats.t.interval() を使えば、t分布に基づく正確な信頼区間を計算できます。
stats.sem() は標準誤差を計算する便利な関数です。
標本サイズと信頼区間の幅
標本サイズが大きいほど、標準誤差が小さくなり、信頼区間も狭くなります。
つまり、より精度の高い推定ができるようになります。
標本サイズを変えて、信頼区間の幅がどう変わるか確認します。
以下、コードです。
np.random.seed(42)
print("【標本サイズと信頼区間の幅】")
print(f"{'n':>6} | {'標本平均':>7} | {'95%CI':>14} | {'CI幅':>6}")
print("-" * 60)
for n in [10, 30, 100, 300]:
sample = np.random.choice(
population,
size=n,
replace=False
)
ci = stats.t.interval(
0.95,
df=n-1,
loc=np.mean(sample),
scale=stats.sem(sample)
)
width = ci[1] - ci[0]
print(
f"{n:>6} | "
f"{np.mean(sample):>10.3f} | "
f"[{ci[0]:.3f}, {ci[1]:.3f}] | "
f"{width:>8.3f}"
)
以下、実行結果です。
【標本サイズと信頼区間の幅】
n | 標本平均 | 95%CI | CI幅
------------------------------------------------------------
10 | 3.241 | [2.482, 4.000] | 1.518
30 | 2.793 | [2.458, 3.129] | 0.671
100 | 3.068 | [2.872, 3.263] | 0.390
300 | 3.045 | [2.936, 3.155] | 0.219
標本サイズが10のときは信頼区間の幅が約1.5ありますが、300になると約0.2まで狭くなります。
「信頼区間が狭い」ということは、「推定の精度が高い」ということを意味します。
信頼区間を使った意思決定
信頼区間は、「数字としての結果」よりも、意思決定にどう使えるかを意識すると理解しやすくなります。
まずは、身近なビジネスの例から見てみましょう。
例:販促キャンペーンは本当に売上を伸ばしたのか?
ある店舗で、販促キャンペーンを実施しました。
- 施策前:1日の売上データを複数日分集めた
- 施策後:同じ条件で、再び売上データを集めた
計算すると……
- 施策前の平均売上:およそ 49
- 施策後の平均売上:およそ 55
……となり、平均だけを見ると「売上は増えていそう」に見えます。
しかし、ここで次の疑問が残ります。
それとも、たまたま良い日が続いただけなのか?
売上は日によって上下します。
そのため、平均との差が少し大きく見えても、それが偶然のばらつきの範囲内である可能性は常に残ります。
ここで役立つのが、「平均との差」の信頼区間です。
差の95%信頼区間を見る
この例で計算した「施策後 − 施策前」の差の95%信頼区間は……
……という範囲になりました。
この数値が意味するのは……
- 効果があったとしても、その大きさは 最低でも約4.5
- 多く見積もっても 約6.5程度
……ということです。
ここで最も重要なのは、信頼区間に 0 が含まれているかです。
この例の場合は……
- 信頼区間はすべて正の値
- 0(=効果なし)は含まれていない
少なくとも、「売上が増えていない」という可能性は排除できます。
よって、販促キャンペーンには、統計的に意味のある効果があったと判断できます
効果があるとは言い切れないケース
別の施策で、平均との差は +2 でしたが、差の95%信頼区間が……
……だったとします。
この場合……
- 売上が増えた可能性もある
- 実は減っていた可能性も否定できない
つまり、効果があったとは結論づけられません。
平均がプラスでも、信頼区間が0をまたいでいれば判断は保留になります。
信頼区間が「意思決定向き」な理由
信頼区間は、次の3つを同時に教えてくれます。
- 効果があるか、ないか
- 効果の大きさはどの程度か
- 最悪の場合でも、どれくらいは期待できるか
これは「有意か/有意でないか」だけを示す仮説検定よりも、ビジネスや現場の判断に直結しやすい情報です。
実務では……
- 平均だけで判断しない
- 必ず「差の信頼区間」を確認する
- 0を含むかどうかで、結論の可否を決める
この考え方を身につけておくと、次に学ぶ 仮説検定も「道具として」理解しやすくなります。
まとめ
この記事では、一部のデータ(標本)から全体(母集団)を推測する「推測統計」の基本を学びました。
母集団と標本という概念を理解することが、推測統計の第一歩です。
母集団は調査したい対象の全体であり、標本はそこから選び出した一部です。私たちは標本から計算した統計量(標本平均など)を使って、未知の母数(母平均など)を推測します。
標本から計算した平均は、抽出のたびに異なる値になります。この「標本平均のばらつき」を表す指標が標準誤差(SE = σ/√n)です。
標本サイズ n が大きくなるほど標準誤差は小さくなり、推定の精度が向上します。また、中心極限定理により、元の母集団がどんな分布であっても、標本サイズが十分に大きければ標本平均の分布は正規分布に近づきます。この定理のおかげで、正規分布に基づく推測統計の手法が広く適用できるのです。
母平均を推定する方法には、点推定(一つの値で推定)と区間推定(幅を持って推定)があります。
95%信頼区間は「同じ方法を繰り返したとき、95%の確率で真の母平均を含む区間」を与えます。ただし、これは「この区間に95%の確率で母平均がある」という意味ではない点に注意が必要です。信頼区間が狭いほど推定精度が高く、標本サイズを増やすことで区間を狭くできます。

