データサイエンスにおいて、高次元のデータセットを効果的に解析し理解することは、常に一つの大きな課題です。
主成分分析(PCA)は、この課題を解決するための強力なツールであり、多次元データの本質を捉え、より低次元の空間で表現することにより、データの洞察を深めるのに役立ちます。
今回は、Boston Housingデータセットを使用して、PCAの概念とそのビジュアル化技術を紹介します。
Boston Housingデータセットには、犯罪率、住宅価格、税率など、ボストンの住宅市場に影響を与える様々な特徴が含まれています。
これらの多次元データを用いて、PCAを実施し、どの特徴が住宅価格に最も大きな影響を与えるのか、またそれらがどのように相互作用しているのかを視覚的に分析していきます。
Contents
はじめに
主成分分析(PCA)とは?
PCAは、多次元データをより低次元の空間に射影することで、データの最も重要な構造を明らかにする手法です。
これは、データの分散を最大化するように新しい軸(主成分)を作り出し、元のデータの次元を削減しつつ、データが持つ情報量を保つことを目的としています。
PCAを適用することで、元の変数がどのように関連しているか、どの変数がデータの分散に最も寄与しているかを視覚的に把握することができます。
なぜPCAが重要なのか?
データサイエンスの分野では、多次元データを効果的に理解することがしばしば課題となります。
例えば、住宅価格の予測において、犯罪率や税率、部屋の数、交通アクセスなど、数多くの要因が複雑に絡み合っています。
これらの多次元データを分析し、重要なパターンや傾向を抽出するために、主成分分析(PCA: Principal Component Analysis)という強力なツールが使われます。
これにより、データの理解が深まり、さらには予測モデルの性能向上にも繋がります。
特に、複数の変数が相互に関連している場合、PCAはこれらの関係性を明確にし、データ分析の効率を大幅に高めます。
Boston Housingデータセットの概要
今回は、Boston Housingデータセットを用いてPCAの概念とその結果の視覚化の方法について説明してきます。
このデータセットは、ボストン市の住宅価格に関する様々な特徴を含んでおり、データサイエンスの分野で広く利用されています。
このデータセットの特徴量(説明変数)は以下です。
- CRIM: 町ごとの犯罪率
- ZN: 25,000平方フィート以上の住宅区画の割合
- INDUS: 町ごとの非小売業地域の割合
- CHAS: チャールズ川に接しているかどうか(バイナリ値)
- NOX: 一酸化窒素濃度(ppm)
- RM: 住宅の平均部屋数
- AGE: 1940年以前に建てられた住宅の割合
- DIS: 主要な雇用センターからの距離
- RAD: 高速道路へのアクセス指数
- TAX: 1万ドルあたりの固定資産税率
- PTRATIO: 町ごとの生徒教師比率
- B: 町ごとの黒人の割合を反映した指標
- LSTAT: 低所得者層の割合
目的変数(ターゲット変数)は以下となります。
- MEDV: 住宅価格の中央値
これらの多様な特徴量をPCAにかけることで、どの変数が住宅価格に最も強く影響を与えているかを理解することができます。
データの準備と前処理
PCAを適用する前に、データの適切な準備と前処理が重要です。データの前処理を正しく行うことで、主成分分析の結果が正確かつ信頼性の高いものになります。
データの読み込み
まずは、Pythonを使ってBoston Housingデータセットを読み込みます。
以下、コードです。
from sklearn.datasets import fetch_openml import pandas as pd # Boston Housingデータセットの読み込み from OpenML boston = fetch_openml(name='boston', version=1, as_frame=True) # データをPandas DataFrameに変換 df = pd.DataFrame(boston.data, columns=boston.feature_names) # 目標変数(住宅価格)を追加 df['MEDV'] = boston.target # データの先頭5行を表示 print(df.head())
以下、実行結果です。
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO \
0 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296.0 15.3
1 0.02731 0.0 7.07 0 0.469 6.421 78.9 4.9671 2 242.0 17.8
2 0.02729 0.0 7.07 0 0.469 7.185 61.1 4.9671 2 242.0 17.8
3 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222.0 18.7
4 0.06905 0.0 2.18 0 0.458 7.147 54.2 6.0622 3 222.0 18.7
B LSTAT MEDV
0 396.90 4.98 24.0
1 396.90 9.14 21.6
2 392.83 4.03 34.7
3 394.63 2.94 33.4
4 396.90 5.33 36.2
データの標準化
PCAを適用する前に、各特徴量のスケールを統一するためにデータを標準化します。
標準化とは、データの各特徴量を平均0、標準偏差1に変換する手法です。
これにより、異なる単位を持つ特徴量間での影響を均等にし、PCAの結果が偏らないようにします。
Pythonでは、scikit-learnのStandardScalerを使用して簡単に標準化を行うことができます。
以下、コードです。
from sklearn.preprocessing import StandardScaler
# 説明変数を抽出
X = df.drop('MEDV', axis=1)
# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 標準化されたデータの確認
print(pd.DataFrame(X_scaled, columns=X.columns).head())
以下、実行結果です。
CRIM ZN INDUS CHAS NOX RM AGE \
0 -0.419782 0.284830 -1.287909 -0.272599 -0.144217 0.413672 -0.120013
1 -0.417339 -0.487722 -0.593381 -0.272599 -0.740262 0.194274 0.367166
2 -0.417342 -0.487722 -0.593381 -0.272599 -0.740262 1.282714 -0.265812
3 -0.416750 -0.487722 -1.306878 -0.272599 -0.835284 1.016303 -0.809889
4 -0.412482 -0.487722 -1.306878 -0.272599 -0.835284 1.228577 -0.511180
DIS RAD TAX PTRATIO B LSTAT
0 0.140214 -0.982843 -0.666608 -1.459000 0.441052 -1.075562
1 0.557160 -0.867883 -0.987329 -0.303094 0.441052 -0.492439
2 0.557160 -0.867883 -0.987329 -0.303094 0.396427 -1.208727
3 1.077737 -0.752922 -1.106115 0.113032 0.416163 -1.361517
4 1.077737 -0.752922 -1.106115 0.113032 0.441052 -1.026501
欠損値の確認と処理
次に、データセット内に欠損値がないかを確認します。
欠損値があると、PCAの計算に悪影響を与える可能性があります。
以下、コードです。
# 欠損値の確認 print(df.isnull().sum())
以下、実行結果です。
CRIM 0 ZN 0 INDUS 0 CHAS 0 NOX 0 RM 0 AGE 0 DIS 0 RAD 0 TAX 0 PTRATIO 0 B 0 LSTAT 0 MEDV 0 dtype: int64
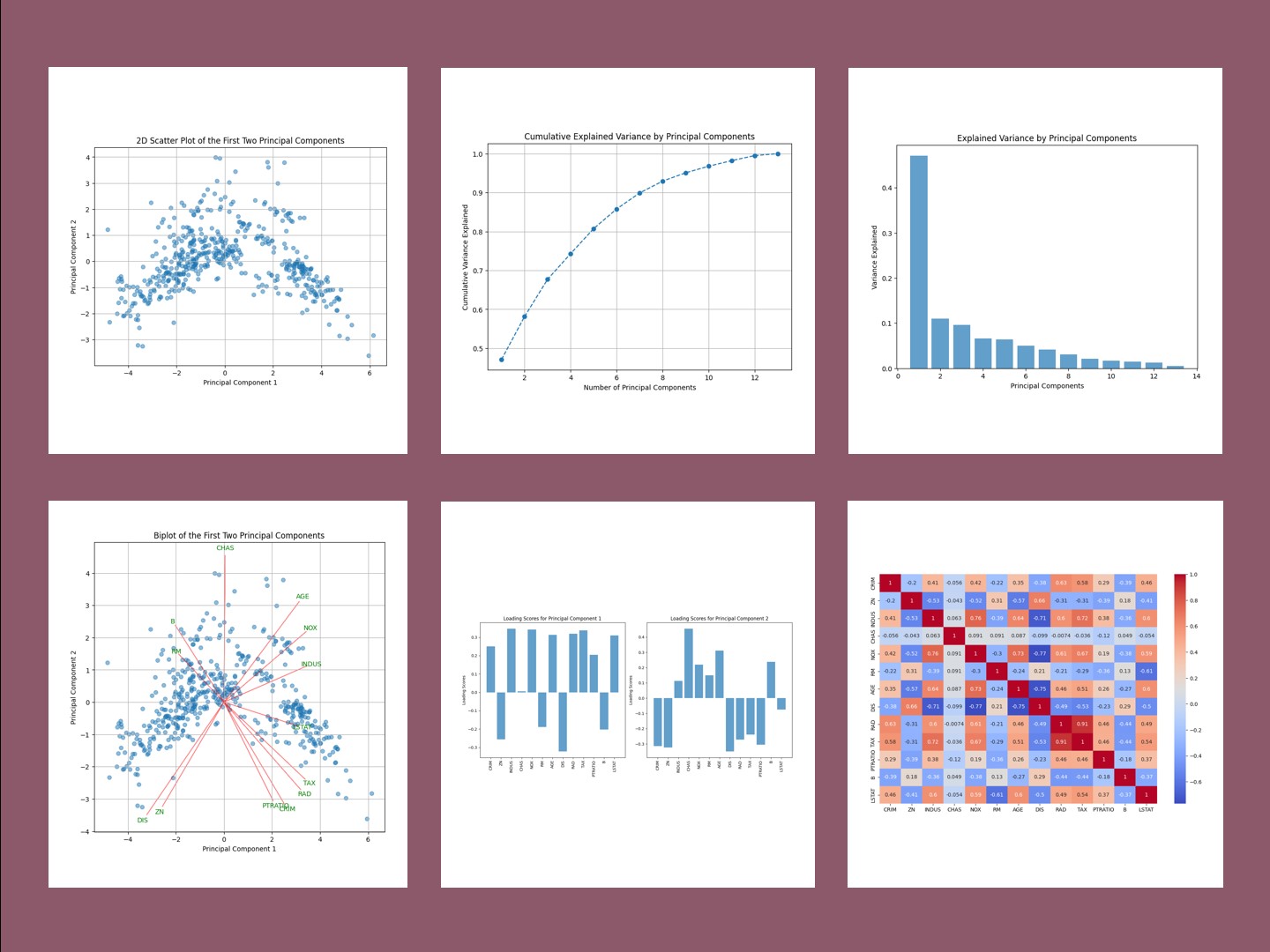
特徴量の相関の確認
PCAを実施する前に、各特徴量間の相関関係を確認することも有益です。
相関が高い特徴量同士は、PCAによって同じ主成分に集約される可能性が高いからです。
以下、コードです。
import seaborn as sns import matplotlib.pyplot as plt # 特徴量の相関行列を計算 df_scaled = pd.DataFrame(X_scaled, columns=X.columns) corr_matrix = df_scaled.corr() # 相関行列のヒートマップを表示 plt.figure(figsize=(12, 8)) sns.heatmap(corr_matrix, annot=True, cmap='coolwarm') plt.show()
以下、実行結果です。
ここまでで、PCAを実施するためのデータの準備が整いました。
データを読み込み、標準化し、必要に応じて欠損値を処理することで、PCAの前提条件を満たすデータセットが完成しました。
このデータを用いて実際にPCAを実施し、その結果を視覚化していきます。
主成分分析の実施
先ほど準備したデータを用いて、主成分分析(PCA)を実施します。
Pythonを使ってPCAを適用し、その結果をビジュアル化してデータの特徴を理解する方法を紹介します。
PCAの実施
まず、scikit-learnライブラリのPCAクラスを使用して、標準化されたデータに対してPCAを実行します。
以下のコードで、PCAを適用し、各主成分がどれだけの分散を説明しているか寄与率を確認します。
from sklearn.decomposition import PCA # PCAの実行 pca = PCA() X_pca = pca.fit_transform(X_scaled) # 主成分が説明する分散の割合を表示 print(pca.explained_variance_ratio_)
explained_variance_ratio_は、各主成分が元のデータの分散をどの程度説明しているかと言った、データの特徴を捉えている寄与率を示します。
これにより、どの主成分がデータの重要な特徴を捉えているかを把握することができます。
以下、実行結果です。
[0.47129606 0.11025193 0.0955859 0.06596732 0.06421661 0.05056978 0.04118124 0.03046902 0.02130333 0.01694137 0.0143088 0.01302331 0.00488533]
第1主成分、第2主成分、…の順番になっています。例えば、第1主成分の寄与率は約47%、第2主成分の寄与率は約11%となっており、寄与率の大きい順に並んでいます。
主成分の数を決定する
PCAでは、通常、全ての主成分を採用する必要はなく、データの大部分の分散を説明する少数の主成分を選択します。
ここでは、累積寄与率を計算し、どの主成分までを採用するかを決定します。
以下、コードです。
import numpy as np # 累積寄与率を計算 cumulative_variance = np.cumsum(pca.explained_variance_ratio_) # 累積寄与率を表示 print(cumulative_variance)
以下、実行結果です。
[0.47129606 0.581548 0.67713389 0.74310121 0.80731782 0.8578876 0.89906884 0.92953786 0.9508412 0.96778257 0.98209137 0.99511467 1. ]
累積寄与率が90%を超えるまでの主成分を選択するのが一般的な手法です。この結果をもとに、必要な主成分の数を決定します。
今回の場合ですと、第7主成分もしくは第8主成分ぐらいまで採用するのがいいでしょう。
主成分の可視化
次に、主成分分析の結果を可視化します。
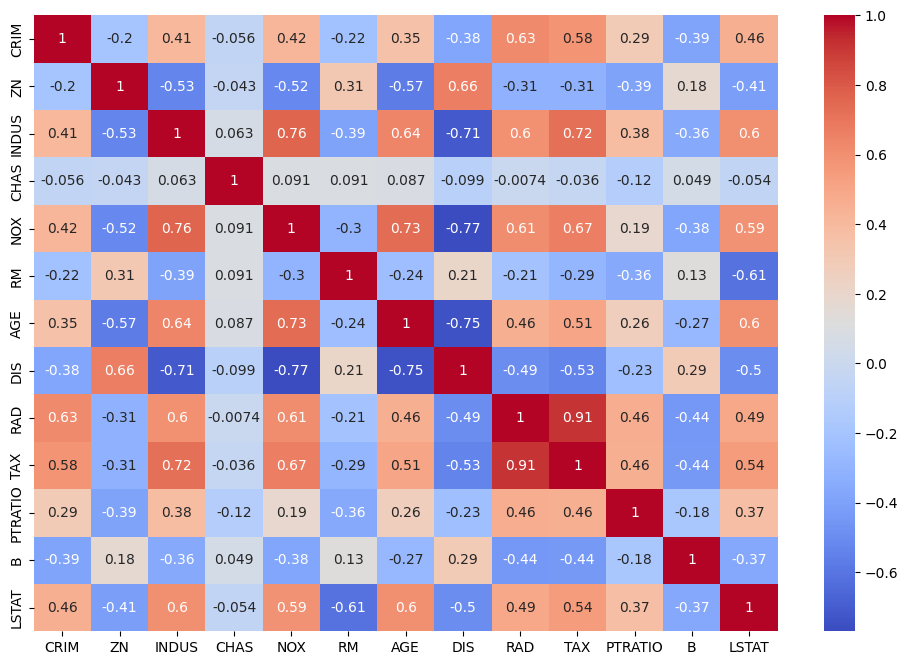
寄与率プロット
まず、各主成分がどれだけの分散を説明しているかを示す「寄与率プロット」を作成します。
以下、コードです。
import matplotlib.pyplot as plt
# 寄与率プロット
plt.figure(figsize=(8, 6))
plt.bar(
range(1, len(pca.explained_variance_ratio_) + 1),
pca.explained_variance_ratio_,
alpha=0.7,
align='center')
plt.xlabel('Principal Components')
plt.ylabel('Variance Explained')
plt.title('Explained Variance by Principal Components')
plt.show()
以下、実行結果です。
このプロットでは、各主成分がデータの分散をどれだけ説明しているかを視覚的に示します。
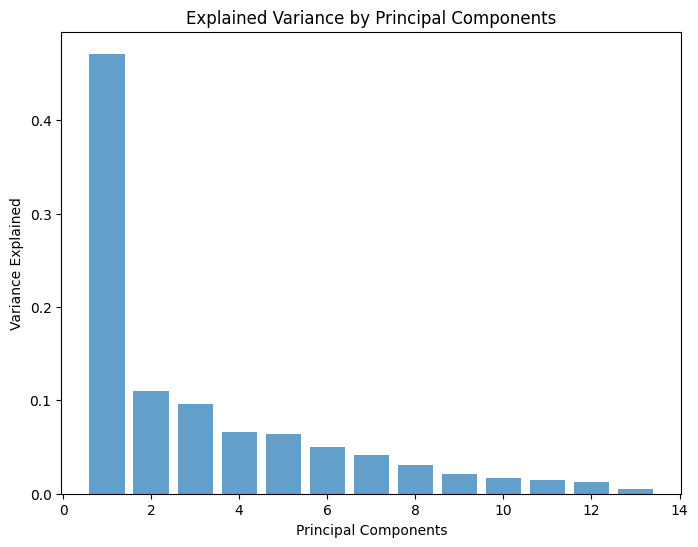
累積寄与率プロット
次に、累積寄与率をプロットし、選択した主成分がどれだけの分散を保持しているかを確認します。
以下、コードです。
# 累積寄与率プロット
plt.figure(figsize=(8, 6))
plt.plot(
range(1, len(cumulative_variance) + 1),
cumulative_variance,
marker='o',
linestyle='--')
plt.xlabel('Number of Principal Components')
plt.ylabel('Cumulative Variance Explained')
plt.title('Cumulative Explained Variance by Principal Components')
plt.grid()
plt.show()
以下、実行結果です。
このプロットは、データの分散を一定割合以上保持するために必要な主成分の数を判断するのに役立ちます。
成分散布図
次に、最初の2つまたは3つの主成分を用いて、データを2Dまたは3Dでプロットし、データの構造を視覚化します。
以下、コードです。横軸が第1主成分、縦軸が第2主成分です。
# 2D成分散布図
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], alpha=0.5)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('2D Scatter Plot of the First Two Principal Components')
plt.grid()
plt.show()
以下、実行結果です。
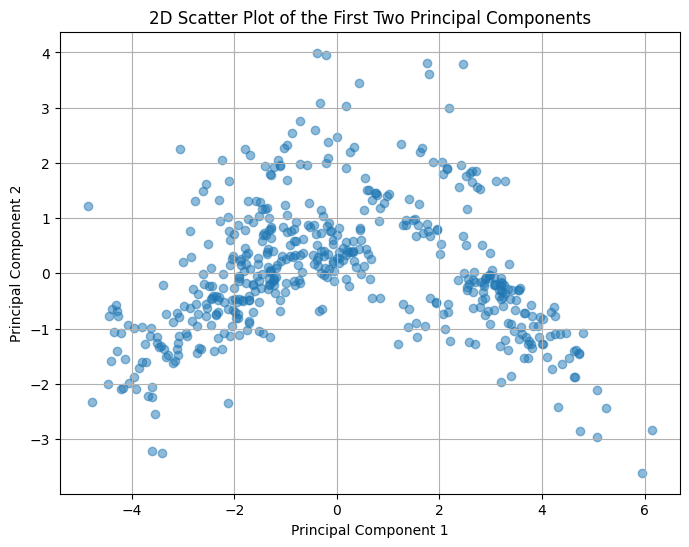
データが2次元または3次元空間にどのように分布しているかを観察し、クラスターやパターンを視覚的に確認します。
ローディングスコアプロット(負荷量プロット)
ローディングスコア(負荷量)は、各変数が主成分にどれだけ寄与しているかを示します。
以下、コードです。
# ローディングスコアの表示
loadings = pd.DataFrame(
pca.components_.T,
columns=[f'PC{i}' for i in range(1, len(pca.components_) + 1)],
index=X.columns)
print(loadings)
以下、実行結果です。
PC1 PC2 PC3 PC4 PC5 PC6 PC7 \
CRIM 0.250951 -0.315252 0.246566 0.061771 0.082157 -0.219660 0.777607
ZN -0.256315 -0.323313 0.295858 0.128712 0.320617 -0.323388 -0.274996
INDUS 0.346672 0.112493 -0.015946 0.017146 -0.007811 -0.076138 -0.339576
CHAS 0.005042 0.454829 0.289781 0.815941 0.086531 0.167490 0.074136
NOX 0.342852 0.219116 0.120964 -0.128226 0.136854 -0.152983 -0.199635
RM -0.189243 0.149332 0.593961 -0.280592 -0.423447 0.059267 0.063940
AGE 0.313671 0.311978 -0.017675 -0.175206 0.016691 -0.071709 0.116011
DIS -0.321544 -0.349070 -0.049736 0.215436 0.098592 0.023439 -0.103900
RAD 0.319793 -0.271521 0.287255 0.132350 -0.204132 -0.143194 -0.137943
TAX 0.338469 -0.239454 0.220744 0.103335 -0.130461 -0.192934 -0.314887
PTRATIO 0.204942 -0.305897 -0.323446 0.282622 -0.584002 0.273153 0.002324
B -0.202973 0.238559 -0.300146 0.168498 -0.345607 -0.803455 0.070295
LSTAT 0.309760 -0.074322 -0.267000 0.069414 0.394561 -0.053216 0.087011
PC8 PC9 PC10 PC11 PC12 PC13
CRIM 0.153350 0.260390 0.019369 -0.109644 0.086761 0.045952
ZN -0.402680 0.358137 0.267527 0.262756 -0.071425 -0.080919
INDUS 0.173932 0.644416 -0.363532 -0.303169 -0.113200 -0.251077
CHAS -0.024662 -0.013728 -0.006182 0.013927 -0.003983 0.035922
NOX 0.080121 -0.018522 0.231056 0.111319 0.804323 0.043630
RM -0.326752 0.047898 -0.431420 0.053162 0.152873 0.045567
AGE -0.600823 -0.067562 0.362779 -0.459159 -0.211936 -0.038551
DIS -0.121812 -0.153291 -0.171213 -0.695693 0.390941 -0.018299
RAD 0.080358 -0.470891 0.021909 0.036544 -0.107026 -0.633490
TAX 0.082774 -0.176563 -0.035168 -0.104836 -0.215191 0.720233
PTRATIO -0.317884 0.254428 0.153430 0.174505 0.209599 0.023398
B -0.004923 -0.044898 -0.096515 0.019275 0.041723 -0.004463
LSTAT -0.424353 -0.195221 -0.600711 0.271382 0.055226 0.024432
この結果を確認することで、例えば、主成分1(PC1)がどの変数に最も強く影響されているかを理解できます。
これにより、主成分1がデータのどの側面を反映しているのかを把握できます。
ここで、視覚化するローディングスコアプロットを作成します。
以下、コードです。第1主成分と第2主成分の負荷量をプロットしています。
# ローディングスコアプロット
loadings = pd.DataFrame(
pca.components_.T,
columns=[f'PC{i}' for i in range(1, len(pca.components_) + 1)],
index=X.columns)
plt.figure(figsize=(12, 6))
# PC1のローディングスコア
plt.subplot(1, 2, 1)
plt.bar(loadings.index, loadings['PC1'], alpha=0.7)
plt.ylabel('Loading Scores')
plt.title('Loading Scores for Principal Component 1')
plt.xticks(rotation=90)
# PC2のローディングスコア
plt.subplot(1, 2, 2)
plt.bar(loadings.index, loadings['PC2'], alpha=0.7)
plt.ylabel('Loading Scores')
plt.title('Loading Scores for Principal Component 2')
plt.xticks(rotation=90)
plt.tight_layout()
plt.show()
以下、実行結果です。
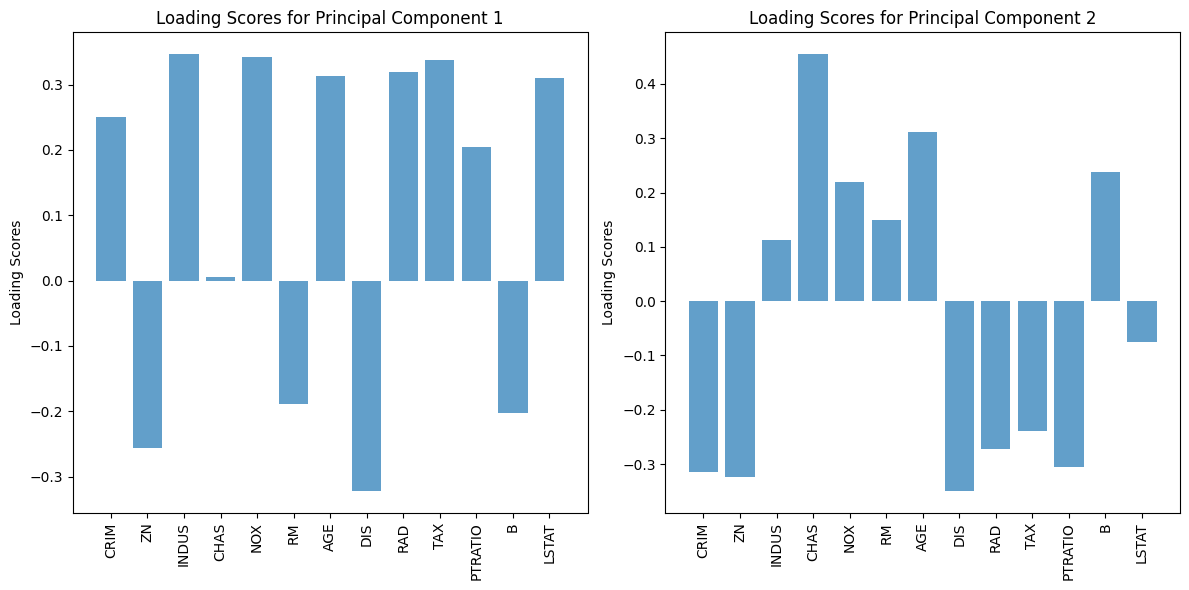
このプロットでは、各変数が特定の主成分にどの程度寄与しているかを視覚的に示します。
これにより、データの特徴が主成分分析によってどのように要約されるかを理解できます。
バイプロットの作成
バイプロットは、各変数が主成分にどのように寄与しているかを示すための強力な可視化手法で、成分散布図に負荷量の情報をプロットしたものです。
以下、コードです。横軸が第1主成分、縦軸が第2主成分です。
# バイプロットの作成
plt.figure(figsize=(8, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], alpha=0.5)
scale_factor = 10 # スケールファクター
for i, feature in enumerate(X.columns):
plt.arrow(
0, 0,
pca.components_[0, i] * scale_factor,
pca.components_[1, i] * scale_factor,
color='r', alpha=0.5)
plt.text(
pca.components_[0, i] * scale_factor * 1.05,
pca.components_[1, i] * scale_factor * 1.05,
feature,
color='g',
ha='center',
va='center')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('Biplot of the First Two Principal Components')
plt.grid()
plt.show()
以下、実行結果です。
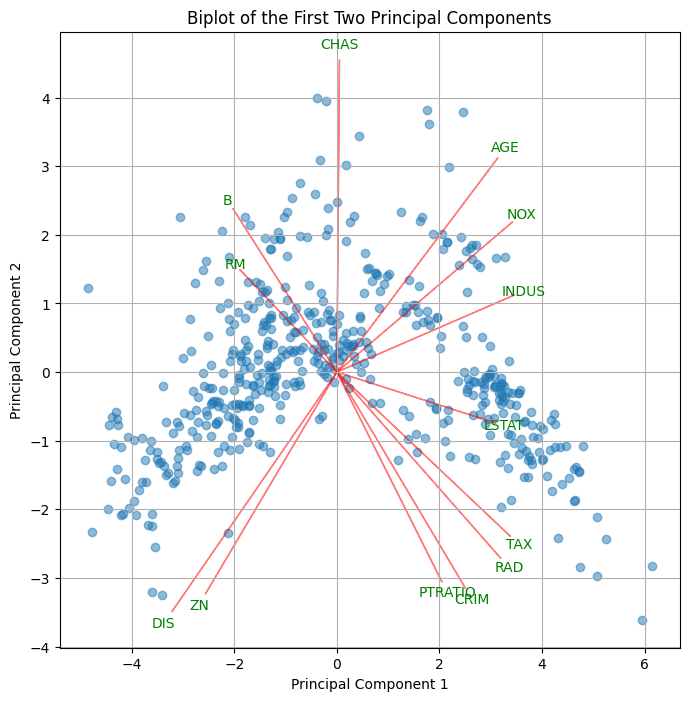
このプロットでは、各変数がどの程度の寄与をしているか、および変数間の相関関係を視覚化できます。
主成分分析の活用と注意点
活用例
主成分分析は、ビジネスや研究においてさまざまな形で活用されています。
データの次元削減
- PCAは、多次元データの次元を削減しつつ、重要な情報を保持するのに非常に有効です。
- 例えば、マーケティングデータや生物学的データなど、特徴量が非常に多い場合にPCAを適用することで、モデルのトレーニング時間を短縮し、過学習を防ぐことができます。
特徴選択
- PCAは、データ中の重要な変数を特定するのにも役立ちます。
- 主成分のローディングスコアを分析することで、どの変数がデータの分散に最も寄与しているかを特定し、それらを予測モデルに組み込むことでモデルの精度を向上させることができます。
可視化による洞察
- PCAを用いた可視化(例えば2D散布図やバイプロット)は、データセット内の隠れたパターンやクラスターを発見するのに有効です。
- 例えば、顧客セグメンテーションを行う際に、顧客の購買行動を主成分に基づいてプロットすることで、異なる顧客グループを視覚的に識別できます。
注意点と限界
PCAには強力な利点がありますが、使用する際にはいくつかの注意点と限界があります。
非線形な関係には不適
- PCAは線形手法であるため、変数間に非線形な関係が存在する場合、うまく機能しないことがあります。
- このような場合には、他の次元削減手法(例えば、カーネルPCAやt-SNE)を検討する必要があります。
主成分の解釈が難しい場合がある
- 主成分は元の変数の線形結合であるため、主成分自体の意味を直接解釈するのが難しい場合があります。
- 特に、複数の変数が似たような重みを持つ場合、主成分の意味を特定するのが困難になることがあります。
まとめ
今回は、主成分分析(PCA)の基本概念から、主成分分析の結果のビジュアル化までをお話ししました。
Boston Housingデータセットを使い、PCAの実行手順や結果の解釈方法を具体的に示し、ローディングスコアやバイプロットを活用して、データの構造を明らかにする方法を紹介しました。
PCAがデータの次元削減や解析を通じて、より深い洞察を得るための強力なツールであることが理解できたと思います。
PCAを活用することで、複雑なデータをシンプルにし、より良い意思決定に役立てることができるでしょう。