前回までに、回帰分析でモデルを作り、統計的検定で係数の有意性を確認しました。
しかし、「統計的に有意」なモデルが必ずしも「良いモデル」とは限りません。
たとえば、気温から売上を予測するモデルが統計的に有意でも、実際の売上の変動の10%しか説明できないなら、予測には使いにくいでしょう。
また、モデルの前提条件が満たされていなければ、得られた結果の信頼性も疑わしくなります。
本記事では、回帰モデルの「成績表」を作成する方法を紹介します。
モデルがデータをどの程度うまく説明できているか、前提条件は満たされているか、問題のあるデータ点はないか、これらを体系的に評価する手法を身につけていきます。
Contents
- 前回と同じサンプルデータ
- サンプルデータ生成
- 回帰分析の実行
- ANOVA(分散分析)
- 変動分解
- 変動の分解定理
- 変動の計算
- 変動の視覚化
- F検定とF統計量
- F検定の必要性
- F統計量の定義と意味
- F検定の仮説設定
- F分布と検定の実施
- 分散分析表
- 決定係数(R²)
- 決定係数の定義と意味
- 自由度調整済み決定係数
- statsmodelsによる回帰分析
- 回帰診断(前提条件の確認)
- ガウス・マルコフの仮定と正規性
- 線形性の診断
- 期待値ゼロの確認
- 等分散性の診断
- 無相関性の診断
- 完全共線性の確認
- 正規性の診断
- 外れ値と影響力のある点の検出
- 問題のあるデータ点の種類
- 標準化残差による外れ値の検出
- てこ比(Leverage)
- Cook’s Distance
- 回帰診断の総合評価
- 診断結果の解釈と活用
- 第1段階:モデル全体の評価
- 第2段階:前提条件の確認
- 第3段階:外れ値と影響力のある点の確認
- 診断結果が良くないときの対策
- 線形性に問題があるとき
- 等分散性に問題があるとき
- 正規性に問題があるとき
- 外れ値・影響力のある点が見つかったとき
- モデル改善の基本的な考え方
- まとめ
前回と同じサンプルデータ
サンプルデータ生成
前回のデータと同じサンプルデータを生成します。
# 数値計算とデータ処理のためのライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from scipy import stats
# 再現性のための乱数シード固定
np.random.seed(42)
# データ生成のパラメータ設定
n = 30 # サンプル数(30日間の営業データ)
# 真のモデルのパラメータ
TRUE_BETA_0 = -150 # 真の切片
TRUE_BETA_1 = 10 # 真の傾き(気温1℃上昇で10杯増加)
SIGMA = 15 # 誤差の標準偏差
print("真のモデル設定:")
print(f" y = {TRUE_BETA_0} + {TRUE_BETA_1}x + ε")
print(f" 誤差の標準偏差 σ = {SIGMA}")
# 説明変数:気温データの生成
# 夏季(7月)の東京の気温分布を想定
mu_temp = 27.5 # 平均気温
sigma_temp = 3.5 # 気温の標準偏差
# 正規分布に従う乱数を生成
temp = np.random.normal(
mu_temp, # 平均
sigma_temp, # 標準偏差
n, # サンプル数
)
# 気温を現実的な範囲に制限
temp = np.clip(
temp, # 制限対象の配列
20, # 下限値
35 # 上限値
)
print(f"\n気温データ生成:")
print(f" 平均: {np.mean(temp):.1f}℃")
print(f" 標準偏差: {np.std(temp):.1f}℃")
print(f" 範囲: {np.min(temp):.1f}℃ ~ {np.max(temp):.1f}℃")
# 誤差項の生成(平均0、標準偏差SIGMAの正規分布に従う)
epsilon = np.random.normal(
0, # 平均
SIGMA, # 標準偏差
n # サンプル数
)
# 真の関係式による理論値
ice_coffee_sales_true = TRUE_BETA_0 + TRUE_BETA_1 * temp
# 観測値(理論値+ノイズ)
ice_coffee_sales = ice_coffee_sales_true + epsilon
print(f"\n売上データ生成:")
print(f" 理論値の平均: {np.mean(ice_coffee_sales_true):.1f}杯")
print(f" 観測値の平均: {np.mean(ice_coffee_sales):.1f}杯")
print(f" ノイズの影響: {np.mean(epsilon):.1f}杯(平均)")
# データフレームの作成
data = pd.DataFrame({
'日付': pd.date_range(
'2024-07-01', # 開始日
periods=n # 期間
),
'気温': temp,
'理論値': ice_coffee_sales_true,
'売上': ice_coffee_sales
})
# 最初の5行を表示
print("\n生成したデータ(最初の5日間):")
print(data.head())
以下、実行結果です。
真のモデル設定:
y = -150 + 10x + ε
誤差の標準偏差 σ = 15
気温データ生成:
平均: 26.8℃
標準偏差: 3.1℃
範囲: 20.8℃ ~ 33.0℃
売上データ生成:
理論値の平均: 118.4杯
観測値の平均: 116.6杯
ノイズの影響: -1.8杯(平均)
生成したデータ(最初の5日間):
日付 気温 理論値 売上
0 2024-07-01 29.238500 142.384995 133.359396
1 2024-07-02 27.016075 120.160749 147.944922
2 2024-07-03 29.766910 147.669099 147.466640
3 2024-07-04 32.830604 178.306045 162.440381
4 2024-07-05 26.680463 116.804632 129.142806
回帰分析の実行
前回と同じ回帰分析(単回帰)を実行します。
# データの準備
x = data['気温'].values
y = data['売上'].values
n = len(x)
# 平均の計算
x_bar = np.mean(x)
y_bar = np.mean(y)
# 平均からの偏差の計算
x_dev = x - x_bar
y_dev = y - y_bar
# 偏差積和・偏差平方和の計算
S_xy = np.sum(x_dev * y_dev) # 偏差積和
S_xx = np.sum(x_dev**2) # xの偏差平方和
# 回帰係数の計算
beta_1_hat = S_xy / S_xx # 傾きの推定値
beta_0_hat = y_bar - beta_1_hat * x_bar # 切片の推定値
print(f"推定した回帰式: ŷ = {beta_0_hat:.2f} + {beta_1_hat:.2f}x")
以下、実行結果です。
推定した回帰式: ŷ = -163.58 + 10.44x
ANOVA(分散分析)
変動分解
変動の分解定理
回帰分析の本質は、データの「ばらつき(変動)」を説明することです。
データがなぜばらつくのか、その理由を数学的に解明しようとするのが回帰分析の目的です。
このばらつきを理解するために、まず「変動」という概念を数学的に定義しましょう。
変動とは、各データ点がある基準値(通常は平均値)からどれだけ離れているかを測る指標です。
変動は次の3つの成分に分解できます。
- 全変動(SST: Total Sum of Squares)
- 回帰変動(SSR: Regression Sum of Squares)
- 残差変動(SSE: Error Sum of Squares)
全変動(SST: Total Sum of Squares)は、データ全体がその平均値からどれだけばらついているかを表します。これは、何も予測をしない場合の、データの自然なばらつきを表しています。
$$
SST = \sum_{i=1}^n (y_i – \bar{y})^2
$$
回帰変動(SSR: Regression Sum of Squares)は、回帰モデルによって説明される変動です。つまり、モデルの予測値が平均からどれだけ変動しているかを表します。これは、モデルが「うまく説明できた」部分です。
$$
SSR = \sum_{i=1}^n (\hat{y}_i – \bar{y})^2
$$
残差変動(SSE: Error Sum of Squares)は、モデルで説明できない変動です。実測値と予測値の差を表し、これは「説明できなかった」部分、つまり誤差です。
$$
SSE = \sum_{i=1}^n (y_i – \hat{y}_i)^2
$$
ちなみに、y_i は i 番目の実測値(実際に観測された売上)、\bar{y}は y の平均値(全データの平均売上)、\hat{y}_i は i 番目の予測値(モデルが予測した売上)を表します。
これら3つの変動には、次の関係が成り立ちます。
$$
SST = SSR + SSE
$$
この式は「全体のばらつき(SST) = モデルで説明できる部分(SSR) + 説明できない部分(SSE)」という意味を持ち、「変動の分解定理」と呼ばれます。
変動の計算
変動の分解を実際に計算し、分解定理を確認します。それぞれの変動がどのような意味を持つのかも理解していきましょう。
# 予測値の計算
y_hat = beta_0_hat + beta_1_hat * x
# 変動の分解
SST = np.sum((y - y_bar)**2) # 全変動
SSR = np.sum((y_hat - y_bar)**2) # 回帰変動
SSE = np.sum((y - y_hat)**2) # 残差変動
print("変動の分解:")
print(f" 全変動 (SST) = {SST:,.2f}")
print(f" 回帰変動 (SSR) = {SSR:,.2f}")
print(f" 残差変動 (SSE) = {SSE:,.2f}")
print(f"\n割合:")
print(f" 回帰変動の割合: {SSR/SST*100:.1f}%")
print(f" 残差変動の割合: {SSE/SST*100:.1f}%")
以下、実行結果です。
変動の分解: 全変動 (SST) = 36,954.46 回帰変動 (SSR) = 31,352.86 残差変動 (SSE) = 5,601.60 割合: 回帰変動の割合: 84.8% 残差変動の割合: 15.2%
回帰変動の割合が大きいということは、モデルがデータのばらつきの大部分を説明できているということです。これは良いモデルの証拠です。
変動の視覚化
変動の分解を視覚的に理解することは、概念を深く理解する上で非常に重要です。グラフを見ることで、各変動が具体的に何を表しているのかが明確になります。
変動の3要素を視覚的に表示します。各グラフの縦線が、それぞれの変動を表しています。
# 変動の視覚化
fig, axes = plt.subplots(3, 1, figsize=(10, 15))
#
# 全変動(SST):データが平均からどれだけ離れているか
#
# 実測値のプロット
axes[0].scatter(
x, y,
alpha=0.6, s=50,
label='実測値'
)
# 平均値のプロット
axes[0].axhline(
y_bar,
color='green', linestyle='--',
label=f'平均 [latex]ȳ[/latex]={y_bar:.1f}'
)
# 実測値と平均値の差のプロット
for i in range(n):
axes[0].plot(
[x[i], x[i]], [y[i], y_bar],
'gray', alpha=0.3, linewidth=1
)
axes[0].set_xlabel('気温')
axes[0].set_ylabel('売上')
axes[0].set_title(f'全変動 SST = {SST:.1f}\n(実測値と平均の差)')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
#
# 回帰変動(SSR):モデルが説明できる変動
#
# 予測値のプロット
axes[1].scatter(x, y_hat, alpha=0.6, color='red', s=50, label='予測値')
# 平均値のプロット
axes[1].axhline(y_bar, color='green', linestyle='--', label=f'平均 [latex]ȳ[/latex]={y_bar:.1f}')
# 回帰直線のプロット
axes[1].plot(x, y_hat, 'r-', alpha=0.5, label='回帰直線')
# 予測値と平均値の差のプロット
for i in range(n):
axes[1].plot(
[x[i], x[i]], [y_hat[i], y_bar],
'red', alpha=0.3, linewidth=1
)
axes[1].set_xlabel('気温')
axes[1].set_ylabel('売上')
axes[1].set_title(f'回帰変動 SSR = {SSR:.1f}\n(予測値と平均の差)')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
#
# 残差変動(SSE):モデルが説明できない変動
#
# 実測値のプロット
axes[2].scatter(
x, y,
alpha=0.6, s=50,
label='実測値'
)
# 回帰直線のプロット
axes[2].plot(
x, y_hat,
'r-', alpha=0.5,
label='回帰直線'
)
# 実測値と予測値の差のプロット
for i in range(n):
axes[2].plot(
[x[i], x[i]], [y[i], y_hat[i]],
'blue', alpha=0.3, linewidth=1
)
axes[2].set_xlabel('気温')
axes[2].set_ylabel('売上')
axes[2].set_title(f'残差変動 SSE = {SSE:.1f}\n(実測値と予測値の差)')
axes[2].legend()
axes[2].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
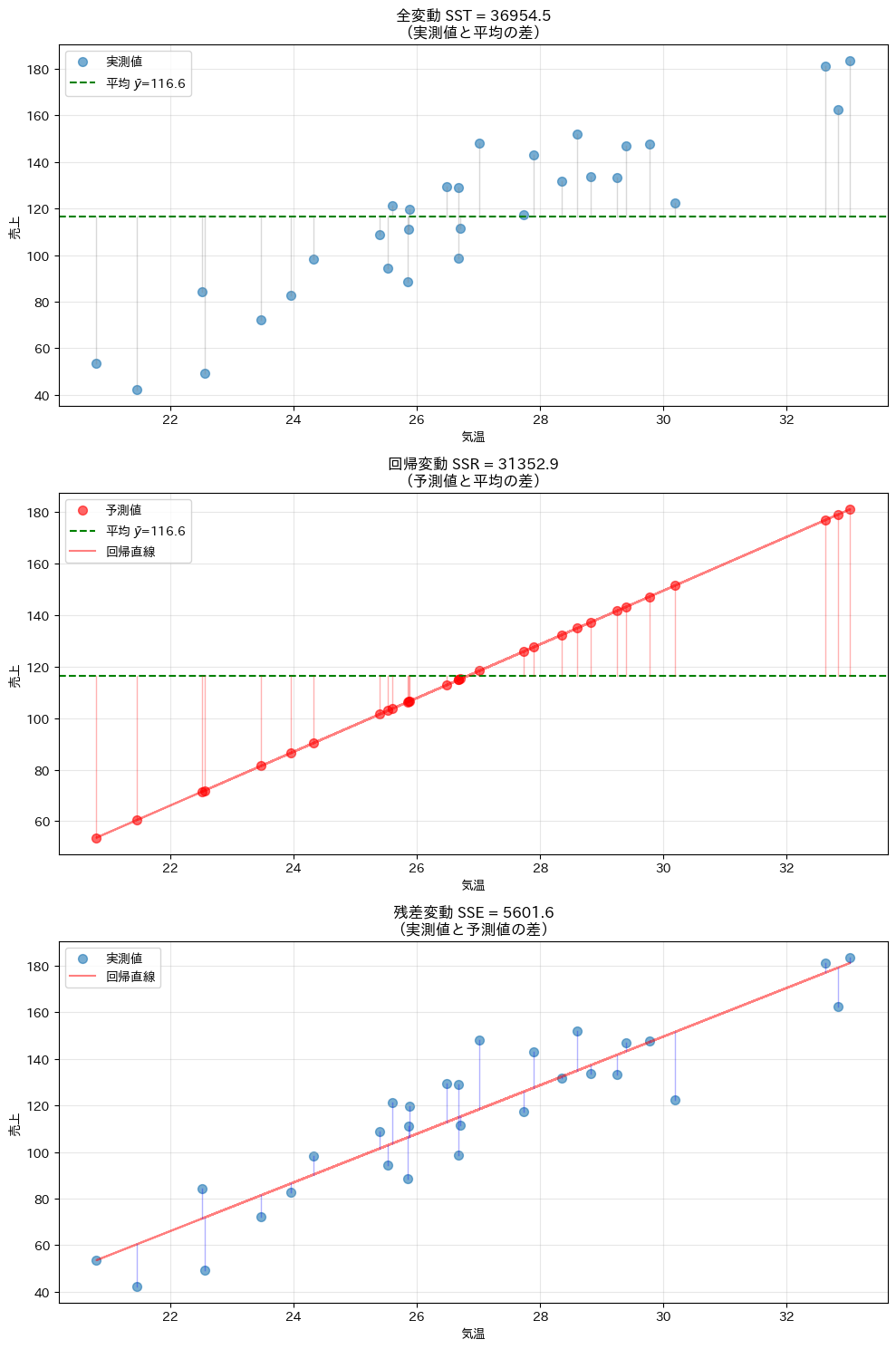
これらのグラフから、変動の分解が何を意味するのかが視覚的に理解できます。
一番上の図の縦線(灰色)は全体のばらつきを、上から二番目の図の縦線(赤)はモデルが説明できた部分を、一番下の図の縦線(青)は説明できなかった部分を表しています。縦線が短いほど、その変動が小さいことを意味します。
F検定とF統計量
F検定の必要性
ここで重要な疑問が生じます。「モデルが説明する変動(SSR)は、本当に意味があるのか、それとも偶然なのか?」この疑問に答えるのがF検定です。
もし気温と売上に全く関係がなかったら、回帰直線はほぼ水平(傾きが0に近い)になります。この場合、SSRは非常に小さくなります。
逆に、気温と売上に強い関係があれば、SSRは大きくなります。
F検定は、観測されたSSRが「偶然では起こりにくいほど大きい」かどうかを統計的に判定します。
F統計量の定義と意味
F統計量は、モデルが説明する変動と説明できない変動の比を表す指標です。
ただし、単純に変動を比較するのではなく、それぞれを自由度で割った「平均的な変動」を比較します。
まず、自由度(degrees of freedom, df)について説明しましょう。
自由度とは、「自由に値を決められる個数」のことです。
たとえば、5つの数の合計が100と決まっている場合、4つの数を自由に決められますが、5つ目は自動的に決まります。この場合、自由度は4です。
回帰分析では、以下の自由度を使います。
- 全体の自由度:n - 1(平均を計算したため1つ減る)
- 回帰の自由度:p(説明変数の数、単回帰では1)
- 誤差の自由度:n - p - 1(p + 1 個のパラメータを推定したため)
平均平方(Mean Square)は、変動を自由度で割った値です。
- 回帰の平均平方:MSR = \displaystyle \frac{SSR}{p}
- 誤差の平均平方:MSE = \displaystyle \frac{SSE}{n-p-1}
そして、F統計量は次のように定義されます。
$$
F = \frac{MSR}{MSE} = \frac{\displaystyle \frac{SSR}{p}}{\displaystyle \frac{SSE}{n-p-1}}
$$
この式の意味を考えてみましょう。
分子(MSR)は「モデルが説明する平均的な変動」、分母(MSE)は「説明できない平均的な変動(誤差)」です。
したがって、F統計量は値が大きいほどモデルの説明力が高いことを示します。
F検定の仮説設定
F検定では、以下の仮説を設定します。
帰無仮説(H_0):すべての回帰係数が0である(モデルに予測力がない)
$$
H_0: \beta_1 = 0
$$
対立仮説(H_1):少なくとも1つの回帰係数が0でない(モデルに予測力がある)
$$
H_1: \beta_1 \neq 0
$$
単回帰の場合、これは傾きが0かどうかの検定と同じですが、重回帰分析では複数の係数を同時に検定することになります。
F分布と検定の実施
帰無仮説が正しいと仮定した場合、F検定で用いられる F統計量は F分布に従います。F分布は、二つのカイ二乗分布の比から導かれる確率分布であり、分子側と分母側に対応する二つの自由度によって、その形が決まります。
F分布は変動の比を表す分布であるため、値は常に正となり、分布の形は右に歪んだものになります。特に右側に長い裾を持つ点が特徴で、自由度が小さい場合ほど歪みが大きくなります。自由度が大きくなるにつれて分布は次第に集中し、極端に大きな値が出にくくなります。
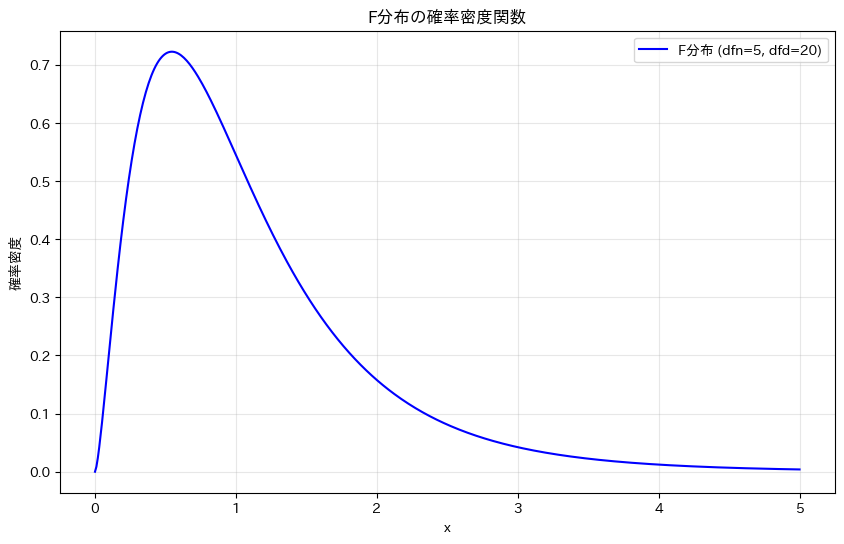
F検定では、このF分布を基準として、観測された F統計量がどの程度起こりにくいかを評価します。
具体的には、まず回帰モデルから F統計量を計算し、その値以上が F分布のもとで得られる確率、すなわち p値を求めます。
そして、その p値があらかじめ定めた有意水準(通常は 0.05)より小さい場合には、帰無仮説を棄却し、モデル全体として統計的に有意であると判断します。
このようにF検定は、回帰モデルが偶然によるものではなく、全体として意味のある説明力を持っているかどうかを判断するための検定です。
分散分析表
分散分析表は、これまでに説明した変動の分解とF検定の結果を、体系的にまとめた表です。この表を見ることで、モデルの性能を総合的に評価できます。
分散分析表を作成し、F検定を実施します。
# 分散分析表(ANOVA)の作成
# 自由度の計算
df_regression = 1 # 回帰の自由度(説明変数の数)
df_error = n - 2 # 誤差の自由度(n - パラメータ数)
df_total = n - 1 # 全体の自由度
# 平均平方の計算
MSR = SSR / df_regression # 回帰の平均平方
MSE = SSE / df_error # 誤差の平均平方
# F統計量の計算
F_statistic = MSR / MSE
# p値の計算(F分布を使用)
p_value_F = 1 - stats.f.cdf(F_statistic, df_regression, df_error)
# 分散分析表の作成
print("="*70)
print("分散分析表(ANOVA: Analysis of Variance)")
print("="*70)
print(f"{'要因'} {'平方和':>7} {'自由度':>7} {'平均平方':>7} {'F値':>8} {'p値':>9}")
print("-"*70)
print(f"{'回帰'} {SSR:>10.2f} {df_regression:>7} {MSR:>12.2f} {F_statistic:>10.3f} {p_value_F:>10.6f}")
print(f"{'誤差'} {SSE:>10.2f} {df_error:>7} {MSE:>12.2f}")
print(f"{'全体'} {SST:>10.2f} {df_total:>7}")
print("="*70)
以下、実行結果です。
====================================================================== 分散分析表(ANOVA: Analysis of Variance) ====================================================================== 要因 平方和 自由度 平均平方 F値 p値 ---------------------------------------------------------------------- 回帰 31352.86 1 31352.86 156.720 0.000000 誤差 5601.60 28 200.06 全体 36954.46 29 ======================================================================
分散分析表の各要素について説明します。
平方和(Sum of Squares)の列は、各変動の大きさを示します。SST = SSR + SSE という関係が成立していることを確認できます。
自由度(Degrees of Freedom)の列は、各変動に対応する自由度を示します。全体の自由度 = 回帰の自由度 + 誤差の自由度という関係があります。
平均平方(Mean Square)の列は、平方和を自由度で割った値です。これは「単位自由度あたりの変動」を表し、異なる要因の変動を公平に比較できます。
F値は、回帰の平均平方を誤差の平均平方で割った値です。この値が1に近い場合、モデルは平均値による予測と大差ないことを意味します。値が大きいほど、モデルの説明力が高いことを示します。
p値は、帰無仮説が正しいと仮定したときに、観測されたF値以上の値が得られる確率です。この値が小さいほど、モデルの有意性が高いことを示します。
今回の結果はF統計量が大きく、p値が非常に小さいことから、モデル全体が統計的に有意であることが分かります。これは、気温が売上を予測する上で確かに有用な変数であることを示しています。
決定係数(R²)
決定係数の定義と意味
決定係数(R²)は、モデルがデータの変動をどの程度説明できているかを表す、最も重要な指標の一つです。
決定係数は次の式で定義されます。
$$
R^2 = \frac{SSR}{SST} = 1 – \frac{SSE}{SST}
$$
SSR/SST は「全変動のうち、モデルが説明できる部分の割合」を表します。これは、全体のばらつきの中で、モデルがうまく捉えた部分の比率です。
- R^2 = 0:モデルに予測力がない(すべての予測値が平均値と同じ)
- R^2 = 1:完全な予測(すべてのデータ点が回帰直線上に乗る)
- 0 < R^2 < 1:モデルが全変動の R^2 \times 100% を説明している
たとえば、R^2 = 0.8 の場合、「モデルはデータの変動の80%を説明できており、残り20%は説明できない」と解釈します。
決定係数を計算します。
# 決定係数の計算
R2 = SSR / SST
R2_alternative = 1 - SSE/SST # 別の計算方法
print("決定係数(Coefficient of Determination):")
print(f" R² = SSR/SST = {SSR:.1f}/{SST:.1f} = {R2:.4f}")
print(f" R² = 1 - SSE/SST = 1 - {SSE:.1f}/{SST:.1f} = {R2_alternative:.4f}")
以下、実行結果です。
決定係数(Coefficient of Determination): R² = SSR/SST = 31352.9/36954.5 = 0.8484 R² = 1 - SSE/SST = 1 - 5601.6/36954.5 = 0.8484
R^2の値から、モデルの説明力を客観的に評価できます。この例では、モデルがデータの変動の大部分を説明できていることが分かります。
自由度調整済み決定係数
決定係数には重要な問題があります。
それは、意味のない説明変数を追加しても、決定係数は必ず増加(または不変)するという性質です。これは、「過学習」につながる可能性があります。
この問題を解決するために導入されたのが自由度調整済み決定係数(Adjusted R²)です。これは、説明変数の数に応じてペナルティを課すことで、より公平なモデル比較を可能にします。
自由度調整済み決定係数は次の式で計算されます。
$$
R^2_{adj} = 1 – \frac{\displaystyle\frac{SSE}{n-p-1}}{\displaystyle\frac{SST}{n-1}} = 1 – (1-R^2)\frac{n-1}{n-p-1}
$$
この式を理解するために、分子と分母を見てみましょう。分子の SSE/(n-p-1) は誤差の平均平方(MSE)、分母の SST/(n-1) は全変動の平均平方です。
つまり、自由度調整済み決定係数は、単純な変動の比ではなく、平均平方の比を使って計算されています。
自由度調整済み決定係数を計算し、通常の決定係数と比較します。
# 自由度調整済み決定係数
p = 1 # 説明変数の数
R2_adj = 1 - (1 - R2) * (n - 1) / (n - p - 1)
print("自由度調整済み決定係数:")
print(f" R²_adj = {R2_adj:.4f}")
print(f" 通常のR² = {R2:.4f}")
以下、実行結果です。
自由度調整済み決定係数: R²_adj = 0.8430 通常のR² = 0.8484
自由度調整済みR^2は、異なる説明変数の数を持つモデルを比較する際に特に重要です。
statsmodelsによる回帰分析
これまで手動で計算してきた統計量は、実はPythonのstatsmodelsライブラリを使えば簡単に得ることができます。statsmodelsは統計分析に特化したライブラリで広く使用されています。
statsmodelsの主な利点は、回帰係数とその標準誤差、t値、p値、信頼区間をすべて一度に計算してくれます。また、決定係数、自由度調整済み決定係数、F統計量なども自動的に計算されます。さらに、残差の診断に必要な統計量も提供してくれます。
statsmodelsを使って回帰分析を実行し、包括的な結果を得ます。
import statsmodels.api as sm # データの準備(切片項を追加) X_sm = sm.add_constant(x) # 定数項(切片)を追加 y_sm = y # 線形回帰モデルの作成と推定 model = sm.OLS(y_sm, X_sm) results = model.fit() # サマリーの表示 print(results.summary())
以下、実行結果です。
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.848
Model: OLS Adj. R-squared: 0.843
Method: Least Squares F-statistic: 156.7
Date: Fri, 19 Dec 2025 Prob (F-statistic): 5.45e-13
Time: 05:06:45 Log-Likelihood: -121.01
No. Observations: 30 AIC: 246.0
Df Residuals: 28 BIC: 248.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -163.5796 22.529 -7.261 0.000 -209.728 -117.431
x1 10.4382 0.834 12.519 0.000 8.730 12.146
==============================================================================
Omnibus: 0.254 Durbin-Watson: 1.895
Prob(Omnibus): 0.881 Jarque-Bera (JB): 0.447
Skew: -0.085 Prob(JB): 0.800
Kurtosis: 2.426 Cond. No. 236.
==============================================================================
statsmodelsのサマリーには、これまで手動で計算してきたすべての統計量が含まれています。一度にすべての情報が得られるため、非常に効率的です。
この出力結果は、大きく分けて「モデル全体の評価」「回帰係数ごとの検定結果」「モデル診断の情報」の3つの観点から読み取ることができます。
まず、表の上段の「モデル全体の評価」です。
============================================================================== Dep. Variable: y R-squared: 0.848 Model: OLS Adj. R-squared: 0.843 Method: Least Squares F-statistic: 156.7 Date: Fri, 19 Dec 2025 Prob (F-statistic): 5.45e-13 Time: 05:06:45 Log-Likelihood: -121.01 No. Observations: 30 AIC: 246.0 Df Residuals: 28 BIC: 248.8 Df Model: 1 Covariance Type: nonrobust ==============================================================================
まず、R-squared(決定係数)は、回帰モデルが目的変数の変動をどの程度説明できているかを示しています。ここでは (R^2 = 0.848) となっており、売上の変動の約85%が気温によって説明されていることを意味します。
また、Adj. R-squared(自由度調整済み決定係数)は説明変数の数を考慮した指標であり、今回のように説明変数が1つの場合には、R-squaredとほぼ同じ値になります。
F-statistic と Prob (F-statistic) は、モデル全体の有意性を検定する F検定の結果です。F統計量が 156.7 と非常に大きく、その p値が (5.45e-13) と極めて小さいことから、「この回帰モデルは、説明変数をまったく使わないモデルと比べて、有意に予測力がある」と判断できます。つまり、モデル全体として統計的に有意であることが確認できます。
次に、中央の表は「回帰係数ごとの検定結果」です。
============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const -163.5796 22.529 -7.261 0.000 -209.728 -117.431 x1 10.4382 0.834 12.519 0.000 8.730 12.146 ==============================================================================
coef は回帰係数の推定値を表し、const は切片、x1 は気温に対応する傾きです。ここでは、気温の傾きが約 10.4382 となっており、「気温が 1 度上昇すると、売上が平均して約 10 杯増加する」ことを意味します。
std err は回帰係数の標準誤差であり、推定値の不確実性の大きさを表します。t は t統計量、P>|t| はその p値です。気温に対応する x1 の p値は 0.000(表示上はほぼ0)となっており、有意水準 5% どころか 1% を大きく下回っています。このことから、「気温と売上の関係は統計的に有意である」と判断できます。
さらに、右端の [0.025, 0.975] は 95% 信頼区間を示しています。この区間が 0 を含んでいない点からも、傾きが 0 ではないという結論が裏付けられます。
最後に、表の下段は「モデル診断の情報」で残差に関する診断指標がまとめられています。
============================================================================== Omnibus: 0.254 Durbin-Watson: 1.895 Prob(Omnibus): 0.881 Jarque-Bera (JB): 0.447 Skew: -0.085 Prob(JB): 0.800 Kurtosis: 2.426 Cond. No. 236. ==============================================================================
Durbin-Watson 統計量は誤差の自己相関を確認するための指標で、2 に近い値であれば大きな問題はないとされます。ここでは 1.895 と 2 に近く、強い自己相関は見られないと考えられます。
また、Omnibus 検定や Jarque–Bera 検定(帰無仮説:誤差は正規分布に従っている、対立仮説:誤差は正規分布に従っていない)の p値はいずれも比較的大きな値を示しており帰無仮説を棄却できません。この結果から、誤差が正規分布から大きく逸脱しているとは言い切れません。
このように、statsmodels のサマリーを読むことで、回帰係数の有意性、モデル全体の有意性、そして仮定の妥当性までを一度に確認できます。
主要な結果を取り出します。
print(f"【回帰係数】")
print(f" 切片: {results.params[0]:.4f}")
print(f" 傾き: {results.params[1]:.4f}")
print(f"【決定係数】")
print(f" R² = {results.rsquared:.4f}")
print(f" 調整済みR² = {results.rsquared_adj:.4f}")
print(f"【F検定】")
print(f" F統計量 = {results.fvalue:.2f}")
print(f" p値 = {results.f_pvalue:.6f}")
print(f"【回帰係数の検定】")
print(f" 傾きのt値 = {results.tvalues[1]:.3f}")
print(f" 傾きのp値 = {results.pvalues[1]:.6f}")
print(f" 傾きの95%信頼区間 = [{results.conf_int()[1,0]:.3f}, {results.conf_int()[1,1]:.3f}]")
print(f"【残差標準誤差】")
print(f" σ̂ = {np.sqrt(results.mse_resid):.2f}")
以下、実行結果です。
【回帰係数】 切片: -163.5796 傾き: 10.4382 【決定係数】 R² = 0.8484 調整済みR² = 0.8430 【F検定】 F統計量 = 156.72 p値 = 0.000000 【回帰係数の検定】 傾きのt値 = 12.519 傾きのp値 = 0.000000 傾きの95%信頼区間 = [8.730, 12.146] 【残差標準誤差】 σ̂ = 14.14
回帰診断(前提条件の確認)
ガウス・マルコフの仮定と正規性
回帰分析が適切に機能するためには、いくつかの重要な前提条件が満たされている必要があります。これらの前提条件を確認することを回帰診断といいます。
前提条件は以下の6つです。
- 線形性:説明変数と目的変数の関係が線形である
- 期待値ゼロ:誤差項の期待値(平均)が0である
- 等分散性:誤差の分散がすべての観測で一定である
- 無相関性:異なる観測の誤差が互いに相関を持たない
- 完全共線性がない:説明変数間に完全な線形関係がない
- 正規性:誤差項が正規分布に従う(検定や信頼区間に必要)
これらの条件が満たされていない場合、推定値は偏ったり、検定結果が信頼できなくなったりする可能性があります。
それでは、各条件を一つずつ診断していきましょう。
線形性の診断
線形性の仮定は、説明変数と目的変数の関係が直線的であることを要求します。
もし真の関係が曲線的なのに直線で近似してしまうと、予測精度が低下し、係数の解釈も誤ったものになります。
線形性を診断する最も基本的な方法は、残差プロットを見ることです。
残差プロットとは、横軸に予測値や説明変数、縦軸に残差をとった散布図です。
線形性を診断するための複数のプロットを作成します。
# 残差の計算
residuals = y - y_hat
# 線形性の診断プロット
fig, axes = plt.subplots(3, 1, figsize=(10, 15))
# 散布図と回帰直線(線形関係の直接的確認)
axes[0].scatter(x, y, alpha=0.6, s=50)
axes[0].plot(x, y_hat, 'r-', linewidth=2, label='回帰直線')
axes[0].set_xlabel('気温')
axes[0].set_ylabel('売上')
axes[0].set_title('【線形性の診断】散布図\n(点が直線の周りにランダムに散らばっていればOK)')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
# 残差 vs 説明変数
axes[1].scatter(x, residuals, alpha=0.6, s=50)
axes[1].axhline(y=0, color='red', linestyle='--', linewidth=2)
axes[1].set_xlabel('気温(説明変数)')
axes[1].set_ylabel('残差')
axes[1].set_title('【線形性の診断】残差 vs 説明変数\n(水平な帯状に散らばっていればOK)')
axes[1].grid(True, alpha=0.3)
# 残差 vs 予測値
axes[2].scatter(y_hat, residuals, alpha=0.6, s=50)
axes[2].axhline(y=0, color='red', linestyle='--', linewidth=2)
axes[2].set_xlabel('予測値')
axes[2].set_ylabel('残差')
axes[2].set_title('【線形性・等分散性の診断】残差 vs 予測値\n(ランダムに散らばっていればOK)')
axes[2].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
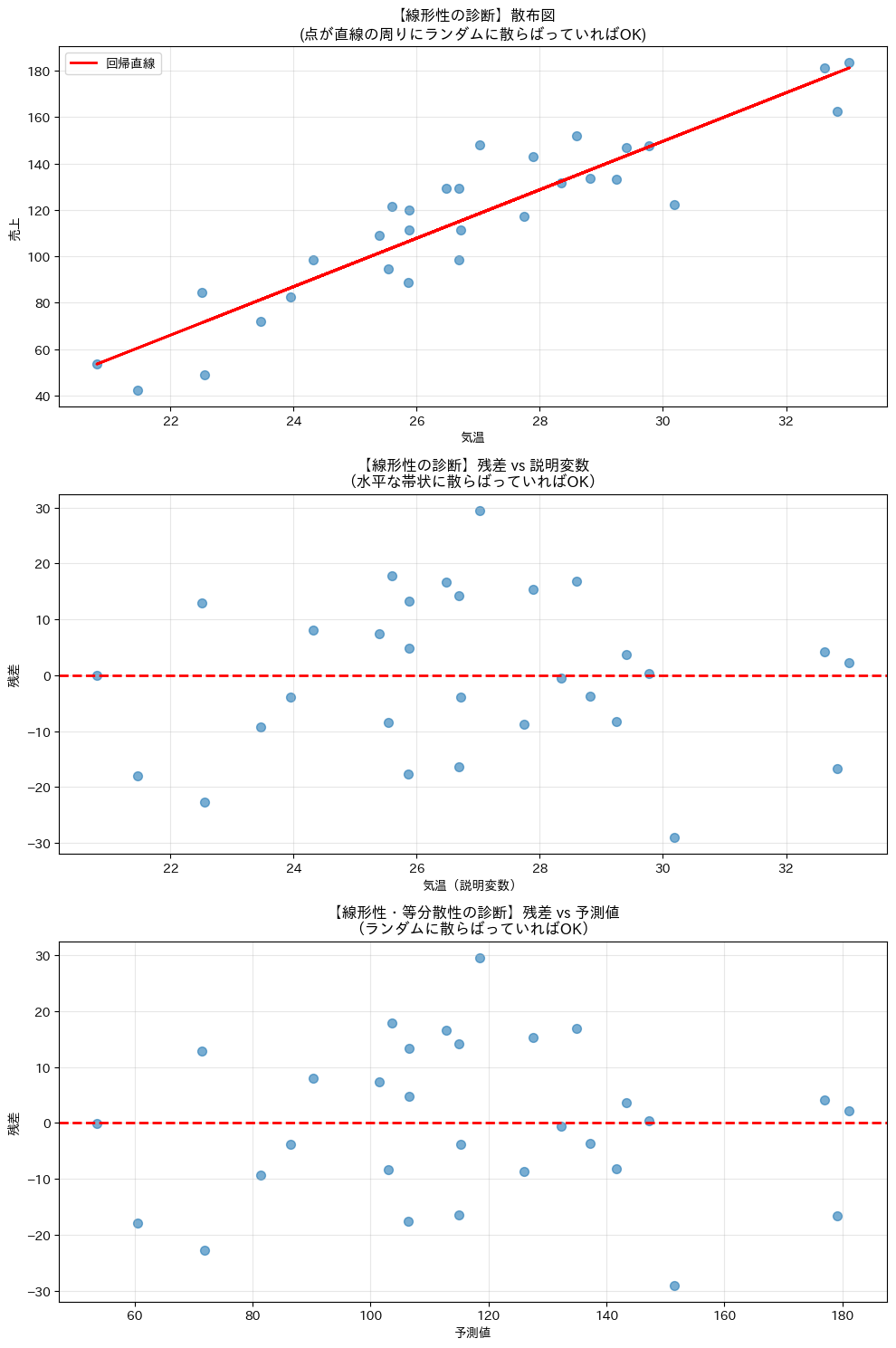
残差プロットに明確なパターンが見られない場合、線形性の仮定は満たされていると判断できます。
もしU字型などのパターンが見られた場合は、変数変換や多項式項の追加を検討する必要があります。
期待値ゼロの確認
期待値ゼロの仮定は、誤差項の平均が0であることを要求します。最小二乗法では、この条件は構造的に満たされるように設計されています。
残差の平均を確認します。
# 残差の平均(期待値)
residual_mean = np.mean(residuals)
print(f"残差の平均: {residual_mean:.10f}")
以下、実行結果です。
残差の平均: 0.0000000000
等分散性の診断
等分散性の仮定は、誤差の分散がすべての観測で一定であることを要求します。この仮定が満たされていない場合、標準誤差の推定が不正確になります。
等分散性を診断するためのScale-Locationプロットを作成します。
import statsmodels.api as sm
# 標準化残差の計算
sigma_hat = np.sqrt(SSE / (n - 2))
stded_res = residuals / sigma_hat
# Scale-Locationプロット
fig, ax = plt.subplots(figsize=(10, 5))
# 予測値と標準化残差の散布図
ax.scatter(
y_hat,
np.sqrt(np.abs(stded_res)),
alpha=0.6,
s=50
)
# 非パラメトリック回帰(LOWESS)を用いてトレンド線を計算
lowess = sm.nonparametric.lowess
trend = lowess(
np.sqrt(np.abs(stded_res)), # 縦軸
y_hat, # 横軸
)
# トレンド線の描画
ax.plot(trend[:, 0], trend[:, 1], 'r-', linewidth=2, label='トレンド')
ax.set_xlabel('予測値')
ax.set_ylabel('√|標準化残差|')
ax.set_title('【等分散性の診断】Scale-Locationプロット')
ax.legend()
plt.show()
以下、実行結果です。
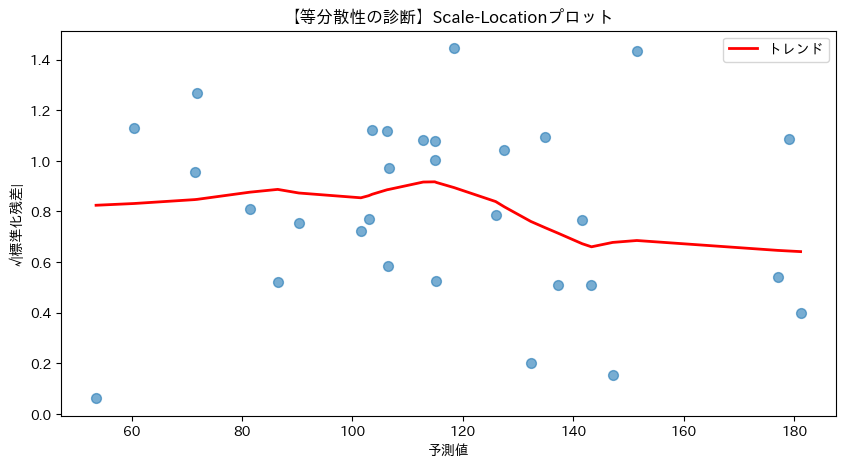
Scale-Locationプロットは、予測値に対する標準化残差の平方根がプロットされたものです。理想的には、プロット上の点がランダムに散らばり予測値の大小に関わらず一定、トレンド線が水平であれば等分散性があると判断できます。
無相関性の診断
無相関性の仮定とは、各観測データの誤差が互いに独立であることを意味します。
簡単に言えば、「あるデータの予測のズレ(残差)が、他のデータのズレと連動していない」という状態です。
この仮定が崩れると、回帰係数の標準誤差が正しく推定されず、p値や信頼区間の信頼性が損なわれます。
実際には、数値指標(Durbin-Watson比など)だけで機械的に判断するのではなく、線形性の診断で利用した残差プロットを確認して、特定の順序やグループにおいて不自然な規則性や偏りが見られないかを総合的に判断します。
完全共線性の確認
完全共線性の仮定は、説明変数間に完全な線形関係がないことを要求します。
単回帰分析では説明変数が1つだけなので、この問題は発生しません。
単回帰では共線性の問題はありませんが、重回帰分析では重要な診断項目となります。
重回帰分析を取り上げたときに紹介します。
正規性の診断
正規性の仮定とは、誤差項が正規分布に従っているという仮定です。
この仮定は回帰係数の推定そのものには必須ではありませんが、t検定・F検定・信頼区間の妥当性を支える前提になります。
正規性の確認では、まず 視覚的な確認を行うのが基本です。特に Q–Qプロット は、残差の分布が正規分布とどの程度近いかを直感的に確認できる代表的な方法です。
Q–Qプロットでは、点が概ね一直線上に並んでいれば、正規性が大きく崩れていないと考えます。
以下では、Q–Qプロットとヒストグラムを用いて、残差の分布を確認します。
# 残差の標準偏差を計算
sigma_hat = np.std(residuals, ddof=1)
# 残差のQ-Qプロットとヒストグラムを可視化
fig, axes = plt.subplots(2, 1, figsize=(10, 10))
#
# Q-Qプロット
#
stats.probplot(
residuals, # データ
dist="norm", # 正規分布に対するプロット
plot=axes[0], # 描画先のAxesオブジェクト
)
axes[0].set_title('Q–Qプロット')
axes[0].grid(True, alpha=0.3)
#
# 残差のヒストグラムと正規分布
#
axes[1].hist(
residuals, # データ
bins=10, # ビンの数
density=True, # 密度を表示
alpha=0.7, # 透明度
color='skyblue', # 塗りつぶし色
edgecolor='black', # 枠線の色
)
# 正規分布のプロット用データを生成
x_val = np.linspace(
residuals.min(), # 最小値
residuals.max(), # 最大値
100, # データ数
)
# 正規分布をプロット
axes[1].plot(
x_val, # 横軸
stats.norm.pdf(x_val, 0, sigma_hat), # 正規分布
'r-', linewidth=2
)
axes[1].set_title('残差のヒストグラム')
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。

視覚的な確認に加えて、正規性を数値として評価する方法として、いくつかの統計的検定が用いられます。
これらの検定はいずれも、「残差が正規分布に従っている」という仮説がデータと矛盾していないかを調べるものです。
まず、Shapiro–Wilk 検定は、残差の分布が正規分布に近いかどうかを直接的に評価する検定で、特にサンプルサイズがそれほど大きくない場合に適しています。
- 帰無仮説 H_0:残差は正規分布に従っている
- 対立仮説 H_1:残差は正規分布に従っていない
p値が小さい場合に、帰無仮説を棄却し対立仮説を採用します。
次に、Jarque–Bera 検定は、分布の形に注目した検定です。具体的には、分布の左右の非対称性(歪み)や、裾の重さ(尖り具合)が、正規分布とどの程度異なるかを評価します。
- 帰無仮説 H_0:残差は正規分布に従っている
- 対立仮説 H_1:残差は正規分布に従っていない
分布の形が正規分布から大きく外れている場合に、p値が小さくなります。
これらの検定は、正規性を完全に証明するものではありませんが、正規性が大きく破れていないかを確認するための補助的な手段として有効です。
# 正規性の統計的検定
shapiro_stat, shapiro_p = stats.shapiro(residuals)
jb_stat, jb_p = stats.jarque_bera(residuals)
# 結果の表示
print(f"Shapiro-Wilk検定 p値: {shapiro_p:.6f}")
print(f"Jarque-Bera検定 p値: {jb_p:.6f}")
以下、実行結果です。
Shapiro-Wilk検定 p値: 0.896303 Jarque-Bera検定 p値: 0.799552
Q-Qプロットの点が直線に近く、統計的検定のp値が0.05より大きい場合、正規性の仮定は満たされていると判断できます。
外れ値と影響力のある点の検出
問題のあるデータ点の種類
回帰分析では、少数のデータ点が結果を大きく左右することがあります。特に注意すべきなのは、「外れ値」(Outlier)、「てこ比の高い点」(High Leverage)、そしてそれらが組み合わさった 「影響力のある点」(Influential Point)です。
外れ値は、モデルの予測から大きく外れた観測で、残差が大きい点を指します。一方、てこ比の高い点は、説明変数の値が極端であるため、回帰直線を強く「引っ張る」位置にある点です。影響力のある点は、この両方の性質を併せ持ち、その点を含めるかどうかで回帰直線自体が大きく変わる可能性があります。
ここで重要なのは、怪しい点を機械的に除外することではありません。入力ミスや特殊な事情(イベント日、異常値など)がないかを確認し、結論が特定の点に強く依存していないか(頑健性)を確かめることが目的です。
標準化残差による外れ値の検出
外れ値の確認には、標準化残差を用いるのが一般的です。標準化残差は、残差をそのばらつきで割ったもので、どの観測が相対的に大きく外れているかを比較しやすくします。
目安として、標準正規分布に基づき、 |\text{標準化残差}|>2 は注意、|\text{標準化残差}|>3 は外れ値の可能性が高いと考えます。
標準化残差を計算し、外れ値候補を確認します。
# 残差の標準化
std_residuals = residuals / sigma_hat
# 外れ値の検出
outliers = np.abs(std_residuals) > 2
extreme_outliers = np.abs(std_residuals) > 3
print("標準化残差による外れ値検出:")
print(f" |標準化残差| > 2 の点: {np.sum(outliers)} 個")
print(f" |標準化残差| > 3 の点: {np.sum(extreme_outliers)} 個")
if np.sum(outliers) > 0:
print("\n注意が必要な点の詳細:")
for i in np.where(outliers)[0]:
print(f"- データ {i+1}:")
print(f" 標準化残差 = {std_residuals[i]:.2f}")
print(f" 気温 = {x[i]:.1f}℃, 売上 = {y[i]:.1f}杯")
print(f" 予測値 = {y_hat[i]:.1f}杯, 残差 = {residuals[i]:.1f}杯")
以下、実行結果です。
標準化残差による外れ値検出: |標準化残差| > 2 の点: 2 個 |標準化残差| > 3 の点: 0 個 注意が必要な点の詳細: - データ 2: 標準化残差 = 2.12 気温 = 27.0℃, 売上 = 147.9杯 予測値 = 118.4杯, 残差 = 29.5杯 - データ 8: 標準化残差 = -2.09 気温 = 30.2℃, 売上 = 122.5杯 予測値 = 151.5杯, 残差 = -29.0杯
標準化残差が大きい点は、モデルから大きく外れており、データの確認が必要です。入力ミスや特殊な状況(イベント日など)の可能性があります。
てこ比(Leverage)
てこ比(leverage)は、各データ点が回帰直線の形をどれだけ左右しやすいかを表す指標です。説明変数が平均から大きく離れている点ほど、回帰直線を「てこの原理」のように強く引っ張るため、てこ比は大きくなります。
単回帰モデルにおける i 番目の観測のてこ比 h_{ii} は、次の式で定義されます。
$$
h_{ii}
=
\frac{1}{n}
+
\frac{(x_i – \bar{x})^2}{S_{xx}},
\qquad
S_{xx} = \sum_{j=1}^{n} (x_j – \bar{x})^2
$$
この式から分かるように、てこ比は 「説明変数が平均からどれだけ離れているか」 によって決まります。目的変数(売上など)が特に極端でなくても、説明変数が極端な値を取る点は、回帰直線を大きく動かす可能性があります。
てこ比がどの程度大きいと「注意が必要か」については、厳密な基準があるわけではありませんが、実務では次の経験則がよく用いられます。
$$
h_{ii} > \frac{2k}{n}
\quad \text{(注意レベル)},
\qquad
h_{ii} > \frac{3k}{n}
\quad \text{(かなり高い)}
$$
ここでも k は切片を含むパラメータ数です。 たとえば、説明変数が 1 個ある単回帰モデルでは、切片を含めて k=2 となり、データ数が n=30 なら、注意レベルは 2k/n \risingdotseq 0.133 程度になります。
# てこ比(単回帰)
leverage = 1/n + (x - x_bar)**2 / S_xx
# 目安
threshold_h = 2 * (2 / n)
# 高いてこ比の点の検出
high_leverage = leverage > threshold_h
print(f"高いてこ比の目安: {threshold_h:.3f}")
print(f"高いてこ比の点: {high_leverage.sum()} 個")
if high_leverage.any():
print("高いてこ比の点:")
for i in np.where(high_leverage)[0]:
print(f"- データ {i+1}:")
print(f" てこ比 = {leverage[i]:.3f}, 標準化残差 = {std_residuals[i]:.2f}")
print(f" 気温 = {x[i]:.1f}℃, 売上 = {y[i]:.1f}杯")
print(f" 予測値 = {y_hat[i]:.1f}杯, 残差 = {residuals[i]:.1f}杯")
# 可視化(データ番号に対するてこ比)
plt.figure(figsize=(10, 5))
plt.stem(range(1, n+1), leverage)
plt.axhline(
threshold_h,
linestyle='--',
linewidth=2,
label=f'目安 [latex]2\\times(2/n) = {threshold_h:.3f}[/latex]'
)
plt.xlabel('データ番号')
plt.ylabel('leverage')
plt.title('てこ比(leverage)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
高いてこ比の目安: 0.133 高いてこ比の点: 5 個 高いてこ比の点: - データ 4: てこ比 = 0.158, 標準化残差 = -1.20 気温 = 32.8℃, 売上 = 162.4杯 予測値 = 179.1杯, 残差 = -16.7杯 - データ 7: てこ比 = 0.166, 標準化残差 = 0.16 気温 = 33.0℃, 売上 = 183.4杯 予測値 = 181.2杯, 残差 = 2.2杯 - データ 14: てこ比 = 0.160, 標準化残差 = -0.00 気温 = 20.8℃, 売上 = 53.5杯 予測値 = 53.6杯, 残差 = -0.1杯 - データ 15: てこ比 = 0.134, 標準化残差 = -1.30 気温 = 21.5℃, 売上 = 42.5杯 予測値 = 60.5杯, 残差 = -18.0杯 - データ 21: てこ比 = 0.150, 標準化残差 = 0.30 気温 = 32.6℃, 売上 = 181.2杯 予測値 = 177.0杯, 残差 = 4.1杯
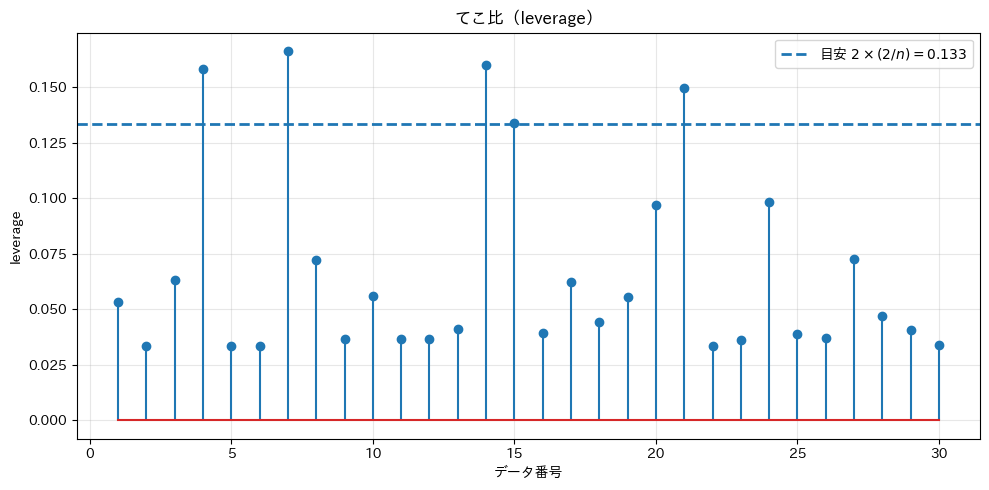
説明変数が複数ある重回帰モデルでは、説明変数行列(切片を含む)\mathbf{X}から計算した以下のハット行列(hat matrix)\mathbf{H} の対角成分 h_{ii} がi番目のデータのてこ比にります。
$$
\mathbf{H} = \mathbf{X}(\mathbf{X}^\top \mathbf{X})^{-1}\mathbf{X}^\top,
\qquad
h_{ii} = H_{ii}
$$
てこ比は常に 0 と 1 の間の値を取り、全データの平均は以下となります。
$$
\frac{1}{n}\sum_{i=1}^n h_{ii} = \frac{k}{n}
$$
ここで n はデータ数、k は 推定しているパラメータ数(切片を含む)です。説明変数が増えるほど、平均的なてこ比も大きくなることが分かります。
先ほどの紹介した基準 h_{ii} > 2k/n(注意レベル)、h_{ii} > 3k/n(かなり高い)は、平均の2倍、3倍という基準です。
statsmodelsライブラリーで簡単に出力することができます。
# X: 説明変数(2次元)、切片を追加
X_sm = sm.add_constant(x)
# モデルのフィッティング
model = sm.OLS(y, X_sm).fit()
# てこ比
leverage = model.get_influence().hat_matrix_diag
n = X_sm.shape[0]
k = X_sm.shape[1] # 切片を含む
# 目安
threshold_h = 2 * k / n
# 高いてこ比の点の検出
high_leverage = leverage > threshold_h
print(f"高いてこ比の目安: {threshold_h:.3f}")
print(f"高いてこ比の点: {high_leverage.sum()} 個")
if high_leverage.any():
print("高いてこ比の点:")
for i in np.where(high_leverage)[0]:
print(f"- データ {i+1}: てこ比 = {leverage[i]:.3f}")
以下、実行結果です。
高いてこ比の目安: 0.133 高いてこ比の点: 5 個 高いてこ比の点: - データ 4: てこ比 = 0.158 - データ 7: てこ比 = 0.166 - データ 14: てこ比 = 0.160 - データ 15: てこ比 = 0.134 - データ 21: てこ比 = 0.150
なお、てこ比が高い点が必ずしも問題になるわけではありません。重要なのは、「てこ比が高く、かつ残差も大きい場合」です。そのような点は、回帰結果に強い影響を与える可能性があります。
- てこ比が高いが、残差が小さい点 → モデルに大きな悪影響は与えない
- てこ比が高く、かつ残差も大きい点 → 回帰結果に強い影響を与える可能性がある
この後者を見つけるために、てこ比と残差を組み合わせた指標として Cook’s Distance を用います。
Cook’s Distance
Cook’s Distance(クックの距離)は、各データ点が回帰モデル全体に与える影響を総合的に評価する指標です。
残差の大きさとてこ比の両方を考慮し、「その点を除外したときに回帰直線がどれだけ変わるか」を一つの数値で表します。
Cook’s Distance は次の式で定義されます。ここで k は推定しているパラメータ数(切片を含む)です。
$$
D_i
=
\frac{(y_i – \hat{y}_i)^2}{k\,\hat{\sigma}^2}
\cdot
\frac{h_{ii}}{(1 – h_{ii})^2}
$$
この式は、Cook’s Distance が 二つの要素の組み合わせによって決まることを示しています。
前半の以下の数式は、残差の大きさをモデル全体のばらつきとパラメータ数で調整したものです。つまり、その点が「どれくらい予測から外れているか」を表しています。
$$
\frac{(y_i – \hat{y}_i)^2}{k\,\hat{\sigma}^2}
$$
一方、後半の以下の数式は、てこ比の高さを反映する項です。てこ比 h_{ii} が大きい点ほど、回帰直線を引っ張りやすく、この項の値も急激に大きくなります。
$$
\frac{h_{ii}}{(1 – h_{ii})^2}
$$
このように Cook’s Distance は、「残差が大きい点」と「てこ比が高い点」の両方を同時に評価する指標になっています。
残差が大きいだけの点や、てこ比が高いだけの点では Cook’s Distance はそれほど大きくなりませんが、両方を併せ持つ点では値が大きくなり、回帰結果に強い影響を与える可能性があることを示します。
そのため、Cook’s Distance は「どのデータ点が回帰直線全体を実質的に左右しているか」を判断するための指標として用いられます。
このCook’s Distance はどの程度の大きさを目安に、影響力のある点として見なせばいいのかという問題が出てきます。実務では、以下の目安を用いることが一般的です。
$$
D_i > \frac{4}{n}
$$
Cook’s Distance を計算し、影響力の大きい点を確認します。
# Cook's Distanceの計算
p = 1 # パラメータ数(傾きのみ)
cooks_d = (residuals**2 / (p * sigma_hat**2)) * (leverage / (1 - leverage)**2)
# 影響力のある点の検出
threshold_4n = 4 / n
influential_points = cooks_d > threshold_4n
print("Cook's Distanceによる影響力のある点の検出:")
print(f" 閾値 (4/n) = {threshold_4n:.3f}")
print(f" 影響力のある点: {np.sum(influential_points)} 個")
if np.sum(influential_points) > 0:
print("\n影響力のある点の詳細:")
for i in np.where(influential_points)[0]:
print(f"- データ {i+1}:")
print(f" Cook's D = {cooks_d[i]:.3f}")
print(f" てこ比 = {leverage[i]:.3f}, 標準化残差 = {std_residuals[i]:.2f}")
print(f" 気温 = {x[i]:.1f}℃, 売上 = {y[i]:.1f}杯")
# Cook's Distanceの可視化
plt.figure(figsize=(10, 5))
plt.stem(
range(1, n+1), cooks_d,
linefmt='b-', markerfmt='bo'
)
plt.axhline(
y=threshold_4n,
color='r', linestyle='--', linewidth=2,
label=f'閾値 4/n = {threshold_4n:.3f}'
)
plt.xlabel('データ番号')
plt.ylabel("Cook's Distance")
plt.title("Cook's Distanceプロット")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
Cook's Distanceによる影響力のある点の検出: 閾値 (4/n) = 0.133 影響力のある点: 5 個 影響力のある点の詳細: - データ 2: Cook's D = 0.162 てこ比 = 0.033, 標準化残差 = 2.12 気温 = 27.0℃, 売上 = 147.9杯 - データ 4: Cook's D = 0.321 てこ比 = 0.158, 標準化残差 = -1.20 気温 = 32.8℃, 売上 = 162.4杯 - データ 8: Cook's D = 0.366 てこ比 = 0.072, 標準化残差 = -2.09 気温 = 30.2℃, 売上 = 122.5杯 - データ 15: Cook's D = 0.299 てこ比 = 0.134, 標準化残差 = -1.30 気温 = 21.5℃, 売上 = 42.5杯 - データ 20: Cook's D = 0.319 てこ比 = 0.097, 標準化残差 = -1.64 気温 = 22.6℃, 売上 = 49.1杯
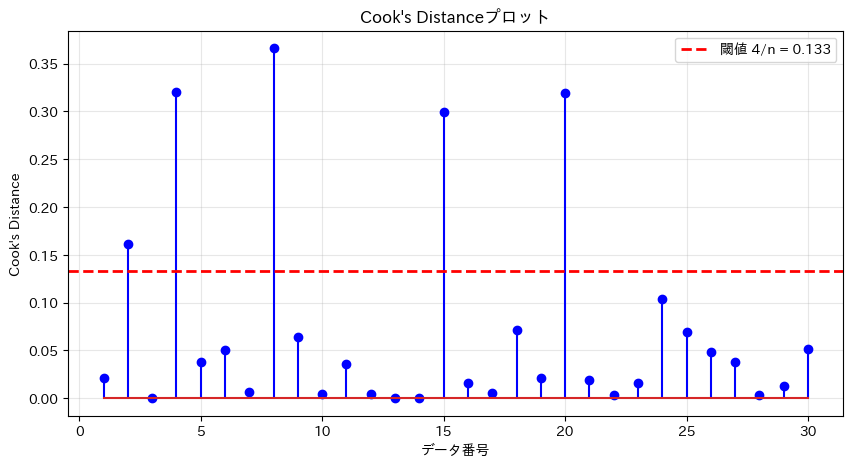
Cook’s Distanceが閾値を超える点は、モデルに大きな影響を与えている可能性があります。
これらの点を除外した場合の分析も行い、結果の頑健性を確認することが重要です。
回帰診断の総合評価
診断結果の解釈と活用
ここまでで行ったANOVAと回帰診断の結果を、どのように解釈し、実際の意思決定に活用すべきか説明します。
回帰分析の結果を使用する際は、以下の3段階で評価することが重要です。
第1段階:モデル全体の評価
まず、モデルが統計的に意味があるかを確認します。F検定が有意でない場合、モデルは予測に使用できません。次に、決定係数(R²)でモデルの説明力を評価します。
第2段階:前提条件の確認
ガウス・マルコフの仮定と正規性が満たされているかを確認します。これらの条件が満たされていない場合、推定値や検定結果の信頼性が低下します。
第3段階:外れ値と影響力のある点の確認
問題のあるデータ点を特定し、それらがモデルに与える影響を評価します。
診断結果が良くないときの対策
回帰分析では、前提となる仮定がうまく満たされていないことがあります。その場合でも、慌てて高度な手法に進む必要はありません。まずは 問題の種類ごとに、基本的な対処を順に検討することが大切です。
線形性に問題があるとき
残差プロットに曲線的なパターン(U字型など)が見られる場合、変数同士の関係が直線では表しきれていない可能性があります。
この場合、まずは 変数変換 を試します。たとえば、関係が指数的に見えるときは対数変換、なだらかな曲線関係が疑われるときは説明変数の2乗項を追加します。
それでも改善しない場合は、多項式回帰や、関係が途中で変わる場合に有効な区分線形回帰(スプライン)を検討します。直線モデル自体が合っていないと判断できるときは、非線形モデルや機械学習手法に切り替えることも選択肢です。
等分散性に問題があるとき
予測値が大きくなるにつれて残差のばらつきも大きくなる場合、等分散性が満たされていません。このままでは、標準誤差や検定結果が不正確になります。
基本的な対処は、目的変数の変換です。売上データなどでは、対数変換によってばらつきが安定することがよくあります。
それでも難しい場合は、ロバスト標準誤差を用いて、検定や信頼区間だけを頑健にする方法が実務ではよく使われます。
正規性に問題があるとき
残差の分布が大きく歪んでいる場合、小標本では検定結果の信頼性が下がることがあります。ただし、データ数が十分に多い場合は、多少の非正規性は大きな問題にならないことも多いです。
まずは 、外れ値が原因でないかを確認します。入力ミスや特殊事情があれば修正・説明します。
次に、対数変換などの変数変換を検討します。それでも影響が大きい場合は、ロバスト回帰や、正規性を仮定しないブートストラップを用いる方法もあります。
外れ値・影響力のある点が見つかったとき
外れ値や影響力のある点が見つかっても、すぐに除外してはいけません。まずはデータが正しいか、特別な事情がないかを確認します。
次に、その点を含めた場合と除外した場合で分析結果を比較し、結論がどれくらい変わるかを確認します。結果が安定していれば問題は小さく、結果が大きく変わる場合は慎重な解釈が必要です。必要に応じて、ロバスト回帰や層別分析を検討します。
モデル改善の基本的な考え方
診断で問題が見つかった場合は、一度にすべてを直そうとしないことが重要です。通常は、「線形性 → 等分散性 → 正規性」の順で対処すると、他の問題も同時に改善されることが多くなります。
変数変換やモデルの見直しで改善しない場合は、データの範囲や量が十分か、重要な変数が欠けていないかも確認します。最終的には、統計的にきれいなモデルだけでなく、実務で意味のある解釈ができるかを重視することが大切です。
まとめ
本記事では、回帰モデルの評価と診断について体系的に学びました。
- F検定とANOVAにより、モデル全体の有意性を評価できます。
- 回帰診断では、ガウス・マルコフの仮定と正規性を確認します。各種のプロットの見方を理解することで、前提条件の違反を視覚的に検出できます。
- 外れ値と影響力のある点の検出により、分析結果の頑健性を確認できます。標準化残差とCook’s Distanceは、問題のある点を特定する強力なツールです。
回帰診断は、モデルの信頼性を保証するために不可欠なプロセスです。単に当てはまりの良いモデルを作るだけでなく、前提条件を満たし、外れ値に対して頑健なモデルを構築することが、実務での成功の鍵となります。
統計的な検定や診断は、最初は複雑に感じるかもしれません。しかし、一つ一つの手法の意味とグラフの見方を理解することで、データが語る真実を正しく読み取ることができるようになります。
第4回では、複数の説明変数を扱う重回帰分析について学びます:
- 重回帰モデルの理論と実装
- 変数選択の手法(前進選択、後退除去、ステップワイズ法)
- 多重共線性の問題と対処(VIF、条件数)
- 交互作用項の導入と解釈
より現実的で複雑な問題に対応できる分析手法を身につけていきましょう。