前回まで、気温からアイスコーヒーの売上を予測する単回帰分析を学びました。
しかし、現実のビジネスで何かを予測する際、影響する要因は一つだけではありません。
たとえば、コンビニエンスストアの売上を考えてみましょう。
売上に影響する要因として、店舗面積、スタッフ数、駐車場の有無、駅からの距離、周辺人口、競合店の数など、数多くの要素が考えられます。
これらの要因を個別に分析しても、全体像は見えてきません。
なぜなら、これらの要因は相互に関連し合っているからです。
たとえば、大きな店舗は駐車場も広く、スタッフも多い傾向があります。
このような場合、店舗面積だけを見て「面積が大きいから売上が高い」と結論づけるのは早計です。
実際には、スタッフの充実や駐車場の利便性が真の要因かもしれません。
重回帰分析(Multiple Regression Analysis)は、このような複数の要因を同時に考慮し、それぞれの要因が目的変数に与える「純粋な効果」を評価できる強力な手法です。
Contents
重回帰分析の理論
重回帰モデルの数学的表現
重回帰分析は、単回帰分析を複数の説明変数に拡張したものです。
単回帰が1つの説明変数から目的変数を予測するのに対し、重回帰は複数の説明変数を同時に使用します。
p 個の説明変数 x_1, x_2, ..., x_p から目的変数 y を予測する重回帰モデルは、次のように表現されます。$$
y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + … + \beta_p x_p + \varepsilon
$$
ここで、\beta_0 は切片(定数項)、\beta_1, \beta_2, ..., \beta_p は各説明変数に対する偏回帰係数、\varepsilon は誤差項を表します。ちなみに、重回帰分析の回帰係数は「偏回帰係数」と呼ばれます。
行列表現による一般化
n 個の観測データがある場合、重回帰モデルは行列を使って簡潔に表現できます。$$
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}
$$
まず、\mathbf{y} は n \times 1 の目的変数ベクトルで、n 個の観測値を縦に並べたものです。y_i は i 番目の観測における目的変数の値を意味します。
$$
\mathbf{y}
=
\begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{pmatrix}
$$
次に、\mathbf{X} は n \times (p+1) のデザイン行列で、各観測に対応する説明変数の値をまとめた行列です。切片をモデルに含めるため、第1列にはすべて 1 が配置されています。ここで x_{ij} は、i 番目の観測における j 番目の説明変数の値を表しています。
$$
\mathbf{X}
=
\begin{pmatrix}
1 & x_{11} & x_{12} & \cdots & x_{1p} \\
1 & x_{21} & x_{22} & \cdots & x_{2p} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n1} & x_{n2} & \cdots & x_{np}
\end{pmatrix}
$$
偏回帰係数をまとめた \boldsymbol{\beta} は (p+1) \times 1 のベクトルで、切片と各説明変数の効果を成分として持ちます。このベクトルに含まれる \beta_0 は切片を表し、\beta_1,\ldots,\beta_p はそれぞれ対応する説明変数の偏回帰係数です。これらは未知のパラメータであり、データから推定される対象となります。
$$
\boldsymbol{\beta}
=
\begin{pmatrix}
\beta_0 \\
\beta_1 \\
\vdots \\
\beta_p
\end{pmatrix}
$$
最後に、\boldsymbol{\varepsilon} は n \times 1 の誤差ベクトルであり、各観測におけるモデルでは説明しきれない部分を表します。
$$
\boldsymbol{\varepsilon}
=
\begin{pmatrix}
\varepsilon_1 \\
\varepsilon_2 \\
\vdots \\
\varepsilon_n
\end{pmatrix}
$$
これらをすべて書き下すと、行列表現の回帰モデルは
$$
\begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{pmatrix}
=
\begin{pmatrix}
1 & x_{11} & \cdots & x_{1p} \\
1 & x_{21} & \cdots & x_{2p} \\
\vdots & \vdots & \ddots & \vdots \\
1 & x_{n1} & \cdots & x_{np}
\end{pmatrix}
\begin{pmatrix}
\beta_0 \\
\beta_1 \\
\vdots \\
\beta_p
\end{pmatrix}
+
\begin{pmatrix}
\varepsilon_1 \\
\varepsilon_2 \\
\vdots \\
\varepsilon_n
\end{pmatrix}
$$
となります。この式は、各観測 i について以下の n 個の式を同時にまとめて表現したものです。
$$
y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \varepsilon_i
$$
最小二乗推定量
単回帰と同様に、最小二乗法を用いて偏回帰係数を推定します。残差平方和を最小化することで、最適な偏回帰係数を求めます。
$$
\text{最小化:} \sum_{i=1}^n (y_i – \hat{y}_i)^2 = (\mathbf{y} – \mathbf{X}\boldsymbol{\beta})^T(\mathbf{y} – \mathbf{X}\boldsymbol{\beta})
$$
この最小化問題を解くと、最小二乗推定量は次の式で与えられます。
$$
\hat{\boldsymbol{\beta}} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}
$$
この式は単回帰の場合の自然な拡張になっています。ただし、\mathbf{X}^T\mathbf{X} が逆行列を持つことが必要です。これが後で説明する多重共線性と関連してきます。
実装:店舗売上データの分析
データの生成と準備
今回利用するサンプルデータを生成します。店舗の売上データです。
このデータには、店舗面積、スタッフ数、駐車場台数、駅からの距離という4つの説明変数が含まれており、これらが相互に関連しながら売上に影響を与える状況を再現します。
まず、必要なライブラリをインポートします。
import numpy as np import pandas as pd from scipy import stats import matplotlib.pyplot as plt import japanize_matplotlib import seaborn as sns
では、店舗データを生成します。
# 再現性のための乱数シード固定
np.random.seed(42)
# データ生成のパラメータ
n_stores = 100 # 100店舗のデータ
#
# 説明変数の生成
#
# 店舗面積(30〜150平方メートル)
floor_area = np.random.uniform(30, 150, n_stores)
# スタッフ数(面積に緩く関連)
staff_base = 0.08 * floor_area + np.random.normal(5, 2, n_stores)
staff_count = np.clip(staff_base, 3, 20).astype(int)
# 駐車場台数(面積と相関)
parking_base = 0.15 * floor_area + np.random.normal(0, 5, n_stores)
parking_spaces = np.clip(parking_base, 0, 30).astype(int)
# 駅からの距離(独立)
distance_from_station = np.random.exponential(1.5, n_stores)
distance_from_station = np.clip(distance_from_station, 0.1, 8)
# 真のモデルのパラメータ
TRUE_BETA = {
'intercept': 50, # 切片5万円
'floor_area': 1.5, # 面積1㎡あたり1.5万円
'staff_count': 12.0, # スタッフ1人あたり12万円
'parking_spaces': 2.5, # 駐車場1台あたり2.5万円
'distance': -8.0 # 駅から1km離れると-8万円
}
# 売上の生成(真のモデル + ノイズ)
daily_sales = (
TRUE_BETA['intercept'] +
TRUE_BETA['floor_area'] * floor_area +
TRUE_BETA['staff_count'] * staff_count +
TRUE_BETA['parking_spaces'] * parking_spaces +
TRUE_BETA['distance'] * distance_from_station +
np.random.normal(0, 25, n_stores) # ノイズ
)
# データフレームの作成
store_data = pd.DataFrame({
'店舗面積': floor_area,
'スタッフ数': staff_count,
'駐車場台数': parking_spaces,
'駅からの距離': distance_from_station,
'日売上': daily_sales
})
print("生成した店舗データの先頭5行:")
print(store_data.head())
print("\n生成した店舗データの概要:")
print(store_data.describe().round(2))
以下、実行結果です。
生成した店舗データの先頭5行:
店舗面積 スタッフ数 駐車場台数 駅からの距離 日売上
0 74.944814 11 11 0.109774 320.563627
1 144.085717 15 28 1.542591 478.724611
2 117.839273 14 16 0.100000 433.496081
3 101.839018 9 28 1.322021 362.965893
4 48.722237 8 10 4.225883 218.344254
生成した店舗データの概要:
店舗面積 スタッフ数 駐車場台数 駅からの距離 日売上
count 100.00 100.00 100.00 100.00 100.00
mean 86.42 11.44 12.61 1.64 336.45
std 35.70 3.14 7.34 1.55 108.76
min 30.66 5.00 0.00 0.10 128.69
25% 53.18 9.00 7.00 0.50 241.49
50% 85.70 11.00 12.00 1.21 322.70
75% 117.62 14.00 17.25 2.37 429.11
max 148.43 19.00 30.00 6.99 579.86
データの探索的分析
重回帰分析を行う前に、データの構造を理解することが重要です。
変数間の関係を視覚化し、潜在的な問題を事前に把握しましょう。
相関行列を計算し、ヒートマップで視覚化します。これにより、変数間の関係が一目で分かります。
# 相関行列の計算
corr_mat = store_data.corr()
# 相関行列のヒートマップ
plt.figure(figsize=(10, 8))
sns.heatmap(
corr_mat, # 表示するデータ(相関行列)
annot=True, # セル内に相関係数を表示
cmap='coolwarm', # カラーマップ
center=0, # カラーマップの中心を0に設定
square=True, # セルを正方形にする
linewidths=1, # セルの境界線の太さ
)
plt.title('変数間の相関行列')
plt.tight_layout()
plt.show()
以下、実行結果です。
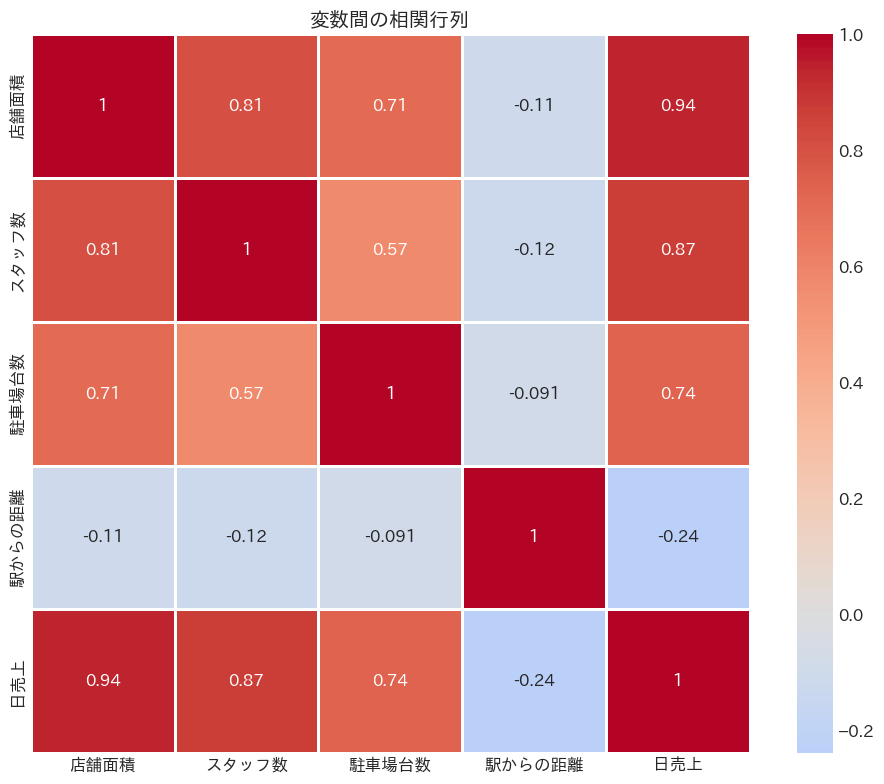
相関行列から、店舗面積とスタッフ数、駐車場台数の間に正の相関があることが分かります。
これは直感的に理解できる関係です(大きな店舗は人も駐車場も多い)。
しかし、このような相関は多重共線性の原因となり、偏回帰係数の解釈を難しくする可能性があります。
散布図行列による関係の視覚化
変数間の関係をより詳しく理解するために、散布図行列を作成します。
これにより、線形関係だけでなく、非線形な関係や外れ値も発見できます。
散布図行列を作成し、各変数ペアの関係を視覚化します。
fig = plt.figure(figsize=(10, 10))
# 変数のリストを作成
variables = store_data.columns.tolist()
# 変数の数を取得
n_vars = len(variables)
# 散布図行列(ペアプロット)を作成
for i in range(n_vars):
for j in range(n_vars):
ax = plt.subplot(n_vars, n_vars, i * n_vars + j + 1)
# 対角線上の場合
if i == j:
# 対角線上:ヒストグラム
ax.hist(
store_data[variables[i]], # データ
bins=20, # ビンの数
edgecolor='white' # 縁取りの色
)
# ヒストグラムのタイトルを設定
if j == 0:
ax.set_ylabel(variables[i])
# X軸のラベルを設定
if i == n_vars - 1:
ax.set_xlabel(variables[j])
# 対角線上でない場合
else:
# 非対角要素:散布図
ax.scatter(
store_data[variables[j]], # X軸のデータ
store_data[variables[i]], # Y軸のデータ
alpha=0.5, s=20
)
# 売上との関係には回帰直線を追加
if variables[i] == '日売上':
# 回帰直線の傾きと切片を計算
z = np.polyfit(
store_data[variables[j]], # X軸のデータ
store_data[variables[i]], # Y軸のデータ
1 # 1次関数
)
# 回帰直線の式を作成
p = np.poly1d(z)
# X軸の範囲を設定
x_line = np.linspace(
store_data[variables[j]].min(),
store_data[variables[j]].max(),
100
)
# 回帰直線をプロット
ax.plot(x_line, p(x_line), "r-", alpha=0.6)
# Y軸のラベルを設定
if j == 0:
ax.set_ylabel(variables[i])
# X軸のラベルを設定
if i == n_vars - 1:
ax.set_xlabel(variables[j])
# グリッドを表示
ax.grid(True, alpha=0.5)
plt.suptitle('散布図行列:変数間の関係')
plt.tight_layout()
plt.show()
以下、実行結果です。
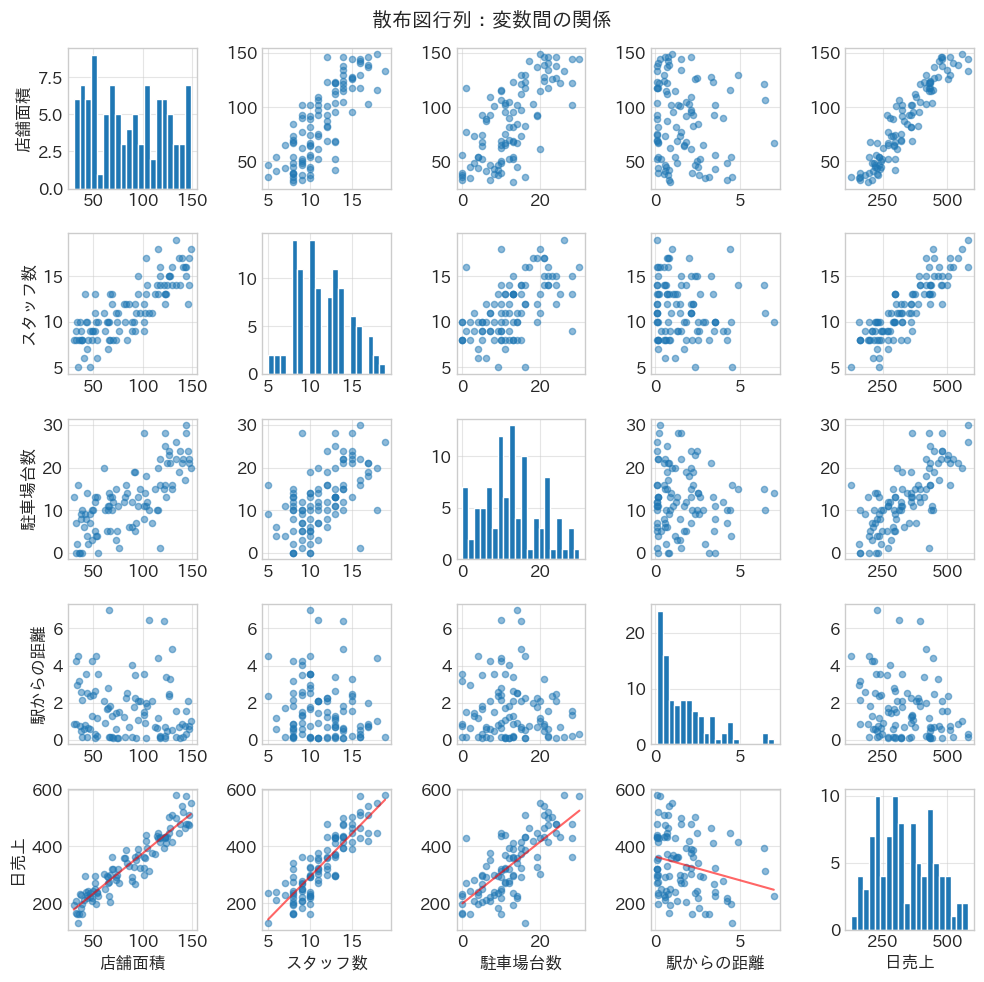
以下、この散布図行列の見方です。
- 対角線:各変数の分布(ヒストグラム)
- 最下行:各説明変数と売上の関係(赤線は単回帰直線)
- その他:説明変数同士の関係
散布図行列から、各変数と売上の関係が概ね線形であることが確認できます。
重回帰分析の実行
最小二乗法による推定
それでは、重回帰分析を実行しましょう。
まず、NumPyの行列演算を使って、理論式通りに偏回帰係数を計算します。
# データの数(n)と説明変数の数(p)を取得
n, p = X.shape
# y: 目的変数
y = store_data['日売上'].values
# X: 説明変数
X = store_data.drop(columns=['日売上'])
# デザイン行列の作成(切片項を追加)
X_with_intercept = np.column_stack([np.ones(n), X.values])
# 行列演算を用いた重回帰分析の実装
XtX = X_with_intercept.T @ X_with_intercept
Xty = X_with_intercept.T @ y
XtX_inv = np.linalg.inv(XtX)
beta_hat = XtX_inv @ Xty
# 結果の表示
feature_names = ['切片'] + X.columns.tolist()
print("="*60)
print("重回帰分析の結果(行列演算による実装)")
print("="*60)
for i, name in enumerate(feature_names):
print(f"{name}:\t{beta_hat[i]:7.3f}", end="")
if i > 0:
true_value = list(TRUE_BETA.values())[i]
print(f"\t(真の値: {true_value:5.1f})")
else:
print(f"\t(真の値: {TRUE_BETA['intercept']:5.1f})")
# 予測値と残差
y_pred = X_with_intercept @ beta_hat
res = y - y_pred
print(f"\n残差の平均:\t{np.mean(res):.2f}")
print(f"残差の標準偏差:\t{np.std(res, ddof=p+1):.2f}")
以下、実行結果です。
============================================================ 重回帰分析の結果(行列演算による実装) ============================================================ 切片: 49.047 (真の値: 50.0) 店舗面積: 1.745 (真の値: 1.5) スタッフ数: 10.960 (真の値: 12.0) 駐車場台数: 2.047 (真の値: 2.5) 駅からの距離: -8.888 (真の値: -8.0) 残差の平均: 0.00 残差の標準偏差: 25.67
推定された偏回帰係数が真の値に近いことが確認できます。
scikit-learnとstatsmodelsによる実装
実務では、ライブラリを使用して効率的に分析を行います。scikit-learnとstatsmodelsの両方で実装し、結果を比較します。
scikit-learnとstatsmodelsで重回帰分析を実行します。
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
# scikit-learnによる実装
lr_model = LinearRegression()
lr_model.fit(X, y)
y_pred_sklearn = lr_model.predict(X)
print("="*60)
print("scikit-learnによる重回帰分析")
print("="*60)
print(f"切片: {lr_model.intercept_:.3f}")
for i, name in enumerate(['店舗面積', 'スタッフ数', '駐車場台数', '駅からの距離']):
print(f"{name}: {lr_model.coef_[i]:.3f}")
# statsmodelsによる実装(詳細な統計情報)
X_sm = sm.add_constant(X)
model = sm.OLS(y, X_sm)
results = model.fit()
print("\n" + "="*60)
print("statsmodelsによる重回帰分析(詳細)")
print("="*60)
print(results.summary())
以下、実行結果です。
============================================================
scikit-learnによる重回帰分析
============================================================
切片: 49.047
店舗面積: 1.745
スタッフ数: 10.960
駐車場台数: 2.047
駅からの距離: -8.888
============================================================
statsmodelsによる重回帰分析(詳細)
============================================================
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.947
Model: OLS Adj. R-squared: 0.944
Method: Least Squares F-statistic: 420.4
Date: Sat, 20 Dec 2025 Prob (F-statistic): 1.78e-59
Time: 13:02:09 Log-Likelihood: -463.88
No. Observations: 100 AIC: 937.8
Df Residuals: 95 BIC: 950.8
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 49.0473 10.705 4.582 0.000 27.794 70.300
店舗面積 1.7448 0.142 12.324 0.000 1.464 2.026
スタッフ数 10.9600 1.388 7.894 0.000 8.204 13.716
駐車場台数 2.0472 0.498 4.110 0.000 1.058 3.036
駅からの距離 -8.8880 1.682 -5.285 0.000 -12.226 -5.550
==============================================================================
Omnibus: 1.085 Durbin-Watson: 1.858
Prob(Omnibus): 0.581 Jarque-Bera (JB): 0.994
Skew: -0.013 Prob(JB): 0.608
Kurtosis: 2.512 Cond. No. 399.
==============================================================================
statsmodelsのサマリーには、各係数の標準誤差、t値、p値、信頼区間など、統計的推論に必要な情報がすべて含まれています。F統計量により、モデル全体の有意性も確認できます。
重回帰分析の回帰係数は「偏回帰係数」と呼ばれ、その解釈には注意が必要です。各係数は「他の説明変数を一定に保った状態での効果」を表します。
標準化偏回帰係数(変数の重要度評価)
なぜ標準化が必要か
回帰係数の大きさを直接比較しても、どの変数が最も重要かは分かりません。なぜなら、変数によって単位やスケールが異なるからです。
たとえば、店舗面積は平方メートル単位で数十から百数十の値を取りますが、スタッフ数は人数単位で数人から十数人の値を取ります。
この問題を解決するのが標準化偏回帰係数です。
すべての変数を平均0、標準偏差1に標準化してから回帰分析を行うことで、係数の大きさを直接比較できるようになります。
標準化偏回帰係数の計算
j 番目の説明変数に対応する標準化偏回帰係数\beta_j^{*} は、次の式で計算されます。$$
\beta_j^{*}
=
\beta_j \times \frac{s_{x_j}}{s_y}
$$
ここで、\beta_j は元の(非標準化)偏回帰係数であり、s_{x_j} は説明変数 x_j の標準偏差、s_y は目的変数 y の標準偏差です。
重要度をランキング
標準化回帰係数を計算し、変数の重要度をランキングします。
from sklearn.preprocessing import StandardScaler
# データの標準化
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_std = scaler_X.fit_transform(X)
y_std = scaler_y.fit_transform(y.reshape(-1, 1)).ravel()
# 標準化データでの回帰分析
lr_std = LinearRegression(fit_intercept=False)
lr_std.fit(X_std, y_std)
# 標準化偏回帰係数
std_coefs = lr_std.coef_
# 重要度ランキング
importance_df = pd.DataFrame({
'変数': X.columns,
'偏回帰係数': lr_model.coef_,
'標準化偏回帰係数': std_coefs,
'絶対値': np.abs(std_coefs)
}).sort_values('絶対値', ascending=False)
print("="*70)
print("標準化偏回帰係数による重要度ランキング")
print("="*70)
print("順位\t 変数\t 偏回帰係数\t標準化偏回帰係数\t重要度")
print("-"*60)
for i, row in enumerate(importance_df.iterrows(), 1):
_, data = row
print(
f"{i:2d}\t{data['変数']:5s}\t{data['偏回帰係数']:6.3f}"
f"\t{data['標準化偏回帰係数']:10.3f}"
f"\t{'*' * int(abs(data['標準化偏回帰係数'])*10)}"
)
以下、実行結果です。標準化偏回帰係数の絶対値が大きい順に並べています。
====================================================================== 標準化偏回帰係数による重要度ランキング ====================================================================== 順位 変数 偏回帰係数 標準化偏回帰係数 重要度 ------------------------------------------------------------ 1 店舗面積 1.745 0.573 ***** 2 スタッフ数 10.960 0.317 *** 3 駐車場台数 2.047 0.138 * 4 駅からの距離 -8.888 -0.126 *
標準化回帰係数により、どの変数が最も重要かが明確になります。
この例では、店舗面積やスタッフ数が売上に大きな影響を与えていることが分かります。
多重共線性と回帰診断
回帰診断
重回帰分析を行う際も、基本的な前提条件は単回帰分析と同じです。これらの条件が大きく崩れていないかを確認することで、回帰結果を安心して解釈できるようになります。
前回(第3回)で紹介した前提条件は次の6つです。
- 線形性:説明変数と目的変数の関係が線形である
- 期待値ゼロ:誤差項の期待値(平均)が0である
- 等分散性:誤差の分散がすべての観測で一定である
- 無相関性:異なる観測の誤差が互いに相関を持たない
- 完全共線性がない:説明変数間に完全な線形関係がない
- 正規性:誤差項が正規分布に従う(検定や信頼区間に必要)
このうち「完全共線性がない」という条件は、説明変数が複数ある重回帰分析で初めて問題になります。単回帰では説明変数が1つしかないため、この点を意識する必要はありませんでした。重回帰では、VIF を用いてこの条件が満たされているかを確認します。
また、実務では「完全に同じ」説明変数がなくても、よく似た情報を持つ説明変数が複数含まれている状態がしばしば起こります。これを多重共線性と呼び、完全共線性ほど深刻ではないものの、回帰係数が不安定になったり、解釈が難しくなったりする原因になります。重回帰分析では、VIF を用いてこのような多重共線性の程度もあわせて確認します。
このように、単回帰で学んだ回帰診断を土台としつつ、重回帰では説明変数どうしの関係にも注意を払うことが重要です。
import statsmodels.api as sm
# 残差の計算
residuals = y - y_pred
# 線形性の診断プロット
fig, axes = plt.subplots(3, 2, figsize=(10, 10))
# 残差 vs 説明変数
for i, column in enumerate(X.columns):
x = X[column]
ax = axes[i // 2, i % 2] # 2列に配置
ax.scatter(x, residuals, alpha=0.6, s=50)
ax.axhline(y=0, color='red', linestyle='--', linewidth=2)
ax.set_xlabel(f'{column}(説明変数)')
ax.set_ylabel('残差')
ax.set_title(f'【線形性の診断】残差 vs {column}'
f'\n(水平な帯状に散らばっていればOK)')
ax.grid(True, alpha=0.3)
# 残差 vs 予測値を別のプロットで表示
ax2 = axes[2, 0]
ax2.scatter(y_pred, residuals, alpha=0.6, s=50)
ax2.axhline(y=0, color='red', linestyle='--', linewidth=2)
ax2.set_xlabel('予測値')
ax2.set_ylabel('残差')
ax2.set_title('【線形性・等分散性の診断】残差 vs 予測値'
'\n(ランダムに散らばっていればOK)')
ax2.grid(True, alpha=0.3)
# Scale-Locationプロット
ax3 = axes[2, 1]
# 予測値と標準化残差の散布図
ax3.scatter(
y_pred,
np.sqrt(np.abs(stded_res)),
alpha=0.6,
s=50
)
# 非パラメトリック回帰(LOWESS)を用いてトレンド線を計算
lowess = sm.nonparametric.lowess
trend = lowess(
np.sqrt(np.abs(stded_res)), # 縦軸
y_pred, # 横軸
)
# トレンド線の描画
ax3.plot(
trend[:, 0], trend[:, 1],
'r-', linewidth=2, label='トレンド')
ax3.set_xlabel('予測値')
ax3.set_ylabel('√|標準化残差|')
ax3.set_title('【等分散性の診断】Scale-Locationプロット'
'\n(ローカルなトレンドが水平線に近ければOK)')
ax3.grid(True, alpha=0.3)
ax3.legend()
plt.tight_layout()
plt.show()
以下、実行結果です。
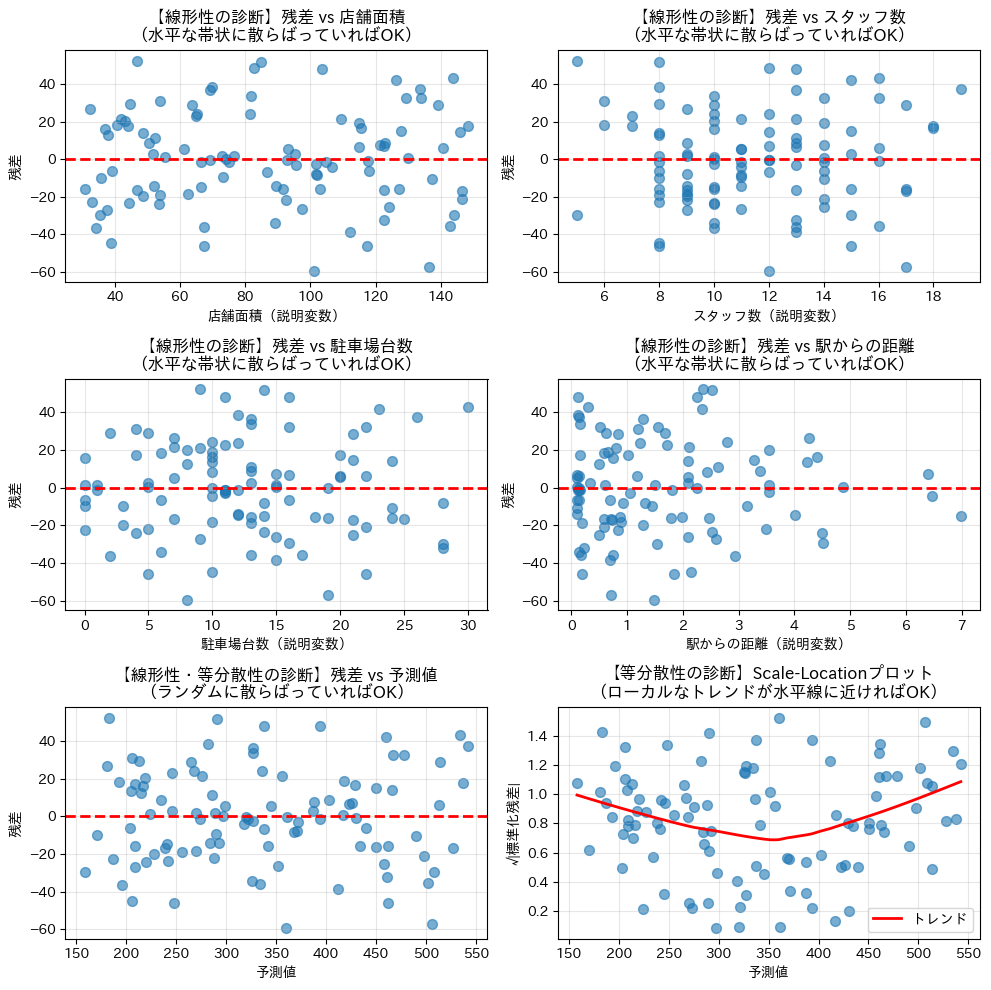
statsmodels の OLS では、多くの診断結果が model.summary() にすでに含まれています。先ほど求めたものがあるので、再掲します。
OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.947 Model: OLS Adj. R-squared: 0.944 Method: Least Squares F-statistic: 420.4 Date: Sun, 21 Dec 2025 Prob (F-statistic): 1.78e-59 Time: 09:57:18 Log-Likelihood: -463.88 No. Observations: 100 AIC: 937.8 Df Residuals: 95 BIC: 950.8 Df Model: 4 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const 49.0473 10.705 4.582 0.000 27.794 70.300 店舗面積 1.7448 0.142 12.324 0.000 1.464 2.026 スタッフ数 10.9600 1.388 7.894 0.000 8.204 13.716 駐車場台数 2.0472 0.498 4.110 0.000 1.058 3.036 駅からの距離 -8.8880 1.682 -5.285 0.000 -12.226 -5.550 ============================================================================== Omnibus: 1.085 Durbin-Watson: 1.858 Prob(Omnibus): 0.581 Jarque-Bera (JB): 0.994 Skew: -0.013 Prob(JB): 0.608 Kurtosis: 2.512 Cond. No. 399. ==============================================================================
この重回帰モデルは、売上(目的変数)を4つの要因で説明しており、決定係数は 0.947 と非常に高く、売上の変動の約95%を説明できています。モデル全体の有意性を示す F 検定の p 値も極めて小さく、モデル全体として統計的に有意であることが分かります。
各説明変数の係数を見ると、店舗面積・スタッフ数・駐車場台数はいずれも正の影響を持っており、値が大きくなるほど売上が増える傾向があります。特にスタッフ数の影響が大きく、1人増えるごとに売上が大きく伸びることが示されています。一方で、駅からの距離は負の係数となっており、駅から遠くなるほど売上が下がる傾向が確認できます。
すべての説明変数は p 値が 0.05 を大きく下回っており、個々の変数も統計的に有意です。また、残差の正規性(Jarque–Bera 検定)についても大きな問題は見られず、回帰モデルの前提条件は概ね満たされていると判断できます。
完全共線性がないという条件については、モデルが問題なく推定されていることから、少なくとも説明変数間に完全な線形関係は存在していないと判断できます。
一方で、条件数(Cond. No.)が 399 とやや大きめ(基準例:30以上でやや注意、100以上で多重共線性が強い可能性、1000以上で偏回帰係数が不安定、など)である点には注意が必要です。
今回の値は深刻な問題を示す水準ではありませんが、将来的に変数を追加する場合や、係数の解釈を厳密に行う際には、VIF などでの追加確認が望まれます。
多重共線性とは
多重共線性(Multicollinearity)とは、複数の説明変数どうしがよく似た動きをしており、強い相関関係を持っている状態のことです。このような状況では、どの変数がどれだけ目的変数に影響しているのかを、はっきり分けて判断することが難しくなります。
たとえば、アイスクリームの売上を予測したいと考え、「気温」と「冷房の使用時間」の2つを説明変数として使ったとします。暑い日ほど冷房の使用時間は長くなるため、この2つの変数は非常によく似た動きをします。このとき、売上が増えた理由が「気温の影響」なのか「冷房の使用時間の影響」なのかを、データだけから正確に分けて判断することは困難になります。
このような状況では、回帰係数はデータのわずかな違いによって大きく変わりやすくなります。ある分析では「気温の影響が大きい」という結果になり、別のデータでは「冷房の使用時間の影響が大きい」という結果になることもあります。しかし、どちらの分析も売上の予測自体はそれなりに当たってしまうため、問題に気づきにくいという特徴があります。
そのため、多重共線性は予測だけを目的とする場合には大きな支障にならないこともありますが、「なぜ売上が伸びたのか」を説明したり、「どの要因に対策を打つべきか」を考えたりする場面では、注意が必要な重要な問題となります。
VIFによる診断
VIF(Variance Inflation Factor)は、各説明変数が他の説明変数とどれほど強く関係しているかを数値で表したもので、多重共線性の代表的な指標です。
VIFを計算するときは、もとの回帰モデルとは別に、説明変数どうしの関係だけを見るための回帰を行います。
具体的には、ある説明変数 x_j を「目的変数」とみなし、残りのすべての説明変数を「説明変数」として回帰を行います。その回帰で得られる決定係数を R_j^2 と呼びます。
- もとの回帰モデル:y = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p + \varepsilon
- VIF 計算のための回帰モデル:x_j = \gamma_0 + \gamma_1 x_1 + \cdots + \gamma_{j-1} x_{j-1} + \gamma_{j+1} x_{j+1} + \cdots + \gamma_p x_p + u
VIF 計算のための回帰モデルから求めた決定係数 R_j^2 は、「x_j が、他の説明変数によってどれだけ説明されてしまっているか」を表しています。
R_j^2 が高いほど、x_j は他の説明変数と強く結びついており、独立した情報をあまり持っていないことを意味します。その結果として、VIFが大きくなり、多重共線性の問題が強いと判断されます。$$
\mathrm{VIF}_j = \frac{1}{1 – R_j^2}
$$
一般に、VIF が 5 未満であれば多重共線性の問題はほとんどないと考えられます。
一方、5 以上になると説明変数どうしの関係が強くなっている可能性があり、10 を超える場合には、回帰係数の解釈が難しくなるほど深刻な多重共線性が疑われます。
これから実行するコードでは、各説明変数の VIF を計算し、多重共線性が問題になっていないかを確認します。
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 説明変数のデータフレームを作成
vif_data = pd.DataFrame()
vif_data["変数"] = X.columns
# VIFを計算してデータフレームに追加
vif_data["VIF"] = [
variance_inflation_factor(X, i)
for i in range(X.shape[1])
]
print("="*60)
print("多重共線性の診断(VIF)")
print("="*60)
print(vif_data.to_string(index=False))
# VIFの視覚化
plt.figure(figsize=(10, 5))
# VIFの値によってバーの色を設定
colors = [
'green' if v < 5 # VIFが5未満の場合は緑
else 'orange' if v < 10 # VIFが5以上10未満の場合はオレンジ
else 'red' for v in vif_data['VIF'] # VIFが10以上の場合は赤
]
# 棒グラフを描画
bars = plt.bar(
vif_data['変数'],
vif_data['VIF'],
color=colors, alpha=0.7
)
plt.axhline(y=5, color='orange', linestyle='--', label='注意レベル (VIF=5)')
plt.axhline(y=10, color='red', linestyle='--', label='深刻レベル (VIF=10)')
plt.ylabel('VIF値')
plt.title('多重共線性の診断:VIF')
plt.legend()
plt.grid(True, alpha=0.3, axis='y')
# 値をバー上に表示
for bar, val in zip(bars, vif_data['VIF']):
plt.text(bar.get_x() + bar.get_width()/2, val + 0.2,
f'{val:.2f}', ha='center', va='bottom')
plt.tight_layout()
plt.show()
以下、実行結果です。
============================================================
多重共線性の診断(VIF)
============================================================
変数 VIF
店舗面積 25.726929
スタッフ数 20.588009
駐車場台数 7.992227
駅からの距離 1.888317
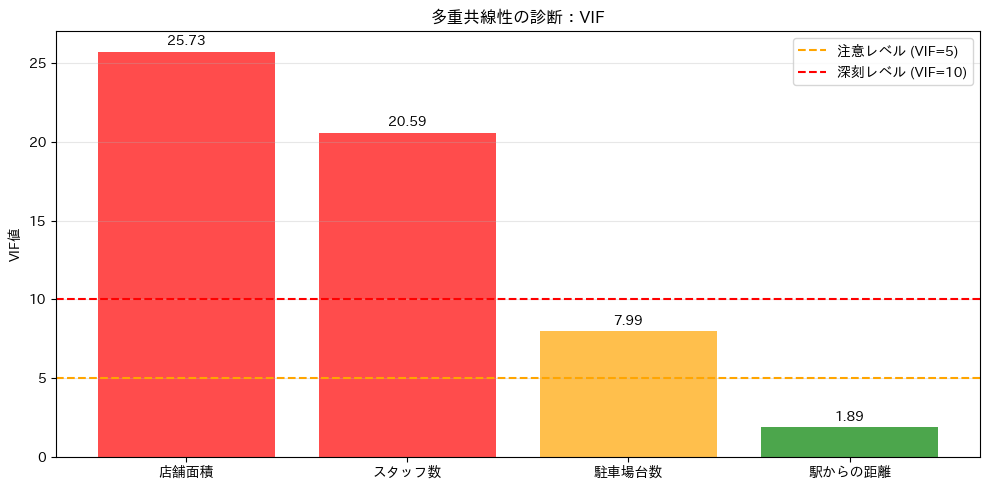
VIF値から、どの変数に多重共線性の問題があるかが分かります。値が高い変数は、他の変数と強く相関している可能性があります。
相関の高い変数ペアの特定
多重共線性の原因を特定するために、相関の高い変数ペアを見つけます。
説明変数間の相関を詳しく分析します。
# 説明変数間の相関行列
X_corr = X.corr()
# 相関の高いペアを特定
high_corr_pairs = []
for i in range(len(X_corr.columns)):
for j in range(i+1, len(X_corr.columns)):
corr_value = X_corr.iloc[i, j]
if abs(corr_value) > 0.5:
high_corr_pairs.append({
'変数1': X_corr.columns[i],
'変数2': X_corr.columns[j],
'相関係数': corr_value
})
if high_corr_pairs:
print("="*60)
print("相関の高い変数ペア(|r| > 0.5)")
print("="*60)
for pair in high_corr_pairs:
print(f"{pair['変数1']} ↔ {pair['変数2']}"
f"\t r = {pair['相関係数']:6.3f}")
else:
print("相関の高い変数ペアはありません(|r| ≤ 0.5)")
以下、実行結果です。
============================================================ 相関の高い変数ペア(|r| > 0.5) ============================================================ 店舗面積 ↔ スタッフ数 r = 0.806 店舗面積 ↔ 駐車場台数 r = 0.708 スタッフ数 ↔ 駐車場台数 r = 0.574
相関の高い変数ペアが特定できれば、それらが多重共線性の原因となっている可能性があります。
多重共線性への対処法
多重共線性が見つかった場合でも、必ずしも分析が失敗というわけではありません。目的に応じて、いくつかの対処法を選ぶことができます。
最もシンプルな方法は、よく似た動きをしている説明変数のうち、どちらか一方をモデルから外すことです。情報が重なっている変数を減らすことで、回帰係数の不安定さを抑えることができます。
変数を単純に削除したくない場合には、関連の深い変数をまとめて一つの指標にする方法もあります。たとえば、相関の高い複数の売上指標を合計や平均として扱うことで、情報を保ったまま多重共線性を弱めることができます。
また、主成分分析を用いると、相関のある複数の変数を、互いに相関のない新しい変数に変換することができます。この方法は、多くの変数を扱う場合に特に有効ですが、変数の意味が分かりにくくなる点には注意が必要です。
回帰手法そのものを工夫する方法としては、Ridge回帰のような正則化を用いる手があります。これは、回帰係数が極端な値にならないように制約を加えることで、多重共線性があっても安定した推定を可能にします。
さらに、データ数を増やすことも一つの対策です。サンプル数が多くなると、回帰係数の推定精度が向上し、多重共線性の影響が相対的に小さくなる場合があります。
このように、多重共線性への対処法は一つではなく、「予測が目的なのか」「変数の意味を説明したいのか」といった分析の目的に応じて、適切な方法を選ぶことが重要です。
Cook’s Distanceによる影響力のある点の検出
重回帰分析でも、影響力のある点を検出することは重要です。Cook’s Distanceは、各データ点がモデル全体に与える影響を測る指標です。
Cook’s Distanceを計算し、影響力のある点を特定します。
from statsmodels.stats.outliers_influence import OLSInfluence
# statsmodelsでCook's Distanceを計算
influence = OLSInfluence(results)
cooks_d = influence.cooks_distance[0]
# 影響力のある点の検出
threshold = 4 / n
influential_points = cooks_d > threshold
print("="*60)
print("Cook's Distanceによる影響力のある点の検出")
print("="*60)
print(f" 閾値 (4/n): {threshold:.3f}")
print(f" 影響力のある点: {np.sum(influential_points)} 個")
if np.sum(influential_points) > 0:
print("\n【影響力のある点の詳細】")
influential_idx = np.where(influential_points)[0]
for idx in influential_idx:
print(f"\n- 店舗 {idx+1}:")
print(f" Cook's D: {cooks_d[idx]:.3f}")
print(f" 実際の売上: {y[idx]:.1f}万円"
f" 予測売上: {y_pred[idx]:.1f}万円"
f" 残差: {residuals[idx]:.1f}万円")
# すべての説明変数を表示
features = ', '.join([
f"{col}={X.iloc[idx, i]:.1f}"
for i, col in enumerate(X.columns)
])
print(f" 特徴: {features}")
# Cook's Distanceの可視化
plt.figure(figsize=(10, 6))
plt.stem(
range(1, n+1), cooks_d,
linefmt='b-', markerfmt='bo', basefmt=' ')
plt.axhline(
y=threshold, color='r', linestyle='--',
label=f'閾値 4/n = {threshold:.3f}')
plt.xlabel('店舗番号')
plt.ylabel("Cook's Distance")
plt.title("Cook's Distanceプロット(重回帰分析)")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
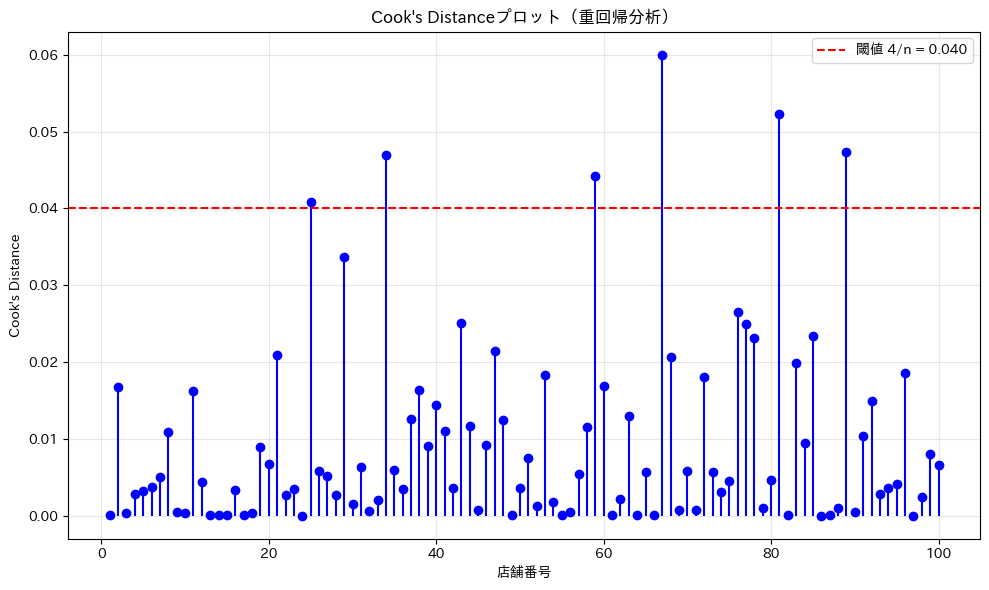
Cook’s Distanceが閾値を超える点は、モデルに大きな影響を与えている可能性があります。これらの店舗は特殊な状況にある可能性があり、個別に調査する価値があります。
最後に、すべての回帰診断結果を統合して、モデルの信頼性を総合的に評価しましょう。
まとめ
本記事では、前回までの単回帰から拡張し、説明変数が複数の場合の重回帰分析についてお話ししました。
重要なポイントを振り返りましょう。
- 重回帰モデルの理論:複数の説明変数から目的変数を予測する数学的枠組みを学びました。偏回帰係数は「他の変数を固定したときの効果」を表すという点が、単回帰との重要な違いです。
- 標準化回帰係数:変数のスケールの違いを調整することで、どの変数が最も重要かを判定できます。これにより、限られたリソースをどこに投入すべきかが明確になります。
- 多重共線性:説明変数間の相関が強い場合に生じる問題と、VIFを使った診断方法を学びました。実際のビジネスデータでは頻繁に遭遇する問題であり、適切な対処が必要です。
- 回帰診断:第3回で学んだ診断手法を重回帰に適用し、モデルの前提条件の確認とCook’s Distanceによる影響力のある点の検出を行いました。
重回帰分析は、複雑な現実世界を理解し、予測するための強力なツールです。
しかし、その力を適切に活用するためには、理論的な理解、実装スキル、そして結果を正しく解釈する能力が必要です。
本記事で学んだ内容を基礎として、実際のデータ分析に挑戦してみてください。
次回は、回帰分析をより実用的にする3つの重要な技術を学びます。
- 変数変換により曲線的な関係を扱う方法
- ダミー変数によりカテゴリカルデータを数値化する方法
- そして交互作用により変数間の相乗効果を捉える方法
これらの技術を身につけることで、現実のデータが持つ複雑な構造をより正確にモデル化できるようになります。