これまでの4回で、回帰分析の基本から重回帰分析まで説明しました。
— 第1回 —
アイスコーヒーは何杯売れる? 単回帰分析で売上予測に挑戦
https://www.salesanalytics.co.jp/datascience/datascience281/
— 第2回 —
その予測、本当に信頼できる? 統計的検定と信頼区間
https://www.salesanalytics.co.jp/datascience/datascience282/
— 第3回 —
モデルの成績表を作ろう! 決定係数とANOVA、そして回帰診断
https://www.salesanalytics.co.jp/datascience/datascience283/
— 第4回 —
複数の要因を同時に分析! 重回帰分析で店舗売上を予測
https://www.salesanalytics.co.jp/datascience/datascience284/
しかし、現実のデータ分析では、もう一歩進んだ技術が必要になることがあります。
たとえば、こんな場面を想像してみてください。
あるカフェのオーナーが、売上予測モデルを改善しようとしています。
これまでの分析で気温が売上に影響することは分かりましたが、よく観察すると、気温が25度までは売上が急増し、それ以降は緩やかになることに気づきました。
これは直線では表現できません。
また、曜日によって売上が大きく異なることも分かってきました。
月曜日と金曜日では、同じ気温でも売上が違うのです。
このような「直線では表せない関係」や「カテゴリー別の違い」をどう扱えばよいでしょうか。
実は、線形回帰モデルは見た目以上に柔軟で、適切な工夫により、これらの複雑な関係も表現できるのです。
本記事では、回帰分析をより実用的にする3つの重要な技術を学びます。
- 変数変換により曲線的な関係を扱う方法
- ダミー変数によりカテゴリカルデータを数値化する方法
- そして交互作用により変数間の相乗効果を捉える方法
これらの技術を身につけることで、現実のデータが持つ複雑な構造をより正確にモデル化できるようになります。
Contents
非線形関係を線形モデルで扱う(変数変換)
なぜ変数変換が必要なのか
線形回帰モデルは「線形」という名前がついていますが、これは必ずしもすべての関係が直線でなければならないという意味ではありません。
適切な変数変換を行うことで、曲線的な関係も扱えるのです。
たとえば、働き始めてからの経験年数と年収の関係を考えてみましょう。
新卒で入社してから数年間は急速に年収が上がりますが、ある程度経験を積むと上昇率は緩やかになります。
このような「最初は急で、後に緩やか」という関係は、対数関数でうまく表現できます。
まず、必要なライブラリをインポートし、データ分析の準備をします。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import japanize_matplotlib from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures from sklearn.metrics import r2_score, mean_squared_error import statsmodels.api as sm from scipy import stats
対数変換
対数変換は、指数関数的な関係を線形化する強力な手法です。
数学的には、指数関数的な関係 y = a \cdot b^x は、対数を取ることで線形関係 \log(y) = \log(a) + x\log(b) に変換されます。
経験年数と年収の関係を例に、対数変換の効果を確認してみましょう。
# 乱数のシード固定
np.random.seed(42)
# 経験年数の生成
experience = np.linspace(0.5, 30, 100)
# 経験年数に基づいて年収を設定
salary_base = 300 + 150 * np.log(experience + 1)
salary = salary_base + np.random.normal(0, 20, 100)
# データフレームの作成
salary_data = pd.DataFrame({
'経験年数': experience,
'年収': salary
})
print("データの先頭5行:")
print(salary_data.head())
print("\nデータの概要:")
print(salary_data.describe().round(1))
以下、実行結果です。
データの先頭5行:
経験年数 年収
0 0.500000 370.754049
1 0.797980 385.234269
2 1.095960 423.955494
3 1.393939 461.401641
4 1.691919 443.855092
データの概要:
経験年数 年収
count 100.0 100.0
mean 15.2 685.1
std 8.6 111.3
min 0.5 370.8
25% 7.9 626.6
50% 15.2 716.5
75% 22.6 779.4
max 30.0 822.5
このデータは、経験年数が増えるにつれて年収が増加しますが、その増加率は徐々に小さくなるという現実的なパターンを反映しています。
まずは何も工夫せず、経験年数と年収の関係をそのまま線形回帰で表します。
# '年収'列を除いたデータを説明変数として設定
X_simple = salary_data.drop(['年収'], axis=1)
# '年収'列を目的変数として設定
y_simple = salary_data['年収']
# 線形回帰モデルのインスタンスを作成
model_simple = LinearRegression()
# モデルをデータにフィットさせる
model_simple.fit(X_simple, y_simple)
# 説明変数を用いて年収を予測
y_pred_simple = model_simple.predict(X_simple)
# 決定係数R^2を計算
r2_simple = r2_score(y_simple, y_pred_simple)
# 散布図と回帰直線をプロット
plt.figure(figsize=(5, 4))
plt.scatter(X_simple, y_simple, alpha=0.5, s=20)
plt.plot(X_simple, y_pred_simple, 'r-', linewidth=2)
plt.xlabel('経験年数')
plt.ylabel('年収(万円)')
plt.title(f'単純な線形回帰\n[latex]R^2 = {r2_simple:.3f}[/latex]')
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
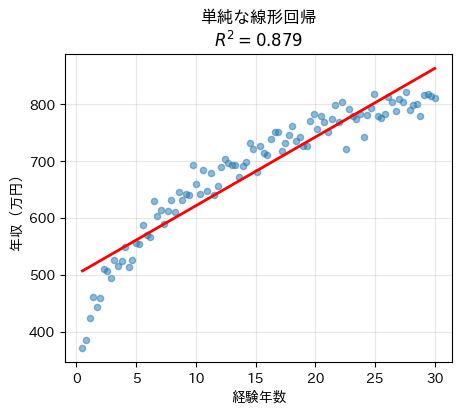
直線は引けていますが、データの増え方(初期は急で、後半は緩やか)を十分に表現できていません。
このように、関係が曲線的な場合、単純な線形回帰では当てはまりが悪くなります。
次に、経験年数を対数変換してから線形回帰を行います。
これは「成長が次第に鈍化する」ような関係を、線形モデルで扱いやすくするための工夫です。
# 説明変数を対数変換
X_log = np.log(X_simple + 1).values.reshape(-1, 1)
# 線形回帰モデルのインスタンスを作成
model_log = LinearRegression()
# モデルをデータにフィットさせる
model_log.fit(X_log, y_simple)
# 説明変数を用いて年収を予測
y_pred_log = model_log.predict(X_log)
# 決定係数R^2を計算
r2_log = r2_score(y_simple, y_pred_log)
# 散布図と回帰直線をプロット
plt.figure(figsize=(5, 4))
plt.scatter(X_simple, salary, alpha=0.5, s=20)
plt.plot(X_simple, y_pred_log, 'r-', linewidth=2)
plt.xlabel('経験年数')
plt.ylabel('年収(万円)')
plt.title(f'対数変換(説明変数)\n[latex]R^2 = {r2_log:.3f}[/latex]')
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
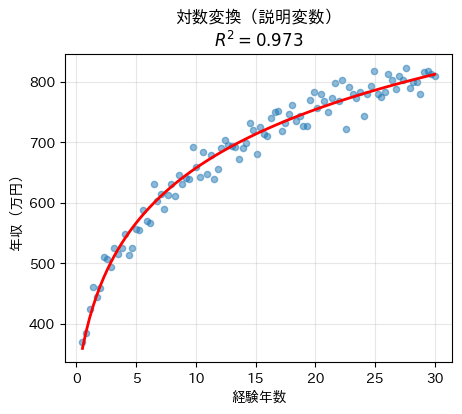
直線がデータの傾向をうまく捉えるようになり、R^2 も改善します。
これは、対数変換によって「曲線的な関係」を見かけ上、線形に近づけられたためです。
最後に、対数変換後の説明変数そのものを横軸に取り、本当に線形関係になっているかを視覚的に確認します。
# 対数変換後の変数どうしの関係を確認
plt.figure(figsize=(5, 4))
plt.scatter(X_log, salary, alpha=0.5, s=20)
plt.plot(X_log, y_pred_log, 'r-', linewidth=2)
plt.xlabel('log(経験年数 + 1)')
plt.ylabel('年収(万円)')
plt.title('対数変換後の線形関係')
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
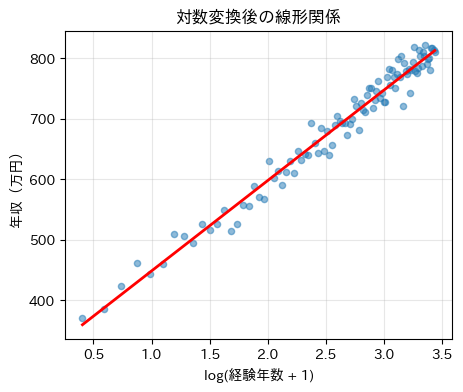
多項式回帰
もう一つの重要な変換は多項式変換です。
売上と広告費の関係を考えてみましょう。
広告費を増やすと売上は増えますが、ある程度を超えると効果が薄れる(収穫逓減の法則)ことがあります。
このような関係は2次関数でうまく表現できます。2次の場合、y = \beta_0 + \beta_1 x + \beta_2 x^2 + \varepsilon となります。
これは x と x^2 を別々の説明変数として扱うことで、線形モデルの枠組みで扱えます。
まず、広告費と売上の間に「収穫逓減(最初は効くが、次第に効きにくくなる)」関係があるという想定で、2次関数的なデータを人工的に作ります。
# 再現性のため乱数シードを固定
np.random.seed(42)
# 広告費(説明変数)
ad_cost = np.linspace(0, 100, 150) # 広告費(万円)
# 2次関数的な関係(収穫逓減)
sales_base = 50 + 5 * ad_cost - 0.03 * ad_cost**2
# ノイズを加えた実際の売上データ
sales = sales_base + np.random.normal(0, 10, 150)
# データフレームの作成
sales_data = pd.DataFrame({
'広告費': ad_cost,
'売上': sales
})
print("データの先頭5行:")
print(sales_data.head())
print("\nデータの概要:")
print(sales_data.describe().round(1))
以下、実行結果です。
データの先頭5行:
広告費 売上
0 0.000000 54.967142
1 0.671141 51.959549
2 1.342282 63.134243
3 2.013423 75.175797
4 2.684564 60.865079
データの概要:
広告費 売上
count 150.0 150.0
mean 50.0 198.8
std 29.2 63.7
min 0.0 52.0
25% 25.0 156.7
50% 50.0 226.6
75% 75.0 249.1
max 100.0 281.3
x と x^2 を別々の説明変数として扱うことで、モデル自体は線形回帰のまま2次曲線を表現できるようにします。
# 説明変数と目的変数の設定
X = sales_data.drop('売上', axis=1)
y = sales_data['売上']
# PolynomialFeaturesで、2次の多項式特徴量x,x^2を生成
poly = PolynomialFeatures(
degree=2, # 2次の多項式
include_bias=False, # バイアス項(切片)を除く
)
# 2次の多項式特徴量に変換
X_poly = poly.fit_transform(X)
print("2次の多項式特徴量の先頭5行:")
print(X_poly[:5])
以下、実行結果です。
2次の多項式特徴量の先頭5行: [[0. 0. ] [0.67114094 0.45043016] [1.34228188 1.80172064] [2.01342282 4.05387145] [2.68456376 7.20688257]]
X_poly の中身は次のようになっています。
$$
X =
\begin{bmatrix}
x & x^2
\end{bmatrix}
$$
これによりモデルは、次のような形の線形回帰問題として推定できます。
$$
売上 = \beta_0 + \beta_1 x + \beta_2 x^2
$$
作成した多項式特徴量を使って、2次の多項式回帰モデルを学習し予測をします。
# 多項式回帰モデルの学習 model_poly = LinearRegression() model_poly.fit(X_poly, y) # 予測値 y_pred_poly = model_poly.predict(X_poly)
比較のため、x だけを使った通常の線形回帰も作ります。
# 1次(線形)モデル model_linear = LinearRegression() model_linear.fit(X, y) # 予測値 y_pred_linear = model_linear.predict(X)
このモデルでは、広告費と売上の関係を「一直線」でしか表現できません。
実データ・1次モデル・2次モデルを同じ図に描き、どちらがデータの傾向をうまく捉えているかを確認します。
# グラフのサイズを設定
plt.figure(figsize=(10, 6))
# 実データの散布図をプロット
plt.scatter(
X, y,
alpha=0.5, s=20, label='実データ'
)
# 1次(線形)モデルの予測値をプロット
plt.plot(
X, y_pred_linear,
'g-', linewidth=2,
label=f'1次(線形): [latex]R^2[/latex] = {r2_score(y, y_pred_linear):.3f}'
)
# 2次(多項式)モデルの予測値をプロット
plt.plot(
X, y_pred_poly,
'r-', linewidth=2,
label=f'2次(多項式): [latex]R^2[/latex] = {r2_score(y, y_pred_poly):.3f}'
)
plt.xlabel('広告費(万円)')
plt.ylabel('売上(万円)')
plt.title('多項式回帰による収穫逓減の表現')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
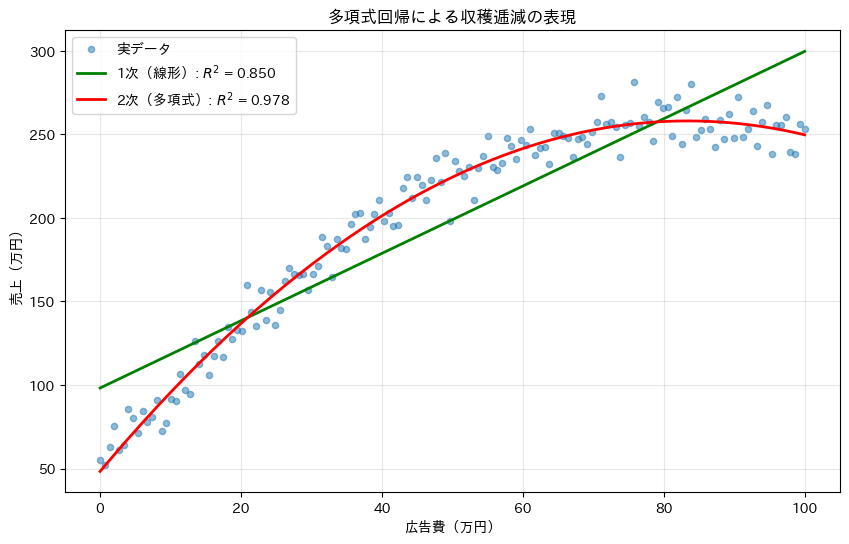
最後に、推定された係数を確認し、収穫逓減が数値として現れているかをチェックします。
print("多項式回帰の係数:")
print(f" 切片: {model_poly.intercept_:.2f}")
print(f" 1次の係数: {model_poly.coef_[0]:.3f}")
print(f" 2次の係数: {model_poly.coef_[1]:.5f}")
以下、実行結果です。
多項式回帰の係数: 切片: 48.28 1次の係数: 5.027 2次の係数: -0.03014
2次の係数が負の値になっていることから、広告費が増えるほど効果が逓減することが数値的に確認できます。
このような洞察は、最適な広告費を決定する際に重要です。
カテゴリカル変数の扱い(ダミー変数)
ダミー変数の基本概念
これまで扱ってきた変数は、気温や売上のような連続的な数値でした。
しかし、現実のデータには「曜日」「地域」「性別」といったカテゴリカル変数も多く存在します。
これらを回帰分析で扱うには、数値化する必要があります。
ダミー変数(dummy variable)は、カテゴリーを0と1の数値で表現する方法です。
たとえば、「週末かどうか」を表すダミー変数は、週末なら1、平日なら0となります。
カフェの売上データで、曜日効果を分析してみましょう。
ここでは実データの代わりに、平日は低め、週末は高めという想定で人工データを作成します。
# 再現性のため乱数シードを固定
np.random.seed(42)
n_weeks = 20 # 20週間分
days = ['月', '火', '水', '木', '金', '土', '日']
# 各曜日の基本売上(土日が高い)
base_sales = {
'月': 100, '火': 110, '水': 115, '木': 120,
'金': 140, '土': 180, '日': 170
}
# データ生成
data_list = []
for week in range(n_weeks):
for day in days:
daily_sales = base_sales[day] + np.random.normal(0, 15)
data_list.append({
'週': week + 1,
'曜日': day,
'売上': daily_sales
})
# データフレームに変換
cafe_data = pd.DataFrame(data_list)
print("データの先頭10行:")
print(cafe_data.head(10))
以下、実行結果です。
データの先頭10行: 週 曜日 売上 0 1 月 107.450712 1 1 火 107.926035 2 1 水 124.715328 3 1 木 142.845448 4 1 金 136.487699 5 1 土 176.487946 6 1 日 193.688192 7 2 月 111.511521 8 2 火 102.957884 9 2 水 123.138401
曜日ごとに売上を平均し、「月曜はいくら、火曜はいくら…」という形で比較します。
# 曜日別の平均売上を計算
day_means = cafe_data.groupby('曜日')['売上'].mean()
# 曜日順に並べ替え
day_means = day_means.reindex(days)
# 棒グラフで表示
plt.figure(figsize=(10, 6))
plt.bar(days, day_means, color='skyblue')
plt.xlabel('曜日')
plt.ylabel('平均売上(万円)')
plt.title('曜日別の平均売上')
plt.grid(True, alpha=0.3, axis='y')
plt.show()
以下、実行結果です。
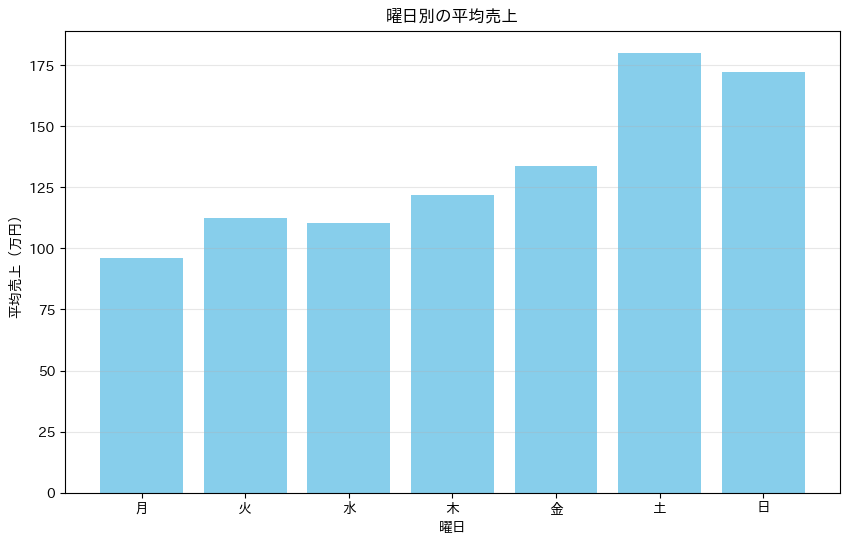
グラフから、週末(土日)の売上が平日より明らかに高いことが分かります。
このような曜日効果を回帰モデルに組み込むために、ダミー変数を使います。
ダミー変数の作成と回帰分析
pandasの`get_dummies()`関数を使ってダミー変数を作成します。
重要な点は、k個のカテゴリーがある場合、k-1個のダミー変数を作ることです。
これは「ダミー変数トラップ」を避けるためです。
# ダミー変数の作成(月曜日を基準カテゴリとする)
dummies = pd.get_dummies(
cafe_data['曜日'], # 変換する変数
prefix='曜日', # 変数名のプレフィックス
drop_first=False # 基準カテゴリを除外しない
)
# 基準カテゴリ(月曜日)を除外
dummies_model = dummies.drop('曜日_月', axis=1)
# ダミー変数を整数型に変換
dummies_model = dummies_model.astype(int)
# 曜日を火曜日始まり日曜日終わりに並べ替え
dummies_model = dummies_model[[
'曜日_火', '曜日_水', '曜日_木',
'曜日_金', '曜日_土', '曜日_日'
]]
# 元のデータと結合
cafe_data_with_dummies = pd.concat([
cafe_data, dummies_model], axis=1)
print("ダミー変数の例(最初の10行):")
print(cafe_data_with_dummies.head(10))
以下、実行結果です。
ダミー変数の例(最初の10行): 週 曜日 売上 曜日_火 曜日_水 曜日_木 曜日_金 曜日_土 曜日_日 0 1 月 107.450712 0 0 0 0 0 0 1 1 火 107.926035 1 0 0 0 0 0 2 1 水 124.715328 0 1 0 0 0 0 3 1 木 142.845448 0 0 1 0 0 0 4 1 金 136.487699 0 0 0 1 0 0 5 1 土 176.487946 0 0 0 0 1 0 6 1 日 193.688192 0 0 0 0 0 1 7 2 月 111.511521 0 0 0 0 0 0 8 2 火 102.957884 1 0 0 0 0 0 9 2 水 123.138401 0 1 0 0 0 0
各曜日に対応するダミー変数が作成されました。すべてのダミー変数が0のときが月曜日を表します。
ダミー変数を使った回帰分析を実行します。p値を出すためにstatsmodelsで実施します。
# 説明変数と目的変数の設定
X = dummies_model.values
y = cafe_data['売上'].values
# 回帰分析の実行
X_with_const = sm.add_constant(X)
model_days = sm.OLS(y, X_with_const).fit()
# 結果を表示
print("回帰分析の結果:")
print("=" * 60)
print(f"決定係数 R²: {model_days.rsquared:.3f}")
print(f"自由度調整済み R²: {model_days.rsquared_adj:.3f}")
print("\n回帰係数(月曜日を基準):")
print("-" * 40)
# 係数と曜日名の対応
column_names = ['切片(月曜日の売上)']
column_names += [f"{col} の 効果" for col in dummies_model.columns]
# 係数とp値を表示
for i, name in enumerate(column_names):
coef = model_days.params[i]
p_val = model_days.pvalues[i]
print(f"{name:20s}: {coef:7.2f} (p値: {p_val:.4f})")
以下、実行結果です。
回帰分析の結果: ============================================================ 決定係数 R²: 0.825 自由度調整済み R²: 0.817 回帰係数(月曜日を基準): ---------------------------------------- 切片(月曜日の売上) : 95.88 (p値: 0.0000) 曜日_火 の 効果 : 16.51 (p値: 0.0003) 曜日_水 の 効果 : 14.54 (p値: 0.0013) 曜日_木 の 効果 : 25.92 (p値: 0.0000) 曜日_金 の 効果 : 37.66 (p値: 0.0000) 曜日_土 の 効果 : 84.18 (p値: 0.0000) 曜日_日 の 効果 : 76.22 (p値: 0.0000)
回帰係数は「月曜日との差」を表します。
たとえば、土曜日の係数84.18は、土曜日は月曜日より平均84.18万円売上が高いことを意味します。
p値が小さい曜日は、月曜日と統計的に有意な差があることを示しています。
ダミー変数の解釈と活用
ダミー変数の係数を正しく解釈することが重要です。予測値を計算して確認してみましょう。
# 予測値を格納する辞書
predictions = {}
# 基準カテゴリー(月曜日)の予測値(切片)
intercept = model_days.params[0]
predictions['月'] = intercept
# 他の曜日の予測値を計算
for i, day in enumerate(days[1:], 1):
predictions[day] = intercept + model_days.params[i]
# 実際の平均と予測値の比較
comparison = pd.DataFrame({
'実際の平均': day_means,
'モデルの予測': predictions
})
# 比較結果を表示
print("曜日別売上の比較:")
print(comparison.round(1))
以下、実行結果です。
曜日別売上の比較: 実際の平均 モデルの予測 月 95.9 95.9 火 112.4 112.4 水 110.4 110.4 木 121.8 121.8 金 133.5 133.5 土 180.1 180.1 日 172.1 172.1
グラフで視覚的に確認します。
# グラフのサイズを設定
fig, ax = plt.subplots(figsize=(10, 6))
# 曜日の数に基づいてx軸の位置を設定
x_pos = np.arange(len(days))
# 棒グラフの幅を設定
width = 0.35
# 実際の平均値を棒グラフで描画
bars1 = ax.bar(
x_pos - width/2, comparison['実際の平均'], width,
label='実際の平均', color='lightblue'
)
# モデルの予測値を棒グラフで描画
bars2 = ax.bar(
x_pos + width/2, comparison['モデルの予測'], width,
label='モデルの予測', color='orange'
)
ax.set_xlabel('曜日')
ax.set_ylabel('売上(万円)')
ax.set_title('曜日別売上:実際vs予測')
ax.set_xticks(x_pos)
ax.set_xticklabels(days)
ax.legend()
ax.grid(True, alpha=0.3, axis='y')
plt.show()
以下、実行結果です。
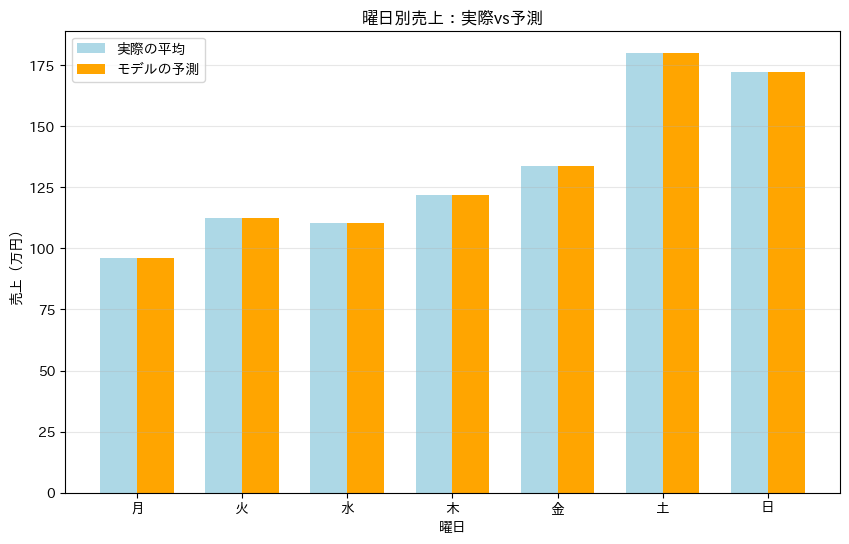
モデルの予測値が実際の平均値とほぼ一致していることから、ダミー変数が曜日効果を適切に捉えていることが分かります。
交互作用:変数同士の相乗効果
交互作用とは何か
これまでは各変数が独立に目的変数に影響すると仮定していました。
しかし、現実には変数同士が影響し合うことがあります。
たとえば、「気温の売上への影響が、平日と週末で異なる」という状況です。
これを交互作用(interaction)と呼びます。
数式では、交互作用項を含むモデルは次のように表されます。
$$
y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1 \times x_2 + \varepsilon
$$
ここで、\beta_3 x_1 \times x_2 が交互作用項です。
気温と週末の交互作用
アイスコーヒーの売上において、気温の効果が平日と週末で異なるかを、人工的に作成したサンプルデータで分析してみましょう。
ということで、サンプルデータを人工的に作ります。
分析に使う説明変数を用意します。ここでは 200日分のデータを想定します。
np.random.seed(42) n_days = 200 # 気温(15〜35℃の一様分布) temperature = np.random.uniform(15, 35, n_days) # 週末フラグ(0=平日, 1=週末) is_weekend = np.random.choice([0, 1], n_days, p=[5/7, 2/7])
売上は次のような仕組みで発生すると仮定し、人工的にデータを生成します。
$$
売上=50+3×気温+30×週末+2×(気温×週末)+ノイズ
$$
sales = (
50
+ 3 * temperature
+ 30 * is_weekend
+ 2 * temperature * is_weekend
+ np.random.normal(0, 10, n_days)
)
生成したデータを、データフレームにします。
df = pd.DataFrame({
"気温": temperature,
"週末": is_weekend,
"売上": sales
})
print("データフレームの先頭5行を表示:")
print(df.head())
以下、実行結果です。
データフレームの先頭5行を表示:
気温 週末 売上
0 22.490802 0 130.527195
1 34.014286 0 152.252897
2 29.639879 0 145.739166
3 26.973170 1 211.763181
4 18.120373 0 107.602782
平日と週末の件数も確認しておきます。
df["週末"].value_counts()
以下、実行結果です。
週末 0 144 1 56 Name: count, dtype: int64
交互作用を視覚的に比較するため、データを 平日と週末 に分割します。
weekday = df[df["週末"] == 0] weekend = df[df["週末"] == 1]
この分割により、それぞれ別々に回帰直線を当てられるようになります。
まずは回帰直線を描かず、点の分布だけを確認します。
plt.figure(figsize=(10, 6))
# 平日のデータをプロット
plt.scatter(
weekday["気温"],
weekday["売上"],
alpha=0.5,
label="平日"
)
# 週末のデータをプロット
plt.scatter(
weekend["気温"],
weekend["売上"],
alpha=0.5,
label="週末"
)
plt.xlabel("気温(℃)")
plt.ylabel("アイスコーヒー売上(杯)")
plt.title("気温と売上の関係(平日 vs 週末)")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
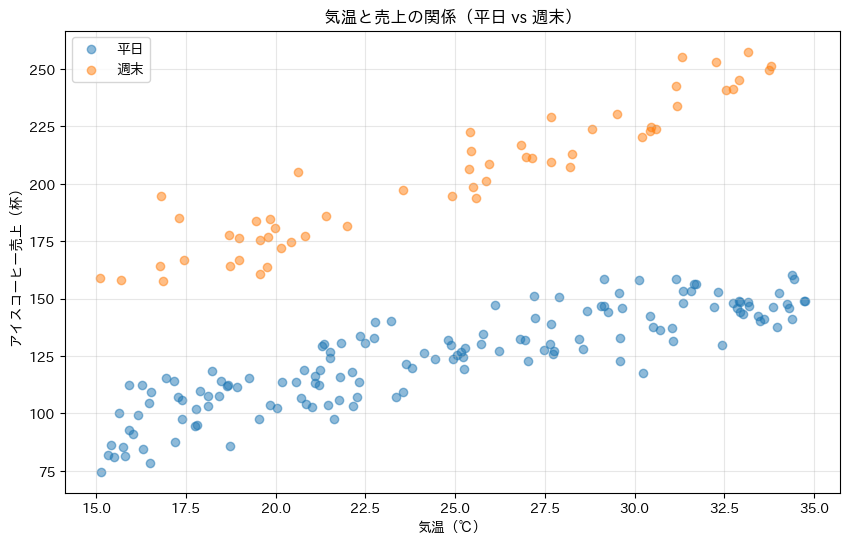
次に、気温と売上の関係を直線(一次式)で近似します。
# 平日のデータに対する線形回帰のパラメータを計算
weekday_fit = np.polyfit(
weekday["気温"],
weekday["売上"],
1
)
# 週末のデータに対する線形回帰のパラメータを計算
weekend_fit = np.polyfit(
weekend["気温"],
weekend["売上"],
1
)
散布図の上に、平日・週末それぞれの回帰直線を描きます。
# 気温の範囲を設定
x_range = np.linspace(15, 35, 100)
# グラフのサイズを設定
plt.figure(figsize=(10, 6))
# 平日のデータをプロット
plt.scatter(
weekday["気温"], weekday["売上"],
alpha=0.5, label="平日"
)
# 週末のデータをプロット
plt.scatter(
weekend["気温"], weekend["売上"],
alpha=0.5, label="週末"
)
# 平日の回帰直線をプロット
plt.plot(
x_range, np.polyval(weekday_fit, x_range),
linewidth=2, label="平日(直線)"
)
# 週末の回帰直線をプロット
plt.plot(
x_range, np.polyval(weekend_fit, x_range),
linewidth=2, label="週末(直線)"
)
plt.xlabel("気温(℃)")
plt.ylabel("アイスコーヒー売上(杯)")
plt.title("気温と売上の関係(平日 vs 週末)")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
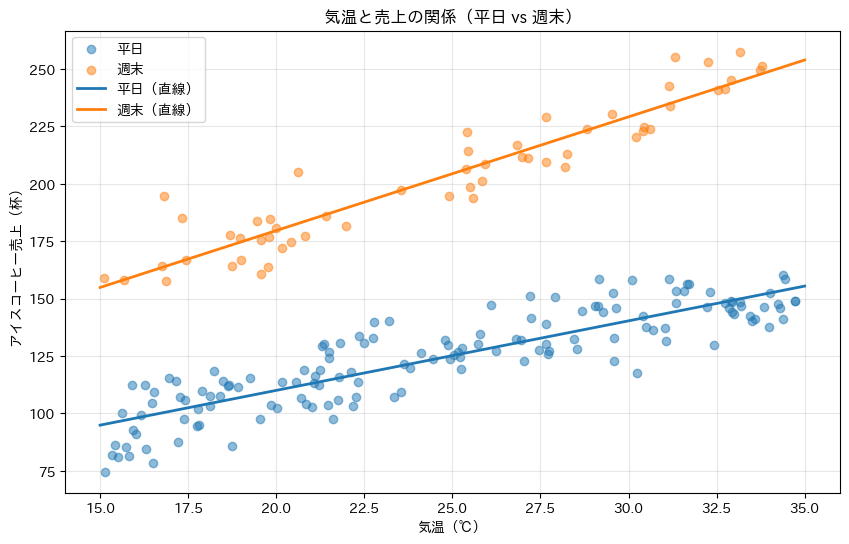
平日と週末の傾きの差を見てみます。
# 平日の傾きを取得
weekday_slope = weekday_fit[0]
# 週末の傾きを取得
weekend_slope = weekend_fit[0]
print(f"平日の傾き: {weekday_slope:.2f}")
print(f"週末の傾き: {weekend_slope:.2f}")
print(f"傾きの差: {weekend_slope - weekday_slope:.2f}")
以下、実行結果です。
平日の傾き: 3.03 週末の傾き: 4.95 傾きの差: 1.92
これが交互作用の効果です。
週末は外出する人が多いため、気温の影響がより顕著に現れると解釈できます。
交互作用を含むモデルの構築
交互作用項を明示的にモデルに含めて分析します。
まず、気温と週末フラグの積を取り、「交互作用項」を新しい列として作成します。
# 新しいデータフレームを作成
interaction_data = df.copy()
# 気温と週末の相互作用項を追加
interaction_data['気温×週末'] = (
interaction_data['気温']
* interaction_data['週末']
)
# データフレームの最初の数行を表示して確認
print(interaction_data.head())
以下、実行結果です。
気温 週末 売上 気温×週末 0 22.490802 0 130.527195 0.00000 1 34.014286 0 152.252897 0.00000 2 29.639879 0 145.739166 0.00000 3 26.973170 1 211.763181 26.97317 4 18.120373 0 107.602782 0.00000
この交互作用を表す変数は、以下の性質を持ちます。
- 平日(週末=0) → 常に 0
- 週末(週末=1) → 気温そのもの
次に、回帰分析に使う変数を整理します。
X = interaction_data[['気温', '週末', '気温×週末']].values y = interaction_data['売上'].values
このとき、モデルは次の形を想定しています。
$$
売上 = \beta_0
+ \beta_1 \cdot 気温
+ \beta_2 \cdot 週末
+ \beta_3 \cdot (気温 \times 週末)
+ \varepsilon
$$
statsmodels を使って、 切片(定数項)を含む線形回帰を実行します。
import statsmodels.api as sm # 定数項を追加して説明変数を拡張 X_with_const = sm.add_constant(X) # 回帰モデルを作成 model_interaction = sm.OLS(y, X_with_const).fit()
add_constant を使うことで、\beta_0(切片)を同時に推定できます。
まずは、係数と統計的有意性を確認します。
print("交互作用を含むモデルの結果:")
print("=" * 60)
print(model_interaction.summary().tables[1])
以下、実行結果です。
交互作用を含むモデルの結果:
============================================================
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 49.5405 3.504 14.139 0.000 42.631 56.450
x1 3.0260 0.138 21.951 0.000 2.754 3.298
x2 31.0806 7.000 4.440 0.000 17.276 44.885
x3 1.9236 0.277 6.952 0.000 1.378 2.469
==============================================================================
ここで注目すべきポイントは以下です。
- x3(気温×週末) の係数
- その符号(正か負か)
- p値(有意かどうか)
交互作用項(気温×週末)の係数が正で有意です。これは、「週末には気温が売上により強く影響する」ことを意味しています。
要するに、「暑い週末ほど、アイスコーヒーの需要が加速する」という行動の違いを数量化したものです。
このことより、たとえば次のような意思決定にそのまま活用できます。
- 週末の仕込み量調整
- 繁忙日の人員配置
- 気温予報と連動したオペレーション
最後に、数値をそのまま式の形にして、直感的に確認します。
print("推定された回帰式:")
print(
f"売上 = {model_interaction.params[0]:.1f} + "
f"{model_interaction.params[1]:.2f}×気温 + "
f"{model_interaction.params[2]:.1f}×週末 + "
f"{model_interaction.params[3]:.2f}×(気温×週末)"
)
以下、実行結果です。
推定された回帰式: 売上 = 49.5 + 3.03×気温 + 31.1×週末 + 1.92×(気温×週末)
全5回のシリーズの振り返り
ここまで5回にわたって回帰分析を学んできました。各回で学んだ内容を振り返り、それらがどのようにつながっているかを確認しましょう。
第1回:単回帰分析の基礎
最小二乗法の原理を学びました。観測データから最も当てはまりの良い直線を見つける方法を、数式の導出からPython実装まで丁寧に理解しました。これがすべての基礎となります。
第2回:統計的検定と信頼区間
推定した係数が「偶然ではなく意味がある」ことを確認する方法を学びました。t検定により係数の有意性を判定し、信頼区間により推定値の不確実性を定量化しました。
第3回:モデルの評価と診断
決定係数でモデルの説明力を測り、ANOVAで全体的な有意性を確認しました。さらに残差診断により、モデルの前提条件が満たされているかを確認する方法を学びました。
第4回:重回帰分析
複数の要因を同時に考慮する方法を学びました。多重共線性の問題とその対処法も理解し、より現実的なモデル構築が可能になりました。
第5回(本記事):変数変換とダミー変数
線形モデルの柔軟性を大幅に高める技術を学びました。非線形関係、カテゴリカル変数、交互作用を適切に扱うことで、複雑な現実のデータに対応できるようになりました。
重要なのは、これらの技術を機械的に適用するのではなく、データの性質と分析の目的に応じて適切に選択・組み合わせることです。
モデルを複雑にすれば精度は上がりますが、解釈が困難になります。ビジネスや研究の現場では、精度と解釈可能性のバランスが重要です。
まとめ
本記事では、回帰分析をより実用的にする3つの重要な技術を学びました。
- 変数変換:対数関数的な関係や2次関数的な関係など、様々な非線形パターンを線形モデルの枠組みで扱えることを学びました。
- ダミー変数:曜日や地域といったカテゴリカルデータを数値化する方法を学びました。
- 交互作用:変数同士の相乗効果を捉える方法を学びました。
これらの技術により、線形回帰という一見単純な手法が、実は非常に柔軟で強力なツールであることが理解できたと思います。重要なのは、データの性質を理解し、適切な変換や変数を選択することです。
5回にわたり、回帰分析の理論と実装を基礎から学んできました。この知識は、データ分析の実務において強力な武器となるはずです。
しかし、ここで学んだことは、あくまでも出発点に過ぎません。実際のデータと向き合い、試行錯誤を重ねることで、真の実力が身についていきます。
データから価値ある洞察を引き出し、より良い意思決定につなげる。それが回帰分析の、そしてデータサイエンスの本質です。
本シリーズが、皆さんのデータ分析の旅の確かな第一歩となることを願っています。
— 第1回 —
アイスコーヒーは何杯売れる? 単回帰分析で売上予測に挑戦
https://www.salesanalytics.co.jp/datascience/datascience281/
— 第2回 —
その予測、本当に信頼できる? 統計的検定と信頼区間
https://www.salesanalytics.co.jp/datascience/datascience282/
— 第3回 —
モデルの成績表を作ろう! 決定係数とANOVA、そして回帰診断
https://www.salesanalytics.co.jp/datascience/datascience283/
— 第4回 —
複数の要因を同時に分析! 重回帰分析で店舗売上を予測
https://www.salesanalytics.co.jp/datascience/datascience284/
— 第5回 —
変数変換とダミー変数で回帰分析をパワーアップ
https://www.salesanalytics.co.jp/datascience/datascience285/