非線形最適化は、ビジネス、工学、データサイエンスなど、多岐にわたる分野で不可欠なツールとなっています。

この複雑で魅力的な領域に飛び込む準備はできていますか？

今回は、線形最適化から非線形最適化への遷移、非線形最適化の基本理論、さらには制約の扱い方や目的関数の設定について扱います。

また、ScyPyを用いた非線形最適化問題の解法についても解説し、実践的な応用例を通じて理論の実用性を検証します。

ビジネスの非線形で複雑な問題に対処するための洞察を得る準備をしましょう！

はじめに

前回の線形最適化の基礎に引き続き、本回ではより複雑かつ現実的な問題に取り組むための非線形最適化に焦点を当てます。

Python SciPyで手を動かしながら学ぶ数理最適化– 第2回: 線形最適化の基礎 –

線形最適化は、目的関数と制約がすべて線形関数で表される最適化問題です。これに対して、非線形最適化では目的関数や制約が非線形関数で表されます。

この非線形性は、問題の解を見つける上で追加の複雑さをもたらし、解法もより高度で多様です。

例えば、凸関数、非凸関数、滑らかな関数、滑らかでない関数など、非線形関数の種類によって適用するアルゴリズムも変わります。

 

非線形最適化の基本理論

　非線形最適化とは

非線形最適化は、目的関数や制約条件が非線形関数で表される最適化問題です。

これらの問題は、一般に解が複数存在したり、局所的な最適解が複数存在する可能性があるなど、線形最適化よりも解くのが難しい特徴を持っています。

非線形最適化の目標は、与えられた制約の下で目的関数を最大化または最小化する解を見つけることです。

 

　非線形最適化問題の特徴と難易度

非線形最適化問題の主な特徴は、問題の解が直感的でなかったり、解析的に解を求めるのが困難な場合が多いことです。

また、非線形関数の性質によっては、局所的な最適解が複数存在する可能性があり、全体の最適解を見つけることがさらに難しくなります。

これらの特徴は、非線形最適化問題の解法選択やアルゴリズムの設計に影響を与え、難易度を高めます。

 

　基本的な非線形関数の種類と例

非線形関数は多岐にわたりますが、いくつかの基本的な種類を紹介します。

• 凸関数（Convex Functions）: 関数の任意の2点を結んだ線分が関数のグラフの上にある場合、その関数は凸関数です。例えば、f(x)=x^2 は凸関数です。
• 非凸関数（Non-Convex Functions）: 凸関数の条件を満たさない関数は非凸関数です。例えば、f(x)=sin(x) は非凸関数です。
• 滑らかな関数（Smooth Functions）: 関数が微分可能であれば、滑らかな関数と言えます。例えば、f(x)=e^x は滑らかな関数です。
• 滑らかでない関数（Non-Smooth Functions）: 微分不可能な点を持つ関数は、滑らかでない関数です。例えば、f(x)=|x| は滑らかでない関数です。

 

これらの基本的な非線形関数の理解は、非線形最適化問題を解く上での第一歩です。

 

制約の扱い方と目的関数の設定

　制約のある非線形最適化と制約のない非線形最適化

非線形最適化問題は、制約があるかないかによって大きく2つのカテゴリに分けられます。

制約のある非線形最適化
このタイプの問題では、目的関数の最適化を行いつつ、一つ以上の制約条件を満たす必要があります。制約条件は不等式や等式で表され、解が制約を満たす範囲内でのみ受け入れられます。

制約のない非線形最適化
ここでは、制約条件を考慮せずに目的関数を最適化します。これは理論的には単純ですが、現実の問題ではしばしば制約条件が存在するため、制約のない問題は比較的少ないです。

 

　目的関数の設定方法と注意点

目的関数は、最適化の目標を数学的に表現したものです。目的関数を設定する際の注意点は以下の通りです。

• 明確な目標: 目的関数は、問題の目標を明確に反映している必要があります。最適化の目標が不明確だと、適切な目的関数を定義できず、適切な解が得られない可能性があります。
• 実現可能性: 目的関数は、実現可能で計算可能であることが重要です。過度に複雑な関数は、計算の難易度を上げ、解の探索を困難にします。可能か限りシンプルにしましょう。

 

　制約条件の設定と種類

制約条件は、問題解決の範囲を限定する役割を果たします。制約条件の主な種類は以下の通りです。

等式制約
形式 g(x)=0 の条件で、解が特定の値に等しいことを要求します。

不等式制約
形式 h(x) \le 0 や h(x) \ge 0  の条件で、解が特定の範囲内にあることを要求します。

 

制約条件の適切な設定は、問題の解法に大きく影響します。現実の問題ではしばしば複数の制約条件が組み合わさり、これらの条件をうまく扱うことが非線形最適化の鍵となります。

 

ScyPyを用いた非線形最適化問題の解法

　ScyPyにおける非線形最適化問題のモデル化

ScyPyのoptimizeモジュールには、非線形最適化問題を解くための様々な関数が含まれています。

たとえば、minimize関数です。

問題をモデル化する際、まず目的関数と制約条件をPythonの関数として定義します。次に、これらの関数をScyPyの最適化関数に渡して、最適な解を求めます。

 

　適切なアルゴリズムの選定

ScyPyには、様々な最適化アルゴリズムが用意されています。問題の種類や特性に応じて適切なアルゴリズムを選ぶことが重要です。

たとえば、minimize関数には一般的な最適化問題に対応し、異なるアルゴリズムを指定することができます。

BFGSやNelder-Meadなど、問題の性質に合わせて選択しましょう。

アルゴリズム	特徴	利点	欠点
Nelder-Mead	微分不要、制約なし	単純、微分困難な関数に適用可能	収束が遅い、大規模問題に不向き
BFGS	勾配利用、準ニュートン法	高速収束、多次元問題に適用	勾配計算必要、非常に非線形問題に収束難
CG	勾配利用、大規模問題に適用	メモリ使用少、大規模問題に有効	勾配計算必要、局所最適解に陥りやすい
Powell	微分不要、制約なし	微分困難な関数に適用可能	収束が遅い、大規模問題に不向き
L-BFGS-B	境界制約付き、準ニュートン法	メモリ使用少、境界制約考慮可能	複雑な制約に対応困難
TNC	勾配利用、非線形制約考慮可能	制約付き問題対応、高速収束可能	勾配・ヘッセ行列計算必要
SLSQP	線形・非線形制約考慮可能	様々な種類の制約対応可能	問題によっては収束困難

 

　実装例とコードの解説

ここでは、f(x_0,x_1)=x_0^2+x_1^2 を最小化する、単純な非線形最適化問題を解く例を示します。

import numpy as np
from scipy.optimize import minimize

# 目的関数の定義
def objective(x):
    return x[0]**2 + x[1]**2

# 初期値
x0 = np.array([1, 1])

# 最適化の実行
result = minimize(objective, x0, method='BFGS')

print("最適解:", result.x)
print("目的関数の値:", result.fun)

 

• numpyライブラリをインポートします。numpy を用いて行列計算を効率よく行うためです。
• scipy.optimize から minimize 関数をインポートします。minimize 関数は一般的な最小化問題（目的関数を最小にするようなパラメータを見つける）を解くためのものです。
• objective 関数を定義します。この関数が最小化するべき目的関数です。ここでは２変数関数 x[0]**2 + x[1]**2 の最小化を目指します。
• 初期値 x0 を np.array([1, 1]) と設定します。最適化問題では、初期値からスタートして目的関数を最小化する方向へ進みます。この初期値は適当に設定しても良いですが、問題によっては初期値が最終結果に影響することもあります。
• minimize 関数を使って最適化を行います。引数には目的関数、初期値、そして最適化アルゴリズムを指定します。ここでは `BFGS` アルゴリズムを使用しています。
• result.x は最適解を表し、result.fun は最適解における目的関数の値を表します。

 

以下、実行結果です。

最適解: [-1.07505143e-08 -1.07505143e-08]
目的関数の値: 2.311471135620994e-16

 

このように、ScyPyを使用すると、比較的簡単に非線形最適化問題をモデル化し、解決することができます。

 

非線形最適化の実践的応用例

　事例: マーケティングキャンペーンの最適化

ABC株式会社は中堅家電メーカーで、新しいスマートホームデバイスの市場投入を控えています。

限られたマーケティング予算を持ち、テレビ、オンライン、紙媒体の3つの広告チャネルにわたって最適に予算を配分したいと考えています。目標は、限られた予算内で最大のリーチ（影響を与える顧客数）を達成することです。リーチは各広告チャネルの広告支出に非線形に依存し、合計予算は制限されています。

定式化すると以下のようになります。

目的関数：
\displaystyle \text{maximize } R=R_{TV}​(x)+R_{Online}​(y)+R_{Print}​(z)

制約条件：
\displaystyle x \times C_{TV}​ + y \times C_{Online} ​+ z \times C_{Print}​ \le B

• R は総リーチ
• R_{TV}(x)、R_{Online}(y)、R_{Print}(z) は各広告チャネルのリーチ関数
• x、y、z は各広告チャネルへの投下量
• C_{TV}、C_{Online}、C_{Print}は各広告チャネルの単位あたりのコスト
• B は総予算

 

リーチ関数は、非線形の曲線で描きます。今回は、次のような関数を使います。

\displaystyle R(x)=base \times (1-e^{-x/shape})

どのような関数なのか、Pythonで描いてみます。横軸が投下量で、縦軸がその効果（リーチ）です。

以下、コードです。

import matplotlib.pyplot as plt
import numpy as np

# Cost per unit
unit_cost = 20000

# Base reach
base_reach = 300000

# Online calculation formula
def online_reach(x):
    return base_reach * (1 - np.exp(-x / 40))

# Online budget range (0 to 5000000 yen)
online_budget = np.linspace(0, 5000000, 100)

# Calculation of reach
reaches = online_reach(online_budget / unit_cost)

# Graph drawing
plt.figure(figsize=(10, 6))
plt.plot(online_budget, reaches)
plt.xlabel('online Advertising Budget (Yen)')
plt.ylabel('online Reach')
plt.title('Relationship between online Advertising Budget and Reach')
plt.grid(True)
plt.show()

 

以下、実行結果です。

 

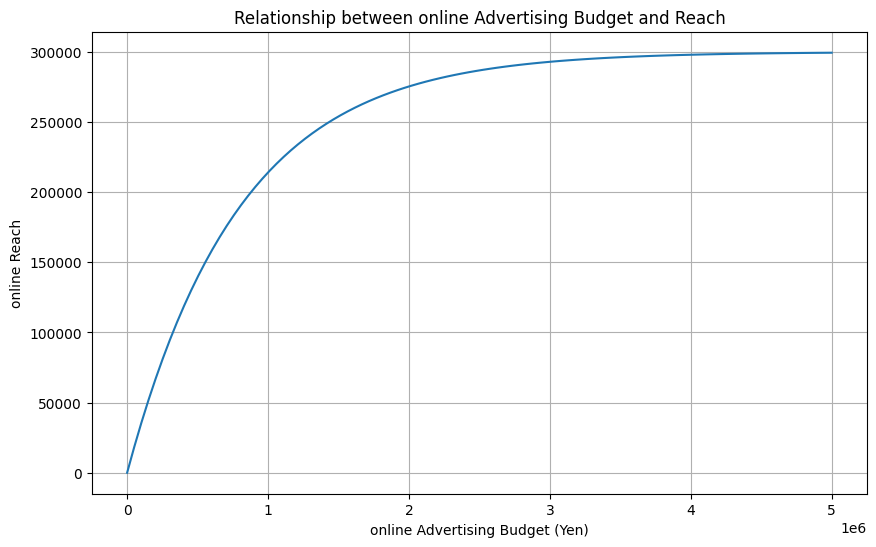
このように、ある一定の投下量を過ぎると飽和するような関数です。このような関数を目的関数に使います。

 

今回の最適化問題をコードにすると、以下のようになります。目的関数に -1 を掛けることで、最大化問題を最小化問題にしています。

import numpy as np
import pandas as pd
from scipy.optimize import minimize

# 広告チャネル
channels = ["テレビ", "オンライン", "紙媒体"]

# 各チャネルの単位あたりのコスト
costs = [50000, 20000, 30000]

# 各チャネルの基本リーチ
base_reach = [600000, 300000, 200000]

df = pd.DataFrame({'cost': costs, 'base': base_reach}, index=channels)

# 目的関数（リーチの最大化）
def objective(x):
    tv_reach = df.loc["テレビ", "base"] * (1 - np.exp(-x[0] / 3500))
    online_reach = df.loc["オンライン", "base"] * (1 - np.exp(-x[1] / 40))
    print_reach = df.loc["紙媒体", "base"] * (1 - np.exp(-x[2] / 3000))
    return -(tv_reach + online_reach + print_reach)

# 制約条件（予算）
def constraint(x):
    return 10000000 - sum(x[i] * df.loc[channels[i], "cost"] for i in range(3))

con = {'type': 'ineq', 'fun': constraint}

# 初期値
x0 = [1, 1, 1]

# 最適化
result = minimize(objective, x0, constraints=con, bounds=[(0, None)]*3)

# 結果
if result.success:
    print("最適解:", result.x)
    print("最大利益:", -1 * result.fun)
else:
    print("最適化問題の解決に失敗しました。")

 

このコードは、総予算10,000,000円の制約の下で、ABC株式会社がテレビ、オンライン、紙媒体の3つの広告チャネルにどのように予算を配分すれば、総リーチを最大化できるかを計算します。

リーチは非線形関数で表され、各広告支出に対するリターンが減少する効果をモデル化しています。制約関数は総予算を超えないようにします。

• `numpy`, `pandas`, および `minimize`（ `scipy.optimize` モジュールから）をインポートします。このコードでは数値計算（`numpy`）、データフレームの操作（`pandas`）、最適化問題の解決（`minimize`）が必要です。
• 広告チャネル（”テレビ”、”オンライン”、”紙媒体”）を定義しています。
• 各チャネルの単位あたりのコストと基本リーチ（達成可能な最大視聴者数）を定義しています。
• `pandas`の`DataFrame`を使用して広告チャネル、単位あたりのコスト、基本リーチを含むデータフレームを作成します。広告チャネルはデータフレームのインデックスとして使用され、コストとリーチは列として使用されます。
• `objective`関数を定義しています。これはこの最適化問題の目的関数であり、各広告チャネルのリーチを最大限にすることを目的としています。リーチはチャネルごとの基本リーチと配分された広告予算（`x`）に基づいて計算され、広告予算が増えるとリーチも増加しますが、その効果は漸逓的に減少します。これは負の指数関数`np.exp(-x / factor)`を使用してモデル化されています。最後に、全体のリーチの負の値（`-`）を返しています。これは最大化問題を`minimize`関数（最小化問題を解くためのもの）で解くためです。
• `constraint`リチターンを定義します。これは総広告予算（`10,000,000`）から各チャネルのコスト`x[i] * df.loc[channels[i], "cost"]`を引いたもので、この値が非負であるという制約条件を表しています。つまり、総広告予算を超えることなく広告を配置することが求められます。
• 単一の制約条件をPythonの辞書で定義します。これは `minimize` 関数に渡される形式でなければなりません。
• `x0` は最適化の初期値であり、各広告チャネルに対する初期広告予算です。この例では全てのチャネルに対して `[1, 1, 1]` と等しく設定されています。
• 最適化の実行を行います。`minimize`関数は目的関数、初期値、制約条件、変数の範囲（この場合は（0,無限大））を引数に取ります。
• 最適化の結果を確認し、成功したかどうかをチェックします。成功した場合は最適解`最適解:`と最大利益（最大リーチ）`最大利益:`を印刷します。そうでなければ、`最適化問題の解決に失敗しました。`というメッセージが表示されます。

 

以下、実行結果です。

最適解: [124.31484801 189.21287998   0.        ]
最大利益: 318289.9996269426

 

最適化の結果は、各広告チャネルにどれだけの予算を割り当てるべきかを示し、ABC株式会社はこれに基づいて最も効果的な予算配分を決定できます。

 

　事例: 航空会社の航空券価格最適化

国際航空会社「SkyBound」は、航空券の価格戦略を最適化する必要があります。

航空券の価格と乗客の予約傾向に非線形の関係があることを認識しています。特定の価格帯では需要が高く、他の価格帯では需要が落ちるという現象が見られます。目標は、様々な路線で航空券の価格を設定し、総収益を最大化することです。

定式化すると以下のようになります。

目的関数：
\displaystyle \text{maximize } Z = \sum_{i \in routes} price_i \times booking_i\left( price_i \right)

制約条件：
\displaystyle minPrice_i \leq price_i \leq maxPrice_i

• price_i は路線 i の料金
• minPrice_i は路線 i の料金price_iの下限
• maxPrice_i は路線 i の料金price_iの上限
• booking_i は料金 price_i で路線 i で見込まれる予約数
• n は、路線数

 

今回は以下の3つの路線（route）で考えます。

• 路線A
• 路線B
• 路線C

 

各路線（route）は価格（price）に応じて需要が変化します。現状手元にあるデータを使い、価格と予想される予約数の関係をグラフ化します。

以下、コードです。

import matplotlib.pyplot as plt 

routes = {
    'A': {'price': [200, 400, 600, 800, 1000], 'bookings': [200, 300, 250, 150, 100]},
    'B': {'price': [250, 450, 650, 850, 1050], 'bookings': [180, 280, 230, 130, 80]},
    'C': {'price': [220, 420, 620, 820, 1020], 'bookings': [210, 310, 260, 160, 110]}
}

plt.figure(figsize=(8,6))

for key, value in routes.items():
    plt.plot(value['price'], value['bookings'], label=key)
    
plt.xlabel('Price')
plt.ylabel('Bookings')
plt.title('Price vs Bookings for each Route')
plt.legend()
plt.grid(True)
plt.show()

 

以下、実行結果です。

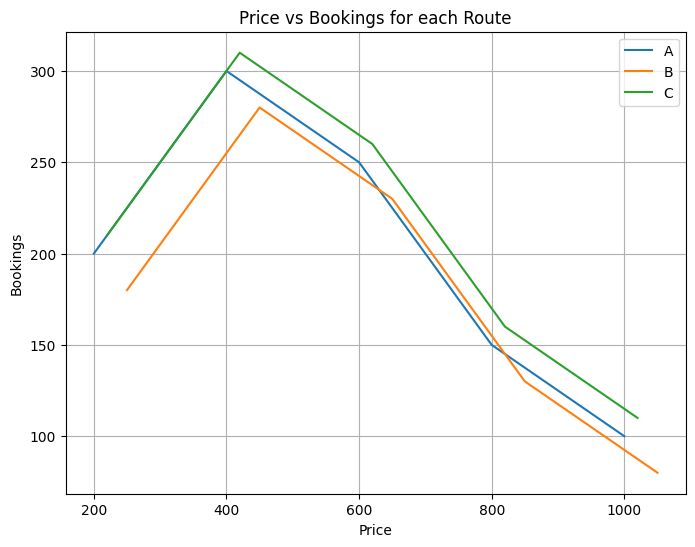
この結果から、どのように需要関数を作るのか、という問題が発生します。

今回は、簡易的に線形補間（NumPyの線形補間）で需要関数を作ることにします。線形補完といっても、非線形な需要関数になります。

 

今回の最適化問題をコードにすると、以下のようになります。目的関数に -1 を掛けることで、最大化問題を最小化問題にしています。

import numpy as np
from scipy.optimize import minimize

# 各路線ごとの価格と予想される予約数の関係
routes = {
    'A': {'price': [200, 400, 600, 800, 1000], 'bookings': [200, 300, 250, 150, 100]},
    'B': {'price': [250, 450, 650, 850, 1050], 'bookings': [180, 280, 230, 130, 80]},
    'C': {'price': [220, 420, 620, 820, 1020], 'bookings': [210, 310, 260, 160, 110]}
}

# 目的関数
def total_revenue(x):
    revenue = 0
    for i, key in enumerate(routes.keys()):
        price_bookings = routes[key]
        price = x[i]
        bookings = np.interp(price, price_bookings['price'], price_bookings['bookings'])
        revenue += price * bookings
    return -revenue  # 最大化問題なので負の値を返す

# 初期値
initial_prices = [400, 450, 420]

# 制約条件
bounds = [(min(r['price']), max(r['price'])) for r in routes.values()]

# 最適化
result = minimize(total_revenue, initial_prices, bounds=bounds)

# 結果表示
if result.success:
    optimal_prices = result.x
    print("最適な価格設定:", optimal_prices)
else:
    print("最適化に失敗しました。")

 

このコードは、非線形最適化を用いて、各路線における航空券の最適な価格設定を求めることを目的としています。total_revenue関数は、設定された価格に基づいて各路線の総収益を計算し、minimize関数を用いてこの収益を最大化します。制約条件は、各路線の航空券価格が現実的な範囲内で設定されることを保証します。最適化の結果、各路線に対して最適な価格が提案され、総収益の増加が期待されます。

• numpy と scipy.optimize モジュールの minimize 関数をインポートしています。これらは最適化問題を解くために必要なライブラリです。
• 各路線（’A’, ‘B’, ‘C’）の価格とその価格に対応する予約数が辞書形式で格納されています。
• total_revenue という目的関数を定義しています。この関数は、各路線の価格と予約数から総収入を算出します。np.interp 関数は、予約数を価格に対して線形補間することで推定します。最大化問題として扱うために、最終的な収入に負の符号をつけて返しています。
• 初期の価格を設定しています。これらの価格が最適化用の初期値として利用されます。
• 各路線の価格の最小値と最大値を用いて制約条件を定義しています。これらは最適化問題での価格の下限と上限を示します。
• minimize 関数を用いて、目的関数を最適化しています。引数には目的関数、初期値、制約条件を渡しています。
• 最後に、最適化の結果をチェックしています。成功した場合は最適な価格設定を出力し、そうでない場合はエラーメッセージを出力します。

 

以下、実行結果です。

最適な価格設定: [599.99990859 649.99999999 620.00007574]

 

最適化の結果は、総収益を最大化する各路線の価格を示し、国際航空会社「SkyBound」はこれに基づいて各路線の価格を決定できます。

 

　事例: 財務におけるポートフォリオ最適化

XYZリバイバルファンドは、株式、債券、不動産、プライベートエクイティなど、多様な資産クラスにわたる投資ポートフォリオを持っています。

しかし、市場の変動性が高くなると、リスクとリターンのバランスが取りづらくなります。この会社は、期待されるリターンを最大化しながらリスクを最小限に抑えるために、ポートフォリオの構成を最適化する必要がありました。

定式化すると以下のようになります。

目的関数：
\displaystyle \text{maximize } w^T r

制約条件：
\displaystyle \begin{array}{rrrrr}w^T \sum w \le \delta\\w^T I = 1 \\w \ge 0\end{array}

• w は各資産に投資する割合のベクトル
• r は各資産の期待リターンのベクトル
• Σ は資産間の共分散行列
• δ は許容される最大リスクレベル
• I は要素がすべて1のベクトル

 

δ は、ポートフォリオのリスク許容度を表します。具体的には、ポートフォリオの収益の分散または標準偏差の最大限度を示しています。つまり、ポートフォリオ全体として許容できる最大のリスク（変動、不確実性）を示します。このリスク許容度は、投資家のリスク許容度（リスクをどれだけ受け入れることができるか）、投資目標、投資期間などに基づいて投資家自身によって設定されます。

一般的に、リスク許容度は投資家のリスク取り扱いの態度や投資目標により異なるため、その設定は個々の投資家によって行う必要があります。許容リスクが高いほど高リターンを狙うことができますが、同時に収益の変動（リスク）も高くなります。逆に、許容リスクが低いと収益も比較的低くなりますが、収益の変動は抑えられます。そのため、リスクとリターンのバランスを考えて適切なリスク許容度を設定することが重要です。

 

今回の最適化問題をコードにすると、以下のようになります。目的関数に -1 を掛けることで、最大化問題を最小化問題にしています。

import numpy as np
from scipy.optimize import minimize

# 資産の期待リターン
expected_returns = np.array([0.12, 0.10, 0.07, 0.09])

# 共分散行列
cov_matrix = np.array([
    [0.10, 0.03, 0.02, 0.04],
    [0.03, 0.08, 0.01, 0.03],
    [0.02, 0.01, 0.07, 0.02],
    [0.04, 0.03, 0.02, 0.09]
])

# 許容される最大リスク
max_risk = 0.08

# 目的関数の定義
def objective(weights):
    return -weights.dot(expected_returns)

# 制約条件の定義
constraints = [
    {'type': 'eq', 'fun': lambda x: np.sum(x) - 1},  # 合計投資比率は1
    {'type': 'ineq', 'fun': lambda x: max_risk - x.dot(cov_matrix).dot(x)}  # リスク制約
]

# 非負制約の定義
bounds = [(0, None)]*len(expected_returns)

# 最適化
initial_weights = np.array([0.25, 0.25, 0.25, 0.25])
result = minimize(objective, initial_weights, constraints=constraints, bounds=bounds)

# 結果表示
if result.success:
    optimal_weights = result.x
    print("最適な価格設定:", optimal_weights)
else:
    print("最適化に失敗しました。")

 

このコードは、XYZ投資会社が自社のポートフォリオを最適化するために使用します。目的関数は、資産の期待リターンの合計を最大化することです。制約条件は、ポートフォリオの総投資比率が1であること、そして許容される最大リスクを超えないことを保証します。

• `numpy`と`scipy.optimize`の`minimize`関数をインポートします。これらは数値最適化を行うためのライブラリです。
• `expected_returns`という配列に各資産の期待リターンを定義します。
• `cov_matrix`という配列に各資産の共分散行列を定義します。共分散行列は資産間の収益の変動の関連性を表しています。
• `max_risk`変数に許容される最大リスクを定義します。
• `objective`関数を定義します。目的関数は各資産への投資の重みに基づいて期待リターンを計算し、その値を最大化するための関数です。
• 制約条件を定義します
  • 合計投資比率は1でなければならないという等式制約
  • リスクが許容最大リスク以下でなければならないという不等式制約
• `minimize` 関数に渡すための資産の重みに対する非負の制約を定義します。
• `minimize` 関数を用いて目的関数を最適化します。初期値（`initial_weights`）、制約条件、および上限下限制約（`bounds`）を引数に渡します。
• 最適化の結果を確認し、最適化が成功したかどうかを表示します。成功した場合、最適な投資比率（`optimal_weights`）を表示します。そうでなければ、エラーメッセージを表示します。

 

以下、実行結果です。

最適な価格設定: [8.33333335e-01 1.66666665e-01 3.67480162e-16 0.00000000e+00]

 

最適化の結果は、各資産に投資する最適な比率を示します。これにより、XYZリバイバルファンドはリスクをコントロールしながら期待されるリターンを最大化するポートフォリオを構築できるようになります。

 

まとめ

今回は、非線形最適化の基本理論から実践的応用例に至るまでを一通り紹介しました。

線形最適化の限界から非線形最適化の必要性へと移行する過程を探求し、非線形最適化の特徴とその解法の基本について理解を深めました。さらに、ScyPyを用いた具体的な解法や、現実世界での応用例についても触れました。

非線形最適化は多くの現実世界の問題に対して重要なツールです。この分野を理解し適用するためには、以下のポイントを押さえることが重要です。

• 非線形性: 非線形関数は予測が難しく、局所的最適解に陥りやすい。
• 制約の管理: 制約条件が問題の難易度を大きく左右する。
• アルゴリズムの選択: 問題に適したアルゴリズムの選定が結果に大きく影響する。
• 実践的応用: 理論と実践の間にはギャップがあるため、現実のデータや状況に適応する柔軟性が求められる。

 

次回は、「整数最適化と組合せ最適化」を取り上げます。これらの最適化問題は、特にスケジューリング、ルーティング、リソース割当などの問題において非常に重要です。整数制約がどのように問題を複雑化させるか、また、これらの問題を効率的に解くためのアルゴリズムや手法について学びます。現実世界で頻繁に遭遇する複雑な問題への対処法を理解するために、次回も是非ご期待ください。

Python SciPyで手を動かしながら学ぶ数理最適化– 第4回: 整数最適化と組合せ最適化 –