前回は、共分散行列の固有値分解によって「主成分の方向」と「その方向での分散」が求まることを学びました。
Pythonで体感する次元削減入門 – PCAと因子分析の基礎のキソ— 第2回 —PCAのしくみを分散・共分散・固有値分解で理解する
固有ベクトルが主成分の方向を、固有値がその方向での分散の大きさを表すのでしたね。
しかし、ここで新たな疑問が生まれます。
「結局、主成分はいくつ使えばいいの?」
元のデータが10次元なら、主成分も10個得られます。でも、10個全部使ったら次元削減になりません。
かといって、1個だけでは情報が失われすぎるかもしれません。
今回は、この「いくつ残すか」問題に答えるための道具、寄与率とスクリープロットを学びます。
Contents
主成分分析と固有値分解
いま、共分散行列を \mathbf{S} とします。このとき、次の式を満たすベクトル \mathbf{v} と数値 \lambda を考えます。
$$
\mathbf{S}\mathbf{v} = \lambda \mathbf{v}
$$
この式は、「ベクトル \mathbf{v} に共分散行列 \mathbf{S} を掛けると、向きは変わらず、長さだけが \lambda 倍になる」ということを意味しています。
このような 向きが保たれる特別な方向 を 固有ベクトル、そのときの 伸び縮みの大きさ を 固有値 と呼びます。
共分散行列に固有値分解を行うと、複数の固有ベクトルと固有値が得られます。これらは、そのまま 主成分分析(PCA)における主成分 に対応しています。
今、固有ベクトルを列に並べた行列 \mathbf{V} とします。
$$
\mathbf{V}
=
\begin{bmatrix}
\mathbf{v}_1 & \mathbf{v}_2 & \cdots & \mathbf{v}_p
\end{bmatrix}
$$
固有値を対角成分に並べた行列\mathbf{\Lambda}とします。
$$
\mathbf{\Lambda}
=
\begin{bmatrix}
\lambda_1 & & \\
& \ddots & \\
& & \lambda_p
\end{bmatrix}
$$
行列\mathbf{V}と行列\mathbf{\Lambda}から、共分散行列は次のように表せます。
$$
\mathbf{S} = \mathbf{V}\mathbf{\Lambda}\mathbf{V}^\top
$$
これは、「共分散行列は、主成分方向と、その方向での分散によって完全に分解できる」ことを意味しています。
寄与率とは何か
会社の売上分析を例に考えてみましょう。
ある会社の売上に影響する要因として、「広告費」「営業人数」「商品数」「立地」など10個の変数があるとします。
PCAを適用すると、10個の主成分が得られます。
第1主成分が売上の変動の40%を説明し、第2主成分が25%を説明するとしたら、この2つだけで全体の65%を説明できることになります。残りの8個の主成分は合わせて35%しか説明しません。
この「全体の分散のうち、各主成分が何%を説明するか」を表す指標が寄与率(explained variance ratio)です。
数学的には、寄与率は次のように計算します。
$$
\text{第k主成分の寄与率} = \frac{\lambda_k}{\displaystyle \sum_{i=1}^{p} \lambda_i}
$$
ここで、λₖ は第k主成分の固有値(=その方向での分散)、分母はすべての固有値の合計です。
固有値の合計は、元のデータの全分散に等しくなります。
準備
ライブラリとデータの読み込み
まずは、必要なライブラリなどを読み込みます。
import numpy as np import pandas as pd from sklearn.datasets import load_iris from sklearn.preprocessing import StandardScaler import matplotlib.pyplot as plt import seaborn as sns import japanize_matplotlib np.random.seed(42)
今回はIrisデータセットを使います。
Irisデータセットは、3種類のアヤメ(Setosa、Versicolor、Virginica)について、4つの特徴量(がく片の長さ・幅、花弁の長さ・幅)を測定したものです。
# Irisデータセットを読み込む
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
# DataFrameにまとめる
df_iris = pd.DataFrame(X, columns=feature_names)
df_iris['species'] = [target_names[i] for i in y]
print(f"サンプル数: {len(df_iris)}")
print(f"特徴量: {feature_names}")
print(f"目的変数(品種): {list(target_names)}")
print()
print(df_iris.head())
以下、実行結果です。
サンプル数: 150 特徴量: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] 目的変数(品種): ['setosa', 'versicolor', 'virginica'] sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \ 0 5.1 3.5 1.4 0.2 1 4.9 3.0 1.4 0.2 2 4.7 3.2 1.3 0.2 3 4.6 3.1 1.5 0.2 4 5.0 3.6 1.4 0.2 species 0 setosa 1 setosa 2 setosa 3 setosa 4 setosa
150個のサンプル(各品種50個ずつ)と4つの特徴量があることが確認できます。
4次元のデータを2次元に削減して可視化することが、今回の目標です。
データの標準化
PCAを行う前に、データを標準化(平均0、標準偏差1に変換)します。
これは、変数ごとにスケール(単位)が異なる場合に重要です。
# 標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print("標準化前の平均と標準偏差:")
print(f" 平均: {X.mean(axis=0).round(2)}")
print(f" 標準偏差: {X.std(axis=0).round(2)}")
print()
print("標準化後の平均と標準偏差:")
print(f" 平均: {X_scaled.mean(axis=0).round(2)}")
print(f" 標準偏差: {X_scaled.std(axis=0).round(2)}")
以下、実行結果です。
標準化前の平均と標準偏差: 平均: [5.84 3.06 3.76 1.2 ] 標準偏差: [0.83 0.43 1.76 0.76] 標準化後の平均と標準偏差: 平均: [-0. -0. -0. -0.] 標準偏差: [1. 1. 1. 1.]
標準化によってすべての変数の平均が0、標準偏差が1になったことが確認できます。
これで、変数間のスケールの違いを気にせずにPCAを適用できます。
共分散行列の固有値分解
標準化したデータの共分散行列(=相関行列)を計算し、固有値分解を行います。
# 共分散行列を計算
n = len(X_scaled)
cov_matrix = (X_scaled.T @ X_scaled) / (n - 1)
# 固有値分解
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 固有値が大きい順にソート
idx = np.argsort(eigenvalues)[::-1]
eigenvalues = eigenvalues[idx].real # 実数部分を取得
eigenvectors = eigenvectors[:, idx].real
print("固有値(各主成分の分散):")
for i, ev in enumerate(eigenvalues):
print(f" 第{i+1}主成分: {ev:.4f}")
以下、実行結果です。
固有値(各主成分の分散): 第1主成分: 2.9381 第2主成分: 0.9202 第3主成分: 0.1477 第4主成分: 0.0209
4つの固有値が大きい順に表示されます。第1主成分の固有値が最も大きく、順に小さくなっていることがわかります。
主成分数の決定
寄与率と累積寄与率を計算する
各主成分の寄与率と、累積寄与率を計算してみましょう。
# 寄与率を計算
total_variance = np.sum(eigenvalues)
explained_ratio = eigenvalues / total_variance
# 累積寄与率を計算
cumulative_ratio = np.cumsum(explained_ratio)
print(
f"{'主成分'} {'固有値':>8}"
f"{'寄与率':>8} {'累積寄与率':>8}"
)
print("-" * 45)
for i in range(len(eigenvalues)):
print(
f"PC{i+1}"
f"{eigenvalues[i]:>14.4f}"
f"{explained_ratio[i]*100:>10.2f}%"
f"{cumulative_ratio[i]*100:>10.2f}%"
)
以下、実行結果です。
主成分 固有値 寄与率 累積寄与率 --------------------------------------------- PC1 2.9381 72.96% 72.96% PC2 0.9202 22.85% 95.81% PC3 0.1477 3.67% 99.48% PC4 0.0209 0.52% 100.00%
各主成分の寄与率と累積寄与率が表示されます。
第1主成分と第2主成分だけで、全体の分散の約95%を説明できることがわかります。
これは、4次元のデータを2次元に減らしても、情報の95%は保持できることを意味します。
スクリープロットを描く
スクリープロット(scree plot)は、固有値(または寄与率)を主成分の順に棒グラフや折れ線グラフで描いたものです。
「スクリー(scree)」とは、山の斜面にたまった岩屑のこと。グラフの形が岩屑の斜面に似ていることから名付けられました。
fig, axes = plt.subplots(2, 1, figsize=(10, 10))
#
# 上: 固有値のスクリープロット
#
ax = axes[0]
# 固有値を棒グラフで表示
x = np.arange(1, len(eigenvalues) + 1)
ax.bar(x, eigenvalues,alpha=0.7)
# 固有値を折れ線グラフで表示
ax.plot(x, eigenvalues, 'ro-', markersize=8, linewidth=2)
# 軸ラベルとタイトルを設定
ax.set_xlabel('主成分')
ax.set_ylabel('固有値',)
ax.set_title('スクリープロット(固有値)')
ax.set_xticks(x)
ax.set_xticklabels([f'PC{i}' for i in x])
ax.grid(True, axis='y', alpha=0.3)
#
# 下: 寄与率と累積寄与率
#
ax = axes[1]
# 寄与率を棒グラフで表示
ax.bar(x, explained_ratio * 100, label='寄与率')
# 累積寄与率を折れ線グラフで表示
ax.plot(
x, cumulative_ratio * 100,
'ro-', markersize=8, linewidth=2, label='累積寄与率'
)
# 80%ラインを水平線で表示
ax.axhline(
y=80, color='green',
linestyle='--', linewidth=2, label='80%ライン'
)
ax.set_xlabel('主成分')
ax.set_ylabel('寄与率 (%)')
ax.set_title('寄与率と累積寄与率')
ax.set_xticks(x)
ax.set_xticklabels([f'PC{i}' for i in x])
ax.set_ylim(0, 105)
ax.legend(loc='center right')
ax.grid(True, axis='y', alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
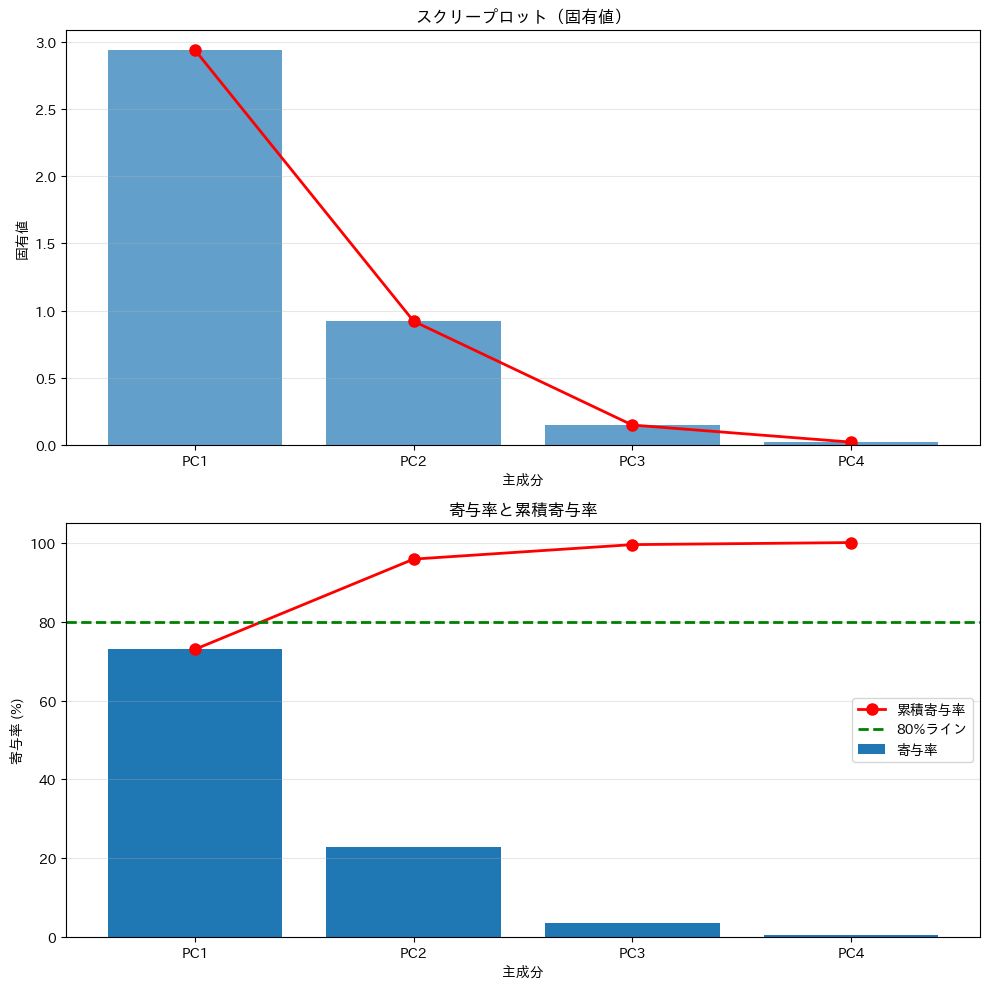
上のグラフでは、第1主成分と第2主成分の固有値が大きく、第3主成分以降は急に小さくなっています。下のグラフでは、累積寄与率が80%を超えるのに必要な主成分数がわかります。
主成分数を決める主な基準
肘法(エルボー法)
スクリープロットの形を見て、曲線が急に平らになる「肘(elbow)」の位置で打ち切る方法を肘法(エルボー法)といいます。
先ほどのグラフを見ると、第2主成分と第3主成分の間で傾きが急に緩やかになっていることがわかります。この「肘」の位置で打ち切り、第1・第2主成分を採用するのが肘法の考え方です。
肘法は視覚的にわかりやすく、直感的に主成分数を決められる方法ですが、必ずしも「肘」がはっきり現れるとは限らないという弱点があります。
データによっては、固有値がなだらかに減少し、「どこが肘なのか判断しづらい」ケースも少なくありません。そのため、肘法だけで主成分数を決めるのではなく、他の基準と併用して判断するのが一般的です。
累積寄与率による判断
最もよく使われるのが、累積寄与率を基準にする方法です。
あらかじめ「どの程度まで情報を残したいか」を決めておき、その割合を超える最小の主成分数を採用します。
たとえば、次のような目安がよく用いられます。
- 可視化や簡易分析なら 80%程度
- 分析の前処理としては 90%前後
- 情報の損失をできるだけ抑えたい場合は 95%程度
今回の例では、第1主成分と第2主成分までで累積寄与率が約95%に達しているため、「95%を保持する」という基準を採用すれば、主成分数は2 と判断できます。
この方法は数値的に明確で、説明もしやすいため、実務やレポートで最も使われる判断基準の一つです。
固有値の大きさに基づく判断(カイザー基準)
固有値そのものの大きさに注目する方法があります。
標準化したデータに対するPCAでは、「固有値が1より大きい主成分のみを採用する」という経験則が知られています。
これは、固有値が1未満の主成分は、元の変数1個分にも満たない情報しか持たないと考えるためです。
今回の結果では、第1主成分の固有値は1を大きく上回っていますが、第2主成分は1未満です。そのため、この基準を用いると、第1主成分のみを採用するという、より強く次元を圧縮した判断になります。
この方法は簡便ですが、やや厳しめに主成分数が少なくなりやすいため、補助的な基準として使われることが多いです。
主成分数は「一つの正解」ではない
主成分数の決定に、唯一の正解はありません。
肘法、累積寄与率、固有値の大きさ、ノイズとの比較、そして分析の目的。これらを総合的に見て、「この目的なら、この主成分数が妥当だ」と説明できることが大切です。
今回の例では、肘法(エルボー法)と累積寄与率(95%)の両方が「第1・第2主成分までで十分」という結論を支持しており、2主成分を採用する判断は自然で妥当だと言えるでしょう。
主成分得点と負荷量
主成分得点
共分散行列に固有値分解を行うと、複数の固有ベクトル \mathbf{v} と固有値 \lambda が得られます。これらは、そのまま 主成分分析(PCA)における主成分 に対応しています。
$$
\mathbf{S}\mathbf{v} = \lambda \mathbf{v}
$$
次に知りたいのは、各データ点はその主成分の方向の上でどれくらいに位置しているのか、という点です。これを表すのが 主成分得点(principal component score) です。
今、中心化されたデータ行列(元のデータの列ごとに平均値で引いた値)を \mathbf{X} とします。
$$
\mathbf{X} \in \mathbb{R}^{n \times p}
$$
第 k 主成分の固有ベクトルを \mathbf{v}_k とすると、第 k 主成分の主成分得点は次の数式で求められます。
$$
\mathbf{z}_k = \mathbf{X}\mathbf{v}_k
$$
これは、元のデータを第 k 主成分の方向に正射影した結果に他なりません。
つまり、主成分得点とは「新しい座標軸(主成分軸)で見たときのデータの座標」です。
固有ベクトルを並べた行列 \mathbf{V} を用いると、すべての主成分得点は次のように書けます。
$$
\mathbf{Z} = \mathbf{X}\mathbf{V}
$$
- \mathbf{Z}:主成分得点行列
- 各列が、第1主成分得点、第2主成分得点、…を表す
この \mathbf{Z} が、PCAによって得られた次元削減後のデータです。
主成分負荷量
主成分得点が「サンプルの位置」を表すのに対し、主成分負荷量(loading)は、各特徴量(変数)がその主成分にどれだけ寄与しているかを表す量です。
第 k 主成分の負荷量ベクトル \mathbf{l}_k は、次のように定義されることが一般的です。
$$
\mathbf{l}_k = \sqrt{\lambda_k}\,\mathbf{v}_k
$$
- \mathbf{v}_k:第 k 主成分の方向(単位ベクトル)
- \lambda_k:その方向に射影したときの分散
- \sqrt{\lambda_k}:その方向での標準偏差
ちなみに、固有ベクトル \mathbf{v}_k は長さ1に正規化されています。これは「向きだけを表す」ベクトルです。一方、\sqrt{\lambda_k} は、ばらつきのスケール(標準偏差)になります。
- \mathbf{v}_k → どちらの方向を向いているか
- \sqrt{\lambda_k}\mathbf{v}_k→ その方向に、どれくらいの強さでデータが広がっているか
つまり、主成分負荷量とは、「主成分の向き」に「その方向でのデータの広がり」を掛け合わせた、各変数が主成分をどれだけ強く構成しているかを表す量となります。
主成分得点の計算と主成分プロット
いよいよ、4次元のIrisデータを2次元に削減して可視化してみましょう。
主成分得点を計算する
データを主成分の方向に射影して、主成分得点(principal component scores)を計算します。
# 上位2つの固有ベクトルを取得
W = eigenvectors[:, :2] # 4×2の行列
# 主成分得点を計算(射影)
Z = X_scaled @ W # 150×2の行列
print("主成分得点の形状:", Z.shape)
print("(150サンプル × 2主成分)")
print()
print("最初の5サンプルの主成分得点:")
print(pd.DataFrame(Z[:5], columns=['PC1', 'PC2']).round(3))
以下、実行結果です。
主成分得点の形状: (150, 2)
(150サンプル × 2主成分)
最初の5サンプルの主成分得点:
PC1 PC2
0 -2.265 -0.480
1 -2.081 0.674
2 -2.364 0.342
3 -2.299 0.597
4 -2.390 -0.647
150個のサンプルそれぞれについて、2つの主成分得点が計算されます。
これが、4次元から2次元に「圧縮」されたデータです。
散布図で3品種を可視化する
2次元に圧縮したデータを散布図にプロットし、3品種がどのように分布しているか確認します。
plt.figure(figsize=(10, 8))
# 品種ごとに色分けしてプロット
colors = ['#E74C3C', '#2ECC71', '#3498DB']
for i, (species, color) in enumerate(zip(target_names, colors)):
mask = y == i
plt.scatter(
Z[mask, 0], Z[mask, 1],
c=color, label=species,
s=80, alpha=0.7, edgecolors='white')
plt.xlabel(f'第1主成分 (寄与率: {explained_ratio[0]*100:.1f}%)')
plt.ylabel(f'第2主成分 (寄与率: {explained_ratio[1]*100:.1f}%)')
plt.title('Irisデータセットの主成分分析')
plt.legend(title='品種')
plt.grid(True, alpha=0.3)
plt.axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
plt.axvline(x=0, color='gray', linestyle='-', linewidth=0.5)
plt.show()
以下、実行結果です。
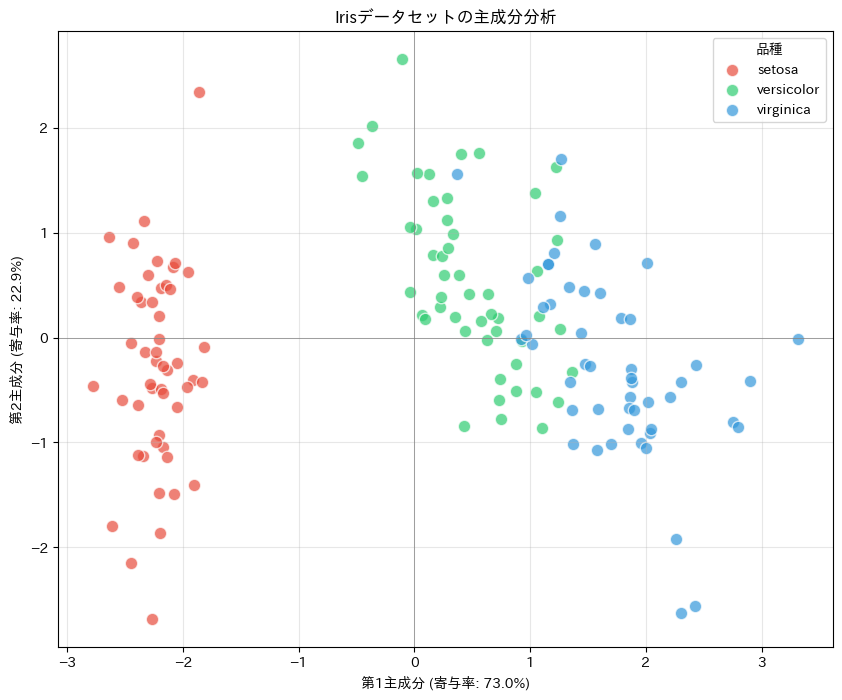
この散布図を見ると、3品種がかなり明確に分離されていることがわかります。
特にSetosaは他の2品種と完全に分離しています。VersicolorとVirginicaも、多少の重なりはあるものの、おおむね分離できています。
4次元のデータを直接見ることはできませんが、2次元に圧縮することで、データの構造を目で見て理解できるようになります。
主成分負荷量の計算とバイプロット
主成分負荷量を計算する
主成分が元のどの特徴量と関係しているかを確認してみましょう。
固有ベクトルの成分を見ると、各特徴量が主成分にどれだけ寄与しているかがわかります。
# 主成分負荷量を計算
loadings = pd.DataFrame(
eigenvectors[:, :2] * np.sqrt(eigenvalues[:2]),
index=feature_names,
columns=['PC1', 'PC2']
)
print("主成分への各特徴量の寄与(主成分負荷量):")
print(loadings.round(3))
以下、実行結果です。
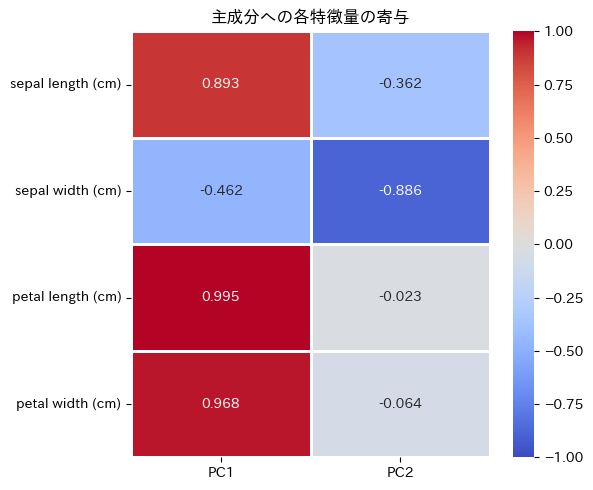
主成分への各特徴量の寄与(主成分負荷量):
PC1 PC2
sepal length (cm) 0.893 -0.362
sepal width (cm) -0.462 -0.886
petal length (cm) 0.995 -0.023
petal width (cm) 0.968 -0.064
固有ベクトルの値(主成分負荷量)は、主成分分析における各特徴量の重みを表します。
PC1(第1主成分)は、sepal length (cm)とpetal length (cm)、 petal width (cm)の主成分負荷量の絶対値が大きく、これらの特徴量が第1主成分に強く影響していることを示しています。
PC2(第2主成分)では、sepal width (cm)の主成分負荷量の絶対値が大きく、他の特徴量よりも第2主成分に強く影響しています。
これにより、データの分散を説明する際に、どの特徴量が重要かを理解することができます。
ヒートマップを描き見てみます。
plt.figure(figsize=(6, 5))
sns.heatmap(
loadings, annot=True,
fmt='.3f', cmap='coolwarm',
center=0, linewidths=1,
vmin=-1, vmax=1
)
plt.title('主成分への各特徴量の寄与')
plt.tight_layout()
plt.show()
以下、実行結果です。
バイプロット
ここまでで、主成分負荷量を用いて「各主成分が、どの特徴量によって構成されているか」を確認しました。
次に有効なのが、バイプロット(biplot)です。
バイプロットは、主成分得点(各サンプルの位置)と主成分負荷量(各特徴量の寄与) 同じ平面上に同時に描画する可視化手法です。
plt.figure(figsize=(10, 8))
# 主成分得点をプロット
for i, (species, color) in enumerate(zip(target_names, colors)):
mask = y == i
plt.scatter(
Z[mask, 0], Z[mask, 1],
c=color, label=species,
s=80, alpha=0.7, edgecolors='white')
# 主成分負荷量をプロット
scale_factor = 2 # 矢印の長さを調整するためのスケールファクター
loadings_corrected = loadings * scale_factor
for i in range(loadings.shape[0]):
plt.arrow(
0, 0,
loadings_corrected.iloc[i, 0],
loadings_corrected.iloc[i, 1],
color='black', alpha=0.5, head_width=0.05
)
plt.text(
loadings_corrected.iloc[i, 0] * 1.05,
loadings_corrected.iloc[i, 1] * 1.1,
loadings_corrected.index[i],
color='black', #ha='center', va='center'
)
plt.xlabel(f'第1主成分 (寄与率: {explained_ratio[0]*100:.1f}%)')
plt.ylabel(f'第2主成分 (寄与率: {explained_ratio[1]*100:.1f}%)')
plt.title('Irisデータセットの主成分分析バイプロット')
plt.legend(title='品種')
plt.grid(True, alpha=0.3)
plt.axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
plt.axvline(x=0, color='gray', linestyle='-', linewidth=0.5)
plt.show()
以下、実行結果です。
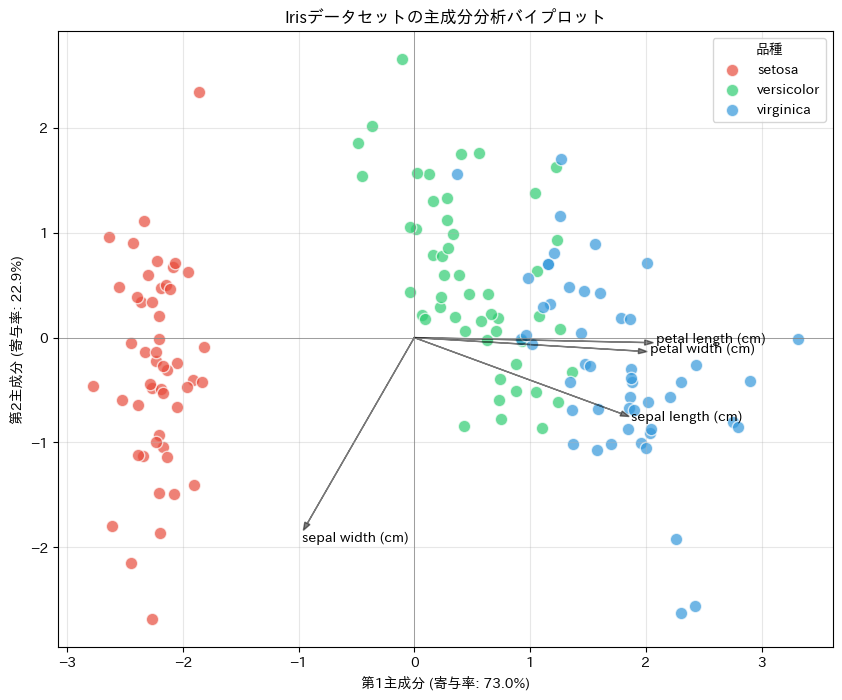
バイプロットにおける特徴量の矢印は、次のように解釈します。
- 矢印の長さが長い → その特徴量は、表示している主成分(PC1・PC2)によってよく説明されている
- 矢印の向き → その特徴量が、どの主成分に正・負の影響を与えているか
- 矢印同士の角度
- 鋭角:正の相関
- 鈍角:負の相関
- 直角:ほぼ無相関
これは、主成分負荷量が「主成分空間における特徴量の方向」を表しているためです。
まとめ
この第3回では、「主成分をいくつ残すか」を決めるための道具を学びました。
寄与率は、各主成分が全体の分散の何%を説明するかを表す指標です。固有値を全固有値の合計で割って計算します。
累積寄与率は、第1主成分から第k主成分までの寄与率の合計です。「上位k個の主成分で、全体の何%の情報を保持できるか」を表します。
スクリープロットは、固有値または寄与率を主成分の順にグラフ化したものです。
主成分数を決める主な基準:
- 累積寄与率が70〜90%を超える
- 固有値が1以上(カイザー基準)
- スクリープロットの肘の位置(エルボー法)
Irisデータセットでは、2主成分で約95%の情報を保持でき、3品種がきれいに分離される様子を確認しました。
第4回では、scikit-learnとstatsmodelsを使って、PCAをより簡単に実行する方法を学びます。
手計算の知識があるからこそ、ライブラリの出力が理解できるようになります。
Pythonで体感する次元削減入門 – PCAと因子分析の基礎のキソ— 第4回 —scikit-learnでさくっとPCAを実施する

