このシリーズでは、第1回から第5回まで、PCAと因子分析の基礎を一歩ずつ学んできました。
— 第1回 —
なぜ「次元を減らす」のか? 情報の海で溺れないために
https://www.salesanalytics.co.jp/datascience/datascience286/
— 第2回 —
PCAのしくみを分散・共分散・固有値分解で理解する
https://www.salesanalytics.co.jp/datascience/datascience288/
— 第3回 —
次元はいくつ残す? 寄与率とスクリープロットの読み方
https://www.salesanalytics.co.jp/datascience/datascience289/
— 第4回 —
scikit-learnでさくっとPCAを実施する
https://www.salesanalytics.co.jp/datascience/datascience290/
— 第5回 —
PCAと因子分析、何が違う?
https://www.salesanalytics.co.jp/datascience/datascience291/
「データが広がる方向を見つける」という直感的な理解から始まり、共分散行列の固有値分解という数学的な仕組み、寄与率による次元数の決定、そしてPCAと因子分析の違いまで、幅広いトピックを扱いました。
最終回となる今回は、PCAを回帰分析に応用する方法を学びます。
具体的には、主成分回帰(Principal Component Regression, PCR)という手法を取り上げます。
「せっかく次元削減を学んだのに、可視化以外に使い道はないの?」という疑問をお持ちの方もいるかもしれません。
実は、PCAは回帰分析における厄介な問題である多重共線性を解決する強力なツールになります。
今回は、この問題とその解決法を、実際にPythonで手を動かしながら学んでいきましょう。
Contents
ライブラリの準備
今回は回帰分析も行うため、scikit-learnの回帰関連モジュールも読み込みます。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import japanize_matplotlib import seaborn as sns from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from sklearn.linear_model import LinearRegression, Ridge from sklearn.pipeline import Pipeline from sklearn.metrics import mean_squared_error, r2_score # VIF計算用 from statsmodels.stats.outliers_influence import variance_inflation_factor
このコードを実行すると、PCAと回帰分析に必要な道具が使えるようになります。
多重共線性とは何か
身近な例で考える
あなたが不動産会社のデータサイエンティストで、マンションの価格を予測するモデルを作りたいとします。
説明変数として「延床面積」「部屋数」「築年数」「駅からの距離」などを使うことを考えます。
ここで問題が起きます。
「延床面積」が大きいマンションは「部屋数」も多い傾向があります。つまり、この2つの変数は強く相関しています。
このように、説明変数同士が強く相関している状態を多重共線性(multicollinearity)といいます。
多重共線性があると、回帰分析で困ったことが起きます。
回帰係数の推定が不安定になり、ちょっとしたデータの変化で係数が大きく変わってしまいます。
また、係数の標準誤差が大きくなり、統計的検定の信頼性が下がります。さらに、係数の符号が直感と逆になることもあります。
たとえば「面積が大きいほど価格が下がる」という、常識に反する結果が出ることがあります。
なぜ多重共線性が問題になるのか
重回帰分析では、目的変数 \mathbf{y} を説明変数の行列 X を用いて次のように表します。
$$
\mathbf{y} = X\boldsymbol{\beta} + \boldsymbol{\varepsilon}
$$
- X:説明変数を並べた行列(各列が1つの説明変数)
- \boldsymbol{\beta}:推定したい回帰係数ベクトル
- \boldsymbol{\varepsilon}:誤差項
最小二乗法による回帰係数の推定値は、次の式で与えられます。
$$
\hat{\boldsymbol{\beta}} = (X^\top X)^{-1} X^\top \mathbf{y}
$$
この式の中で重要なのが、行列 X^\top X です。
説明変数同士が強く相関している場合、次のようになります。
- ある説明変数が、別の説明変数のほぼ線形結合として表せてしまう
- つまり、X の列ベクトルが互いに似た方向を向く
このとき X^\top X は 行列式が 0 に近い状態(ほぼ特異行列) になり、(X^\top X)^{-1}の計算が不安定になります。
この逆行列が、数学的に不安定になるため、多重共線性が強いモデルでは次のような問題が発生します。
- 係数の符号や大きさが直感に反する
- 推定値のばらつきが大きくなる
- 解釈が難しくなる
多重共線性のあるサンプルデータを生成
実際に多重共線性のあるデータを作成して、問題を体験してみましょう。
以下のコードでは、互いに相関の高い5つの説明変数と、それらから生成される目的変数を作成します。
# サンプル数
n = 100
# 基礎となる潜在変数(2つ)
z1 = np.random.normal(0, 1, n)
z2 = np.random.normal(0, 1, n)
# 5つの説明変数(互いに相関がある)
x1 = z1 + np.random.normal(0, 0.1, n)
x2 = z1 + np.random.normal(0, 0.15, n) # x1と強く相関
x3 = z1 + np.random.normal(0, 0.2, n) # x1, x2と強く相関
x4 = z2 + np.random.normal(0, 0.1, n)
x5 = z2 + np.random.normal(0, 0.15, n) # x4と強く相関
# 説明変数をまとめる
X = np.column_stack([x1, x2, x3, x4, x5])
feature_names = ['x1', 'x2', 'x3', 'x4', 'x5']
# 目的変数(真の関係: y = 2*z1 + 3*z2 + noise)
y = 2 * z1 + 3 * z2 + np.random.normal(0, 0.5, n)
print(f"説明変数の形状: {X.shape}")
print(f"目的変数の形状: {y.shape}")
以下、実行結果です。
説明変数の形状: (100, 5) 目的変数の形状: (100,)
100サンプル×5変数の説明変数と、それに対応する目的変数が生成されます。
x1, x2, x3は互いに強く相関し、x4, x5も互いに強く相関するように設計されています。
説明変数間の相関を確認してみましょう。
# 相関行列を計算
df_X = pd.DataFrame(X, columns=feature_names)
corr_matrix = df_X.corr()
# ヒートマップで可視化
plt.figure(figsize=(8, 6))
sns.heatmap(
corr_matrix,
annot=True, fmt='.2f', cmap='coolwarm',
center=0, linewidths=1,
vmin=-1, vmax=1
)
plt.title('説明変数間の相関行列')
plt.show()
以下、実行結果です。
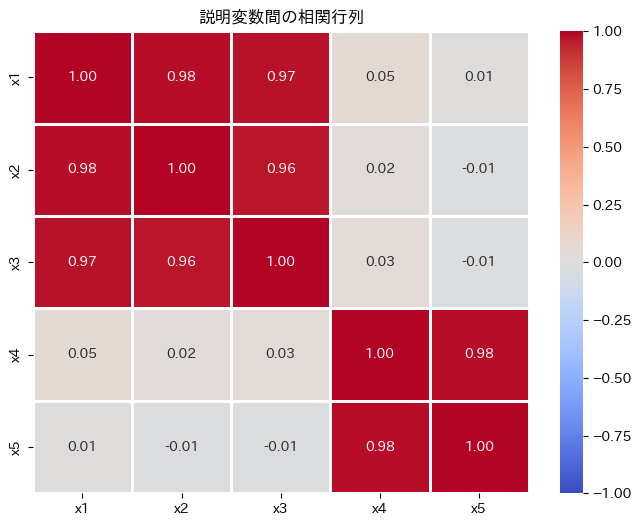
このヒートマップを見ると、x1-x2-x3のグループとx4-x5のグループ内で非常に高い相関(0.9以上)があることがわかります。
これが多重共線性の典型的なパターンです。
VIF(分散膨張係数)で多重共線性を検出する
多重共線性の程度を定量的に測る指標として、VIF(Variance Inflation Factor, 分散膨張係数)があります。
VIFは、ある説明変数が他の説明変数でどれだけ説明できるかを表します。
VIFの解釈の目安として、1であれば多重共線性なし、1〜5であれば軽度の多重共線性、5〜10であれば中程度の多重共線性があり注意が必要、10以上であれば深刻な多重共線性があり対処が必要とされています。
# VIFを計算する関数
def calculate_vif(X, feature_names):
vif_data = pd.DataFrame()
vif_data['変数'] = feature_names
vif_data['VIF'] = [variance_inflation_factor(X, i) for i in range(X.shape[1])]
return vif_data
# VIFを計算
vif_result = calculate_vif(X, feature_names)
print("=== VIF(分散膨張係数) ===")
print(vif_result.round(2))
以下、実行結果です。
=== VIF(分散膨張係数) === 変数 VIF 0 x1 47.38 1 x2 32.68 2 x3 20.95 3 x4 29.48 4 x5 29.44
VIFが10を大きく超える変数があれば、多重共線性が深刻であることを示しています。
通常の重回帰分析を試してみる
多重共線性のあるデータに対して、通常の重回帰分析を適用するとどうなるか確認してみましょう。
# データを標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 通常の重回帰分析
ols = LinearRegression()
ols.fit(X_scaled, y)
# 結果を表示
print("=== 通常の重回帰分析(OLS)の結果 ===")
print()
coef_df = pd.DataFrame({
'変数': feature_names,
'回帰係数': ols.coef_
})
print(coef_df.round(3))
print(f"\nR²スコア: {r2_score(y, ols.predict(X_scaled)):.3f}")
以下、実行結果です。
=== 通常の重回帰分析(OLS)の結果 === 変数 回帰係数 0 x1 1.300 1 x2 0.082 2 x3 0.526 3 x4 1.575 4 x5 1.430 R²スコア: 0.971
ランダムにサンプルを選択(ブートストラップ)することで、データをわずかに変えたときに、係数がどれだけ変化するか確認してみましょう。
# 異なるサブサンプルで回帰を繰り返し、係数のばらつきを確認
coefficients_list = []
for i in range(100):
# ランダムにサンプルを選択(ブートストラップ)
idx = np.random.choice(n, n, replace=True)
X_boot = X_scaled[idx]
y_boot = y[idx]
# 回帰を実行
model = LinearRegression()
model.fit(X_boot, y_boot)
coefficients_list.append(model.coef_)
coef_array = np.array(coefficients_list)
# 係数の標準偏差を計算
coef_std = pd.DataFrame({
'変数': feature_names,
'係数の平均': coef_array.mean(axis=0),
'係数の標準偏差': coef_array.std(axis=0)
})
print("=== ブートストラップによる係数の安定性評価 ===")
print(coef_std.round(3))
以下、実行結果です。
=== ブートストラップによる係数の安定性評価 === 変数 係数の平均 係数の標準偏差 0 x1 1.315 0.419 1 x2 0.081 0.365 2 x3 0.525 0.291 3 x4 1.616 0.351 4 x5 1.390 0.340
ブートストラップによる係数の安定性評価の結果を分析したところ、以下のような結論に至りました。
- x2 は非常に不安定です。標準偏差が平均よりも大きいため、モデルにおいて注意が必要です。
- x1 と x3 は中程度の不安定性を示しています。
- x4 と x5 は比較的安定しており、平均に対する標準偏差が低いため、信頼性の高い予測変数と考えられます。
この分析に基づき、特に x2 の不安定性に注意を払いながら、モデルの改善を検討することが重要です。
主成分回帰(PCR)で多重共線性を解決する
ここで登場するのが主成分回帰(Principal Component Regression, PCR)です。PCRの基本的なアイデアは非常にシンプルです。
まず、説明変数にPCAを適用して主成分を抽出します。次に、元の説明変数の代わりに主成分を使って回帰を行います。
なぜこれで多重共線性が解決するのでしょうか?
それは、PCAで得られる主成分は互いに直交(無相関)しているからです。無相関な変数間には多重共線性は存在しません。
PCRを数式で理解する
PCRのアイデアを数式で確認しましょう。
まず、標準化された説明変数の行列を X(サンプル数 n × 変数の数 p)とします。PCAを適用すると、主成分得点の行列 Z が得られます。
$$
Z = XV
$$
ここで、V は固有ベクトルを列に並べた行列です。第2回で学んだように、Z の各列が主成分得点(PC1, PC2, …)に対応します。
通常の重回帰では、X を使って回帰係数 \boldsymbol{\beta} を推定しますが、PCRでは Z の一部(上位 k 個の主成分)を使います。
上位 k 個の主成分だけを取り出した行列を Z_k とすると、PCRは次の回帰モデルを推定します。
$$
\mathbf{y} = Z_k \boldsymbol{\gamma} + \boldsymbol{\varepsilon}
$$
ここで \boldsymbol{\gamma} は主成分空間での回帰係数です。
この回帰係数の推定値は、通常の最小二乗法と同じ形式で求められます。
$$
\hat{\boldsymbol{\gamma}} = (Z_k^\top Z_k)^{-1} Z_k^\top \mathbf{y}
$$
ここで重要なのは、主成分 Z_k の列同士は互いに直交しているという点です。
直交しているということは、Z_k^\top Z_k が対角行列になることを意味します。対角行列の逆行列は常に安定して計算できるため、多重共線性の問題が解消されるのです。
PCRを手順を追って実装する
まず、PCAを適用して主成分を抽出します。
# PCAを適用(全成分を抽出)
pca = PCA()
Z = pca.fit_transform(X_scaled)
# 寄与率を確認
print("=== PCAの結果 ===")
for i, ratio in enumerate(pca.explained_variance_ratio_):
cumsum = sum(pca.explained_variance_ratio_[:i+1])
print(f"PC{i+1}: 寄与率 {ratio*100:.1f}%, 累積 {cumsum*100:.1f}%")
以下、実行結果です。
=== PCAの結果 === PC1: 寄与率 59.0%, 累積 59.0% PC2: 寄与率 39.6%, 累積 98.6% PC3: 寄与率 0.8%, 累積 99.4% PC4: 寄与率 0.3%, 累積 99.7% PC5: 寄与率 0.3%, 累積 100.0%
元のデータが2つの潜在変数から生成されているため、最初の2つの主成分で大部分の分散が説明されています。
主成分で回帰を行う
次に、抽出した主成分を説明変数として回帰分析を行います。
# 第1主成分と第2主成分の主成分得点を抽出
n_components = 2
Z_reduced = Z[:, :n_components]
# 主成分で回帰分析を実施
pcr = LinearRegression()
pcr.fit(Z_reduced, y)
# 結果を表示
print(f"=== 主成分回帰(PCR, {n_components}成分)の結果 ===")
print()
print("主成分空間での回帰係数:")
for i, coef in enumerate(pcr.coef_):
print(f" PC{i+1}: {coef:.3f}")
print(f"\nR²スコア: {r2_score(y, pcr.predict(Z_reduced)):.3f}")
以下、実行結果です。
=== 主成分回帰(PCR, 2成分)の結果 === 主成分空間での回帰係数: PC1: 1.188 PC2: 2.091 R²スコア: 0.970
主成分は互いに無相関なので、係数の推定は安定しています。
元の変数での係数に変換する
主成分空間での係数を、元の変数空間に戻すことができます。
主成分空間での回帰係数 \hat{\boldsymbol{\gamma}} を、元の変数空間での係数 \hat{\boldsymbol{\beta}} に変換する方法を数式で確認しましょう。
主成分得点は Z = XV という関係で元のデータと結びついていました。これを使って、予測値を2通りの方法で表現できます。
主成分空間での予測は次のようになります。
$$
\hat{\mathbf{y}} = Z_k \hat{\boldsymbol{\gamma}}
$$
一方、元の変数空間での予測は次のようになります。
$$
\hat{\mathbf{y}} = X \hat{\boldsymbol{\beta}}
$$
$$
\hat{\mathbf{y}} = Z_k \hat{\boldsymbol{\gamma}} = X V_k \hat{\boldsymbol{\gamma}}
$$
この式と \hat{\mathbf{y}} = X \hat{\boldsymbol{\beta}} を比較すると、元の変数空間での回帰係数は次のように求められます。
$$
\hat{\boldsymbol{\beta}} = V_k \hat{\boldsymbol{\gamma}}
$$
つまり、主成分空間での係数に固有ベクトル行列を掛けることで、元の変数空間での係数に変換できるのです。
# 元の変数空間での係数に変換
# β_original = V @ β_pc(Vは固有ベクトル行列)
V = pca.components_[:n_components].T
beta_original = V @ pcr.coef_
print("=== 元の変数空間での係数(PCRから変換) ===")
coef_pcr_df = pd.DataFrame({
'変数': feature_names,
'PCR係数': beta_original,
'OLS係数': ols.coef_
})
print(coef_pcr_df.round(3))
以下、実行結果です。
=== 元の変数空間での係数(PCRから変換) === 変数 PCR係数 OLS係数 0 x1 0.664 1.300 1 x2 0.623 0.082 2 x3 0.627 0.526 3 x4 1.523 1.575 4 x5 1.498 1.430
このコードを実行すると、PCRとOLSの係数を比較できます。
scikit-learnのPipelineを使った実装
実務では、データの標準化から主成分分析、回帰分析をPipelineにまとめると便利です。
# Pipelineを構築
pcr_pipeline = Pipeline([
('scaler', StandardScaler()),
('pca', PCA(n_components=2)),
('regressor', LinearRegression())
])
# 学習
pcr_pipeline.fit(X, y)
# 予測
y_pred = pcr_pipeline.predict(X)
print("=== Pipeline PCRの結果 ===")
print(f"R²スコア: {r2_score(y, y_pred):.3f}")
以下、実行結果です。
=== Pipeline PCRの結果 === R²スコア: 0.970
PLS回帰
PCRの発展形として、PLS回帰(Partial Least Squares Regression)があります。PCRとPLSの違いを簡単に説明しておきましょう。
PCRは、説明変数Xの分散を最大化する方向で主成分を抽出します。つまり、目的変数yのことは考慮せずに次元削減を行います。
一方、PLS回帰は、説明変数Xと目的変数yの共分散を最大化する方向で成分を抽出します。つまり、yの予測に役立つ方向を優先的に抽出します。
この違いを数式で表現してみましょう。
PCAでは、説明変数 X の共分散行列 X^\top X の固有値問題を解きます。これは、X の分散を最大化する方向 \mathbf{w} を見つけることに相当します。
$$
\text{PCA: } \max_{\mathbf{w}} \mathbf{w}^\top X^\top X \mathbf{w}
$$
一方、PLSでは説明変数 X と目的変数 \mathbf{y} の共分散を最大化する方向を探します。
$$
\text{PLS: } \max_{\mathbf{w}} \mathbf{w}^\top X^\top \mathbf{y} \mathbf{y}^\top X \mathbf{w}
$$
PCAが「X の中でばらつきが大きい方向」を見つけるのに対し、PLSは「X と \mathbf{y} が一緒に変動する方向」を見つけます。
たとえば、ある主成分が X の分散の多くを説明していても、目的変数 \mathbf{y} とほとんど関係がなければ、予測には役立ちません。PLSはこの問題を避け、予測に直接役立つ成分を優先的に抽出します。
このため、PLS回帰はPCRよりも少ない成分数で高い予測精度を達成できることが多いです。
from sklearn.cross_decomposition import PLSRegression
# PLS回帰
pls = PLSRegression(n_components=2)
pls.fit(X_scaled, y)
print("=== PLS回帰の結果 ===")
print(f"R²スコア: {r2_score(y, pls.predict(X_scaled)):.3f}")
# PCRとの比較
print("\n=== PCR vs PLS(2成分での比較) ===")
print(f"PCR R²: {r2_score(y, pcr.predict(Z_reduced)):.3f}")
print(f"PLS R²: {r2_score(y, pls.predict(X_scaled)):.3f}")
以下、実行結果です。
=== PLS回帰の結果 === R²スコア: 0.970 === PCR vs PLS(2成分での比較) === PCR R²: 0.970 PLS R²: 0.970
まとめ
この第6回では、PCAを回帰分析に応用する方法を学びました。
多重共線性は、説明変数同士が強く相関している状態で、回帰係数の推定を不安定にします。VIF(分散膨張係数)が10を超える変数があれば、注意が必要です。
主成分回帰(PCR)は、説明変数にPCAを適用して互いに無相関な主成分を抽出し、それを使って回帰を行う手法です。主成分は直交しているため、多重共線性の問題が解消されます。成分数は交差検証で選択します。
scikit-learnのPipelineを使うと、標準化→PCA→回帰という一連の処理をまとめることができます。
PLS回帰は、PCRの発展形で、目的変数との共分散を最大化する成分を抽出します。予測が目的の場合、PCRより効率的なことが多いです。
全6回にわたるシリーズ「Pythonで体感する次元削減入門」を完走しました。
— 第1回 —
なぜ「次元を減らす」のか? 情報の海で溺れないために
https://www.salesanalytics.co.jp/datascience/datascience286/
— 第2回 —
PCAのしくみを分散・共分散・固有値分解で理解する
https://www.salesanalytics.co.jp/datascience/datascience288/
— 第3回 —
次元はいくつ残す? 寄与率とスクリープロットの読み方
https://www.salesanalytics.co.jp/datascience/datascience289/
— 第4回 —
scikit-learnでさくっとPCAを実施する
https://www.salesanalytics.co.jp/datascience/datascience290/
— 第5回 —
PCAと因子分析、何が違う?
https://www.salesanalytics.co.jp/datascience/datascience291/
— 第6回 —
次元削減を回帰に活かす主成分回帰(PCR)
https://www.salesanalytics.co.jp/datascience/datascience292/
振り返ると、第1回では「データが広がる方向を見つける」というPCAの直感を学び、第2回では共分散行列と固有値分解という数学的基盤を理解しました。
第3回では寄与率とスクリープロットで次元数を決める方法を習得し、第4回ではscikit-learnでPCAを効率的に実行する方法を学びました。
第5回ではPCAと因子分析の本質的な違いの理解しました。そして今回の第6回では、PCAを回帰分析に応用する主成分回帰を学びました。
次元削減は、データサイエンスの基礎でありながら、奥が深いテーマです。このシリーズで学んだ知識を土台に、ぜひ実際のデータ分析で活用してみてください。
最後までお読みいただき、ありがとうございました!

