前回、k-means法を学んだときに「K=3」と決め打ちでクラスタ数を指定しました。
でも、ちょっと待ってください。なぜ3なのでしょうか? 2でも4でも5でもいいはずです。
この疑問は、日常生活でも遭遇します。
たとえば、本棚を整理するとき。あなたは本をいくつのカテゴリに分けますか?
「小説」「技術書」「漫画」の3つ?
それとも「日本文学」「海外文学」「プログラミング」「データサイエンス」「少年漫画」「少女漫画」の6つ?
さらに細かく分けることもできるし、逆に「読み物」「仕事用」の2つだけにすることもできます。
正解はないのです。目的や好みによって、最適な分け方は変わります。
クラスター分析でも同じです。データに「正解のクラスタ数」が書いてあるわけではありません。
しかし、データから「ちょうどいいクラスタ数」を推定する方法はあります。
今回は、その代表的な手法であるエルボー法とシルエット分析を学びましょう。
Contents
なぜクラスタ数の決定が難しいのか
k-means法の目標は「クラスタ内のばらつきを最小化する」ことでした。
前回学んだ目的関数を思い出してみましょう。
$$
J = \sum_{k=1}^{K} \sum_{\mathbf{x}_i \in C_k} \|\mathbf{x}_i – \boldsymbol{\mu}_k\|^2
$$
この値(inertia、またはSSE: Sum of Squared Errors)は、クラスタ数Kを増やせば必ず減少します。
極端な話、K=n(データ数と同じ)にすれば、各データが1つのクラスタになり、ばらつきは0になります。
しかし、それでは「グループ分け」の意味がありません。100人の顧客を100グループに分けても、たとえばマーケティング施策には使えません。
つまり、クラスタ数の決定は「ばらつきの最小化」と「グループの意味のある数」のトレードオフなのです。
Pythonの準備
今回使うライブラリをインポートしましょう。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import japanize_matplotlib from sklearn.cluster import KMeans from sklearn.preprocessing import StandardScaler from sklearn.datasets import make_blobs from sklearn.metrics import silhouette_score, silhouette_samples # 乱数シードを固定 np.random.seed(42)
silhouette_scoreとsilhouette_samplesは、後ほど学ぶシルエット分析で使用します。
サンプルデータを準備する
まずは、分析に使うサンプルデータを生成しましょう。
今回は「本当のクラスタ数」がわかっているデータを使って、手法の妥当性を確認します。
# 4つのクラスタを持つサンプルデータを生成
X, y_true = make_blobs(
n_samples=300,
centers=4, # 本当のクラスタ数は4
cluster_std=0.8,
random_state=42
)
print(f"データの形状: {X.shape}")
print(f"本当のクラスタ数: {len(np.unique(y_true))}")
このデータには「本当は4つのクラスタがある」ことを覚えておいてください。
エルボー法やシルエット分析で、この「4」を発見できるか試してみましょう。
データを可視化する
まずはデータを散布図で確認します。
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], s=50, alpha=0.6)
plt.title('Sample Data (True K=4)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
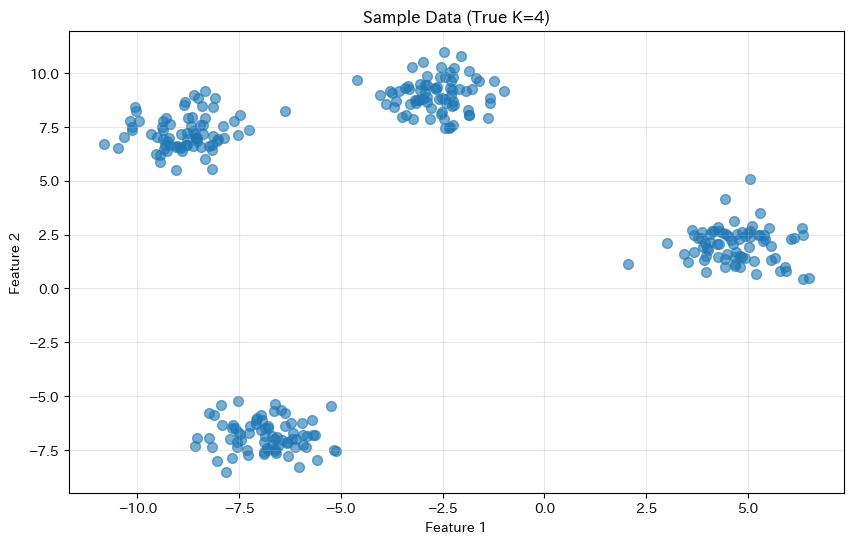
目視でも4つのグループがなんとなく見えるでしょうか?
しかし、実際のデータでは次元が高かったり、クラスタの境界が曖昧だったりして、目視では判断できないことがほとんどです。
そこで定量的な手法が必要になります。
エルボー法(Elbow Method)
考え方
エルボー法は最もシンプルで広く使われている手法です。
考え方は以下の通りです。
- Step 1:K=1, 2, 3, … と順番にクラスタ数を変えてk-meansを実行
- Step 2:各Kでのinertia(クラスタ内誤差平方和)を記録
- Step 3:横軸にK、縦軸にinertiaをプロット
- Step 4:グラフが「肘(エルボー)」のように折れ曲がる点を探す
inertiaはKを増やすほど減少しますが、適切なクラスタ数を超えると減少幅が小さくなります。
この「減少幅が急に緩やかになる点」が、ちょうど肘を曲げたような形に見えることから「エルボー法」と呼ばれています。
エルボー法を実装する
では、実際にエルボー法を実装してみましょう。K=1から10までのinertiaを計算します。
# 各クラスタ数でのinertiaを計算
K_range = range(1, 11)
inertias = []
for k in K_range:
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
kmeans.fit(X)
inertias.append(kmeans.inertia_)
# 結果を表示
for k, inertia in zip(K_range, inertias):
print(f"K={k}: inertia = {inertia:.1f}")
以下、実行結果です。
K=1: inertia = 19780.3 K=2: inertia = 9211.2 K=3: inertia = 1919.4 K=4: inertia = 362.5 K=5: inertia = 329.3 K=6: inertia = 294.6 K=7: inertia = 261.6 K=8: inertia = 232.0 K=9: inertia = 209.1 K=10: inertia = 188.7
K=1のときにinertiaが最も大きく、Kが増えるにつれて減少していることがわかります。
しかし、数値だけでは「どこで減少が緩やかになるか」がわかりにくいですね。
エルボーカーブを描く
inertiaの推移をグラフで可視化しましょう。
plt.figure(figsize=(10, 6))
plt.plot(
K_range, inertias,
'bo-', linewidth=2, markersize=10
)
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Inertia (Within-cluster Sum of Squares)')
plt.title('Elbow Method')
plt.xticks(K_range)
plt.grid(True, alpha=0.3)
# K=4の位置に縦線を追加(参考)
plt.axvline(
x=4,
color='r', linestyle='--', alpha=0.7,
label='Elbow point (K=4)'
)
plt.legend()
plt.show()
以下、実行結果です。
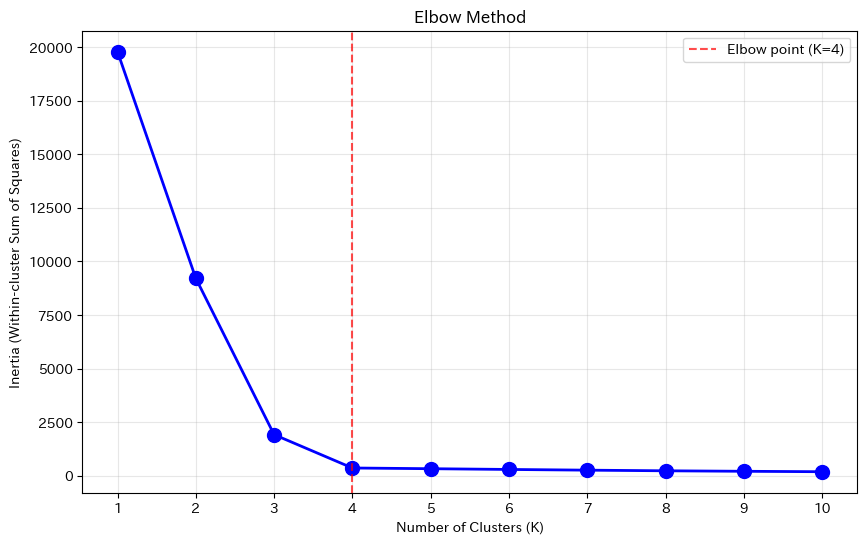
グラフを見ると、K=4あたりで曲線が「肘」のように曲がっていることがわかります。
K=1からK=4までは急激に減少していますが、K=4以降は減少幅が緩やかになっています。
これは「4つのクラスタに分けると大幅に改善するが、5つ以上に分けてもあまり変わらない」ことを意味しています。
したがって、K=4が適切と判断できます。
エルボー法の弱点
エルボー法は直感的でわかりやすいのですが、「肘」が明確でない場合があります。
# 肘が曖昧なデータを生成
X_ambiguous, _ = make_blobs(
n_samples=300,
centers=4,
cluster_std=10,
random_state=42
)
# エルボーカーブを計算
inertias_ambiguous = []
for k in K_range:
kmeans = KMeans(
n_clusters=k,
random_state=42,
n_init=10
)
kmeans.fit(X_ambiguous)
inertias_ambiguous.append(kmeans.inertia_)
# プロット
plt.figure(figsize=(10, 6))
plt.plot(
K_range, inertias_ambiguous,
'bo-', linewidth=2, markersize=10
)
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Inertia')
plt.title('Elbow Method (Ambiguous Case)')
plt.xticks(K_range)
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
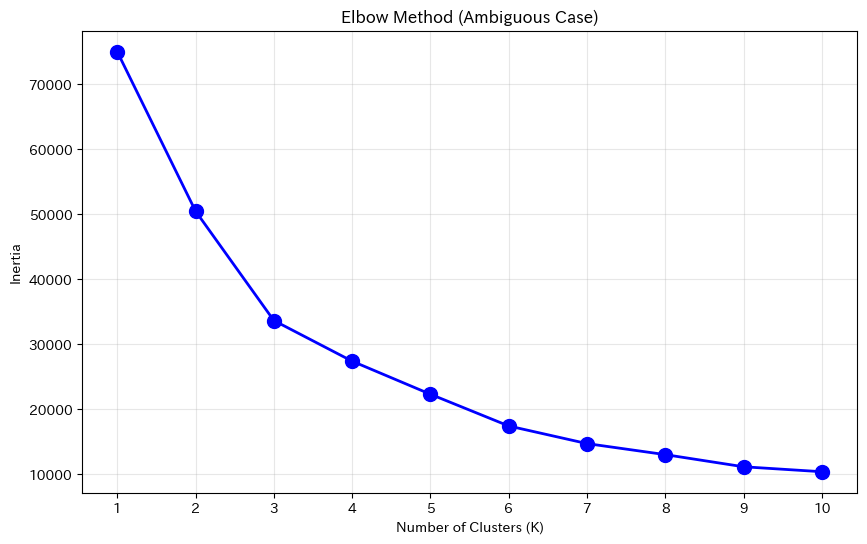
クラスタの境界が曖昧なデータ(標準偏差を大きくしたもの)では、カーブがなだらかになり、「肘」の位置が特定しにくくなります。
このような場合は、次に紹介するシルエット分析が役立ちます。
シルエット分析(Silhouette Analysis)
考え方
シルエット分析は、各データ点が「どれだけ適切なクラスタに割り当てられているか」を評価する手法です。
各データ点について、シルエット係数という値を計算します。
$$
s(i) = \frac{b(i) – a(i)}{\max(a(i), b(i))}
$$
- a(i):データ点iと、同じクラスタ内の他の点との平均距離(凝集度)
- b(i):データ点iと、最も近い他クラスタの点との平均距離(分離度)
シルエット係数は-1から+1の範囲の値を取ります。
- +1に近い:そのデータ点は正しいクラスタに割り当てられている(同クラスタ内で近く、他クラスタとは遠い)
- 0に近い:クラスタの境界付近にある(どちらのクラスタでもよい)
- -1に近い:間違ったクラスタに割り当てられている可能性が高い
全データ点のシルエット係数の平均値がシルエットスコアです。この値が高いほど、良いクラスタリングと言えます。
シルエットスコアを計算する
各クラスタ数でのシルエットスコアを計算してみましょう。
# 各クラスタ数でのシルエットスコアを計算
# K=1ではシルエットスコアは定義できないため、K=2から
K_range_sil = range(2, 11)
silhouette_scores = []
for k in K_range_sil:
kmeans = KMeans(
n_clusters=k,
random_state=42,
n_init=10
)
labels = kmeans.fit_predict(X)
score = silhouette_score(X, labels)
silhouette_scores.append(score)
print(f"K={k}: silhouette score = {score:.3f}")
以下、実行結果です。
K=2: silhouette score = 0.603 K=3: silhouette score = 0.778 K=4: silhouette score = 0.834 K=5: silhouette score = 0.698 K=6: silhouette score = 0.588 K=7: silhouette score = 0.449 K=8: silhouette score = 0.332 K=9: silhouette score = 0.344 K=10: silhouette score = 0.359
K=4のときにシルエットスコアが最も高くなっています。
これは「4つのクラスタが最も適切」であることを示しています。
シルエットスコアをグラフ化する
結果をグラフで可視化しましょう。
plt.figure(figsize=(10, 6))
plt.plot(
K_range_sil, silhouette_scores,
'go-', linewidth=2, markersize=10
)
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Silhouette Score')
plt.title('Silhouette Analysis')
plt.xticks(K_range_sil)
plt.grid(True, alpha=0.3)
# 最大値の位置を強調
best_k = K_range_sil[np.argmax(silhouette_scores)]
plt.axvline(
x=best_k,
color='r', linestyle='--', alpha=0.7,
label=f'Best K={best_k}'
)
plt.legend()
plt.show()
以下、実行結果です。
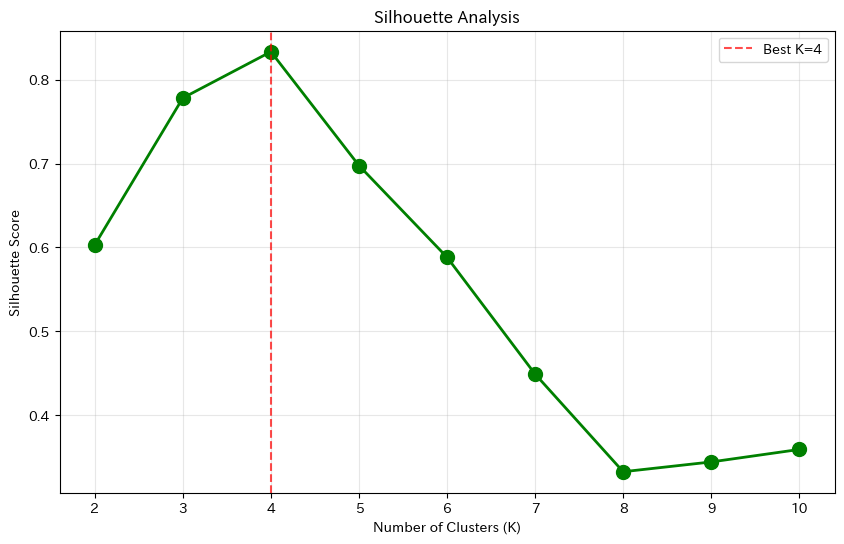
シルエットスコアが最大となるKを選ぶことで、最適なクラスタ数を決定できます。
エルボー法と同様に、K=4が選ばれました。
シルエットプロットで詳細を確認する
シルエット分析のもう一つの強力なツールがシルエットプロットです。
各クラスタ内のデータ点ごとのシルエット係数を可視化することで、クラスタの「質」を詳しく確認できます。
"""シルエットプロットを描画する関数"""
def plot_silhouette(X, n_clusters_list):
fig, axes = plt.subplots(
len(n_clusters_list), 1,
figsize=(10, 3 * len(n_clusters_list))
)
if len(n_clusters_list) == 1:
axes = [axes]
for ax, n_clusters in zip(axes, n_clusters_list):
kmeans = KMeans(
n_clusters=n_clusters,
random_state=42,
n_init=10
)
labels = kmeans.fit_predict(X)
silhouette_vals = silhouette_samples(X, labels)
silhouette_avg = silhouette_score(X, labels)
y_lower = 10
for i in range(n_clusters):
cluster_silhouette_vals = silhouette_vals[labels == i]
cluster_silhouette_vals.sort()
cluster_size = len(cluster_silhouette_vals)
y_upper = y_lower + cluster_size
color = plt.cm.viridis(i / n_clusters)
ax.fill_betweenx(np.arange(y_lower, y_upper),
0, cluster_silhouette_vals,
facecolor=color, alpha=0.7)
ax.text(-0.05, y_lower + 0.5 * cluster_size, str(i))
y_lower = y_upper + 10
ax.axvline(
x=silhouette_avg,
color='red', linestyle='--',
label=f'Average: {silhouette_avg:.3f}'
)
ax.set_xlabel('Silhouette Coefficient')
ax.set_ylabel('Cluster')
ax.set_title(f'Silhouette Plot (K={n_clusters})')
ax.legend()
plt.tight_layout()
plt.show()
この関数を使って、K=2~7の場合を比較してみましょう。
# K=2~7のシルエットプロットを描画 plot_silhouette(X, range(2, 7))
以下、実行結果です。
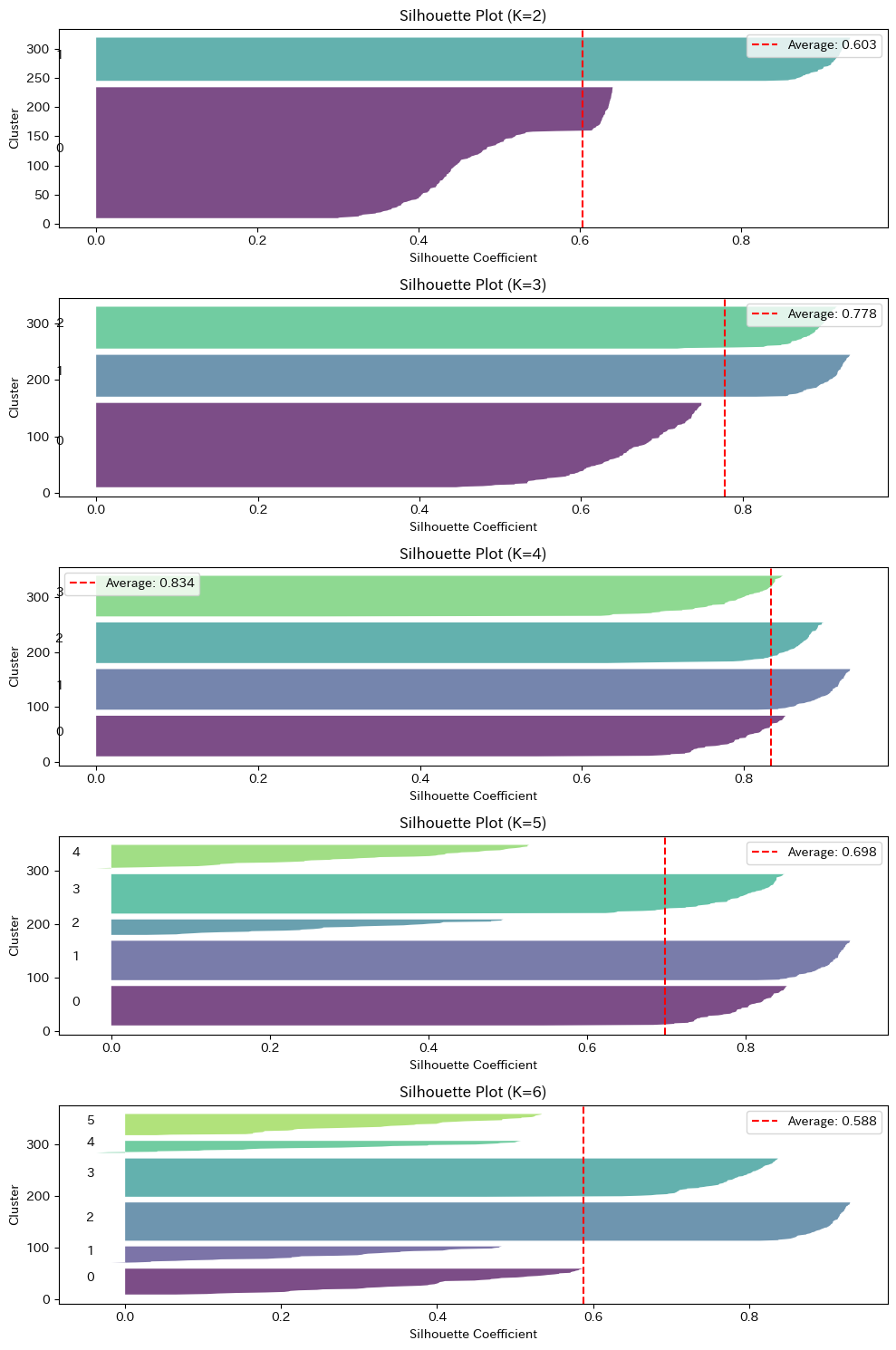
良いクラスタリングの特徴は以下の通りです。
- 各クラスタの幅(N数)がほぼ均等
- すべてのクラスタが平均線(赤い点線)を超えている
- 負の値を持つデータ点が少ない
K=4のプロットが最もバランスが良く、全てのクラスタが平均線を超えていることが確認できるはずです。
統計と直感のバランス
エルボー法やシルエット分析は強力なツールですが、最終的な判断は人間が行う必要があります。
たとえば、シルエットスコアはK=4が最大だったとしても、ビジネス的にはK=3の方が施策を打ちやすいかもしれません。逆に、K=5にした方が各セグメントの特徴が明確になることもあります。
実務でクラスタ数を決める際は、以下の観点を総合的に考慮しましょう。
| 観点 | 確認事項 |
|---|---|
| 統計的指標 | エルボー法とシルエット分析で推奨されるK |
| ビジネス的解釈 | 各クラスタに意味のある名前をつけられるか |
| 施策の実行可能性 | そのクラスタ数に対して施策を打てるか |
| クラスタサイズ | 極端に小さい/大きいクラスタがないか |
| 安定性 |
統計的な「最適」と、ビジネス的な「最適」は必ずしも一致しません。 両方のバランスを取ることが、実務では重要です。
迷ったときは、候補となるいくつかのKでクラスタリングを行い、結果を比較するのも有効です。
まとめ
今回は、クラスタ数の決め方を2つ紹介しました。
| 概要 | 特徴・補足 | |
|---|---|---|
| エルボー法 | クラスタ数を変えながら inertia を計算し、グラフが「肘」のように曲がる点を探す | シンプルで直感的だが、曲がり点が不明確な場合もある |
| シルエット分析 | 各データ点の「正しいクラスタへの所属度」を評価する |
実務では、複数の手法を組み合わせて判断するようにします。このとき、統計的な最適とビジネス的な最適のバランスを取る必要あり、最終判断は人間が行います。
以下、判断基準です。
- 各クラスタに意味のある解釈ができるか
- 施策に活用できるクラスタ数か
- 極端なサイズのクラスタがないか
クラスタ数を決めて、データを分類できました。しかし、これで終わりではありません。
次回の最終回では、クラスタープロファイリングのお話しをします。
「クラスタ0」「クラスタ1」という数字のラベルを、「プレミアム顧客」「ライトユーザー」といった意味のある名前に変換し、ビジネス施策につなげる方法を解説します。

