こんにちは!「Pythonで始める分類モデル入門」もいよいよ最終回です。
- 第1回 —分類問題ってなに? ロジスティック回帰で「合格予測」を作ろう
- 第2回 —データの「形」から分ける — 線形判別分析(LDA)入門
- 第3回 —「もし〜なら」で分ける — 決定木の仕組みと過学習対策
- 第4回 —木を束ねて森にする — ランダムフォレストで精度向上
これまでの4回で、ロジスティック回帰、線形判別分析、決定木、ランダムフォレストと、様々な分類モデルを学んできました。
モデルの性能を評価する際、私たちは「正解率」を使ってきましたが、実は正解率だけでは不十分な場合があります。
今回は、分類モデルを正しく評価するための様々な指標を学びます。
「良いモデルとは何か」は、問題の性質によって変わります。
この視点を身につけることで、実務で本当に役立つモデルを作れるようになります。
Contents
- 正解率99%のモデル、実は役立たず?
- 必要なライブラリを読み込もう
- 不均衡データの問題を体験しよう
- 混同行列:予測結果を4つに分類する
- モデルを作って混同行列を見てみよう
- 混同行列をヒートマップで可視化しよう
- 4つの数値を取り出して分析しよう
- 評価指標その1:適合率(Precision)
- 評価指標その2:再現率(Recall)
- 適合率と再現率のトレードオフ
- 評価指標その3:F1スコア
- 評価指標その4:特異度(Specificity)
- 分類レポートでまとめて確認しよう
- ROC曲線とAUC
- 閾値を変えると何が変わるか
- 適合率-再現率曲線(PR曲線)
- 問題に応じた指標の選び方
- 偽陽性(誤検知)のコストが高い場合 → 適合率を重視
- 例①:スパムフィルター
- 例②:クレジットカードの利用停止判定
- 例③:人事の不正・懲戒対象の検知
- 偽陰性(見逃し)のコストが高い場合 → 再現率を重視
- 例①:がん検診
- 例②:不正取引検出
- 例③:製造業の不良品検出
- 例④:セキュリティ侵入検知
- 両方のバランスが重要な場合 → F1スコアを重視
- 例①:顧客離反(チャーン)予測
- 例②:採用書類の一次スクリーニング
- 例③:商品レビューのネガティブ判定
- 複数モデルを比較しよう
- ROC曲線を並べて比較しよう
- 実務での評価指標活用
- ステップ1:問題の性質を理解する
- ステップ2:適切な指標を選ぶ
- ステップ3:混同行列で詳細を確認する
- ステップ4:閾値を調整する
- ステップ5:ビジネス指標と結びつける
- まとめ
正解率99%のモデル、実は役立たず?
いきなりですが、クイズです。
あなたはクレジットカード会社で働いていて、不正利用を検出するモデルを作りました。
1万件の取引データでテストしたところ、正解率99%を達成しました。素晴らしい成果でしょうか?
答えは「データによる」です。
たとえば、クレジットカードの不正利用は全取引が約1%とします。
この場合、「すべての取引を正常と予測する」という何も考えないモデルでも、正解率は99%になります。
しかし、このモデルは不正取引を1件も検出できません。
これが正解率の落とし穴です。
クラスの割合が偏っている(不均衡データ)場合、正解率は誤解を招く指標になります。
必要なライブラリを読み込もう
今回使うライブラリを読み込みます。評価指標の計算にはsklearn.metricsモジュールを使います。
以下、コードです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.linear_model import LogisticRegression
from sklearn import tree
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
# 評価指標
from sklearn.metrics import (
confusion_matrix,
accuracy_score,
precision_score,
recall_score,
f1_score,
classification_report,
roc_curve,
auc,
precision_recall_curve
)
# 乱数のシードを固定
np.random.seed(42)
不均衡データの問題を体験しよう
まずは、不均衡データの問題を実際に体験してみましょう。不正取引検出のデータを作成します。
以下、コードです。
# 不正取引検出のデータを生成(不正は全体の2%)
n_transactions = 5000
n_fraud = 100 # 不正取引は2%
# 正常取引のデータ
normal_amount = np.random.exponential(
5000,
n_transactions - n_fraud
)
normal_time = np.random.uniform(
6, 23,
n_transactions - n_fraud
)
# 不正取引のデータ(金額が大きく、深夜が多い傾向)
fraud_amount = np.random.exponential(
15000,
n_fraud
)
fraud_time = np.random.uniform(
0, 6,
n_fraud
)
# 結合
amount = np.concatenate([
normal_amount,
fraud_amount
])
time = np.concatenate([
normal_time,
fraud_time
])
is_fraud = np.array(
[0] * (n_transactions - n_fraud) + [1] * n_fraud)
# シャッフル
shuffle_idx = np.random.permutation(len(amount))
amount, time, is_fraud = (
amount[shuffle_idx],
time[shuffle_idx],
is_fraud[shuffle_idx]
)
print(f"全取引数: {len(is_fraud)}")
print(f"不正取引数: {is_fraud.sum()} ({is_fraud.mean()*100:.1f}%)")
print(f"正常取引数: {len(is_fraud) - is_fraud.sum()} ({(1-is_fraud.mean())*100:.1f}%)")
以下、実行結果です。
全取引数: 5000 不正取引数: 100 (2.0%) 正常取引数: 4900 (98.0%)
不正取引が全体の約2%しかない、非常に不均衡なデータが作成されました。
このようなデータで「すべて正常」と予測すると、正解率は約98%になりますが、不正は1件も検出できません。
混同行列:予測結果を4つに分類する
混同行列(Confusion Matrix)は、分類モデルの予測結果を4つのカテゴリに整理した表です。
これを理解することが、評価指標の第一歩です。
2クラス分類(陽性/陰性)の場合、予測結果は以下の4つに分かれます。
| 予測:陽性 | 予測:陰性 | |
|---|---|---|
| 実際:陽性 | 真陽性(TP) | 偽陰性(FN) |
| 実際:陰性 | 偽陽性(FP) |
- :実際に陽性で、陽性と予測した(正解)
- 真陰性(True Negative, TN):実際に陰性で、陰性と予測した(正解)
- 偽陽性(False Positive, FP):実際は陰性なのに、陽性と予測した(誤り)
- 偽陰性(False Negative, FN)
不正取引検出の例で言えば、TPは「不正を正しく検出」、TNは「正常を正しく正常と判定」、FPは「正常を誤って不正と判定(誤検知)」、FNは「不正を見逃した(検出漏れ)」となります。
モデルを作って混同行列を見てみよう
実際にモデルを作成し、混同行列を確認してみましょう。
以下、コードです。
# 特徴量とラベルを準備
X = np.column_stack([amount, time])
y = is_fraud
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42)
# ロジスティック回帰モデルを訓練
model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# 正解率を計算
accuracy = accuracy_score(y_test, y_pred)
print(f"正解率: {accuracy*100:.1f}%")
以下、実行結果です。
正解率: 99.4%
正解率はかなり高く見えますが、これだけでは本当に良いモデルかわかりません。
混同行列を見てみましょう。
以下、コードです。
# 混同行列を計算
cm = confusion_matrix(y_test, y_pred)
print("【混同行列】")
print(f" 予測:正常 予測:不正")
print(f"実際:正常 {cm[0,0]:>6} {cm[0,1]:>6}")
print(f"実際:不正 {cm[1,0]:>6} {cm[1,1]:>6}")
以下、実行結果です。
【混同行列】
予測:正常 予測:不正
実際:正常 1477 0
実際:不正 9 14
混同行列を見ると、モデルの「中身」がわかります。
正常取引はほとんど正しく判定できていますが、不正取引の検出状況はどうでしょうか?
混同行列をヒートマップで可視化しよう
混同行列をより見やすくヒートマップで表示してみましょう。
以下、コードです。
# ヒートマップで可視化
plt.figure(figsize=(8, 6))
plt.imshow(cm, cmap='Blues')
plt.colorbar()
# ラベルを追加
classes = ['Normal', 'Fraud']
tick_marks = [0, 1]
plt.xticks(tick_marks, classes)
plt.yticks(tick_marks, classes)
# 数値を表示
for i in range(2):
for j in range(2):
plt.text(
j, i,
str(cm[i, j]),
ha='center', va='center', fontsize=20,
color='white' if cm[i, j] > cm.max()/2 else 'black'
)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.tight_layout()
plt.show()
以下、実行結果です。
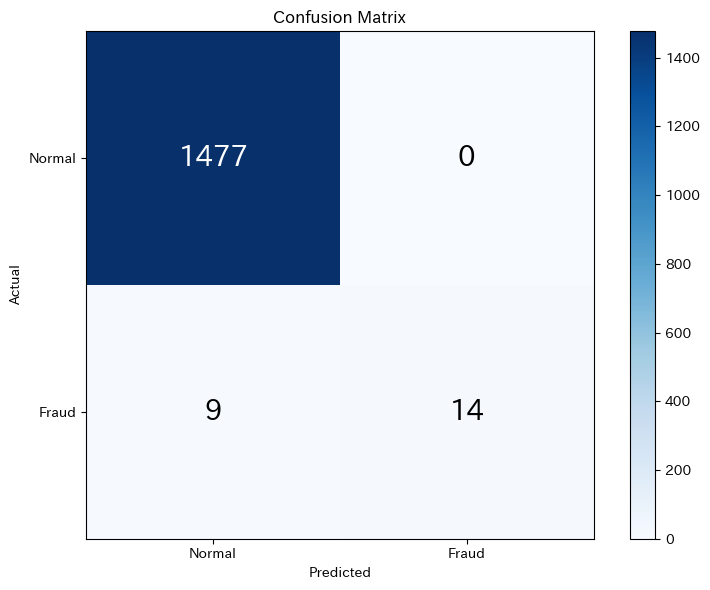
ヒートマップにより、どの種類の正解・誤りが多いかが一目でわかります。
対角線上(左上と右下)が正解、それ以外が誤りです。
4つの数値を取り出して分析しよう
混同行列の各要素を取り出して、詳しく分析してみましょう。
以下、コードです。
# 混同行列の要素を取り出す
TN, FP, FN, TP = cm.ravel()
print("【混同行列の内訳】")
print(f"真陰性(TN): {TN}件 - 正常取引を正しく「正常」と判定")
print(f"偽陽性(FP): {FP}件 - 正常取引を誤って「不正」と判定(誤検知)")
print(f"偽陰性(FN): {FN}件 - 不正取引を「正常」と判定(見逃し)")
print(f"真陽性(TP): {TP}件 - 不正取引を正しく「不正」と検出")
print()
print(f"不正取引 {TP + FN}件 中、{TP}件を検出(検出率: {TP/(TP+FN)*100:.1f}%)")
print(f"正常取引 {TN + FP}件 中、{FP}件を誤検知(誤検知率: {FP/(TN+FP)*100:.1f}%)")
以下、実行結果です。
【混同行列の内訳】 真陰性(TN): 1477件 - 正常取引を正しく「正常」と判定 偽陽性(FP): 0件 - 正常取引を誤って「不正」と判定(誤検知) 偽陰性(FN): 9件 - 不正取引を「正常」と判定(見逃し) 真陽性(TP): 14件 - 不正取引を正しく「不正」と検出 不正取引 23件 中、14件を検出(検出率: 60.9%) 正常取引 1477件 中、0件を誤検知(誤検知率: 0.0%)
この結果から、モデルの強みと弱みが見えてきます。
FPが多いと顧客に迷惑がかかり、FNが多いと金銭的損失が発生します。
どちらをより避けたいかは、ビジネスの状況によって異なります。
評価指標その1:適合率(Precision)
適合率(Precision)は、「陽性と予測したもののうち、実際に陽性だった割合」です。
$$
\text{適合率} = \frac{TP}{TP + FP}
$$
不正取引検出で言えば、「不正と判定した取引のうち、本当に不正だった割合」です。
適合率が低いと、正常な取引を誤って不正と判定してしまう(誤検知が多い)ことを意味します。
以下、コードです。
# 適合率を計算
precision = precision_score(y_test, y_pred)
print(f"適合率: {precision*100:.1f}%")
print(
f"「不正」と判定した{TP + FP}件のうち、"
f"本当に不正だったのは{TP}件({precision*100:.1f}%)"
)
以下、実行結果です。
適合率: 100.0% 「不正」と判定した14件のうち、本当に不正だったのは14件(100.0%)
適合率が高いほど、「不正と判定されたら本当に不正である可能性が高い」ことを意味します。
評価指標その2:再現率(Recall)
再現率(Recall)は、「実際に陽性のもののうち、正しく陽性と予測できた割合」です。感度(Sensitivity)や検出率とも呼ばれます。
$$
\text{再現率} = \frac{TP}{TP + FN}
$$
不正取引検出で言えば、「実際の不正取引のうち、どれだけを検出できたか」です。
再現率が低いと、不正を見逃してしまう(検出漏れが多い)ことを意味します。
以下、コードです。
# 再現率を計算
recall = recall_score(y_test, y_pred)
print(f"再現率: {recall*100:.1f}%")
print(
f"実際の不正取引{TP + FN}件のうち、"
f"\n - {TP}件を検出できた({recall*100:.1f}%)"
f"\n - {FN}件は見逃した({FN/(TP+FN)*100:.1f}%)"
)
以下、実行結果です。
再現率: 60.9% 実際の不正取引23件のうち、 - 14件を検出できた(60.9%) - 9件は見逃した(39.1%)
再現率が高いほど、「不正を見逃さない」ことを意味します。
適合率と再現率のトレードオフ
ここで非常に重要な概念を理解しましょう。
適合率と再現率は、多くの場合トレードオフの関係にあります。
つまり、適合率を上げようとすると再現率が下がり、再現率を上げようとすると適合率が下がる傾向があります。
なぜでしょうか?
不正取引検出を例に考えます。
「少しでも怪しい取引はすべて不正と判定する」という厳しい基準を設けると、不正を見逃すことは減ります(再現率が上がる)。
しかし、正常な取引まで不正と判定してしまう可能性が高まります(適合率が下がる)。
逆に、「明らかに不正とわかるものだけを不正と判定する」という緩い基準にすると、誤検知は減ります(適合率が上がる)。
しかし、巧妙な不正を見逃してしまう可能性が高まります(再現率が下がる)。
実際に確認してみましょう。
以下、コードです。
# 予測確率を取得
y_prob = model.predict_proba(X_test)[:, 1]
# 閾値を変えて適合率・再現率を計算
print("【閾値を変えた場合の適合率・再現率】")
print("-" * 50)
print(f"{'閾値':>7} {'適合率':>7} {'再現率':>7}")
print("-" * 50)
for threshold in [0.1, 0.3, 0.5, 0.7, 0.9]:
y_pred_th = (y_prob >= threshold).astype(int)
if y_pred_th.sum() > 0:
# 適合率を計算
prec = precision_score(
y_test, y_pred_th, zero_division=0
)
# 再現率を計算
rec = recall_score(
y_test, y_pred_th
)
# 表示
print(
f"{threshold:>8.1f} "
f"{prec:>10.1%} "
f"{rec:>10.1%}"
)
以下、実行結果です。
【閾値を変えた場合の適合率・再現率】
--------------------------------------------------
閾値 適合率 再現率
--------------------------------------------------
0.1 78.6% 95.7%
0.3 90.0% 78.3%
0.5 100.0% 60.9%
0.7 100.0% 39.1%
0.9 100.0% 30.4%
閾値を下げると再現率が上がり(より多くを「不正」と判定)、閾値を上げると適合率が上がる(確信度の高いものだけを「不正」と判定)傾向が見えます。
評価指標その3:F1スコア
適合率と再現率のバランスを取った指標がF1スコアです。F1スコアは適合率と再現率の調和平均です。
$$
\text{F1} = 2 \times \frac{\text{適合率} \times \text{再現率}}{\text{適合率} + \text{再現率}} = \frac{2 \cdot TP}{2 \cdot TP + FP + FN}
$$
なぜ単純な平均ではなく調和平均を使うのでしょうか?
調和平均は、どちらか一方だけが高くても値が大きくなりません。両方がバランスよく高い場合にのみ、F1スコアも高くなります。
以下、コードです。
# F1スコアを計算
f1 = f1_score(y_test, y_pred)
print(f"適合率: {precision*100:.1f}%")
print(f"再現率: {recall*100:.1f}%")
print(f"F1スコア: {f1:.3f}")
以下、実行結果です。
適合率: 100.0% 再現率: 60.9% F1スコア: 0.757
F1スコアは0から1の値を取り、1に近いほど良いモデルです。
適合率と再現率のどちらも一定レベル以上を保ちたい場合に有用な指標です。
評価指標その4:特異度(Specificity)
特異度(Specificity)は、「実際に陰性のもののうち、正しく陰性と予測できた割合」です。再現率の「陰性版」と言えます。
$$
\text{特異度} = \frac{TN}{TN + FP}
$$
以下、コードです。
# 特異度を計算
specificity = TN / (TN + FP)
print(f"特異度: {specificity*100:.1f}%")
print(
f"正常取引{TN + FP}件のうち、"
f"{TN}件を正しく「正常」と判定"
)
以下、実行結果です。
特異度: 100.0% 正常取引1477件のうち、1477件を正しく「正常」と判定
この例の特異度は、「正常なものを正常と判定する能力」を示します。
医療診断では、健康な人を誤って病気と診断しないことも重要なので、特異度も重視されます。
分類レポートでまとめて確認しよう
scikit-learnのclassification_report関数を使うと、これらの指標を一度にまとめて表示できます。
以下、コードです。
print("【分類レポート】")
print(
classification_report(
y_test, # 実測
y_pred, # 予測
target_names=['Normal', 'Fraud'] # クラス名を指定
)
)
以下、実行結果です。
【分類レポート】
precision recall f1-score support
Normal 0.99 1.00 1.00 1477
Fraud 1.00 0.61 0.76 23
accuracy 0.99 1500
macro avg 1.00 0.80 0.88 1500
weighted avg 0.99 0.99 0.99 1500
分類レポートには、各クラスごとの適合率(precision)、再現率(recall)、F1スコア(f1-score)、サンプル数(support)が表示されます。
macro avgは各クラスの単純平均、weighted avgはサンプル数で重み付けした平均です。不均衡データでは、weighted avgの方が全体像を表していることが多いです。
ROC曲線とAUC
閾値を変えると何が変わるか
ロジスティック回帰などのモデルは、まず「確率」を予測し、その確率が閾値(通常は0.5)を超えたら陽性と判定します。
この閾値を変えることで、適合率と再現率のバランスを調整できます。
ROC曲線(Receiver Operating Characteristic curve)は、閾値を0から1まで変化させたときの真陽性率(再現率)と偽陽性率(1-特異度)の関係を描いたグラフです。
以下、コードです。
plt.figure(figsize=(8, 6))
# ROC曲線を計算
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
# AUCを計算
roc_auc = auc(fpr, tpr)
# ROC曲線を描画
plt.plot(
fpr, # 偽陽性率(1-特異度)
tpr, # 真陽性率(再現率)
'b-',
label=f'ROC Curve (AUC = {roc_auc:.3f})'
)
# 対角線を描画
plt.plot(
[0, 1], # x軸の範囲
[0, 1], # y軸の範囲
'r--',
label='Random Classifier'
)
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Recall)')
plt.title('ROC Curve')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
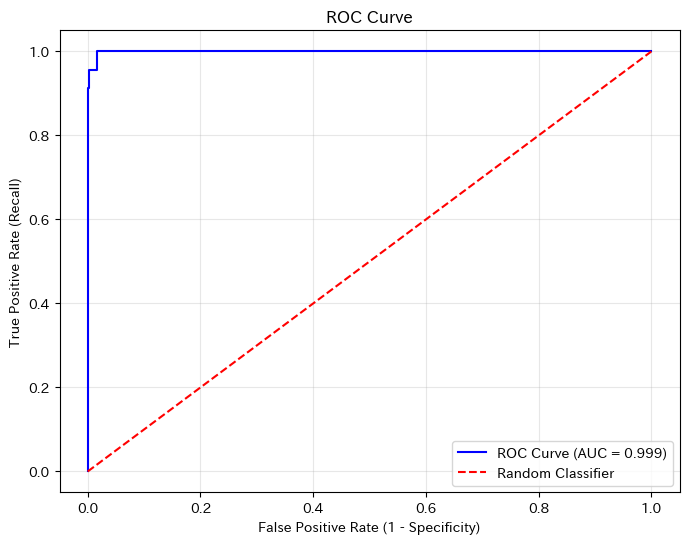
青い曲線がROC曲線です。曲線が左上に近いほど良いモデルです。
赤い対角線はランダムに予測した場合の性能を表し、これより上にあれば「当てずっぽうよりまし」なモデルと言えます。
AUCは、ROC曲線の下の面積です。0から1の値を取り、以下のように解釈できます。
- AUC = 0.5:ランダム分類器と同程度(コインを投げるのと同じ)
- AUC = 0.7〜0.8:まずまずの性能
- AUC = 0.8〜0.9:良い性能
- AUC = 0.9以上:非常に良い性能
- AUC = 1.0:完璧な分類(理論上の最高値)
適合率-再現率曲線(PR曲線)
ROC曲線は広く使われていますが、クラスが非常に不均衡な場合(陽性が1%以下など)、ROC曲線は過度に楽観的な評価を与えることがあります。
このような場合には、適合率-再現率曲線(PR曲線)がより適切です。
以下、コードです。
# PR曲線を計算
precision_curve, recall_curve, _ = precision_recall_curve(
y_test, # 実測値
y_prob # 予測確率
)
# PR曲線を描画
plt.figure(figsize=(8, 6))
plt.plot(
recall_curve, # 再現率
precision_curve, # 適合率
'g-'
)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
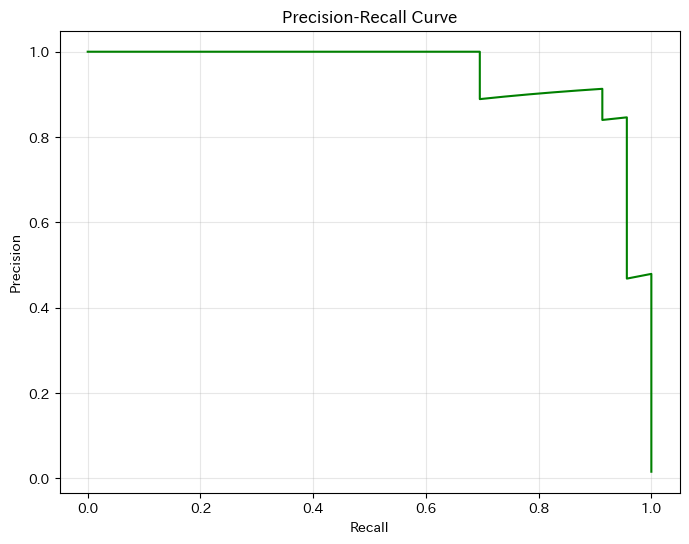
PR曲線では、右上(再現率も適合率も高い)に近いほど良いモデルです。
曲線が右下に急降下するモデルは、再現率(Recall)を上げようとすると適合率(Precision)が大きく犠牲になることを示しています。
問題に応じた指標の選び方
どの指標を重視すべきかは、問題の性質によって大きく異なります。これが、分類モデルを評価するうえで 最も重要なポイント です。
偽陽性(誤検知)のコストが高い場合 → 適合率を重視
「本当は問題ないもの」を誤って問題ありと判定すると、 業務や顧客に大きな悪影響が出るケースです。
例①:スパムフィルター
重要なメールを誤ってスパムと判定すると、 商談や契約に関わる連絡を見逃してしまう可能性があります。
「疑わしいものはすべてスパムにする」という方針では、重要なメールまでブロックされてしまいます。
この場合は、適合率を重視し、 「確実にスパムと判断できるものだけをブロックする」という設計の方が安全です。
例②:クレジットカードの利用停止判定
不正利用を疑ってカードを停止すると、正規ユーザーが決済できなくなり、大きな不満につながります。
多少の不正を見逃すリスクがあっても、 誤って正規利用を止めないことが重視される場面では、適合率の高いモデルが求められます。
例③:人事の不正・懲戒対象の検知
誤って無実の社員を不正と判定すると、信頼関係や組織文化に深刻なダメージを与えます。
このようなケースでは、「本当に問題があると確信できるケースだけを拾う」ために、適合率を重視する判断が合理的です。
偽陰性(見逃し)のコストが高い場合 → 再現率を重視
「本当は問題があるもの」を見逃すと、 重大な損失やリスクにつながるケースです。
例①:がん検診
がんを見逃すと、命に関わります。
多少の誤検知によって精密検査が増えたとしても、「がんを見逃さないこと」が最優先です。
この場合は、再現率を重視し、「少しでも疑わしければ陽性とする」判断が適切になります。
例②:不正取引検出
不正を見逃すと、直接的な金銭的損失が発生します。
誤検知による調査コストはかかりますが、不正を放置するよりは許容されることが多いです。
そのため、多くの不正検知システムでは再現率を重視した設計が採られます。
例③:製造業の不良品検出
不良品を見逃して市場に流出すると、リコールやブランド毀損につながります。
多少の良品を不良品として弾いてしまっても、「不良品を確実に除去する」ことが優先されるため、
再現率が重視されます。
例④:セキュリティ侵入検知
サイバー攻撃を見逃すと、情報漏洩やサービス停止といった深刻な被害が発生します。
アラートが多少多くなっても、攻撃を見逃さないことが重要なため、再現率を高く設定することが一般的です。
両方のバランスが重要な場合 → F1スコアを重視
適合率と再現率のどちらも一定レベル以上を保ちたい場合には、F1スコアを評価指標として重視します。
F1スコアは、適合率と再現率の調和平均であり、どちらか一方だけが高いモデルを評価しすぎない、という特徴があります。
例①:顧客離反(チャーン)予測
離反しそうな顧客を見逃すと、売上機会を失います。
一方で、離反しない顧客に過剰な引き止め施策を行うと、コストや顧客体験の悪化につながります。
このように……
- 見逃しも困る
- 誤検知も多すぎては困る
……というケースでは、適合率と再現率のバランスを反映するF1スコアが有効です。
例②:採用書類の一次スクリーニング
有望な応募者を誤って落とすのは避けたい一方、明らかに要件を満たさない応募者ばかりを通してしまうと、面接担当者の負担が増えてしまいます。
一次選考では……
- 有望な人材をできるだけ拾う
- ノイズとなる応募を過剰に増やさない
……という両立が求められるため、F1スコアを重視したモデル評価が適しています。
例③:商品レビューのネガティブ判定
クレームや重大な不満を見逃すと、ブランド毀損や炎上につながる可能性があります。
一方で、軽微な不満まで大量に検知してしまうと、対応工数が膨れ上がってしまいます。
このように、「重要なものは拾いたいが、過剰反応も避けたい」という状況では、F1スコアが適した指標になります。
いい流れです。その締めとして自然につながり、「評価指標は固定ではなく、設計対象である」ことが伝わる節を用意します。
複数モデルを比較しよう
最後に、複数のモデルを様々な指標で比較する実践をしてみましょう。
以下、コードです。
# 複数のモデルを訓練
models = {
'Logistic Regression': LogisticRegression(
random_state=42
),
'Decision Tree': tree.DecisionTreeClassifier(
random_state=42
),
'Random Forest': RandomForestClassifier(
n_estimators=100,
random_state=42
),
}
# 各モデルの評価指標を計算
results = []
for name, model in models.items():
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
y_prob = model.predict_proba(X_test)[:, 1]
# ROC-AUCを計算
fpr, tpr, _ = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr)
results.append({
'Model': name,
'Accuracy': accuracy_score(y_test, y_pred),
'Precision': precision_score(y_test, y_pred, zero_division=0),
'Recall': recall_score(y_test, y_pred),
'F1': f1_score(y_test, y_pred),
'AUC': roc_auc
})
# 結果を表示
results_df = pd.DataFrame(results)
print("【モデル比較】")
print(results_df.to_string(index=False))
以下、実行結果です。
【モデル比較】
Model Accuracy Precision Recall F1 AUC
Logistic Regression 0.994 1.0 0.608696 0.756757 0.998852
Decision Tree 1.000 1.0 1.000000 1.000000 1.000000
Random Forest 1.000 1.0 1.000000 1.000000 1.000000
正解率だけでなく、複数の指標を比較することで、各モデルの特性がより明確になります。
ROC曲線を並べて比較しよう
複数モデルのROC曲線を同じグラフに描いて比較してみましょう。
以下、コードです。
plt.figure(figsize=(8, 6))
for name, model in models.items():
y_prob = model.predict_proba(X_test)[:, 1]
fpr, tpr, _ = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr)
plt.plot(
fpr,
tpr,
'--',
label=f'{name} (AUC={roc_auc:.3f})'
)
plt.plot(
[0, 1],
[0, 1],
'k:',
label='Random'
)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve Comparison')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
以下、実行結果です。
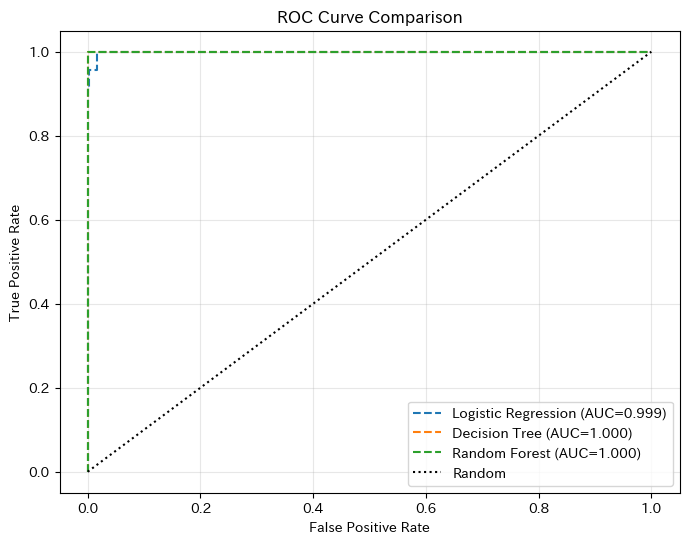
ROC曲線がより左上に位置するモデルが、より良い識別能力を持っています。AUCの値と合わせて、どのモデルが優れているかを判断できます。
実務での評価指標活用
実務で分類モデルを評価する際のポイントをまとめます。
ステップ1:問題の性質を理解する
まず「偽陽性と偽陰性のどちらのコストが高いか」を考えます。これがわからないと、適切な指標を選べません。
ステップ2:適切な指標を選ぶ
FPのコストが高い場合は適合率、FNのコストが高い場合は再現率、バランスが重要な場合はF1スコア、モデル比較にはAUCを使います。
ステップ3:混同行列で詳細を確認する
数値だけでなく、混同行列を見て「どんな誤りをしているか」を把握します。
ステップ4:閾値を調整する
必要に応じて、予測の閾値を調整して適合率と再現率のバランスを取ります。
ステップ5:ビジネス指標と結びつける
最終的には、「このモデルでいくらのコスト削減/売上増加が見込めるか」というビジネス指標と結びつけて評価します。
まとめ
今回学んだことを振り返りましょう。
正解率の落とし穴として、不均衡データでは正解率だけでは不十分です。「すべてを多数派クラスと予測」しても高い正解率が出てしまうため、混同行列で詳細を確認する必要があります。
混同行列は、予測結果をTP、TN、FP、FNの4つに分類した表です。ここから様々な評価指標を計算できます。
主要な評価指標として、適合率は「陽性と予測したもののうち、本当に陽性だった割合」(予測の信頼性)、再現率は「実際の陽性のうち、正しく陽性と予測できた割合」(検出能力)、F1スコアは適合率と再現率の調和平均(バランス指標)、AUCは閾値に依存しない総合的な指標(モデル比較向き)です。
指標の選び方は、問題の性質によって決まります。FPのコストが高ければ適合率、FNのコストが高ければ再現率を重視します。モデルを作る前に「何を最も避けたいか」を明確にすることが重要です。
全5回を通じて、分類モデルの基礎から評価方法まで学んできました。最後に、シリーズ全体を振り返ります。
第1回:ロジスティック回帰では、シグモイド関数で確率を予測し、オッズ比で係数を解釈する方法を学びました。
第2回:線形判別分析(LDA)では、データの分布を推定して分類する「生成的アプローチ」を学び、ロジスティック回帰との使い分けを理解しました。
第3回:決定木では、人間の意思決定に近い「条件分岐」によるモデルと、過学習の問題・対策を学びました。
第4回:ランダムフォレストでは、複数の決定木を組み合わせるアンサンブル学習で、精度と安定性を向上させる方法を学びました。
第5回:評価指標では、正解率だけでなく、問題に応じた適切な指標を選ぶ重要性を学びました。
これらの知識を組み合わせることで、実務で本当に役立つ分類モデルを構築できるようになります。
全5回、お付き合いいただきありがとうございました!このシリーズが、皆さんの機械学習の学習の第一歩になれば幸いです。

