前回、データを一つの数字で代表させる「代表値」を学びました。
https://www.salesanalytics.co.jp/datascience/datascience308/
しかし、平均だけを見ていると、大事なことを見落としてしまいます。
たとえば、2つのクラスのテスト結果を考えてみましょう。
- クラスA:78点、80点、79点、81点、77点(平均79点)
- クラスB:60点、95点、70点、100点、70点(平均79点)
どちらも平均は同じ79点です。
しかし、クラスAは全員が平均付近に集まっているのに対し、クラスBは60点から100点まで大きくバラついています。
もしあなたが先生なら、この2つのクラスには全く異なる指導が必要だと感じるでしょう。
この「ばらつきの大きさ」を数値化したものが、今回学ぶ分散と標準偏差です。
Contents
まずは「ばらつき」を目で確認する
2つのクラスのデータを作成し、平均が同じでも分布が異なることを確認します。
以下、コードです。
import numpy as np
import matplotlib.pyplot as plt
# クラスA:みんな平均付近
class_A = np.array([78, 80, 79, 81, 77])
# クラスB:ばらつきが大きい
class_B = np.array([60, 95, 70, 100, 70])
print("【クラスA】")
print(f" データ: {class_A}")
print(f" 平均: {np.mean(class_A)}点")
print("\n【クラスB】")
print(f" データ: {class_B}")
print(f" 平均: {np.mean(class_B)}点")
以下、実行結果です。
【クラスA】 データ: [78 80 79 81 77] 平均: 79.0点 【クラスB】 データ: [ 60 95 70 100 70] 平均: 79.0点
どちらも平均は79点ですが、データを見比べると明らかに性質が違います。
クラスAは77〜81点の狭い範囲に収まっていますが、クラスBは60〜100点と40点もの幅があります。
この違いをグラフで視覚的に確認します。各生徒の点数を点でプロットし、平均からの距離を可視化します。
以下、コードです。
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
for ax, data, name in zip(
axes,
[class_A, class_B],
['クラスA', 'クラスB']
):
ax.scatter(
range(len(data)),
data, s=100
)
ax.axhline(
np.mean(data),
color='red', linestyle='--',
label=f'平均: {np.mean(data)}点'
)
ax.set_ylim(50, 110)
ax.set_xlabel('生徒')
ax.set_ylabel('点数')
ax.set_title(name)
ax.legend()
plt.tight_layout()
plt.show()
以下、実行結果です。
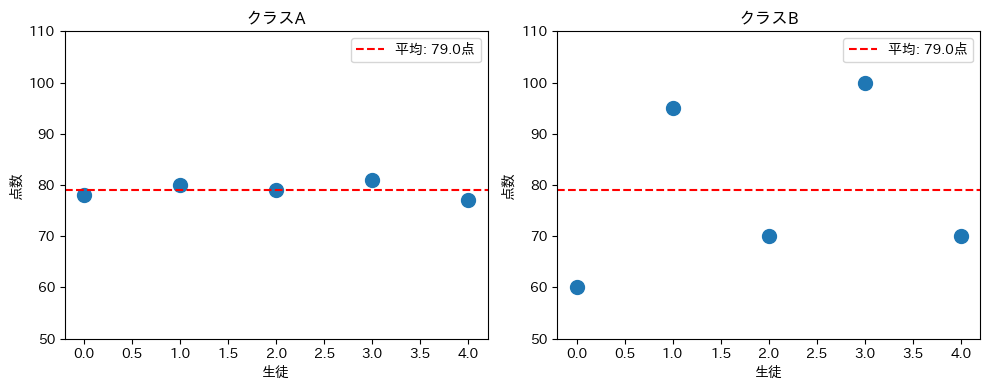
赤い破線が平均(79点)を示しています。
クラスAでは各点が破線の近くに集まっていますが、クラスBでは破線から大きく離れた点がいくつもあります。
この「平均からの距離」がばらつきの正体です。
偏差:平均からどれだけ離れているか
偏差とは?
偏差とは、各データが平均からどれだけ離れているかを表す値です。計算は単純で、「各データ − 平均」で求められます。
$$
\text{偏差} = x_i – \bar{x}
$$
クラスAとクラスBの偏差をそれぞれ計算します。
まず、クラスAです。
以下、コードです。
# クラスAの偏差
mean_A = np.mean(class_A)
deviation_A = class_A - mean_A
print("【クラスA】")
print(f" 平均: {mean_A}点")
print(f" 各データ: {class_A}")
print(f" 偏差: {deviation_A}")
以下、実行結果です。
【クラスA】 平均: 79.0点 各データ: [78 80 79 81 77] 偏差: [-1. 1. 0. 2. -2.]
偏差は「平均より何点高いか(低いか)」を表します。
78点の生徒は平均79点より1点低いので偏差は-1、81点の生徒は平均より2点高いので偏差は+2となります。
次に、クラスBの偏差も計算して比較します。
以下、コードです。
# クラスBの偏差
mean_B = np.mean(class_B)
deviation_B = class_B - mean_B
print("【クラスB】")
print(f" 平均: {mean_B}点")
print(f" 各データ: {class_B}")
print(f" 偏差: {deviation_B}")
以下、実行結果です。
【クラスB】 平均: 79.0点 各データ: [ 60 95 70 100 70] 偏差: [-19. 16. -9. 21. -9.]
クラスBでは偏差が-19や+21といった大きな値になっています。
これはクラスAの偏差(-2〜+2程度)と比べてはるかに大きく、ばらつきが大きいことを数値で確認できます。
偏差の合計は必ずゼロになる
ここで一つ重要な性質があります。偏差をすべて足し合わせると、必ずゼロになります。
偏差の合計を計算して、この性質を確認します。
以下、コードです。
print(f"クラスAの偏差の合計: {np.sum(deviation_A)}")
print(f"クラスBの偏差の合計: {np.sum(deviation_B)}")
以下、実行結果です。
クラスAの偏差の合計: 0.0 クラスBの偏差の合計: 0.0
どちらも合計はゼロ(または浮動小数点の誤差でほぼゼロ)になります。
これは平均の定義から必然的に導かれる性質です。
プラスの偏差とマイナスの偏差が打ち消し合うため、偏差の合計でばらつきを測ることはできません。
なぜ「二乗」するのか?
打ち消し合いを防ぐ工夫
偏差の合計がゼロになってしまう問題を解決するため、統計学では偏差を二乗します。
二乗すればマイナスの値もプラスになるため、打ち消し合いが起きません。
偏差を二乗した値を計算します。
以下、コードです。
# 偏差の二乗
squared_dev_A = deviation_A ** 2
squared_dev_B = deviation_B ** 2
print("【クラスA】")
print(f" 偏差: {deviation_A}")
print(f" 偏差の二乗: {squared_dev_A}")
print(f" 二乗の合計: {np.sum(squared_dev_A)}")
print("\n【クラスB】")
print(f" 偏差: {deviation_B}")
print(f" 偏差の二乗: {squared_dev_B}")
print(f" 二乗の合計: {np.sum(squared_dev_B)}")
以下、実行結果です。
【クラスA】 偏差: [-1. 1. 0. 2. -2.] 偏差の二乗: [1. 1. 0. 4. 4.] 二乗の合計: 10.0 【クラスB】 偏差: [-19. 16. -9. 21. -9.] 偏差の二乗: [361. 256. 81. 441. 81.] 二乗の合計: 1220.0
二乗することで、すべての値がプラスになりました。
クラスAの二乗の合計は10、クラスBは1070と、大きな差が出ています。
これでばらつきの違いを数値として捉えられるようになりました。
絶対値ではダメなのか?
「マイナスをなくすなら絶対値でもいいのでは?」と思うかもしれません。
実際、絶対値を使った「平均絶対偏差」という指標も存在します。
しかし、二乗には数学的に扱いやすいという大きなメリットがあります。
微分可能であること、後に学ぶ正規分布や最小二乗法と相性が良いことなど、統計学の理論体系の中で二乗は特別な役割を果たしています。
分散(Variance):ばらつきの指標
分散の定義
分散は、偏差の二乗の平均です。これにより、データの個数に依存しない「ばらつきの大きさ」を表せます。
n 個のデータ x_1, x_2, \ldots, x_n の分散 \sigma^2(シグマの二乗)は次の式で計算されます。$$
\sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2
$$
分散を手計算の手順で求めます。
以下、コードです。
# クラスAの分散(手計算)
n_A = len(class_A)
var_A_manual = np.sum(squared_dev_A) / n_A
print("【クラスAの分散を手計算】")
print(
f" 偏差の二乗の合計: {np.sum(squared_dev_A)}"
)
print(
f" データ数: {n_A}"
)
print(
f" 分散 = {np.sum(squared_dev_A)} / {n_A}"
f" = {var_A_manual}"
)
以下、実行結果です。
【クラスAの分散を手計算】 偏差の二乗の合計: 10.0 データ数: 5 分散 = 10.0 / 5 = 2.0
クラスAの分散は2.0と計算されました。偏差の二乗の合計(10)をデータ数(5)で割っています。
クラスBの分散も計算し、比較します。
以下、コードです。
# クラスBの分散(手計算)
n_B = len(class_B)
var_B_manual = np.sum(squared_dev_B) / n_B
print("【2つのクラスの分散を比較】")
print(f" クラスAの分散: {var_A_manual}")
print(f" クラスBの分散: {var_B_manual}")
以下、実行結果です。
【2つのクラスの分散を比較】 クラスAの分散: 2.0 クラスBの分散: 244.0
クラスAの分散は2.0、クラスBの分散は244.0です。
クラスBはクラスAの122倍もばらついていることがわかります。
平均だけでは見えなかった違いが、分散によって明確に数値化されました。
NumPyで分散を計算する
実務では np.var() 関数を使って一行で分散を計算します。
以下、コードです。
# NumPyで分散を計算
print(f"クラスAの分散(NumPy): {np.var(class_A)}")
print(f"クラスBの分散(NumPy): {np.var(class_B)}")
以下、実行結果です。
クラスAの分散(NumPy): 2.0 クラスBの分散(NumPy): 244.0
手計算と同じ結果が得られます。
標準偏差(Standard Deviation):解釈しやすい指標
分散の問題点
分散には一つ困った点があります。単位が「元のデータの二乗」になってしまうことです。
テストの点数なら、分散の単位は「点²(点の二乗)」です。
「このクラスの分散は214点²です」と言われても、直感的にわかりにくいですよね。
標準偏差の定義
この問題を解決するため、分散の平方根をとったものが標準偏差です。
標準偏差の単位は元のデータと同じになるため、解釈が容易になります。
$$
\sigma = \sqrt{\sigma^2} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2}
$$
標準偏差を計算し、元のデータと比較しやすい形にします。
以下、コードです。
# 標準偏差 = 分散の平方根
std_A = np.sqrt(var_A_manual)
std_B = np.sqrt(var_B_manual)
print("【標準偏差】")
print(f" クラスA: {std_A:.2f}点")
print(f" クラスB: {std_B:.2f}点")
以下、実行結果です。
【標準偏差】 クラスA: 1.41点 クラスB: 15.62点
クラスAの標準偏差は約1.41点、クラスBは約15.62点です。
これは「データが平均からだいたいどのくらい離れているか」を表しています。
クラスAでは平均±1〜2点程度、クラスBでは平均±16点程度のばらつきがあると解釈できます。
NumPyの std() 関数を使って標準偏差を計算します。
以下、コードです。
# NumPyで標準偏差を計算
print(f"クラスAの標準偏差(NumPy): {np.std(class_A):.2f}点")
print(f"クラスBの標準偏差(NumPy): {np.std(class_B):.2f}点")
以下、実行結果です。
クラスAの標準偏差(NumPy): 1.41点 クラスBの標準偏差(NumPy): 15.62点
np.std() を使えば一行で標準偏差を求められます。実務ではこちらを使いましょう。
母分散と標本分散:n で割るか、n-1 で割るか
2種類の分散
ここまで「データ数 n で割る」分散を計算してきましたが、実はもう一つの計算方法があります。
n-1 で割る方法です。
- 母分散:n で割る(全データがわかっている場合)
- 標本分散(不偏分散):n-1 で割る(一部のデータから全体を推測する場合)
同じデータに対して、n で割る場合と n-1 で割る場合を比較します。
以下、コードです。
data = np.array([72, 85, 68, 90, 75])
n = len(data)
# 母分散(n で割る)
var_population = np.var(data)
# 標本分散(n-1 で割る)
var_sample = np.var(data, ddof=1)
print(f"データ: {data}")
print(f"データ数 n = {n}")
print(f"\n母分散(n で割る): {var_population:.2f}")
print(f"標本分散(n-1 で割る): {var_sample:.2f}")
以下、実行結果です。
データ: [72 85 68 90 75] データ数 n = 5 母分散(n で割る): 67.60 標本分散(n-1 で割る): 84.50
同じデータでも、割る数が違うと分散の値が変わります。
標本分散のほうが少し大きくなります。
なぜ n-1 で割るのか?
標本(一部のデータ)から母集団(全体)の分散を推測するとき、n で割ると過小評価してしまうことが知られています。
n-1 で割ることで、この偏りを補正し、より正確な推定ができます。
この「n-1」は自由度と呼ばれます。
詳しい数学的証明は省きますが、直感的には「平均を計算するときに1つの情報を使ってしまったので、自由に動ける情報が1つ減る」と理解できます。
シミュレーションで、n-1 で割るほうが正確であることを確認します。
以下、コードです。
np.random.seed(42)
# 母集団(真の分散がわかっている)
population = np.random.normal(
loc=70, # 平均
scale=10, # 標準偏差
size=1000000 # データ数
)
# 母集団の真の分散
true_variance = np.var(population)
# 母集団から標本を繰り返し抽出し分散を計算
n_samples = 1000 # 標本を抽出する回数
sample_size = 10 # 標本のサイズ
var_n_list = [] # n で割った分散
var_n1_list = [] # n-1 で割った分散
for _ in range(n_samples):
# 母集団からサンプリング
sample = np.random.choice(
population, # 母集団
size=sample_size, # サンプルサイズ
replace=False # 重複なし
)
# n で割った分散を計算しリストに追加
var_n_list.append(np.var(sample, ddof=0)) # n で割る
# n-1 で割った分散を計算しリストに追加
var_n1_list.append(np.var(sample, ddof=1)) # n-1 で割る
print(f"母集団の真の分散: {true_variance:.2f}")
print(f"n で割った分散の平均: {np.mean(var_n_list):.2f}")
print(f"n-1 で割った分散の平均: {np.mean(var_n1_list):.2f}")
以下、実行結果です。
母集団の真の分散: 100.04 n で割った分散の平均: 89.98 n-1 で割った分散の平均: 99.98
n で割った分散は真の分散より小さめに、n-1 で割った分散は真の分散に近い値になります。
標本から母集団を推測する場合は、n-1 で割る標本分散(不偏分散)を使うのが適切です。
実務での使い分け
| 状況 | 使う分散 | NumPyでの指定 |
|---|---|---|
| 手元のデータそのもの(データのすべて)を記述したい | 母分散(n で割る) | np.var(data) または ddof=0 |
| 標本から母集団を推測したい | 標本分散(n-1 で割る) |
多くの統計ソフトや論文では、デフォルトで n-1 を使います。
NumPyはデフォルトで n を使うので、推測統計の文脈では ddof=1 を明示的に指定する習慣をつけましょう。
標準偏差の実践的な解釈
平均 ± 標準偏差でデータの範囲をつかむ
標準偏差は「データが平均からどのくらい散らばっているか」を表します。
正規分布に従うデータの場合、以下のような目安があります。
- 平均 ± 1標準偏差の範囲に約68%のデータが入る
- 平均 ± 2標準偏差の範囲に約95%のデータが入る
- 平均 ± 3標準偏差の範囲に約99.7%のデータが入る
正規分布に従うデータを生成し、この法則を確認します。
以下、コードです。
np.random.seed(42)
# 平均70、標準偏差10の正規分布からデータを生成
data = np.random.normal(loc=70, scale=10, size=1000)
mean = np.mean(data)
std = np.std(data, ddof=1)
# 各範囲に入るデータの割合を計算
within_1std = (
np.sum((data >= mean - std) & (data <= mean + std))
/ len(data) * 100
)
within_2std = (
np.sum((data >= mean - 2*std) & (data <= mean + 2*std))
/ len(data) * 100
)
within_3std = (
np.sum((data >= mean - 3*std) & (data <= mean + 3*std))
/ len(data) * 100
)
print(f"平均: {mean:.1f}, 標準偏差: {std:.1f}")
print(
f"\n平均 ± 1標準偏差({mean-std:.1f}〜{mean+std:.1f})に入る割合"
f": {within_1std:.1f}%"
)
print(
f"平均 ± 2標準偏差({mean-2*std:.1f}〜{mean+2*std:.1f})に入る割合"
f": {within_2std:.1f}%"
)
print(
f"平均 ± 3標準偏差({mean-3*std:.1f}〜{mean+3*std:.1f})に入る割合"
f": {within_3std:.1f}%"
)
以下、実行結果です。
平均: 70.2, 標準偏差: 9.8 平均 ± 1標準偏差(60.4〜80.0)に入る割合: 68.6% 平均 ± 2標準偏差(50.6〜89.8)に入る割合: 95.6% 平均 ± 3標準偏差(40.8〜99.6)に入る割合: 99.7%
約68%、95%、99.7%という理論値に近い結果が得られます。
この法則を使えば、「平均70点、標準偏差10点」と聞いただけで、「大体の人は60〜80点くらいで、50点以下や90点以上はかなり珍しい」と推測できます。
可視化でばらつきを直感的に理解する
ヒストグラムに平均と標準偏差の範囲を重ねて表示します。
以下、コードです。
plt.figure(figsize=(10, 5))
# ヒストグラム
plt.hist(data, bins=30, edgecolor='black', alpha=0.7, density=True)
# 平均
plt.axvline(
mean,
color='red', linestyle='-', linewidth=2,
label=f'平均: {mean:.1f}'
)
# ± 1標準偏差
plt.axvline(
mean - std,
color='orange', linestyle='--', linewidth=2,
label=f'±1σ: {mean-std:.1f}, {mean+std:.1f}'
)
plt.axvline(
mean + std,
color='orange', linestyle='--', linewidth=2
)
# ± 2標準偏差
plt.axvline(
mean - 2*std,
color='green', linestyle=':', linewidth=2,
label=f'±2σ: {mean-2*std:.1f}, {mean+2*std:.1f}'
)
plt.axvline(
mean + 2*std,
color='green', linestyle=':', linewidth=2
)
plt.xlabel('値')
plt.ylabel('密度')
plt.title('正規分布と標準偏差の関係')
plt.legend()
plt.show()
以下、実行結果です。
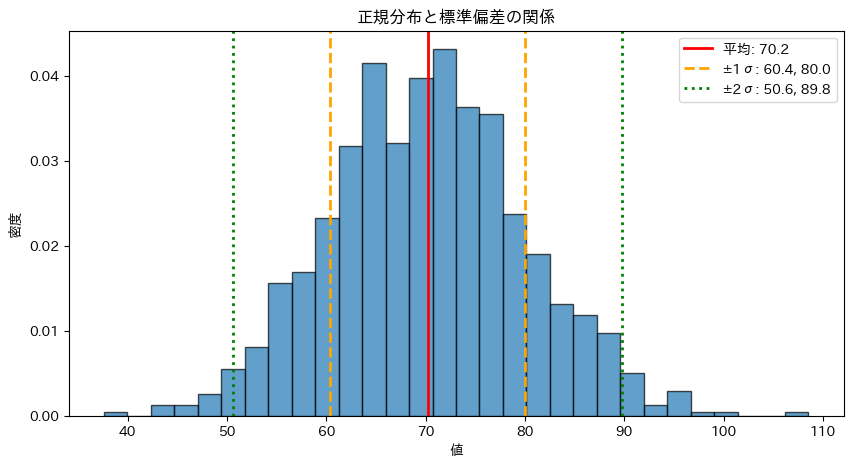
ヒストグラムの山の中心に赤い線(平均)があり、オレンジの線(±1σ)の間に大部分のデータが収まっています。
緑の線(±2σ)の外にあるデータはごくわずかです。
標準偏差がデータの「広がり」を数値化していることが視覚的に理解できます。
まとめ
今回は、データの「ばらつき」を数値化する方法として、分散と標準偏差を学びました。
平均だけではデータの性質を十分に表現できません。
平均が同じ79点でも、全員が78〜80点に集中しているクラスと、60〜100点までばらついているクラスでは、教育的な対応も分析結果の解釈も全く異なります。この違いを捉えるのが分散と標準偏差です。
分散は、各データが平均からどれだけ離れているか(偏差)を二乗し、その平均を取ったものです。偏差をそのまま合計するとプラスとマイナスが打ち消し合ってゼロになってしまうため、二乗することでこの問題を回避しています。
数式では \sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 と表され、Pythonでは np.var(data) で計算できます。
標準偏差は分散の平方根で、元のデータと同じ単位を持つため解釈が容易です。「平均±標準偏差」という形で、データのおおよその範囲を把握できます。
正規分布では、平均±1標準偏差に約68%、±2標準偏差に約95%のデータが収まるという目安があります。Pythonでは np.std(data) で計算できます。
また、標本から母集団を推測する場合は、n ではなく n-1 で割る標本分散(不偏分散)を使います。NumPyでは ddof=1 を指定することで標本分散を計算できます。

