第1〜3回で学んだコレスポンデンス分析(CA)は、「学部 × メニュー」のように2つのカテゴリ変数の関係を可視化する手法でした。
- 第1回 —クロス集計表の「その先」へ ― コレスポンデンス分析って何?
- 第2回 —期待と現実のズレを測る ― 独立性・期待度数・カイ二乗
- 第3回 —数学のキモをつかむ ― SVDで次元を圧縮する仕組み
しかし、実際のアンケート調査やマーケティングデータでは、分析したいカテゴリ変数が3つも4つもあるのが普通です。
たとえば、あるECサイトの顧客調査で次のような質問があったとしましょう。
- 性別:男性 / 女性
- 年代:20代 / 30代 / 40代 / 50代以上
- よく使うデバイス:スマートフォン / PC / タブレット
- 好きな商品カテゴリ:ファッション / 家電 / 食品 / 書籍
これら4つの変数の間にどんな関係があるのかを、一枚のマップにまとめて俯瞰できたら便利だと思いませんか?
「スマホで買い物する20代女性はファッションが好き」「PCを使う40代男性は家電に関心がある」といったパターンが、マップを一目見るだけでわかるようになります。
この問いに答えるのが、今回紹介する多重コレスポンデンス分析(MCA: Multiple Correspondence Analysis)です。
MCAは、CAを3つ以上のカテゴリ変数に拡張した手法です。
今回は、MCAに必要なインジケータ行列とBurt行列という2つの新しい道具を学び、顧客セグメンテーションの事例でその威力を体感します。
Contents
ライブラリのインポート
今回も prince ライブラリを使います。MCAの実行も prince がサポートしています。
以下、コードです。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import japanize_matplotlib import prince
ステップ1:アンケートデータを作る
まずは分析対象となるサンプルデータを用意しましょう。
架空のECサイト顧客300人に対するアンケートの回答データを生成します。
各行が1人の回答者、各列が1つの質問項目(カテゴリ変数)に対応しています。
以下、コードです。
n_respondents = 300 # 回答者数
# 回答データを生成(傾向を持たせたデータ)
np.random.seed(42)
gender = np.random.choice(
['男性', '女性'],
n_respondents, p=[0.45, 0.55]
)
age = np.random.choice(
['20代', '30代', '40代', '50代以上'],
n_respondents,
p=[0.30, 0.30, 0.25, 0.15]
)
device = np.random.choice(
['スマートフォン', 'PC', 'タブレット'],
n_respondents,
p=[0.50, 0.35, 0.15]
)
category = np.random.choice(
['ファッション', '家電', '食品', '書籍'],
n_respondents,
p=[0.30, 0.25, 0.25, 0.20]
)
survey = pd.DataFrame({
'性別': gender,
'年代': age,
'デバイス': device,
'好きなカテゴリ': category
})
print(f"回答者数: {len(survey)}人")
print(f"変数の数: {len(survey.columns)}個\n")
print("【先頭5件】")
print(survey.head())
以下、実行結果です。
回答者数: 300人 変数の数: 4個 【先頭5件】 性別 年代 デバイス 好きなカテゴリ 0 男性 20代 スマートフォン ファッション 1 女性 30代 スマートフォン ファッション 2 女性 30代 スマートフォン ファッション 3 女性 40代 スマートフォン 食品 4 男性 40代 スマートフォン 家電
各行が1人の回答者を表し、4つの列にそれぞれカテゴリ値(「男性」「20代」「スマートフォン」「ファッション」など)が入っています。
CAではクロス集計表(2変数の集計結果)が入力でしたが、MCAの入力はこのような個体レベルの生データです。
ここが大きな違いです。では、この生データをMCAが内部でどう処理しているのか、順を追って見ていきましょう。
ステップ2:インジケータ行列 ― ダミー変数化で「0と1の表」に変換する
なぜ変換が必要なのか
「男性」「20代」「スマートフォン」……といった文字データは、そのままでは数学的に扱えません。
足し算も掛け算もできないからです。
そこで、カテゴリの値を0と1の数値に変換します。
この操作をダミー変数化(one-hot encoding)と呼び、変換後の行列をインジケータ行列(indicator matrix)と呼びます。
インジケータ行列の定義
N 人の回答者と Q 個のカテゴリ変数があるとします。変数 q のカテゴリ数を J_q とすると、全カテゴリ数の合計は J = \sum_{q=1}^{Q} J_q です。
インジケータ行列 Z は N \times J の行列で、その (i, j) 要素は次のように定義されます。
$$
z_{ij} = \begin{cases} 1 & \text{(回答者 } i \text{ がカテゴリ } j \text{ に該当する場合)} \\ 0 & \text{(それ以外)} \end{cases}
$$
今回のデータでは N = 300(回答者数)、Q = 4(変数の数:性別・年代・デバイス・好きなカテゴリ)です。
カテゴリ数は性別が2、年代が4、デバイスが3、好きなカテゴリが4なので、合計 J = 2 + 4 + 3 + 4 = 13 列になります。
pandasの pd.get_dummies() を使えば、インジケータ行列を一行で作れます。
以下、コードです。
# インジケータ行列 Z を作成(ダミー変数化)
Z = pd.get_dummies(survey)
print(
"インジケータ行列の形状: "
f"{Z.shape}({Z.shape[0]}人 × "
f"{Z.shape[1]}カテゴリ)\n"
)
print("【先頭5行】")
print(Z.head())
以下、実行結果です。
インジケータ行列の形状: (300, 13)(300人 × 13カテゴリ) 【先頭5行】 性別_女性 性別_男性 年代_20代 年代_30代 年代_40代 年代_50代以上 デバイス_PC デバイス_スマートフォン \ 0 False True True False False False False True 1 True False False True False False False True 2 True False False True False False False True 3 True False False False True False False True 4 False True False False True False False True デバイス_タブレット 好きなカテゴリ_ファッション 好きなカテゴリ_家電 好きなカテゴリ_書籍 好きなカテゴリ_食品 0 False True False False False 1 False True False False False 2 False True False False False 3 False False False False True 4 False False True False False
インジケータ行列の重要な性質
インジケータ行列にはいくつか便利な性質があります。理解のために確認しておきましょう。
以下、コードです。
print("【インジケータ行列の性質】")
print(f"各行の合計(Trueの数):")
print(
f" 最小={Z.sum(axis=1).min()},"
f" 最大={Z.sum(axis=1).max()}"
)
print(f"\n各列の合計(各カテゴリの該当者数):")
print(Z.sum(axis=0))
以下、実行結果です。
【インジケータ行列の性質】 各行の合計(Trueの数): 最小=4, 最大=4 各列の合計(各カテゴリの該当者数): 性別_女性 164 性別_男性 136 年代_20代 86 年代_30代 86 年代_40代 74 年代_50代以上 54 デバイス_PC 100 デバイス_スマートフォン 161 デバイス_タブレット 39 好きなカテゴリ_ファッション 93 好きなカテゴリ_家電 57 好きなカテゴリ_書籍 70 好きなカテゴリ_食品 80 dtype: int64
各行の合計は必ず Q(変数の数)になります。これは各回答者が各変数について1つだけカテゴリを選んでいるためです。
各列の合計は、そのカテゴリに該当する回答者の人数を表します。
ステップ3:Burt行列 ― すべての変数ペアの関係を一覧にする
Burt行列の定義
インジケータ行列 Z の次に登場するのがBurt行列です。
Burt行列 B は、インジケータ行列の転置とインジケータ行列の積として定義されます。
$$
B = Z^T Z
$$
つまり Burt行列は、すべてのカテゴリペアの共起度数(同時に該当する人数)を一枚にまとめた表です。
以下、コードです。
# インジケータ行列 Z の要素を整数型に変換
Z = Z.astype(int)
# Burt行列 B = Z^T Z
B = Z.T @ Z
print(
"Burt行列の形状: "
f"{B.shape}"
f"({B.shape[0]}×{B.shape[1]})\n"
)
print("【Burt行列(一部を表示)】")
print(B.iloc[:6, :6])
以下、実行結果です。
Burt行列の形状: (13, 13)(13×13)
【Burt行列(一部を表示)】
性別_女性 性別_男性 年代_20代 年代_30代 年代_40代 年代_50代以上
性別_女性 164 0 49 47 42 26
性別_男性 0 136 37 39 32 28
年代_20代 49 37 86 0 0 0
年代_30代 47 39 0 86 0 0
年代_40代 42 32 0 0 74 0
年代_50代以上 26 28 0 0 0 54
Burt行列の構造を読み解く
Burt行列は、ブロック構造を持っています。ヒートマップで全体像を確認してみましょう。
以下、コードです。
plt.figure(figsize=(10, 8))
sns.heatmap(
B,
annot=True, fmt='d', cmap='YlOrRd',
linewidths=0.5, square=True
)
plt.title('Burt行列のヒートマップ')
plt.tight_layout()
plt.show()
以下、実行結果です。
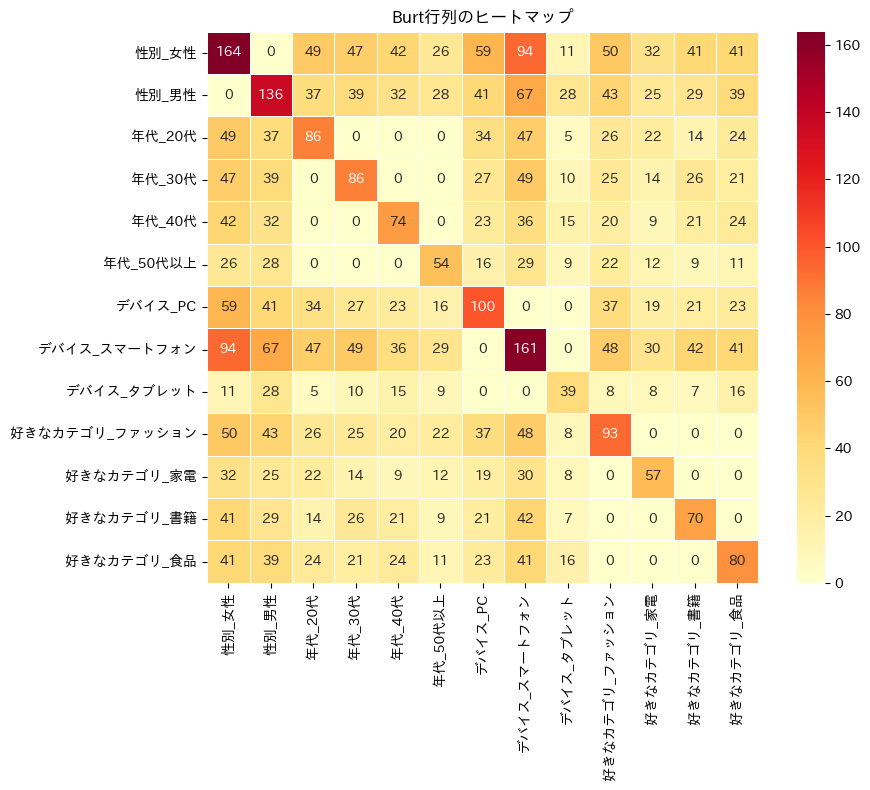
対角ブロック(左上から右下へ並ぶ正方形の領域)は、同じ変数内のカテゴリどうしの関係を表しています。
対角要素は各カテゴリの該当者数になり、非対角要素は0になります。なぜなら、1人の回答者が同じ変数で2つのカテゴリに該当することはないからです(たとえば「男性」かつ「女性」はあり得ない)。
非対角ブロックは、異なる変数間のカテゴリどうしの共起度数です。
たとえば「男性」行と「20代」列の値は「男性かつ20代の回答者数」を表しています。これはまさに、2変数のクロス集計表を切り出したものにほかなりません。
つまり Burt行列とは、すべての変数ペアについてのクロス集計表を一枚に貼り合わせた「超クロス集計表」なのです。
MCAは、このBurt行列(またはそれと等価な情報を持つインジケータ行列)に対して、CAと同様の次元削減を行います。
ステップ4:MCAを実行する
prince による実行
MCAの内部計算は、インジケータ行列 Z を対応行列に変換し、CAと同じくSVDで次元削減する操作です。
prince.MCA を使えば、元の個体×変数のDataFrameをそのまま渡すだけで実行できます。
以下、コードです。
# MCAを実行(2次元に圧縮)
mca = prince.MCA(
n_components=2,
random_state=42
)
mca = mca.fit(survey)
print("【MCA 寄与率】")
for i, pct in enumerate(mca.percentage_of_variance_):
print(
f" 第{i+1}次元: {pct:.2f}%"
)
print(
" 累積寄与率: "
f"{sum(mca.percentage_of_variance_[:2]):.2f}%"
)
以下、実行結果です。
【MCA 寄与率】 第1次元: 14.68% 第2次元: 13.39% 累積寄与率: 28.06%
MCAの寄与率に関する注意点
ここで一つ重要な注意があります。MCAの寄与率は、CAに比べてかなり低い値になることが多いです。
たとえばCAでは累積寄与率が80%を超えることも珍しくありませんが、MCAでは30〜40%程度にとどまることがあります。
これはMCAの欠陥ではなく、構造的な性質です。
インジケータ行列の「同じ変数内のカテゴリ間の関係」はすべて0(例:男性と女性の組み合わせは0)であり、ここに含まれる「自明なイナーシャ」が総イナーシャを膨らませてしまうためです。
このため、MCAの寄与率はCAほど直感的に解釈しにくく、低い値でもマップの構造が有用な場合があることを覚えておきましょう。
カテゴリの座標を確認する
MCAは各カテゴリに座標を割り当てます。ここがMCAの最大の魅力です。
4つの変数に属する全13カテゴリが、同じ2次元空間上に配置されます。
以下、コードです。
# カテゴリの座標を取得
col_coords = mca.column_coordinates(survey)
col_coords.columns = ['次元1', '次元2']
print("【カテゴリの座標】")
print(col_coords.round(4))
以下、実行結果です。
【カテゴリの座標】
次元1 次元2
性別__女性 -0.5128 -0.2666
性別__男性 0.6183 0.3215
年代__20代 -0.6192 0.5808
年代__30代 -0.1088 -0.6461
年代__40代 0.6487 -0.6287
年代__50代以上 0.2706 0.9655
デバイス__PC -0.4280 0.3394
デバイス__スマートフォン -0.2145 -0.2765
デバイス__タブレット 1.9832 0.2712
好きなカテゴリ__ファッション -0.3088 0.5019
好きなカテゴリ__家電 -0.3125 0.8124
好きなカテゴリ__書籍 -0.1180 -1.2112
好きなカテゴリ__食品 0.6849 -0.1025
13個のカテゴリそれぞれに(次元1, 次元2)の座標が割り当てられました。
この座標をプロットすれば、異なる変数に属するカテゴリ間の関係性が一目でわかるマップになります。
ステップ5:MCAマップを描く
いよいよMCAマップを描きましょう。
異なる変数のカテゴリを色分けすることで、「どの変数のどのカテゴリが、どの位置にあるか」が読み取りやすくなります。
以下、コードです。
fig, ax = plt.subplots(figsize=(10, 8))
# 変数ごとに色とマーカーを定義
colors = {
'性別': '#2E86AB',
'年代': '#E94F37',
'デバイス': '#44AF69',
'好きなカテゴリ': '#D6A100'
}
markers = {
'性別': 'o',
'年代': 's',
'デバイス': '^',
'好きなカテゴリ': 'D'
}
# 各カテゴリをプロット
for cat_name in col_coords.index:
# 右側の区切りで変数名とラベルに分割する
if '__' in cat_name:
base = cat_name.rsplit('__', 1)
var_name = base[0]
label_text = base[1]
else:
base = cat_name.rsplit('_', 1)
var_name = base[0]
label_text = base[1] if len(base) > 1 else cat_name
# 変数名に基づいて色とマーカーを取得
color = colors.get(var_name, 'gray')
marker = markers.get(var_name, 'o')
# 座標を取得
x, y = col_coords.loc[cat_name]
# color を使用し、facecolors 指定で確実に塗りつぶし色を反映
ax.scatter(
x, y,
s=200, color=color, marker=marker,
edgecolors='white', linewidths=2
)
ax.annotate(
label_text, (x, y),
fontsize=11, fontweight='bold',
xytext=(10, 10),
textcoords='offset points', color=color
)
# 原点の十字線
ax.axhline(
y=0, color='gray',
linestyle='--', linewidth=0.8
)
ax.axvline(
x=0, color='gray',
linestyle='--', linewidth=0.8
)
# 軸ラベルとタイトル
ax.set_xlabel(
'次元1(寄与率: '
f'{mca.percentage_of_variance_[0]:.2f}%)'
)
ax.set_ylabel(
'次元2(寄与率: '
f'{mca.percentage_of_variance_[1]:.2f}%)'
)
ax.set_title(
'MCAマップ:顧客アンケートの多変量カテゴリ関係'
)
# 凡例
from matplotlib.lines import Line2D
legend_elements = [
Line2D(
[0], [0],
marker=markers[v], color='w',
markerfacecolor=colors[v],
markeredgecolor='white',
markeredgewidth=2,
markersize=12,
label=v
)
for v in colors
]
ax.legend(handles=legend_elements, loc='best')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
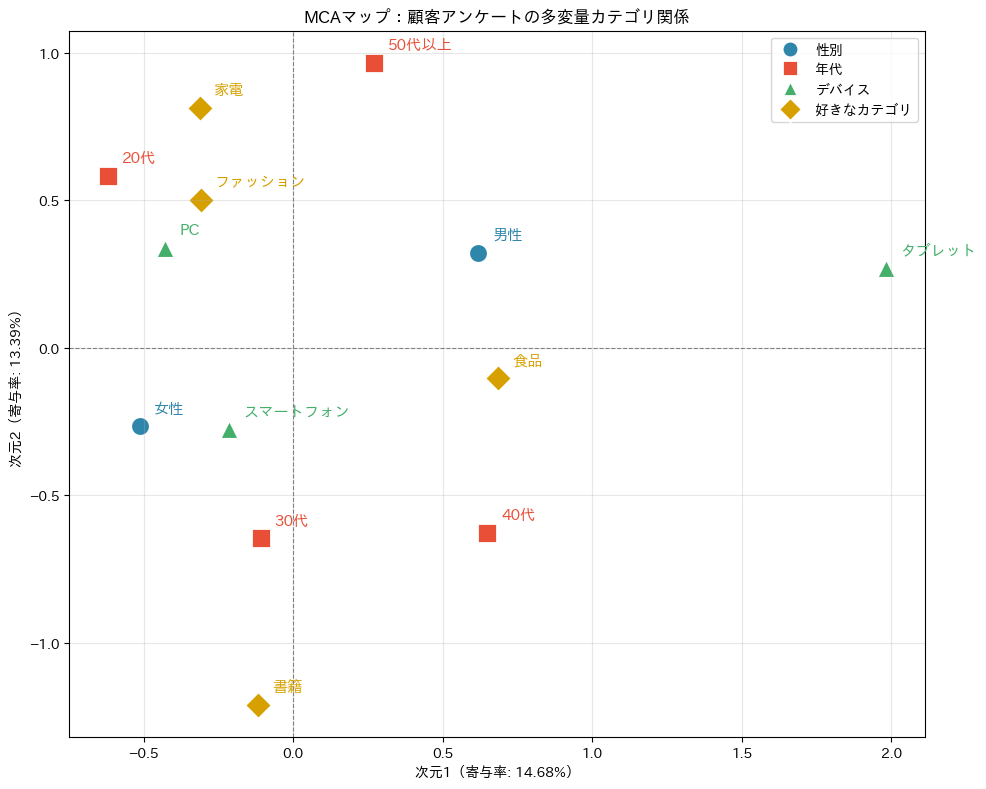
このマップの読み方は、基本的にはCAマップと同じです。
近くにあるカテゴリどうしは関連が強い(同じ人が選びやすい組み合わせ)、原点から遠いカテゴリほど個性的(特定のパターンと強く結びつく)、原点をはさんで反対側にあるカテゴリは対照的です。
MCAの最大のポイントは、異なる変数のカテゴリが同じ空間にあることです。
たとえば「20代」「スマートフォン」「ファッション」が近くに固まっていれば、「スマートフォンで買い物する20代はファッションに関心が高い」という顧客像が浮かび上がります。
ステップ6:個体(回答者)もマップに配置する
MCAのもう一つの強力な機能は、カテゴリだけでなく個体(回答者)も同じマップ上にプロットできることです。
これにより、回答者がどのカテゴリ群に近いかを視覚的に把握できます。
MCAにおける個体 i の座標は、その個体が該当するカテゴリの座標を平均したものとして計算されます。
個体 i の第 k 次元の座標 \psi_{ik} は、次の式で表されます。
$$
\psi_{ik} = \frac{1}{Q} \sum_{j \in C_i} \gamma_{jk}
$$
ここで Q はカテゴリ変数の数、C_i は個体 i が該当するカテゴリの集合、\gamma_{jk} は第3回で学んだカテゴリ j の第 k 次元の座標です。
つまり、4つの質問に対する回答のカテゴリ座標を単純に平均したものが、その回答者の位置になります。
以下、コードです。
# 個体(回答者)の座標を取得
row_coords = mca.row_coordinates(survey)
row_coords.columns = ['次元1', '次元2']
print(
"個体座標の形状: "
f"{row_coords.shape}"
f"({row_coords.shape[0]}人 × 2次元)\n"
)
print("【先頭5人の座標】")
print(row_coords.head().round(4))
以下、実行結果です。
個体座標の形状: (300, 2)(300人 × 2次元)
【先頭5人の座標】
次元1 次元2
0 -0.2281 0.5137
1 -0.4981 -0.3131
2 -0.4981 -0.3131
3 0.2637 -0.5805
4 0.3219 0.1041
カテゴリと個体を重ねてプロットしてみましょう。
個体は薄い灰色の小さな点で、カテゴリは大きなマーカーで描きます。
以下、コードです。
fig, ax = plt.subplots(figsize=(10, 8))
# 変数ごとに色とマーカーを定義
colors = {
'性別': '#2E86AB',
'年代': '#E94F37',
'デバイス': '#44AF69',
'好きなカテゴリ': '#D6A100'
}
markers = {
'性別': 'o',
'年代': 's',
'デバイス': '^',
'好きなカテゴリ': 'D'
}
# 個体を薄い灰色でプロット
ax.scatter(
row_coords['次元1'], row_coords['次元2'],
marker='*',
s=50, c='gray', alpha=0.4
)
# 各カテゴリをプロット
for cat_name in col_coords.index:
# 右側の区切りで変数名とラベルに分割する
if '__' in cat_name:
base = cat_name.rsplit('__', 1)
var_name = base[0]
label_text = base[1]
else:
base = cat_name.rsplit('_', 1)
var_name = base[0]
label_text = base[1] if len(base) > 1 else cat_name
# 変数名に基づいて色とマーカーを取得
color = colors.get(var_name, 'gray')
marker = markers.get(var_name, 'o')
# 座標を取得
x, y = col_coords.loc[cat_name]
# color を使用し、facecolors 指定で確実に塗りつぶし色を反映
ax.scatter(
x, y,
s=200, color=color, marker=marker,
edgecolors='white', linewidths=2
)
ax.annotate(
label_text, (x, y),
fontsize=11, fontweight='bold',
xytext=(10, 10),
textcoords='offset points', color=color
)
# 原点の十字線
ax.axhline(
y=0, color='gray',
linestyle='--', linewidth=0.8
)
ax.axvline(
x=0, color='gray',
linestyle='--', linewidth=0.8
)
# 軸ラベルとタイトル
ax.set_xlabel(
'次元1(寄与率: '
f'{mca.percentage_of_variance_[0]:.2f}%)'
)
ax.set_ylabel(
'次元2(寄与率: '
f'{mca.percentage_of_variance_[1]:.2f}%)'
)
ax.set_title(
'MCAマップ:顧客アンケートの多変量カテゴリ関係'
)
# 凡例
from matplotlib.lines import Line2D
legend_elements = [
Line2D(
[0], [0],
marker='*', color='w',
markerfacecolor='gray',
markersize=12,
label='個体(回答者)'
)
] + [
Line2D(
[0], [0],
marker=markers[v], color='w',
markerfacecolor=colors[v],
markeredgecolor='white',
markeredgewidth=2,
markersize=12,
label=v
)
for v in colors
]
ax.legend(handles=legend_elements, loc='best')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
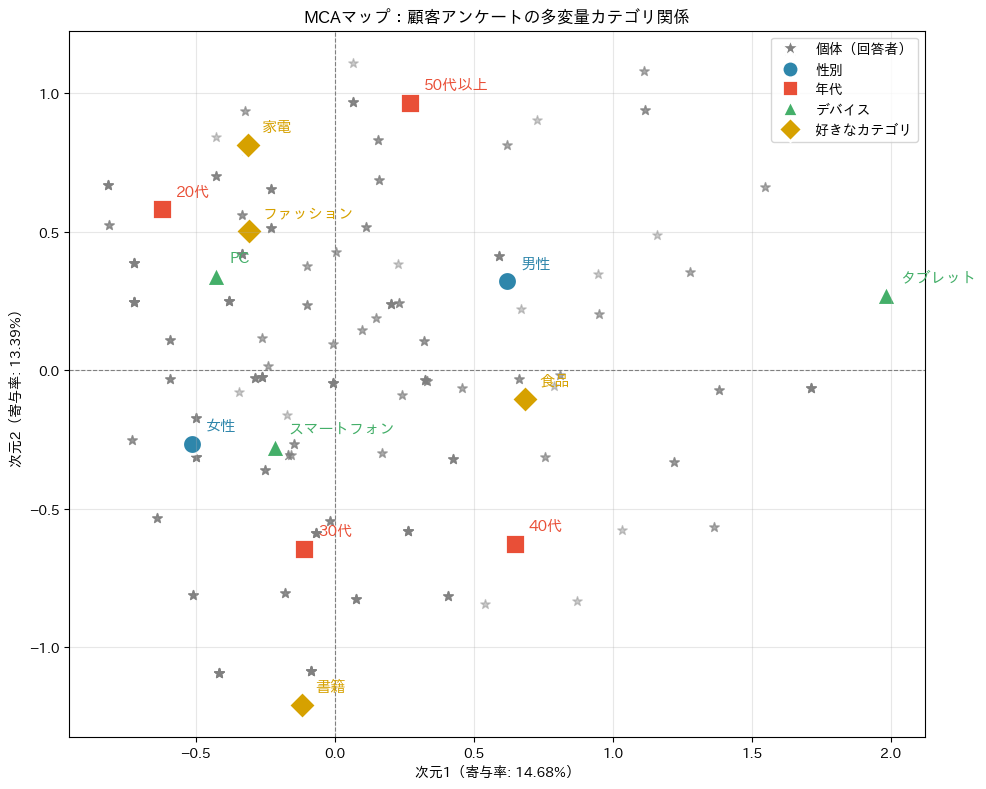
灰色の点(★)の「密集地帯」を見てください。カテゴリのマーカーの近くに回答者が集まっていることが確認できるはずです。
あるカテゴリに近い回答者は、そのカテゴリに該当する人(またはそれと似た回答パターンを持つ人)です。
ステップ7:顧客セグメンテーションへの応用
MCAの座標を使えば、回答者を似た回答パターンのグループにまとめる顧客セグメンテーションが可能です。
MCAで次元を圧縮したあとに、K-meansなどのクラスタリング手法を適用するのが定番のアプローチです。
MCAの座標に対してK-meansクラスタリングを実行し、回答者を3つのグループに分けてみましょう。
以下、コードです。
from sklearn.cluster import KMeans
# MCA座標に対してK-meansクラスタリング(3グループ)
kmeans = KMeans(
n_clusters=3,
random_state=42,
n_init=10
)
survey['セグメント'] = kmeans.fit_predict(row_coords)
print("【各セグメントの人数】")
print(
survey['セグメント'].value_counts().sort_index()
)
以下、実行結果です。
【各セグメントの人数】 セグメント 0 146 1 88 2 66 Name: count, dtype: int64
各セグメントにどんな回答者が多いのかを確認してみましょう。セグメントごとに、各カテゴリの出現比率を集計します。
以下、コードです。
# セグメントごとのカテゴリ分布
for seg in sorted(survey['セグメント'].unique()):
print(f"\n{'='*40}")
print(f"セグメント {seg}({(survey['セグメント']==seg).sum()}人)")
print('='*40)
seg_data = survey[survey['セグメント'] == seg]
for col in ['性別', '年代', 'デバイス', '好きなカテゴリ']:
dist = seg_data[col].value_counts(normalize=True)
top = dist.index[0]
print(f" {col}: {top}({dist.iloc[0]*100:.0f}%)")
以下、実行結果です。
======================================== セグメント 0(146人) ======================================== 性別: 女性(58%) 年代: 20代(49%) デバイス: PC(51%) 好きなカテゴリ: ファッション(48%) ======================================== セグメント 1(88人) ======================================== 性別: 女性(80%) 年代: 30代(48%) デバイス: スマートフォン(76%) 好きなカテゴリ: 書籍(65%) ======================================== セグメント 2(66人) ======================================== 性別: 男性(85%) 年代: 40代(42%) デバイス: タブレット(58%) 好きなカテゴリ: 食品(52%)
MCAマップ上にセグメントを色分けして表示すると、各グループの特徴がより直感的にわかります。
以下、コードです。
fig, ax = plt.subplots(figsize=(10, 8))
# セグメントごとの色とマーカー(形)を指定
seg_colors = {0: '#2E86AB', 1: '#E94F37', 2: '#44AF69'}
seg_markers = {0: 'o', 1: 's', 2: '^'}
# セグメントごとにプロット
for seg in sorted(survey['セグメント'].unique()):
mask = survey['セグメント'] == seg
ax.scatter(
row_coords.loc[mask, '次元1'],
row_coords.loc[mask, '次元2'],
s=100, c=seg_colors[seg],
marker=seg_markers.get(seg, 'o'),
alpha=0.6, edgecolors='white',
linewidths=0.5, label=f'セグメント {seg}'
)
# カテゴリも重ねる(黒で統一)
for cat_name in col_coords.index:
# 右側の区切りでラベル抽出(__ または _ のどちらにも対応)
if '__' in cat_name:
label_text = cat_name.rsplit('__', 1)[1]
else:
parts = cat_name.rsplit('_', 1)
label_text = parts[1] if len(parts) > 1 else cat_name
x, y = col_coords.loc[cat_name]
ax.scatter(
x, y, s=120, c='black', marker='x', linewidths=2)
ax.annotate(
label_text, (x, y), fontsize=10, fontweight='bold',
xytext=(8, 8), textcoords='offset points')
ax.axhline(y=0, color='gray', linestyle='--', linewidth=0.8)
ax.axvline(x=0, color='gray', linestyle='--', linewidth=0.8)
ax.set_xlabel(f'次元1(寄与率: {mca.percentage_of_variance_[0]:.2f}%)')
ax.set_ylabel(f'次元2(寄与率: {mca.percentage_of_variance_[1]:.2f}%)')
ax.set_title('MCA + K-means による顧客セグメンテーション')
# 凡例(形も反映)
from matplotlib.lines import Line2D
legend_handles = [
Line2D(
[0], [0],
marker=seg_markers.get(seg, 'o'), color='w',
markerfacecolor=seg_colors[seg],
markeredgecolor='white', markeredgewidth=0.5,
markersize=10, label=f'セグメント {seg}')
for seg in sorted(survey['セグメント'].unique())
]
# カテゴリ用の凡例要素
legend_handles.append(
Line2D(
[0], [0],
marker='x', color='black', linestyle='None',
markersize=8, label='カテゴリ')
)
ax.legend(handles=legend_handles, loc='best')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
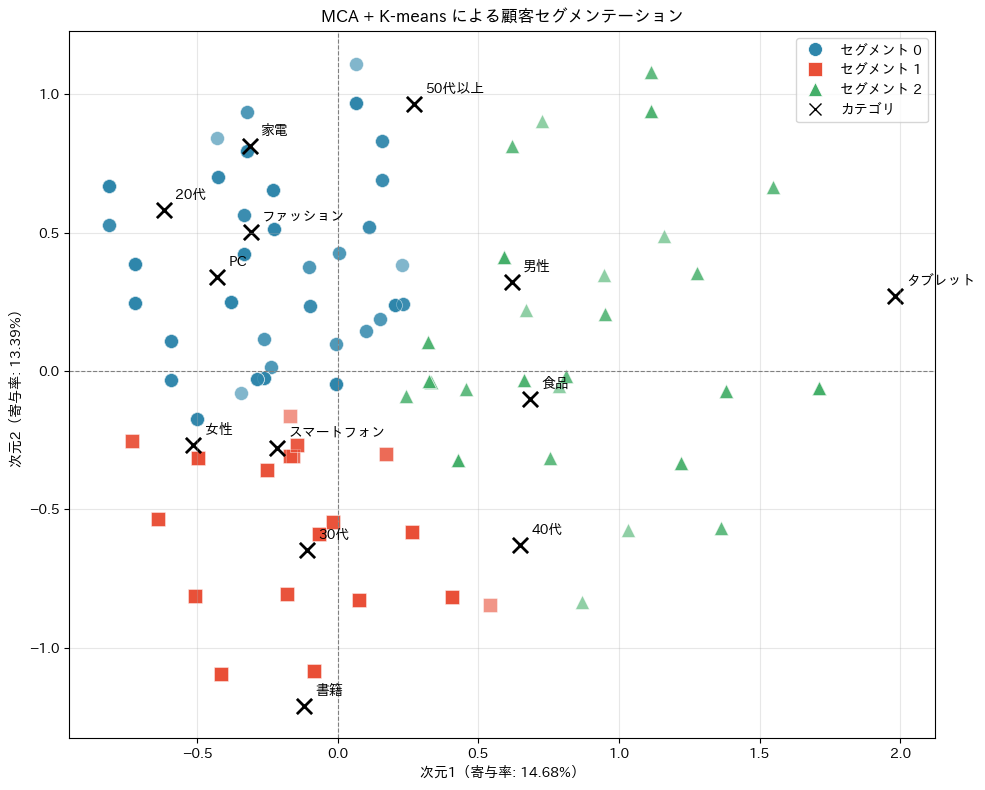
マップ上で色のかたまりを見ると、各セグメントがどの位置に分布しているかがわかります。
近くにあるカテゴリラベル(×印)を読むことで、「セグメント0は○○が多い20代のスマホユーザー」のような人物像を描くことができます。
このように、MCAで次元圧縮 → クラスタリングでグループ化 → カテゴリの位置から解釈という流れは、マーケティングリサーチや社会調査で非常によく使われるパターンです。
CA と MCA の比較
ここまでの内容をふまえ、CAとMCAの違いを整理しておきましょう。
| 観点 | CA(コレスポンデンス分析) | MCA(多重コレスポンデンス分析) |
|---|---|---|
| 入力データ | クロス集計表(2変数の集計) | 個体 × 変数の表(生データ) |
| 扱える変数の数 | 2つのカテゴリ変数 | |
| 内部表現 | 対応行列 P | インジケータ行列 Z またはBurt行列 B = Z^T Z |
| 分析の核 | P の標準化残差をSVD | Z から構成される対応行列をSVD |
| 寄与率の目安 | 累積70%以上で信頼性が高い | CAより低くなりやすい(構造的な性質) |
| 個体のプロット | 通常はカテゴリのみ | カテゴリと個体の両方が可能 |
MCAの数学的な仕組みは、本質的にはCAの拡張です。
インジケータ行列 Z から対応行列を作り、第3回で学んだのと同じ手順(標準化残差 → SVD → 座標計算)で分析を行います。
つまり、第1〜3回で学んだCAの理論がそのままMCAの土台になっています。
まとめ
今回は、カテゴリ変数が3つ以上ある場合に使える多重コレスポンデンス分析(MCA)を学びました。
インジケータ行列 Z について。個体 × 変数の生データを、0と1のダミー変数に変換した N \times J の行列です。各行はちょうど Q 個の1を含みます(Q は変数の数)。pd.get_dummies() で簡単に作成できます。
Burt行列 B について。インジケータ行列の転置とインジケータ行列の積 B = Z^T Z として定義される J \times J の正方行列です。すべての変数ペアについてのクロス集計表を一枚に貼り合わせた「超クロス集計表」であり、対角ブロックには各カテゴリの該当者数が、非対角ブロックにはカテゴリ間の共起度数が入ります。
MCAマップについて。異なる変数に属するカテゴリがすべて同じ2次元空間上に配置されます。近いカテゴリどうしは同じ回答者に選ばれやすい組み合わせです。さらに個体(回答者)もマップ上にプロットでき、個体の座標はその人が該当するカテゴリ座標の平均 \psi_{ik} = \frac{1}{Q}\sum_{j \in C_i} \gamma_{jk} として計算されます。
顧客セグメンテーションについて。MCA座標にK-meansなどのクラスタリングを適用することで、似た回答パターンの回答者をグループ化できます。MCAで次元圧縮→クラスタリング→カテゴリ位置で解釈、という流れはマーケティングリサーチの定番手法です。
ここまでの4回で、CA・MCAの実行方法と数学的な仕組みをひと通り学んできました。
しかし、マップを描いただけでは分析は終わりではありません。「この軸は何を意味しているのか」「どの点の解釈が信頼できるのか」「どの点がこの次元を特徴づけているのか」を判断するための定量的な指標が必要です。
最終回の第5回では、寄与度(contribution)、cos²(表現の質)、距離の解釈という3つの指標を学びます。

