Pythonで始める分類モデル入門— 第3回 —「もし〜なら」で分ける — 決定木の仕組みと過学習対策

こんにちは！「Pythonで始める分類モデル入門」の第3回です。

前回までに学んだロジスティック回帰やLDAは、どちらもデータを「直線」で分割する手法でした。

https://www.salesanalytics.co.jp/datascience/datascience302/

数学的にはエレガントですが、現実世界のデータは直線で分けられるほど単純ではないこともあります。

今回学ぶ決定木（Decision Tree）は、私たちが日常的に行っている「もし〜なら〜」という条件分岐の思考をそのままモデル化した手法です。

直感的に理解しやすく、結果の説明もしやすいという大きな魅力があります。

私たちは毎日「決定木」を使っている

実は、あなたは毎日のように「決定木」的な思考をしています。

たとえば、休日の朝に「今日は何をしようか」と考えるとき、こんな風に考えませんか？

「天気は良い？」→ はい →「体調は良い？」→ はい → 外出しよう
「天気は良い？」→ はい →「体調は良い？」→ いいえ → 家でゆっくり
「天気は良い？」→ いいえ →「見たい映画がある？」→ はい → 映画館へ
「天気は良い？」→ いいえ →「見たい映画がある？」→ いいえ → 家で読書

このように、質問を繰り返して最終的な判断に到達するプロセスが、まさに決定木の考え方です。

機械学習における決定木は、「どんな質問を」「どの順番で」「どんな基準で」行えば最も正確に分類できるかを、データから自動的に学習します。

必要なライブラリを読み込もう

今回使うライブラリを読み込みます。決定木の可視化にはplot_tree関数を使います。

以下、コードです。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 乱数のシードを固定
np.random.seed(42)

顧客の購買データを作ってみよう

今回は「年齢と年収から、高額商品を購入するかどうかを予測する」問題に取り組みます。ECサイトのマーケティング担当者になったつもりで考えてみましょう。

以下、コードです。

# 200人分の顧客データを生成
n_samples = 200

# 年齢（20〜70歳）と年収（200〜1200万円）をランダムに生成
age = np.random.randint(20, 70, n_samples)
income = np.random.randint(200, 1200, n_samples)

# 購入ルール：年収600万以上、または年齢40以上かつ年収400万以上なら購入しやすい
purchase_prob = (
    (income >= 600) | ((age >= 40) &amp; (income >= 400))
).astype(float)
# 確率的な要素を加える（現実のデータはノイズを含む）
purchase_prob = purchase_prob * 0.8 + 0.1  # 80%の確率で購入、10%のベースライン
purchase = np.random.binomial(1, purchase_prob)

# DataFrameにまとめる
df = pd.DataFrame({
    'age': age,
    'income': income,
    'purchase': purchase
})

print(f"データ数: {len(df)}人")
print(f"購入者数: {purchase.sum()}人 ({purchase.mean()*100:.1f}%)")
print(df.head(10))

以下、実行結果です。

データ数: 200人
購入者数: 130人 (65.0%)
   age  income  purchase
0   28    1058         1
1   69     634         1
2   46     646         1
3   21    1193         1
4   24     507         0
5   48     448         1
6   56     365         0
7   57     680         0
8   38    1183         1
9   27     534         0

このデータには意図的に「直線では分けにくい」パターンを入れています。

「年収が高ければ購入する」という単純なルールに加えて、「年齢が高くて中程度の年収でも購入する」というルールがあるため、ロジスティック回帰のような直線では完璧に分離できません。

データの分布を確認しよう

散布図でデータを可視化して、購入者と非購入者の分布を確認しましょう。

以下、コードです。

plt.figure(figsize=(10, 7))

# 購入していない顧客をプロット
plt.scatter(
    df[df['purchase']==0]['age'], 
    df[df['purchase']==0]['income'],
    c='#E94F37', s=60, alpha=0.6, 
    label='Not Purchase'
)

# 購入者をプロット
plt.scatter(
    df[df['purchase']==1]['age'], 
    df[df['purchase']==1]['income'],
    c='#2E86AB', s=60, alpha=0.6, 
    label='Purchase'
)

plt.xlabel('Age')
plt.ylabel('Income (10K JPY)')
plt.title('Customer Purchase Pattern')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

以下、実行結果です。

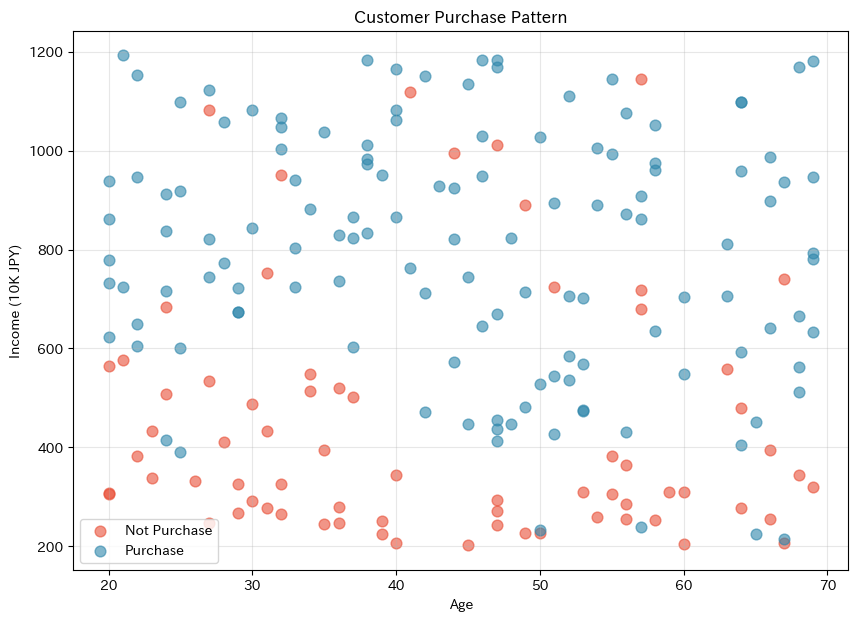
グラフを見ると、単純な直線では2つのグループを分けられないことがわかります。

購入者（青、Purchase）は「年収が高い領域」と「年齢が高くて年収が中程度の領域」の両方に分布しています。

このような複雑なパターンを捉えるのが決定木の得意技です。

決定木の構造を理解しよう

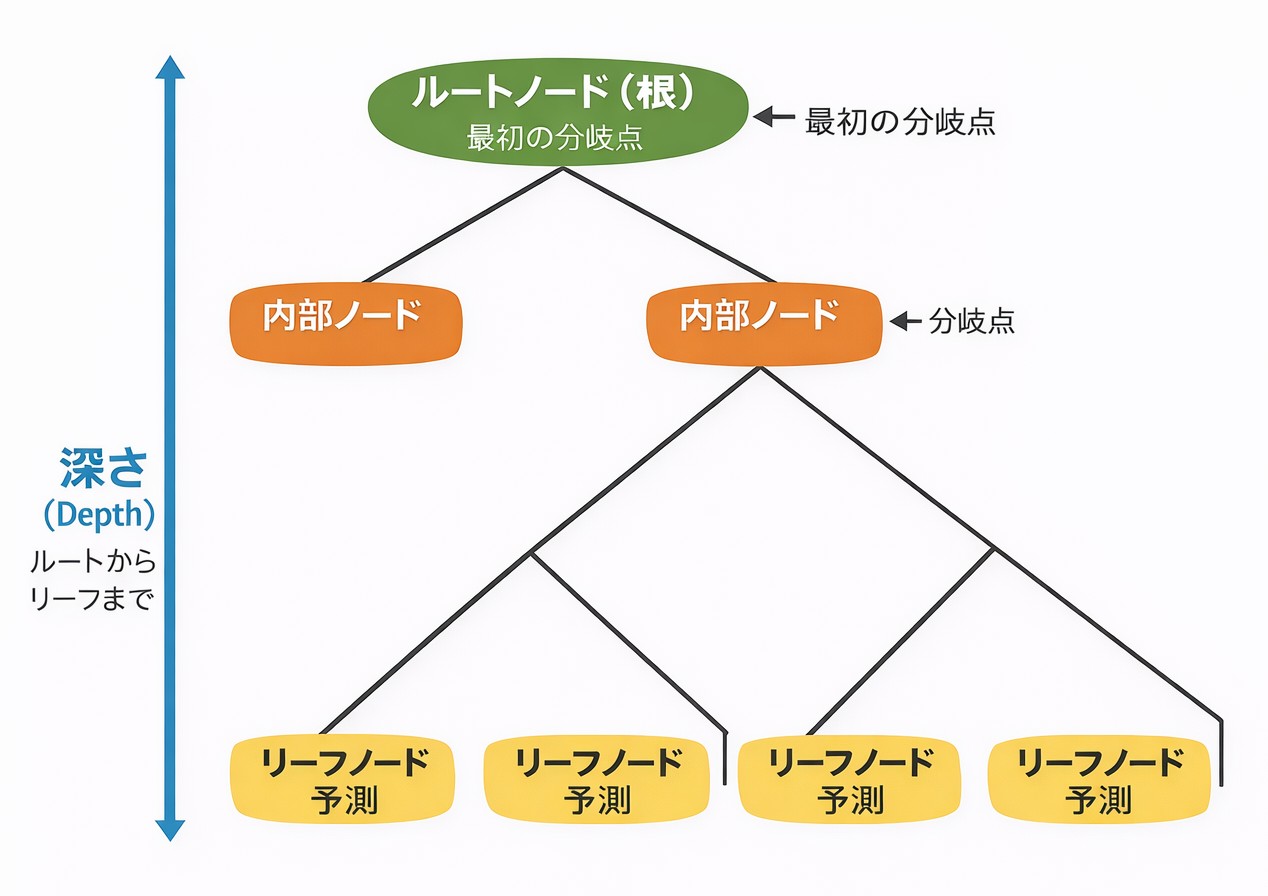
決定木は、木を逆さまにしたような構造をしています。

専門用語を整理しておきましょう。

ルートノード（根）は木の一番上にある最初の分岐点です
内部ノードは途中の分岐点です
リーフノード（葉）は木の末端で、ここで最終的な予測が出力されます
深さ（Depth）はルートからリーフまでの分岐の回数です

決定木の学習とは、「どの特徴量で」「どの値を基準に」「どの順番で」分岐するかを、データから自動的に決定することです。

最初の決定木を作ってみよう

まずはシンプルな決定木を作成してみましょう。scikit-learnを使えば数行で実装できます。

以下、コードです。

# 特徴量とラベルを準備
X = df[['age', 'income']].values
y = df['purchase'].values

# 決定木モデルを作成（まずは深さ制限なし）
tree_model = DecisionTreeClassifier(random_state=42)
tree_model.fit(X, y)

print("【決定木の基本情報】")
print(
    f"木の深さ: {tree_model.get_depth()}"
)
print(
    f"葉の数: {tree_model.get_n_leaves()}"
)
print(
    f"訓練データの正解率: "
    f"{accuracy_score(y, tree_model.predict(X))*100:.1f}%"
)

以下、実行結果です。

【決定木の基本情報】
木の深さ: 13
葉の数: 33
訓練データの正解率: 100.0%

深さ制限なしで学習すると、かなり深い木が作られることがわかります。

訓練データに対する正解率は非常に高いですが、これが良いこととは限りません（後で詳しく説明します）。

決定木を可視化しよう

決定木の最大の魅力は、モデルの判断過程を視覚的に確認できることです。

ただし、深すぎる木は見づらいので、まずは深さを2に制限した木を可視化します。

以下、コードです。

# 深さを2に制限した決定木を作成
tree_simple = DecisionTreeClassifier(
    max_depth=2, # 深さを2に制限
    random_state=42
)
tree_simple.fit(X, y)

# 決定木を可視化
plt.figure(figsize=(10, 10))
plot_tree(
    tree_simple, # 可視化するモデル
    feature_names=['age', 'income'], # 特徴量の名前
    class_names=['Not Purchase', 'Purchase'], # クラスの名前
    filled=True, # 色を塗る
    rounded=True # 角を丸める
)

plt.title('Decision Tree Visualization (max_depth=2)')
plt.tight_layout()
plt.show()

以下、実行結果です。

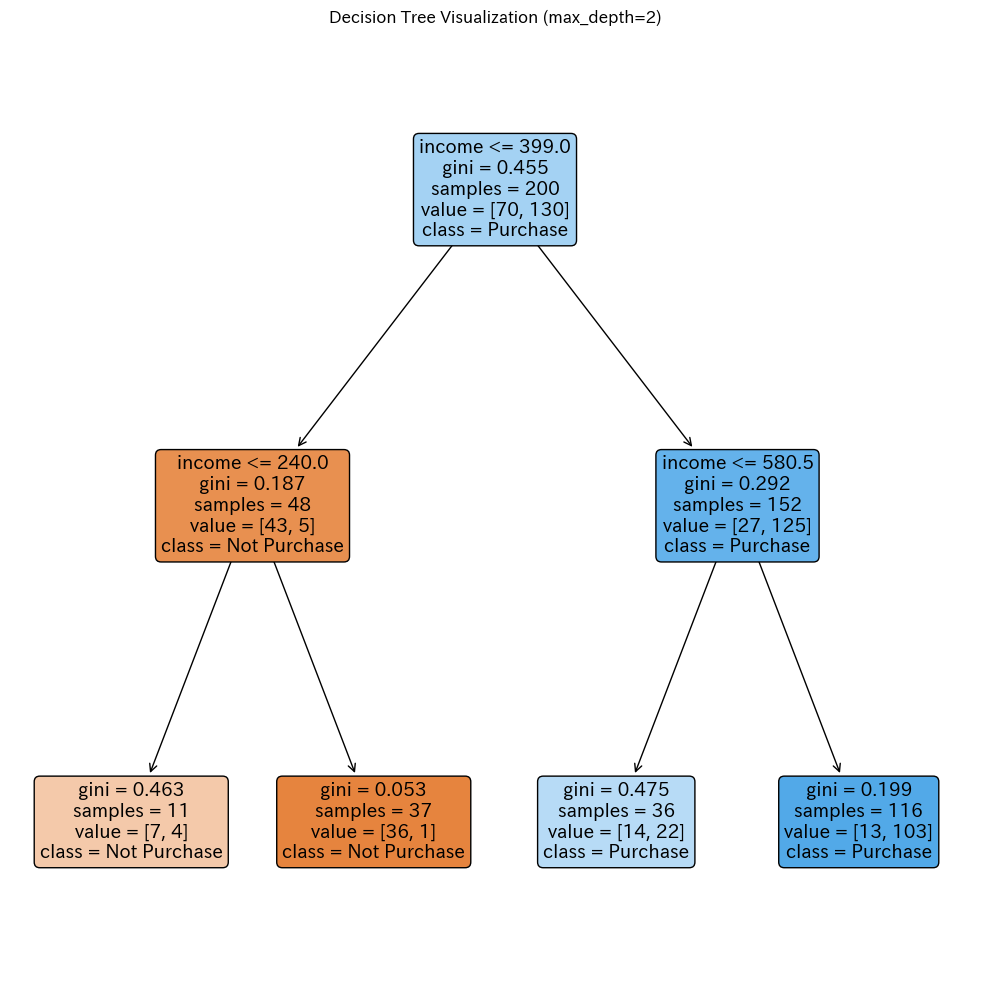
各ノード（箱）の中身を読み解いてみましょう。

一番上の行は分岐条件です（例：「income <= 399.0」）。この条件がTrueなら左の子ノードへ、Falseなら右の子ノードへ進みます。

giniは「ジニ不純度」という指標で、そのノードにどれだけ混ざったデータがあるかを表します。0に近いほど「純粋」（片方のクラスだけ）で、0.5に近いほど「不純」（両クラスが混在）です。

samplesはそのノードに到達したサンプル数です。

valueは各クラスのサンプル数で、[非購入者数, 購入者数]の形式です。

classは多数決による予測クラスです。

分岐基準を数学的に理解しよう：ジニ不純度

決定木は「どの変数のどこで分岐するのが最も良いか」を自動的に判断します。

その基準となるのがジニ不純度（Gini Impurity）です。

ジニ不純度とは、 ノード内のクラス分布 ${p_k}$ （クラス $k$ の割合）に基づいてクラスを確率的に割り当てたとき、真のクラスと一致しない確率を意味します。

数式で書くと次のようになります。
$$
\text{Gini} = 1 – \sum_{k=1}^{K} p_k^2
$$

2クラス分類の場合、購入者の割合を $p$ とすると次のようになります。
$$
\text{Gini} = 1 – p^2 – (1-p)^2 = 2p(1-p)
$$

この値は $p = 0$ （全員非購入）または $p = 1$ （全員購入）のとき最小値0、 $p = 0.5$ （半々）のとき最大値0.5になります。

実際に計算して確認してみましょう。

以下、コードです。

# ジニ不純度を計算する関数
# クラス1の割合pからジニ不純度を計算
def gini_impurity(p):
    return 2 * p * (1 - p)

# いくつかの割合でジニ不純度を計算
print("【ジニ不純度の例】")
for p in [0.0, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0]:
    print(
        f"購入者の割合 {p:.1f} → "
        f"Gini = {gini_impurity(p):.3f}"
    )

以下、実行結果です。

【ジニ不純度の例】
購入者の割合 0.0 → Gini = 0.000
購入者の割合 0.1 → Gini = 0.180
購入者の割合 0.3 → Gini = 0.420
購入者の割合 0.5 → Gini = 0.500
購入者の割合 0.7 → Gini = 0.420
購入者の割合 0.9 → Gini = 0.180
購入者の割合 1.0 → Gini = 0.000

この結果から、データが一方のクラスに偏っているほど（純粋なほど）ジニ不純度が低くなることがわかります。

決定木は、分岐後のジニ不純度ができるだけ低くなる（つまり、純粋なグループに分かれる）ような分岐点を探します。

ジニ不純度を可視化しよう

ジニ不純度がどのような形をしているか、グラフで確認してみましょう。

以下、コードです。

plt.figure(figsize=(10, 6))

# クラス1の割合の範囲を設定
p_values = np.linspace(0, 1, 100)

# ジニ不純度を計算
gini_values = 2 * p_values * (1 - p_values)

# ジニ不純度のグラフをプロット
plt.plot(p_values, gini_values, 'b-', linewidth=3)

# ジニ不純度の下側を塗りつぶす
plt.fill_between(p_values, gini_values, alpha=0.3)

# ジニ不純度が最大になる点を赤い破線で示す
plt.axvline(
    x=0.5, 
    color='red', linestyle='--', alpha=0.7, 
    label='Maximum Impurity'
)

plt.xlabel('Proportion of Class 1 (p)')
plt.ylabel('Gini Impurity')
plt.title('Gini Impurity vs Class Proportion')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

以下、実行結果です。

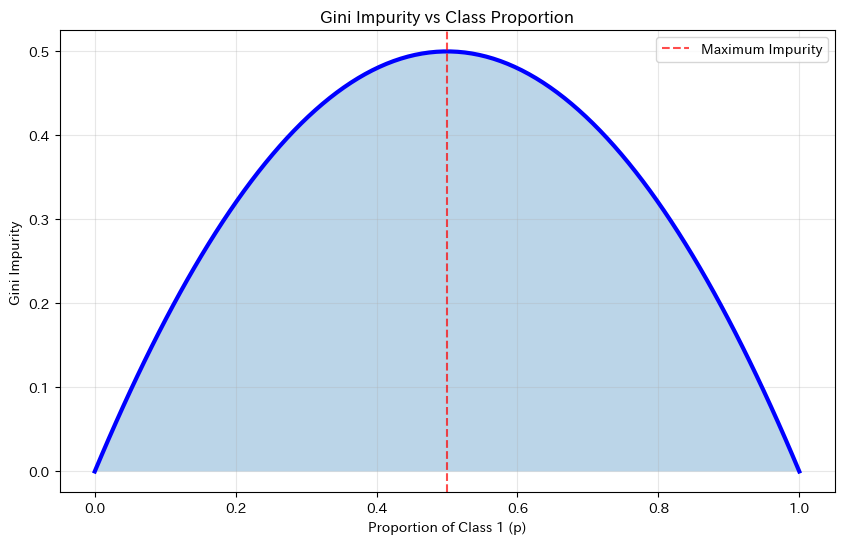
グラフは逆U字型になっています。

p=0.5のとき最大値0.5をとり、両端（p=0またはp=1）で0になります。

これは、クラスが半々に混ざっているとき最も「不純」で、どちらか一方だけになると「純粋」になることを視覚的に示しています。

情報利得：分岐の良さを測る

決定木は、分岐によってどれだけジニ不純度が減少するかを計算し、最も減少が大きい分岐を選びます。

この減少量を情報利得（Information Gain）と呼びます。
$$
\text{情報利得} = \text{Gini}_{\text{親}} – \left( \frac{n_{\text{左}}}{n} \cdot \text{Gini}_{\text{左}} + \frac{n_{\text{右}}}{n} \cdot \text{Gini}_{\text{右}} \right)
$$

つまり、親ノードのジニ不純度から、子ノードのジニ不純度の加重平均を引いた値です。

具体例で計算してみましょう。10人の顧客データがあり、6人が購入者だとします。

以下、コードです。

# 親ノード：10人中6人が購入者
n_total = 10
n_purchase_parent = 6
gini_parent = gini_impurity(n_purchase_parent / n_total)
print(f"親ノード: {n_purchase_parent}/{n_total}人が購入者")
print(f"親ノードのジニ不純度: {gini_parent:.3f}")
print()

# 分岐案1: 左に6人（購入5人）、右に4人（購入1人）
n_left1, n_purchase_left1 = 6, 5
n_right1, n_purchase_right1 = 4, 1
gini_left1 = gini_impurity(n_purchase_left1 / n_left1)
gini_right1 = gini_impurity(n_purchase_right1 / n_right1)
gini_children1 = (n_left1/n_total) * gini_left1 + (n_right1/n_total) * gini_right1
info_gain1 = gini_parent - gini_children1

print("【分岐案1】左(5/6購入), 右(1/4購入)")
print(f"  左のGini: {gini_left1:.3f}, 右のGini: {gini_right1:.3f}")
print(f"  子ノードの加重平均Gini: {gini_children1:.3f}")
print(f"  情報利得: {info_gain1:.3f}")
print()

# 分岐案2: 左に5人（購入3人）、右に5人（購入3人）
n_left2, n_purchase_left2 = 5, 3
n_right2, n_purchase_right2 = 5, 3
gini_left2 = gini_impurity(n_purchase_left2 / n_left2)
gini_right2 = gini_impurity(n_purchase_right2 / n_right2)
gini_children2 = (n_left2/n_total) * gini_left2 + (n_right2/n_total) * gini_right2
info_gain2 = gini_parent - gini_children2

print("【分岐案2】左(3/5購入), 右(3/5購入)")
print(f"  左のGini: {gini_left2:.3f}, 右のGini: {gini_right2:.3f}")
print(f"  子ノードの加重平均Gini: {gini_children2:.3f}")
print(f"  情報利得: {info_gain2:.3f}")

以下、実行結果です。

親ノード: 6/10人が購入者
親ノードのジニ不純度: 0.480

【分岐案1】左(5/6購入), 右(1/4購入)
  左のGini: 0.278, 右のGini: 0.375
  子ノードの加重平均Gini: 0.317
  情報利得: 0.163

【分岐案2】左(3/5購入), 右(3/5購入)
  左のGini: 0.480, 右のGini: 0.480
  子ノードの加重平均Gini: 0.480
  情報利得: 0.000

分岐案1の方が情報利得が大きいため、決定木はこちらの分岐を選択します。

直感的にも、分岐案1の方がデータをより「きれいに」分けていることがわかりますね。

決定境界を可視化しよう

決定木がどのような境界でデータを分けているか確認してみましょう。

以下、コードです。

# メッシュグリッドを作成
h = 1
x_min, x_max = X[:, 0].min() - 5, X[:, 0].max() + 5
y_min, y_max = X[:, 1].min() - 50, X[:, 1].max() + 50
xx, yy = np.meshgrid(
    np.arange(x_min, x_max, h),
    np.arange(y_min, y_max, h)
)

# 深さ2の決定木で予測
Z = tree_simple.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(10, 7))

# 決定木の境界を描画
plt.contourf(xx, yy, Z, alpha=0.3, cmap='RdBu')

# 非購入者を描画
plt.scatter(
    X[y==0, 0], X[y==0, 1], 
    c='#E94F37', s=60, alpha=0.7, 
    label='Not Purchase'
)
# 購入者を描画
plt.scatter(
    X[y==1, 0], X[y==1, 1], 
    c='#2E86AB', s=60, alpha=0.7, 
    label='Purchase'
)

plt.xlabel('Age')
plt.ylabel('Income (10K JPY)')
plt.title('Decision Tree Boundary (max_depth=2)')
plt.legend()
plt.show()

以下、実行結果です。

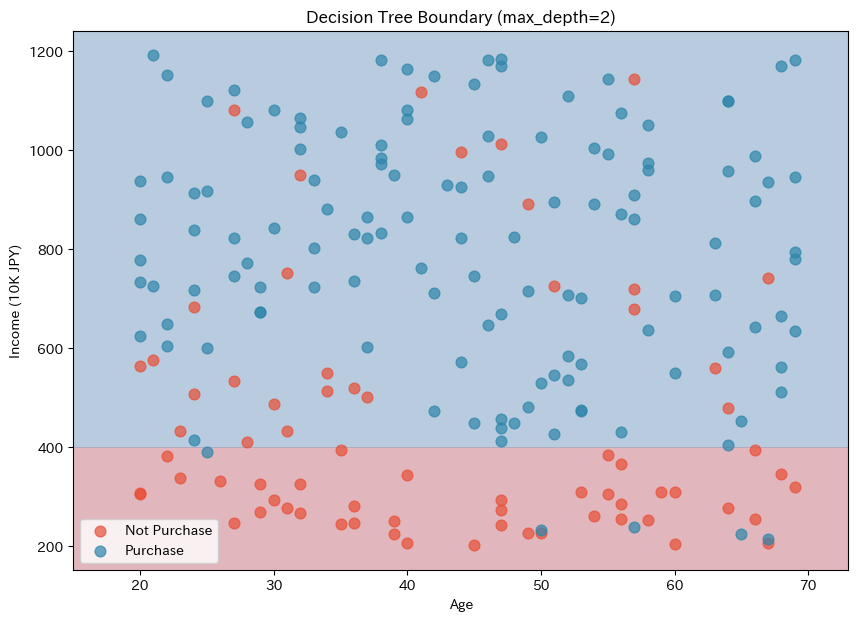
ロジスティック回帰やLDAとは全く異なる境界が描かれています。決定木の境界は軸に平行な直線の組み合わせになります。

これは、各分岐が「年齢 <= 〇〇」「年収 <= 〇〇」のように、単一の特徴量に基づく条件だからです。

この「階段状」の境界が、決定木が複雑なパターンを捉えられる理由であり、同時に過学習しやすい原因でもあります。

過学習：決定木の落とし穴

ここで決定木の大きな問題点、過学習（Overfitting）について学びましょう。

過学習とは、モデルが訓練データに「適合しすぎて」しまい、新しいデータに対する予測性能が低下する現象です。

訓練データの本質的なパターンだけでなく、たまたま含まれていたノイズまで学習してしまうのです。

訓練データとテストデータに分けて、過学習を確認してみましょう。

以下、コードです。

# データを訓練用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42)

# 深さ制限なしの決定木
tree_overfit = DecisionTreeClassifier(random_state=42)
tree_overfit.fit(X_train, y_train)

print("【深さ制限なしの決定木】")
print(f"木の深さ: {tree_overfit.get_depth()}")
print(f"葉の数: {tree_overfit.get_n_leaves()}")
print(
    f"訓練データの正解率: "
    f"{accuracy_score(y_train, tree_overfit.predict(X_train))*100:.1f}%"
)
print(
    f"テストデータの正解率: "
    f"{accuracy_score(y_test, tree_overfit.predict(X_test))*100:.1f}%"
)

以下、実行結果です。

【深さ制限なしの決定木】
木の深さ: 12
葉の数: 33
訓練データの正解率: 100.0%
テストデータの正解率: 83.3%

訓練データでは非常に高い正解率なのに、テストデータでは性能が落ちています。

これが過学習の典型的な症状です。

モデルが訓練データを「暗記」してしまい、本質的なパターンを学習できていないのです。

なぜ過学習が起きるのか

深すぎる決定木は、訓練データの一つ一つのサンプルに合わせて分岐を作ってしまいます。

極端な場合、すべてのサンプルを個別に覚えてしまい、「汎化能力」（未知のデータに対する予測能力）が失われます。

決定境界を見ると、過学習の様子がよくわかります。

以下、コードです。

fig, axes = plt.subplots(2, 1, figsize=(10, 14))

#
# 上：深さ制限なし
#

# メッシュ上の各点を予測し、決定境界（領域）を可視化するための配列Zを作成
Z_overfit = tree_overfit.predict(np.c_[xx.ravel(), yy.ravel()]) 
Z_overfit = Z_overfit.reshape(xx.shape)

# 決定境界を描画
axes[0].contourf(xx, yy, Z_overfit, alpha=0.3, cmap='RdBu')

# purchase=0のデータを赤色でプロット
axes[0].scatter(
    X_train[y_train==0, 0], X_train[y_train==0, 1], 
    c='#E94F37', s=60, alpha=0.7
)
# purchase=1のデータを青色でプロット
axes[0].scatter(
    X_train[y_train==1, 0], X_train[y_train==1, 1], 
    c='#2E86AB', s=60, alpha=0.7
)

axes[0].set_title(f'No Depth Limit (depth={tree_overfit.get_depth()})')
axes[0].set_xlabel('Age')
axes[0].set_ylabel('Income')

#
# 下：深さ3に制限
#

# 深さ3に制限した決定木
tree_pruned = DecisionTreeClassifier(
    max_depth=3, 
    random_state=42
)
tree_pruned.fit(X_train, y_train)

# メッシュ上の各点を予測し、決定境界（領域）を可視化するための配列Zを作成
Z_pruned = tree_pruned.predict(np.c_[xx.ravel(), yy.ravel()])
Z_pruned = Z_pruned.reshape(xx.shape)

# 決定境界を描画
axes[1].contourf(xx, yy, Z_pruned, alpha=0.3, cmap='RdBu')

# purchase=0のデータを赤色でプロット
axes[1].scatter(
    X_train[y_train==0, 0], X_train[y_train==0, 1], 
    c='#E94F37', s=60, alpha=0.7
)
# purchase=1のデータを青色でプロット
axes[1].scatter(
    X_train[y_train==1, 0], X_train[y_train==1, 1], 
    c='#2E86AB', s=60, alpha=0.7
)

axes[1].set_title(f'max_depth=3 (depth={tree_pruned.get_depth()})')
axes[1].set_xlabel('Age')
axes[1].set_ylabel('Income')

plt.tight_layout()
plt.show()

以下、実行結果です。

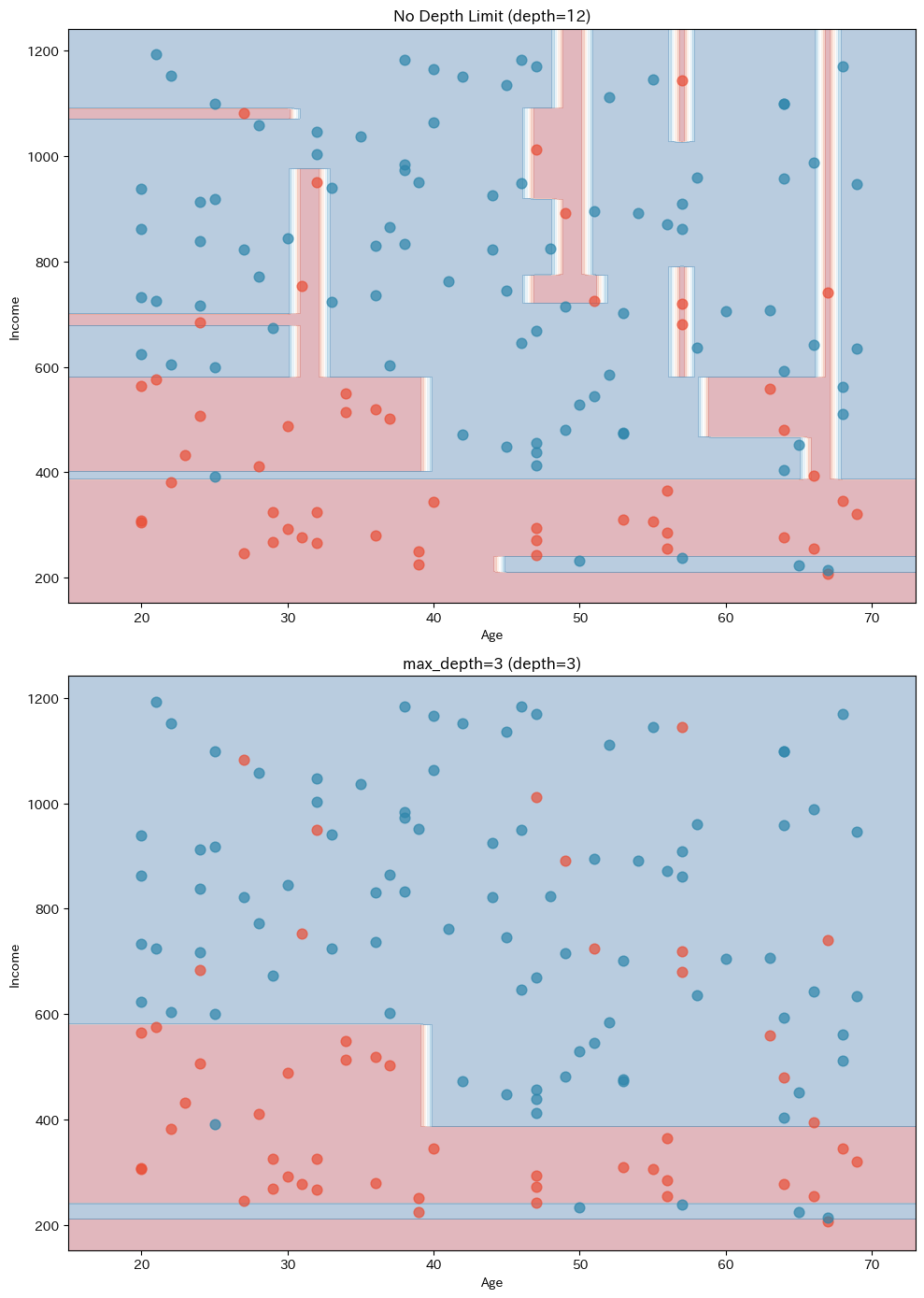
上の図（深さ制限なし）は、境界が非常に複雑で、個々のデータ点に合わせて細かく曲がりくねっています。

これは訓練データのノイズまで学習してしまっている証拠です。

下の図（深さ3）は、境界がシンプルで、データの大まかな傾向を捉えています。

過学習を防ぐ方法

過学習を防ぐために、決定木の「成長」を制限する方法がいくつかあります。

max_depth（最大深さ）：木がどれだけ深く成長できるかを制限します。
min_samples_split（分岐に必要な最小サンプル数）：ノードを分岐するために必要な最小サンプル数を指定します。
min_samples_leaf（葉の最小サンプル数）：葉ノードに含まれるサンプルの最小数を指定します。

これらのパラメータを調整して、過学習を抑制してみましょう。

以下、コードです。

# パラメータを調整した決定木
tree_tuned = DecisionTreeClassifier(
    max_depth=4,
    min_samples_split=10,
    min_samples_leaf=5,
    random_state=42
)
tree_tuned.fit(X_train, y_train)

print("【パラメータ調整後の決定木】")
print(f"木の深さ: {tree_tuned.get_depth()}")
print(f"葉の数: {tree_tuned.get_n_leaves()}")
print(
    f"訓練データの正解率: "
    f"{accuracy_score(y_train, tree_tuned.predict(X_train))*100:.1f}%"
)
print(
    f"テストデータの正解率: "
    f"{accuracy_score(y_test, tree_tuned.predict(X_test))*100:.1f}%"
)

以下、実行結果です。

【パラメータ調整後の決定木】
木の深さ: 4
葉の数: 11
訓練データの正解率: 86.4%
テストデータの正解率: 93.3%

訓練データの正解率は下がりましたが、テストデータの正解率は向上しています。

これが適切な「汎化」ができている状態です。

最適な深さを探そう

どのくらいの深さが最適かを調べるために、深さを変えながら精度を比較してみましょう。

以下、コードです。

# 深さを1から15まで変えて精度を計算
depths = range(1, 16)
train_scores = []
test_scores = []

for depth in depths:
    tree = DecisionTreeClassifier(max_depth=depth, random_state=42)
    tree.fit(X_train, y_train)
    train_scores.append(accuracy_score(y_train, tree.predict(X_train)))
    test_scores.append(accuracy_score(y_test, tree.predict(X_test)))

# グラフで可視化
plt.figure(figsize=(10, 6))
plt.plot(
    depths, train_scores, 
    'b-o', linewidth=2, markersize=8, 
    label='Training'
)
plt.plot(
    depths, test_scores, 
    'r-s', linewidth=2, markersize=8, 
    label='Test'
)
plt.xlabel('Tree Depth')
plt.ylabel('Accuracy')
plt.title('Accuracy vs Tree Depth')
plt.legend()
plt.grid(True, alpha=0.3)
plt.xticks(depths)
plt.show()

以下、実行結果です。

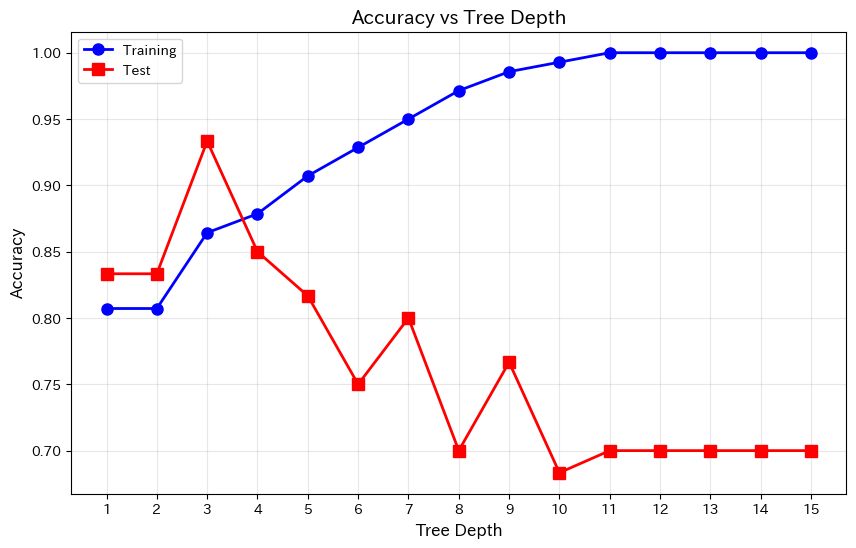
このグラフは非常に重要な示唆を与えてくれます。

訓練データの精度（青線）は深さが増すほど上がり続けますが、テストデータの精度（赤線）はある深さで頭打ちになるか、下がり始めます。

この「乖離」が過学習の兆候です。テスト精度が最大になる深さ付近が、最適な複雑さと言えます。

エントロピーによる分岐基準

ジニ不純度の他に、エントロピーという指標も分岐基準として使えます。

エントロピーは情報理論に基づく概念で、データの「乱雑さ」や「不確実性」を測ります。
$$
\text{Entropy} = -\sum_{k=1}^{K} p_k \log_2(p_k)
$$

2クラスの場合、次のようになります。
$$
\text{Entropy} = -p \log_2(p) – (1-p) \log_2(1-p)
$$

エントロピーも、データが純粋（一方のクラスだけ）なら0、半々なら最大値1になります。

以下、コードです。

# エントロピーを計算する関数
# クラス1の割合pからエントロピーを計算（0や1の場合は0を返す）
def entropy(p):
    if p == 0 or p == 1:
        return 0
    return -p * np.log2(p) - (1-p) * np.log2(1-p)

# ジニ不純度とエントロピーを比較
p_values = np.linspace(0.001, 0.999, 100)
gini_values = [gini_impurity(p) for p in p_values]
entropy_values = [entropy(p) for p in p_values]

plt.figure(figsize=(10, 6))

# ジニ不純度をプロット
plt.plot(
    p_values, gini_values, 
    'b-', linewidth=2, 
    label='Gini Impurity'
)

# エントロピーをプロット
plt.plot(
    p_values, entropy_values, 
    'r-', linewidth=2, 
    label='Entropy'
)

plt.xlabel('Proportion of Class 1 (p)')
plt.ylabel('Impurity / Entropy')
plt.title('Gini Impurity vs Entropy')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

以下、実行結果です。

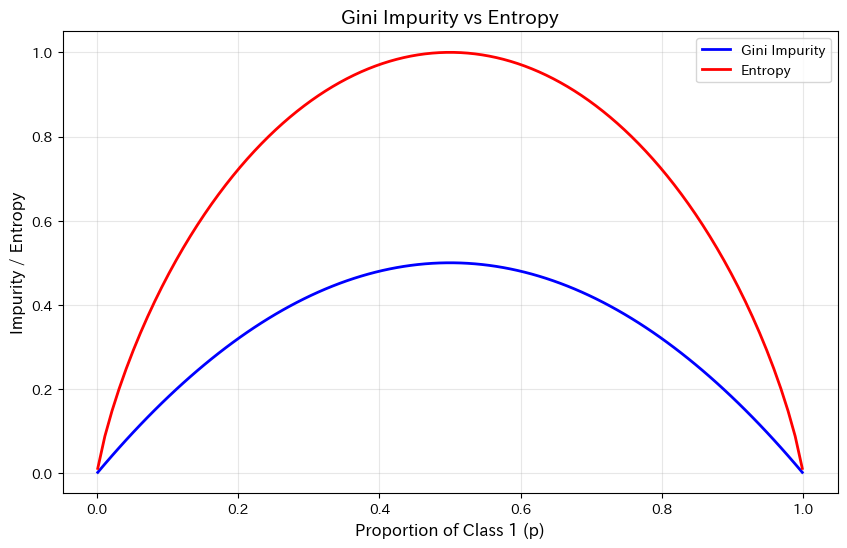
両方とも似た形をしていますね。

実用上、どちらを使っても結果に大きな違いはないことが多いです。

scikit-learnのデフォルトはジニ不純度（criterion='gini'）ですが、criterion='entropy'で切り替えることもできます。

決定木の長所と短所

ここまで学んできた決定木の特徴を整理しましょう。

　長所

長所として、まずモデルの解釈性が高いことが挙げられます。

木構造を可視化すれば、なぜその予測になったかを説明できます。ビジネスの意思決定では、この「説明のしやすさ」が非常に重要です。

また、前処理が少なくて済むのも魅力です。

特徴量のスケーリング（標準化など）が不要で、カテゴリ変数も扱いやすいです。

さらに、非線形な関係を捉えられます。

ロジスティック回帰やLDAでは難しい複雑なパターンも学習できます。

　短所

短所としては、過学習しやすいことが最大の弱点です。パラメータ調整が必要です。

また、不安定という問題もあります。データが少し変わるだけで、木の構造が大きく変わることがあります。

そして、最適な木を見つけることが難しいという計算上の課題もあります。

決定木の学習は「貪欲法」と呼ばれる近似的な方法を使っており、理論的に最適な木が見つかる保証はありません。

新しいデータを予測してみよう

最後に、調整した決定木モデルで新しい顧客の購入を予測してみましょう。

以下、コードです。

# 予測したい顧客のデータ
new_customers = [
    [25, 300],   # 若くて年収低め
    [55, 500],   # 中年で年収中程度
    [35, 800],   # 若めで年収高め
    [45, 450],   # 中年で年収中程度
]

print("【新規顧客の購入予測】")
print("-" * 50)

for age, income in new_customers:
    pred = tree_tuned.predict([[age, income]])[0]
    # 決定木は確率も出力できる
    prob = tree_tuned.predict_proba([[age, income]])[0]
    result = "Purchase" if pred == 1 else "Not Purchase"
    
    print(
        f"年齢{age}歳, 年収{income}万円 → {result}"
    )
    print(
        f" - 非購入確率: {prob[0]*100:.1f}%\n"
        f" - 購入確率: {prob[1]*100:.1f}%"
    )

以下、実行結果です。

【新規顧客の購入予測】
--------------------------------------------------
年齢25歳, 年収300万円 → Not Purchase
 - 非購入確率: 100.0%
 - 購入確率: 0.0%
年齢55歳, 年収500万円 → Purchase
 - 非購入確率: 0.0%
 - 購入確率: 100.0%
年齢35歳, 年収800万円 → Purchase
 - 非購入確率: 5.4%
 - 購入確率: 94.6%
年齢45歳, 年収450万円 → Purchase
 - 非購入確率: 0.0%
 - 購入確率: 100.0%

決定木も確率を出力できますが、この確率は「その葉に到達した訓練データの割合」なので、ロジスティック回帰の確率とは解釈が異なることに注意してください。