Pythonで学ぶコレスポンデンス分析入門
— 第2回 —
期待と現実のズレを測る ― 独立性・期待度数・カイ二乗

122
Pythonで学ぶコレスポンデンス分析入門— 第2回 —期待と現実のズレを測る ― 独立性・期待度数・カイ二乗

前回（第1回）では、prince ライブラリを使ってコレスポンデンス分析のマップをいきなり描いてみました。

Pythonで学ぶコレスポンデンス分析入門— 第1回 —クロス集計表の「その先」へ ― コレスポンデンス分析って何？

マップ上で近い点どうしは関連が強い、という直感的な読み方を体験できたと思います。

しかし、あのマップの座標はどうやって計算されているのか、まだブラックボックスのままでした。

今回はその仕組みの第一歩として、コレスポンデンス分析の「エンジン」にあたる「独立性からのズレ」という考え方を掘り下げます。

具体的には、次の3つを順にお話しします。

  • 独立性とは何か ― 「学部とメニューが無関係だったら」の世界を考える
  • 期待度数 ― その「無関係な世界」での理論値を計算する
  • カイ二乗検定 ― そもそも関連があるのかを統計的に確かめる

この3つがわかると、コレスポンデンス分析が「何のズレを、どう可視化しているのか」がクリアになります。

ライブラリと前回のデータ

まずは前回と同じライブラリとデータを用意します。

今回は統計検定のために `scipy.stats` も追加でインポートします。

以下、コードです。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
from scipy import stats

plt.rcParams['figure.figsize'] = [10, 8]
sns.set_style("whitegrid")
np.random.seed(42)

 

続けて、前回と同じ「学部 × メニュー」のクロス集計表を作ります。

以下、コードです。

# 学部（行）× メニュー（列）のクロス集計表
data = {
    'カレー':   [45, 30, 25, 35],
    'ラーメン': [40, 25, 20, 30],
    'パスタ':   [20, 35, 40, 25],
    '定食':     [35, 30, 25, 40],
    'サラダ':   [10, 30, 40, 20]
}
index = ['工学部', '経済学部', '文学部', '理学部']

cross_table = pd.DataFrame(data, index=index)

print("【クロス集計表（観測度数）】")
print(cross_table)
print(f"\n合計人数: {cross_table.values.sum()}人")

 

以下、実行結果です。

【クロス集計表（観測度数）】
      カレー  ラーメン  パスタ  定食  サラダ
工学部    45    40   20  35   10
経済学部   30    25   35  30   30
文学部    25    20   40  25   40
理学部    35    30   25  40   20

合計人数: 600人

 

この表の数字（実際に観測された人数）を観測度数と呼びます。

今回のキーワードは、この観測度数と、これから計算する期待度数の「ズレ」です。

 

ステップ1：「独立」ってどういう状態？

　サイコロのたとえで考える

「学部とメニュー選択が独立である」とは、一言でいえば「学部を知っても、その学生がどのメニューを選ぶかの予測に役立たない」という状態です。

サイコロの例で考えるとわかりやすいでしょう。

赤いサイコロと青いサイコロを同時に振るとき、赤いサイコロの出目が「3」だったとしても、青のサイコロの出目には何の影響もありません。

これが独立です。

食堂の例に戻ると、「独立」とは……

  • 工学部だろうが文学部だろうが、カレーを選ぶ確率は同じ
  • パスタを選ぶ確率も同じ

……という状態です。

学部ごとに好みの偏りがまったくない世界を想像してください。

 

　もし独立だったら、表はどうなるはず？

このことを確かめるために、まずはクロス集計表の周辺度数（行と列の合計）を計算してみましょう。

周辺度数は、「各学部の総回答数」と「各メニューの総選択数」に相当します。

以下、コードです。

# 各学部の合計
row_totals = cross_table.sum(axis=1)  
# 各メニューの合計
col_totals = cross_table.sum(axis=0)  
# 全体の合計
grand_total = cross_table.values.sum() 

print("【行の合計（学部別の回答数）】")
print(row_totals)
print(f"\n【列の合計（メニュー別の選択数）】")
print(col_totals)
print(f"\n総計: {grand_total}人")

 

以下、実行結果です。

【行の合計（学部別の回答数）】
工学部     150
経済学部    150
文学部     150
理学部     150
dtype: int64

【列の合計（メニュー別の選択数）】
カレー     135
ラーメン    115
パスタ     120
定食      130
サラダ     100
dtype: int64

総計: 600人

 

この周辺度数が、次のステップで「期待度数」を計算するための材料になります。

 

ステップ2：期待度数を計算する

　期待度数の考え方

期待度数とは、「もし2つの変数が完全に独立（無関係）だったら、各セルの値はいくつになるはずか」を表す理論値です。

考え方はシンプルです。

全600人のうち工学部は150人なので、工学部の割合は 150/600 = 25% です。

また、カレーは全体で135人に選ばれているので、カレーの割合は 135/600 = 22.5% です。

もし学部とメニューが独立なら、「工学部 かつ カレー」の人数は、この2つの割合を掛け算して全体に戻すだけで求まります。

$$
\text{期待度数} = \frac{\text{行の合計} \times \text{列の合計}}{\text{総計}}
$$

工学部×カレーの場合は 150 \times 135 \div 600 = 33.75 人です。

それでは全セルの期待度数をまとめて計算してみましょう。

np.outer() を使えば、行の合計と列の合計の「外積」（すべての組み合わせの掛け算）を一度に計算できます。

以下、コードです。

# 期待度数 = (行の合計 × 列の合計) / 総計
expected = (
    np.outer(row_totals, col_totals) 
    / grand_total
)
expected_df = pd.DataFrame(
    expected,
    index=cross_table.index,
    columns=cross_table.columns
)

print("【期待度数（独立の場合の理論値）】")
print(expected_df.round(2))

 

以下、実行結果です。

【期待度数（独立の場合の理論値）】
        カレー   ラーメン   パスタ    定食   サラダ
工学部   33.75    28.75    30.0    32.5   25.0
経済学部  33.75    28.75    30.0    32.5   25.0
文学部   33.75    28.75    30.0    32.5   25.0
理学部   33.75    28.75    30.0    32.5   25.0

 

各セルに「学部とメニューが無関係だったら何人になるはずか」の理論値が入った表が得られます。

これが期待度数表です。

 

　観測度数と期待度数を並べて比較する

数字だけでは違いがつかみにくいので、観測度数と期待度数を色で比較してみましょう。

2つのヒートマップを横に並べて表示します。

以下、コードです。

fig, axes = plt.subplots(2, 1, figsize=(10, 12))

# 観測度数（実際のデータ）のヒートマップ
sns.heatmap(
    cross_table, 
    annot=True, fmt='d', cmap='YlOrRd',
    linewidths=0.5, ax=axes[0], 
    vmin=10, vmax=50
)
axes[0].set_title('観測度数（実際のデータ）')

# 期待度数（独立の場合の理論値）のヒートマップ
sns.heatmap(
    expected_df, 
    annot=True, fmt='.1f', cmap='YlOrRd',
    linewidths=0.5, ax=axes[1], 
    vmin=10, vmax=50
)
axes[1].set_title('期待度数（独立の場合の理論値）')

plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

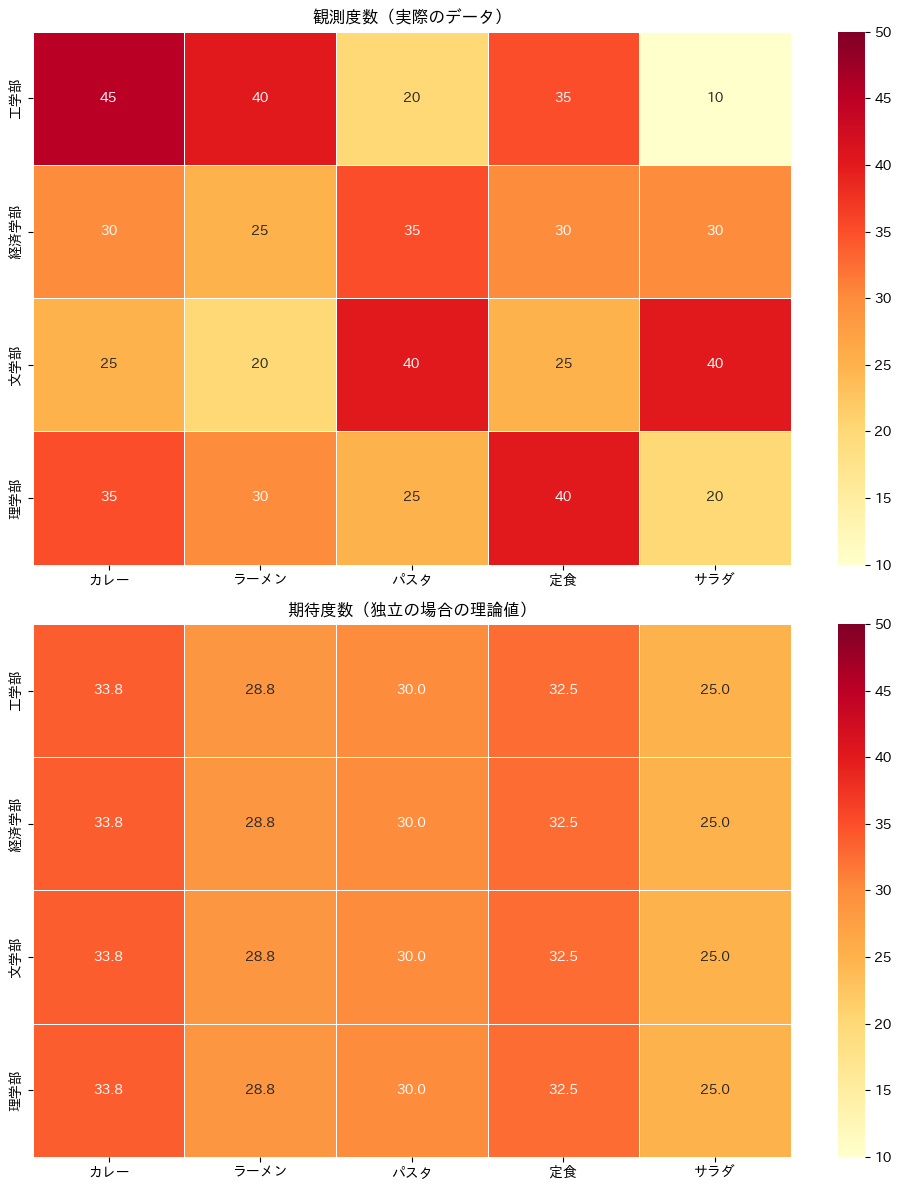
2つのヒートマップを見比べてみてください。

期待度数（下）は色のムラが少なく、どのセルも似たような値になっていることがわかります。

これが「学部とメニューが無関係な世界」の姿です。

一方、観測度数（上）にはメリハリがあり、学部によってメニューの好みに偏りがあることが見て取れます。

 

ステップ3：「ズレ」を数値化する ― 残差

　観測度数 − 期待度数 ＝ 残差

観測度数と期待度数の差を残差（residual）と呼びます。

残差が正なら「独立の仮定より多い＝好まれている」、負なら「独立の仮定より少ない＝避けられている」ことを意味します。

以下、コードです。

# 残差 = 観測度数 − 期待度数
residuals = cross_table - expected_df

print("【残差（観測度数 − 期待度数）】")
print(residuals.round(2))

 

以下、実行結果です。

【残差（観測度数 − 期待度数）】
        カレー   ラーメン   パスタ   定食   サラダ
工学部   11.25   11.25   -10.0    2.5   -15.0
経済学部  -3.75   -3.75    5.0   -2.5     5.0
文学部   -8.75   -8.75    10.0   -7.5    15.0
理学部    1.25    1.25    -5.0    7.5    -5.0

 

たとえば「工学部×カレー」は正の値、「工学部×サラダ」は負の値になるはずです。

工学部の学生はカレーを期待以上に選び、サラダは期待以下しか選んでいない、ということです。

 

　残差のヒートマップで「ズレの地図」を描く

残差を色で可視化すると、「どの組み合わせが独立からズレているか」が一目でわかります。

赤系（正）が「期待より多い」、青系（負）が「期待より少ない」を表します。

以下、コードです。

plt.figure(figsize=(10, 6))

# 残差のヒートマップ
sns.heatmap(
    residuals, 
    annot=True, fmt='.1f', cmap='RdBu_r',
    center=0, linewidths=0.5,
    cbar_kws={'label': '残差（観測 − 期待）'}
)
plt.title('残差のヒートマップ：独立性からのズレ')
plt.xlabel('メニュー')
plt.ylabel('学部')
plt.tight_layout()
plt.show()

以下、実行結果です。

 

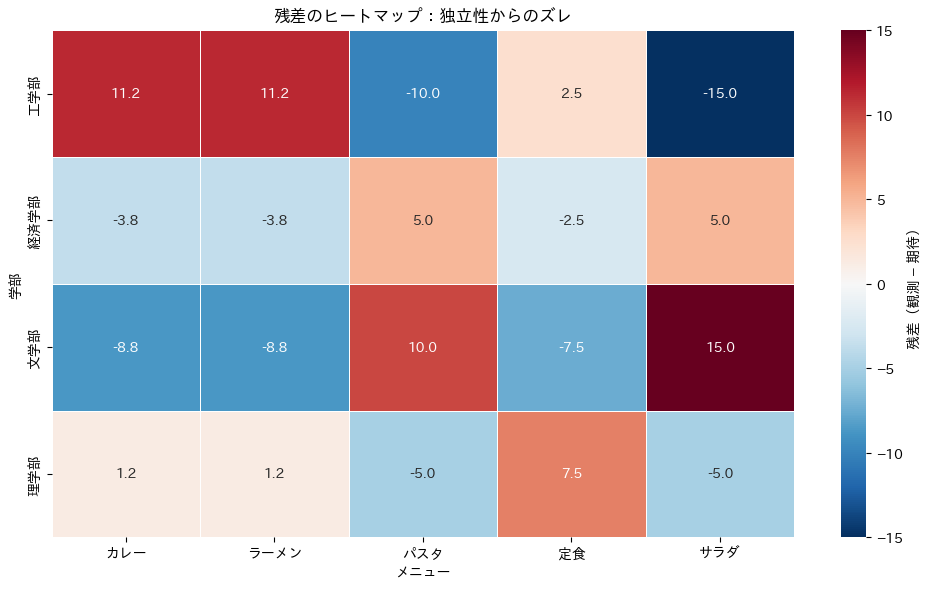
このヒートマップを眺めると、前回のコレスポンデンス分析マップで「近くにあった」学部とメニューのペアは、ここでも赤く表示されていることがわかると思います。

つまり、コレスポンデンス分析マップの「近さ」は、この残差の情報を低次元に圧縮したものなのです。

 

ステップ4：残差を「公平に」比較する ― 標準化残差

　生の残差の問題点

先ほどの残差には一つ弱点があります。

周辺度数（合計人数）が大きいセルほど、残差の絶対値も大きくなりやすいのです。

たとえば工学部（150人）と経済学部（150人）は同じ合計なので比較しやすいですが、もし合計が大きく違う学部があれば、残差の単純比較は不公平になります。

この問題を解消するのが標準化残差です。

各残差を期待度数の平方根で割ることで、スケールを揃えます。
$$
\text{標準化残差} = \frac{\text{観測度数} – \text{期待度数}}{\sqrt{\text{期待度数}}}
$$

以下、コードです。

# 標準化残差（ピアソン残差）
standardized_residuals = (
    (cross_table - expected_df) 
    / np.sqrt(expected_df)
)

print("【標準化残差】")
print(standardized_residuals.round(4))

 

以下、実行結果です。

【標準化残差】
         カレー    ラーメン     パスタ      定食  サラダ
工学部    1.9365   2.0981   -1.8257    0.4385  -3.0
経済学部  -0.6455  -0.6994   0.9129   -0.4385   1.0
文学部   -1.5062  -1.6319    1.8257   -1.3156   3.0
理学部    0.2152   0.2331   -0.9129    1.3156  -1.0

 

標準化することで、どのセルの「ズレ」も同じ基準で比較できるようになりました。

絶対値が大きいセルほど、独立の仮定から強くズレていることを意味します。目安として絶対値が2を超えると「かなり特徴的な偏り」と考えてよいでしょう。

実はこの標準化残差こそが、コレスポンデンス分析で特異値分解（SVD）にかけられる行列の正体です。

第3回で詳しく扱いますが、「コレスポンデンス分析は標準化残差の構造を低次元に要約している」と覚えておくと、全体の見通しがよくなります。

ヒートマップでも確認しておきましょう。

以下、コードです。

plt.figure(figsize=(10, 6))
# 標準化残差のヒートマップ
sns.heatmap(
    standardized_residuals, 
    annot=True, fmt='.2f',
    cmap='RdBu_r', center=0, linewidths=0.5,
    cbar_kws={'label': '標準化残差'}
)
plt.title('標準化残差のヒートマップ')
plt.xlabel('メニュー')
plt.ylabel('学部')
plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

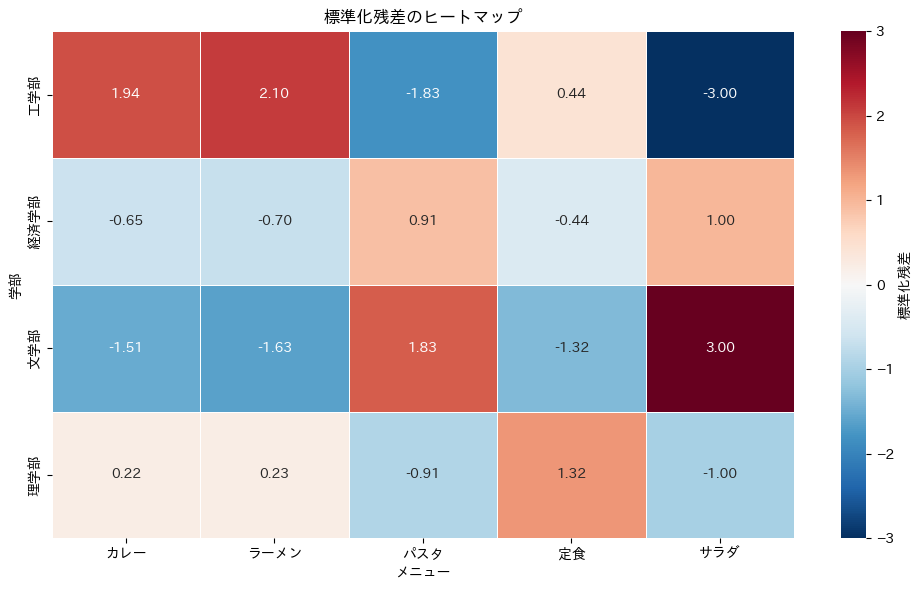
先ほどの生の残差ヒートマップと見比べてみてください。

パターン自体は似ていますが、値のスケールが統一されたことで、「どのズレが本当に大きいのか」がより正確に読み取れるようになっています。

 

ステップ5：カイ二乗検定 ― 「そもそも関連はあるの？」を確かめる

　なぜ検定が必要なのか

ここまで残差を見てきましたが、一つ注意が必要です。

たとえ2つの変数が本当に独立（無関係）であっても、有限のサンプルデータでは偶然のバラつきによって残差がゼロにならないことがあります。

たまたまカレーが多く選ばれた日にアンケートを取っただけかもしれません。

そこで、「この残差のパターンは、偶然では説明できないほど大きいのか？」を客観的に判定する方法がカイ二乗検定（\chi^2 検定）です。

 

　カイ二乗統計量の計算

カイ二乗統計量は、先ほどの標準化残差を二乗して全セル分足し合わせたものです。

$$
\chi^2 = \sum_{i,j} \frac{(O_{ij} – E_{ij})^2}{E_{ij}}
$$

ここで O_{ij} は観測度数、E_{ij} は期待度数です。

この値が大きいほど「独立とは言えない（＝関連がある）」と判断できます。

まずは手計算で値を確かめてみましょう。

以下、コードです。

# カイ二乗統計量を手計算で求める
chi2_manual = (
    (cross_table - expected_df) ** 2 
    / expected_df
).values.sum()

print(f"カイ二乗統計量（手計算）: {chi2_manual:.4f}")

 

以下、実行結果です。

カイ二乗統計量（手計算）: 46.2697

 

　scipy を使った検定

手計算で仕組みを確認できたところで、`scipy.stats.chi2_contingency()` を使って正式な検定を行います。

この関数はカイ二乗統計量に加えて、p値や自由度もまとめて返してくれます。

以下、コードです。

chi2, p_value, dof, expected_scipy = stats.chi2_contingency(
    cross_table)

print(f"カイ二乗統計量: {chi2:.4f}")
print(f"自由度:         {dof}")
print(f"p値:            {p_value:.6f}")

 

以下、実行結果です。

カイ二乗統計量: 46.2697
自由度:         12
p値:            0.000006

 

結果の読み方を説明します。

p値は「本当は独立なのに、たまたまこれだけ大きなカイ二乗統計量が出る確率」を表します。

一般に p値が 0.05 未満であれば「偶然とは考えにくい＝学部とメニューに有意な関連がある」と結論づけます。

今回のデータでは p値が 0.05 を大きく下回るので、「学部とメニュー選択には統計的に有意な関連がある」と判断でき、コレスポンデンス分析を進める意味があると確認できます。

ここで覚えておいてほしい重要なポイントがあります。

コレスポンデンス分析を実行する前に、必ずカイ二乗検定を行うべきです。

もし検定で有意な関連が認められなければ、コレスポンデンス分析のマップに描かれる構造は「たまたまの偶然」に過ぎず、信頼できません。

カイ二乗検定はいわば「分析のゴーサイン」を出す事前チェックの役割を果たします。

 

ステップ6：総イナーシャ ― カイ二乗とコレスポンデンス分析をつなぐ橋

　総イナーシャとは

コレスポンデンス分析にはイナーシャ（慣性, inertia）という重要な概念があります。

総イナーシャは、クロス集計表全体の「独立からのズレの大きさ」を一つの数値にまとめたもので、実はカイ二乗統計量を総度数で割っただけのシンプルな関係があります。
$$
\text{総イナーシャ} = \frac{\chi^2}{n}
$$

ここで n は総度数（全体の人数）です。

以下、コードです。

total_inertia = chi2 / grand_total

print(f"カイ二乗統計量: {chi2:.4f}")
print(f"総度数:         {grand_total}")
print(f"総イナーシャ:   {total_inertia:.4f}")

 

以下、実行結果です。

カイ二乗統計量: 46.2697
総度数:         600
総イナーシャ:   0.0771

 

総イナーシャの値が大きいほど、2つの変数間の関連が強いことを意味します。

そしてコレスポンデンス分析は、この総イナーシャを各次元に分配する作業です。

「第1次元が全体の何%を説明しているか」が寄与率であり、第1回で見た「次元1の寄与率: ○○%」という数字の正体はここにあります。

 

　第1回のマップとつなげて理解する

ここで、前回の分析結果と今回の内容をつなげてみましょう。

princeで改めてコレスポンデンス分析を実行し、イナーシャの分配を確認します。

以下、コードです。

import prince

# コレスポンデンス分析のインスタンスを作成
ca = prince.CA(n_components=2, random_state=42)
# データ（クロス集計結果）を与えて学習
ca = ca.fit(cross_table)

# 各次元の寄与率と、対応するイナーシャを確認
for i, pct in enumerate(ca.percentage_of_variance_):
    inertia_i = total_inertia * pct / 100
    print(
        f"第{i+1}次元: "
        f"寄与率 {pct:.1f}%（"
        f"イナーシャ {inertia_i:.4f}）"
    )

print(
    "\n累積寄与率: "
    f"{sum(ca.percentage_of_variance_[:2]):.1f}%"
)

 

以下、実行結果です。

第1次元: 寄与率 95.7%（イナーシャ 0.0738）
第2次元: 寄与率 4.1%（イナーシャ 0.0032）

累積寄与率: 99.8%

 

総イナーシャという「ズレの総量」を各次元に配分し、上位2次元で十分な割合を説明できていれば、2次元マップの信頼性が高いと判断できます。

目安として累積寄与率が70%以上あれば十分です。

 

まとめ

今回学んだことを、一枚の流れ図として整理しておきましょう。

クロス集計表（観測度数）
↓
期待度数の計算
（もし独立だったら何人？）
↓
残差 = 観測度数 − 期待度数
（独立からのズレ）
↓
標準化残差 = 残差 / √期待度数
（スケールを揃えて公平に比較）
↓
カイ二乗検定 → 関連は有意か？
（分析のゴーサイン）
↓
総イナーシャ = χ² / n
（ズレの総量）
↓
コレスポンデンス分析（SVD）
（次元ごとにイナーシャを分配 → マップ化）
↓
2次元マップで関係性を可視化！

今回のポイントを改めてまとめます。

独立性と期待度数について。「2つの変数が独立」とは、一方を知っても他方の予測に役立たない状態のことです。期待度数は「独立だった場合の理論値」であり、\text{行の合計} \times \text{列の合計} \div \text{総計} で求まります。

残差と標準化残差について。観測度数と期待度数の差（残差）が、独立からの「ズレ」を表します。標準化残差はスケールを揃えたもので、コレスポンデンス分析が実際にSVDで分解する対象の行列そのものです。

カイ二乗検定について。コレスポンデンス分析の前に必ず行う事前チェックです。p値 < 0.05 なら「有意な関連あり」と判断でき、分析を進めるゴーサインになります。

総イナーシャについて。カイ二乗統計量を総度数で割ったもので、「ズレの総量」を表します。コレスポンデンス分析は、この総イナーシャを各次元に分配する操作です。

今回、コレスポンデンス分析が「標準化残差の構造を低次元に要約するもの」であることがわかりました。では、その「要約」は具体的にどんな数学で実現されているのでしょうか？

次回の第3回では、いよいよコレスポンデンス分析の心臓部である特異値分解（SVD）に踏み込みます。

対応行列、行プロファイル、標準化残差行列を順に計算し、SVDによって座標が生まれる過程をPythonで一歩ずつ追いかけます。「なぜ2次元マップに落とせるのか」を数式とコードの両面から納得できる回になりますので、お楽しみに。