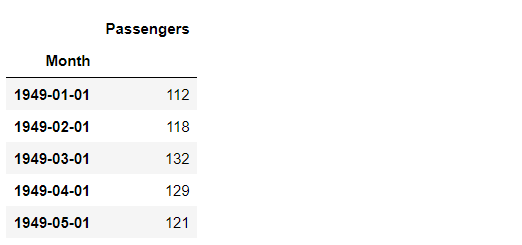Pythonで時系列解析・超入門（その2）

指数平滑化法（Exponential Smoothing model）で予測する方法

14331
Pythonで時系列解析・超入門（その2）指数平滑化法（Exponential Smoothing model）で予測する方法

ビジネスの世界で発生するデータの多くは、時間的概念の紐付いた時系列データです。

例えば、売上金額や受注件数、販売量、生産量、在庫量、PV（ページビュー）数、見込み顧客数、既存顧客数、離反顧客数、故障件数、広告宣伝費、人件費、従業員数、離職者数、などなど。

前回、「時系列データに対する3つの特徴把握方法（成分分解・定常性・コレログラム）」というお話しをしました。

Pythonで時系列解析・超入門（その1）時系列データに対する3つの特徴把握方法（変動成分・定常性・コレログラム）

今回は、「指数平滑化法（Exponential Smoothing model）で予測する方法」について説明していきます。

指数平滑化法は、ARIMA系のモデルと並ぶ代表的な古典的な時系列モデルです。

準備（必要なライブラリーとデータの読み込み）

必要なライブラリーを読み込みます。

以下、コードです。

# ライブラリーの読み込み
import pandas as pd
import numpy as np

from statsmodels.tsa.holtwinters import SimpleExpSmoothing
from statsmodels.tsa.holtwinters import Holt
from statsmodels.tsa.holtwinters import ExponentialSmoothing

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error

import matplotlib.pyplot as plt

plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

 

次に、データセットを読み込みます。

今回利用する時系列データのデータセットは、Airline Passengers（飛行機乗客数）は、Box and Jenkins (1976) の有名な時系列データです。サンプルデータとして、よく利用されます。

弊社のHPからもダウンロードできます。

弊社のHP上のURLからダウンロード
https://www.salesanalytics.co.jp/591h

では、データセットを読み込みます。

以下、コードです。

# データセットの読み込み
url='https://www.salesanalytics.co.jp/591h' #データセットのあるURL
df=pd.read_csv(url,                      #読み込むデータのURL
               index_col='Month',        #変数「Month」をインデックスに設定
               parse_dates=True)         #インデックスを日付型に設定

df.head() #確認

 

以下、実行結果です。

 

グラフ化し確認します。

以下、コードです。

# プロット
df.plot()
plt.title('Passengers')                            #グラフタイトル
plt.ylabel('Monthly Number of Airline Passengers') #タテ軸のラベル
plt.xlabel('Month')                                #ヨコ軸のラベル
plt.show()

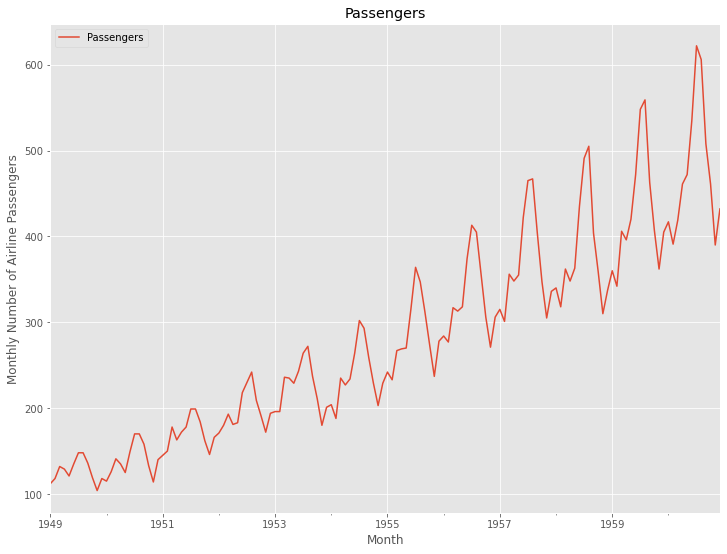
以下、実行結果です。

 

見るからに、トレンド成分と季節成分がありそうです。どうすれば定常状態になるかを検討することで、見当をつけることができます。前回扱っていますので、以下の前回の記事を参考にして頂ければと思います。

 

予測モデルを作ってテストをしていきますので、データセットを学習データとテストデータに分割します。テストデータの期間は直近12ヶ月間で、それより前の期間が学習データです。

以下、コードです。

# 学習データとテストデータ（直近12ヶ月間）に分割
train = df.iloc[:-12, :] #学習データ
test = df.iloc[-12:, :]  #テストデータ

 

学習データで予測モデルを構築し、構築した予測モデルをテストデータで予測精度検証します。

 

予測精度の評価指標

今回の予測精度の評価指標は、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。 

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • n ・・・実測値・予測値の数

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

今回検討するモデル

今回検討するのは、以下の3つのモデルです。

  • Simple Exponential Smoothing model（単純指数平滑化法モデル）
  • Holt’s Linear Smoothing model（Holtの線形指数平滑法モデル）
  • Holt-Winter’s Seasonal Smoothing model（ホルト-ウィンターズ法モデル）

 

Simple Exponential Smoothing model
（単純指数平滑化法モデル）

Simple Exponential Smoothing model（単純指数平滑化法モデル）の特徴です。

  • トレンド成分：なし
  • 季節成分：なし

トレンド成分も季節成分もなさそうな、時系列データをモデル化する手法です。

 

数式で表現すると、時系列データ y_1,y_2,\cdots,y_n に対し、以下のようになります。

\hat{y}_{t+1} = \alpha {y}_{t} + (1 - \alpha ) \hat{y}_{t}
\hat{y}_{t+1} は 1 期先の予測値です。

 

では、学習データでモデルを構築します。

以下、コードです。

# モデルの学習
SES_model = SimpleExpSmoothing(train)
SES_model_fit = SES_model.fit(smoothing_level=0.5)

 

構築したモデルをテストデータで精度検証します。

以下、コードです。

# テストデータで精度検証
SES_pred = SES_model_fit.forecast(12) #予測

print('RMSE:')
print(np.sqrt(mean_squared_error(test, SES_pred)))
print('MAE:')
print(mean_absolute_error(test, SES_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(test, SES_pred))

 

以下、実行結果です。

 

グラフで確認してみます。

以下、コードです。

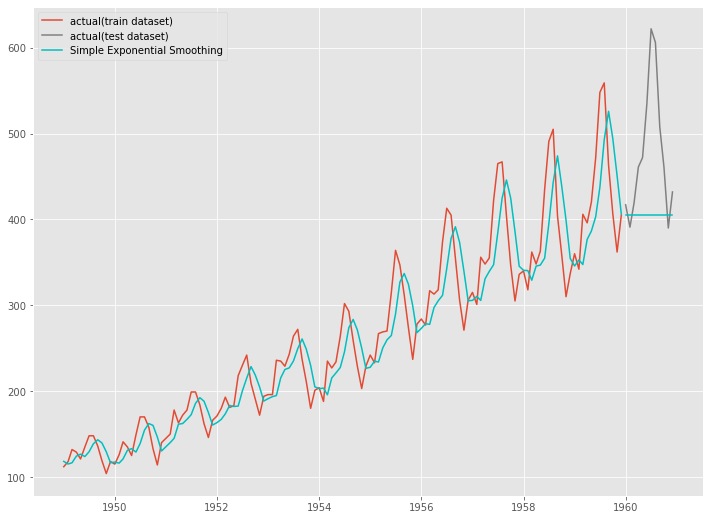
# グラフ化
fig, ax = plt.subplots()
ax.plot(train.index, train.values, label="actual(train dataset)")
ax.plot(test.index, test.values, label="actual(test dataset)", color="gray")
ax.plot(train.index, SES_model_fit.fittedvalues, color="c")
ax.plot(test.index, SES_pred, label="Simple Exponential Smoothing", color="c") 
plt.legend()

 

以下、実行結果です。

 

Holt’s Linear Smoothing model
（Holtの線形指数平滑法モデル）

Holt’s Linear Smoothing model（Holtの線形指数平滑法モデル）の特徴です。

  • トレンド成分：あり
  • 季節成分：なし

トレンド成分はありそうだが、季節成分がなさそうな時系列データをモデル化する手法です。

 

数式で表現すると、時系列データ y_1,y_2,\cdots,y_n に対し、以下のようになります。

\hat{y}_{t+h} =  l_{t} + h b_{t}  l_{t} = \alpha y_{t} + (1-\alpha) (l_{t-1} + b_{t-1}) b_{t} = \beta (l_{t} - l_{t-1}) + (1-\beta) b_{t-1}
\hat{y}_{t+h} は h 期先の予測値です。

 

では、学習データでモデルを構築します。

以下、コードです。

# モデルの学習
Holt_model = Holt(train)
Holt_model_fit = Holt_model.fit(smoothing_level=.3,
                                smoothing_trend=.2)

 

構築したモデルをテストデータで精度検証します。

以下、コードです。

# テストデータで精度検証
Holt_pred = Holt_model_fit.forecast(12) #予測

print('RMSE:')
print(np.sqrt(mean_squared_error(test, Holt_pred)))
print('MAE:')
print(mean_absolute_error(test, Holt_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(test, Holt_pred))

 

以下、実行結果です。

 

グラフで確認してみます。

以下、コードです。

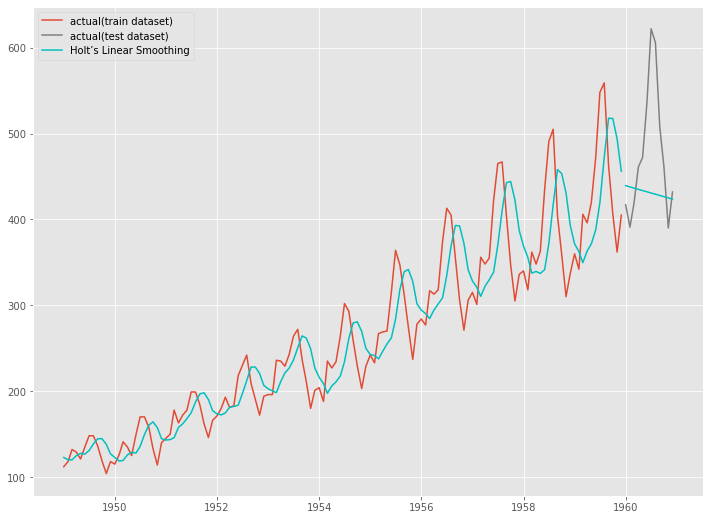
# グラフ化
fig, ax = plt.subplots()
ax.plot(train.index, train.values, label="actual(train dataset)")
ax.plot(test.index, test.values, label="actual(test dataset)", color="gray")
ax.plot(train.index, Holt_model_fit.fittedvalues, color="c")
ax.plot(test.index, Holt_pred, label="Holt’s Linear Smoothing", color="c") 
plt.legend()

 

以下、実行結果です。

 

Holt-Winter’s Seasonal Smoothing model
（ホルト-ウィンターズ法モデル）

Holt-Winter’s Seasonal Smoothing model（ホルト-ウィンターズ法モデル）の特徴です。

  • トレンド成分：あり（なしにもできる）
  • 季節成分：あり（なしにもできる）

Holt-Winter’s Seasonal Smoothing model（ホルト-ウィンターズ法モデル）は、トレンド成分を考慮したりしなかったり、季節成分を考慮したりしなかったりと、非常に使い勝手がいいです。

 

数式で表現すると、時系列データ y_1,y_2,\cdots,y_n に対し、以下のようになります。

\hat{y}_{t+h} =  l_{t} + h b_{t} + S_{t-m+h_m^+}  l_{t} = \alpha (y_{t} - S_{t-m}) + (1-\alpha) (l_{t-1} + b_{t-1}) b_{t} = \beta (l_{t} - l_{t-1}) + (1-\beta) b_{t-1} S_{t} = \gamma (y_{t} - l_{t} - b_{t-1}) + (1-\gamma) S_{t-m}
\hat{y}_{t+h} は h 期先の予測値です。ちなみに、mは季節成分の周期で、h_m^+ = \lfloor (h-1) \mod m \rfloor +1 です。\mod は余りを取得する剰余演算で、 \lfloor x \rfloor は x 以下の最大の整数を返す床関数です。

 

では、学習データでモデルを構築します。

以下、コードです。

# モデルの学習
HW_model = ExponentialSmoothing(train,
                                trend = 'additive',    #加法
                                seasonal = 'additive', #加法
                                seasonal_periods = 12)
HW_model_fit = HW_model.fit()

 

構築したモデルをテストデータで精度検証します。

以下、コードです。

# テストデータで精度検証
HW_pred = HW_model_fit.forecast(12) #予測

print('RMSE:')
print(np.sqrt(mean_squared_error(test, HW_pred)))
print('MAE:')
print(mean_absolute_error(test, HW_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(test, HW_pred))

 

以下、実行結果です。

 

グラフで確認してみます。

以下、コードです。

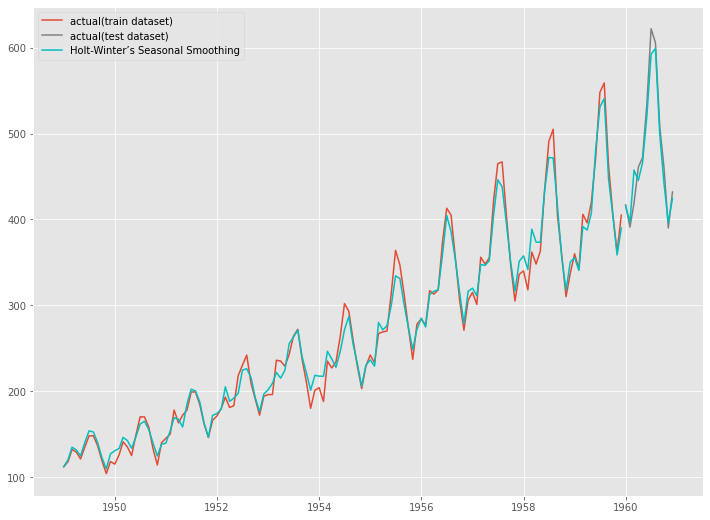
# グラフ化
fig, ax = plt.subplots()
ax.plot(train.index, train.values, label="actual(train dataset)")
ax.plot(test.index, test.values, label="actual(test dataset)", color="gray")
ax.plot(train.index, HW_model_fit.fittedvalues, color="c")
ax.plot(test.index, HW_pred, label="Holt-Winter’s Seasonal Smoothing", color="c") 
plt.legend()

 

以下、実行結果です。

 

次回

今回は、「指数平滑化法（Exponential Smoothing model）で予測する方法」について説明しました。

次回は、「ARIMA系モデルで予測する方法」について説明していきます。

Pythonで時系列解析・超入門（その3）ARIMA系モデルで予測する方法