ディープラーニングは、近年急速に発展し、さまざまな分野で応用されている技術です。
画像認識や自然言語処理、音声認識など、多岐にわたる分野で驚異的な成果を上げています。
今回は、TensorFlowという強力なライブラリを使って、ディープラーニングを始めるためのステップを解説していきます。
ディープラーニングの基本概念から始め、実際にモデルを構築し、トレーニング、評価、さらには応用方法まで、説明していきます。
生まれて初めての方にも安心して学べるよう、具体的なコード例とともに進めていきますので、ぜひ一緒にディープラーニングの世界に踏み出しましょう。
Contents
はじめに
ディープラーニングの概要
ディープラーニングは、機械学習の一分野であり、ニューラルネットワークを用いてデータから複雑なパターンを学習する手法です。
従来の機械学習アルゴリズムと異なり、ディープラーニングは多層のニューラルネットワークを使用するため、「ディープ(深層)」という名前が付いています。
これにより、画像、音声、テキストなどの高度なデータを処理し、驚異的な精度で予測や分類を行うことができます。
ディープラーニングの主な特徴としては、以下の点が挙げられます。
自動特徴抽出
ディープラーニングはデータから自動的に特徴を抽出し、手動での特徴エンジニアリングを大幅に減少させます。ただ、減少するだけで無くなるわけではありません。
高い汎化性能
膨大なデータを使用することで、高い汎化性能を発揮し、新しいデータにも強い適応力を持ちます。ただ、時間が掛かります。
並列処理の利用
GPUを活用することで、大規模なデータの処理を効率的に行うことができます。ただ、処理を効率的に行ったとしても、時間の掛かるものは掛かります。
TensorFlowの役割と特徴
TensorFlowは、Googleが開発したオープンソースのディープラーニングライブラリです。
強力で柔軟なAPIを提供し、研究者やエンジニアがディープラーニングモデルを簡単に構築、トレーニング、評価できるように設計されています。
以下はTensorFlowの主な特徴です。
豊富なタスクに対応
画像認識、自然言語処理、音声認識など、多岐にわたるタスクに対応できます。
高いパフォーマンス
GPUやTPUなどのハードウェアアクセラレーションを活用し、大規模なデータセットを効率的に処理します。
柔軟性と拡張性
モジュラー設計により、ユーザーは自身のニーズに合わせてカスタマイズや拡張が可能です。既存のモデルに新しい層を追加したり、独自の損失関数を定義することも容易です。
活発なコミュニティ
世界中の研究者や開発者が参加する活発なコミュニティが存在し、多くのリソースやサポートが提供されています。
TensorFlowのインストール
TensorFlowをインストールします。
以下、コードです。
pip install tensorflow
TensorFlowが正しくインストールされたかを確認します。
Pythonを開いて以下のコードを実行します。
import tensorflow as tf print(tf.__version__)
TensorFlowのバージョンが表示されれば、インストールは成功です。
データセットの準備
サンプルデータの準備から始めます。
ここでは、アヤメ(Iris)のデータセットを使用します。このデータセットは、ディープラーニングの基本的な例としてよく使用されます。
次に、データの前処理を行い、トレーニングセットとテストセットに分割します。
データの読み込みと確認
まず、IrisデータセットをPandasを用いて読み込み、データの概要を確認します。
以下、コードです。
import pandas as pd from sklearn.datasets import load_iris # Irisデータセットの読み込み iris = load_iris() data = pd.DataFrame(iris.data, columns=iris.feature_names) data['target'] = iris.target # データの確認 print(data.head()) print(data.info()) print(data.describe())
以下、実行結果です。
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
target
0 0
1 0
2 0
3 0
4 0
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 sepal length (cm) 150 non-null float64
1 sepal width (cm) 150 non-null float64
2 petal length (cm) 150 non-null float64
3 petal width (cm) 150 non-null float64
4 target 150 non-null int64
dtypes: float64(4), int64(1)
memory usage: 6.0 KB
None
sepal length (cm) sepal width (cm) petal length (cm) \
count 150.000000 150.000000 150.000000
mean 5.843333 3.057333 3.758000
std 0.828066 0.435866 1.765298
min 4.300000 2.000000 1.000000
25% 5.100000 2.800000 1.600000
50% 5.800000 3.000000 4.350000
75% 6.400000 3.300000 5.100000
max 7.900000 4.400000 6.900000
petal width (cm) target
count 150.000000 150.000000
mean 1.199333 1.000000
std 0.762238 0.819232
min 0.100000 0.000000
25% 0.300000 0.000000
50% 1.300000 1.000000
75% 1.800000 2.000000
max 2.500000 2.000000
特徴量のスケーリング
標準化を行い、すべての特徴量を同じスケールにします。
以下、コードです。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data.drop('target', axis=1))
# スケーリングされたデータをDataFrameに変換
scaled_data = pd.DataFrame(scaled_data, columns=iris.feature_names)
scaled_data['target'] = data['target']
print(scaled_data.head())
以下、実行結果です。
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \ 0 -0.900681 1.019004 -1.340227 -1.315444 1 -1.143017 -0.131979 -1.340227 -1.315444 2 -1.385353 0.328414 -1.397064 -1.315444 3 -1.506521 0.098217 -1.283389 -1.315444 4 -1.021849 1.249201 -1.340227 -1.315444 target 0 0 1 0 2 0 3 0 4 0
トレーニングセットとテストセットの分割
次に、データをトレーニングセット(train)とテストセット(test)に分割します。
以下、コードです。
from sklearn.model_selection import train_test_split
X = scaled_data.drop('target', axis=1)
y = scaled_data['target']
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.2,
random_state=42)
print(f'Training set size: {X_train.shape}')
print(f'Test set size: {X_test.shape}')
以下、実行結果です。
Training set size: (120, 4) Test set size: (30, 4)
モデルの構築
Kerasを用いてディープラーニングモデルを定義し、層の追加や調整、そして活性化関数の選択について説明します。
Kerasを用いたモデルの定義
KerasはTensorFlowの高レベルなAPIであり、Kerasを通じて簡単にニューラルネットワークをTensorFlowで構築することができます。
まず、基本的なモデルを定義しましょう。
以下、コードです。
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# モデルの定義
model = Sequential()
# 入力層と隠れ層の追加
model.add(
Dense(
units=10, activation='relu',
input_shape=(X_train.shape[1],)
)
)
# さらに隠れ層を追加
model.add(
Dense(units=10, activation='relu')
)
# 出力層の追加
model.add(
Dense(units=3, activation='softmax')
)
# モデルの概要を表示
model.summary()
以下、実行結果です。
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 10) 50
dense_2 (Dense) (None, 10) 110
dense_3 (Dense) (None, 3) 33
=================================================================
Total params: 193
Trainable params: 193
Non-trainable params: 0
_________________________________________________________________
ニューラルネットワークの各層は、ネットワーク全体の学習能力に大きな影響を与えます。このコードでは、入力層と2つの隠れ層、そして出力層を持つシンプルなモデルを構築しました。
- 入力層:
input_shapeパラメータは、入力データの形状を指定します。Irisデータセットでは、4つの特徴量があるため、input_shape=(4,)となります。 - 隠れ層: 隠れ層には、任意の数のユニット(ノード)を持つことができます。ここでは10ユニットを持つ隠れ層を2つ追加しています。活性化関数としてReLUを使用しています。
- 出力層: 出力層のユニット数は分類するクラスの数に対応します。Irisデータセットでは3つのクラス(setosa, versicolor, virginica)があるため、出力層のユニット数は3です。活性化関数としてソフトマックス関数を使用しています。
活性化関数は、各層の出力を非線形に変換するために使用されます。
以下に一般的な活性化関数をいくつか紹介します。
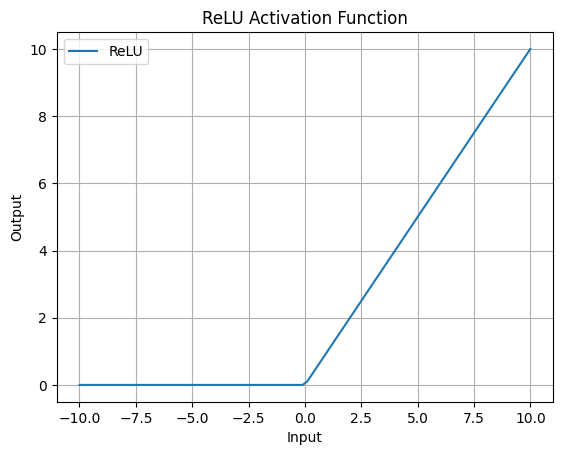
ReLU (Rectified Linear Unit)
隠れ層でよく使用される活性化関数で、負の値を0に変換し、正の値はそのまま通過させます。計算がシンプルで、勾配消失問題を緩和します。
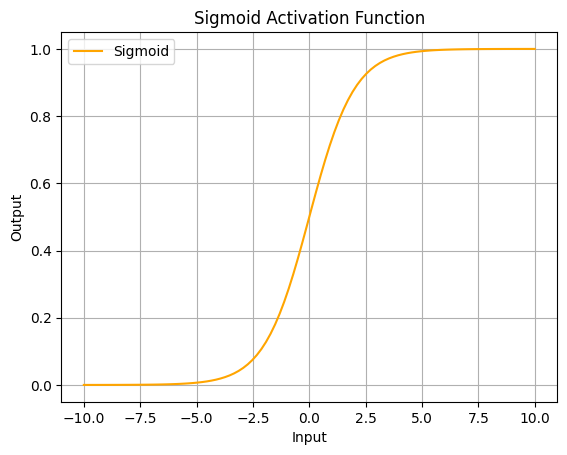
Sigmoid
出力を0から1の範囲に変換します。2クラス分類問題の出力層でよく使用されます。
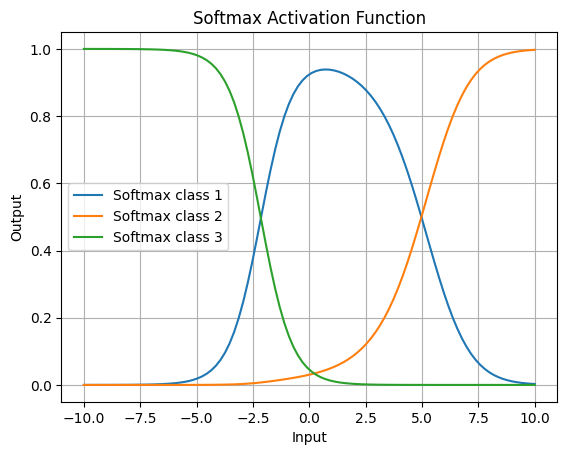
Softmax
複数クラス分類問題の出力層で使用され、出力を確率として解釈できるようにします。複数クラスの合計を1(100%)になるように調整する関数です。
モデルのコンパイル
モデルをコンパイルする必要があります。
モデルのコンパイルには、最適化アルゴリズムの設定、学習率と損失関数の設定、そして評価指標の選定しておく必要があります。
最適化アルゴリズムの設定
最適化アルゴリズムは、モデルの重みを更新するためのルールを定めます。
一般的な最適化アルゴリズムとして、以下のものがあります。
SGD (確率的勾配降下法)
SGDは、機械学習アルゴリズムの中で最も基本的な最適化手法の一つで、損失関数の勾配を計算し、その勾配の反対方向にパラメータを更新することで、損失関数を最小化します。
Adam
Adamは、確率的勾配降下法に基づく最適化アルゴリズムで、勾配の一階モーメントと二階モーメントの両方を利用し、学習率の調整を自動的に行い、収束を早めます。
RMSprop
RMSpropは、学習率を適応的に調整する最適化アルゴリズムで、勾配の二乗平均を利用して、各パラメータごとに学習率を調整します。
今回は、一般的によく使用されるAdamを使用します。
学習率と損失関数の設定
損失関数は、モデルの予測の誤差を測定するために使用されます。
分類問題では、一般的に以下の損失関数が使用されます。
- 二値分類:
binary_crossentropy - 多クラス分類:
categorical_crossentropyまたはsparse_categorical_crossentropy
Irisデータセットは多クラス分類問題なので、今回はsparse_categorical_crossentropyを使用します。
評価指標の選定
評価指標は、モデルの性能を評価するために使用されます。
一般的な評価指標には、以下のものがあります。
- accuracy: 正解率
- precision: 適合率
- recall: 再現率
今回は、最も分かりやすい正解率(accuracy)を使用します。
モデルのコンパイル
では、以上の設定でモデルをコンパイルします。
以下、コードです。
# モデルのコンパイル
model.compile(
optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
上記のコードでは、Adam最適化アルゴリズムを使用し、損失関数としてsparse_categorical_crossentropy、評価指標として正解率(accuracy)を設定しています。
これで、モデルのコンパイルが完了しました。
モデルのトレーニング
コンパイルしたモデルを用いてトレーニングを行います。
トレーニングにはバッチサイズとエポック数の設定をし、モデルをトレーニング(学習)します。このとき、トレーニングの進行状況をモニタリングします。
バッチサイズとエポック数の設定
バッチサイズ
- モデルが一度に処理するデータのサンプル数です。
- 小さすぎるとトレーニングが遅くなり、大きすぎるとメモリを大量に消費します。
- 一般的には32や64が使用されます。
エポック数
- トレーニングデータ全体を何回繰り返して学習するかを示します。
- エポック数が多すぎると過学習のリスクがあり、少なすぎると十分な学習ができません。
トレーニング(学習)
トレーニングデータを用いてモデルをトレーニング(学習)します。
以下、コードです。
# モデルのトレーニング(学習)
history = model.fit(
X_train, y_train,
validation_data=(X_test, y_test),
epochs=50,
batch_size=32)
上記のコードでは、以下の設定を行っています。
- トレーニングデータ(X_train, y_train)を指定
- テストデータ(X_test, y_test)を指定
- エポック数を50に設定
- バッチサイズを32に設定
以下、実行結果です。
Epoch 1/50 4/4 [==============================] - 0s 44ms/step - loss: 1.0195 - accuracy: 0.5083 - val_loss: 0.9661 - val_accuracy: 0.6667 Epoch 2/50 4/4 [==============================] - 0s 6ms/step - loss: 0.9993 - accuracy: 0.5500 - val_loss: 0.9428 - val_accuracy: 0.6667 Epoch 3/50 4/4 [==============================] - 0s 6ms/step - loss: 0.9785 - accuracy: 0.5667 - val_loss: 0.9204 - val_accuracy: 0.7000 Epoch 4/50 4/4 [==============================] - 0s 6ms/step - loss: 0.9583 - accuracy: 0.5833 - val_loss: 0.8990 - val_accuracy: 0.7333 Epoch 5/50 4/4 [==============================] - 0s 6ms/step - loss: 0.9391 - accuracy: 0.6167 - val_loss: 0.8773 - val_accuracy: 0.7667 Epoch 6/50 4/4 [==============================] - 0s 6ms/step - loss: 0.9203 - accuracy: 0.6250 - val_loss: 0.8555 - val_accuracy: 0.7667 Epoch 7/50 4/4 [==============================] - 0s 6ms/step - loss: 0.9006 - accuracy: 0.6500 - val_loss: 0.8341 - val_accuracy: 0.7667 Epoch 8/50 4/4 [==============================] - 0s 6ms/step - loss: 0.8813 - accuracy: 0.6583 - val_loss: 0.8132 - val_accuracy: 0.7667 Epoch 9/50 4/4 [==============================] - 0s 6ms/step - loss: 0.8612 - accuracy: 0.6750 - val_loss: 0.7925 - val_accuracy: 0.7667 Epoch 10/50 4/4 [==============================] - 0s 6ms/step - loss: 0.8430 - accuracy: 0.6917 - val_loss: 0.7712 - val_accuracy: 0.7667 Epoch 11/50 4/4 [==============================] - 0s 6ms/step - loss: 0.8231 - accuracy: 0.6833 - val_loss: 0.7505 - val_accuracy: 0.8000 Epoch 12/50 4/4 [==============================] - 0s 6ms/step - loss: 0.8038 - accuracy: 0.7000 - val_loss: 0.7304 - val_accuracy: 0.8667 Epoch 13/50 4/4 [==============================] - 0s 6ms/step - loss: 0.7848 - accuracy: 0.7083 - val_loss: 0.7107 - val_accuracy: 0.8667 Epoch 14/50 4/4 [==============================] - 0s 6ms/step - loss: 0.7667 - accuracy: 0.7333 - val_loss: 0.6912 - val_accuracy: 0.8667 Epoch 15/50 4/4 [==============================] - 0s 6ms/step - loss: 0.7486 - accuracy: 0.7667 - val_loss: 0.6721 - val_accuracy: 0.8667 Epoch 16/50 4/4 [==============================] - 0s 6ms/step - loss: 0.7306 - accuracy: 0.7667 - val_loss: 0.6536 - val_accuracy: 0.8667 Epoch 17/50 4/4 [==============================] - 0s 6ms/step - loss: 0.7137 - accuracy: 0.7750 - val_loss: 0.6357 - val_accuracy: 0.8667 Epoch 18/50 4/4 [==============================] - 0s 6ms/step - loss: 0.6973 - accuracy: 0.7833 - val_loss: 0.6182 - val_accuracy: 0.8667 Epoch 19/50 4/4 [==============================] - 0s 6ms/step - loss: 0.6811 - accuracy: 0.8000 - val_loss: 0.6015 - val_accuracy: 0.8667 Epoch 20/50 4/4 [==============================] - 0s 6ms/step - loss: 0.6652 - accuracy: 0.8083 - val_loss: 0.5853 - val_accuracy: 0.8667 Epoch 21/50 4/4 [==============================] - 0s 6ms/step - loss: 0.6499 - accuracy: 0.8083 - val_loss: 0.5695 - val_accuracy: 0.8667 Epoch 22/50 4/4 [==============================] - 0s 6ms/step - loss: 0.6354 - accuracy: 0.8083 - val_loss: 0.5540 - val_accuracy: 0.8667 Epoch 23/50 4/4 [==============================] - 0s 6ms/step - loss: 0.6212 - accuracy: 0.8167 - val_loss: 0.5393 - val_accuracy: 0.8667 Epoch 24/50 4/4 [==============================] - 0s 6ms/step - loss: 0.6068 - accuracy: 0.8167 - val_loss: 0.5252 - val_accuracy: 0.9000 Epoch 25/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5934 - accuracy: 0.8167 - val_loss: 0.5119 - val_accuracy: 0.9000 Epoch 26/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5804 - accuracy: 0.8167 - val_loss: 0.4990 - val_accuracy: 0.9000 Epoch 27/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5680 - accuracy: 0.8167 - val_loss: 0.4864 - val_accuracy: 0.9000 Epoch 28/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5558 - accuracy: 0.8250 - val_loss: 0.4741 - val_accuracy: 0.9000 Epoch 29/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5441 - accuracy: 0.8250 - val_loss: 0.4625 - val_accuracy: 0.9000 Epoch 30/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5333 - accuracy: 0.8250 - val_loss: 0.4515 - val_accuracy: 0.9000 Epoch 31/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5218 - accuracy: 0.8333 - val_loss: 0.4407 - val_accuracy: 0.9000 Epoch 32/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5112 - accuracy: 0.8333 - val_loss: 0.4307 - val_accuracy: 0.9000 Epoch 33/50 4/4 [==============================] - 0s 6ms/step - loss: 0.5012 - accuracy: 0.8333 - val_loss: 0.4213 - val_accuracy: 0.9000 Epoch 34/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4916 - accuracy: 0.8333 - val_loss: 0.4121 - val_accuracy: 0.9000 Epoch 35/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4820 - accuracy: 0.8417 - val_loss: 0.4033 - val_accuracy: 0.9000 Epoch 36/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4733 - accuracy: 0.8417 - val_loss: 0.3948 - val_accuracy: 0.9000 Epoch 37/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4648 - accuracy: 0.8417 - val_loss: 0.3869 - val_accuracy: 0.9000 Epoch 38/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4571 - accuracy: 0.8500 - val_loss: 0.3793 - val_accuracy: 0.9000 Epoch 39/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4488 - accuracy: 0.8500 - val_loss: 0.3719 - val_accuracy: 0.9000 Epoch 40/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4415 - accuracy: 0.8500 - val_loss: 0.3648 - val_accuracy: 0.9000 Epoch 41/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4345 - accuracy: 0.8500 - val_loss: 0.3579 - val_accuracy: 0.9000 Epoch 42/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4275 - accuracy: 0.8500 - val_loss: 0.3517 - val_accuracy: 0.9000 Epoch 43/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4208 - accuracy: 0.8500 - val_loss: 0.3455 - val_accuracy: 0.9000 Epoch 44/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4145 - accuracy: 0.8500 - val_loss: 0.3395 - val_accuracy: 0.9000 Epoch 45/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4083 - accuracy: 0.8583 - val_loss: 0.3339 - val_accuracy: 0.9333 Epoch 46/50 4/4 [==============================] - 0s 6ms/step - loss: 0.4025 - accuracy: 0.8667 - val_loss: 0.3284 - val_accuracy: 0.9333 Epoch 47/50 4/4 [==============================] - 0s 6ms/step - loss: 0.3967 - accuracy: 0.8667 - val_loss: 0.3230 - val_accuracy: 0.9333 Epoch 48/50 4/4 [==============================] - 0s 6ms/step - loss: 0.3913 - accuracy: 0.8667 - val_loss: 0.3177 - val_accuracy: 0.9333 Epoch 49/50 4/4 [==============================] - 0s 6ms/step - loss: 0.3859 - accuracy: 0.8667 - val_loss: 0.3126 - val_accuracy: 0.9333 Epoch 50/50 4/4 [==============================] - 0s 6ms/step - loss: 0.3809 - accuracy: 0.8750 - val_loss: 0.3078 - val_accuracy: 0.9333
トレーニングの進行状況のモニタリング
トレーニングの進行状況をモニタリングするために、トレーニングと検証の損失および精度の推移をプロットします。
以下、コードです。
import matplotlib.pyplot as plt
# トレーニングの進行状況をプロット
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label='val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(loc='upper right')
plt.show()
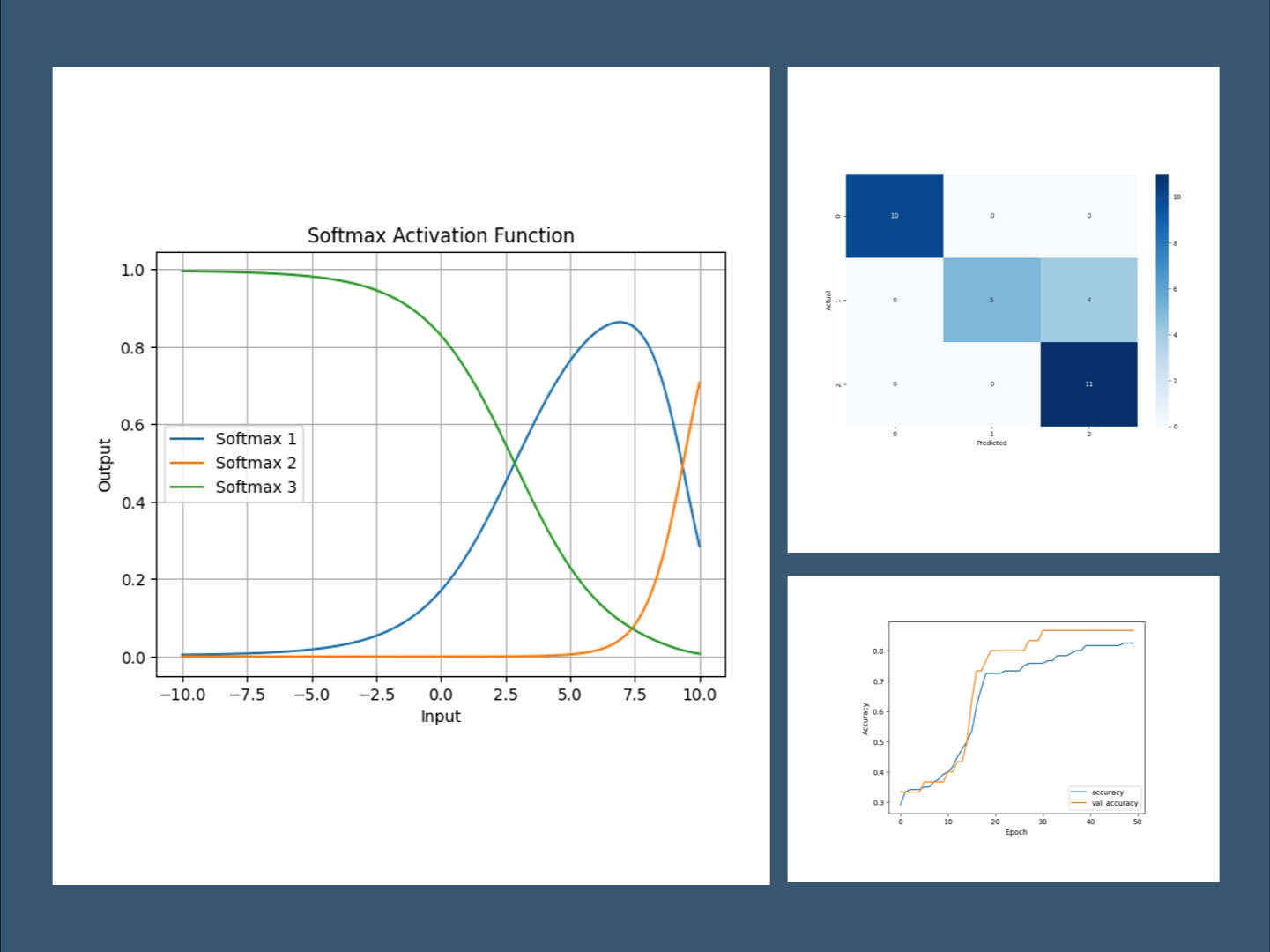
以下、実行結果です。
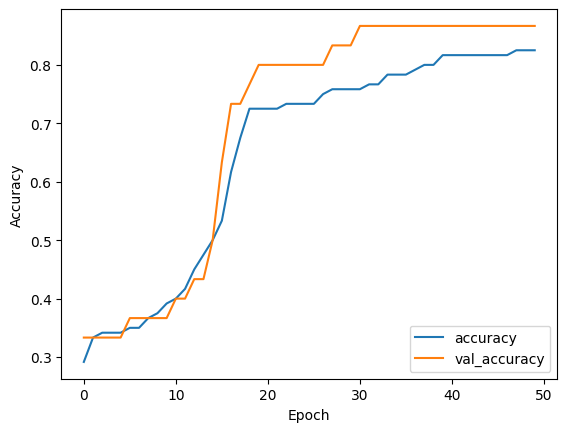
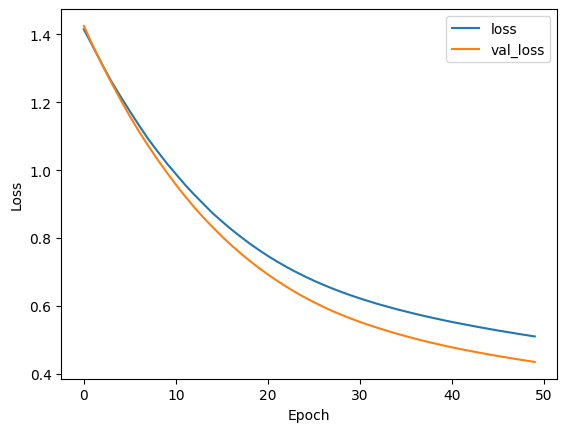
このプロットにより、トレーニングと検証の精度および損失の推移を視覚的に確認することができます。
これにより、トレーニングの進行状況や過学習の兆候を判断できます。
モデルの評価と予測
トレーニングしたモデルを評価し、新しいデータに対する予測を行う方法について説明します。
モデルの評価にはテストデータを使用し、予測結果を分析します。
モデルの評価
まず、テストデータを用いてモデルの性能を評価します。
model.evaluate関数を使用して、テストデータに対する損失と精度を計算します。
以下、コードです。
# モデルの評価
test_loss, test_accuracy = model.evaluate(X_test, y_test)
print(f'Test Loss: {test_loss}')
print(f'Test Accuracy: {test_accuracy}')
以下、実行結果です。
1/1 [==============================] - 0s 17ms/step - loss: 0.4352 - accuracy: 0.8667 Test Loss: 0.43519648909568787 Test Accuracy: 0.8666666746139526
予測結果の分析
次に、新しいデータに対して予測を行い、その結果を分析します。
ここでは、テストデータを使って予測を行います。
以下、コードです。
# テストデータに対する予測
predictions = model.predict(X_test)
# 最初の5つの予測結果を表示
for i in range(5):
print(f'Predicted: {predictions[i]}, Actual: {y_test.iloc[i]}')
以下、実行結果です。最初の5つの予測結果のみ表示しています。
1/1 [==============================] - 0s 71ms/step Predicted: [0.21028955 0.38535288 0.40435767], Actual: 1 Predicted: [0.97337353 0.01331554 0.01331093], Actual: 0 Predicted: [0.06612273 0.07690746 0.8569697 ], Actual: 2 Predicted: [0.18027289 0.3610332 0.45869386], Actual: 1 Predicted: [0.17180614 0.27961496 0.548579 ], Actual: 1
予測結果は、ソフトマックス関数の出力として各クラスの確率が返されます。
最も高い確率を持つクラスを予測クラスとして解釈します。
予測の可視化
予測結果を可視化することで、モデルの性能を視覚的に評価できます。
以下に、混同行列を使用した可視化の例を示します。
以下、コードです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
import seaborn as sns
# 予測クラスの取得
predicted_classes = np.argmax(predictions, axis=1)
# 混同行列の作成
conf_matrix = confusion_matrix(y_test, predicted_classes)
# 混同行列のプロット
plt.figure(figsize=(10, 7))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Blues')
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()
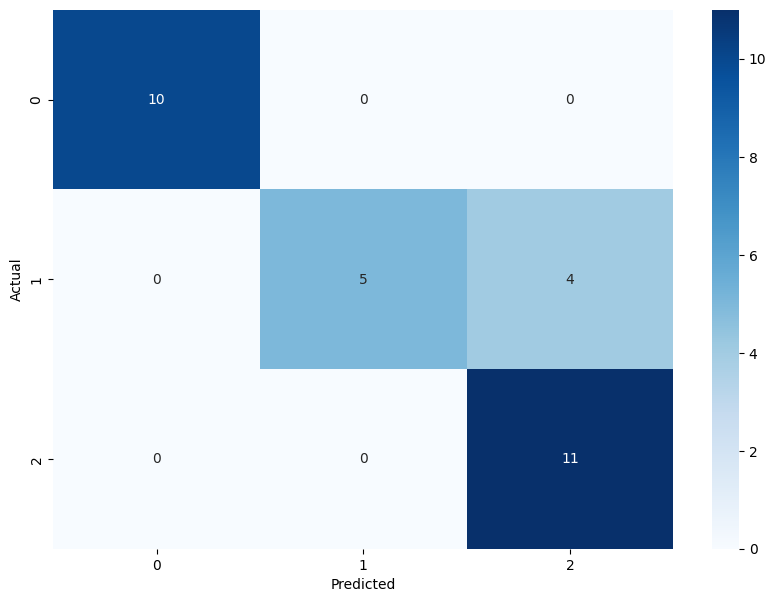
このコードでは、予測クラスを取得し、混同行列を作成してプロットします。
混同行列により、各クラスごとの正しい予測と誤った予測の数を視覚的に確認できます。
以下、実行結果です。
まとめ
ディープラーニングの基本的な流れを、TensorFlowを用いて段階的に説明しました。
- ディープラーニングの基本概念とTensorFlowの役割
- データセットの準備、トレーニングセットとテストセットの分割
- Kerasを用いた基本的なモデルの構築方法
- モデルのコンパイルとトレーニング、進行状況のモニタリング
- トレーニングしたモデルの評価と予測結果の分析
今後もディープラーニングの技術を磨き、新たな応用方法を探求していきましょう。