何かと便利なベイズ推定、ビジネスの世界でも活用が進んでいます。
MCMCというアルゴリズムが手軽に利用できるなったことが、大きな要因の1つでしょう。MCMCとは、マルコフ連鎖を利用したモンテカルロシミュレーションです。手軽にMCMCでベイズ推定を実現するのがPyMC3というPythonのパッケージです。
MCMCそのものの理解は脇においておくとしても、ベイズ推定そのものの理解を脇においておくわけには行きません。
ということで前回は、「コイン投げの例を使ってベイズ推定を何となく理解しよう」というお話しをしました。
前回は、PyMC3は登場しませんでした。コイン投げの場合、登場するまでもない、という感じでしたが、通常はそうは行きません。
今回は、「コイン投げの例を使ってPyMC3ベイズ推定を何となく理解しよう」というお話しをします。
今回も前回と同じコイン投げの例でお話しを進めます。
コイン投げ

コイン投げの例で説明を進めていきます。
コインには表と裏があります。コインを投げると、表になったり裏になったりします。それを数字で記録していきます。
- 表:1
- 裏:0
そうすると、次のような0-1のデータが手に入ります。
0010010111011001010101011111000…00101110
100回コイン投げをしたとします。このとき……
- 表;56回
- 裏:44回
……でたとします。
このコインの表の出る確率は、どうでしょうか?
このデータがなければ、0.5と考えるかもしれません。このデータから、0.56(=56/100)と考えるかもしれません。
ベイズ推定
以下、ベイズの定理です。
\displaystyle p(\theta|data)=\frac{p(data|\theta)\cdot p(\theta)}{p(data)}- 推定対象:\theta(今回の例では、表の出る確率)
- データ:data
- 事前分布(prior):p(\theta)
- 尤度(likelhood):p(data|\theta)
- 規格化定数(normalization):p(data)
- 事後分布(posterior):p(\theta|data)
これは、得られたデータ(data)を使って、推定対象(\theta)の分布を更新していく式になっています。
更新前の推定対象(\theta)の分布を事前分布(prior)、更新後の推定対象(\theta)の分布を、事後分布(posterior)と言います。
PyMC3で何ができるのか?
コイン投げのケースでは、ベルヌーイ分布(もしくは二項分布)とベータ分布が上手く連動し、事前分布も事後分布もベータ分布であるという幸運な状況が生まれました。
ベルヌーイ分布(もしくは二項分布)とベータ分布については、以下の記事を参考にしてください。
Pythonで描く二項分布とベータ分布
このような幸運な状況は他でも起こりますが、一般的ではありません。このような幸運な状況は、共役分布が存在するかどうかで決まります。今回の例ですと、ベルヌーイ分布(もしくは二項分布)の共役分布がベータ分布だから生まれた幸運です。ここでは共役分布とは何か、という説明はいたしません。
このような幸運な状況がないと、ベイズ推定は簡単ではありません。そこで登場するのがPyMC3です。似たようなPythonライブラリーは他にもありますが、今回はPyMC3でいきます。
PyMC3を使い事後分布を計算していきます。
前回も話しましたが、ベイズの定理のp(data)の計算はやっかいです。PyMC3を使っても、事後分布を綺麗な数式で表現することはできません。例えば、ベータ分布のような綺麗な数式で求めることはできません。
では、PyMC3は事後分布の何を得ることができるのか?
PyMC3はMCMCというアルゴリズムなどを活用し、 分母にあるp(data)を明示的に計算することなく、事後分布から好きなだけサンプルを得ることができます。
要は、事後分布を表す数式を得ることなく(知ることなく)、その分布からサンプリングしたときに得られるデータを、好きなだけ得られるのです。
事後分布からサンプルを得ることができれば、平均や分散、中央値や標準偏差などの、統計量を推定することができます。ヒストグラムや確率密度を可視化することもできます。
要は、事後分布の重要な情報を抽出することができるのです。
それが予測値であれば、予測の分布を得ることができるということです。予測の分布が得られれば、その分布の平均値や中央値、最頻値などを予測値としてもいいでしょう。分散や標準偏差から、予測のばらつきも知ることができます。各予測値が実現確率も求めることもできます。
PyMC3で求めるコイン投げの事後分布
PyMC3をまだインストールされていない方は、例えばコマンドプロンプト上で、以下のコードでインストールしてください。
pip install pymc3
先ず、必要なライブラリーを読み込みます。
以下、コードです。
# ライブラリー読み込み
import numpy as np
import pymc3 as pm
import arviz as az
import matplotlib.pyplot as plt
# グラフの表示設定
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ
次に、コイン投げデータを作ります。ランダムな0-1データです。
- 1:表
- 0:裏
以下、コードです。
# 0以上2未満の整数値をランダムに出力する tosses = np.random.randint(0, 2, 100) tosses
以下、実行結果です。
このデータに対し、PyMC3で事後分布から得られるデータを生成します。
以下の3つを設定する必要があります。
- 事前分布の定義
- 尤度の定義
- 事後分布からデータ生成
以下、コードです。
with pm.Model() as model:
# 事前分布の定義
theta = pm.Beta('theta', 1, 1)
# 尤度の定義
data = pm.Bernoulli('data', theta, observed=tosses)
# 事後分布からデータ生成
trace = pm.sample(return_inferencedata=True)
以下、実行中の様子です。少々時間が掛かります。
簡単にコードを説明します。
コイン投げの例ということで、今回は事前分布としてベータ分布 Beta(\alpha = 1,\beta = 1) を設定します。今回は、以下のように設定します。
theta = pm.Beta('theta', 1, 1)
尤度としてベルヌーイ分布を設定します。Observedは、先程作ったコイン投げデータを設定します。今回は、以下のように設定します。
data = pm.Bernoulli('data', theta, observed=tosses)
事後分布からデータ生成するには、今回は以下のように設定します。
trace = pm.sample()
事後分布から得られるデータは、traceに格納されます。
結果を見てみます。
以下、コードです。
trace
以下、実行結果です。
色々な情報が含まれています。
事後分布のサンプルデータのみ抽出してみます。
以下、コードです。
trace.posterior.theta.values
以下、実行結果です。
事後分布から得られたデータのサマリーを見てみます。
以下、コードです。
az.summary(trace)
以下、実行結果です。
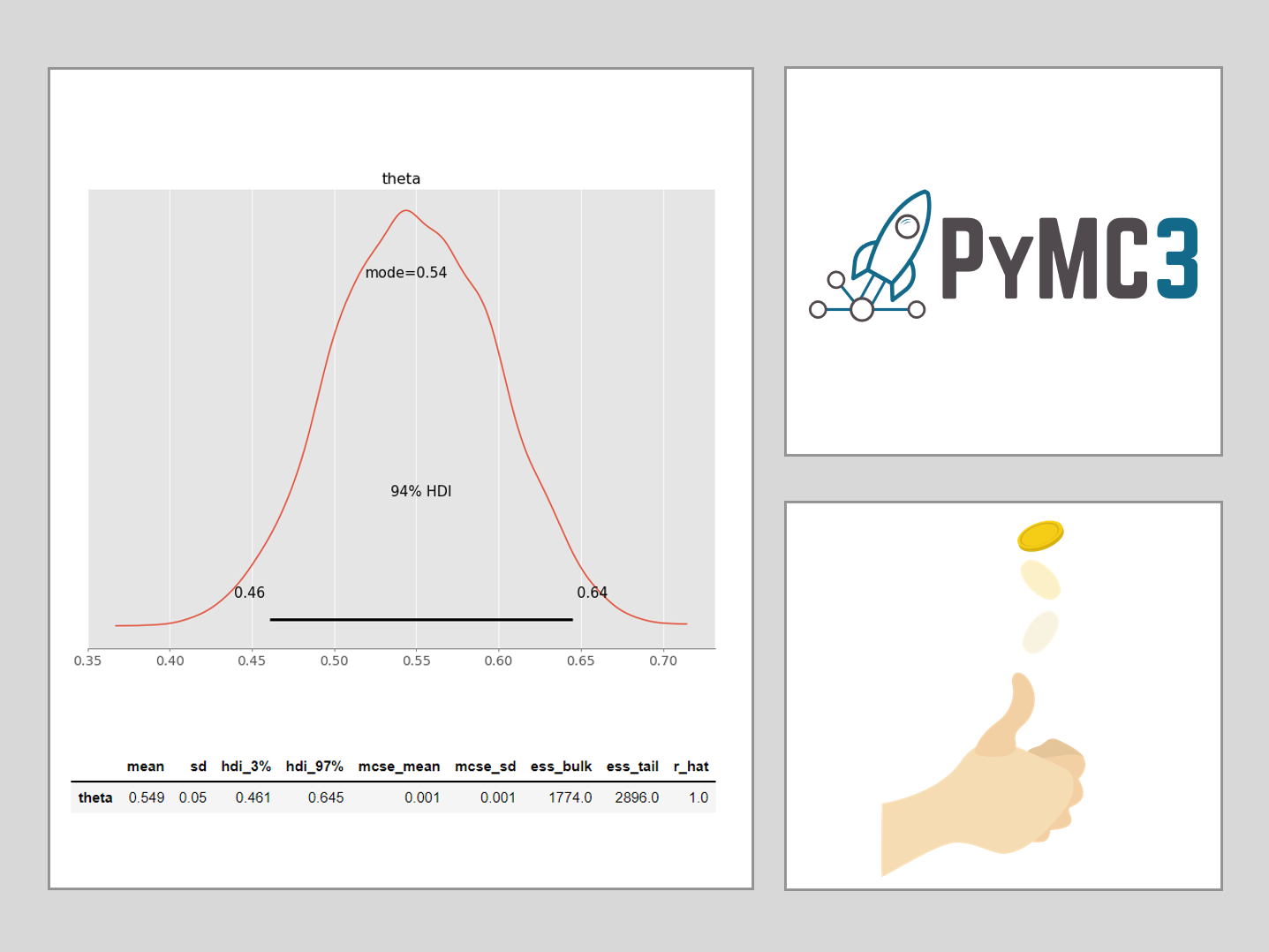
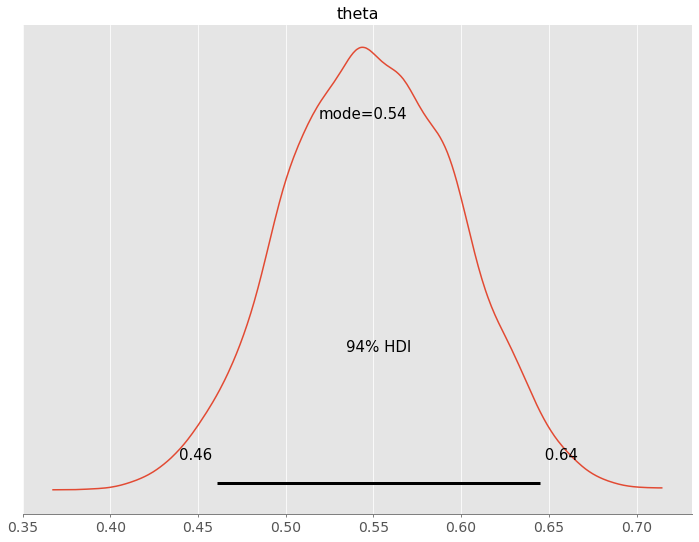
プロットしてみます。最頻値(mode)も出力します。
以下、コードです。
az.plot_posterior(trace, point_estimate='mode')
以下、実行結果です。
まとめ
今回は、「コイン投げの例を使ってPyMC3ベイズ推定を何となく理解しよう」というお話しをしました。
次回は、ちょっとレベルを上げて、「PyMC3によるベイズ型線形回帰モデル」というお話しをします。