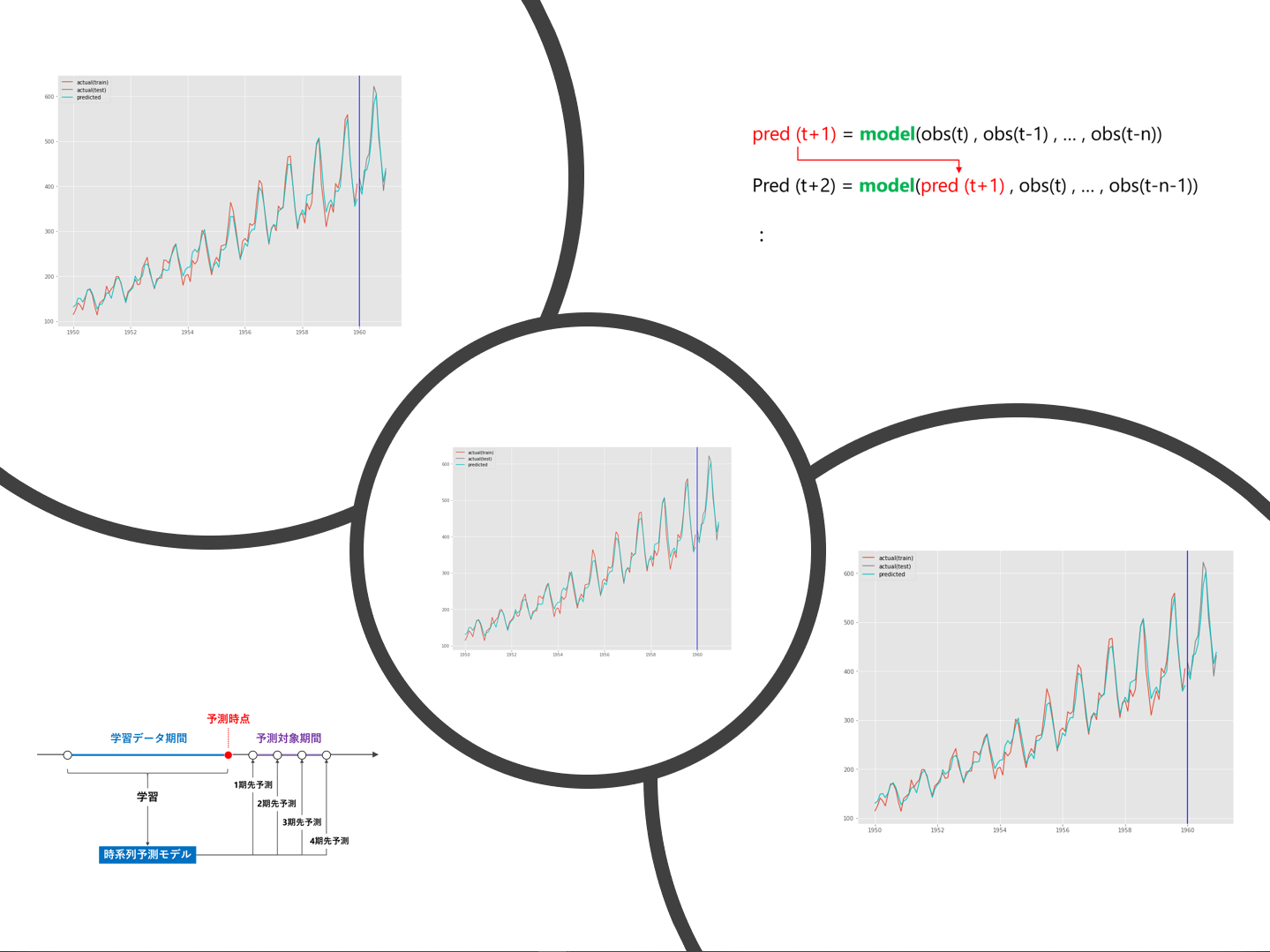
Pythonで時系列解析・超入門（その12）

テーブルデータ系モデルで複数先予測
（正則化項付き線形回帰）

3223
Pythonで時系列解析・超入門（その12）テーブルデータ系モデルで複数先予測（正則化項付き線形回帰）

時系列予測モデルの基本は1期先予測です。例えば、時系列データが日単位である場合、1期先予測とは、学習データ期間の次の日を予測することです。

実務上は、1期先だけではなく、もっと先を予測することが多いです。例えば、2期先予測（翌々日）、3期先予測（翌翌々日）、…などです。複数先予測（Multi-Step ahead prediction）です。

 

 

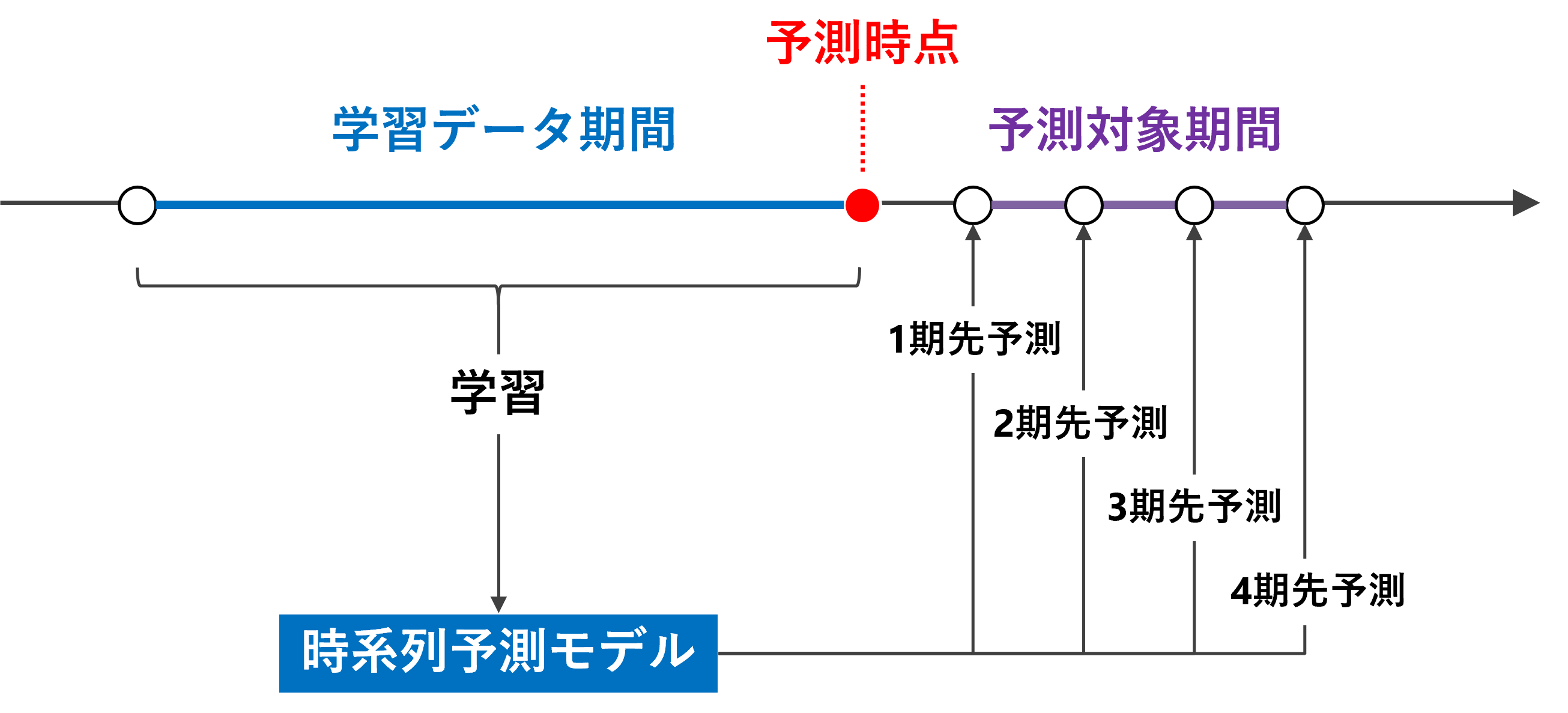
複数先予測（Multi-Step ahead prediction）を実現する方法の1つとして、「1期先予測モデルを1つ作り再帰的に利用する方法」があります。

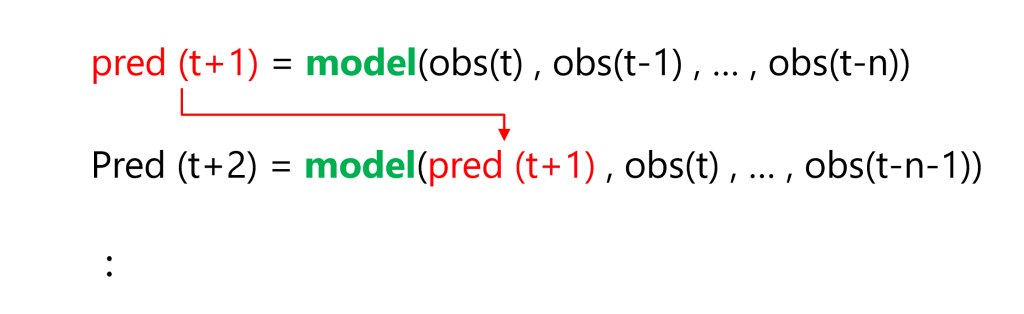
これは、1期先予測モデルを使いまわして、複数先予測を実現しようという考え方です。

例えば、過去90日間のデータを使う予測モデルの場合、利用するデータ期間をスライドさせながら……

  • 1期先予測：1期先予測対象日前の過去90日間のデータを使う
  • 2期先予測：1期先予測対象日前の過去89日間のデータ＋前日の予測値のデータを使う
  • 3期先予測：1期先予測対象日前の過去88日間のデータ＋前日と前々日の予測値のデータを使う

……といった感じで、予測データを使いながら予測を実施します。

予測モデルが1つで済むというのが利点です。ただ、2期先予測、3期先予測、……をするとき、その前までの予測値を過去の観測データの代わりに予測データを利用するという気持ち悪さは生まれます。

前回は、「テーブルデータ系モデルで複数先予測（線形回帰）」というお話しをしました。

Pythonで時系列解析・超入門（その11）テーブルデータ系モデルで複数先予測（線形回帰）

今回は、前回と同じ時系列特徴量付きデータセットを使い、以下の3つの正則化項付き線形回帰モデルで時系列予測モデルを構築し複数先予測（Multi-Step ahead prediction）を実施します。

  • Ridge回帰
  • Lasso回帰
  • Elastic Net回帰

必要なライブラリーの読み込み

先ず、必要なライブラリーなどを読み込みます。

以下、コードです。

import numpy as np
import pandas as pd
import datetime

from sklearn.linear_model import RidgeCV
from sklearn.linear_model import LassoCV
from sklearn.linear_model import ElasticNetCV

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

 

利用するデータ

今回利用するデータは、前回準備した時系列特徴量付きデータセットです。

以下からダウンロードできます。

dataset.csv
https://www.salesanalytics.co.jp/6ro8

 

このURLから直接データセットを読み込めます。

以下、コードです。

url='https://www.salesanalytics.co.jp/6ro8'
df=pd.read_csv(url,                         #読み込むデータのURL
               index_col='Month',           #変数「Month」をインデックスに設定
               parse_dates=True)            #インデックスを日付型に設定
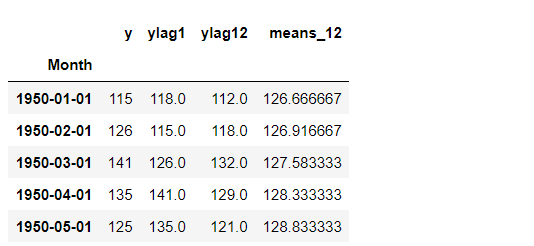
df.head() #確認

 

以下、実行結果です。

 

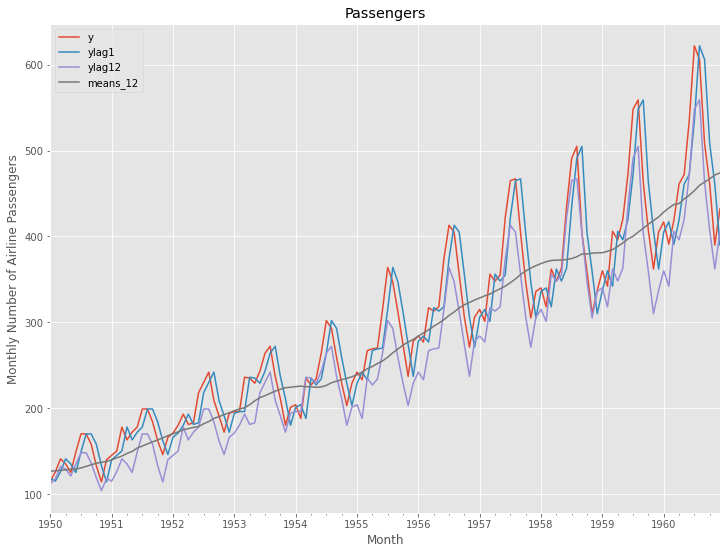
グラフ化し確認します。

以下、コードです。

# プロット
df.plot()
plt.title('Passengers')                            #グラフタイトル
plt.ylabel('Monthly Number of Airline Passengers') #タテ軸のラベル
plt.xlabel('Month')                                #ヨコ軸のラベル
plt.show()

 

以下、実行結果です。

 

次に、読み込んだデータセットを、学習データとテストデータに分割します。

以下、コードです。

# 学習データ
train = df.iloc[:-12]
y_train = train['y']              #目的変数y
X_train = train.drop('y', axis=1) #説明変数X

# テストデータ
test = df.iloc[-12:]  #テストデータ
y_test = test['y']              #目的変数y
X_test = test.drop('y', axis=1) #説明変数X

 

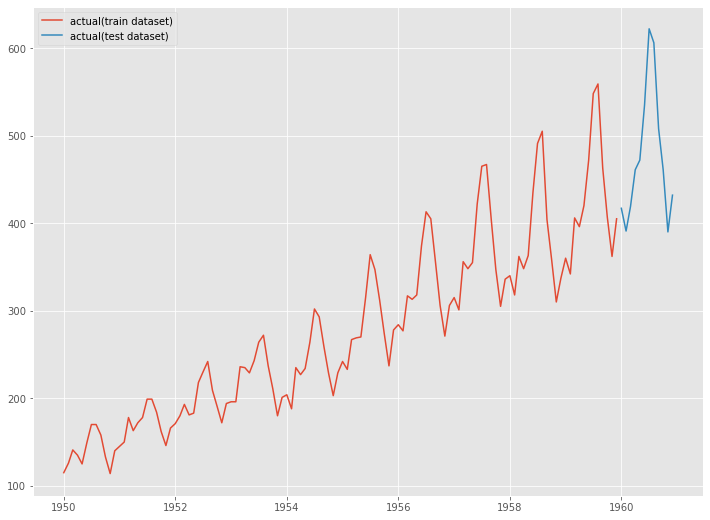
グラフ化します。

以下、コードです。

# グラフ化
fig, ax = plt.subplots()
ax.plot(y_train.index, y_train.values, label="actual(train dataset)")
ax.plot(y_test.index, y_test.values, label="actual(test dataset)")
plt.legend()

 

以下、実行結果です。

 

学習データで正則化項付き線形回帰モデルを構築し、構築したモデルをテストデータで精度検証します。

 

予測精度の評価指標

今回の予測精度の評価指標は、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。 

以下の記号を使い精度指標の説明をします。

  • y_i^{actual} ・・・i番目の実測値
  • y_i^{pred} ・・・i番目の予測値
  • n ・・・実測値・予測値の数

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

 

Ridge回帰で予測モデル構築

　学習データで学習

学習データを使って、Ridge回帰モデルを学習します。

以下、コードです。

regressor = RidgeCV(alphas=np.linspace(1, 10000000, 1000)/100, cv = 10)
regressor.fit(X_train, y_train)

 

これは、1期先予測モデルです。

 

　予測の実施（学習期間）

学習データ期間の目的変数yの値を予測します。学習データ期間の説明変数Xのデータは既知なので、学習し求めた予測モデルをそのまま利用します。

以下、コードです。

train_pred = regressor.predict(X_train)

 

　予測の実施（テストデータ期間）

テストデータ期間の目的変数yの値を予測します。テストデータ期間の説明変数Xのデータは未知のものが混在しているので、工夫が必要です。

要は、「1期先予測モデルを1つ作り再帰的に利用する方法」で「複数先予測」（Multi-Step ahead prediction）を実施していきます。

以下、コードです。

# 学習データのコピー
y_train_new = y_train.copy()

# 説明変数Xを更新しながら予測を実施
for i in range(len(y_test)):
    
    #当期の予測の実施
    X_value =  X_test.iloc[i:(i+1),:]
    y_value_pred = regressor.predict(X_value)
    y_value_pred = pd.Series(y_value_pred,index=[X_value.index[0]])
    y_train_new = pd.concat([y_train_new,y_value_pred])
    
    #次期の説明変数Xの計算
    lag1_new = y_train_new[-1] #ylag1
    lag12_new = y_train_new[-12] #ylag12
    means_12_new = y_train_new[-12:].mean() #means_12
    
    #次期の説明変数Xの更新
    X_test.iloc[(i+1):(i+2),0] = lag1_new
    X_test.iloc[(i+1):(i+2),1] = lag12_new
    X_test.iloc[(i+1):(i+2),2] = means_12_new
    
# 予測値の代入
test_pred = y_train_new[-12:]

 

　予測モデルのテスト（テストデータ利用）

テストデータで精度検証します。

以下、コードです。

print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

グラフ化します。

以下、コードです。

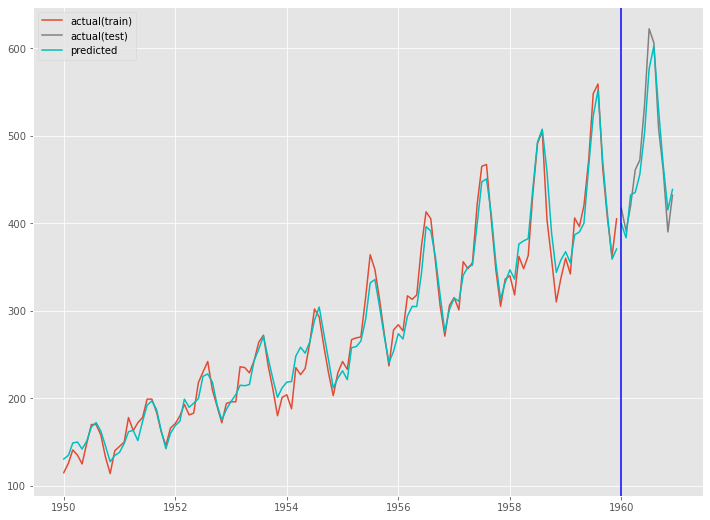
fig, ax = plt.subplots()

ax.plot(train.index, y_train, label='actual(train)')
ax.plot(test.index, y_test, label='actual(test)', color='gray')
ax.plot(train.index, train_pred, color='c')
ax.plot(test.index, test_pred, label="predicted", color="c") 
ax.axvline(datetime.datetime(1960,1,1),color='blue')
ax.legend()

plt.show()

 

以下、実行結果です。

 

Lasso回帰で予測モデル構築

　学習データで学習

学習データを使って、Lasso回帰モデルを学習します。

以下、コードです。

regressor = LassoCV(alphas=np.linspace(1, 10000000, 1000)/100, cv = 10)
regressor.fit(X_train, y_train)

 

これは、1期先予測モデルです。

 

　予測の実施（学習期間）

学習データ期間の目的変数yの値を予測します。学習データ期間の説明変数Xのデータは既知なので、学習し求めた予測モデルをそのまま利用します。

以下、コードです。

train_pred = regressor.predict(X_train)

 

　予測の実施（テストデータ期間）

テストデータ期間の目的変数yの値を予測します。テストデータ期間の説明変数Xのデータは未知のものが混在しているので、工夫が必要です。

要は、「1期先予測モデルを1つ作り再帰的に利用する方法」で「複数先予測」（Multi-Step ahead prediction）を実施していきます。

以下、コードです。

# 学習データのコピー
y_train_new = y_train.copy()

# 説明変数Xを更新しながら予測を実施
for i in range(len(y_test)):
    
    #当期の予測の実施
    X_value =  X_test.iloc[i:(i+1),:]
    y_value_pred = regressor.predict(X_value)
    y_value_pred = pd.Series(y_value_pred,index=[X_value.index[0]])
    y_train_new = pd.concat([y_train_new,y_value_pred])
    
    #次期の説明変数Xの計算
    lag1_new = y_train_new[-1] #ylag1
    lag12_new = y_train_new[-12] #ylag12
    means_12_new = y_train_new[-12:].mean() #means_12
    
    #次期の説明変数Xの更新
    X_test.iloc[(i+1):(i+2),0] = lag1_new
    X_test.iloc[(i+1):(i+2),1] = lag12_new
    X_test.iloc[(i+1):(i+2),2] = means_12_new
    
# 予測値の代入
test_pred = y_train_new[-12:]

 

　予測モデルのテスト（テストデータ利用）

テストデータで精度検証します。

以下、コードです。

print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

グラフ化します。

以下、コードです。

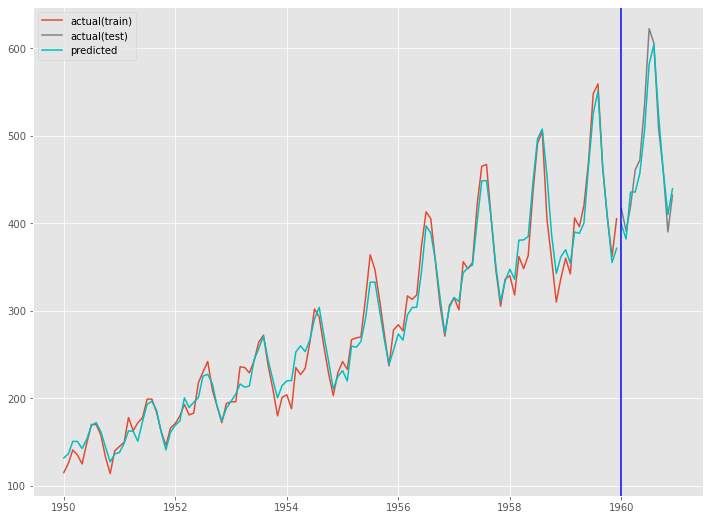
fig, ax = plt.subplots()

ax.plot(train.index, y_train, label='actual(train)')
ax.plot(test.index, y_test, label='actual(test)', color='gray')
ax.plot(train.index, train_pred, color='c')
ax.plot(test.index, test_pred, label="predicted", color="c") 
ax.axvline(datetime.datetime(1960,1,1),color='blue')
ax.legend()

plt.show()

 

以下、実行結果です。

 

Elastic net回帰で予測モデル構築

　学習データで学習

学習データを使って、Elastic net回帰モデルを学習します。

以下、コードです。

regressor = ElasticNetCV(alphas=np.linspace(1, 10000000, 1000)/100, 
                         l1_ratio=np.linspace(0, 10000, 1000)/10000,
                         cv = 10)
regressor.fit(X_train, y_train)

 

これは、1期先予測モデルです。

 

　予測の実施（学習期間）

学習データ期間の目的変数yの値を予測します。学習データ期間の説明変数Xのデータは既知なので、学習し求めた予測モデルをそのまま利用します。

以下、コードです。

train_pred = regressor.predict(X_train)

 

　予測の実施（テストデータ期間）

テストデータ期間の目的変数yの値を予測します。テストデータ期間の説明変数Xのデータは未知のものが混在しているので、工夫が必要です。

要は、「1期先予測モデルを1つ作り再帰的に利用する方法」で「複数先予測」（Multi-Step ahead prediction）を実施していきます。

以下、コードです。

# 学習データのコピー
y_train_new = y_train.copy()

# 説明変数Xを更新しながら予測を実施
for i in range(len(y_test)):
    
    #当期の予測の実施
    X_value =  X_test.iloc[i:(i+1),:]
    y_value_pred = regressor.predict(X_value)
    y_value_pred = pd.Series(y_value_pred,index=[X_value.index[0]])
    y_train_new = pd.concat([y_train_new,y_value_pred])
    
    #次期の説明変数Xの計算
    lag1_new = y_train_new[-1] #ylag1
    lag12_new = y_train_new[-12] #ylag12
    means_12_new = y_train_new[-12:].mean() #means_12
    
    #次期の説明変数Xの更新
    X_test.iloc[(i+1):(i+2),0] = lag1_new
    X_test.iloc[(i+1):(i+2),1] = lag12_new
    X_test.iloc[(i+1):(i+2),2] = means_12_new
    
# 予測値の代入
test_pred = y_train_new[-12:]

 

　予測モデルのテスト（テストデータ利用）

テストデータで精度検証します。

以下、コードです。

print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

 

以下、実行結果です。

 

グラフ化します。

以下、コードです。

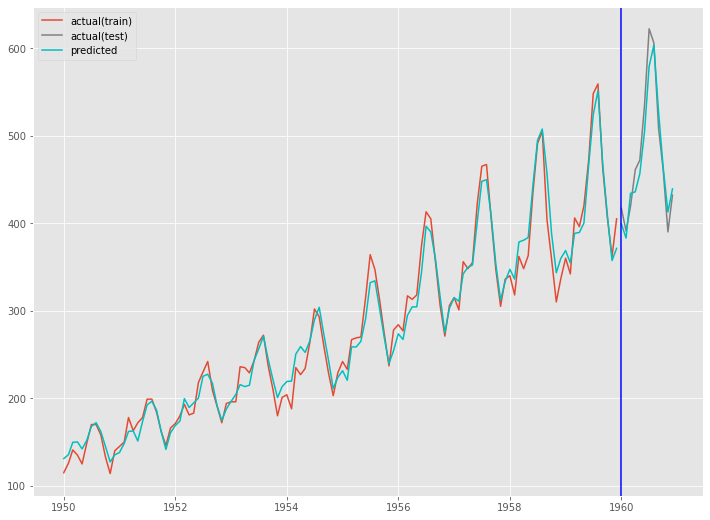
fig, ax = plt.subplots()

ax.plot(train.index, y_train, label='actual(train)')
ax.plot(test.index, y_test, label='actual(test)', color='gray')
ax.plot(train.index, train_pred, color='c')
ax.plot(test.index, test_pred, label="predicted", color="c") 
ax.axvline(datetime.datetime(1960,1,1),color='blue')
ax.legend()

plt.show()

 

以下、実行結果です。

 

まとめ

今回は、前回と同じ時系列特徴量付きデータセットを使い、以下の3つの正則化項付き線形回帰モデルで時系列予測モデルを構築し複数先予測（Multi-Step ahead prediction）を実施しました。

  • Ridge回帰
  • Lasso回帰
  • Elastic Net回帰

そこで利用した方法は「1期先予測モデルを1つ作り再帰的に利用する方法」というものでした。

次回は、今回と同じ時系列特徴量付きデータセットを使い、ディシジョンツリー（決定木）で時系列予測モデルを構築します。

Pythonで時系列解析・超入門（その13）テーブルデータ系モデルで複数先予測（ディシジョンツリー）

初めての方へ
メルマガ
サービス
お問合せ