【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！

– 【第3回】Pythonによる大域的最適化手法の実装（決定論的手法編） –

382
【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第3回】Pythonによる大域的最適化手法の実装（決定論的手法編） –

前回は、メタヒューリスティクスを中心に、非線形計画問題の大域的最適化に挑戦しました。

メタヒューリスティクスは、問題依存性が低く、大域的最適解の探索に適した手法ですが、その性能はアルゴリズムの選択とパラメータ設定に大きく依存することを確認しました。

【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第2回】Pythonによる大域的最適化手法の実装（メタヒューリスティクス編） –

ただ、メタヒューリスティクスは大域的最適解を保証しません。近づくだけです。

どうしても大域的最適解を得たい場合にはどうすればいいでしょうか？

決定論的手法です。

要するに、大域的最適解にこだわるなら決定論的手法、スピードを重視するならメタヒューリスティックス、といった感じです。

ということで今回は、もう一つの大域的最適化手法である決定論的手法に着目します。

決定論的手法は、メタヒューリスティクスとは異なり、数学的な理論に基づいて大域的最適性を保証する手法です。代表的な決定論的手法として、区間分割法や分枝限定法などがあります。

決定論的手法は、大域的最適性を保証できる強力な手法ですが、計算量の爆発や問題の定式化の難しさなどの課題もあります。

これらの課題を理解し、問題の特性に応じて適切な手法を選択することが、非線形計画問題の大域的最適化に挑戦する上で重要です。

Contents

決定論的大域的最適化手法の概要

決定論的大域的最適化手法は、数学的な理論に基づいて大域的最適性を保証する手法です。

決定論的手法の定義と特徴、代表的な手法、適用領域について説明します。

 

　決定論的手法の定義と特徴

決定論的手法は、以下のような特徴を持っています。

  • アルゴリズムの進行が一意に定まる
  • 大域的最適性を理論的に保証できる
  • 厳密解を求めることができる
  • 問題の数学的構造を利用する

 

決定論的手法は、問題の数学的構造を利用して、大域的最適解を厳密に求めることを目的とします。これは、メタヒューリスティクスが確率的な探索を行うのとは対照的です。

 

　代表的な決定論的大域的最適化手法

代表的な決定論的大域的最適化手法には、以下のようなものがあります。

手法 特徴 メリット デメリット
区間分割法
  • 区間演算を用いて探索空間を分割
  • 大域的最適解を含む区間を特定
  • 区間の幅が十分小さくなるまで分割を繰り返す
  • 大域的最適性を保証
  • 実装が比較的容易
  • 区間演算により効率的な探索が可能
  • 次元の増加に伴い計算量が指数的に増加
  • 区間演算の精度に依存
  • 非線形制約の扱いが難しい
分枝限定法
  • 探索空間を分枝し、部分空間に分割
  • 限定操作で非有望な部分空間を削除
  • 部分空間が十分小さくなるまで分枝と限定を繰り返す
  • 大域的最適性を保証
  • 問題の数学的構造を利用可能
  • 強力な限定操作により効率的な探索が可能
  • 問題の定式化が難しい
  • 計算量が指数的に増加する可能性がある
  • 非線形制約の扱いが難しい
リプシッツ最適化
  • 目的関数のリプシッツ定数を利用
  • 最小点を中心に最適解の存在範囲を絞り込む
  • 存在範囲内でランダムに新しい探索点を生成
  • 勾配情報が不要
  • 目的関数の評価に時間がかかる問題に有効
  • 実装が比較的容易
  • リプシッツ定数の適切な設定が難しい
  • 理論的な収束性は保証されていない
  • 探索点の生成方法に依存

 

区間分割法と分枝限定法は、大域的最適性を保証できる強力な手法ですが、次元の増加に伴い計算量が指数的に増加する可能性があります。

リプシッツ最適化は、勾配情報が不要で、目的関数の評価に時間がかかる問題に有効ですが、リプシッツ定数の適切な設定が難しく、理論的な収束性は保証されていません。

これらの手法を適用する際は、問題の特性をよく理解し、各手法のメリットとデメリットを考慮して、適切な手法を選択することが重要です。

 

　決定論的手法の適用領域

決定論的手法は、以下のような問題に適用されます。

  • 低次元の問題
  • 目的関数が滑らかな問題
  • 厳密解が求められる問題
  • 問題の数学的構造が明らかな問題

 

決定論的手法は、問題の数学的構造を利用するため、問題の定式化が重要です。また、計算量が問題の規模に対して指数的に増加する場合があるため、高次元の問題や大規模な問題への適用は難しい場合があります。

決定論的手法は、大域的最適性を保証できる強力な手法ですが、適用可能な問題のクラスが限定的であるという特徴があります。

区間分割法の概要とPythonでの実装

区間分割法は、区間演算を用いて探索空間を分割しながら大域的最適解を求める決定論的手法です。

ここでは、区間分割法の基本的なアイデア、アルゴリズム、Pythonでの実装例について説明します。

 

　区間分割法の基本的なアイデア

区間分割法の基本的なアプローチは、以下の通りです。

  • 探索空間を区間で表現する
  • 区間を分割しながら、大域的最適解を含む区間を特定する
  • 区間の幅が十分小さくなったら、その区間を大域的最適解の近似とみなす

 

区間分割法では、区間演算を用いて、区間に対する目的関数の値の範囲を効率的に計算します。これにより、大域的最適解を含まない区間を早期に発見し、探索空間を縮小することができます。

 

　区間演算の概要

区間演算は、実数演算を区間に拡張したものです。区間 [a, b] に対する基本的な演算は、以下のように定義されます。

加法
二つの区間の加算は、各区間の下限を加えたものと、上限を加えたもので新しい区間を形成します。

\displaystyle [a, b] + [c, d] = [a + c, b + d]

 

減法
二つの区間の減算は、最初の区間の下限から第二の区間の上限を引いたものと、最初の区間の上限から第二の区間の下限を引いたもので新しい区間を形成します。

\displaystyle [a, b] - [c, d] = [a - d, b - c]

 

乗法
二つの区間の乗算においては、各区間の端点を乗じた全ての組み合わせの中で最小値と最大値を求め、それらで新しい区間を形成します。

\displaystyle [a, b] \times [c, d] = [\min(ac, ad, bc, bd), \max(ac, ad, bc, bd)]

 

除法
二つの区間の除算は、最初の区間を第二の区間の逆数を乗じた区間として計算します。ただし、第二の区間に0が含まれていない場合に限ります。

\displaystyle [a, b] \div [c, d] = [a, b] \times [1/d, 1/c] \quad \text{ただし、}0 \notin [c, d]

 

区間演算を用いることで、関数の値の範囲を効率的に計算することができます。

 

　区間分割法のアルゴリズム

区間分割法のアルゴリズムは、以下のようなステップからなります。

  • ステップ 1 : 初期区間を設定する
  • ステップ 2 : 区間を分割する（分割ルール）
  • ステップ 3 : 大域的最適解を含まない区間を削除する（削除ルール）
  • ステップ 4 : 区間の幅が許容誤差以下になるまで、ステップ 2 と 3 を繰り返す（終了条件）

 

分割ルールには、等分割法や黄金分割法などがあります。削除ルールには、目的関数の下界を用いる方法などがあります。終了条件は、区間の幅に基づいて設定されます。

 

　Pythonでの区間分割法の実装

mpmathは、Pythonで高精度な数値計算を行うためのライブラリです。区間演算もサポートしているため、区間分割法の実装に使うことができます。

mpmathは、以下のコマンドを使ってインストールできます。

pip install mpmath

インストールが完了したら、以下のようにしてmpmathをインポートできます。

from mpmath import mp, iv

ここで、mpはmpmathのモジュールで、ivは区間を表すクラスです。

 

　　1変量目的関数の最適化例

以下で、目的関数 (x-2)^2 を最小化する解を探索します。最適解は x=2 で、最適値は 0 です。

from mpmath import mp, iv

# 目的関数を定義します
def objective(x):
    return (x - 2) ** 2

# 区間分割法を実装します
def interval_division(f, x_range, eps):
    stack = [(x_range, None)]  # 探索範囲とその関数値の区間を保持
    best_x = None  # 最適解のxの値
    best_f_x = iv.mpf([float('inf'), float('inf')])  # 最適値を無限大で初期化
    while stack:
        x, _ = stack.pop()  # 探索区間を取り出す
        f_x = f(x)  # 関数値を計算
        if f_x.delta < eps:  # 許容誤差内か確認
            if f_x.a < best_f_x.a:  # 最小値で更新
                best_x = x
                best_f_x = f_x
        else:
            mid = x.mid  # 区間の中点を計算
            stack.append((iv.mpf((x.a, mid)), f_x))  # 左区間を追加
            stack.append((iv.mpf((mid, x.b)), f_x))  # 右区間を追加
    return best_x, best_f_x  # 最適解のxの値の区間と最適値を返す

# 探索範囲とパラメータの定義
x_range = iv.mpf([-5, 5])  # 探索範囲を定義
eps = 1e-5  # 許容誤差を設定

# 区間分割法で最適解を探索
result, best_f_x = interval_division(objective, x_range, eps)

# 最適解と最適値を表示
print(f"Optimal solution: {result.mid}")
print(f"Optimal value: {best_f_x.a}")

 

このコードを簡単に説明します。

目的関数の定義

  • objective(x)として定義され、(x - 2) ** 2を計算。
  • この関数はx = 2で最小値0を取る。

区間分割法の実装

  • 関数interval_division(f, x_range, eps)で実装。
  • fは目的関数、x_rangeは探索範囲、epsは許容誤差。
  • アルゴリズムの流れ：
    • 探索範囲をスタックに追加し、スタックが空になるまで次を繰り返す。
    • スタックから探索範囲を取り出し、目的関数の値を計算。
    • 計算された関数値の区間の幅がeps未満の場合、現在の最適値と比較し更新。
    • そうでない場合、探索範囲を二分し、スタックに追加して再探索。

探索範囲とパラメータの定義

  • x_range = iv.mpf([-5, 5])で探索範囲を [-5,5] に設定。
  • eps = 1e-5で許容誤差を 10^{-5} に設定。

最適解の探索と表示

  • interval_division関数を使用して最適解を探索。
  • 計算された最適解の中点(result.mid)と最適値(best_f_x.a)を表示。

 

以下、実行結果です。

Optimal solution: [1.99951171875, 1.99951171875]
Optimal value: [0.0, 0.0]

 

結果は区間として出力されます。出力される下限と上限が同じ値の場合はどちらか一方を、異なる場合は下限と上限の中点を採用して頂ければと思います。

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：x=2.0
  • 最適値（Optimal value）：0.0

 

　　2変量目的関数の最適化例

以下で、目的関数 (x_0 - 2) ^ 2 + (x_1 - 3) ^ 2 を最小化する解を探索します。最適解は (x_0,x_1)=(2,3) で、最適値は 0 です。

from mpmath import mp, iv

# 目的関数を定義します
def objective(x0, x1):
    return (x0 - 2) ** 2 + (x1 - 3) ** 2

# 区間分割法を実装します
def interval_division(f, x0_range, x1_range, eps):
    stack = [((x0_range, x1_range), None)]  # 探索範囲とその関数値の区間を保持
    best_x = None  # 最適解のx0, x1の値
    best_f_x = iv.mpf([float('inf'), float('inf')])  # 最適値を無限大で初期化
    while stack:
        (x0, x1), _ = stack.pop()  # 探索区間を取り出す
        f_x = f(x0, x1)  # 関数値を計算
        if f_x.delta < eps:  # 許容誤差内か確認
            if f_x.a < best_f_x.a:  # 最小値で更新
                best_x = (x0, x1)
                best_f_x = f_x
        else:
            mid_x0 = x0.mid  # x0区間の中点を計算
            mid_x1 = x1.mid  # x1区間の中点を計算
            stack.append(((iv.mpf((x0.a, mid_x0)), iv.mpf((x1.a, mid_x1))), f_x))  # 左下区間を追加
            stack.append(((iv.mpf((x0.a, mid_x0)), iv.mpf((mid_x1, x1.b))), f_x))  # 左上区間を追加
            stack.append(((iv.mpf((mid_x0, x0.b)), iv.mpf((x1.a, mid_x1))), f_x))  # 右下区間を追加
            stack.append(((iv.mpf((mid_x0, x0.b)), iv.mpf((mid_x1, x1.b))), f_x))  # 右上区間を追加
    return best_x, best_f_x  # 最適解のx0, x1の値の区間と最適値を返す

# 探索範囲とパラメータの定義
x0_range = iv.mpf([-5, 5])  # 探索範囲を定義(x0)
x1_range = iv.mpf([-5, 5])  # 探索範囲を定義(x1)
eps = 1e-3  # 許容誤差を設定

# 区間分割法で最適解を探索
result, best_f_x = interval_division(objective, x0_range, x1_range, eps) 

# 最適解と最適値を表示
print(f"Optimal solution: x0 = {result[0].mid}, x1 = {result[1].mid}")
print(f"Optimal value: {best_f_x.a}")

 

以下、実行結果です。

Optimal solution: x0 = [2.0062500000000000888, 2.0062500000000000888], x1 = [3.0062500000000000888, 3.0062500000000000888]
Optimal value: [0.0, 0.0]

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：(x_0,x_1)=(2.0,3.0)
  • 最適値（Optimal value）：0.0

 

　　多峰性関数を目的関数にした例

前回同様、多数の局所最適解を持つことが知られている以下のAckley関数を目的関数にし最小化する例を示します。最適解は (x_0,x_1)=(-3,4) で、最適値は 0 です。

 

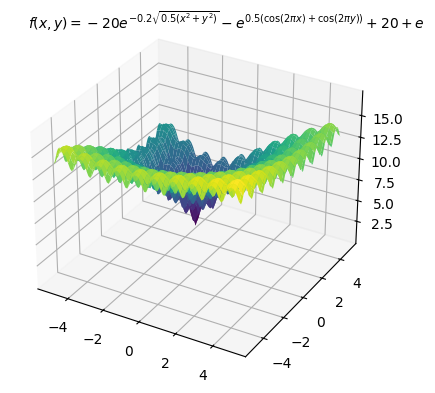
以下、コードです。変数の上下限制約のみ入れています。

from mpmath import mp, iv

# 目的関数の定義
def objective(x0, x1):
    a = 20
    b = 0.2
    c = 2 * iv.pi
    n = 2
    x_offset = [x0 + iv.mpf('3'), x1 - iv.mpf('4')]  # オフセット値も区間数として扱う
    sum_sq_term = -a * iv.exp(-b * iv.sqrt(sum(x**2 for x in x_offset) / n))
    cos_term = -iv.exp(sum(iv.cos(c * x) for x in x_offset) / n)
    return sum_sq_term + cos_term + a + iv.e

# 区間分割法を実装します
def interval_division(f, x0_range, x1_range, eps):
    stack = [((x0_range, x1_range), None)]
    best_x = None
    best_f_x = iv.mpf(['inf', 'inf'])
    while stack:
        (x0, x1), _ = stack.pop()
        f_x = f(x0, x1)
        if f_x.delta < eps:
            if f_x.a < best_f_x.a:
                best_x = (x0, x1)
                best_f_x = f_x
        else:
            mid_x0 = x0.mid
            mid_x1 = x1.mid
            # 4つの区間に分割して追加する際の範囲の指定方法を修正
            stack.append(((iv.mpf((x0.a, mid_x0)), iv.mpf((x1.a, mid_x1))), None))
            stack.append(((iv.mpf((x0.a, mid_x0)), iv.mpf((mid_x1, x1.b))), None))
            stack.append(((iv.mpf((mid_x0, x0.b)), iv.mpf((x1.a, mid_x1))), None))
            stack.append(((iv.mpf((mid_x0, x0.b)), iv.mpf((mid_x1, x1.b))), None))
    return best_x, best_f_x

# 探索範囲とパラメータの定義
x0_range = iv.mpf([-5, 5])
x1_range = iv.mpf([-5, 5])
eps = 1e-3

# 区間分割法で最適解を探索
result, best_f_x = interval_division(objective, x0_range, x1_range, eps)

# 最適解と最適値を表示
print(f"Optimal solution: x0 = {result[0].mid}, x1 = {result[1].mid}")
print(f"Optimal value: {best_f_x.a}")

 

以下、実行結果です。

Optimal solution: x0 = [-2.9999023437500000888, -2.9999023437500000888], x1 = [4.0000976562500003553, 4.0000976562500003553]
Optimal value: [-3.1086244689504383132e-15, -3.1086244689504383132e-15]

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：(x_0,x_1)=(-3.0,4.0)
  • 最適値（Optimal value）：0.0

 

　　制約付き非線形計画問題

前回同様、以下の非線形計画問題を扱います。最適解は (x_0,x_1)=(1,1) で、最適値は 0 です。

\displaystyle \begin{array}{ll} \displaystyle \min_{x \in \mathbb{R}^2} \quad & f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2 \\ \text{subject to} \quad & x_0-2x_1 - 2 \leq 0 \\ & e^{x_1}- 8 \leq 0 \\ & x_0^2 + x_1^2 - 10 \leq 0 \\ & -5 \leq x_0 \leq 5 \\ & -5 \leq x_1 \leq 5 \end{array}

 

制約条件はペナルティとして目的関数に組み込み最適化します。

以下、コードです。

from mpmath import mp, iv

# 区間演算の初期化
mp.dps = 15  # 小数点以下の桁数を設定
iv.dps = 15  # 区間演算での小数点以下の桁数を設定

# 目的関数を定義
def objective(x0, x1):
    return (1 - x0) ** 2 + 100 * (x1 - x0 ** 2) ** 2

# 制約関数を定義
def constraint_functions(x0, x1):
    c1 = x0 - 2 * x1 - 2
    c2 = iv.exp(x1) - 8
    c3 = x0 ** 2 + x1 ** 2 - 10
    return c1, c2, c3

# ペナルティ関数を定義
def calculate_penalty(x0, x1):
    c1, c2, c3 = constraint_functions(x0, x1)
    # 必要であれば区間のカスタムmax関数を実装、またはロジックを調整
    penalty = max(0, c1) + max(0, c2) + max(0, c3)
    return penalty

# ペナルティを含む目的関数を定義
def objective_with_penalty(x0, x1):
    obj = objective(x0, x1)
    penalty = calculate_penalty(x0, x1)
    return obj + penalty * 1e10

# 区間分割法を定義
def interval_division(f, x0_range, x1_range, eps):
    stack = [((x0_range, x1_range), None)]  # 探索スタック
    best_x = None  # 最適解
    best_f_x = iv.mpf('inf')  # 最適な関数の値を無限大で初期化
    while stack:
        ((x0, x1), _) = stack.pop()  # スタックから探索区間を取り出す
        f_x = f(x0, x1)  # 関数値を計算
        if f_x.b - f_x.a < eps:  # 許容誤差内かチェック
            if f_x.a < best_f_x.a:  # 最適値を更新
                best_x = (x0, x1)
                best_f_x = f_x
        else:  # 分割を続ける
            mid_x0 = x0.mid  # 中点計算（x0）
            mid_x1 = x1.mid  # 中点計算（x1）
            stack.append(((iv.mpf((x0.a, mid_x0)), iv.mpf((x1.a, mid_x1))), None))  # 左下区間を追加
            stack.append(((iv.mpf((x0.a, mid_x0)), iv.mpf((mid_x1, x1.b))), None))  # 左上区間を追加
            stack.append(((iv.mpf((mid_x0, x0.b)), iv.mpf((x1.a, mid_x1))), None))  # 右下区間を追加
            stack.append(((iv.mpf((mid_x0, x0.b)), iv.mpf((mid_x1, x1.b))), None))  # 右上区間を追加
    return best_x, best_f_x  # 最適解とその関数値を返す

# 探索範囲とパラメータの定義
x0_range = iv.mpf([-5, 5])
x1_range = iv.mpf([-5, 5])
eps = 1e-3  # 許容誤差を設定

# 区間分割法で最適解を探索
result, best_f_x = interval_division(objective_with_penalty, x0_range, x1_range, eps)

# 最適解とその関数値を表示
print(f"Optimal solution: x0 = {result[0].mid}, x1 = {result[1].mid}")
print(f"Optimal value: {best_f_x}")

 

以下、実行結果です。

Optimal solution: x0 = [1.0006249999999998757, 1.0006249999999998757], x1 = [1.0018750000000000711, 1.0018750000000000711]
Optimal value: [0.0, 0.00062656249999997338639]

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：(x_0,x_1)=(1.0,1.0)
  • 最適値（Optimal value）：0.0

 

　区間分割法の適用例と性能評価

区間分割法は、低次元の非線形最適化問題に対して有効です。特に、目的関数が連続で、区間演算が容易に行える問題に適しています。

区間分割法の性能は、問題の性質や実装方法に依存します。一般に、区間分割法は、問題の次元が高くなるにつれて、計算量が指数的に増加します。そのため、高次元の問題への適用は難しい場合があります。

また、区間分割法は、厳密解を求めることができますが、計算量が多いという欠点があります。実用的な問題に適用する際は、許容誤差を適切に設定し、計算量とのトレードオフを考慮する必要があります。

区間分割法は、大域的最適性を保証する決定論的手法の一つですが、適用可能な問題のクラスが限定的であるという特徴があります。問題の特性をよく理解し、適切な手法を選択することが重要です。

 

分枝限定法の概要とPythonでの実装

分枝限定法は、探索空間を分枝しながら、限定操作によって非有望な部分空間を削除し、大域的最適解を求める決定論的手法です。

ここでは、分枝限定法の基本的なアイデア、アルゴリズム、Pythonでの実装例について説明します。

 

　分枝限定法の基本的なアイデア

分枝限定法の基本的なアイデアは、以下の通りです。

  • 分枝操作 ：探索空間を部分空間に分割する
  • 限定操作 ：各部分空間に対して、最適解の上界と下界を計算する
  • 枝刈り：上界が現在の最良解より悪い部分空間を削除する

 

　分枝限定法のアルゴリズム

分枝限定法のアルゴリズムは、以下のようなステップからなります。

  • ステップ 1 ：初期の部分空間を設定する
  • ステップ 2 ：部分空間を分枝する（分枝操作）
  • ステップ 3 ：各部分空間に対して、上界と下界を計算する（限定操作）
  • ステップ 4 ：上界が現在の最良解より悪い部分空間を削除する（枝刈り）
  • ステップ 5 ：部分空間が十分小さくなるまで、ステップ 2 ～ 4 を繰り返す

 

分枝変数の選択ルールには、最も広い区間を選ぶ方法や、最も制約式に違反している変数を選ぶ方法などがあります。探索の打ち切り条件は、部分空間の大きさや上下界の差に基づいて設定されます。

 

　Pythonでの分枝限定法の実装

　　1変量目的関数の最適化例

以下で、目的関数 (x-2)^2 を最小化する解を探索します。最適解は x=2 で、最適値は 0 です。

import heapq
from typing import Callable, Tuple

# 目的関数を定義
def objective(x):
    return (x[0] - 2) ** 2

# 分枝限定法の関数を定義
def branch_and_bound(f: Callable[[Tuple[float, ...]], float], x_range: Tuple[Tuple[float, float], ...], eps: float) -> Tuple[float, ...]:
    best_solution = None
    best_value = float('inf')
    # 初期区間の中心で目的関数を評価し、キューに追加します
    mid = tuple((a + b) / 2 for a, b in x_range)
    queue = [(-f(mid), x_range)]

    while queue:
        _, current_range = heapq.heappop(queue)

        mid = tuple((a + b) / 2 for a, b in current_range)
        f_mid = f(mid)

        # これまでの最良値よりも良い結果を見つけた場合、解と値を更新します
        if f_mid < best_value:
            best_solution = mid
            best_value = f_mid

        # 全ての区間の幅がeps以下になるまで続けます
        if all(b - a <= eps for a, b in current_range):
            continue

        # 区間を分割し、それぞれの区間の中心で目的関数を評価し、キューに追加します
        for i in range(len(current_range)):
            if current_range[i][1] - current_range[i][0] > eps:
                left_range = list(current_range)
                left_range[i] = (current_range[i][0], mid[i])
                heapq.heappush(queue, (-f(tuple((a + b) / 2 for a, b in left_range)), tuple(left_range)))

                right_range = list(current_range)
                right_range[i] = (mid[i], current_range[i][1])
                heapq.heappush(queue, (-f(tuple((a + b) / 2 for a, b in right_range)), tuple(right_range)))

    return best_solution

# 探索範囲とパラメータの定義
x_range = ((-5, 5),)  # 探索範囲を設定します。
eps = 1e-3  # 許容誤差を設定します

# 分枝限定法で最適解を探索
result = branch_and_bound(objective, x_range, eps) 

# 最適解とその関数値を表示
print(f"Optimal solution: {result}") 
print(f"Optimal value: {objective(result)}")

 

このコードを簡単に説明します。

目的関数の定義

  • objective(x)関数を定義し、(x[0] - 2) ** 2を計算。
  • この関数は、x = 2で最小値0を取る。

分枝限定法の実装

  • branch_and_bound(f, x_range, eps)関数を定義。
  • fは目的関数、x_rangeは探索範囲、epsは許容誤差。
  • アルゴリズムの流れ
    • 初期区間の中心点で目的関数を評価し、優先度付きキューに追加。
    • キューから区間を取り出し、中心点で目的関数を評価。
    • 評価結果がこれまでの最良値よりも良ければ、解と値を更新。
    • 全ての区間の幅がeps以下になるまで、以下を繰り返す
      • 区間を分割
      • それぞれの中心で目的関数を評価
      • キューに追加

探索範囲とパラメータの定義

  • x_range = ((-5, 5),)で、探索範囲を (-5,5) に設定。
  • eps = 1e-3で、許容誤差を 10^{-3} に設定。

最適解の探索と表示

  • branch_and_bound関数を使用して最適解を探索。
  • 計算された最適解とその時の目的関数の値を表示。

 

以下、実行結果です。

Optimal solution: (2.0001220703125,)
Optimal value: 1.4901161193847656e-08

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：x=2.0
  • 最適値（Optimal value）：0.0

 

　　2変量目的関数の最適化例

以下で、目的関数 (x_0 - 2) ^ 2 + (x_1 - 3) ^ 2 を最小化する解を探索します。最適解は (x_0,x_1)=(2,3) で、最適値は 0 です。

import heapq
from typing import Callable, Tuple

# 目的関数を定義
def objective(x):
    return (x[0] - 2) ** 2 + (x[1] - 3) ** 2

# 分枝限定法の関数を定義
def branch_and_bound(f: Callable[[Tuple[float, float]], float], x_range: Tuple[Tuple[float, float]], eps: float) -> Tuple[float, float]:
    best_solution = None
    best_value = float('inf')
    # 初期区間の中心で目的関数を評価し、キューに追加します。
    mid = tuple((a + b) / 2 for a, b in x_range)
    queue = [(-f(mid), x_range)]
    
    while queue:
        _, current_range = heapq.heappop(queue)  # キューから現在の範囲を取得します。
        
        mid = tuple((a + b) / 2 for a, b in current_range)  # 新しい中心を計算します。
        f_mid = f(mid)  # 中心で目的関数を評価します。
        
        if f_mid < best_value:  # 最良値を更新する場合
            best_solution = mid
            best_value = f_mid
        
        if all(b - a <= eps for a, b in current_range):  # 全ての区間が十分に小さくなった場合
            continue

        # 区間を分割し、キューに追加します。
        for i in range(len(current_range)):
            if current_range[i][1] - current_range[i][0] > eps:
                left_range = list(current_range)
                left_range[i] = (current_range[i][0], mid[i])  # 左側の区間
                heapq.heappush(queue, (-f(tuple((a + b) / 2 for a, b in left_range)), tuple(left_range)))
                
                right_range = list(current_range)
                right_range[i] = (mid[i], current_range[i][1])  # 右側の区間
                heapq.heappush(queue, (-f(tuple((a + b) / 2 for a, b in right_range)), tuple(right_range)))

    return best_solution

# 探索範囲とパラメータの定義
x_range = ((-5, 5), (-5, 5))  # 探索範囲を設定します。
eps = 1e-3  # 許容誤差を設定します。

# 分枝限定法で最適解を探索
result = branch_and_bound(objective, x_range, eps) 

# 最適解とその関数値を表示
print(f"Optimal solution: {result}")
print(f"Optimal value: {objective(result)}")

 

以下、実行結果です。

Optimal solution: (2.0, 3.0)
Optimal value: 0.0

 

  • 最適解（Optimal solution）：(x_0,x_1)=(2.0,3.0)
  • 最適値（Optimal value）：0.0

 

　　多峰性関数を目的関数にした例

先ほどと同様、多数の局所最適解を持つことが知られている以下のAckley関数を目的関数にし最小化する例を示します。最適解は (x_0,x_1)=(-3,4) で、最適値は 0 です。

 

以下、コードです。変数の上下限制約のみ入れています。

import numpy as np
import heapq
from typing import Callable, Tuple

# 目的関数の定義
def objective(x):
    a = 20
    b = 0.2
    c = 2 * np.pi
    n = len(x)
    x_offset = np.array([x[0] + 3, x[1] - 4])
    sum_sq_term = -a * np.exp(-b * np.sqrt(sum(x_offset**2) / n))
    cos_term = -np.exp(sum(np.cos(c * x_offset) / n))
    return sum_sq_term + cos_term + a + np.e

# 分枝限定法の関数を定義
def branch_and_bound(f: Callable[[Tuple[float, float]], float], x_range: Tuple[Tuple[float, float]], eps: float) -> Tuple[float, float]:
    best_solution = None
    best_value = float('inf')
    # 初期区間の中心で目的関数を評価し、キューに追加します。
    mid = tuple((a + b) / 2 for a, b in x_range)
    queue = [(-f(mid), x_range)]
    
    while queue:
        _, current_range = heapq.heappop(queue)  # キューから現在の範囲を取得します。
        
        mid = tuple((a + b) / 2 for a, b in current_range)  # 新しい中心を計算します。
        f_mid = f(mid)  # 中心で目的関数を評価します。
        
        if f_mid < best_value:  # 最良値を更新する場合
            best_solution = mid
            best_value = f_mid
        
        if all(b - a <= eps for a, b in current_range):  # 全ての区間が十分に小さくなった場合
            continue

        # 区間を分割し、キューに追加します。
        for i in range(len(current_range)):
            if current_range[i][1] - current_range[i][0] > eps:
                left_range = list(current_range)
                left_range[i] = (current_range[i][0], mid[i])  # 左側の区間
                heapq.heappush(queue, (-f(tuple((a + b) / 2 for a, b in left_range)), tuple(left_range)))
                
                right_range = list(current_range)
                right_range[i] = (mid[i], current_range[i][1])  # 右側の区間
                heapq.heappush(queue, (-f(tuple((a + b) / 2 for a, b in right_range)), tuple(right_range)))

    return best_solution

# 探索範囲とパラメータの定義
x_range = ((-5, 5), (-5, 5))  # 探索範囲を設定します。
eps = 1e-3  # 許容誤差を設定します。

# 分枝限定法で最適解を探索
result = branch_and_bound(objective, x_range, eps) 

# 最適解とその関数値を表示
print(f"Optimal solution: {result}")
print(f"Optimal value: {objective(result)}")

 

以下、実行結果です。

Optimal solution: (-3.0, 4.0)
Optimal value: 4.440892098500626e-16

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：(x_0,x_1)=(-3.0,4.0)
  • 最適値（Optimal value）：0.0

 

　　制約付き非線形計画問題

先ほどと同様、以下の非線形計画問題を扱います。最適解は、(x_0,x_1)=(1,1)です。

\displaystyle \begin{array}{ll} \displaystyle \min_{x \in \mathbb{R}^2} \quad & f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2 \\ \text{subject to} \quad & x_0-2x_1 - 2 \leq 0 \\ & e^{x_1}- 8 \leq 0 \\ & x_0^2 + x_1^2 - 10 \leq 0 \\ & -5 \leq x_0 \leq 5 \\ & -5 \leq x_1 \leq 5 \end{array}

 

以下、コードです。

import numpy as np
import heapq
from typing import Callable, Tuple

目的関数を定義
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約関数を定義
def constraint_functions(x):
    c1 = x[0] - 2 * x[1] - 2
    c2 = np.exp(x[1]) - 8
    c3 = x[0]**2 + x[1]**2 - 10
    return c1, c2, c3

# ペナルティ関数を定義
def calculate_penalty(x):
    c1, c2, c3 = constraint_functions(x)
    penalty = np.max([0, c1]) + np.max([0, c2]) + np.max([0, c3])
    return penalty

# ペナルティを加えた目的関数を再定義
def objective_with_penalty(x):
    obj = objective(x)
    penalty = calculate_penalty(x)
    return obj + penalty * 1e10

# 分岐限定法の関数を定義
def branch_and_bound(f: Callable[[Tuple[float, float]], float], x_range: Tuple[Tuple[float, float]], eps: float) -> Tuple[float, float]:
    best_solution = None
    best_value = float('inf')
    # 初期区間の中心で目的関数を評価し、キューに追加します
    mid = tuple((a + b) / 2 for a, b in x_range)
    queue = [(-f(mid), x_range)]
    
    while queue:
        _, current_range = heapq.heappop(queue)
        
        mid = tuple((a + b) / 2 for a, b in current_range)
        f_mid = f(mid)
        
        # これまでの最良値よりも良い結果を見つけた場合、解とその値を更新します
        if f_mid < best_value:
            best_solution = mid
            best_value = f_mid
        
        # 全ての区間の幅がeps以下になるまで続けます
        if all(b - a <= eps for a, b in current_range):
            continue

        # 区間を分割し、それぞれの区間の中心で目的関数を評価し、キューに追加します
        for i in range(len(current_range)):
            if current_range[i][1] - current_range[i][0] > eps:
                left_range = list(current_range)
                left_range[i] = (current_range[i][0], mid[i])
                heapq.heappush(queue, (-f(tuple((a + b) / 2 for a, b in left_range)), tuple(left_range)))
                
                right_range = list(current_range)
                right_range[i] = (mid[i], current_range[i][1])
                heapq.heappush(queue, (-f(tuple((a + b) / 2 for a, b in right_range)), tuple(right_range)))

    return best_solution

# 探索範囲とパラメータの定義
x_range = ((-5, 5), (-5, 5))  # 探索範囲を設定します。
eps = 1e-3  # 許容誤差を設定します

# 分岐限定法で最適解を探索
result = branch_and_bound(objective_with_penalty, x_range, eps)

# 最適解とその関数値を表示
print(f"Optimal solution: {result}")
print(f"Optimal value: {objective(result)}")

 

以下、実行結果です。

Optimal solution: (1.0, 1.0)
Optimal value: 0.0

 

  • 最適解（Optimal solution）：(x_0,x_1)=(1.0,1.0)
  • 最適値（Optimal value）：0.0

 

　分枝限定法の適用例と性能評価

分枝限定法は、整数計画問題や非凸非線形計画問題に対して有効です。特に、問題の数学的構造を利用した強力な限定操作を行うことができる場合に、効率的に解を求めることができます。

分枝限定法の性能は、問題の性質や実装方法に大きく依存します。分枝操作や限定操作の設計には、問題に関する深い洞察が必要です。また、枝刈りの効果を最大限に引き出すためには、良い上界と下界を計算する必要があります。

分枝限定法は、大域的最適性を保証する決定論的手法の一つですが、計算量が指数的になるという欠点があります。実用的な問題に適用する際は、問題のサイズや構造を考慮し、適切な実装方法を選択する必要があります。

 

リプシッツ最適化の概要とPythonでの実装

リプシッツ最適化は、目的関数がリプシッツ連続であることを利用した大域的最適化手法です。

ここでは、リプシッツ最適化の基本的なアイデア、アルゴリズム、Pythonでの実装例について説明します。

 

　リプシッツ最適化の基本的なアイデア

関数 f: X \to \mathbb{R} がリプシッツ連続であるとは、ある定数 L > 0 が存在して、任意の x, y \in X に対して以下の不等式が成り立つことをいいます。

\displaystyle |f(x) - f(y)| \leq L |x - y|

この定数 L をリプシッツ定数と呼びます。リプシッツ最適化は、目的関数のリプシッツ定数を利用して、大域的最適解の存在範囲を絞り込む手法です。

 

　リプシッツ最適化のアルゴリズム

リプシッツ最適化のアルゴリズムは、以下のようなステップからなります。

  • ステップ 1 ：探索点を初期化する
  • ステップ 2 ：探索点の中で目的関数値が最小の点を求める
  • ステップ 3 ：最小点を中心として、リプシッツ定数を利用して、最適解の存在範囲を求める
  • ステップ 4 ：存在範囲内でランダムに新しい探索点を生成する
  • ステップ 5 ：ステップ 2 ～ 4 を繰り返す

 

リプシッツ定数が小さいほど、最適解の存在範囲を狭く絞り込むことができます。

 

　Pythonでのリプシッツ最適化の実装

　　1変量目的関数の最適化例

以下で、目的関数 (x-2)^2 を最小化する解を探索します。最適解は x=2 で、最適値は 0 です。

import numpy as np

# 目的関数の定義
def objective(x):
    return (x[0] - 2) ** 2

# リプシッツ最適化関数の定義
def lipschitz_optimization(f, x_range, L, n_iter):
    dim = len(x_range)  # 次元数 
    best_solution = None  # 最適解の初期値
    best_value = float('inf')  # 最小値の初期値
    
    # ランダムな点を生成
    points = np.random.uniform(
        low=x_range[:, 0], 
        high=x_range[:, 1], 
        size=(int(n_iter), dim))
    values = np.apply_along_axis(f, 1, points)
    
    # 反復処理
    for i in range(int(n_iter)):
        # 最小値とそのインデックスを探索
        min_index = np.argmin(values)
        min_point = points[min_index]
        min_value = values[min_index]
        
        # 最小値がこれまでの最小値より小さい場合、更新
        if min_value < best_value:
            best_solution = min_point
            best_value = min_value
        
        # 新しい点を生成
        radius = (best_value - min_value) / L
        new_point = np.random.uniform(
            low=np.maximum(min_point - radius, x_range[:, 0]),
            high=np.minimum(min_point + radius, x_range[:, 1]))
        
        # 新しい点を追加
        points[i] = new_point
        values[i] = f(new_point)
    
    # 最適解を返す
    return best_solution

# 探索範囲とパラメータの定義
x_range = np.array([[-5, 5]])
L = 100
n_iter = 1e+3

# リプシッツ最適化で最適解を探索
result = lipschitz_optimization(objective, x_range, L, n_iter)

# 最適解とその関数値を表示
print(f"Optimal solution: {result}")
print(f"Optimal value: {objective(result)}")

 

このコードを簡単に説明します。

目的関数の定義

  • objective(x)関数を定義し、(x[0] - 2) ** 2を計算。

リプシッツ最適化関数の定義

  • lipschitz_optimization(f, x_range, L, n_iter)でリプシッツ最適化を行う関数を定義。fは目的関数、x_rangeは探索範囲、Lはリプシッツ定数、n_iterは反復回数。
  • アルゴリズムの流れ
    • ランダムな点の生成と初期評価
      • 探索範囲内でランダムに点を生成。
      • それらに対して目的関数の値を計算。
    • 反復処理
      • 各反復で、最小値を持つ点を探し、その点と値を更新する。
      • 新しい点を生成し、その点で目的関数を評価、ポイントセットに追加。
    • 最適解の更新
      • これまでの最小値と比較
      • 新しい点がこれまでの最小値よりも小さい場合、最適解と最小値を更新。
    • 新しい点の生成
      • 新しい点は、現在の最適解周辺で、許容される範囲内（リプシッツ定数に基づく）でランダムに選ばれる。

探索範囲とパラメータの定義

  • x_range = np.array([[-5, 5]])で、探索範囲を設定。
  • L = 100でリプシッツ定数を、n_iter = 1e+3で反復回数を設定。

最適解の探索と表示

  • 計算された最適解とその時の目的関数の値を表示。

 

以下、実行結果です。

Optimal solution: [1.99999289]
Optimal value: 5.048695467079511e-11

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：x=2.0
  • 最適値（Optimal value）：0.0

 

　　2変量目的関数の最適化例

以下で、目的関数 (x_0 - 2) ^ 2 + (x_1 - 3) ^ 2 を最小化する解を探索します。最適解は (x_0,x_1)=(2,3) で、最適値は 0 です。

import numpy as np

# 目的関数を定義します
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約関数を定義します
def constraint_functions(x):
    c1 = x[0] - 2 * x[1] - 2
    c2 = np.exp(x[1]) - 8
    c3 = x[0]**2 + x[1]**2 - 10
    return c1, c2, c3

# ペナルティ関数を計算します
def calculate_penalty(x):
    c1, c2, c3 = constraint_functions(x)
    penalty = np.max([0, c1]) + np.max([0, c2]) + np.max([0, c3])
    return penalty

# ペナルティを加えた目的関数を定義します
def objective_with_penalty(x):
    obj = objective(x)
    penalty = calculate_penalty(x)
    return obj + penalty * 1e10

# リプシッツ最適化関数を定義します
def lipschitz_optimization(f, x_range, L, n_iter):
    dim = len(x_range)  # 次元数
    best_solution = None  # 最適解の初期値
    best_value = float('inf')  # 最小値の初期値
    
    # ランダムに点を生成します
    points = np.random.uniform(
        low=x_range[:, 0], 
        high=x_range[:, 1], 
        size=(int(n_iter), 
        dim))
    values = np.apply_along_axis(f, 1, points)
    
    # 反復処理を実行します
    for i in range(int(n_iter)):
        min_index = np.argmin(values)  # 最小値のインデックスを取得します
        min_point = points[min_index]  # 最小値の点を取得します
        min_value = values[min_index]  # 最小値を取得します
        
        # 最小値がこれまでの最小値より小さい場合、最適解を更新します
        if min_value < best_value:
            best_solution = min_point
            best_value = min_value
        
        # 新しい点を生成し、探索範囲を更新します
        radius = (best_value - min_value) / L
        new_point = np.random.uniform(
            low=np.maximum(min_point - radius, x_range[:, 0]),
            high=np.minimum(min_point + radius, x_range[:, 1]))
        
        # 新しい点を点集合に追加します
        points[i] = new_point
        values[i] = f(new_point)
    
    # 最適解を返します
    return best_solution

# 探索範囲とパラメータの定義
x_range = np.array([[-5, 5], [-5, 5]])
L = 100
n_iter = 1e+3

# リプシッツ最適化で最適解を探索
result = lipschitz_optimization(objective, x_range, L, n_iter)

# 最適解とその関数値を表示
print(f"Optimal solution: {result}")
print(f"Optimal value: {objective(result)}")

 

以下、実行結果です。

Optimal solution: [2.00020143 2.99966573]
Optimal value: 1.5230960876838183e-07

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：(x_0,x_1)=(2.0,3.0)
  • 最適値（Optimal value）：0.0

 

　　多峰性関数を目的関数にした例

先ほどと同様、多数の局所最適解を持つことが知られている以下のAckley関数を目的関数にし最小化する例を示します。最適解は (x_0,x_1)=(-3,4) で、最適値は 0 です。

 

以下、コードです。変数の上下限制約のみ入れています。

import numpy as np

# 目的関数の定義
def objective(x):
    a = 20
    b = 0.2
    c = 2 * np.pi
    n = len(x)
    x_offset = np.array([x[0] + 3, x[1] - 4])
    sum_sq_term = -a * np.exp(-b * np.sqrt(sum(x_offset**2) / n))
    cos_term = -np.exp(sum(np.cos(c * x_offset) / n))
    return sum_sq_term + cos_term + a + np.e

# リプシッツ最適化関数を定義します
def lipschitz_optimization(f, x_range, L, n_iter):
    dim = len(x_range)  # 次元数
    best_solution = None  # 最適解の初期値
    best_value = float('inf')  # 最小値の初期値
    
    # ランダムに点を生成します
    points = np.random.uniform(
        low=x_range[:, 0], 
        high=x_range[:, 1], 
        size=(int(n_iter), 
        dim))
    values = np.apply_along_axis(f, 1, points)
    
    # 反復処理を実行します
    for i in range(int(n_iter)):
        min_index = np.argmin(values)  # 最小値のインデックスを取得します
        min_point = points[min_index]  # 最小値の点を取得します
        min_value = values[min_index]  # 最小値を取得します
        
        # 最小値がこれまでの最小値より小さい場合、最適解を更新します
        if min_value < best_value:
            best_solution = min_point
            best_value = min_value
        
        # 新しい点を生成し、探索範囲を更新します
        radius = (best_value - min_value) / L
        new_point = np.random.uniform(
            low=np.maximum(min_point - radius, x_range[:, 0]),
            high=np.minimum(min_point + radius, x_range[:, 1]))
        
        # 新しい点を点集合に追加します
        points[i] = new_point
        values[i] = f(new_point)
    
    # 最適解を返します
    return best_solution

# 探索範囲とパラメータを定義します
x_range = np.array([[-5, 5], [-5, 5]])
L = 100
n_iter = 1e+7

# リプシッツ最適化で最適解を探索
result = lipschitz_optimization(objective, x_range, L, n_iter)

# 最適解とその関数値を表示
print(f"Optimal solution: {result}")
print(f"Optimal value: {objective(result)}")

 

以下、実行結果です。

Optimal solution: [-3.00004028  3.999941  ]
Optimal value: 0.00020219320324033063

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：(x_0,x_1)=(-3.0,4.0)
  • 最適値（Optimal value）：0.0

 

　　制約付き非線形計画問題

先ほどと同様、以下の非線形計画問題を扱います。最適解は、(x_0,x_1)=(1,1)です。

\displaystyle \begin{array}{ll} \displaystyle \min_{x \in \mathbb{R}^2} \quad & f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2 \\ \text{subject to} \quad & x_0-2x_1 - 2 \leq 0 \\ & e^{x_1}- 8 \leq 0 \\ & x_0^2 + x_1^2 - 10 \leq 0 \\ & -5 \leq x_0 \leq 5 \\ & -5 \leq x_1 \leq 5 \end{array}

 

以下、コードです。

import numpy as np

# 目的関数を定義します
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約関数を定義します
def constraint_functions(x):
    c1 = x[0] - 2 * x[1] - 2
    c2 = np.exp(x[1]) - 8
    c3 = x[0]**2 + x[1]**2 - 10
    return c1, c2, c3

# ペナルティ関数を計算します
def calculate_penalty(x):
    c1, c2, c3 = constraint_functions(x)
    penalty = np.max([0, c1]) + np.max([0, c2]) + np.max([0, c3])
    return penalty

# ペナルティを加えた目的関数を定義します
def objective_with_penalty(x):
    obj = objective(x)
    penalty = calculate_penalty(x)
    return obj + penalty * 1e10

# リプシッツ最適化関数を定義します
def lipschitz_optimization(f, x_range, L, n_iter):
    dim = len(x_range)  # 次元数
    best_solution = None  # 最適解の初期値
    best_value = float('inf')  # 最小値の初期値
    
    # ランダムに点を生成します
    points = np.random.uniform(
        low=x_range[:, 0], 
        high=x_range[:, 1], 
        size=(int(n_iter), 
        dim))
    values = np.apply_along_axis(f, 1, points)
    
    # 反復処理を実行します
    for i in range(int(n_iter)):
        min_index = np.argmin(values)  # 最小値のインデックスを取得します
        min_point = points[min_index]  # 最小値の点を取得します
        min_value = values[min_index]  # 最小値を取得します
        
        # 最小値がこれまでの最小値より小さい場合、最適解を更新します
        if min_value < best_value:
            best_solution = min_point
            best_value = min_value
        
        # 新しい点を生成し、探索範囲を更新します
        radius = (best_value - min_value) / L
        new_point = np.random.uniform(
            low=np.maximum(min_point - radius, x_range[:, 0]),
            high=np.minimum(min_point + radius, x_range[:, 1]))
        
        # 新しい点を点集合に追加します
        points[i] = new_point
        values[i] = f(new_point)
    
    # 最適解を返します
    return best_solution

# 探索範囲とパラメータの定義
x_range = np.array([[-5, 5], [-5, 5]])
L = 100
n_iter = 1e+3

# リプシッツ最適化で最適解を探索
result = lipschitz_optimization(objective, x_range, L, n_iter)

# 最適解とその関数値を表示
print(f"Optimal solution: {result}")
print(f"Optimal value: {objective(result)}")

 

以下、実行結果です。

Optimal solution: [0.99982209 0.99960475]
Optimal value: 1.8739385868110952e-07

 

以下は小数点2桁目を四捨五入した結果です。

  • 最適解（Optimal solution）：(x_0,x_1)=(1.0,1.0)
  • 最適値（Optimal value）：0.0

 

決定論的手法の特徴と適用上の留意点

決定論的大域的最適化手法は、大域的最適性を保証できる強力な手法ですが、適用にはいくつかの留意点があります。

ここでは、決定論的手法の長所と短所、適用上の留意点について説明します。

 

　決定論的手法の長所

決定論的手法には、以下のような長所があります。

大域的最適性の保証
決定論的手法は、理論的に大域的最適性を保証することができます。これは、メタヒューリスティクスにはない大きな利点です。

厳密解の導出
決定論的手法は、数値的な誤差を除いて、厳密な最適解を求めることができます。これは、高い精度が要求される問題に適しています。

問題の構造の利用
決定論的手法は、問題の数学的構造を利用することで、効率的な探索を行うことができます。例えば、凸性や単調性などの性質を利用することで、強力な限定操作を行うことができます。

 

　決定論的手法の短所

決定論的手法には、以下のような短所もあります。

計算量の爆発
決定論的手法は、問題のサイズが大きくなると、計算量が指数的に増加する傾向があります。これは、高次元の問題や大規模な問題への適用を難しくしています。

問題の定式化の難しさ
決定論的手法を適用するためには、問題を適切に定式化する必要があります。しかし、現実の問題を数理最適化問題として定式化することは容易ではありません。

非線形制約への対応の難しさ
決定論的手法は、非線形の制約条件を扱うことが難しい場合があります。特に、非凸の制約条件がある場合は、限定操作の設計が困難になります。

 

　決定論的手法の適用上の留意点

決定論的手法を適用する際は、以下のような点に留意する必要があります。

問題の定式化
決定論的手法を適用するためには、問題を適切に定式化する必要があります。目的関数や制約条件の設定が不適切だと、良い解が得られない可能性があります。

計算量の管理
決定論的手法は、計算量が爆発的に増加する可能性があるため、計算量を適切に管理する必要があります。問題のサイズや求める解の精度に応じて、打ち切り条件を設定するなどの工夫が必要です。

効率的なアルゴリズムの選択
決定論的手法には、様々なアルゴリズムがあります。問題の特性に合ったアルゴリズムを選択することが重要です。また、アルゴリズムのパラメータも、問題に応じて適切に設定する必要があります。

 

決定論的手法は、大域的最適性を保証できる強力な手法ですが、適用には注意が必要です。問題の特性をよく理解し、適切な定式化とアルゴリズムの選択を行うことが重要です。

 

決定論的手法とメタヒューリスティクスの使い分け

非線形最適化問題を解く際には、決定論的手法とメタヒューリスティクスのどちらを使うべきか、判断に迷うことがあります。

ここでは、両者の比較を行い、問題の特性に応じた手法の選択について議論します。

 

　決定論的手法とメタヒューリスティクスの比較

決定論的手法とメタヒューリスティクスの主な違いは以下の通りです。

特性 決定論的手法 メタヒューリスティクス
大域的最適性の保証 理論的に保証される 保証されない（確率的な手法）
計算効率 問題の数学的構造を利用して効率的だが、問題の次元が高いと計算量が指数的に増加する可能性がある 比較的スケーラブルだが、収束速度が遅い場合がある
問題の定式化の難易度 問題を適切に定式化する必要がある。特に非線形制約がある場合は定式化が難しい 問題の定式化に対する要求が緩やかで、非線形制約がある場合でも適用しやすい

 

簡単に言うと、大域的最適解にこだわるなら決定論的手法、スピードを重視するならメタヒューリスティックス、といった感じです。

 

　問題の特性に応じた手法の選択

問題の特性に応じて、適切な手法を選択することが重要です。以下のような観点から、手法を選択することができます。

問題の規模と次元
問題の規模が小さく、次元が低い場合は、決定論的手法が適しています。問題の規模が大きく、次元が高い場合は、メタヒューリスティクスが適しています。

目的関数の性質
目的関数が滑らかで、勾配情報が利用可能な場合は、決定論的手法が適しています。目的関数が非滑らかで、勾配情報が利用できない場合は、メタヒューリスティクスが適しています。

制約条件の種類
線形制約条件のみの場合は、決定論的手法が適しています。非線形制約条件がある場合は、メタヒューリスティクスが適しています。

 

実際の問題では、これらの観点が複合的に絡み合っています。問題の特性をよく理解し、複数の手法を試すことが重要です。

 

　ハイブリッド手法の可能性

決定論的手法とメタヒューリスティクスは、相互に補完的な関係にあります。両者を組み合わせたハイブリッド手法を使うことで、それぞれの長所を活かすことができます。

決定論的手法とメタヒューリスティクスの組み合わせ
メタヒューリスティクスで得られた解を、決定論的手法の初期解として使うことで、効率的に高精度な解を得ることができます。また、決定論的手法で求めた解の近傍を、メタヒューリスティクスで集中的に探索することで、大域的最適解を得ることができます。

大域的最適性と計算効率のバランス
ハイブリッド手法を使うことで、大域的最適性と計算効率のバランスを取ることができます。例えば、決定論的手法で大まかな解を求めた後、メタヒューリスティクスでその解の近傍を探索することで、大域的最適性を保ちつつ、計算効率を向上させることができます。

 

ハイブリッド手法は、非線形最適化問題に対する有力なアプローチの一つです。問題の特性に合わせて、適切な手法を組み合わせることが重要です。

 

まとめ

今回は、非線形計画問題の大域的最適化に対する決定論的アプローチについて解説しました。

区間分割法と分枝限定法は、大域的最適性を保証する代表的な決定論的手法であり、区間演算や問題の数学的構造を利用することで、効率的に大域的最適解を求めることができます。また、リプシッツ最適化は、目的関数のリプシッツ定数を利用して、大域的最適解を求める手法であり、勾配情報が利用できない場合や、目的関数の評価に時間がかかる場合に有効です。

決定論的手法は、大域的最適性を保証できる一方で、計算量の爆発や問題の定式化の難しさなどの課題があります。したがって、問題の特性をよく理解し、適切な手法を選択することが重要です。さらに、決定論的手法とメタヒューリスティクスは、相互に補完的な関係にあるため、両者を組み合わせたハイブリッド手法を使うことで、大域的最適性と計算効率のバランスを取ることができます。

非線形計画問題の大域的最適化は、現実世界の様々な問題に応用可能な重要な技術であり、問題の特性に合わせて、決定論的手法とメタヒューリスティクスを適切に使い分けることが求められます。

次回は、ハイブリッド手法の詳細と、実際の応用事例について解説します。

【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第4回】Pythonによる大域的最適化のハイブリッド手法 –

初めての方へ
メルマガ
サービス
お問合せ