前回の第1回の記事では、Two-Model法を用いてアップリフトスコアを計算する方法を学びました。
前回出力したアップリフトスコアの数値の羅列だけでは、どの顧客にアプローチすべきか、モデルがどの程度うまく機能しているかを判断することは困難です。
ということで、アップリフト分析の結果を視覚的に理解し、ビジネス上の意思決定に活用するための可視化手法を解説します。
効果的な可視化は、データに隠された物語を明らかにし、経営層や現場のマーケティング担当者が直感的に理解できる形で情報を提示します。
今回は、前回出力したアップリフトスコアのCSVファイル(uplift_analysis_results.csv)を使い、累積効果曲線、Qini曲線、セグメント別効果分析という3つの重要な可視化手法の基礎的な内容を説明していきます。
Contents
累積効果曲線:ROIを最大化する顧客選定
累積効果とは?
累積効果曲線は、アップリフトスコアの高い顧客から順にアプローチした場合の効果を可視化する手法です。
顧客をアップリフトスコア \hat{\tau}(x_i) で降順でソートし、上位 k % の顧客を選択した場合の累積効果 G(k) を以下のように定義します。
$$\displaystyle G(k) = \frac{1}{n_k} \sum_{i \in S_k} \left[ Y_i \cdot T_i – Y_i \cdot (1 – T_i) \cdot \frac{p}{1-p} \right]$$
ここで、S_k は上位 k % に含まれる顧客の集合、n_k はその人数、p は全体での処置群の割合を表します。
Y_i \cdot T_i は処置群での購入者数を表し、Y_i \cdot (1 - T_i) は対照群での購入者数を表します。対照群の項に \frac{p}{1-p} という重みを掛けているのは、処置群と対照群のサンプルサイズの違いを調整するためです。
簡易版として、次のような平均的累積効果 \bar{G}(k) を考えることもできます。
$$\displaystyle \bar{G}(k) = \frac{\displaystyle \sum_{i \in S_k} (Y_i|T_i=1)}{n_{k,T=1}} – \frac{\displaystyle \sum_{i \in S_k} (Y_i|T_i=0)}{n_{k,T=0}}$$
この式は、選択された顧客群における処置群の平均成功率と対照群の平均成功率の差を表しており、より直感的に理解しやすい形となっています。
前回のアップリフトの結果を読み込み
それでは、前回作成したアップリフトモデル(Two-Model法)の結果を読み込みましょう。
まず、第1回で計算したアップリフト分析の結果を保存したCSVファイル(uplift_analysis_results.csv)を読み込みます。ここで、必要なライブラリも併せてインポートします。
以下、コードです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
# 第1回の分析結果を読み込む
data = pd.read_csv('uplift_analysis_results.csv')
print(f"データサイズ: {len(data)}行")
print(f"カラム: {data.columns.tolist()}")
print(f"\nデータの概要:")
print(data.describe())
以下、実行結果です。
データサイズ: 1500行
カラム: ['age', 'purchase_history', 'last_purchase_days', 'email_open_rate', 'uplift_score', 'treatment', 'actual_purchase']
データの概要:
age purchase_history last_purchase_days email_open_rate \
count 1500.000000 1500.000000 1500.000000 1500.000000
mean 35.155013 5.000000 30.808248 0.285448
std 9.906750 2.199824 31.162798 0.160688
min 4.804878 0.000000 0.038902 0.003482
25% 28.531849 3.000000 8.849122 0.159892
50% 35.174812 5.000000 20.588723 0.260370
75% 41.358947 6.000000 43.154383 0.389858
max 67.430930 15.000000 216.619996 0.901874
uplift_score treatment actual_purchase
count 1500.000000 1500.000000 1500.000000
mean 0.246967 0.510667 0.333333
std 0.221353 0.500053 0.471562
min -0.400000 0.000000 0.000000
25% 0.090000 0.000000 0.000000
50% 0.250000 1.000000 0.000000
75% 0.400000 1.000000 1.000000
max 0.840000 1.000000 1.000000
読み込んだデータセットは、アップリフト分析に関連する情報を含むもので、以下の変数を持っています。
- age (float64): 顧客の年齢
- purchase_history (int64): 過去の購入回数
- last_purchase_days (float64): 最後の購入からの日数
- email_open_rate (float64): メールの開封率
- uplift_score (float64): アップリフトスコア(顧客がキャンペーンに反応する可能性を示すスコア)
- treatment (int64): キャンペーンの対象かどうか(1: 対象、0: 非対象)
- actual_purchase (int64): 実際に購入したかどうか(1: 購入、0: 購入なし)
データセットには1500件のレコードが含まれており、基本統計量は以下です。
- age: 平均35.16歳、最小4.80歳、最大67.43歳。
- purchase_history: 平均5回、最小0回、最大15回。
- last_purchase_days: 平均30.81日、最小0.04日、最大216.62日。
- email_open_rate: 平均0.285、最小0.003、最大0.902。
- uplift_score: 平均0.247、最小-0.4、最大0.84。
- treatment: 平均0.511(約半数がキャンペーン対象)。
- actual_purchase: 平均0.333(約33%が購入)。
このデータは、顧客の行動やキャンペーンの効果を分析するために使用されます。
Pythonによる累積効果曲線の実装
それでは、前回作成したTwo-Model法の結果を使用して、累積効果曲線を描画してみましょう。
アップリフトスコアの高い順にインデックスを並べ替え、各パーセンタイルで選択された顧客群における処置群と対照群の購入率の差を計算することで、累積効果を計算する関数calculate_cumulative_gainを作成します。
以下、コードです。
"""
累積効果を計算する関数
Parameters:
-----------
y_true : array-like
実際の購入フラグ
uplift_scores : array-like
アップリフトスコア
treatment : array-like
処置フラグ(1=クーポンあり、0=なし)
n_bins : int
分割数(デフォルト20)
Returns:
--------
percentiles : list
パーセンタイル
gains : list
各パーセンタイルでの累積効果
"""
def calculate_cumulative_gain(y_true, uplift_scores, treatment, n_bins=20):
# スコアの降順でインデックスをソート
sorted_indices = np.argsort(-uplift_scores)
percentiles = []
gains = []
for i in range(1, n_bins + 1):
# 上位i/n_bins割合の顧客を選択
n_selected = int(len(sorted_indices) * i / n_bins)
selected_indices = sorted_indices[:n_selected]
# 選択された顧客群での処置群と対照群の成果を計算
selected_treatment = treatment[selected_indices]
selected_outcome = y_true[selected_indices]
# 処置群の平均購入率
treatment_outcome = selected_outcome[selected_treatment == 1].mean()
# 対照群の平均購入率
control_outcome = selected_outcome[selected_treatment == 0].mean()
# 累積効果(差分)
gain = treatment_outcome - control_outcome if not np.isnan(treatment_outcome - control_outcome) else 0
percentiles.append(i * 100 / n_bins)
gains.append(gain)
return percentiles, gains
次に、この累積効果を描画する関数plot_cumulative_gain_curveを作成します。
以下、コードです。
"""
累積効果曲線を描画する関数
"""
def plot_cumulative_gain_curve(y_true, uplift_scores, treatment):
percentiles, gains = calculate_cumulative_gain(
y_true, # 実際の購入フラグ
uplift_scores, # アップリフトスコア
treatment, # 処置フラグ
n_bins=50 # 分割数
)
plt.figure(figsize=(10, 6))
# 累積効果曲線
plt.plot(
percentiles,
gains,
'b-',
linewidth=2.5,
label='累積効果曲線'
)
# ゼロラインを追加
plt.axhline(y=0, color='gray', linestyle='--', alpha=0.7)
# 最大効果点をマーク
max_gain_idx = np.argmax(gains)
plt.scatter(
percentiles[max_gain_idx],
gains[max_gain_idx],
color='red',
s=100,
zorder=5
)
plt.annotate(
f'最大効果\n({percentiles[max_gain_idx]:.0f}%, {gains[max_gain_idx]:.3f})',
xy=(percentiles[max_gain_idx], gains[max_gain_idx]),
xytext=(percentiles[max_gain_idx] + 10, gains[max_gain_idx] - 0.01),
arrowprops=dict(arrowstyle='->', color='red'),
fontsize=10
)
plt.xlabel('顧客の割合 (%)', fontsize=12)
plt.ylabel('平均アップリフト効果', fontsize=12)
plt.title(
'累積効果曲線:どこまでアプローチすべきか?',
fontsize=14,
fontweight='bold'
)
plt.grid(True, alpha=0.3)
plt.legend(fontsize=11)
# 背景に薄い色を追加
plt.fill_between(
percentiles,
0,
gains,
where=(np.array(gains) > 0),
alpha=0.1,
color='blue',
label='正の効果領域'
)
plt.tight_layout()
plt.show()
これらの関数を使い、累積効果を計算し可視化します。
以下、コードです。
plot_cumulative_gain_curve(
data['actual_purchase'].values,
data['uplift_score'].values,
data['treatment'].values
)
以下、実行結果です。
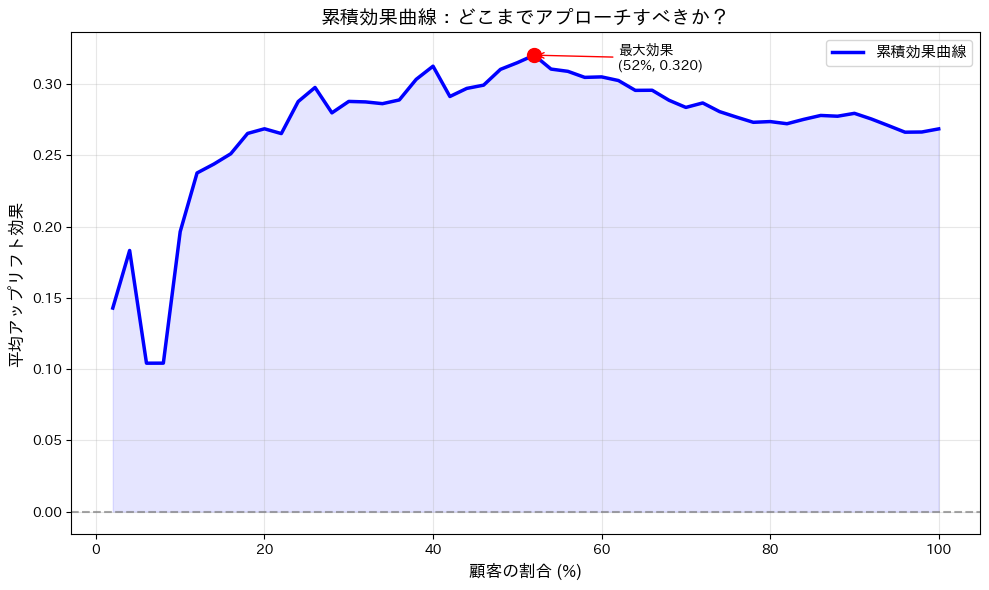
この累積効果曲線の見方について、簡単に解説します。
- 横軸: 顧客の割合(パーセンタイル)
- 縦軸: 平均アップリフト効果(処置群と対照群の購入率の差)
以下、主な要素です。
| 要素 | 説明 |
|---|---|
| 青い線 (累積効果曲線) | 顧客をスコア順に選別した際の累積効果を示します。例えば、最初の10%の顧客では累積効果が約20%となり、これは処置群が対照群よりも約20%高い購入率を持つことを意味します。 |
| 赤い点 (最大効果点) | 累積効果が最大となるポイントを示します。この点の座標は、最大効果が得られる顧客の割合とその効果値を表し、どの程度の顧客にアプローチすべきかを判断する参考にできます。 |
| 灰色の破線 (ゼロライン) | 効果がゼロの基準を示します。累積効果がこの線を超える領域では、処置が対照群よりも効果的であることを意味します。 |
| 青い影 (正の効果領域) | 累積効果が正となる領域を視覚的に強調しています。この領域は、処置が有効である顧客群を示します。 |
この結果を基に、マーケティング施策のターゲットを絞り込むことができます。
例えば、累積効果が最大となる顧客の割合までをターゲットとすることで、効果的な施策を実施することが可能です。
Qini曲線:モデル性能の総合評価
Qini係数とは?
Qini曲線 g(\cdot) は、アップリフトモデルの性能を評価するための標準的な手法です。
この曲線は、ジニ係数の概念をアップリフト分析に応用したもので、施策効果がどの程度特定の顧客群に集中しているかを測定します。
Qini曲線上の点 (f, g(f)) は、全顧客の割合 f に対するQini値 g(f) として定義されます。
$$\displaystyle g(f) = \frac{N_T^{Y=1}(f)}{N_T(f)} – \frac{N_C^{Y=1}(f)}{N_C(f)}$$
ここで、N_T(f) と N_C(f) はそれぞれ上位 f 割合に含まれる処置群と対照群の人数、N_T^{Y=1}(f) と N_C^{Y=1}(f) はその中での購入者数を表します。
正規化されたQini係数 Q は、Qini曲線の下の面積(Area Under the Uplift Curve, AUUC)として計算されます。
$$\displaystyle Q = \int_0^1 g(f) df$$
実際の計算では、台形則を用いて数値積分を行います。
$$\displaystyle Q \approx \sum_{i=1}^{n} \frac{g(f_{i-1}) + g(f_i)}{2} \cdot (f_i – f_{i-1})$$
PythonによるQini曲線の実装
では、モデル性能を評価するためのQini曲線を計算する関数を定義します。
以下、コードです。
"""
Qini曲線の計算
Parameters:
-----------
y_true : array-like
実際の購入フラグ
uplift_scores : array-like
アップリフトスコア
treatment : array-like
処置フラグ
Returns:
--------
fractions : array
顧客の割合
qini_values : array
Qini値
"""
def calculate_qini_curve(y_true, uplift_scores, treatment):
# スコアで降順ソート
indices = np.argsort(-uplift_scores)
y_sorted = y_true[indices]
t_sorted = treatment[indices]
n = len(indices)
fractions = np.arange(0, n + 1) / n
# 累積和の計算
cum_treatment = np.insert(np.cumsum(t_sorted), 0, 0)
cum_control = np.insert(np.cumsum(1 - t_sorted), 0, 0)
cum_y_treatment = np.insert(np.cumsum(y_sorted * t_sorted), 0, 0)
cum_y_control = np.insert(np.cumsum(y_sorted * (1 - t_sorted)), 0, 0)
# Qini値の計算(ゼロ除算を回避)
qini_values = np.zeros(len(fractions))
for i in range(1, len(fractions)):
if cum_treatment[i] > 0 and cum_control[i] > 0:
qini_values[i] = (cum_y_treatment[i] / cum_treatment[i] -
cum_y_control[i] / cum_control[i]) * i / n
return fractions, qini_values
次に、Qini曲線の下の面積を表すAUUC(Area Under the Uplift Curve)を計算する関数と、Qini曲線を描画する関数を定義します。
モデルの相対的な性能を視覚的に理解できるように、この関数ではQini曲線に加えランダムモデル(基準線)を表示します。
以下、コードです。
"""
AUUC(Area Under the Uplift Curve)の計算
"""
def calculate_auuc(fractions, qini_values):
return np.trapz(qini_values, fractions)
"""
Qini曲線を描画する関数
"""
def plot_qini_curve(
y_true,
uplift_scores,
treatment,
model_name="Two-Model"
):
fractions, qini_values = calculate_qini_curve(
y_true,
uplift_scores,
treatment
)
auuc = np.trapz(qini_values, fractions)
# 全体を対象とした時の最終的なQini値
final_qini_value = qini_values[-1]
plt.figure(figsize=(10, 8))
# 1. Qini曲線
plt.plot(fractions * 100, qini_values, 'b-', linewidth=2.5,
label=f'{model_name} (AUUC={auuc:.4f})')
# 2. ランダムモデル
plt.plot([0, 100], [0, final_qini_value], 'k--', linewidth=1.5,
alpha=0.7, label='ランダムモデル')
# 3. 理論的上限
perfect_x = [0, 50, 100]
perfect_y = [0, max(qini_values) * 1.1, final_qini_value]
plt.xlabel('顧客の割合 (%)', fontsize=12)
plt.ylabel('Qini値', fontsize=12)
plt.title(
'Qini曲線:モデル性能の評価',
fontsize=14,
fontweight='bold'
)
plt.grid(True, alpha=0.3)
plt.legend(loc='upper left', fontsize=11)
# AUUCの領域を塗りつぶし
plt.fill_between(
fractions * 100,
0,
qini_values,
alpha=0.1,
color='blue'
)
plt.tight_layout()
plt.show()
これらの関数を使い、を計算し可視化します。
以下、コードです。
# 実際のデータでQini曲線を描画
plot_qini_curve(
data['actual_purchase'].values,
data['uplift_score'].values,
data['treatment'].values
)
# AUUCの値を詳しく分析
fractions, qini_values = calculate_qini_curve(
data['actual_purchase'].values,
data['uplift_score'].values,
data['treatment'].values
)
auuc = calculate_auuc(fractions, qini_values)
print(f"\nモデル性能指標:")
print(f"AUUC (Area Under Uplift Curve): {auuc:.4f}")
print(f"最大Qini値: {max(qini_values):.4f}")
print(f"最大値を達成する顧客割合: {fractions[np.argmax(qini_values)]*100:.1f}%")
以下、実行結果です。
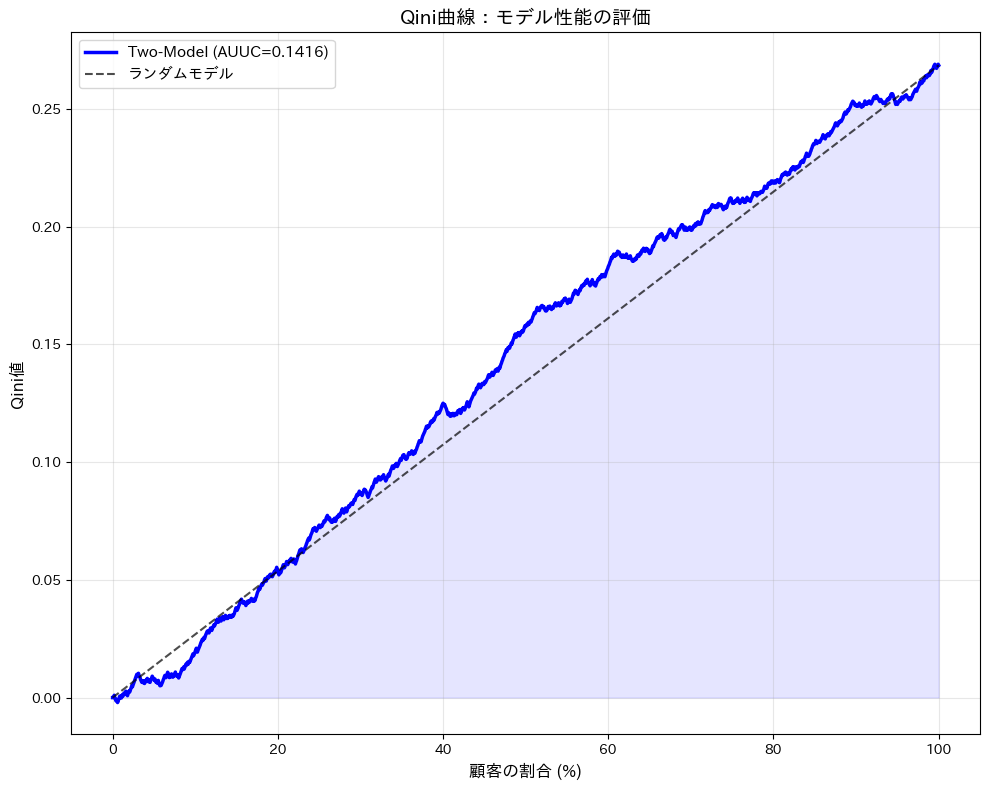
モデル性能指標: AUUC (Area Under Uplift Curve): 0.1416 最大Qini値: 0.2690 最大値を達成する顧客割合: 99.5%
Qini曲線は、アップリフトモデルの性能を評価するための重要な指標です。この曲線は、顧客をスコア順に選別した際の累積効果を視覚的に示しています。
- 横軸: 顧客の割合(パーセンタイル)
- 縦軸: Qini値(処置群と対照群の購入率の差を累積した値)
以下、主な要素です。
| 要素 | 説明 |
|---|---|
| 青い線(Qini曲線) | 顧客をスコア順に選別した際の累積効果を示します。例えば、最初の50%の顧客ではQini値が約0.1416であり、これは処置群が対照群よりも効果的であることを示しています。 |
| ランダムモデル(黒い破線) | ランダムに顧客を選んだ場合の基準線です。この線よりもQini曲線が上にある場合、モデルがランダム選択よりも優れていることを意味します。 |
| AUUC (Area Under the Uplift Curve) | Qini曲線の下の面積を表します。面積が大きいほど、モデルの性能が高いことを示します。今回のAUUCは0.1416であり、完全にランダムに顧客を選んだ場合と比べて、14.16%分より効果的に「施策に反応する顧客」をターゲティングできる、と大まかに解釈できます。 |
| 最大Qini値とその達成割合 | 最大Qini値は0.2690で、これはモデルが最も効果的であるポイントを示します。この値を達成する顧客割合は99.5%であり、ほぼ全ての顧客を対象にした場合に最大効果が得られることを意味します。 |
この結果を基に、マーケティング施策のターゲットを絞り込むことができます。
例えば、Qini曲線が最大となる顧客の割合までをターゲットとすることで、効果的な施策を実施することが可能です。
また、AUUCの値を他のモデルと比較することで、どのモデルが最も効果的であるかを判断できます。
セグメント別ヒートマップ
アップリフト効果は顧客の特性によって大きく異なることがあります。
年齢層と購買履歴という2つの軸でセグメント化し、各セグメントでの平均アップリフト効果を可視化してみましょう。
実際のデータを使用して、どのセグメントに対して施策が最も効果的かを探ります。
まず、セグメント別のアップリフト効果のヒートマップを作成する関数を作ります。
以下、コードです。
"""
セグメント別アップリフト効果のヒートマップを作成
Parameters:
-----------
data : DataFrame
顧客データ
uplift_scores : array-like
アップリフトスコア
age_bins : list
年齢の区切り
purchase_bins : list
購買履歴の区切り
"""
def create_segment_heatmap(
data,
uplift_scores,
age_bins=[20, 30, 40, 50, 60],
purchase_bins=[0, 2, 5, 10, 20]
):
# データのコピーを作成
df = data.copy()
df['uplift_score'] = uplift_scores
# ビニング
df['age_group'] = pd.cut(
df['age'], bins=age_bins,
labels=[f'{age_bins[i]}-{age_bins[i+1]}歳'
for i in range(len(age_bins)-1)]
)
df['purchase_group'] = pd.cut(
df['purchase_history'],
bins=purchase_bins,
labels=[f'{purchase_bins[i]}-{purchase_bins[i+1]}回'
for i in range(len(purchase_bins)-1)]
)
# セグメント別平均アップリフトスコア
segment_matrix = df.pivot_table(
values='uplift_score',
index='purchase_group',
columns='age_group',
aggfunc='mean'
)
# ヒートマップの作成
plt.figure(figsize=(10, 8))
# カラーマップの設定(負の値は赤、正の値は青)
sns.heatmap(
segment_matrix,
annot=True,
fmt='.3f',
cmap='RdBu',
center=0,
cbar_kws={'label': '平均アップリフトスコア'},
linewidths=0.5,
linecolor='gray'
)
plt.title(
'セグメント別アップリフト効果の分析',
fontsize=14,
fontweight='bold'
)
plt.xlabel('年齢層', fontsize=12)
plt.ylabel('購買履歴', fontsize=12)
# 注釈を追加
plt.text(
0.5,
-0.15,
'青色:施策効果が高い | 赤色:施策効果が低い(または逆効果)',
transform=plt.gca().transAxes,
ha='center',
fontsize=10,
bbox=dict(
boxstyle="round,pad=0.3",
facecolor="lightyellow"
)
)
plt.tight_layout()
plt.show()
return segment_matrix
この関数を実行し、セグメント別アップリフト効果のヒートマップを作成します。
以下、コードです。
# 実際のデータでセグメント別ヒートマップを作成
segment_matrix = create_segment_heatmap(data, data['uplift_score'].values)
# セグメント別の統計情報を出力
print("\nセグメント別の分析結果:")
print(f"最も効果が高いセグメント: {segment_matrix.max().max():.3f}")
print(f"最も効果が低いセグメント: {segment_matrix.min().min():.3f}")
print(f"\n効果が高い上位3セグメント:")
top_segments = segment_matrix.unstack().sort_values(ascending=False).head(3)
for (purchase, age), score in top_segments.items():
print(f" 購買履歴{purchase}, {age}: {score:.3f}")
以下、実行結果です。
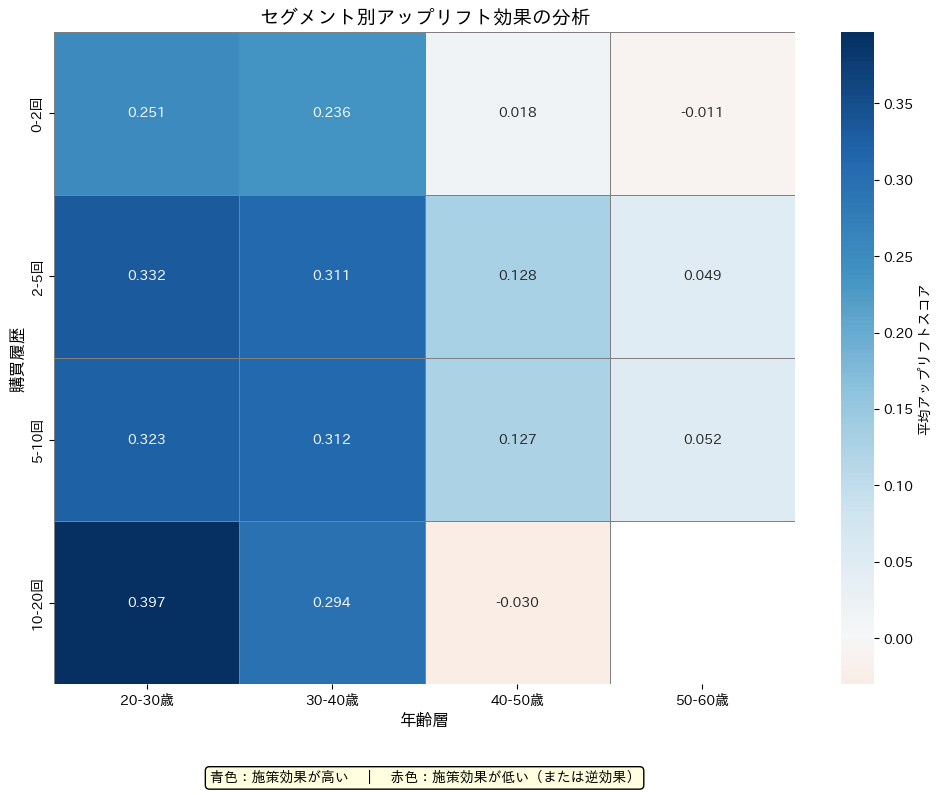
セグメント別の分析結果: 最も効果が高いセグメント: 0.397 最も効果が低いセグメント: -0.030 効果が高い上位3セグメント: 購買履歴20-30歳, 10-20回: 0.397 購買履歴20-30歳, 2-5回: 0.332 購買履歴20-30歳, 5-10回: 0.323
セグメント別ヒートマップは、顧客を年齢層と購買履歴の2軸で分割し、それぞれのセグメントにおける平均アップリフトスコアを視覚的に示しています。
- 横軸: 年齢層(例: 20-30歳, 30-40歳)
- 縦軸: 購買履歴(例: 0-2回, 2-5回)
- 色の濃淡: 平均アップリフトスコア(青色は効果が高い、赤色は効果が低いまたは逆効果)
以下、主な要素です。
| 要素 | 説明 |
|---|---|
| 青色の領域 | 青色が濃いほど、そのセグメントで施策が効果的であることを示します。例えば、”20-30歳”かつ”10-20回”の購買履歴を持つセグメントでは、平均アップリフトスコアが0.397と最も高い効果を示しています。 |
| 赤色の領域 | 赤色が濃いほど、そのセグメントで施策が逆効果である可能性を示します。今回の結果では、最も効果が低いセグメントのスコアは-0.030です。 |
| セグメントの分布 | 年齢層と購買履歴の組み合わせによって、施策の効果が異なることがわかります。特定のセグメントにおいて施策が特に効果的であることが視覚的に確認できます。 |
以下が、最も効果が高いセグメントです。
- 齢層: 20-30歳
- 購買履歴: 10-20回
- 平均アップリフトスコア: 0.397
このヒートマップを活用することで、マーケティング施策のターゲットを絞り込むことができます。
例えば、効果が高いセグメント(青色の領域)に対して重点的に施策を実施することで、効率的なリソース配分が可能です。
一方で、効果が低いまたは逆効果のセグメント(赤色の領域)を避けることで、無駄なコストを削減できます。
アップリフトスコアの分布を可視化します。関数を定義後に実行し表示します。
以下、コードです。
"""
アップリフトスコアの分布を可視化
"""
def plot_score_distribution(uplift_scores, title="アップリフトスコアの分布"):
plt.figure(figsize=(10, 6))
# ヒストグラム
n, bins, patches = plt.hist(
uplift_scores,
bins=50,
alpha=0.7,
color='skyblue',
edgecolor='black'
)
# 色分け(正の値は青、負の値は赤)
for i in range(len(patches)):
if bins[i] + (bins[i+1] - bins[i])/2 < 0:
patches[i].set_facecolor('lightcoral')
# 統計量を表示
mean_score = np.mean(uplift_scores)
median_score = np.median(uplift_scores)
plt.axvline(
0,
color='black',
linestyle='--',
linewidth=2,
label='効果なし'
)
plt.axvline(
mean_score,
color='green',
linestyle='--',
linewidth=2,
label=f'平均値 ({mean_score:.3f})'
)
plt.axvline(
median_score,
color='orange',
linestyle='--',
linewidth=2,
label=f'中央値 ({median_score:.3f})'
)
# パーセンタイル情報
p25 = np.percentile(uplift_scores, 25)
p75 = np.percentile(uplift_scores, 75)
plt.axvspan(p25, p75, alpha=0.2, color='gray',
label=f'四分位範囲 ({p25:.3f} - {p75:.3f})')
plt.xlabel('アップリフトスコア', fontsize=12)
plt.ylabel('顧客数', fontsize=12)
plt.title(title, fontsize=14, fontweight='bold')
plt.legend(loc='upper right', fontsize=10)
plt.grid(True, alpha=0.3, axis='y')
# 統計情報のテキストボックス
stats_text = f'顧客数: {len(uplift_scores):,}\n'
stats_text += f'正の効果: {(uplift_scores > 0).sum():,} ({(uplift_scores > 0).mean():.1%})\n'
stats_text += f'負の効果: {(uplift_scores < 0).sum():,} ({(uplift_scores < 0).mean():.1%})'
plt.text(
0.02,
0.98,
stats_text,
transform=plt.gca().transAxes,
verticalalignment='top',
bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5),
fontsize=10
)
plt.tight_layout()
plt.show()
この関数を実行します。
以下、コードです。
plot_score_distribution(data['uplift_score'].values)
以下、実行結果です。
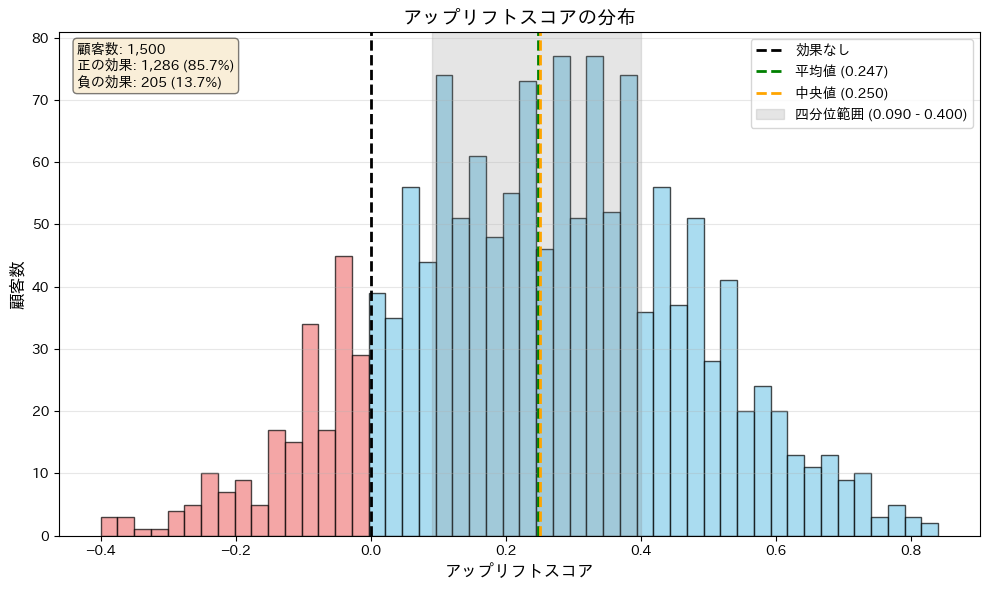
このヒストグラムは、顧客ごとのアップリフトスコアの分布を視覚的に示しています。
- 横軸: アップリフトスコア(施策の効果を示す指標)
- 縦軸: 顧客数
以下、主な要素です。
| 要素 | 説明 |
|---|---|
| スコアの分布 | スコアは正の値と負の値に分布しており、正のスコアは施策が効果的な顧客を、負のスコアは施策が逆効果である顧客を示します。 |
| 統計量の表示 | 緑の破線は平均値、オレンジの破線は中央値、灰色の影はスコアの25%点から75%点までの四分位範囲をそれぞれ表します。 |
| ゼロライン | 黒の破線はスコアがゼロの基準を示します。この線より右側が効果的な顧客、左側が逆効果の顧客の領域です。 |
| 色分け | 正のスコアを持つバーは青色、負のスコアを持つバーは赤色で表示され、効果的な顧客と逆効果の顧客を視覚的に区別できます。 |
| 統計情報のテキストボックス | 全体の顧客数、スコアが正の顧客数とその割合、スコアが負の顧客数とその割合といった集計情報が表示されます。 |
- 正のスコアの顧客: 施策が効果的であるため、積極的にアプローチする
- 負のスコアの顧客: 施策が逆効果である可能性があるため、アプローチを控えるか、別の施策を検討する
また、スコアの分布を分析することで、モデルの性能や施策の全体的な効果を評価することができます。
これまでに実装した可視化手法を組み合わせて、実際のビジネス意思決定に活用する例を見てみましょう。
そのための関数を作成します。
以下、コードです。
"""
アップリフト分析の統合ダッシュボード
"""
def create_uplift_dashboard(data):
fig = plt.figure(figsize=(16, 12))
# アップリフトスコアと関連データを抽出
uplift_scores = data['uplift_score'].values
y_true = data['actual_purchase'].values
treatment = data['treatment'].values
# 1. アップリフトスコアの分布
plt.subplot(2, 2, 1)
n, bins, patches = plt.hist(
uplift_scores,
bins=40,
alpha=0.7,
color='skyblue',
edgecolor='black'
)
for i in range(len(patches)):
if bins[i] + (bins[i+1] - bins[i])/2 < 0:
patches[i].set_facecolor('lightcoral')
plt.axvline(
0,
color='black',
linestyle='--',
linewidth=2
)
plt.axvline(
uplift_scores.mean(),
color='green',
linestyle='--',
linewidth=1.5
)
plt.xlabel('アップリフトスコア')
plt.ylabel('顧客数')
plt.title('スコア分布')
plt.grid(True, alpha=0.3)
# 2. 累積効果曲線
plt.subplot(2, 2, 2)
percentiles, gains = calculate_cumulative_gain(
y_true,
uplift_scores,
treatment,
n_bins=50
)
plt.plot(
percentiles,
gains,
'b-',
linewidth=2.5
)
plt.axhline(
y=0,
color='gray',
linestyle='--',
alpha=0.7
)
max_idx = np.argmax(gains)
plt.scatter(
percentiles[max_idx],
gains[max_idx],
color='red',
s=100,
zorder=5
)
plt.xlabel('顧客の割合 (%)')
plt.ylabel('平均効果')
plt.title('累積効果曲線')
plt.grid(True, alpha=0.3)
# 3. Qini曲線
plt.subplot(2, 2, 3)
fractions, qini_values = calculate_qini_curve(
y_true,
uplift_scores,
treatment
)
auuc = calculate_auuc(
fractions,
qini_values
)
plt.plot(
fractions * 100,
qini_values,
'g-',
linewidth=2.5,
label=f'AUUC={auuc:.4f}'
)
final_qini_value = qini_values[-1]
plt.plot(
[0, 100],
[0, final_qini_value],
'k--',
linewidth=1.5,
alpha=0.7,
label='ランダムモデル'
)
plt.xlabel('顧客の割合 (%)')
plt.ylabel('Qini値')
plt.title('Qini曲線')
plt.legend()
plt.grid(True, alpha=0.3)
# 4. ROI分析
plt.subplot(2, 2, 4)
# ROIシミュレーション
roi_percentiles = []
roi_values = []
coupon_cost = 15 # クーポンコスト(仮定)
average_purchase_value = 100 # 平均購入金額(仮定)
for p in range(0, 101, 1):
n_selected = int(len(uplift_scores) * p / 100)
selected_indices = np.argsort(-uplift_scores)[:n_selected]
# 期待利益の計算
incremental_purchases = uplift_scores[selected_indices].sum()
incremental_revenue = incremental_purchases * average_purchase_value
total_cost = n_selected * coupon_cost
roi = (incremental_revenue - total_cost) / total_cost * 100 if total_cost > 0 else 0
roi_percentiles.append(p)
roi_values.append(roi)
plt.plot(
roi_percentiles,
roi_values,
'r-',
linewidth=2.5
)
plt.axhline(
y=0,
color='gray',
linestyle='--',
alpha=0.7
)
max_roi_idx = np.argmax(roi_values)
plt.scatter(
roi_percentiles[max_roi_idx],
roi_values[max_roi_idx],
color='red',
s=150,
zorder=5
)
plt.xlabel('ターゲット顧客の割合 (%)')
plt.ylabel('ROI (%)')
plt.title('期待ROI分析')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 分析結果のサマリーを出力
print("\n=== 分析結果サマリー ===")
print(f"データ件数: {len(data)}件")
print(f"処置群の割合: {treatment.mean():.1%}")
print(f"全体の購入率: {y_true.mean():.1%}")
print(f"\n--- アップリフトスコア ---")
print(f"平均値: {uplift_scores.mean():.3f}")
print(f"標準偏差: {uplift_scores.std():.3f}")
print(f"正の効果を持つ顧客: {(uplift_scores > 0).sum()}人 ({(uplift_scores > 0).mean():.1%})")
print(f"\n--- 最適化指標 ---")
print(f"最大累積効果を達成する顧客割合: {percentiles[max_idx]:.0f}%")
print(f"AUUC(モデル性能): {auuc:.4f}")
print(f"最大ROIを達成する顧客割合: {roi_percentiles[max_roi_idx]}%")
print(f"最大ROI: {roi_values[max_roi_idx]:.1f}%")
この関数を実行しダッシュボードを表示します。
以下、コードです。
create_uplift_dashboard(data)
以下、実行結果です。
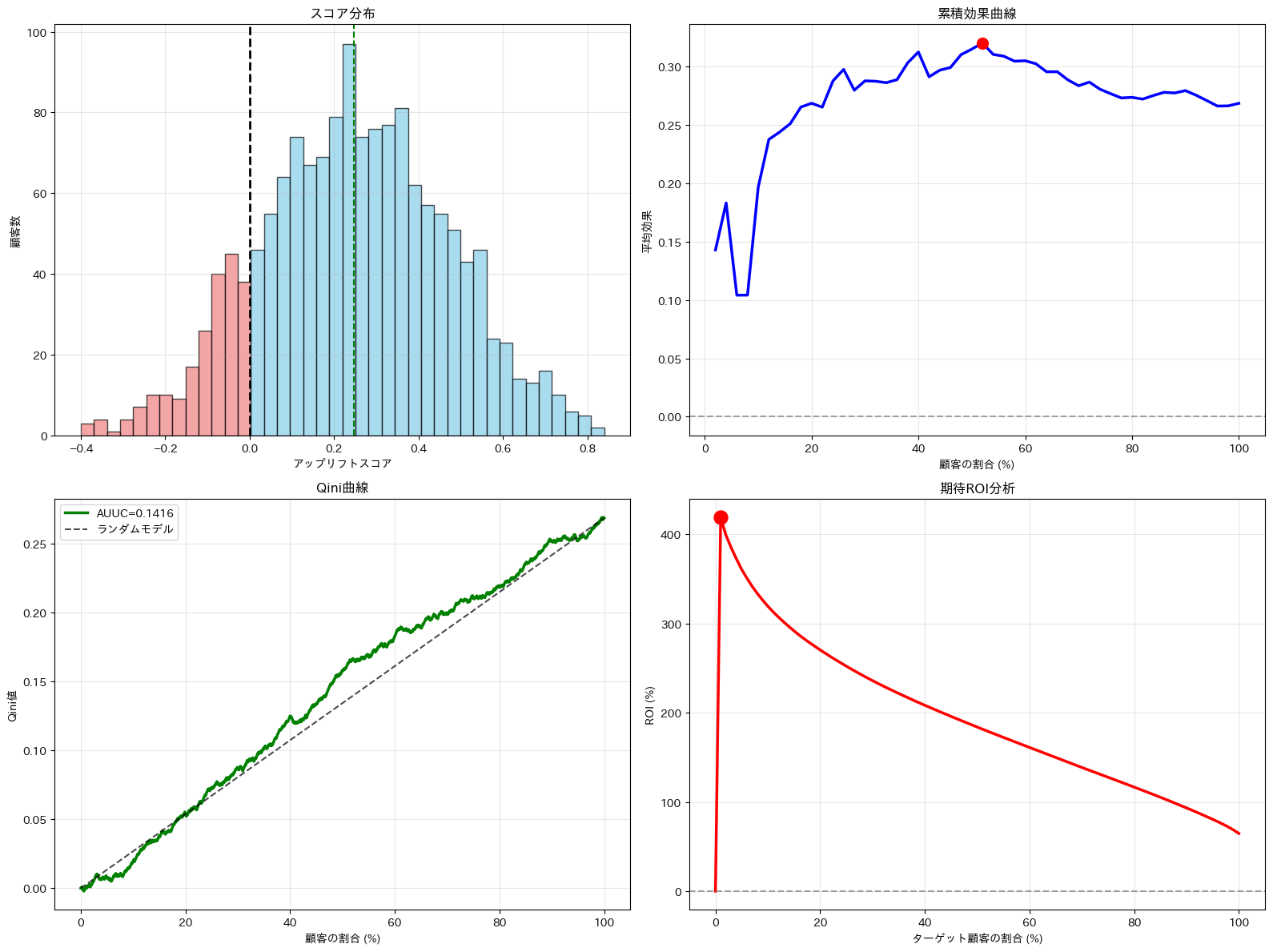
=== 分析結果サマリー === データ件数: 1500件 処置群の割合: 51.1% 全体の購入率: 33.3% --- アップリフトスコア --- 平均値: 0.247 標準偏差: 0.221 正の効果を持つ顧客: 1286人 (85.7%) --- 最適化指標 --- 最大累積効果を達成する顧客割合: 52% AUUC(モデル性能): 0.1416 最大ROIを達成する顧客割合: 1% 最大ROI: 419.1%
スコア分布により全体的な効果の分布を把握し、累積効果曲線で最適なターゲティング範囲を特定し、Qini曲線でモデルの性能を評価し、ROI分析により実際のビジネス価値を定量化しています。
これらのアップリフト分析の結果を実際のビジネスアクションに変換する関数を作成し実行します。
以下、コードです。
"""
分析結果に基づくビジネス戦略の提案
"""
def generate_business_recommendations(data, top_percent=20):
uplift_scores = data['uplift_score'].values
# 上位セグメントの特定
top_percent_threshold = np.percentile(uplift_scores, 100 - top_percent)
top_customers = data[data['uplift_score'] >= top_percent_threshold]
print("\n=== ビジネス戦略の提案 ===")
# 1. ターゲティング戦略
print("\n1. ターゲティング戦略")
print(f" - 上位{top_percent}%の顧客({len(top_customers)}人)に集中的にアプローチ")
print(f" - 平均年齢: {top_customers['age'].mean():.1f}歳")
print(f" - 平均購買履歴: {top_customers['purchase_history'].mean():.1f}回")
print(f" - 平均メール開封率: {top_customers['email_open_rate'].mean():.1%}")
# 2. セグメント別アプローチ
print("\n2. セグメント別アプローチ")
# 年齢層別の効果
age_groups = pd.cut(
data['age'],
bins=[0, 30, 40, 50, 100],
labels=['20-30歳', '30-40歳', '40-50歳', '50歳以上'])
age_analysis = data.groupby(age_groups)['uplift_score'].agg(['mean', 'count'])
print(" 年齢層別の平均効果:")
for age, row in age_analysis.iterrows():
print(f" - {age}: {row['mean']:.3f} (n={row['count']})")
# 3. 施策除外対象
negative_effect = data[data['uplift_score'] < 0]
print(f"\n3. 施策除外対象")
print(f" - 負の効果を持つ顧客: {len(negative_effect)}人 ({len(negative_effect)/len(data):.1%})")
print(f" - これらの顧客には別のアプローチ(ロイヤルティプログラム等)を検討")
# 4. 期待効果
print("\n4. 期待効果の試算")
# 上位セグメントのみにアプローチした場合の試算
selected_uplift = top_customers['uplift_score'].mean()
print(f" - 上位{top_percent}%の平均アップリフト効果: {selected_uplift:.3f}")
print(f" - 全体平均と比較して: {selected_uplift / uplift_scores.mean():.1f}倍の効果")
# 5. 実施タイミングの提案
print("\n5. 実施タイミングの提案")
last_purchase_analysis = top_customers.groupby(
pd.cut(
top_customers['last_purchase_days'],
bins=[0, 7, 14, 30, 100]
)
).size()
print(f" 最終購入からの経過日数分布(上位{top_percent}%):")
for interval, count in last_purchase_analysis.items():
print(f" - {interval}: {count}人")
# ビジネス戦略の提案を生成
generate_business_recommendations(data, top_percent=20)
この関数を実行し、ビジネスアクション案を提示します。今回はアップリフトスコアの上位20%の顧客に絞ったケースで検討します。
以下、コードです。
generate_business_recommendations(data, top_percent=20)
以下、実行結果です。
=== ビジネス戦略の提案 === 1. ターゲティング戦略 - 上位20%の顧客(304人)に集中的にアプローチ - 平均年齢: 30.0歳 - 平均購買履歴: 5.2回 - 平均メール開封率: 27.6% 2. セグメント別アプローチ 年齢層別の平均効果: - 20-30歳: 0.330 (n=445.0) - 30-40歳: 0.302 (n=590.0) - 40-50歳: 0.117 (n=365.0) - 50歳以上: 0.028 (n=100.0) 3. 施策除外対象 - 負の効果を持つ顧客: 205人 (13.7%) - これらの顧客には別のアプローチ(ロイヤルティプログラム等)を検討 4. 期待効果の試算 - 上位20%の平均アップリフト効果: 0.554 - 全体平均と比較して: 2.2倍の効果 5. 実施タイミングの提案 最終購入からの経過日数分布(上位20%): - (0, 7]: 86人 - (7, 14]: 42人 - (14, 30]: 66人 - (30, 100]: 98人
まとめ
今回は、アップリフト分析の結果を効果的に可視化し、ビジネス上の意思決定に活用する方法を解説しました。
主要な学習ポイントは以下の通りです。
- 累積効果曲線により、施策対象を上位何パーセントに絞るべきかを数値的に判断できるようになりました。
- Qini曲線とAUUCにより、構築したモデルがランダムな選択と比較してどの程度優れているかを定量的に評価できるようになりました。
- セグメント別ヒートマップにより、年齢や購買履歴といった顧客属性による効果の違いを視覚的に把握できるようになりました。
これらの可視化手法は単なる分析ツールではなく、マーケティング戦略の科学的根拠となる重要な意思決定支援ツールです。
グラフィカルな表現により、数値の羅列では見えなかった施策効果の全体像が直感的に理解できるようになります。
実際のビジネスでは、これらの分析結果を基に、限られたマーケティング予算を最も効果的に配分し、ROIを最大化することが可能となります。
次回は、これらの分析結果を実際のビジネス運用に落とし込み、継続的な改善サイクルを構築する方法について解説します。
モデルの定期的な更新、効果測定の仕組み、そして組織への導入方法など、実践的な運用ノウハウをお伝えします。

