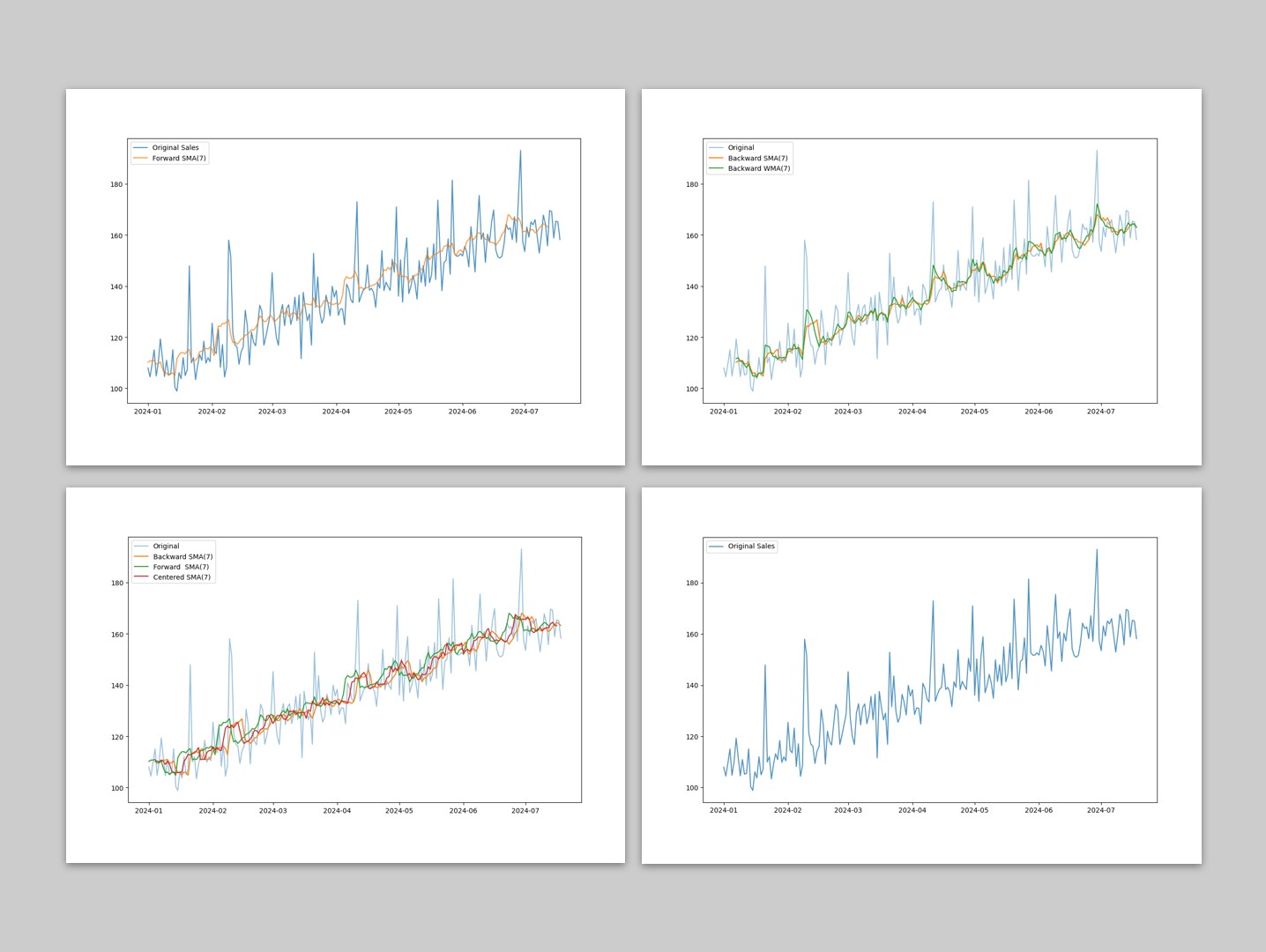
移動平均による時系列分析

日々の売上やアクセス数といった時系列データは、ノイズや季節性の影響で「本当の流れ」が見えにくくなりがちです。

そんなときに役立つのが移動平均（Moving Average）です。

シンプルながら、データのトレンドや周期性をなめらかに表現できる強力な手法です。

今回は、カフェの日次売上を模したサンプルデータを使いながら……

窓の位置取り（後方・前方・中央）による違い
窓幅 $k$ の選び方が与える影響
加重移動平均（WMA）や指数移動平均（EMA）といった発展形

……を、コードとグラフを交えて丁寧に解説します。

Contents

サンプルデータ
移動平均の「窓の位置取り」
　後方移動平均（Backward SMA）
　前方移動平均（Forward SMA）
　中央移動平均（Centered SMA）
　3 種類の移動平均を重ねてみる
　窓幅 k を変えたときの見え方
重みづけのある平滑
　後方加重移動平均（Backward WMA）
　後方指数移動平均（Backward EMA）
まとめ

サンプルデータ

今回利用するサンプルとして利用する時系列データ $y_t$ を人工的に作ります。

適当に作ってもあれなので、地方の小さなカフェの日次売上を、以下を想定し生成します。

このカフェは、開店から少しずつお客さんが増えており、平日はランチ需要で安定、土日は家族連れがやや増えます。
ときどきチラシ配布や駅前イベントがあり、その日は売上が大きく伸びます。
一方で、雨の強い日はお客さんが減ることもあります。

このような時系列データを生成します。

以下、コードです。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 再現性のための乱数シード
np.random.seed(42)

# 期間を決める（200日、2024-01-01 から）
T = 200
idx = pd.date_range('2024-01-01', periods=T, freq='D')

# 1) 緩やかな上昇トレンド（100 → 160 へ直線的に上がるイメージ）
trend = np.linspace(100, 160, T)

# 2) 曜日による季節性（週内パターン：月〜金は+5、土は+10、日は+8 など）
weekday = pd.Series(idx.weekday, index=idx)  # Monday=0 ... Sunday=6
season = (
    np.where(weekday <= 4, 5.0, 0.0)  # 平日
    + np.where(weekday == 5, 10.0, 0.0)  # 土曜
    + np.where(weekday == 6, 8.0, 0.0)   # 日曜
)

# 3) ランダムノイズ（標準偏差 6 程度）
noise = np.random.normal(0, 6, T)

# 4) 散発的イベント（10日おきに+25、たまに+40）
event = np.zeros(T)
event_days = np.arange(20, T, 20)
event[event_days] = 25.0
# さらにランダムで強めのイベント
extra_days = np.random.choice(np.arange(15, T-5), size=3, replace=False)
event[extra_days] += 40.0

# 日次売上を作る
y = trend + season + event + noise
s = pd.Series(y, index=idx, name='sales')

df = pd.DataFrame({'date': idx, 'sales': s.values})

# CSV 保存
df.to_csv('sample_sales.csv', index=False)

# グラフをプロット
plt.figure(figsize=(10,6))
plt.plot(s, label='Original Sales', alpha=0.8)
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。

サンプルデータはCSVファイル（sample_sales.csv）に保存しています。

移動平均の「窓の位置取り」

移動平均の本質は「どこを平均するか」にあります。

同じ窓幅 $k$ でも、窓の位置によって意味も用途も変わります。

ここでは、後方（Backward）・前方（Forward）・中央（Centered）の順に紹介します。

　後方移動平均（Backward SMA）

後方移動平均は、時点 $t$ における当日から過去方向の $k$ 点の平均です。

将来を参照しないため、予測やオンライン運用、機械学習の特徴量として安全に使えます（データリークをしない）。

以下、数式です。

$$
\operatorname{SMA}^{(B)}_{t,k} \,=\, \frac{1}{k} \sum_{i=0}^{k-1} y_{t-i} \quad (t\ge k)
$$

この式は「当日 $y_t$ と過去の $k-1$ 点を合計し、均等に割る」ということを意味しています。

たとえば、 $k=7$ なら「当日と過去 6 日」を平均して、その平均値を「今日の平滑化値」として使います。

実装上は、元の時系列データ $y_t$ の先頭の $k-1$ 点は過去が足りないため欠損値（NaN）となります。

そのため、NaN のままにするか、部分窓（min_periods）を許すかを選ぶ必要があります。

部分窓を選んだ場合、欠損値がなくなり便利ですが、数値の安定性は下がる点に注意してください。

実装するときは、Pandas の rolling を使い、center=False（デフォルト）で計算します。

以下、コードです。

import pandas as pd

# CSV 読み込み
s = pd.read_csv(
    'sample_sales.csv', 
    parse_dates=['date']    
).set_index('date')['sales']

# 後方SMA(7)：当日と過去6日を均等平均（先頭はデータ不足でNaN）
sma_b7 = s.rolling(window=7, min_periods=7).mean()

# グラフをプロット
plt.figure(figsize=(10,6))
plt.plot(s, label='Original Sales', alpha=0.8)
plt.plot(sma_b7, label='Backward SMA(7)', alpha=0.8)
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。

　前方移動平均（Forward SMA）

前方移動平均は、時点 $t$ における当日から未来方向の $k$ 点を平均します。

未来を参照するため、予測やオンライン処理、学習用の特徴量としては使えません（データリークするため）。

一方で、事後的な見通し線や右寄せの平滑線を描く用途では役立ちます。

式は後方と対称的で、平均の取り方を「未来側」に反転させます。

$$
\operatorname{SMA}^{(F)}_{t,k} \,=\, \frac{1}{k} \sum_{i=0}^{k-1} y_{t+i} \quad (t\le T-k+1)
$$

直感的には「今日から先の $k-1$ 日を含めて平均する」ことになります。

元の時系列データ $y_t$ の末尾近くではデータが足りないため（未来のデータがないため）、計算できずNaN（欠損）になります。

Pandas の rolling は後方窓を前提にしているので、時系列をいったん反転して後方平均をとり、再び反転するという方法で実装します。

以下、コードです。

# 前方SMA(7)：時系列を反転 → 後方SMA → 再反転
s_rev = s.iloc[::-1] #データを反転
sma_f7 = s_rev.rolling(window=7,min_periods=7).mean().iloc[::-1]

# グラフをプロット
plt.figure(figsize=(10,6))
plt.plot(s, label='Original Sales', alpha=0.8)
plt.plot(sma_f7, label='Forward SMA(7)', alpha=0.8)
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。

　中央移動平均（Centered SMA）

中央移動平均は、時点 $t$ の前後対称に $k$ 点をとって平均します。

トレンドや季節性の把握に適しています。

ただし将来データを含むため、やはり可視化・事後分析専用です。

中央では奇数窓（ $k=2m+1$ ）が解釈しやすく、式もすっきりします。

$$
\operatorname{SMA}^{(C)}_{t,k} \,=\, \frac{1}{2m+1} \sum_{i=-m}^{m} y_{t+i} \quad (k=2m+1)
$$

これは「過去 $m$ 日・当日・未来 $m$ 日の平均」を作ることを意味しています。

Pandas では center=True を指定するだけで実行できます。

端点では前後のデータが足りないため、前後それぞれ $m$ 点が NaN （欠損）になります。

以下、コードです。

# 中央SMA(7)：前後3日 + 当日の平均
sma_c7 = s.rolling(window=8, center=True, min_periods=7).mean()

# グラフをプロット
plt.figure(figsize=(10,6))
plt.plot(s, label='Original Sales', alpha=0.8)
plt.plot(sma_c7, label='Central SMA(7)', alpha=0.8)
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。

偶数窓の場合 ( $k=2m$ )には、中心が「2つの点の間」になるため、本来は中央に配置できません。

pandas の実装では「中央を右寄りにずらして配置」しています。たとえば、 window=6 の場合には6点の中央は3番と4番目の間の点ですが存在しないので、平均は 4番目の要素に割り当てられる。

つまり pandas の中心化は「完全な対称化」ではなく、「便宜的に右寄りに置く」という仕様になっています。

　3 種類の移動平均を重ねてみる

実際に3つの曲線を重ねて眺めましょう。

以下、コードです。

import matplotlib.pyplot as plt

plt.figure(figsize=(10,6))
plt.plot(s, label='Original', alpha=0.45)
plt.plot(sma_b7, label='Backward SMA(7)')
plt.plot(sma_f7, label='Forward  SMA(7)')
plt.plot(sma_c7, label='Centered SMA(7)')
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。

予測・運用・特徴量では後方を使う、構造把握の可視化では中央を使う、といった住み分けを守ると、解釈の齟齬やデータリークを未然に防げます。

　窓幅 $k$ を変えたときの見え方

移動平均を求めるとき、窓幅 $k$ の選択は非常に重要です。

小さな $k$ は変化への反応が速いものの、ノイズも残りやすい。

大きな $k$ はノイズが残り難く滑らかですが、ラグ（遅れ）が増え、たとえば変化点検出では発見が遅れます。

ここでは後方SMAで $k$ を変え、見え方の違いを確かてみましょう。

以下、コードです。

sma_b3  = s.rolling(3).mean()
sma_b14 = s.rolling(14).mean()
sma_b30 = s.rolling(30).mean()

plt.figure(figsize=(10,6))
plt.plot(s, label='Original', alpha=0.35)
plt.plot(sma_b3,  label='Backward SMA(3)')
plt.plot(sma_b14, label='Backward SMA(14)')
plt.plot(sma_b30, label='Backward SMA(30)')
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。

この比較から、週のザワつきを軽くならすなら 7 日、月の大きな流れを見たいなら 30 日のように、目的に応じて $k$ を選ぶ感覚がつかめます。

活用場面の文脈に照らして、「何のノイズを消したいのか、どの周期を見たいのか」を言葉にし、それに対応する $k$ を決めるのが健全です。

重みづけのある平滑

すべてを均等に平均するのが SMA でした。

直近の情報をより尊重したいときは、加重移動平均（WMA）と指数移動平均（EMA）が役立ちます。

　後方加重移動平均（Backward WMA）

WMA は、過去側 $k$ 点に重み $w_0, w_1, \dots, w_{k-1}$ を付けて平均します。

新しいデータほど重い重みを付ける（ $w_0 > w_1 > \cdots$ ）と、変化にやや敏感になります。

$$
\operatorname{WMA}^{(B)}_{t,k} \,=\, \frac{\sum_{i=0}^{k-1} w_i\, y_{t-i}}{\sum_{i=0}^{k-1} w_i}, \quad w_i>0
$$

Pandas では rolling().apply() を使って実装します。

今回は、線形に増える重み（1,2,3,4,5,6,7）を例にします。

以下、コードです。

import numpy as np
weights = np.arange(1, 8) # 新しいほど重い 1..7
weights = weights / weights.sum() # 重みの正規化
wma_b7 = s.rolling(
    window=7
).apply(
    lambda x: np.dot(x, weights), 
    raw=True
)

# グラフをプロット
plt.figure(figsize=(10,6))
plt.plot(s, label='Original', alpha=0.45)
plt.plot(sma_b7, label='Backward SMA(7)')
plt.plot(wma_b7, label='Backward WMA(7)')
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。

　後方指数移動平均（Backward EMA）

EMA のポイントは $\alpha$ の設定にあります。

\alpha

が大きいほど変化への反応が速く（要は、直近の重みを大きくする）、ノイズも拾いやすくなります。

一般的に「期間」を $k$ とすると $\alpha = 2/(k+1)$ とすることが多いようです（もちろん、絶対ではない）。

$$
\operatorname{EMA}^{(B)}_t \,=\, \alpha y_t \,+\, (1-\alpha)\,\operatorname{EMA}^{(B)}_{t-1}, \quad 0<\alpha\le 1
$$

Pandas の ewm を使うことで計算できます。

以下、コードです。

ema_b7 = s.ewm(span=7, adjust=False).mean()

# グラフをプロット
plt.figure(figsize=(10,6))
plt.plot(s, label='Original', alpha=0.45)
plt.plot(sma_b7, label='Backward SMA(7)')
plt.plot(ema_b7, label='Backward EMA(7)')
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。

SMA と EMA を一緒にプロットすると、EMA のほうが立ち上がりや下落にやや敏感であることが視覚的に確認できます。

以下、コードです。

# グラフをプロット
plt.figure(figsize=(10,6))
plt.plot(s, label='Original', alpha=0.45)
plt.plot(wma_b7, label='Backward WMA(7)')
plt.plot(ema_b7, label='Backward EMA(7)')
plt.legend()
plt.tight_layout()
plt.show()

以下、実行結果です。