前回の記事では、なぜAIの判断根拠を説明することが重要なのか、そしてXAI(説明可能AI)がどのような場面で活用されているかを学びました。
今回はいよいよ実践編です。
実際に手を動かしながら、DALEXというライブラリを使って、AIモデルの中身を「見える化」する体験をしていきましょう。
料理のレシピを順番に実行するように、一つずつ進めていけば、必ずゴールにたどり着けます。
「なぜAIがその判断をしたのか」を可視化できるようになっているはずです。
Contents
環境構築:DALEXを使う準備を整えよう
Google ColabやJupyter Notebookを開いて、以下のコマンドを実行しましょう。すでにインストールされている場合は必要ありません。
# 必要なライブラリをインストール !pip install dalex # DALEX本体:XAIの主役 !pip install xgboost # XGBoost:高性能な機械学習モデル !pip install pandas # pandas:データを扱うための基本ツール !pip install numpy # numpy:数値計算の基礎ライブラリ !pip install scikit-learn # scikit-learn:機械学習の定番ライブラリ !pip install matplotlib # matplotlib:グラフ描画用
インストールが完了したら、実際に使えるか確認してみましょう。
# ライブラリをインポート(道具箱から必要な道具を取り出すイメージ)
import dalex as dx
import pandas as pd
import numpy as np
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings('ignore') # 不要な警告を非表示に
# バージョン確認(正しくインストールされたかチェック)
print(f"DALEX version: {dx.__version__}")
以下、実行結果です。インストールされたタイミングで、バージョンは異なります。
DALEX version: 1.7.2
サンプルデータで学習
データの準備
今回は、機械学習の入門でよく使われる「タイタニック号の乗客データ」を使います。
このデータセットは、1912年に沈没したタイタニック号の乗客情報と、その人が生存したかどうかを記録したものです。
年齢、性別、チケットクラスなどの情報から、生存確率を予測するモデルを作り、その判断根拠を可視化していきます。
# タイタニックデータセットを読み込む
titanic = dx.datasets.load_titanic()
# データの中身を確認
print("最初の5行を表示:")
print(titanic.head())
print(f"\nデータの形状: {titanic.shape}")
print(f"行数(乗客数): {titanic.shape[0]}, 列数(特徴量): {titanic.shape[1]}")
# 各列の意味を理解しよう
print("\n各列の説明:")
print("- survived: 生存したか(1=生存、0=死亡)")
print("- class: チケットクラス(1st, 2nd, 3rd)")
print("- gender: 性別")
print("- age: 年齢")
print("- sibsp: 同乗した兄弟・配偶者の数")
print("- parch: 同乗した親・子供の数")
print("- fare: 運賃")
print("- embarked: 乗船港")
以下、実行結果です。
最初の5行を表示: gender age class embarked fare sibsp parch survived 0 male 42.0 3rd Southampton 7.11 0 0 0 1 male 13.0 3rd Southampton 20.05 0 2 0 2 male 16.0 3rd Southampton 20.05 1 1 0 3 female 39.0 3rd Southampton 20.05 1 1 1 4 female 16.0 3rd Southampton 7.13 0 0 1 データの形状: (2207, 8) 行数(乗客数): 2207, 列数(特徴量): 8 各列の説明: - survived: 生存したか(1=生存、0=死亡) - class: チケットクラス(1st, 2nd, 3rd) - gender: 性別 - age: 年齢 - sibsp: 同乗した兄弟・配偶者の数 - parch: 同乗した親・子供の数 - fare: 運賃 - embarked: 乗船港
データの前処理
予測する目的変数 y は survived(1=生存、0=死亡)、説明変数 X は目的変数以外です。説明変数 X には文字列などのカテゴリカルな変数と、数値データにより構成されます。
機械学習モデルは数値しか理解できません。そのため、文字データを数値に変換する必要があります。get_dummies関数は通常、文字列やカテゴリカルな変数をダミー変数に変換します。数値データはそのまま保持され、ダミー化されません。
# データの前処理
# カテゴリ変数(文字データ)を数値に変換
X = pd.get_dummies(titanic.drop('survived', axis=1)) # 説明変数(予測に使う情報)
y = titanic['survived'] # 目的変数(予測したい結果)
訓練データとテストデータに分割します。訓練データでモデルを学習し、テストデータで検証します。
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(
X, # 説明変数
y, # 目的変数
test_size=0.25, # テストデータの割合
random_state=42
)
print(f"訓練データ: {X_train.shape[0]}件")
print(f"テストデータ: {X_test.shape[0]}件")
以下、実行結果です。
訓練データ: 1655件 テストデータ: 552件
XGBoostモデルの構築
いよいよ機械学習モデルを構築します。XGBoostは、多くのデータ分析コンペティションで優勝実績のある強力なアルゴリズムです。決定木を何本も組み合わせて、より正確な予測を行います。
# XGBoostモデルを構築
model = xgb.XGBClassifier(
n_estimators=100, # 決定木の数(多いほど複雑だが時間もかかる)
max_depth=3, # 各決定木の深さ(深いほど複雑)
learning_rate=0.1, # 学習の速度(小さいほど慎重に学習)
random_state=42 # 再現性のための種
)
# モデルを訓練(学習させる)
model.fit(X_train, y_train)
# モデルの性能を評価
y_pred = model.predict(X_test)
accuracy = (y_pred == y_test).mean()
print(f"予測精度(Accuracy): {accuracy:.4f}")
以下、実行結果です。
予測精度(Accuracy): 0.7899
モデルをDALEXで解釈する
Explainerオブジェクトの作成
ここからが本題です。構築したXGBoostモデルは高い予測精度を持っていますが、なぜその予測をしたのかは分かりません。
DALEXのExplainerオブジェクトは、このブラックボックスなモデルに「説明能力」を与えます。
# Explainerオブジェクトを作成
explainer = dx.Explainer(
model, # 解釈したいモデル
X_test, # テストデータ(説明変数)
y_test, # テストデータ(目的変数)
label='XGBoost生存予測モデル' # モデルの名前(グラフに表示される)
)
# Explainerの基本情報を確認
print("Explainerの準備完了!")
print(f"モデルタイプ: {explainer.model_type}")
print(f"データサイズ: {explainer.data.shape}")
以下、実行結果です。
Preparation of a new explainer is initiated -> data : 552 rows 17 cols -> target variable : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray. -> target variable : 552 values -> model_class : xgboost.sklearn.XGBClassifier (default) -> label : XGBoost生存予測モデル -> predict function : <function yhat_proba_default="" at="" 0x7f1f63f77880=""> will be used (default) -> predict function : Accepts pandas.DataFrame and numpy.ndarray. -> predicted values : min = 0.023, mean = 0.329, max = 0.994 -> model type : classification will be used (default) -> residual function : difference between y and yhat (default) -> residuals : min = -0.99, mean = -0.0106, max = 0.919 -> model_info : package xgboost A new explainer has been created! Explainerの準備完了! モデルタイプ: classification データサイズ: (552, 17) </function>
特徴量重要度の可視化
最初は「特徴量重要度」の可視化です。
これは、モデルが予測する際に「どの情報を重視しているか」を示すもので、まるでテストで「どの科目の配点が高いか」を知るようなものです。
DALEXの特徴量重要度は、Permutation Feature Importance(PFI) の一種です。
PFI(Permutation Feature Importance)とは「ある特徴量の値をランダムに並べ替え、その状態で再度予測し、モデルの損失がどれだけ悪化するかを測定する」ことで、特徴量の重要度を計るアプローチをとったものです。
# 変数重要度を計算
vi = explainer.model_parts()
# 結果を表示
print("変数重要度の数値:")
print(vi.result)
以下、実行結果です。
変数重要度の数値:
variable dropout_loss label
0 embarked_Queenstown 0.190058 XGBoost生存予測モデル
1 parch 0.193999 XGBoost生存予測モデル
2 embarked_Cherbourg 0.196008 XGBoost生存予測モデル
3 class_engineering crew 0.196223 XGBoost生存予測モデル
4 gender_male 0.196937 XGBoost生存予測モデル
5 _full_model_ 0.196937 XGBoost生存予測モデル
6 class_victualling crew 0.197201 XGBoost生存予測モデル
7 embarked_Southampton 0.197603 XGBoost生存予測モデル
8 embarked_Belfast 0.199068 XGBoost生存予測モデル
9 class_2nd 0.200734 XGBoost生存予測モデル
10 class_restaurant staff 0.206355 XGBoost生存予測モデル
11 class_1st 0.207063 XGBoost生存予測モデル
12 sibsp 0.208310 XGBoost生存予測モデル
13 fare 0.213577 XGBoost生存予測モデル
14 class_deck crew 0.229165 XGBoost生存予測モデル
15 class_3rd 0.239079 XGBoost生存予測モデル
16 age 0.245238 XGBoost生存予測モデル
17 gender_female 0.388568 XGBoost生存予測モデル
18 _baseline_ 0.501912 XGBoost生存予測モデル
この出力した表のdropout_loss は、各条件での「モデルの損失」を表す数値です。
「モデルの損失」とは、モデルの予測値と実際の正解値とのズレを定量的に測った指標です。損失が小さいほど、モデルは正確に予測できていることを意味します。
たとえば、gender_female(性別の女性フラグ)という変数だけを ランダムに並び替え(=無効化) した状態で計算した「モデルの損失」が0.388568ということです。
これは、「ある変数を使えなくしたとき、モデルの性能がどれだけ悪化するか」を測ったものです。
そのため、「モデルの損失」が大きいほど、重要な変数であるということになります。
ここで、この出力の_baseline_と_full_model_に着目します。これは、Dalexの特徴量重要度分析における2つの基準点で、モデル全体の性能を測るための「両端の比較軸」となっています。
| 項目 | 値 | 意味 |
|---|---|---|
_baseline_ |
0.501912 | どの変数も使わない(=完全にランダムな予測)ときの損失値 |
_full_model_ |
0.196937 | すべての変数を使ったときの損失値(最良の状態) |
ここで、_baseline_ − _full_model_を計算してみます。
0.501912 – 0.196937 = 0.304975
すべての「説明変数」を使うことによって誤差を 0.305 改善できたことになります。
逆の見方をすると、最良の状態(_full_model_)から全変数を除くと、モデルの損失が0.305悪化することを意味します。
このことを、各変数に対し適用してみます。
つまり、最良の状態(_full_model_)から各変数を除くと、損失どの程度増えるか(悪化するのか)を考えてみましょう。
たとえば、gender_female を除外すると、モデルの損失が0.127悪化します。
| 項目 | 値 | 意味 |
|---|---|---|
full_model(_full_model_) |
0.1969 | すべての変数を使ったときのモデルの損失(=最も良い状態) |
| gender_female 除外時 | 0.3886 | 性別の情報を壊した(使えなくした)ときの損失 |
| 差(悪化量) | 0.3886 – 0.1969 = +0.1917 | 性別を除外したことで損失が0.127増加 |
この悪化量(dropout_loss の差分)をグラフ化します。
vi.plot(show=True)
以下、実行結果です。
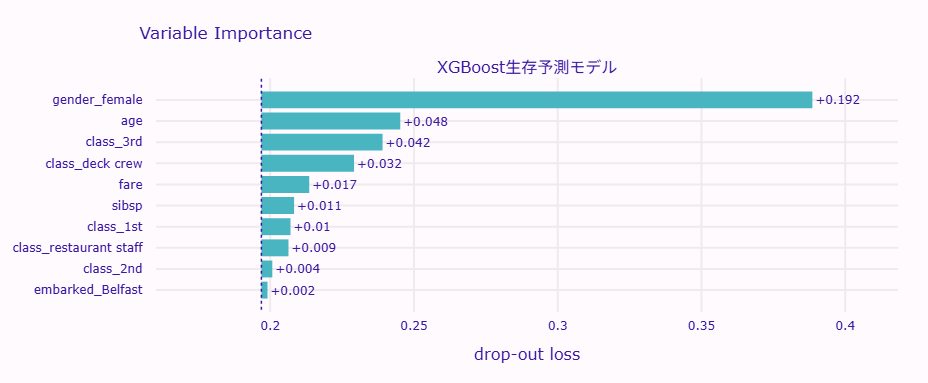
棒が長いほど、その特徴量が重要であることを示しています。
このタイタニックのデータでは、通常以下のような傾向が見られます。
- 性別(gender)が最も重要:当時の「女性と子供を優先」という避難ルールを反映
- チケットクラス(class)も重要:上級クラスの乗客ほど生存率が高い
- 年齢(age)の影響:若い人ほど生存率が高い傾向
このように、特徴量重要度を見ることで、モデルが現実の状況を適切に学習できているかを確認できます。
Break Down分析で個別予測を説明
次に、特定の乗客一人について、なぜモデルがその予測をしたのかを詳しく見てみましょう。
これは医師が患者一人一人に合わせた診断をするようなものです。
# テストデータから一人の乗客を選択
passenger_index = 0 # 最初の乗客を選択
single_passenger = X_test.iloc[[passenger_index]]
# この乗客の情報を確認
print("選択した乗客の情報:")
for col, val in single_passenger.iloc[0].items():
print(f" {col}: {val}")
以下、実行結果です。
選択した乗客の情報: age: 20.0 fare: 0.0 sibsp: 0 parch: 0 gender_female: True gender_male: False class_1st: False class_2nd: False class_3rd: False class_deck crew: False class_engineering crew: False class_restaurant staff: True class_victualling crew: False embarked_Belfast: False embarked_Cherbourg: False embarked_Queenstown: False embarked_Southampton: True
選択した乗客の予測(生存確率)を実施します。
# 予測結果
prediction = model.predict_proba(single_passenger)[0][1]
actual = y_test.iloc[passenger_index]
print(f"モデルの予測生存確率: {prediction:.2%}")
print(f"実際の結果: {'生存' if actual == 1 else '死亡'}")
以下、実行結果です。予測結果だけでなく、実際の結果も表示しています。
モデルの予測生存確率: 65.71% 実際の結果: 生存
この予測結果の要因を分解します。個別予測のBreak Downプロット(寄与分解図) です。
# 予測の要因分解
bd = explainer.predict_parts(
single_passenger,
type='break_down' # 段階的に要因を分解する手法
)
# 結果を可視化
bd.plot(show=True)
以下、実行結果です。
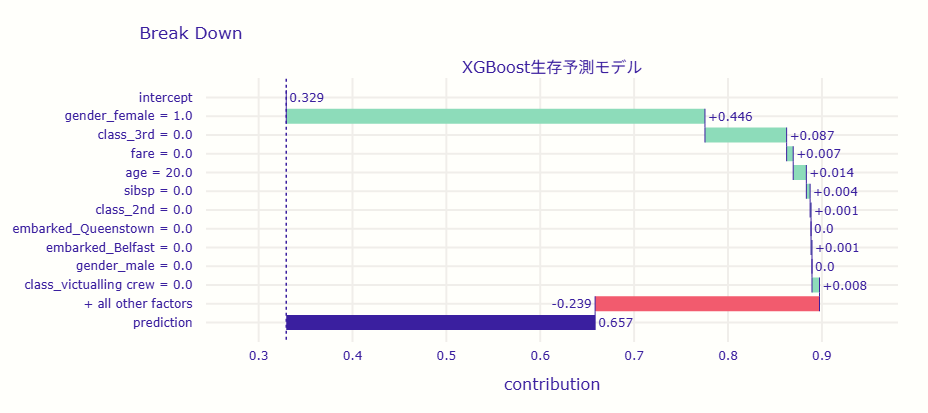
このグラフは、 一人の乗客に対して、モデルが「なぜこの人は生存すると予測したのか」を可視化しています。
縦軸には特徴量(性別、年齢、船室など)、横軸にはそれぞれの特徴がどの程度、 生存確率(予測値)を押し上げたか・押し下げたか が示されています。
モデル全体の平均的な生存確率(ベースライン)は 0.33(33%)ですが、この乗客は最終的に 0.657(65.7%)の生存確率 と予測されています。
以下では、どの特徴がどのようにこの予測に影響したのかを見ていきます。
| 特徴量 | 寄与値 | 寄与方向 | 解釈 |
|---|---|---|---|
| intercept(ベースライン) | 0.329 | – | 平均的な生存確率の出発点。ここから各特徴を加算していく。 |
| gender_female = 1.0 | +0.446 | ⬆️ プラス | 女性であることが最も大きく生存確率を押し上げた(救助の優先対象)。 |
| class_3rd = 0.0 | +0.087 | ⬆️ プラス | 3等船室ではない(=上位クラスである)ことが生存率にプラスに寄与。 |
| fare = 0.0 | +0.007 | ⬆️ プラス | 運賃に関する条件がわずかにプラスに作用。 |
| age = 20.0 | +0.014 | ⬆️ プラス | 20歳という年齢(若年層)であることが生存率を少し上げた。 |
| sibsp = 0.0 | +0.004 | ⬆️ プラス | 同行家族(兄弟・配偶者)がいないことがごくわずかにプラス。 |
| class_2nd = 0.0 | +0.001 | ⬆️ プラス | 2等船室ではない条件による微小なプラス補正。 |
| embarked_Queenstown = 0.0 | 0.0 | – | 寄与なし。 |
| embarked_Belfast = 0.0 | +0.001 | ⬆️ プラス | Belfast出発ではないことによる微小なプラス補正。 |
| gender_male = 0.0 | 0.0 | – | 寄与なし(gender_femaleですでに説明されているため)。 |
| class_victualling crew = 0.0 | +0.008 | ⬆️ プラス | 給養部員(Victualling crew)ではないことがわずかにプラス。 |
| + all other factors | -0.239 | ⬇️ マイナス | 【重要】 その他の変数の合計が大きく足を引っ張っている。上記以外の要因が複合して、最終的な生存確率を約24%押し下げた。 |
| prediction | 0.657 | – | 最終的な予測確率(約65.7%)。 |
この乗客は、「若い女性で上級船室にいた」 という特徴を持っており、Titanicの生存者によく見られる典型的なパターンに一致しています。そのため、ベースライン(33%)より高い 65.7% の生存確率 が予測されました。
寄与の内訳を見ると、性別(女性) が最も強い要因であり、次いで 船室の等級 が生存確率を押し上げています。年齢や運賃といった他の要素は補助的にプラス寄与をしています。
全体として、このモデルは「社会的優先順位(女性・上級船室・若年)」という歴史的な救助傾向を学習しており、この乗客を「ほぼ確実に生存」と判断したことが理解できます。
まとめ
今回は、DALEXの環境構築から始めて、実際にモデルを構築し、その判断根拠を可視化するところまで体験しました。
特徴量重要度を見ることで、モデルがどの特徴を重視しているかが分かり、Break Down分析によって個別の予測がなぜそうなったのかを理解できました。
これはXAIの世界への最初の一歩にすぎません。
次回は、より高度な手法であるPDP(Partial Dependence Plot)やICE(Individual Conditional Expectation)を学び、特徴量と予測結果の関係をさらに深く理解していきます。
これらの手法を使えば、「年齢が10歳上がると生存確率はどう変化するか」「運賃と生存率の関係は線形なのか、それとも閾値があるのか」といった、より複雑な問いに答えることができるようになります。
DALEXで実践する説明可能AI超入門— 第3回 —グローバル解釈で全体像を把握するPFI・PDP・ALE・Surrogate Model

