「AIが不良品と判定した理由が分からない。だから改善のしようがない」
多くの製造現場が、AIのブラックボックス問題に直面しています。
高精度な品質検査AIを導入しても、なぜその判断をしたのか説明できなければ、現場の改善活動につながりません。
第3回では、PDP、ALE、Surrogate Modelといったグローバル解釈手法で、AIモデル全体の振る舞いを理解する方法をお話ししました。
DALEXで実践する説明可能AI超入門— 第3回 —グローバル解釈で全体像を把握するPFI・PDP・ALE・Surrogate Model
第4回では、SHAPやBreak Downによるローカル解釈で、個々の予測を詳細に分解する技術をお話ししました。
DALEXで実践する説明可能AI超入門— 第4回 —ローカル解釈(SHAP/Break Down/Ceteris Paribus)で個別予測を説明する
今回は、これらの手法を製造現場の実際の課題解決に活用します。
プレス加工の品質管理というケースを通じて、以下のグローバル解釈手法を実践します。
- Permutation Importance:品質に最も影響する要因のランク付け
- PDP(Partial Dependence Plot):各パラメータの最適値の発見
- ALE(Accumulated Local Effects):パラメータ間の相関を考慮した正確な影響評価
- Surrogate Model(代理モデル):AIの判断ルールを人間が読める形で可視化
Contents
製造現場におけるAIのジレンマと突破口
とある工場長の苦悩

金属プレス加工を専門とする中堅メーカーの工場長、田中さんの一日は、いつも生産ラインの巡回から始まります。
この工場では昨年、最新のAI品質検査システムを導入しました。カメラとセンサーで製品を検査し、0.1秒で良品と不良品を判定する高性能なシステムです。
しかし、田中さんの表情は晴れません。先週の品質会議での出来事が、頭から離れないのです。
品質保証部から提出された報告書には、AIが不良品と判定した製品の写真が並んでいました。しかし、30年のキャリアを持つ検査主任の山田さんが首をかしげながら言いました。
「工場長、これらの半分以上は、私の目では良品に見えます。逆に、AIが良品と判定したこちらの製品には、微細なクラックが入っています」
田中さんがAIシステムの担当者に理由を尋ねても、返ってきた答えは「ディープラーニングの判断プロセスは複雑で、なぜそう判定したかは説明が困難です」というものでした。これでは、どう改善すれば良いのか分かりません。
実は、このような状況は田中さんの工場だけの問題ではありません。経済産業省の調査によると、製造業でAIを導入した企業の約60%が「判断根拠が不明確」という課題を抱えているのです。
高い投資をしてAIを導入しても、現場の改善活動につながらなければ、その価値は半減してしまいます。
さらに深刻なのは、現場作業者のモチベーションへの影響です。プレス加工担当の若手オペレーター、鈴木さんは困惑しています。
「AIが不良品と言うから、とりあえず作り直していますが、何が悪いのか分からないので、同じミスを繰り返してしまうんです。以前は山田主任が『ここの圧力が高すぎる』と具体的に教えてくれたのに」
このギャップこそが、製造現場におけるAIのジレンマの本質です。
AIは確かに検査スピードを10倍に向上させ、見逃し率も人間の3%から0.5%に減少させました。
しかし、その判断プロセスがブラックボックス化することで、最も重要な「なぜ」という問いに答えられなくなってしまったのです。
現場が求める「納得できる説明」とは

では、製造現場が本当に必要としている「説明」とは、どのようなものでしょうか。
田中工場長が現場の声を集めてみると、3つの要素が浮かび上がってきました。
現場の言葉で理解できる説明
第一に、現場の言葉で理解できる説明です。
「ニューラルネットワークの第3層の活性化関数が…」という説明では、現場は動きません。
「温度が設定値より5度高いことが、不良の主な原因です」という具体的な説明が必要なのです。
これは単に技術用語を避けるということではなく、現場の改善アクションに直結する形で情報を提供することを意味します。
リアルタイムでの説明
第二に、リアルタイムでの説明です。
製造ラインは止まりません。不良品が発生したその瞬間に「なぜ」が分かれば、即座に調整が可能です。
後日レポートで説明されても、すでに100個の不良品が生産された後では遅すぎるのです。
第4回で紹介した Break Down法が計算速度で優れているのは、まさにこのニーズに応えるためです。
改善提案を含む説明
第三に、改善提案を含む説明です。
「温度が高すぎる」だけでなく、「温度を3度下げると、不良率が15%から5%に改善する見込みです」という予測が欲しいのです。
これにより、調整の効果を事前に把握し、最適なパラメータを探索できます。
第3回で紹介した PDPは、まさにこのような「もし~したら」の分析を可能にします。
興味深いことに、ベテラン技術者の山田主任は、XAIに対して前向きな姿勢を示しています。
「私の経験では、プレス圧力と材料温度には相関があると感じていました。でも、それを数値で証明することはできなかった。AIがそれを可視化してくれるなら、私の勘を次世代に伝える助けになります」
実際、XAIを適切に活用すれば、ベテランの暗黙知とAIの分析力を融合できます。
山田主任が「このパターンは危険」と感じる製品について、SHAPで分析すると、確かに複数のパラメータが通常とは異なる組み合わせになっていることが判明しました。
人間の直感には、単純な閾値判定では捉えられない、複雑なパターン認識が含まれているのです。
また、新人教育の観点からも、XAIは革新的なツールとなります。
従来、品質判定のスキルを身につけるには、数年の経験が必要でした。
しかし、XAIが「この製品が不良な理由」を具体的に示すことで、新人も短期間で品質の勘所を理解できるようになります。
プレス加工ラインでの品質異常検知システム構築
製造データの準備と特徴理解
プレス加工の現場です。巨大な金型が、轟音とともに金属板を押し潰し、一瞬で複雑な形状の部品を作り出します。

この瞬間に、温度、圧力、速度など、無数のパラメータが品質を左右します。このデータを使って品質を予測するAIシステムを構築します。
まず、必要なライブラリをインポートし、基本的な設定を行います。
これらのライブラリは、データ処理(pandas、numpy)、可視化(matplotlib、seaborn)、機械学習(sklearn、xgboost)、そして説明可能AI(dalex)のための道具箱となります。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
import dalex as dx
import warnings
warnings.filterwarnings('ignore')
import japanize_matplotlib # 日本語表示のため
次に、サンプルデータ(manufacturing_data.csv)を読み込みます。以下からダウンロードできます。
# CSVファイルから製造データを読み込む
manufacturing_data = pd.read_csv(
'manufacturing_data.csv'
)
# データの最初の5行を表示
print(manufacturing_data.head())
以下、実行結果です。
プレス温度 プレス圧力 プレス速度 材料厚 潤滑油温度 金型温度 \
0 153.973713 171.382887 44.429593 2.076540 45.874070 107.064483
1 148.893886 187.094225 46.845346 2.107341 30.605095 104.062440
2 155.181508 193.795917 45.289699 2.049869 38.361025 108.948530
3 162.184239 228.315315 47.260021 1.805750 39.791700 118.263275
4 148.126773 208.348297 48.929248 1.984458 40.079543 99.952655
環境湿度
0 61.609176
1 58.681402
2 68.456782
3 64.119259
4 72.408029
ここで、データ全体の基本統計を確認します。これにより、データの健全性をチェックできます。
# データの基本統計を確認
print("="*60)
print("製造パラメータの基本統計:")
print("="*60)
print(manufacturing_data.describe().round(2))
以下、実行結果です。
============================================================
製造パラメータの基本統計:
============================================================
プレス温度 プレス圧力 プレス速度 材料厚 潤滑油温度 金型温度 環境湿度
count 3000.00 3000.00 3000.00 3000.00 3000.00 3000.00 3000.00
mean 150.26 200.52 50.09 2.00 39.95 105.24 59.85
std 7.89 15.03 5.03 0.10 4.93 7.44 8.74
min 124.07 150.06 31.82 1.61 21.72 78.15 36.63
25% 144.98 190.28 46.66 1.93 36.48 100.06 53.31
50% 150.19 200.56 50.15 2.00 39.95 105.22 59.76
75% 155.39 210.57 53.54 2.07 43.31 110.41 66.44
max 181.41 251.43 72.40 2.39 58.06 133.39 85.66
このデータセットは、製造業におけるプレス加工ラインの製品に関するものです。
- プレス温度 (℃): プレス加工時の温度で、通常は150℃が最適です。温度の変動は製品の品質に影響を与える可能性があります。
- プレス圧力 (MPa): プレス加工時の圧力で、通常は200MPaが標準です。圧力が不適切だと、成形不良や亀裂の原因となることがあります。
- プレス速度 (mm/s): プレス加工の速度で、速すぎても遅すぎても問題が生じます。速すぎると材料に負荷がかかり、遅すぎると温度管理が困難になります。
- 材料厚 (mm): 材料の厚さで、ロットごとにわずかなバラツキがあります。材料メーカーの公差内でも、品質に影響する場合があります。
- 潤滑油温度 (℃): 潤滑油の温度で、温度管理が重要です。潤滑油の温度が不適切だと、摩擦係数が変化し品質に影響を与える可能性があります。
- 金型温度 (℃): プレス温度と相関があります。
- 環境湿度 (%): 季節変動があり、時間帯による湿度変化をあります(日中と夜間の差)。
このデータセットは、製造パラメータ(変数)は製品の品質に影響を与える可能性があり、これらのデータを分析し、製造プロセスの改善点を見つけることを目的にしています。
次に、品質を決定しているロジックを実装します。これは事例の製造現場で利用している経験などに基にしたものです。
# 品質スコアの計算
def calculate_quality_score(row):
"""
製造パラメータから品質スコアを計算
低いスコアほど不良の可能性が高い
"""
score = 100 # 基準スコア
# 温度の影響(最適値150℃から離れるほどスコア低下)
temp_deviation = abs(row['プレス温度'] - 150)
score -= temp_deviation * 1.5
# 圧力の影響(最適値200MPaから離れるほどスコア低下)
pressure_deviation = abs(row['プレス圧力'] - 200)
score -= pressure_deviation * 0.8
# 速度の影響(速すぎても遅すぎても問題)
speed_deviation = abs(row['プレス速度'] - 50)
score -= speed_deviation * 1.2
# 温度と圧力の相互作用
# 高温高圧の組み合わせは材料に過度な負荷をかける
if row['プレス温度'] > 155 and row['プレス圧力'] > 210:
score -= 15
# 低温低圧の組み合わせは成形不良を起こしやすい
if row['プレス温度'] < 145 and row['プレス圧力'] < 190:
score -= 15
# 材料厚の影響(厚すぎる材料は特別な調整が必要)
if row['材料厚'] > 2.15:
score -= 10
# 環境要因の影響
if row['環境湿度'] > 75:
score -= 5 # 高湿度は品質に悪影響
# 潤滑油温度の管理不良
if row['潤滑油温度'] < 35 or row['潤滑油温度'] > 45:
score -= 8
return score
# 品質スコアを計算
manufacturing_data['品質スコア'] = manufacturing_data.apply(
calculate_quality_score, axis=1
)
print("品質スコアの分布:")
print(f" 平均: {manufacturing_data['品質スコア'].mean():.1f}")
print(f" 標準偏差: {manufacturing_data['品質スコア'].std():.1f}")
print(f" 最小値: {manufacturing_data['品質スコア'].min():.1f}")
print(f" 最大値: {manufacturing_data['品質スコア'].max():.1f}")
以下、実行結果です。
品質スコアの分布: 平均: 70.8 標準偏差: 14.5 最小値: 9.6 最大値: 98.4
品質スコアを基に、不良品判定を行います。実際の製造現場と同様に、一定の閾値を下回った製品を不良品とします。
# 不良品判定(品質スコアが閾値以下を不良品とする)
threshold = 65 # 閾値
manufacturing_data['不良品'] = (
manufacturing_data['品質スコア'] < threshold
).astype(int)
# 不良率の確認
不良率 = manufacturing_data['不良品'].mean()
print(f"全体の不良率: {不良率:.2%}")
print(f" 良品数: {(manufacturing_data['不良品'] == 0).sum()}個")
print(f" 不良品数: {(manufacturing_data['不良品'] == 1).sum()}個")
以下、実行結果です。
全体の不良率: 29.53% 良品数: 2114個 不良品数: 886個
データの可視化により、品質に影響する要因を直感的に理解できます。
# データの可視化準備
fig, axes = plt.subplots(4, 1, figsize=(8, 24))
# 1. 温度と圧力の散布図(良品・不良品の分布)
good_products = manufacturing_data[manufacturing_data['不良品'] == 0]
defect_products = manufacturing_data[manufacturing_data['不良品'] == 1]
axes[0].scatter(
good_products['プレス温度'],
good_products['プレス圧力'],
alpha=0.5, label='良品', color='blue'
)
axes[0].scatter(
defect_products['プレス温度'],
defect_products['プレス圧力'],
alpha=0.5, label='不良品', color='red'
)
axes[0].set_xlabel('プレス温度(℃)')
axes[0].set_ylabel('プレス圧力(MPa)')
axes[0].set_title('図1:温度と圧力による品質分布')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
# 2. 品質スコアのヒストグラム
axes[1].hist(
manufacturing_data['品質スコア'],
bins=30, edgecolor='black', alpha=0.7
)
axes[1].axvline(
x=threshold, color='red', linestyle='--',
label=f'不良品閾値({threshold})'
)
axes[1].set_xlabel('品質スコア')
axes[1].set_ylabel('頻度')
axes[1].set_title('図2:品質スコアの分布')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
# 3. パラメータ相関行列の計算
correlation_matrix = manufacturing_data[
manufacturing_data.columns[0:8]
].corr()
# 相関行列のヒートマップ
im = axes[2].imshow(
correlation_matrix,
cmap='coolwarm',
aspect='auto',
vmin=-1,
vmax=1
)
axes[2].set_xticks(range(len(correlation_matrix.columns)))
axes[2].set_yticks(range(len(correlation_matrix.columns)))
axes[2].set_xticklabels(
correlation_matrix.columns,
rotation=45,
ha='right'
)
axes[2].set_yticklabels(correlation_matrix.columns)
axes[2].set_title('図3:パラメータ間の相関関係')
plt.colorbar(im, ax=axes[2])
# 4. 時系列での不良率変化(時間帯別)
manufacturing_data['時間帯グループ'] = np.arange(len(manufacturing_data)) % 24
hourly_defect = manufacturing_data.groupby(
'時間帯グループ'
)['不良品'].mean()
axes[3].plot(
hourly_defect.index,
hourly_defect.values,
marker='o'
)
axes[3].set_xlabel('時間帯')
axes[3].set_ylabel('不良率')
axes[3].set_title('図4:時間帯別の不良率推移')
axes[3].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
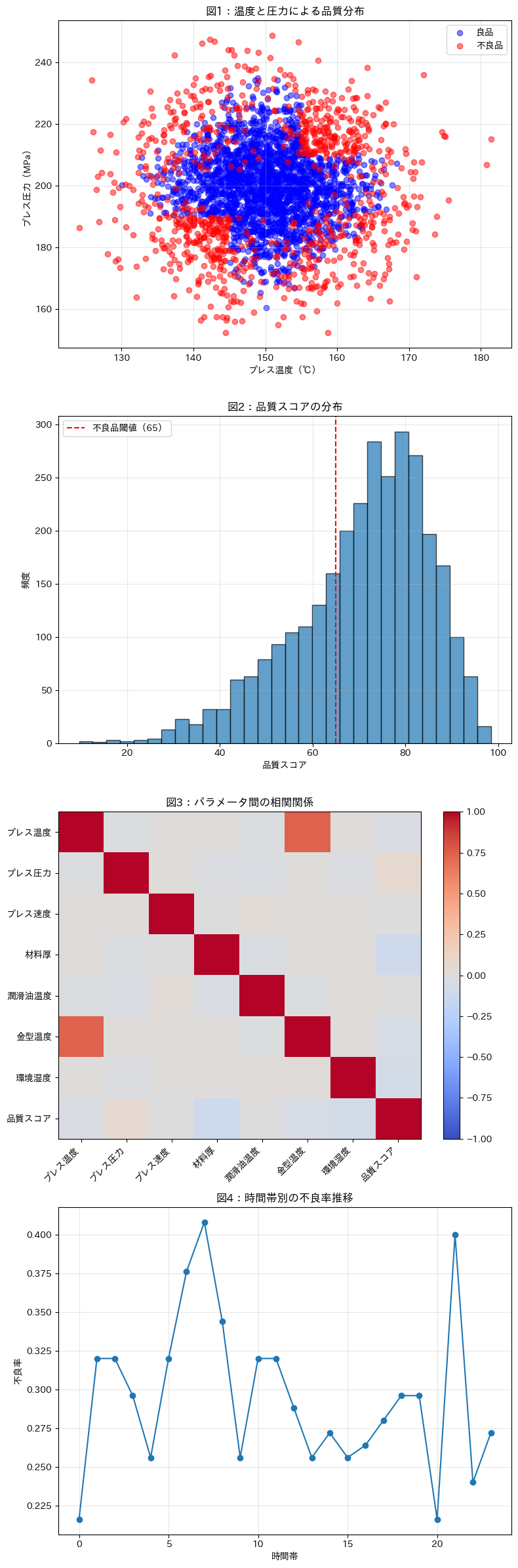
温度と圧力による品質分布(図1)
- この散布図は、プレス温度とプレス圧力の関係が製品の品質にどのように影響するかを示しています。
- 青い点は良品を、赤い点は不良品を表しています。
- 不良品は特定の温度と圧力の組み合わせに集中しており、特に高温高圧または低温低圧の領域で多く見られます。
品質スコアの分布(図2)
- このヒストグラムは、全製品の品質スコアの分布を示しています。
- 赤い破線は不良品の閾値を示しており、これを下回るスコアの製品が不良品と判定されます。
- スコアの分布から、製品の多くが閾値を上回っていることがわかりますが、一定数の製品が不良品として分類されることも確認できます。
パラメータ間の相関関係(図3)
- このヒートマップは、製造パラメータ間の相関関係を視覚化したものです。
- プレス温度と金型温度の間に強い正の相関が見られ、これはプレス温度が金型温度に影響を与えていることを示唆しています。
- 他のパラメータ間の相関は比較的弱いことがわかります。
時間帯別の不良率推移(図4)
- この折れ線グラフは、時間帯ごとの不良率の変化を示しています。
- 特定の時間帯に不良率が上昇する傾向が見られ、これはシフトや環境条件の変化が品質に影響を与えている可能性を示唆しています。
品質スコアと相関の強い要因が何なのかを見てみましょう。相関係数の絶対値の高い要因3つを出力します。
# 相関の強い要因トップ3を表示
print("品質スコアと最も相関の高いパラメータ(絶対値):")
quality_correlations = correlation_matrix[
'品質スコア'
].drop('品質スコア').abs().sort_values(ascending=False)
for i, (param, corr) in enumerate(quality_correlations.head(3).items(), 1):
print(f" ランク{i} - {param}: 相関係数の絶対値 {corr:.3f}")
以下、実行結果です。
品質スコアと最も相関の高いパラメータ(絶対値): ランク1 - 材料厚: 相関係数の絶対値 0.104 ランク2 - 環境湿度: 相関係数の絶対値 0.064 ランク3 - プレス圧力: 相関係数の絶対値 0.061
この品質スコアと最も相関の高いパラメータの結果によると、以下の3つのパラメータが品質スコアに対して最も強い相関を持っています。
- 材料厚: 相関係数の絶対値が0.104で、品質スコアに最も影響を与えるパラメータです。材料の厚さが製品の品質に与える影響は、厚すぎる材料が特別な調整を必要とするため、品質スコアに直接的な影響を及ぼす可能性があります。
- 環境湿度: 相関係数の絶対値が0.064で、品質スコアに対して2番目に強い相関を持っています。高湿度の環境は製品の品質に悪影響を及ぼすことがあり、特に湿度が高いときに不良品が増える傾向が見られます。
- プレス圧力: 相関係数の絶対値が0.061で、3番目に強い相関を持つパラメータです。プレス圧力が適切でない場合、成形不良や亀裂の原因となることがあり、これが品質スコアに影響を与える要因となっています。
これらのパラメータは、製品の品質を管理する上で重要な指標となり、製造プロセスの最適化において考慮すべき要素です。
異常検知モデルの構築と基本評価
データの特性を理解できたところで、品質を予測するAIモデルを構築します。
RandomForestとXGBoostという2つの強力なアルゴリズムを使い、どちらがプレス加工の品質予測に適しているかを検証します。
まず、データを訓練用とテスト用に分割します。これは、モデルの汎化性能を適切に評価するために重要なステップです。
# 特徴量と目的変数の分離
# 品質スコアは実際の運用では分からないので除外
X = manufacturing_data.drop(['不良品', '品質スコア'], axis=1)
y = manufacturing_data['不良品']
print("モデル構築のためのデータ準備:")
print(f" 特徴量の数: {X.shape[1]}")
print(f" 特徴量: {list(X.columns)}")
# 訓練データとテストデータに分割(75:25)
# stratifyで良品と不良品の比率を保つ
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.25,
random_state=42,
stratify=y # 不良品の比率を保持
)
print("\nデータセットのサイズ:")
print(f" 訓練データ: {len(X_train)}件")
print(f" テストデータ: {len(X_test)}件")
print(f"\n不良率の確認:")
print(f" 訓練データの不良率: {y_train.mean():.2%}")
print(f" テストデータの不良率: {y_test.mean():.2%}")
以下、実行結果です。
モデル構築のためのデータ準備: 特徴量の数: 8 特徴量: ['プレス温度', 'プレス圧力', 'プレス速度', '材料厚', '潤滑油温度', '金型温度', '環境湿度', '時間帯グループ'] データセットのサイズ: 訓練データ: 2250件 テストデータ: 750件 不良率の確認: 訓練データの不良率: 29.56% テストデータの不良率: 29.47%
RandomForestモデルを構築します。このアルゴリズムは、複数の決定木を組み合わせることで、安定した予測を実現します。
# RandomForestモデルの構築
print("="*60)
print("RandomForestモデルの構築")
print("="*60)
rf_model = RandomForestClassifier(
n_estimators=100, # 100本の決定木を使用
max_depth=10, # 各決定木の最大深さ
min_samples_split=20, # ノード分割の最小サンプル数
min_samples_leaf=10, # 葉ノードの最小サンプル数
random_state=42
)
# モデルの訓練
rf_model.fit(X_train, y_train)
# 予測の実行
y_pred_rf = rf_model.predict(X_test)
y_pred_proba_rf = rf_model.predict_proba(X_test)[:, 1]
print(f"\nテストデータでの予測結果:")
print(f" 予測された不良品数: {y_pred_rf.sum()}個")
print(f" 実際の不良品数: {y_test.sum()}個")
# 性能評価
from sklearn.metrics import classification_report, confusion_matrix
print("\nRandomForestの性能評価:")
print("-" * 50)
print(classification_report(
y_test,
y_pred_rf,
target_names=['良品', '不良品']
))
# 混同行列の表示
cm_rf = confusion_matrix(y_test, y_pred_rf)
print("\n混同行列:")
print(f" 真の良品を良品と判定: {cm_rf[0,0]}個")
print(f" 真の良品を不良品と判定(過検出): {cm_rf[0,1]}個")
print(f" 真の不良品を良品と判定(見逃し): {cm_rf[1,0]}個")
print(f" 真の不良品を不良品と判定: {cm_rf[1,1]}個")
以下、実行結果です。
============================================================
RandomForestモデルの構築
============================================================
テストデータでの予測結果:
予測された不良品数: 180個
実際の不良品数: 221個
RandomForestの性能評価:
--------------------------------------------------
precision recall f1-score support
良品 0.90 0.97 0.94 529
不良品 0.92 0.75 0.82 221
accuracy 0.91 750
macro avg 0.91 0.86 0.88 750
weighted avg 0.91 0.91 0.90 750
混同行列:
真の良品を良品と判定: 514個
真の良品を不良品と判定(過検出): 15個
真の不良品を良品と判定(見逃し): 56個
真の不良品を不良品と判定: 165個
続いて、XGBoostモデルも構築し、性能を比較します。
# XGBoostモデルの構築
print("="*60)
print("XGBoostモデルの構築")
print("="*60)
xgb_model = XGBClassifier(
n_estimators=100,
max_depth=6,
learning_rate=0.1,
random_state=42
)
# モデルの訓練と予測
xgb_model.fit(X_train, y_train)
y_pred_xgb = xgb_model.predict(X_test)
y_pred_proba_xgb = xgb_model.predict_proba(X_test)[:, 1]
print(f"\nテストデータでの予測結果:")
print(f" 予測された不良品数: {y_pred_xgb.sum()}個")
print(f" 実際の不良品数: {y_test.sum()}個")
# XGBoostの性能評価
print("\nXGBoostの性能評価:")
print("-" * 50)
print(classification_report(
y_test,
y_pred_xgb,
target_names=['良品', '不良品']
))
cm_xgb = confusion_matrix(y_test, y_pred_xgb)
print("\n混同行列:")
print(f" 真の良品を良品と判定: {cm_xgb[0,0]}個")
print(f" 真の良品を不良品と判定(過検出): {cm_xgb[0,1]}個")
print(f" 真の不良品を良品と判定(見逃し): {cm_xgb[1,0]}個")
print(f" 真の不良品を不良品と判定: {cm_xgb[1,1]}個")
以下、実行結果です。
============================================================
XGBoostモデルの構築
============================================================
テストデータでの予測結果:
予測された不良品数: 190個
実際の不良品数: 221個
XGBoostの性能評価:
--------------------------------------------------
precision recall f1-score support
良品 0.93 0.99 0.96 529
不良品 0.96 0.83 0.89 221
accuracy 0.94 750
macro avg 0.95 0.91 0.92 750
weighted avg 0.94 0.94 0.94 750
混同行列:
真の良品を良品と判定: 522個
真の良品を不良品と判定(過検出): 7個
真の不良品を良品と判定(見逃し): 38個
真の不良品を不良品と判定: 183個
製造現場では、見逃し(不良品を良品と判定)と過検出(良品を不良品と判定)のコストが異なります。この観点から両モデルを評価しましょう。
まずは、評価するための関数を作成します。
# 製造現場特有の評価指標を計算
def calculate_manufacturing_metrics(y_true, y_pred, model_name):
"""製造業で重要な品質管理指標を計算"""
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
print(f"\n{model_name}の製造現場視点での評価:")
print("="*50)
# 見逃し率(不良品を良品と誤判定)
miss_rate = fn / (fn + tp) if (fn + tp) > 0 else 0
print(f"見逃し率: {miss_rate:.2%}")
print(f" → {fn}個の不良品を見逃しています")
# 過検出率(良品を不良品と誤判定)
false_alarm_rate = fp / (fp + tn) if (fp + tn) > 0 else 0
print(f"過検出率: {false_alarm_rate:.2%}")
print(f" → {fp}個の良品を不良品と誤判定しています")
# コスト計算(見逃しコストは過検出の10倍と仮定)
miss_cost = 10000 # 不良品流出のコスト(円/個)
false_alarm_cost = 1000 # 良品廃棄のコスト(円/個)
total_cost = fn * miss_cost + fp * false_alarm_cost
print(f"\n推定損失コスト:")
print(f" 見逃しによる損失: {fn * miss_cost:,}円")
print(f" 過検出による損失: {fp * false_alarm_cost:,}円")
print(f" 合計損失: {total_cost:,}円")
return {
'見逃し数': fn,
'過検出数': fp,
'見逃し率': miss_rate,
'過検出率': false_alarm_rate,
'推定損失': total_cost
}
次に、この関数を使い評価します。両モデルの製造指標を比較します。
# 両モデルの製造指標を比較
rf_metrics = calculate_manufacturing_metrics(
y_test,
y_pred_rf,
"RandomForest"
)
xgb_metrics = calculate_manufacturing_metrics(
y_test,
y_pred_xgb,
"XGBoost"
)
# 比較結果の表示
print()
print("="*60)
print("モデル比較結果")
print("="*60)
comparison_df = pd.DataFrame({
'RandomForest': rf_metrics,
'XGBoost': xgb_metrics
}).T
print(comparison_df.to_string())
print("\n推奨モデル: ", end="")
if comparison_df.loc['RandomForest', '推定損失'] < comparison_df.loc['XGBoost', '推定損失']:
print("RandomForest(トータルコストが低い)")
selected_model = rf_model
selected_model_name = "RandomForest"
else:
print("XGBoost(トータルコストが低い)")
selected_model = xgb_model
selected_model_name = "XGBoost"
以下、実行結果です。
RandomForestの製造現場視点での評価:
==================================================
見逃し率: 25.34%
→ 56個の不良品を見逃しています
過検出率: 2.84%
→ 15個の良品を不良品と誤判定しています
推定損失コスト:
見逃しによる損失: 560,000円
過検出による損失: 15,000円
合計損失: 575,000円
XGBoostの製造現場視点での評価:
==================================================
見逃し率: 17.19%
→ 38個の不良品を見逃しています
過検出率: 1.32%
→ 7個の良品を不良品と誤判定しています
推定損失コスト:
見逃しによる損失: 380,000円
過検出による損失: 7,000円
合計損失: 387,000円
============================================================
モデル比較結果
============================================================
見逃し数 過検出数 見逃し率 過検出率 推定損失
RandomForest 56.0 15.0 0.253394 0.028355 575000.0
XGBoost 38.0 7.0 0.171946 0.013233 387000.0
推奨モデル: XGBoost(トータルコストが低い)
RandomForestモデルとXGBoostモデルの性能を比較しました。
両モデルは製品の品質を予測するために使用され、特に不良品を見逃すことや良品を過検出することが製造現場での重要な指標となります。
RandomForestモデルでは、見逃し率が25.34%であり、56個の不良品を見逃しました。また、過検出率は2.84%で、15個の良品を不良品と誤判定しました。これにより、見逃しによる損失が560,000円、過検出による損失が15,000円となり、合計損失は575,000円でした。
一方、XGBoostモデルでは、見逃し率が17.19%で、38個の不良品を見逃しました。過検出率は1.32%で、7個の良品を不良品と誤判定しました。見逃しによる損失は380,000円、過検出による損失は7,000円で、合計損失は387,000円でした。
この結果から、XGBoostモデルはRandomForestモデルよりも見逃し率と過検出率が低く、トータルコストも低いため、製造現場での異常検知において推奨されるモデルとなります。
XGBoostモデルは不良品をより正確に検出し、良品を誤判定することが少ないため、製品の品質管理においてより効果的です。
Permutation Importanceで品質要因をランク付け
どの製造パラメータが品質に最も影響しているのでしょうか。第3回で学んだPermutation Importanceを使って、各パラメータの重要度を定量的に評価します。
print("="*70)
print("Permutation Importanceによる品質要因分析")
print("="*70)
# DALEXのExplainerを作成
# 選択されたモデル(RandomForestまたはXGBoost)を使用
explainer = dx.Explainer(
selected_model,
X_test,
y_test,
label=f"{selected_model_name}品質予測"
)
# Permutation Importanceを計算
importance = explainer.model_parts(
loss_function='1-auc', # AUCの低下を重要度として使用
B=100, # 100回の繰り返しで安定した結果を得る
variable_groups=None
)
# 結果を整理して表示
importance_df = importance.result
# 特徴量ごとの重要度を集計
importance_summary = importance_df.groupby('variable').agg({
'dropout_loss': ['mean', 'std']
}).round(4)
importance_summary.columns = ['平均重要度', '標準偏差']
importance_summary = importance_summary.sort_values(
'平均重要度',
ascending=False
)
# ベースラインとの差分を計算
baseline = importance_df[
importance_df['variable'] == '_baseline_'
]['dropout_loss'].mean()
print("\n特徴量重要度ランキング:")
print("="*60)
for idx, (var, row) in enumerate(importance_summary.iterrows(), 1):
if var not in ['_baseline_', '_full_model_']:
impact = (row['平均重要度'] - baseline) * 100
print(f"\n{idx-1}位: {var}")
print(f" 重要度スコア: {row['平均重要度']:.4f} (±{row['標準偏差']:.4f})")
print(f" 品質への影響度: {impact:.2f}%")
# 具体的な改善提案
if idx <= 3: # トップ3の要因について詳細分析
factor_mean = X_train[var].mean()
factor_std = X_train[var].std()
print(f" 現状: 平均 {factor_mean:.2f} (標準偏差 {factor_std:.2f})")
# 重要度を可視化
importance.plot(show=True)
print("\n可視化完了: 各パラメータの重要度が棒グラフで表示されています")
以下、実行結果です。
====================================================================== Permutation Importanceによる品質要因分析 ====================================================================== Preparation of a new explainer is initiated -> data : 750 rows 8 cols -> target variable : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray. -> target variable : 750 values -> model_class : xgboost.sklearn.XGBClassifier (default) -> label : XGBoost品質予測 -> predict function : <function yhat_proba_default at 0x7f81fff02f20> will be used (default) -> predict function : Accepts pandas.DataFrame and numpy.ndarray. -> predicted values : min = 0.000549, mean = 0.268, max = 0.999 -> model type : classification will be used (default) -> residual function : difference between y and yhat (default) -> residuals : min = -0.874, mean = 0.0269, max = 0.994 -> model_info : package xgboost A new explainer has been created! 特徴量重要度ランキング: ============================================================ 1位: プレス圧力 重要度スコア: 0.2629 (±nan) 品質への影響度: -23.96% 現状: 平均 199.57 (標準偏差 15.08) 2位: プレス温度 重要度スコア: 0.2592 (±nan) 品質への影響度: -24.33% 現状: 平均 150.14 (標準偏差 7.90) 3位: プレス速度 重要度スコア: 0.0335 (±nan) 品質への影響度: -46.90% 4位: 潤滑油温度 重要度スコア: 0.0330 (±nan) 品質への影響度: -46.95% 5位: 材料厚 重要度スコア: 0.0281 (±nan) 品質への影響度: -47.44% 6位: 環境湿度 重要度スコア: 0.0167 (±nan) 品質への影響度: -48.58% 7位: 金型温度 重要度スコア: 0.0163 (±nan) 品質への影響度: -48.62% 8位: 時間帯グループ 重要度スコア: 0.0161 (±nan) 品質への影響度: -48.64%
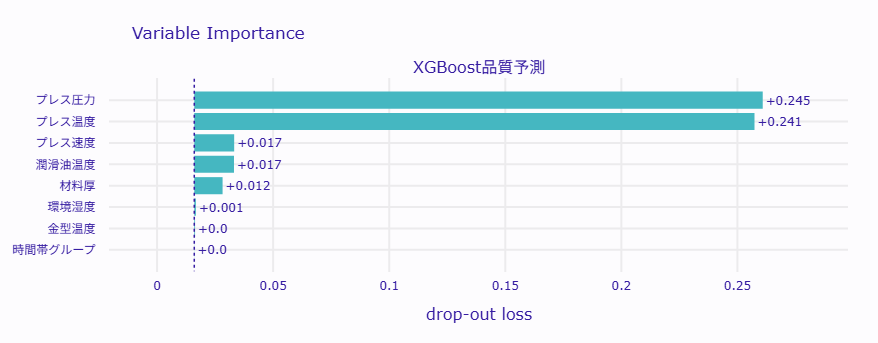
この分析では、製品の品質に影響を与える製造パラメータの重要度を評価しました。重要度は、モデルの予測性能に与える影響度として計算され、特定のパラメータがどれだけ品質に影響を与えるかを示しています。
1位は「プレス圧力」で、重要度スコアは0.2629です。これは、プレス圧力が品質に最も大きな影響を与えることを示しています。現状では平均199.57 MPaで、標準偏差は15.08です。プレス圧力の管理が品質向上に重要であることがわかります。
2位は「プレス温度」で、重要度スコアは0.2592です。プレス温度も品質に大きな影響を与えています。平均は150.14℃で、標準偏差は7.90です。温度管理が品質において重要な要素であることが示されています。
3位は「プレス速度」で、重要度スコアは0.0335です。プレス速度は品質に対する影響度が比較的小さいですが、依然として重要な要因です。
その他の要因として、「潤滑油温度」、「材料厚」、「環境湿度」、「金型温度」、「時間帯グループ」が続きます。これらの要因は、品質に対する影響度が低いですが、製造プロセスの最適化において考慮すべき要素です。
この分析結果は、製造プロセスにおける品質管理の改善に役立ちます。特に、プレス圧力とプレス温度の管理が品質向上において重要であることが示されています。
PDPで見る品質との関係と最適値の発見
Partial Dependence Plot(PDP)を使って、各製造パラメータ(変数)が品質にどのように影響するかを可視化します。これにより、最適な操業条件をデータから特定していきます。
# 最も重要な2つのパラメータのPDPを計算
print("重要度上位2つのパラメータについてPDP分析を実施")
# PDPを計算
# プレス温度
pdp_temp = explainer.model_profile(
type='pdp',
variables=['プレス温度']
)
# プレス圧力
pdp_pressure = explainer.model_profile(
type='pdp',
variables=['プレス圧力']
)
# PDPデータから最適値を特定
# プレス温度
temp_pdp_data = pdp_temp.result[
pdp_temp.result['_vname_'] == 'プレス温度'
]
# プレス圧力
pressure_pdp_data = pdp_pressure.result[
pdp_pressure.result['_vname_'] == 'プレス圧力'
]
# 最適値(不良率が最小となる値)を見つける
# プレス温度
optimal_temp_idx = temp_pdp_data['_yhat_'].idxmin()
optimal_temp = temp_pdp_data.loc[
optimal_temp_idx,
'_x_'
]
optimal_temp_defect_rate = temp_pdp_data.loc[
optimal_temp_idx,
'_yhat_'
]
# プレス圧力
optimal_pressure_idx = pressure_pdp_data['_yhat_'].idxmin()
optimal_pressure = pressure_pdp_data.loc[
optimal_pressure_idx,
'_x_'
]
optimal_pressure_defect_rate = pressure_pdp_data.loc[
optimal_pressure_idx,
'_yhat_'
]
print("\n\n" + "="*50)
print("PDP分析による最適操業条件")
print("="*50)
print(f"\nプレス温度の最適値: {optimal_temp:.1f}℃")
print(f" この温度での予測不良率: {optimal_temp_defect_rate:.3f}")
print(f"\nプレス圧力の最適値: {optimal_pressure:.1f}MPa")
print(f" この圧力での予測不良率: {optimal_pressure_defect_rate:.3f}")
# PDPの可視化
fig, axes = plt.subplots(2, 1, figsize=(8, 12))
# 温度のPDP
axes[0].plot(
temp_pdp_data['_x_'],
temp_pdp_data['_yhat_'],
linewidth=2,
color='darkblue'
)
axes[0].axvline(x=optimal_temp, color='red', linestyle='--',
label=f'最適値: {optimal_temp:.1f}℃')
axes[0].axhline(y=optimal_temp_defect_rate, color='gray',
linestyle=':', alpha=0.5)
axes[0].set_xlabel('プレス温度(℃)')
axes[0].set_ylabel('予測不良率')
axes[0].set_title('温度が品質に与える影響')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
# 圧力のPDP
axes[1].plot(
pressure_pdp_data['_x_'],
pressure_pdp_data['_yhat_'],
linewidth=2,
color='darkgreen'
)
axes[1].axvline(x=optimal_pressure, color='red', linestyle='--',
label=f'最適値: {optimal_pressure:.1f}MPa')
axes[1].axhline(y=optimal_pressure_defect_rate, color='gray',
linestyle=':', alpha=0.5)
axes[1].set_xlabel('プレス圧力(MPa)')
axes[1].set_ylabel('予測不良率')
axes[1].set_title('圧力が品質に与える影響')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
重要度上位2つのパラメータについてPDP分析を実施 Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 62.19it/s] Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 64.23it/s] ================================================== PDP分析による最適操業条件 ================================================== プレス温度の最適値: 148.6℃ この温度での予測不良率: 0.062 プレス圧力の最適値: 198.6MPa この圧力での予測不良率: 0.046
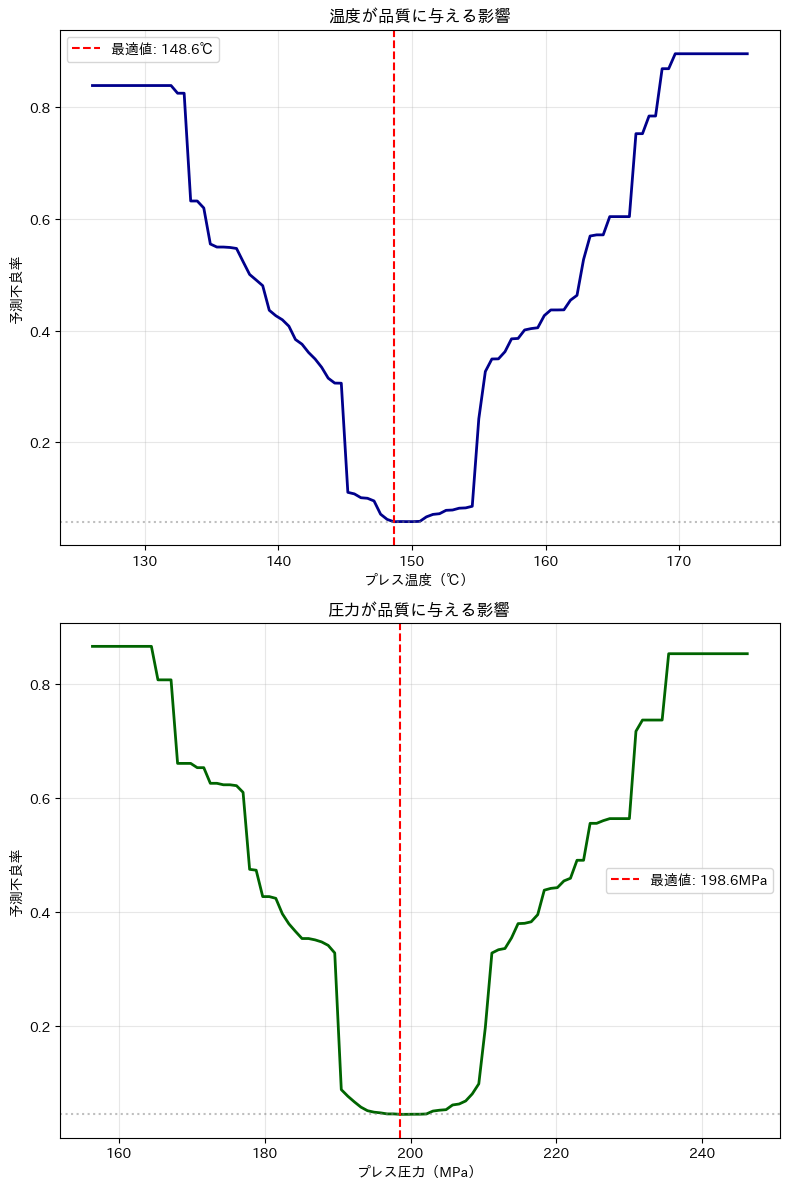
PDP(Partial Dependence Plot)分析は、特定の製造パラメータが製品の品質にどのように影響を与えるかを視覚的に示すための手法です。
今回は、プレス温度とプレス圧力の2つの重要なパラメータについて、品質への影響を評価しました。
- PDPグラフの曲線は、各パラメータ値での予測不良率を示しています。曲線が低いほど、不良率が低く、品質が良いことを意味します。
- 赤い縦線は最適値を示しており、この値で不良率が最小となります。製造プロセスを最適化するためには、この最適値に近づけることが重要です。
- 曲線の傾きが急な部分は、わずかな変化で品質が大きく変わる敏感な領域です。この領域では、パラメータの管理が特に重要です。
具体的な結果として、プレス温度の最適値は148.6℃で、この温度での予測不良率は0.044です。
また、プレス圧力の最適値は198.6MPaで、この圧力での予測不良率は0.047です。
これらの最適値を目指して製造プロセスを調整することで、製品の品質を向上させることができます。
ということで、各パラメータのPDPを計算して最適値を見つけます。
# 各パラメータのPDPを計算して最適値を見つける
optimal_values = {}
num_vars = len(X_train.columns)
fig, axes = plt.subplots(4, 2, figsize=(12, 12))
axes = axes.flatten()
# 各変数ごとにPDPを計算して最適値を見つける
for i, variable in enumerate(X_train.columns):
# PDPを計算
pdp = explainer.model_profile(type='pdp', variables=[variable])
pdp_data = pdp.result[pdp.result['_vname_'] == variable]
optimal_idx = pdp_data['_yhat_'].idxmin()
optimal_value = pdp_data.loc[optimal_idx, '_x_']
optimal_values[variable] = optimal_value
# PDPの可視化
axes[i].plot(pdp_data['_x_'], pdp_data['_yhat_'], linewidth=2)
axes[i].axvline(x=optimal_value, color='red', linestyle='--', label=f'最適値: {optimal_value:.2f}')
axes[i].set_xlabel(variable)
axes[i].set_ylabel('予測不良率')
axes[i].set_title(f'{variable}が品質に与える影響')
axes[i].legend()
axes[i].grid(True, alpha=0.3)
# 余分なサブプロットを非表示にする
for j in range(i + 1, len(axes)):
axes[j].set_visible(False)
plt.tight_layout()
plt.show()
以下、実行結果です。
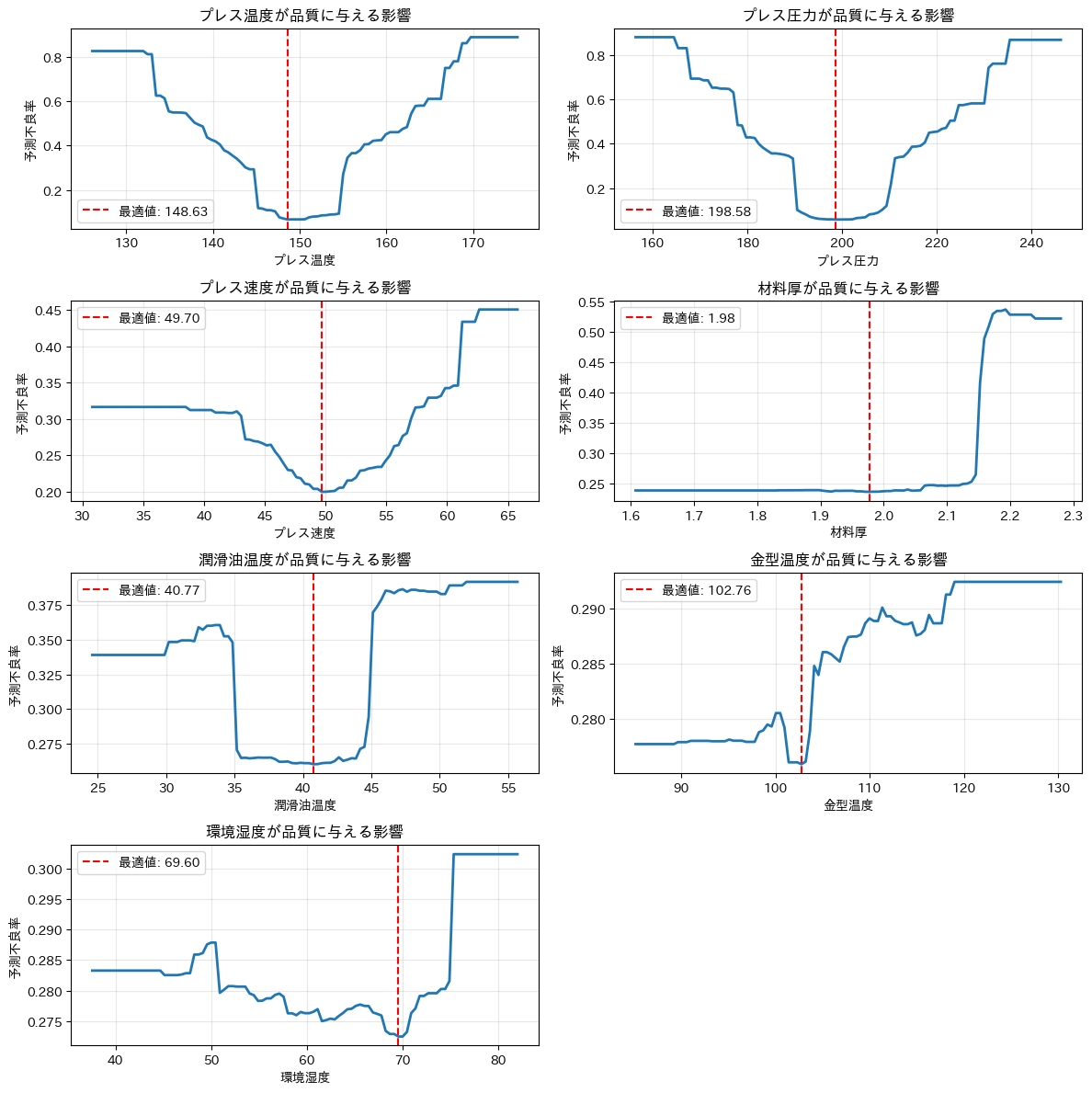
最適条件での改善効果を試算します。ただし、常に最適条件を保つことが難しいので、最適条件に対し±10%のぶれがあることを想定しています。
# 現状と最適条件での不良率を比較
print("="*60)
print("最適化による改善効果の試算")
print("="*60)
# 現在の平均的な操業条件
current_conditions = pd.DataFrame([X_train.mean()])
print("\n現在の平均的な操業条件:")
for col in current_conditions.columns[:-1]:
print(f" {col}: {current_conditions[col].values[0]:.2f}")
# 現状の不良率を計算(元データで計算)
current_defect_prob = selected_model.predict(X_test).mean()
print(f"\n現状の予測不良率: {current_defect_prob:.2%}")
# 最適条件を設定(すべてのパラメータを最適化)
optimal_conditions = pd.DataFrame([X_train.mean()])
for variable, value in optimal_values.items():
optimal_conditions[variable] = value
print("\n最適化後の操業条件:")
for col in optimal_conditions.columns[:-1]:
print(f" {col}: {optimal_conditions[col].values[0]:.2f}(変更)")
# 最適化後の予測不良率を計算(テストデータで評価)
np.random.seed(42) # 再現性のためにシードを設定
fluctuation = np.random.uniform(-0.1, 0.1, size=(X_test.shape[0], X_test.shape[1]-1)) # -10%から+10%の範囲でぶれる
# 最適値に対してぶれを加える
optimal_values_df = pd.DataFrame(optimal_values, index=X_test.index)
X_test_fluctuated = optimal_values_df * (1 + fluctuation)
X_test_fluctuated['時間帯グループ'] = X_test['時間帯グループ']
# ぶれたデータセットでの予測不良率を計算
optimal_defect_prob = selected_model.predict(X_test_fluctuated).mean()
print(f"\n最適化後の予測不良率: {optimal_defect_prob:.2%}")
# 改善効果の計算
if current_defect_prob > 0:
improvement = (current_defect_prob - optimal_defect_prob) / current_defect_prob * 100
else:
improvement = 0
print(f"\n改善効果: {improvement:.1f}%の不良率削減")
# コスト削減効果の試算
print("\n" + "="*60)
print("年間コスト削減効果の試算")
print("="*60)
daily_production = 1000 # 日産1000個
annual_days = 250 # 年間稼働日数
defect_cost = 10000 # 不良品1個あたりのコスト(円)
print(f"前提条件:")
print(f" 日産数: {daily_production:,}個")
print(f" 年間稼働日数: {annual_days}日")
print(f" 不良品1個あたりコスト: {defect_cost:,}円")
annual_production = daily_production * annual_days
current_defects = annual_production * current_defect_prob
optimal_defects = annual_production * optimal_defect_prob
saved_defects = current_defects - optimal_defects
print(f"\n年間生産数: {annual_production:,}個")
print(f"現状の年間不良品数: {current_defects:,.0f}個")
print(f"最適化後の年間不良品数: {optimal_defects:,.0f}個")
print(f"削減される不良品数: {saved_defects:,.0f}個")
annual_saving = saved_defects * defect_cost
print(f"\n年間コスト削減額: {annual_saving:,.0f}円")
if annual_saving > 10000000:
print(f" → {annual_saving/10000000:.1f}千万円の削減効果!")
以下、実行結果です。
============================================================ 最適化による改善効果の試算 ============================================================ 現在の平均的な操業条件: プレス温度: 150.14 プレス圧力: 199.57 プレス速度: 50.05 材料厚: 2.00 潤滑油温度: 40.24 金型温度: 105.28 環境湿度: 59.89 現状の予測不良率: 25.33% 最適化後の操業条件: プレス温度: 148.63(変更) プレス圧力: 198.58(変更) プレス速度: 49.70(変更) 材料厚: 1.98(変更) 潤滑油温度: 40.77(変更) 金型温度: 102.76(変更) 環境湿度: 69.60(変更) 最適化後の予測不良率: 22.13% 改善効果: 12.6%の不良率削減 ============================================================ 年間コスト削減効果の試算 ============================================================ 前提条件: 日産数: 1,000個 年間稼働日数: 250日 不良品1個あたりコスト: 10,000円 年間生産数: 250,000個 現状の年間不良品数: 63,333個 最適化後の年間不良品数: 55,333個 削減される不良品数: 8,000個 年間コスト削減額: 80,000,000円 → 8.0千万円の削減効果!
まず、現状の不良率は25.33%です。
最適化アルゴリズムを用いて最適な操業条件を特定し評価しました。 プレス温度を148.63、プレス圧力を198.58、その他金型温度や環境湿度なども含めて条件を変更しました。
これらの最適値に基づいて操業条件を調整した場合、予測不良率は22.13%となり、現状と比較して12.6%の不良率削減という明確な改善効果が確認されました。
年間コスト削減効果の試算では、日産数1,000個、年間稼働日数250日、不良品1個あたりのコストを10,000円と仮定しました。
現状の年間不良品数は63,333個ですが、最適化後は55,333個となり、削減される不良品数は8,000個にのぼります。これにより、年間8,000万円(8.0千万円)のコスト削減効果が見込まれます。
この結果から、操業条件の最適化(パラメータの微調整)を行うことで、製造プロセスの効率化および大幅なコストメリットを享受できる可能性が高いことが示されました。
ALEで相関を考慮した影響を正確に把握する
PDPは強力な手法ですが、製造現場のデータには注意すべき点があります。
プレス温度と金型温度には強い相関があることを、先ほどの相関行列で確認しました。PDPは「プレス温度だけを変化させて、他のパラメータは固定」という計算を行いますが、実際の製造現場では「プレス温度が上がれば金型温度も上がる」という関係があります。
このような相関がある場合、PDPは現実にはありえない組み合わせ(例:プレス温度が高いのに金型温度が低い)も計算に含めてしまい、結果が歪む可能性があります。
ALE(Accumulated Local Effects)は、この問題を解決する手法です。実際のデータ分布に沿って影響を計算するため、パラメータ間の相関があっても正確な影響を把握できます。
# ALE(Accumulated Local Effects)プロファイルを計算
# プレス温度に対するALEを計算
ale_temp = explainer.model_profile(
type='accumulated', # ALEプロファイルを指定
variables=['プレス温度'] # 対象変数は「プレス温度」
)
# プレス圧力に対するALEを計算
ale_pressure = explainer.model_profile(
type='accumulated', # ALEプロファイルを指定
variables=['プレス圧力'] # 対象変数は「プレス圧力」
)
# プレス温度のALEプロファイルをプロット
ale_temp.plot(show=True)
# プレス圧力のALEプロファイルをプロット
ale_pressure.plot(show=True)
以下、実行結果です。
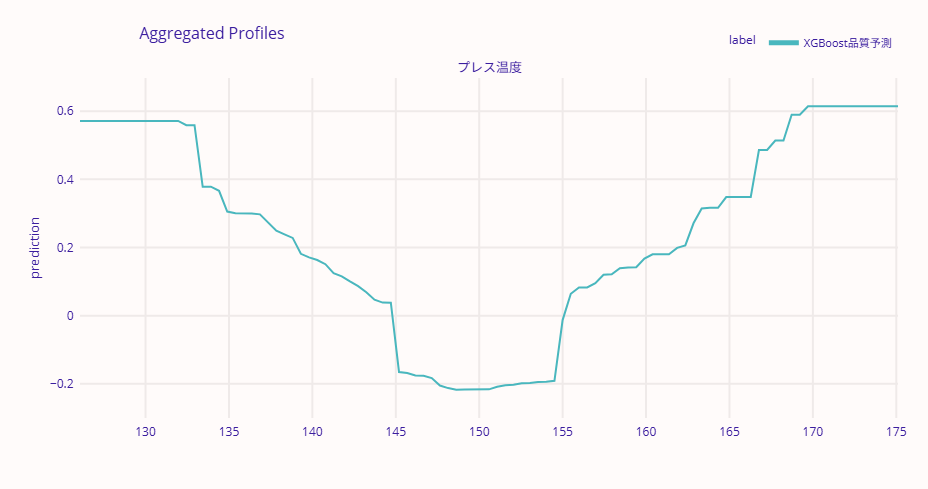
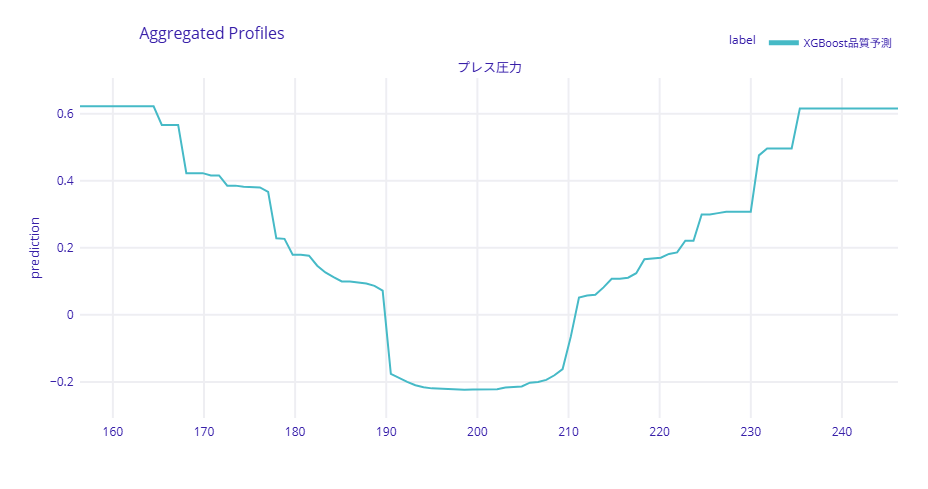
ALEのグラフでは、y軸が予測値(不良率)を示しています。PDPと同様に、各パラメータ値での予測不良率を確認できますが、ALEは実際のデータ分布に基づいた計算を行うため、相関の影響を受けにくい結果が得られます。
PDPとALEの曲線が大きく異なる場合、それはパラメータ間の相関が強いことを示唆しています。
製造現場では、PDPで大まかな傾向を把握し、ALEで相関の影響を確認するという使い方が効果的です。両者の結果が一致していれば、その解釈に自信を持つことができます。
重要なパラメータについて、ALEを一括で計算して比較します。
# ALE(Accumulated Local Effects)プロファイルを計算
# 複数の変数に対するALEを計算
ale_multi = explainer.model_profile(
type='accumulated', # ALEプロファイルを指定
variables=[ # 対象変数をリストで指定
'プレス温度', # プレス温度の影響を評価
'プレス圧力', # プレス圧力の影響を評価
'プレス速度', # プレス速度の影響を評価
'潤滑油温度' # 潤滑油温度の影響を評価
]
)
# ALEプロファイルをプロットして可視化
ale_multi.plot(show=True)
以下、実行結果です。
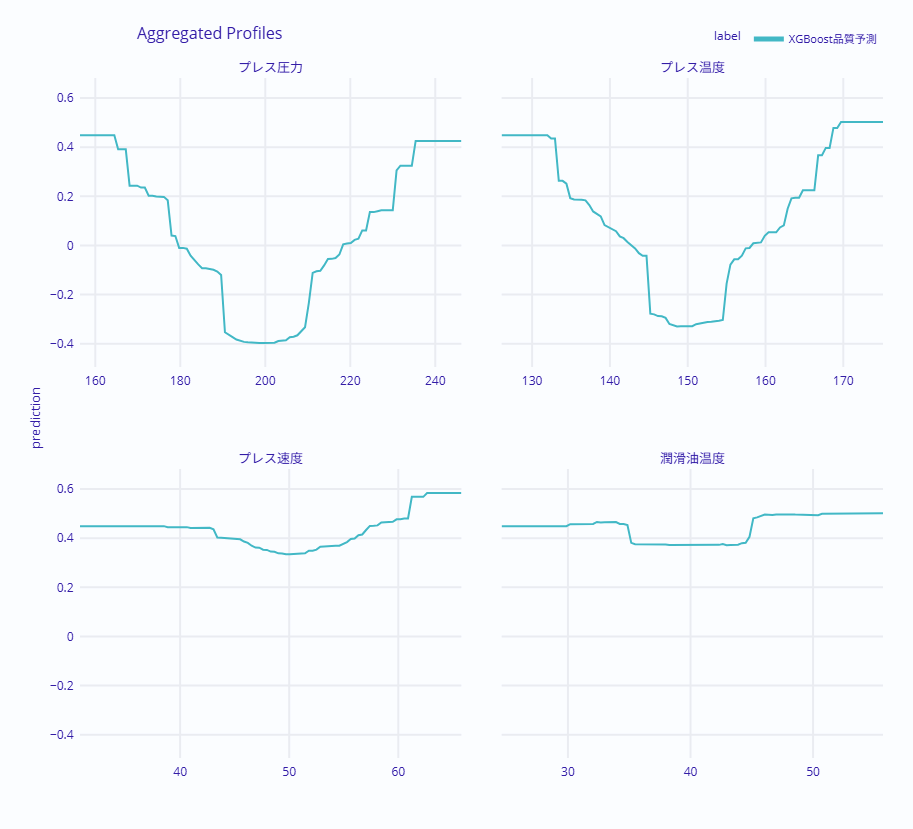
4つのパネルが表示され、各パラメータが品質に与える影響を比較できます。曲線の傾きが急な部分は、わずかな変化で品質が大きく変わる敏感な領域です。この領域では、パラメータの管理を特に厳密に行う必要があります。
Surrogate Modelで判断ルールを可視化する
ここまでの分析で、各パラメータの重要度や最適値を把握できました。しかし、現場の作業者にとっては「結局、どういうルールで良品・不良品が決まるのか」を一目で理解できる形が欲しいところです。
Surrogate Model(代理モデル)は、複雑なXGBoostモデルの判断ロジックを、人間が読める決定木で近似する手法です。
XGBoostの予測結果を「正解」として、シンプルな決定木を学習させます。
# 必要なライブラリをインポート
from sklearn.tree import DecisionTreeClassifier, plot_tree
# 選択されたモデル(XGBoost)の予測結果を取得
xgb_predictions = selected_model.predict(X_test)
# Surrogateモデルとして決定木を作成
surrogate_tree = DecisionTreeClassifier(
max_depth=4, # 木の最大深さ
min_samples_leaf=30, # 葉ノードに必要な最小サンプル数
random_state=42 # 乱数シードを固定
)
# Surrogateモデルを学習
#(XGBoostモデルの予測結果をターゲットとして使用)
surrogate_tree.fit(X_test, xgb_predictions)
# Surrogateモデルの忠実度を計算
# 忠実度: Surrogateモデルの予測が元のモデルの予測と一致する割合
fidelity = (surrogate_tree.predict(X_test) == xgb_predictions).mean()
print(f"忠実度: {fidelity:.2%}")
以下、実行結果です。
忠実度: 89.47%
忠実度は、代理モデルが元のXGBoostモデルの予測をどれだけ再現できているかを示します。89%以上の忠実度があれば、代理モデルは元のモデルの振る舞いをかなりよく捉えていると言えます。
代理モデル(決定木)を可視化します。
# プロットのサイズを指定
plt.figure(figsize=(12, 12))
# 決定木を可視化
plot_tree(
surrogate_tree, # 代理モデル(決定木)
feature_names=X.columns.tolist(), # 特徴量の名前を指定
class_names=['良品', '不良品'], # クラス名を指定
filled=True, # ノードを色付け
rounded=True, # ノードの形状を丸みを帯びた形に
fontsize=10, # フォントサイズを指定
proportion=True # ノード内の割合を表示
)
# グラフのタイトルを設定
plt.title('品質判定の決定ルール(代理モデル)')
# レイアウトを調整
plt.tight_layout()
# グラフを表示
plt.show()
以下、実行結果です。
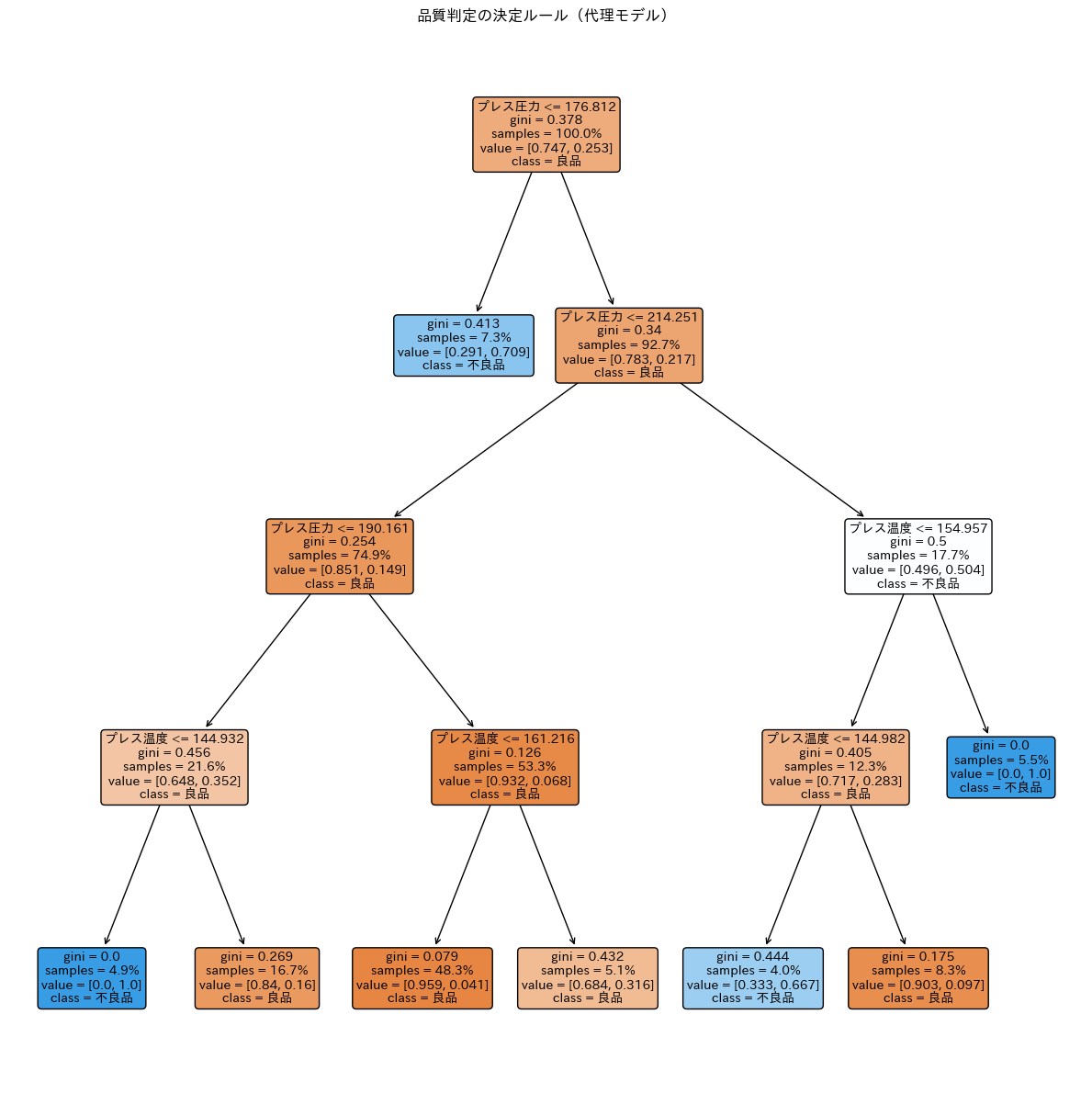
決定木のグラフでは、各ノードの分岐条件と、末端(リーフノード)での予測クラスが表示されます。色が濃いほど、そのクラスへの確信度が高いことを示します。
グラフだけでなく、ルールをテキストとして出力することで、現場での活用がしやすくなります。
# 必要なライブラリをインポート
from sklearn.tree import export_text
# surrogate_tree(代理モデル)からルールを抽出
# feature_namesには特徴量の名前をリスト形式で渡す
tree_rules = export_text(
surrogate_tree, # 決定木モデル
feature_names=X.columns.tolist() # 特徴量の名前を指定
)
# 抽出したルールを出力
print(tree_rules)
以下、実行結果です。
|--- プレス圧力 <= 176.81 | |--- class: 1 |--- プレス圧力 > 176.81 | |--- プレス圧力 <= 214.25 | | |--- プレス圧力 <= 190.16 | | | |--- プレス温度 <= 144.93 | | | | |--- class: 1 | | | |--- プレス温度 > 144.93 | | | | |--- class: 0 | | |--- プレス圧力 > 190.16 | | | |--- プレス温度 <= 161.22 | | | | |--- class: 0 | | | |--- プレス温度 > 161.22 | | | | |--- class: 0 | |--- プレス圧力 > 214.25 | | |--- プレス温度 <= 154.96 | | | |--- プレス温度 <= 144.98 | | | | |--- class: 1 | | | |--- プレス温度 > 144.98 | | | | |--- class: 0 | | |--- プレス温度 > 154.96 | | | |--- class: 1
この決定ルールから、AIモデルの判断ロジックを人間の言葉で解釈できます。
以下は、代理モデルから読み取れる主要ルールです。
- 圧力が低すぎる(176.81以下)場合:
- 温度条件に関わらず、一律で不良品(class: 1)と判定される。
- 圧力が中程度(176.81〜214.25)の場合:
- 圧力が190.16を超えていれば、温度に関わらず基本的に良品。
- 圧力が190.16以下の場合は、温度が144.93より高ければ良品だが、低いと不良品になる。
- 圧力が高すぎる(214.25超)場合:
- 条件が厳しくなる。温度が約145〜155(144.98〜154.96)の範囲内でなければ不良品となりやすい。
これは、Permutation ImportanceやPDPで得た知見と一致しており、モデルが「圧力と温度の複雑な相互作用」を具体的に学習していることを示しています。特に高圧条件下での温度管理の重要性が示唆されています。
代理モデルの決定ルールは、以下のような形で現場に展開できます。
- オペレーター向けチェックリストとして、「圧力が177を下回っていないか」「高圧(215超)時は温度が145〜155の範囲に入っているか」といった確認項目を作成できます。
- アラートシステムとして、圧力が214.25を超えた際、温度が適正範囲(約145〜155)を外れそうになったら即座に警告を出す仕組みを構築できます。
- 新人教育として、「低圧時は即不良につながるが、高圧時は温度管理さえ徹底すれば良品になる可能性がある」といった具体的な挙動を説明できます。
ただし、代理モデルはあくまで「近似」であり、元のモデルの100%を再現しているわけではありません。忠実度を確認し、「このルールはモデル全体の約○%を説明している」と注記を添えることが重要です。
まとめ
今回は、製造現場が直面するAIのブラックボックス問題を、XAIの手法を使って見える化しました。
- Permutation Importanceにより、品質に最も影響する要因を特定
- PDPにより、各パラメータの最適値を科学的に決定
- ALEにより、パラメータ間の相関を考慮した正確な影響を把握
- Surrogate Modelにより、AIの判断ルールを人間が読める形で可視化
これらのグローバル解釈手法を組み合わせることで、モデル全体の振る舞いを多角的に理解できます。
次回(第6回)では、個別不良品の原因究明にフォーカスし、SHAPやBreak Downを使った詳細な要因分解を行います。
さらにICEによる設備個体差の発見など、より高度な分析手法を実践していきます。
製造現場でのAI活用は、「説明できるAI」によって新たな段階に入りました。人間の経験とAIの分析力を融合させることで、これまでにない品質改善が可能になるのです。
DALEXで実践する説明可能AI超入門— 第6回 —製造業でのXAI実践(その2)- 個別不良品の原因究明と改善アクション

