データサイエンスの第一歩として避けて通れない「回帰分析」。
教科書などに書かれている数式を眺めるだけでは、なかなか実感が湧かないのではないでしょうか。
本記事では、カフェのアイスコーヒー売上という身近な題材を使い、回帰分析の理論を数式で理解しながら、同時にPythonで手を動かして実装することで、「分かる」から「使える」レベルまで引き上げます。
Contents
- 回帰分析の基礎のキソ
- 変数間の関係を数式で表現する
- 確率的な関係のモデル化
- なぜ「回帰」というのか?
- データなどの準備と探索的分析
- 必要なライブラリのインポート
- 利用するデータの生成
- 散布図による関係性の視覚化
- 相関係数の計算
- 最小二乗法の理論と実装
- 最小二乗法の数学的定式化
- 正規方程式の導出
- 最小二乗法のステップバイステップ実装
- 相関係数と回帰係数の関係
- 行列表現による最小二乗法
- 回帰直線の可視化と残差分析
- 予測値と残差の計算
- 回帰直線の可視化
- 残差プロット
- モデルの評価
- 変動の分解
- 決定係数(R²)
- 自由度調整済み決定係数
- 残差標準誤差
- 新しいデータでの予測
- 実装の効率化
- NumPyによる効率的な実装
- scikit-learnによる実装
- statsmodelsによる実装
- まとめ
回帰分析の基礎のキソ
変数間の関係を数式で表現する
私たちの身の回りには、2つの量の間に何らかの関係がある現象がたくさんあります。
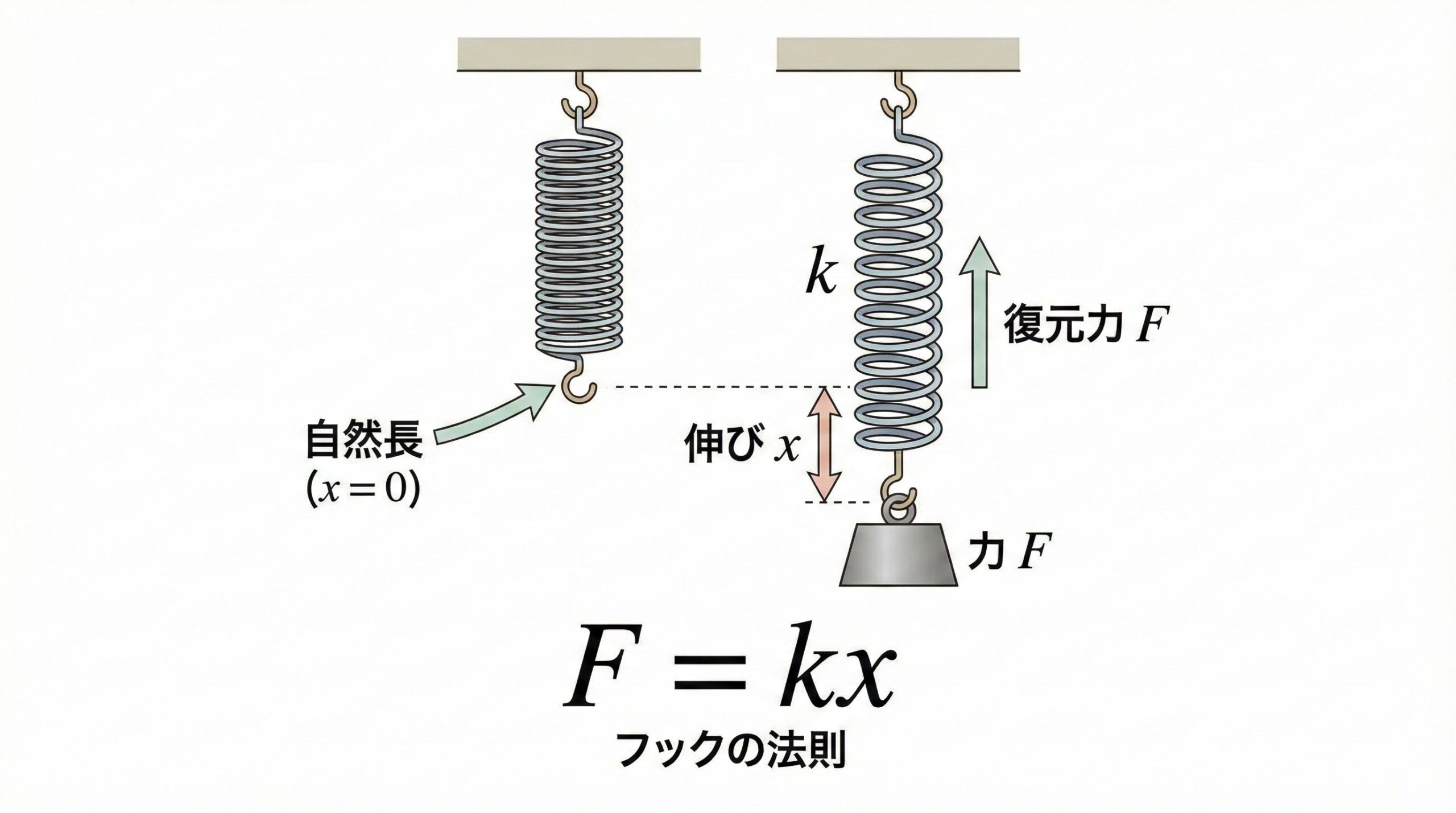
たとえば、物理学では「ばねに加わる力 F が伸び x に比例する」というフックの法則があり、次のような数式で表現できます。
$$F = kx$$
ここで k はばねの硬さを表す定数で、「どれだけ伸ばすと、どれだけ元に戻ろうとする力が生じるか」を定量的に示しています。
同様に化学の分野では、化学反応の速さが温度にどのように依存するかを、次のようなアレニウスの式で表します。
$$k = A \exp(-E_a / RT)$$
この式は、温度 T が高くなるほど反応が起こりやすくなり、活性化エネルギー E_a が大きい反応ほど進みにくいことを説明します。
さらに経済学では、価格と需要量の関係を次のような需要曲線で表し、価格 P が上がると需要量 Q が減少するという人間の行動パターンを数式として表現します。
$$Q = a – bP$$
このように、物理現象、化学反応、経済行動といった異なる対象であっても、変数間の関係を数式で表すことで、現象を理解し、予測し、比較できるようにしている点は共通しています。
これらはすべて、ある変数 x から別の変数 y を予測する問題として定式化できます。回帰分析は、このような変数間の関係を統計的に推定する手法です。
確率的な関係のモデル化
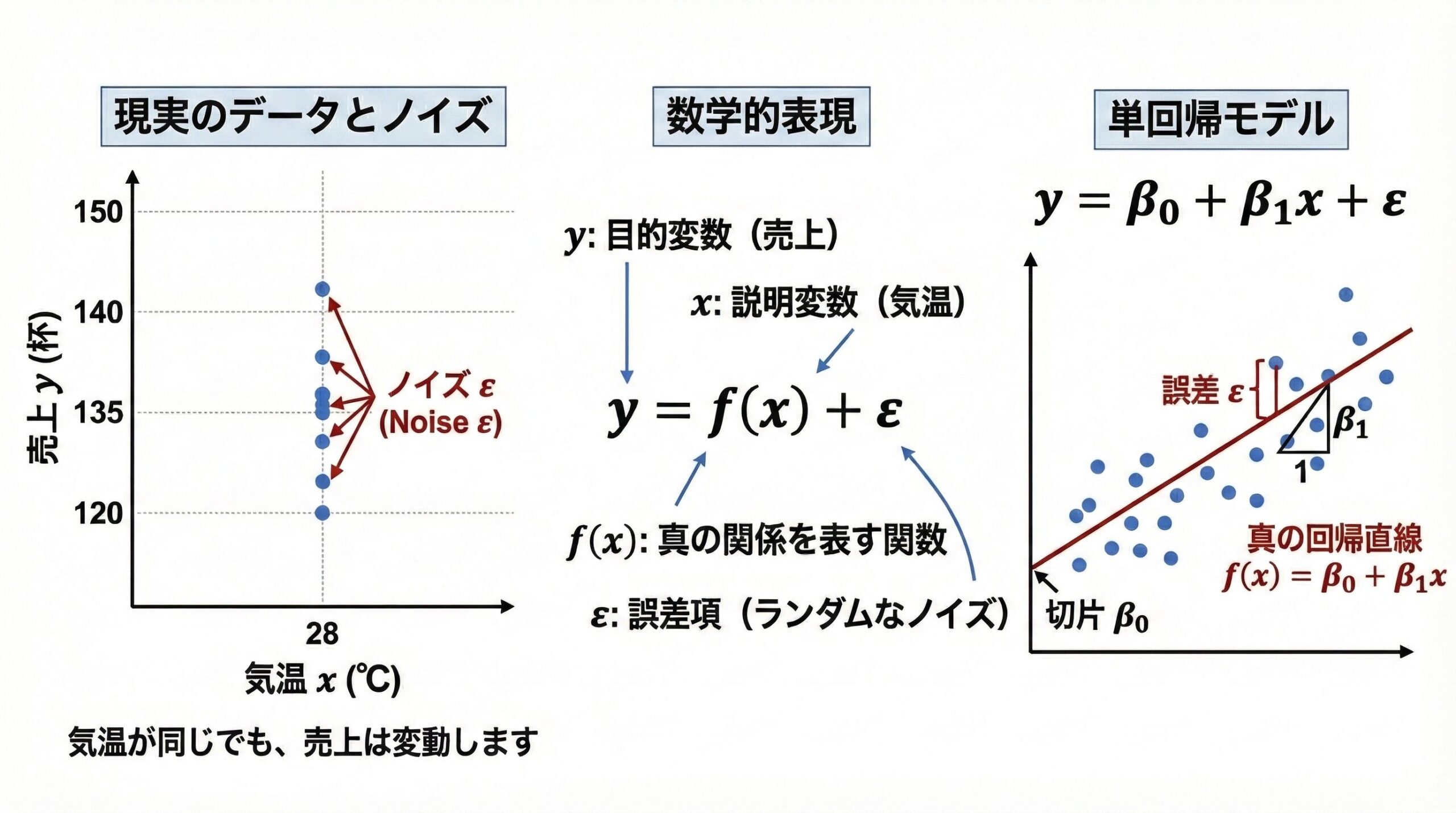
現実のデータには必ずノイズ(誤差)が含まれます。
気温が同じ28℃でも、日によってアイスコーヒーの売上は変動します。
これを数学的に表現すると次のようになります。
$$y = f(x) + \varepsilon$$
ここで、y は目的変数(予測したい量、例:売上)、x は説明変数(予測に使う量、例:気温)、f(x) は x と y の真の関係を表す関数、\varepsilon(イプシロン)は誤差項(ランダムなノイズ)を表します。
最も単純なケースとして、f(x) が線形関数(直線)の場合を考えると、次ようになります。
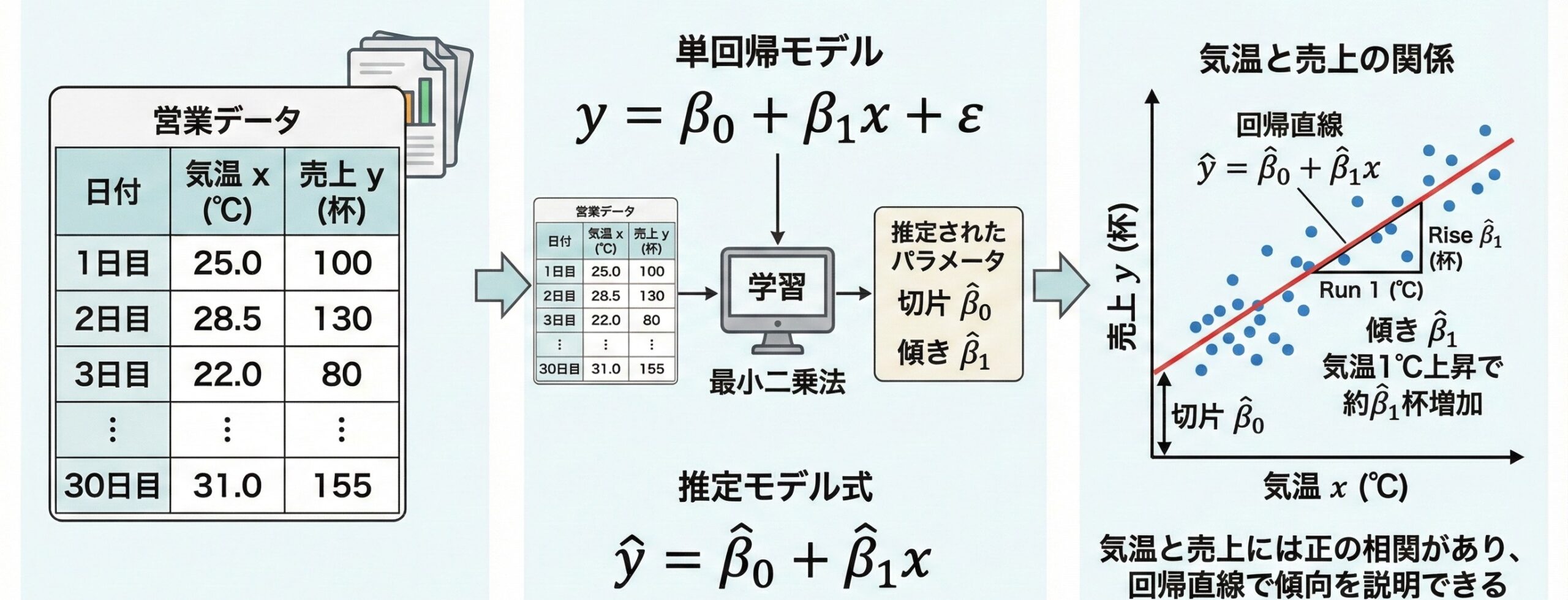
$$y = \beta_0 + \beta_1 x + \varepsilon$$
これが「単回帰モデル」(Simple Linear Regression Model)の基本式です。
\beta_0(ベータ・ゼロ)は切片(intercept)で直線がy軸と交わる点、\beta_1(ベータ・ワン)は傾き(slope)で直線の傾き具合を表します。誤差項 \varepsilon は平均0、分散\sigma^2(シグマの2乗)の正規分布に従うと仮定します。
$$\varepsilon \sim N(0, \sigma^2)$$
なぜ「回帰」というのか?
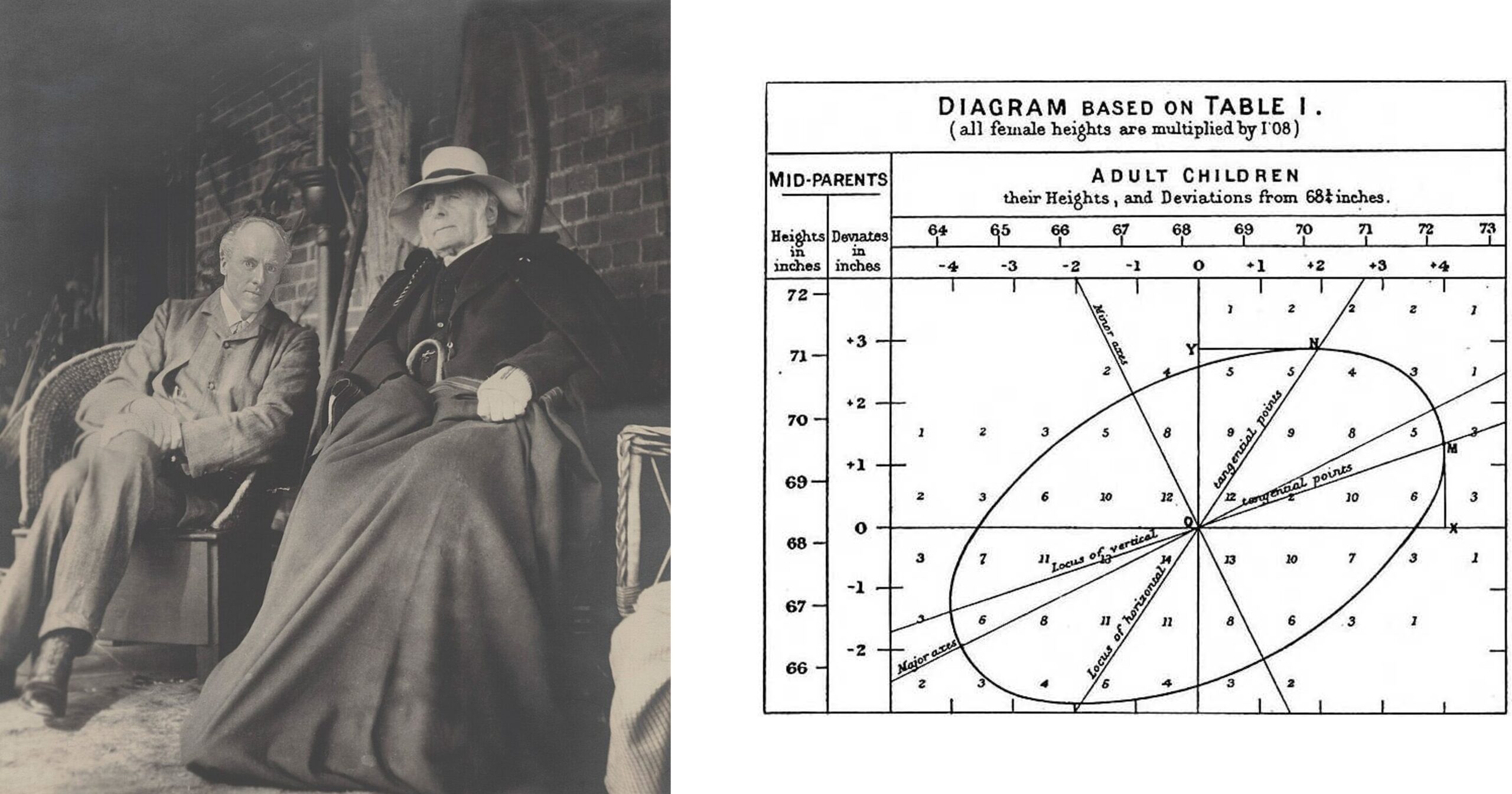
「回帰(Regression)」という言葉は、もともと現代的な予測手法を指していたわけではなく、19世紀の統計学者フランシス・ゴルトンの研究に由来しています。
ゴルトンは親と子の身長データを詳細に分析する中で、非常に背の高い親を持つ子どもは親ほど極端に高身長にはならず、逆に非常に背の低い親を持つ子どもも親ほど低くならない傾向があることに気づきました。
つまり、子どもの身長は親の身長から「平均的な値」へと近づく傾向を示していたのです。ゴルトンはこの現象を「平均への回帰(regression toward the mean)」と呼びました。
当初の回帰は、極端な値が次の世代や次の観測ではより平均的な値に近づくという現象そのものを指していましたが、その後、この考え方は数学的に一般化されました。
現在の統計学やデータ分析において「回帰」とは、ある変数(説明変数)が別の変数(目的変数)にどのような影響を与えているか、その関係をデータから推定するための手法全般を指します。
言い換えれば、もともとは身長データの中で見出された「平均へ戻る傾向」を説明するための概念が、やがてさまざまな分野で変数間の関係を数量的に捉えるための基礎的な統計手法へと発展していったのです。
データなどの準備と探索的分析
必要なライブラリのインポート
まず、Pythonで回帰分析を行うために必要な基本的なライブラリをインポートします。NumPyは数値計算、pandasはデータ操作、matplotlibは可視化のための必須ツールです。
# 数値計算とデータ処理のためのライブラリ import numpy as np import pandas as pd import matplotlib.pyplot as plt import japanize_matplotlib import seaborn as sns from scipy import stats # 乱数シードの固定 np.random.seed(42)
これで分析環境の準備が整いました。乱数シードを固定することで、乱数を使った処理の結果の再現性が保証されます。
利用するデータの生成
30日分のカフェの営業データを想定して、今回利用する分析用のデータを生成していきます。
まずは、真のモデルのパラメータ(回帰分析の数式の切片と係数)を設定します。
# データ生成のパラメータ設定
n = 30 # サンプル数(30日間の営業データ)
# 真のモデルのパラメータ
TRUE_BETA_0 = -150 # 真の切片
TRUE_BETA_1 = 10 # 真の傾き(気温1℃上昇で10杯増加)
SIGMA = 15 # 誤差の標準偏差
print("真のモデル設定:")
print(f" y = {TRUE_BETA_0} + {TRUE_BETA_1}x + ε")
print(f" 誤差の標準偏差 σ = {SIGMA}")
以下、実行結果です。
真のモデル設定: y = -150 + 10x + ε 誤差の標準偏差 σ = 15
これが、回帰分析で得られる真のモデルの状態です。
次に、説明変数である「気温データ」を生成します。気温データは、東京の夏を想定しています。
# 説明変数:気温データの生成
# 夏季(7月)の東京の気温分布を想定
mu_temp = 27.5 # 平均気温
sigma_temp = 3.5 # 気温の標準偏差
# 正規分布に従う乱数を生成
temp = np.random.normal(
mu_temp, # 平均
sigma_temp, # 標準偏差
n, # サンプル数
)
# 気温を現実的な範囲に制限
temp = np.clip(
temp, # 制限対象の配列
20, # 下限値
35 # 上限値
)
print(f"気温データ生成:")
print(f" 平均: {np.mean(temp):.1f}℃")
print(f" 標準偏差: {np.std(temp):.1f}℃")
print(f" 範囲: {np.min(temp):.1f}℃ ~ {np.max(temp):.1f}℃")
以下、実行結果です。
気温データ生成: 平均: 26.8℃ 標準偏差: 3.1℃ 範囲: 20.8℃ ~ 33.0℃
誤差項も生成します。
# 誤差項の生成(平均0、標準偏差SIGMAの正規分布に従う)
epsilon = np.random.normal(
0, # 平均
SIGMA, # 標準偏差
n # サンプル数
)
生成した気温xと誤差項εのデータを、真のモデル(y = -150 + 10x + ε)に代入し目的変数である売上yを求めます。
このとき、-150 + 10xは気温xに対する売上の理論値で、この理論値に誤差項εを加えた-150 + 10x + εが売上の観測値になります。
# 真の関係式による理論値
ice_coffee_sales_true = TRUE_BETA_0 + TRUE_BETA_1 * temp
# 観測値(理論値+ノイズ)
ice_coffee_sales = ice_coffee_sales_true + epsilon
print(f"売上データ生成:")
print(f" 理論値の平均: {np.mean(ice_coffee_sales_true):.1f}杯")
print(f" 観測値の平均: {np.mean(ice_coffee_sales):.1f}杯")
print(f" ノイズの影響: {np.mean(epsilon):.1f}杯(平均)")
以下、実行結果です。
売上データ生成: 理論値の平均: 126.0杯 観測値の平均: 125.7杯 ノイズの影響: -0.3杯(平均)
これで、目的変数y(売上)と説明変数X(説明変数)のデータが揃いました。これを扱いやすいデータフレームにします。
# データフレームの作成
data = pd.DataFrame({
'日付': pd.date_range(
'2024-07-01', # 開始日
periods=n # 期間
),
'気温': temp,
'理論値': ice_coffee_sales_true,
'売上': ice_coffee_sales
})
# 最初の5行を表示
print("生成したデータ(最初の5日間):")
print(data.head())
以下、実行結果です。
生成したデータ(最初の5日間):
日付 気温 理論値 売上
0 2024-07-01 25.822890 108.228902 109.685065
1 2024-07-02 26.850194 118.501936 133.031611
2 2024-07-03 23.627828 86.278276 75.747480
3 2024-07-04 23.313277 83.132768 78.217836
4 2024-07-05 30.343840 153.438404 147.556781
このデータセットの基本統計量(平均や標準偏差など)を見てみます。
# データの基本統計量
print("データの基本統計量:")
print(data[['気温', '売上']].describe())
以下、実行結果です。
データの基本統計量:
気温 売上
count 30.000000 30.000000
mean 27.600734 125.703562
std 3.329652 34.015087
min 20.000000 47.580714
25% 25.700503 110.254227
50% 27.589637 129.498166
75% 30.081989 153.311436
max 32.976253 177.629745
この結果は、30日分の「気温」と「売上」のデータについて、全体的な分布(基本統計量)の特徴をまとめたものです。
気温の平均(mean)は約27.6度で、最も低い日(min)は20度、最も高い日(max)は約33度となっており、標準偏差(std)は約3.3度なので、日ごとの気温は平均の前後に比較的まとまって分布していることが分かります。
一方、売上の平均(mean)は約126で、最小値(min)は約48、最大値(max)は約178と幅が広く、標準偏差(std)も約34と気温に比べてばらつきが大きいことが読み取れます。
このことから、気温は一定の範囲に収まっているのに対し、売上は日によって大きく変動しており、気温以外の要因も売上に影響している可能性があることが読み取れます。
このように、基本統計量を眺めることで、全体的な分布の特徴を掴むことができます。そのため、データセットを手に入れたら、基本統計量を出して各変数の特徴を掴むといいでしょう。
散布図による関係性の視覚化
データの関係性を視覚的に確認するため、散布図を作成します。説明変数が横軸に、目的変数が縦軸になります。
# 散布図の作成
fig, ax = plt.subplots(figsize=(8, 6))
# 散布図のプロット
ax.scatter(
data['気温'], # x軸
data['売上'], # y軸
s=80, # マーカーのサイズ
alpha=0.7, # マーカーの透明度
color='dodgerblue', # マーカーの色
edgecolor='navy', # マーカーの枠線の色
linewidth=1 # マーカーの枠線の太さ
)
# 軸ラベルとタイトルの設定
ax.set_xlabel('気温 $x$ [℃]')
ax.set_ylabel('アイスコーヒー売上 $y$ [杯]')
ax.set_title('観測データの散布図')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
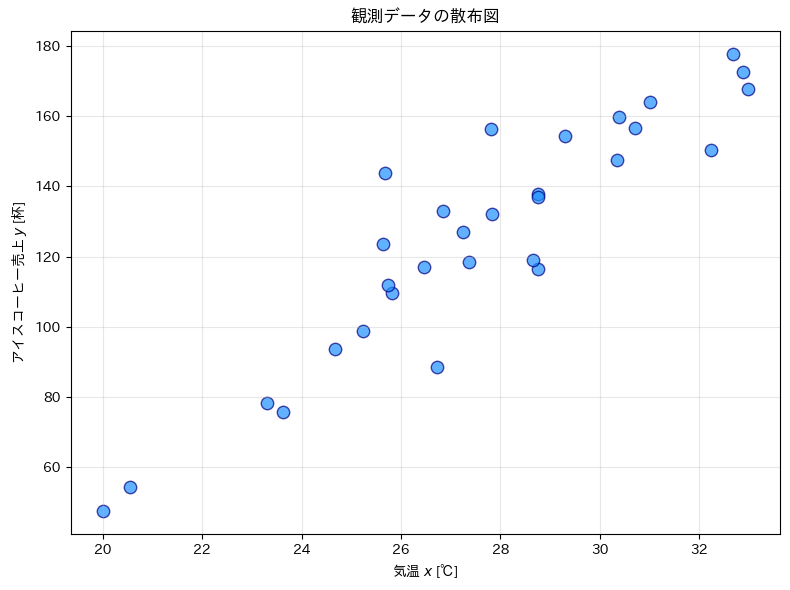
散布図から、気温と売上に正の相関(右上がりの傾向)があることが視覚的に確認できます。この線形関係を数式で表現することが、回帰分析の目的の1つです。
相関係数の計算
相関係数は、2つの変数の「線形関係の強さ」を表す指標です。数学的には、共分散をそれぞれの標準偏差で正規化した量として定義されます。
まず、共分散は次の式で表されます。
$$
\mathrm{Cov}(X, Y)
= \frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})(y_i – \bar{y})
$$
これは、X と Y が同時に平均からどの方向(プラス or マイナス)に、どの程度ずれているかを測る量です。
次に、標準偏差です。これは分散の平方根として定義されます。変数 (X) の標準偏差は以下です。
$$
\sigma_X = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})^2}
$$
同様に、変数 Y の標準偏差は以下です。
$$
\sigma_Y = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i – \bar{y})^2}
$$
これらを用いると、相関係数r は次のように定義されます。
$$
\displaystyle
r
= \frac{\mathrm{Cov}(X, Y)}{\sigma_X \sigma_Y}
= \frac{\displaystyle\frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})(y_i – \bar{y})}
{\displaystyle\sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i – \bar{x})^2}
\cdot
\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i – \bar{y})^2}}
$$
このように、相関係数は「一緒に増減する度合い(共分散)」を、それぞれのばらつきの大きさ(標準偏差)で割ることで、-1 から +1 の範囲に正規化された指標となっています。
では、相関係数をNumPyの関数corrcoefを使い求めてみます。
corrcoef は、2つ以上の変数について相関行列を返す関数です。相関行列とは、各変数同士の相関係数を行列の形でまとめたもので、対角成分には必ず 1(自分自身との相関)、非対角成分には変数同士の相関係数が並びます。
# 相関行列の計算
r = np.corrcoef(
data['気温'], # x軸
data['売上'] # y軸
)[0, 1] # xとyの相関係数は相関行列の[0,1]要素
# 相関係数の表示
print(f"相関係数 r = {r:.2f}")
以下、実行結果です。
相関係数 r = 0.92
相関係数は -1 から 1 までの値をとり、絶対値が 1 に近いほど強い線形関係を示します。正の値は正の相関(xが増えるとyも増える)、負の値は負の相関(xが増えるとyは減る)を意味します。
最小二乗法の理論と実装
最小二乗法の数学的定式化
観測データ (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) が与えられたとき、これらのデータに最も「よく当てはまる」直線を見つけたいと考えます。この直線を回帰直線と呼びます。
この回帰直線は、次にように表現します。ここで、ハット記号「^」は推定値を意味し、\hat{\beta}_0 は切片の推定値、\hat{\beta}_1 は傾きの推定値を表します。
$$
\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x
$$
各データ点における実測値と予測値の差を「残差」(residual)と呼びます。
$$
e_i = y_i – \hat{y}_i = y_i – (\hat{\beta}_0 + \hat{\beta}_1 x_i)
$$
最小二乗法では、すべての残差の二乗を足し合わせた値である「残差平方和」(Sum of Squared Errors, SSE)S(\beta_0, \beta_1)を最小にする直線を「最良の直線」とします。
$$
\displaystyle S(\beta_0, \beta_1) = \sum_{i=1}^n e_i^2 = \sum_{i=1}^n (y_i – \beta_0 – \beta_1 x_i)^2
$$
なぜ二乗するかというと、正負の残差が打ち消し合わないようにするため、また、大きな外れ値により大きなペナルティを与えるためです。
この残差平方和をデータ数 n で割ったものを、「平均二乗誤差」(Mean Squared Error, MSE)と呼びます。
$$
\displaystyle
\mathrm{MSE}
= \frac{1}{n} S(\beta_0, \beta_1)
$$
したがって、SSE を最小化することと MSE を最小化することは本質的に同じであり、単にスケール(平均か合計か)の違いにすぎません。
実務や機械学習では、データ数に依存しない指標として MSE がよく用いられますが、その背後にある考え方は、最小二乗法とまったく同一です。
正規方程式の導出
S(\beta_0, \beta_1) を最小化するパラメータ(\hat{\beta}_0 と\hat{\beta}_1 )を見つけるために、偏微分を使います。極値(最小値など)では偏微分が0になる性質を利用します。まず、β_0 で偏微分して 0 にします。
$$
\frac{\partial S}{\partial \beta_0}
=\frac{\partial}{\partial \beta_0}\sum_{i=1}^{n}(y_i-\beta_0-\beta_1 x_i)^2
=\sum_{i=1}^{n} 2(y_i-\beta_0-\beta_1 x_i)\cdot(-1)
$$
したがって
$$
\frac{\partial S}{\partial \beta_0}
=-2\sum_{i=1}^{n}(y_i-\beta_0-\beta_1 x_i)=0
$$
この式から以下が導き出せます。
$$
n\beta_0 + \beta_1\sum_{i=1}^{n}x_i=\sum_{i=1}^{n}y_i
$$
次に、β_1 で偏微分して 0 にしていきます。
同様に
$$
\frac{\partial S}{\partial \beta_1}
=\frac{\partial}{\partial \beta_1}\sum_{i=1}^{n}(y_i-\beta_0-\beta_1 x_i)^2
=\sum_{i=1}^{n} 2(y_i-\beta_0-\beta_1 x_i)\cdot(-x_i)
$$
よって
$$
\frac{\partial S}{\partial \beta_1}
=-2\sum_{i=1}^{n}x_i(y_i-\beta_0-\beta_1 x_i)=0
$$
この式から以下が導き出せます。
$$
\beta_0\sum_{i=1}^{n}x_i + \beta_1\sum_{i=1}^{n}x_i^2 = \sum_{i=1}^{n}x_i y_i
$$
このβ_1 を偏微分して 0 にし得られた式と、先ほどβ_0 を偏微分して 0 にし得られた、2つの式からなら連立方程式を「正規方程式」(normal equations)と呼びます。
$$
\begin{cases}
\displaystyle n\beta_0 + \beta_1\sum_{i=1}^{n}x_i=\sum_{i=1}^{n}y_i\\
\displaystyle \beta_0\sum_{i=1}^{n}x_i + \beta_1\sum_{i=1}^{n}x_i^2 = \sum_{i=1}^{n}x_i y_i
\end{cases}
$$
この正規方程式を解くと、以下が得られます。これが求めるS(\beta_0, \beta_1) を最小化するパラメータ(\hat{\beta}_0 と\hat{\beta}_1 )です。
$$
\begin{cases}
\displaystyle \hat{\beta}_1=\frac{S_{xy}}{S_{xx}}
=\frac{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2}\\
\displaystyle \hat{\beta}_0=\bar{y}-\hat{\beta}_1\bar{x}
\end{cases}
$$
ここで、\bar{x} と \bar{y} はそれぞれ x と y の平均値、S_{xy} は x と y の偏差積和S_{xy}=\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})、S_{xx} は x の偏差平方和S_{xx}=\sum_{i=1}^{n}(x_i-\bar{x})^2を表します。
最小二乗法のステップバイステップ実装
正規方程式で導いた数式を、実際にPythonで実装して確認します。
# データの準備
x = data['気温'].values
y = data['売上'].values
n = len(x)
# 平均の計算
x_bar = np.mean(x)
y_bar = np.mean(y)
# 平均からの偏差の計算
x_dev = x - x_bar
y_dev = y - y_bar
# 偏差積和・偏差平方和の計算
S_xy = np.sum(x_dev * y_dev) # 偏差積和
S_xx = np.sum(x_dev**2) # xの偏差平方和
# 回帰係数の計算
beta_1_hat = S_xy / S_xx # 傾きの推定値
beta_0_hat = y_bar - beta_1_hat * x_bar # 切片の推定値
print(f"推定回帰式:\t ŷ = {beta_0_hat:.2f} + {beta_1_hat:.2f}x")
print(f"真の回帰式:\t y = {TRUE_BETA_0} + {TRUE_BETA_1}x")
以下、実行結果です。
推定回帰式: ŷ = -133.19 + 9.38x 真の回帰式: y = -150 + 10x
推定された回帰係数(9.380)が真の値(10)にかなり近いことが分かります。これは最小二乗法が適切に機能していることを示しています。
相関係数と回帰係数の関係
単回帰分析において、相関係数 r と回帰係数 \hat{\beta}_1 には以下の重要な関係があります。
$$
\hat{\beta}_1 = r \times \frac{s_y}{s_x}
$$
ここで、s_x と s_y はそれぞれ x と y の標準偏差です。この式から、回帰係数が相関係数に標準偏差の比(スケール調整)を掛けたものであることを示しています。
相関係数と回帰係数の関係を確認するために、相関係数と標準偏差から回帰係数を求めてみます。
# 偏差平方和の計算
S_xy = np.sum(x_dev * y_dev) # xとyの偏差積和
S_xx = np.sum(x_dev**2) # xの偏差平方和
S_yy = np.sum(y_dev**2) # yの偏差平方和
# 相関係数の計算
r = S_xy / np.sqrt(S_xx * S_yy)
# 標準偏差の計算
s_x = np.sqrt(S_xx / n)
s_y = np.sqrt(S_yy / n)
# 回帰係数(rから計算)
beta_1_from_r = r * (s_y / s_x)
print(f"相関係数 r = {r:.2f}")
print(f"回帰係数(先ほど計算):\t {beta_1_hat:.2f}")
print(f"回帰係数(rから計算):\t {beta_1_from_r:.2f}")
print(f"差: {abs(beta_1_hat - beta_1_from_r):.10f}")
以下、実行結果です。
相関係数 r = 0.92 回帰係数(先ほど計算): 9.38 回帰係数(rから計算): 9.38 差: 0.0000000000
この結果より、相関の強さrと変数のスケール(標準偏差の比)から回帰係数が決まることが理解できます。
行列表現による最小二乗法
複数の説明変数がある場合への拡張を見据えて、行列を使った表現も見ていきます。
回帰モデルを行列で表現すると次のようになります。
$$
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}
$$
ここで、\mathbf{y} は n \times 1 の目的変数ベクトル、\mathbf{X} は n \times 2 のデザイン行列(第1列はすべて1、第2列は説明変数)、\boldsymbol{\beta} は 2 \times 1 の回帰係数ベクトル、\boldsymbol{\varepsilon} は n \times 1 の誤差ベクトルです。
具体的には、各行が 1 つの観測データに対応し、次のような形になります。
$$
\begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{pmatrix}
=
\begin{pmatrix}
1 & x_1 \\
1 & x_2 \\
\vdots & \vdots \\
1 & x_n
\end{pmatrix}
\begin{pmatrix}
\beta_0 \\
\beta_1
\end{pmatrix}
+
\begin{pmatrix}
\varepsilon_1 \\
\varepsilon_2 \\
\vdots \\
\varepsilon_n
\end{pmatrix}
$$
この式は、各観測 i について
$$
y_i = \beta_0 + \beta_1 x_i + \varepsilon_i
$$
という単回帰モデルを、すべてまとめて表現したものになっています。
先ほど正規方程式から求めたような最小二乗推定量は、行列表現を用いると次のように簡潔に書けます。
$$
\hat{\boldsymbol{\beta}} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}
$$
ここで、\mathbf{X}^T は行列 \mathbf{X} の転置行列であり、行と列を入れ替えたものを意味します。また、(\mathbf{X}^T\mathbf{X})^{-1} は行列 \mathbf{X}^T\mathbf{X} の逆行列を表します。
この式は、正規方程式を行列として解いた結果です。何よりも、説明変数が増えても同じ形で自然に拡張できる点が、行列表現の大きな利点です。
では、行列演算による最小二乗法を実装します。
まずは、デザイン行列 \mathbf{X} を作ります。
# デザイン行列
X = np.column_stack([
np.ones(n), # 切片項(全ての値が1のベクトル)
x # 説明変数(気温)
])
print(f"デザイン行列 X の形状: {X.shape}")
print("\nXの最初の5行:")
print(X[:5])
以下、実行結果です。
デザイン行列 X の形状: (30, 2) Xの最初の5行: [[ 1. 29.23849954] [ 1. 27.01607495] [ 1. 29.76690988] [ 1. 32.8306045 ] [ 1. 26.68046319]]
行列計算で解を求めます。
# 行列計算で解を求める
XtX = X.T @ X # X^T X (2×2行列)
Xty = X.T @ y # X^T y (2×1ベクトル)
XtX_inv = np.linalg.inv(XtX) # (X^T X)^(-1) (2×2行列)
beta_hat_matrix = XtX_inv @ Xty
print(f"切片:\t{beta_hat_matrix[0]:.2f}")
print(f"傾き:\t{beta_hat_matrix[1]:.2f}")
以下、実行結果です。
切片: -133.19 傾き: 9.38
先ほど求めた結果と行列演算の結果は完全に一致します。行列表現の利点は、説明変数が複数ある重回帰分析への拡張が容易なことです。
回帰直線の可視化と残差分析
予測値と残差の計算
推定された回帰式を使って予測値を計算し、実測値との差(残差)を求めます。
# 予測値の計算
y_hat = beta_0_hat + beta_1_hat * x
# 残差の計算
residuals = y - y_hat
# 基本統計量
print(f"残差の平均:\t {np.mean(residuals):.2f}")
print(f"残差の標準偏差:\t {np.std(residuals):.2f}")
print(f"残差の最小値:\t {np.min(residuals):.2f}")
print(f"残差の最大値:\t {np.max(residuals):.2f}")
以下、実行結果です。
残差の平均: -0.00 残差の標準偏差: 13.25 残差の最小値: -29.02 残差の最大値: 36.07
残差の平均が0に非常に近いことは、最小二乗法の重要な性質です。これは推定が偏りなく行われていることを示しています。
回帰直線の可視化
データ点と回帰直線を重ねて表示し、モデルの適合ぐあいを視覚的に確認します。
# 散布図の作成
fig, ax = plt.subplots(figsize=(8, 6))
# 散布図のプロット
ax.scatter(
data['気温'], # x軸
data['売上'], # y軸
s=80, # マーカーのサイズ
alpha=0.7, # マーカーの透明度
color='dodgerblue', # マーカーの色
edgecolor='navy', # マーカーの枠線の色
linewidth=1, # マーカーの枠線の太さ
label='観測値'
)
# 推定された回帰式のプロット
# xの範囲を100点の等間隔な点で生成
x_range = np.linspace(
data['気温'].min(), # xの最小値
data['気温'].max(), # xの最大値
100 # 100点の等間隔な点を生成
)
# 推定された回帰式のyの値を計算
y_pred = beta_0_hat + beta_1_hat * x_range
# 回帰式のプロット
ax.plot(
x_range, # x軸
y_pred, # y軸
color='red', # 線の色
linewidth=2, # 線の太さ
label='推定回帰式' # 凡例
)
# 重心点を強調
ax.scatter(
x_bar, # x軸
y_bar, # y軸
s=200, # マーカーのサイズ
color='green', # マーカーの色
marker='*', # マーカーの形
label=f'重心 ({x_bar:.1f}, {y_bar:.1f})' # 凡例
)
# 軸ラベルとタイトルの設定
ax.set_xlabel('気温 $x$ [℃]')
ax.set_ylabel('アイスコーヒー売上 $y$ [杯]')
ax.set_title('観測データの散布図と推定回帰式')
ax.legend() # 凡例の表示
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
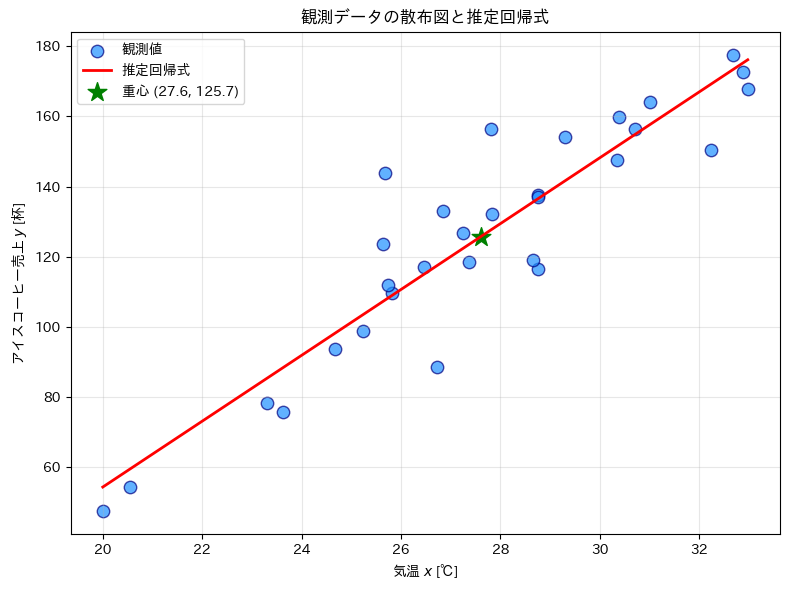
回帰直線が必ず重心(\bar{x}, \bar{y})を通ることが確認できます。これは最小二乗法の数学的性質の一つです。
残差プロット
残差プロットは、線形の回帰モデルの仮定が概ね満たされているかを確認するための重要な診断ツールです。特に、線形性や等分散性といった仮定を、データから視覚的に点検する目的で用いられます。
線形回帰モデルでは、主に次のような仮定を置いています。
- 説明変数と目的変数の関係が、直線で近似できること(線形性)
- 残差同士が互いに独立であること(独立性)
- 残差の平均が 0 であること(零平均性)
- 残差のばらつきが、説明変数(あるいはそれらの線形結合である予測値)の大きさによらず、概ね一定であること(等分散性)
- 残差が正規分布に従うこと(正規性)※回帰係数の推定自体には必須ではない
これらの仮定が大きく破れている場合、推定された回帰係数の解釈や、検定・信頼区間などの統計的推論が不適切になる可能性があります。
以下では、残差プロットを作成し、モデルの妥当性を視覚的に確認します。
# 残差プロット(上下配置)
fig, axes = plt.subplots(2, 1, figsize=(10, 10))
# 上: 予測値 vs 残差(線形性・等分散性)
axes[0].scatter(y_hat, residuals, s=60, alpha=0.6, color='green')
axes[0].axhline(y=0, color='red', linestyle='--', linewidth=1)
axes[0].set_xlabel('予測値 $\hat{y}$ [杯]')
axes[0].set_ylabel('残差 $e_i$ [杯]')
axes[0].set_title('残差プロット(線形性・等分散性の確認)')
axes[0].grid(True, alpha=0.3)
# 下: 残差のヒストグラム(正規性の参考)
axes[1].hist(
residuals, bins=10, density=True,
alpha=0.7, color='purple', edgecolor='black'
)
residual_mean = np.mean(residuals)
residual_std = np.std(residuals, ddof=1)
x_norm = np.linspace(residuals.min(), residuals.max(), 200)
y_norm = stats.norm.pdf(x_norm, residual_mean, residual_std)
axes[1].plot(
x_norm, y_norm, 'r-', linewidth=2,
label=f'N({residual_mean:.2f}, {residual_std:.2f}²)'
)
axes[1].set_xlabel('残差 [杯]')
axes[1].set_ylabel('確率密度')
axes[1].set_title('残差の分布(正規性の確認・参考)')
axes[1].legend()
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
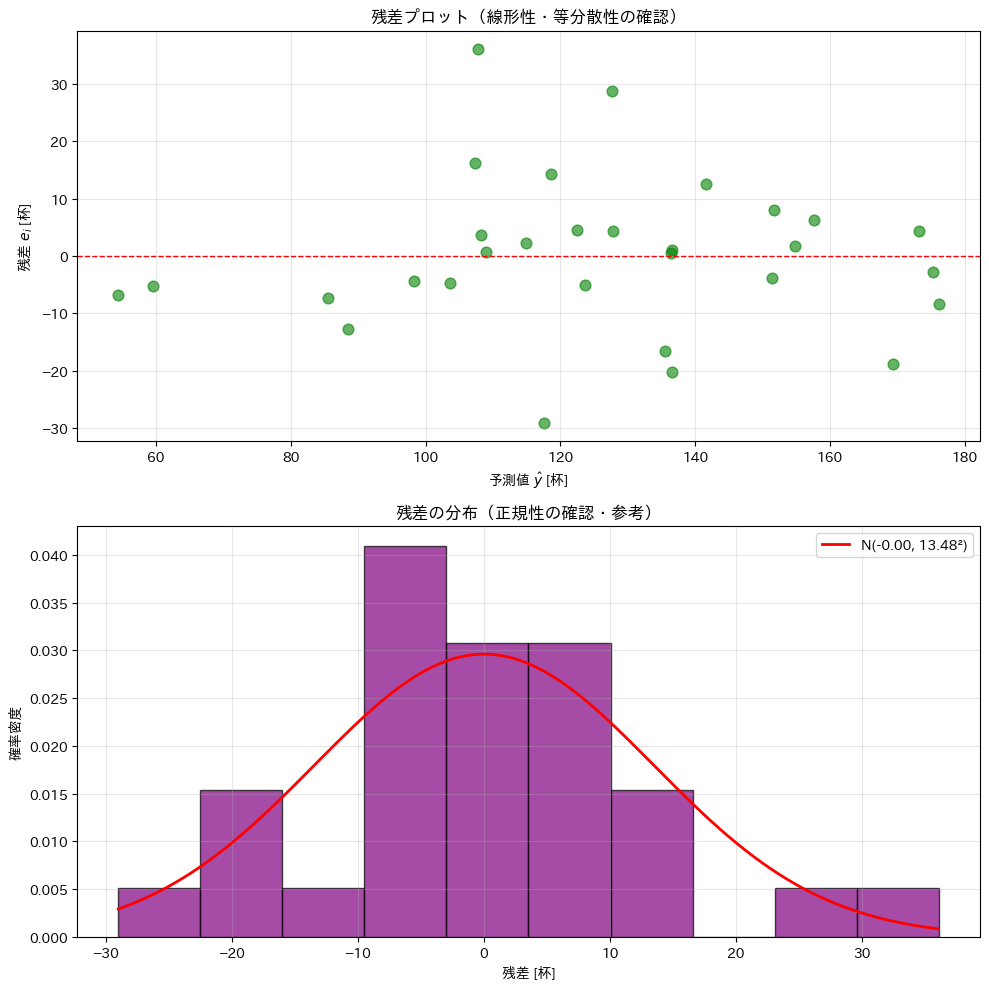
上段の「予測値 vs 残差」の図を見ると、残差はおおむね 0 の周りに散らばっており、予測値が大きくなるにつれて一方向に増減するといった明確な傾向は見られません。
このことから、説明変数と目的変数の関係を直線で近似するという線形性の仮定は、大きくは破れていないと考えられます。
また、予測値の水準によって残差のばらつきが一方的に広がったり狭まったりする、いわゆる扇形(ファン型)のパターンも明確には確認されません。
したがって、残差の分散が予測値(説明変数の線形結合)によらず概ね一定であるという等分散性の仮定も、概ね妥当と判断できます。
ただし、いくつか比較的大きな正負の残差が見られるため、外れ値の影響については注意が必要です。
下段の残差ヒストグラムを見ると、分布はおおよそ左右対称で、重ねて描いた正規分布曲線とも大きく乖離していません。
このことから、残差の分布は概ね正規分布に近い形をしているといえます。ただし、裾の部分ではやや厚みがあり、完全な正規分布とは言い切れない点も見て取れます。
総合すると、この回帰モデルは、線形性・等分散性といった基本的な仮定については大きな問題は見られず、回帰係数の解釈や予測を行う上では概ね妥当なモデルであると評価できます。
モデルの評価
変動の分解
回帰分析では、データの変動(ばらつき)を以下の3つに分解します。
全変動(Total Sum of Squares, SST)
$$
\displaystyle \sum_{i=1}^n (y_i – \bar{y})^2
$$
回帰変動(Regression Sum of Squares, SSR)
$$
\displaystyle \sum_{i=1}^n (\hat{y}_i – \bar{y})^2
$$
残差変動(Error Sum of Squares, SSE)
$$
\displaystyle \sum_{i=1}^n (y_i – \hat{y}_i)^2
$$
これらには以下の重要な関係があります。
$$
SST=SSR+SSE
$$
この式は、「全体のばらつき(SST) = モデルで説明できる部分(SSR)+ 説明できない部分(SSE)」を意味しています。
変動の分解を計算し、関係式を確認します。
# 変動の分解
SST = np.sum((y - y_bar)**2) # 全変動
SSR = np.sum((y_hat - y_bar)**2) # 回帰変動
SSE = np.sum((y - y_hat)**2) # 残差変動(残差平方和)
print(f"全変動\t SST = {SST:.2f}")
print(f"回帰変動\t SSR = {SSR:.2f} ({SSR/SST*100:.1f}%)")
print(f"残差変動\t SSE = {SSE:.2f} ({SSE/SST*100:.1f}%)")
以下、実行結果です。
全変動 SST = 33553.76 回帰変動 SSR = 28287.97 (84.3%) 残差変動 SSE = 5265.78 (15.7%)
この回帰モデルが全変動の大部分(84.3%)を説明できていることが分かります。残りの部分(15.7%)は誤差(ノイズ)によるものです。
決定係数(R²)
決定係数R^2は、回帰モデルがデータの変動をどの程度説明できているかを表す指標です。
$$
R^2 = \frac{SSR}{SST} = 1 – \frac{SSE}{SST}
$$
R^2 は0から1の値をとり、1に近いほどモデルの当てはまりが良いことを示します。単回帰分析の場合、決定係数は相関係数の2乗に等しくなります。
$$
R^2 = r^2
$$
決定係数を計算し、相関係数との関係を確認します。
# 決定係数の計算
R2 = SSR / SST # または 1 - SSE/SST
r_squared = r**2
print(f"決定係数 \t R² = {R2:.4f}")
print(f"相関係数の2乗\t r² = {r_squared:.4f}")
以下、実行結果です。
決定係数 R² = 0.8431 相関係数の2乗 r² = 0.8431
単回帰分析では R^2 = r^2 という関係が成り立つことが確認できました。決定係数の値から、モデルがデータをよく説明できていることが分かります。
自由度調整済み決定係数
自由度調整済み決定係数R^2_{adj}は、説明変数を増やすと必ず大きくなってしまうという決定係数 R^2 の性質を考慮し、説明変数の数に応じた補正を加えた指標です。
不要な説明変数を追加しても過大にモデルの当てはまりを評価してしまわないよう、データ数と説明変数の数(自由度)を踏まえて調整されています。
そのため、モデルの複雑さと当てはまりの良さをバランスよく評価する際に用いられ、異なる説明変数の数を持つ回帰モデル同士を比較する場合に特に有用です。
自由度調整済み決定係数R^2_{adj}を数式で表現すると、次のようになります。
$$
R^2_{adj} = 1 – \frac{\displaystyle \frac{SSE}{n-p-1}}{\displaystyle \frac{SST}{n-1}}
$$
ここで、n はサンプル数、p は説明変数の数です。
自由度調整済み決定係数を計算します。
# 自由度調整済み決定係数
p = 1 # 説明変数の数
R2_adj = 1 - (SSE/(n-p-1)) / (SST/(n-1))
print(f"決定係数 \t R² = {R2:.4f}")
print(f"自由度調整済み\t R²_adj = {R2_adj:.4f}")
print(f"差 \t R²-R²_adj = {R2 - R2_adj:.4f}")
以下、実行結果です。
決定係数 R² = 0.8431 自由度調整済み R²_adj = 0.8375 差 R²-R²_adj = 0.0056
サンプル数が少ない場合や説明変数が多い場合は、自由度調整済みR^2_{adj}がより適切な指標となります。通常のR²より少し小さい値になることが確認できます。
残差標準誤差
残差標準誤差sは、回帰モデルによる予測が実際のデータからどの程度ずれているかを平均的に表す指標です。
$$
s = \sqrt{\frac{SSE}{n-p-1}}
$$
ここで、SSE は残差平方和、n は観測数、p は説明変数の数を表します。分母の n - p - 1 は自由度であり、回帰係数を推定した分だけ失われた自由度を考慮しています。
残差標準誤差sは、誤差項の分散(\sigma^2)の推定値の平方根に相当し、残差の標準偏差の推定値と解釈できます。
したがって、残差標準誤差が小さいほど、回帰直線の周りにデータが密集しており、モデルの予測精度が高いことを意味します。
残差標準誤差を計算し、真の値と比較します。
# 残差標準誤差
s = np.sqrt(SSE / (n - 2))
print(f"残差標準誤差 s = {s:.2f}杯")
print(f"真の標準偏差 σ = {SIGMA}杯")
以下、実行結果です。
残差標準誤差 s = 13.71杯 真の標準偏差 σ = 15杯
残差標準誤差 s は、回帰モデルによる予測値の周りに、実際の観測値がどの程度ばらついているかを表す指標であり、正規分布を仮定すると、残差の多くは平均しておよそ ±s 杯程度の範囲に収まります。
今回は、推定された s は真の標準偏差 \sigma に近い値となっており、誤差分散が適切に推定できていることが確認できます。
新しいデータでの予測
推定された回帰式を使って、様々な気温での売上を予測します。
# 予測に使う気温のリスト
test_temps = np.array([23, 25, 27, 30, 32, 34])
# 予測値の計算
predictions = beta_0_hat + beta_1_hat * test_temps
# 結果の表示
for temp, pred in zip(test_temps, predictions):
print(f"気温 {temp}℃ → 予測売上 {pred:.1f}杯")
以下、実行結果です。
気温 23℃ → 予測売上 82.5杯 気温 25℃ → 予測売上 101.3杯 気温 27℃ → 予測売上 120.1杯 気温 30℃ → 予測売上 148.2杯 気温 32℃ → 予測売上 167.0杯 気温 34℃ → 予測売上 185.7杯
気温が1℃上がるごとに、売上が約10杯ずつ増加していることが確認できます。ただし、データの範囲外(20-35℃の外)での予測(外挿)は注意が必要です。
実装の効率化
NumPyによる効率的な実装
NumPyのpolyfit関数を使えば、最小二乗法を1行で実行できます。
# NumPyによる回帰分析
coefficients = np.polyfit(
x, # 説明変数
y, # 目的変数
deg=1, # deg=1は1次式(直線)
)
print(f"切片: {coefficients[1]:.2f}")
print(f"傾き: {coefficients[0]:.2f}")
以下、実行結果です。
切片: -133.19 傾き: 9.38
NumPyの関数でも全く同じ結果が得られることが確認できました。実務ではこのような効率的な実装を使います。
scikit-learnによる実装
scikit-learnは機械学習の標準的なライブラリで、より高度な分析にも対応できます。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
# データの準備(scikit-learnは2次元配列にする必要がある)
X_sklearn = x.reshape(-1, 1)
# モデルの作成と学習
model = LinearRegression()
model.fit(X_sklearn, y)
# 予測と評価
y_pred = model.predict(X_sklearn)
r2_sklearn = r2_score(y, y_pred)
print(f"切片: {model.intercept_:.2f}")
print(f"傾き: {model.coef_[0]:.2f}")
print(f"決定係数 R²: {r2_sklearn:.4f}")
以下、実行結果です。
切片: -133.19 傾き: 9.38 決定係数 R²: 0.8431
scikit-learnでも同じ結果が得られ、さらに様々な評価指標も簡単に計算できます。実務での回帰分析では、このようなライブラリを活用することが一般的です。
statsmodelsによる実装
statsmodels は、回帰係数の推定だけでなく、決定係数・標準誤差・t値・p値など、統計的推論に必要な情報をまとめて出力できるライブラリです。
import statsmodels.api as sm
# データの準備(切片項を明示的に追加)
X_sm = sm.add_constant(x) # 定数項(切片)を追加
# 目的変数の準備
y_sm = y
# モデルの作成と学習
model = sm.OLS(y_sm, X_sm)
results = model.fit()
# 結果の表示
print(f"切片: {results.params[0]:.2f}")
print(f"傾き: {results.params[1]:.2f}")
print(f"決定係数 R²: {results.rsquared:.4f}")
以下、実行結果です。
切片: -133.19 傾き: 9.38 決定係数 R²: 0.8431
scikit-learn と同様に、回帰係数や決定係数は同じ値が得られていることが分かります。
statsmodels では、次のような統計的情報も簡単に確認できます。
print(results.summary())
以下、実行結果です。
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.843
Model: OLS Adj. R-squared: 0.837
Method: Least Squares F-statistic: 150.4
Date: Sun, 14 Dec 2025 Prob (F-statistic): 8.89e-13
Time: 12:58:01 Log-Likelihood: -120.08
No. Observations: 30 AIC: 244.2
Df Residuals: 28 BIC: 247.0
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -133.1915 21.257 -6.266 0.000 -176.735 -89.648
x1 9.3800 0.765 12.264 0.000 7.813 10.947
==============================================================================
Omnibus: 3.715 Durbin-Watson: 1.784
Prob(Omnibus): 0.156 Jarque-Bera (JB): 2.213
Skew: 0.477 Prob(JB): 0.331
Kurtosis: 3.928 Cond. No. 236.
==============================================================================
これにより、回帰係数(coef)だけでなく回帰係数(coef)の標準誤差(std err)やt 値(t)、p 値(P>|t| )、自由度調整済み決定係数(Adj. R-squared:)などが一括して表示されます。
そのため、次のような使い分けが実務ではよく行われます。
- 機械学習的な予測重視 → scikit-learn
- 統計的な解釈・推論重視 → statsmodels
まとめ
気温データから売上を予測するという身近な例を通じて、回帰分析の本質を理論と実装の両面から学びました。
- 最小二乗法の原理
- 正規方程式の解
- 相関係数と回帰係数の関係
- 決定係数
- 変動の分解
これらの概念は、より高度な統計手法を学ぶ上での基礎となります。特に、行列表現による一般化は、重回帰分析への拡張において重要です。
第2回では、今回求めた回帰係数の統計的性質について学びます。
- 回帰係数の標準誤差と信頼区間
- t検定による統計的有意性の判定
- p値の正しい理解と解釈
- 仮説検定の枠組みと実務での活用
今回の「気温が1℃上がると10.2杯増える」という結果が、偶然ではなく統計的に意味のあるものかを判定する方法を学びます。