Pythonで体感する次元削減入門 – PCAと因子分析の基礎のキソ— 第2回 —PCAのしくみを分散・共分散・固有値分解で理解する

前回は、「次元削減」の考え方と、PCAの基本的なアイデアをお話しいたしました。

具体的には、2次元の従業員評価データを使って、様々な角度に射影したときの分散を計算し、「データが最も広がっている方向」を探しました。

Pythonで体感する次元削減入門 – PCAと因子分析の基礎のキソ— 第1回 —なぜ「次元を減らす」のか？情報の海で溺れないために

しかし、前回のやり方には問題があります。

前回のやり方とは、0度から180度まで1度刻み変化させながら、分散が最大になる方向を探すやり方です。

この1度刻み変化させながら全部試すのは、2次元だから何とかなりましたが、変数が10個、100個になったらどうでしょう？

すべての方向を試すのは現実的ではありません。

今回は、共分散行列と固有値分解という数学的な道具を使って、「最大分散の方向」を一発で見つける方法を学びます。

Contents

ライブラリの準備とデータの用意
分散の復習
2つの変数の連動を測る「共分散」
すべての関係を1つの表にまとめる「共分散行列」
データが広がっている方向を見つける「固有値分解」
固有ベクトルを散布図に重ねる
前回の結果と比較する
固有値 = その方向の分散
2つの主成分は直交している
まとめ

ライブラリの準備とデータの用意

まずは、前回と同じデータを用意しましょう。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib

# 乱数のシードを固定して再現性を確保
np.random.seed(42)  

# 前回と同じ従業員評価データを作成
n_employees = 50
base_ability = np.random.normal(0, 1, n_employees)
接客スキル = base_ability * 3 + np.random.normal(0, 1, n_employees) + 50
商品知識 = base_ability * 2 + np.random.normal(0, 1.5, n_employees) + 50

df = pd.DataFrame({'接客スキル': 接客スキル, '商品知識': 商品知識})
print(df.head().round(1))

以下、実行結果です。

   接客スキル  商品知識
0   51.8  48.9
1   49.2  49.1
2   51.3  50.8
3   55.2  51.8
4   50.3  49.3

前回と同じ50人分の従業員評価データです。

分散の復習

PCAを理解するために、まず分散（variance）を復習しましょう。分散とは、データが平均からどれくらい散らばっているかを表す指標で、分散の値は大きいほど、データのばらつきが大きいことを意味します。

分散は、次のように計算します。

各データから平均を引く（偏差を求める）
偏差を2乗する（マイナスをなくす）
2乗した値の平均を取る

数式で書くと、 $n$ 個のデータ $x_1, x_2, \dots, x_n$ の分散 $\sigma^2$ は次のようになります。

$$
\sigma^2 = \frac{1}{n-1}\sum_{i=1}^{n} (x_i – \bar{x})^2
$$
ここで、 $\bar{x}$ は平均値です。分母が $n$ ではなく $n-1$ なのは、標本から母集団の分散を推定するための補正（不偏分散）です。

接客スキルの分散を計算してみましょう。NumPyの関数でも求めています。

x = df['接客スキル'].values
n = len(x)
x_mean = np.mean(x)

# 分散を求める
x_deviation = x - x_mean
x_deviation_squared = x_deviation ** 2
variance_manual = np.sum(x_deviation_squared) / (n - 1)

# NumPyの関数で計算（ddof=1で不偏分散）
variance_numpy = np.var(x, ddof=1)

print(f"平均: {x_mean:.2f}")
print(f"分散: {variance_manual:.2f}")
print(f"分散（NumPy）: {variance_numpy:.2f}")

以下、実行結果です。

平均: 49.34
分散: 9.15
分散（NumPy）: 9.15

このコードを実行すると、NumPyの結果が一致することが確認できます。

2つの変数の連動を測る「共分散」

次に、共分散（covariance）を理解しましょう。共分散は、2つの変数がどれくらい「一緒に動くか」を表す指標です。

接客スキルが高い人は商品知識も高い傾向がある、というのが前回確認した「正の相関」でした。共分散は、この「連動の強さ」を数値化したものです。

共分散の計算方法は、分散とよく似ています。

各データから平均を引く（偏差を求める）
2つの変数の偏差を掛け合わせる
その平均を取る

数式で書くと、共分散 $\mathrm{Cov}(x,y)$ は次のようになります。

$$
\mathrm{Cov}(x,y) = \frac{1}{n-1}\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})
$$
共分散のプラスマイナスの符号には、重要な意味があります。

正の共分散：一方が平均より大きいとき、他方も大きい傾向（右上がの関係）
負の共分散：一方が平均より大きいとき、他方は小さい傾向（右下がりの関係）
ゼロに近い共分散：2つの変数に連動性がない

接客スキルと商品知識の共分散を計算してみましょう。NumPyの関数でも求めています。

x_values = df['接客スキル'].values
y_values = df['商品知識'].values
n = len(x_values)

# 平均を計算
x_mean = np.mean(x_values)
y_mean = np.mean(y_values)

# 共分散を求める
x_deviation = x_values - x_mean
y_deviation = y_values - y_mean
covariance_manual = np.sum(x_deviation * y_deviation) / (n - 1)

# NumPyの関数で共分散を計算
covariance_matrix_numpy = np.cov(x_values, y_values)
covariance_numpy = covariance_matrix_numpy[0, 1]

print(f"共分散: {covariance_manual:.2f}")
print(f"共分散 (NumPy): {covariance_numpy:.2f}")

以下、実行結果です。

共分散: 4.57
共分散 (NumPy): 4.57

今回は正の共分散が得られました。

これは、接客スキルが高い人は商品知識も高い傾向があることを数値で確認したことになります。

すべての関係を1つの表にまとめる「共分散行列」

変数が2つだけなら共分散は1つですが、変数が増えると、すべてのペアの共分散を考える必要があります。これをまとめたものが共分散行列です。

2つの変数（接客スキル、商品知識）の場合、共分散行列は2×2の表になります。

	接客スキル	商品知識
接客スキル	接客の分散	共分散
商品知識	共分散	商品の分散

対角線上には各変数の分散が、対角線の外には変数間の共分散が並びます。自分自身との共分散は分散に等しいので、これは自然な構造です。

では、共分散行列を計算します。

# データを中心化
X_centered = df.values - df.values.mean(axis=0)

# 共分散行列を計算
n = len(X_centered)
S = (X_centered.T @ X_centered) / (n - 1)

print("共分散行列:")
print(S.round(2))
print()

# 共分散行列を計算（NumPyの関数）
S_numpy = np.cov(df['接客スキル'], df['商品知識'])
print("共分散行列（NumPy）:")
print(S_numpy.round(2))

以下、実行結果です。

共分散行列:
[[9.15 4.57]
 [4.57 5.09]]

共分散行列（NumPy）:
[[9.15 4.57]
 [4.57 5.09]]

2×2の共分散行列が表示されます。対角成分が各変数の分散、非対角成分が共分散です。

この行列には、2つの変数の「ばらつき」と「連動」に関するすべての情報が詰まっています。

共分散行列をヒートマップで可視化してみましょう。

# 共分散行列をDataFrameに変換
S_df = pd.DataFrame(
    S, 
    index=['接客スキル', '商品知識'],
    columns=['接客スキル', '商品知識']
)

# 共分散行列をヒートマップで表示
plt.figure(figsize=(6, 5))
sns.heatmap(
    S_df, annot=True, 
    fmt='.2f', cmap='Blues', 
    square=True, linewidths=1
)
plt.title('共分散行列')
plt.tight_layout()
plt.show()

以下、実行結果です。

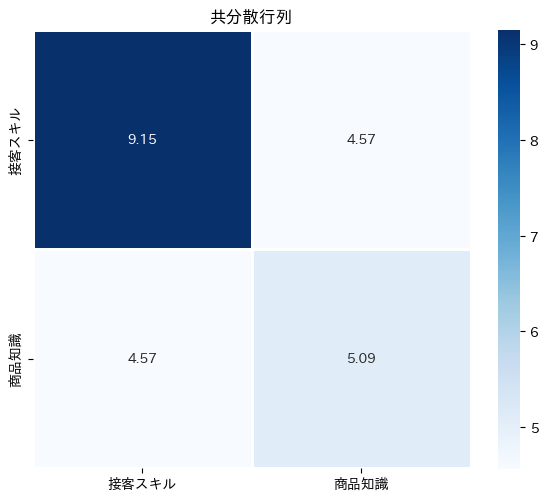
このヒートマップを見ると、対角成分（分散）と非対角成分（共分散）の大きさを一目で比較できます。非対角成分が大きいということは、2つの変数が強く連動していることを示しています。

データが広がっている方向を見つける「固有値分解」

ここからが、今回の内容の中でも特に重要なポイントです。

共分散行列に固有値分解を行うことで、「データがどの方向に、どれだけ広がっているか」を数学的に捉えることができます。

固有値分解とは、行列をデータの広がりを表す方向（固有ベクトル）とその方向にどれだけ広がっているか（固有値）の組に分解する操作です。

いま、共分散行列を $\mathbf{S}$ とします。このとき、次の式を満たすベクトル $\mathbf{v}$ と数値 $\lambda$ を考えます。
$$
\mathbf{S}\mathbf{v} = \lambda \mathbf{v}
$$
この式は、「ベクトル $\mathbf{v}$ に共分散行列 $\mathbf{S}$ を掛けると、向きは変わらず、長さだけが $\lambda$ 倍になる」ということを意味しています。

このような向きが保たれる特別な方向を固有ベクトル、そのときの伸び縮みの大きさを固有値と呼びます。

共分散行列に固有値分解を行うと、複数の固有ベクトルと固有値が得られます。これらは、そのまま主成分分析（PCA）における主成分に対応しています。

共分散行列の場合、次のような意味を持ちます。

各固有ベクトル：データをその方向に射影したとき、分散が最も大きくなる方向や、その次に大きくなる方向
対応する固有値：その方向に射影したときの分散の大きさ

つまり、固有値分解を行うことで、幾つかの主成分をまとめて得られるのです。

分散が最も大きい方向（第1主成分）
第1主成分と直交し、次に分散が大きい方向（第2主成分）
高次元では、第3主成分、第4主成分、……

前回のように角度を少しずつ変えながら探していた「分散が最大になる方向」は、固有値分解によって計算だけで得られることになります。

それでは、NumPy の np.linalg.eig() を使って、共分散行列を固有値分解してみましょう。

# 共分散行列の固有値分解
eigenvalues, eigenvectors = np.linalg.eig(S)

print("固有値:")
print(eigenvalues.round(3))
print()
print("固有ベクトル（列ベクトルとして格納）:")
print(eigenvectors.round(3))

以下、実行結果です。

固有値:
[12.118  2.124]

固有ベクトル（列ベクトルとして格納）:
[[ 0.838 -0.545]
 [ 0.545  0.838]]

共分散行列 $\mathbf{S}$ に対して、次の関係が成り立っています。
$$
\begin{align}
\mathbf{S}\mathbf{v}_1 &= \lambda_1 \mathbf{v}_1 \quad (\mathbf{v}_1 = \begin{bmatrix} 0.838 \\ 0.545\end{bmatrix},\lambda_1 = 12.118) \\
\mathbf{S}\mathbf{v}_2 &= \lambda_2 \mathbf{v}_2 \quad (\mathbf{v}_2 = \begin{bmatrix} -0.545 \\ 0.838\end{bmatrix},\lambda_2 = 2.124)
\end{align}
$$
ここで、 $\lambda_1 > \lambda_2$ であるため次のようになります。

$\mathbf{v}_1$ は第1主成分（分散が最も大きい方向）
$\mathbf{v}_2$ は第2主成分（第1主成分に直交し、次に分散が大きい方向）

固有値が大きい順に並べ替えて、見てみましょう。

# 固有値が大きい順にソート
idx = np.argsort(eigenvalues)[::-1]
eigenvalues_sorted = eigenvalues[idx]
eigenvectors_sorted = eigenvectors[:, idx]

print("=== 第1主成分 ===")
print(f"固有値（分散）: {eigenvalues_sorted[0]:.3f}")
print(f"固有ベクトル（方向）: {eigenvectors_sorted[:, 0].round(3)}")
print()
print("=== 第2主成分 ===")
print(f"固有値（分散）: {eigenvalues_sorted[1]:.3f}")
print(f"固有ベクトル（方向）: {eigenvectors_sorted[:, 1].round(3)}")

以下、実行結果です。

=== 第1主成分 ===
固有値（分散）: 12.118
固有ベクトル（方向）: [0.838 0.545]

=== 第2主成分 ===
固有値（分散）: 2.124
固有ベクトル（方向）: [-0.545  0.838]

固有ベクトルを散布図に重ねる

固有値分解で得られた方向が、本当に「データが広がっている方向」なのか、散布図で確認してみましょう。

plt.figure(figsize=(8, 8))

# 中心化したデータをプロット
plt.scatter(
    X_centered[:, 0], X_centered[:, 1], 
    alpha=0.5, s=60, label='データ点'
)

# 第1主成分の方向（固有値の大きさに応じて矢印を伸ばす）
v1 = eigenvectors_sorted[:, 0]
scale1 = np.sqrt(eigenvalues_sorted[0]) * 2  # 見やすさのためスケール調整
plt.arrow(
    0, 0, v1[0]*scale1, v1[1]*scale1,
    head_width=0.3, head_length=0.2, 
    fc='red', ec='red', linewidth=2
)
plt.text(
    v1[0]*scale1 - 0.5, v1[1]*scale1 + 0.5, 
    f'第1主成分\n(λ={eigenvalues_sorted[0]:.1f})', 
    fontsize=10, color='red'
)

# 第2主成分の方向
v2 = eigenvectors_sorted[:, 1]
scale2 = np.sqrt(eigenvalues_sorted[1]) * 2
plt.arrow(
    0, 0, v2[0]*scale2, v2[1]*scale2,
    head_width=0.3, head_length=0.2, 
    fc='green', ec='green', linewidth=2
)
plt.text(
    v2[0]*scale2 - 1.5, v2[1]*scale2 + 0.5, 
    f'第2主成分\n(λ={eigenvalues_sorted[1]:.1f})', 
    fontsize=10, color='green'
)

# 原点を中心に縦横の線を引く
plt.axhline(
    y=0, color='gray', 
    linestyle='-', linewidth=0.5
)
plt.axvline(
    x=0, color='gray', 
    linestyle='-', linewidth=0.5
)

plt.xlabel('接客スキル（中心化後）')
plt.ylabel('商品知識（中心化後）')
plt.title('固有ベクトル = 主成分の方向')
plt.axis('equal')
plt.grid(True, alpha=0.3)
plt.legend(loc='lower right')
plt.show()

以下、実行結果です。

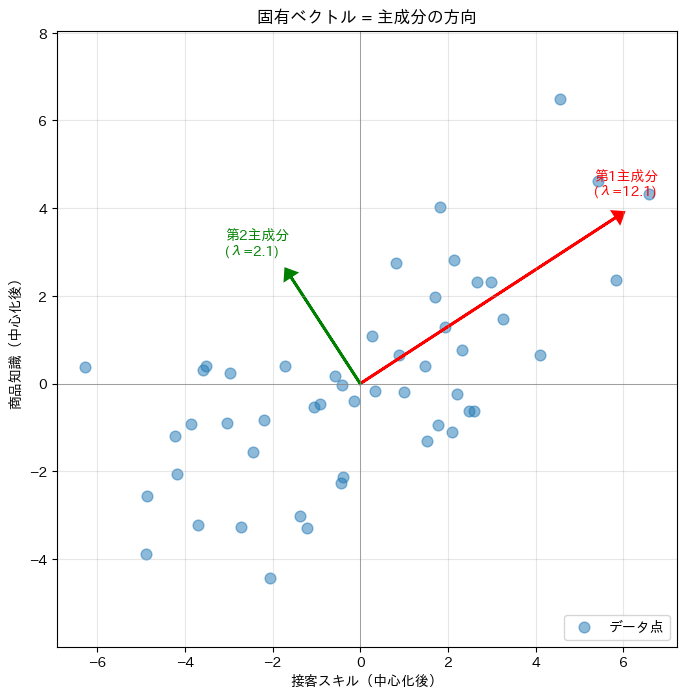
データの散布図に主成分の方向が矢印として重ねて表示されます。赤い矢印（第1主成分）がデータの長軸方向を、緑の矢印（第2主成分）が短軸方向を指していることが確認できるはずです。

前回の結果と比較する

前回は0度から180度まで1度刻みで最大分散の方向を探しました。固有値分解で得られた方向と一致するか確認してみましょう。

# 固有ベクトル（第1主成分）から角度を計算
v1 = eigenvectors_sorted[:, 0]
angle_eigen = np.degrees(np.arctan2(v1[1], v1[0]))
if angle_eigen < 0:
    angle_eigen += 180  # 0〜180度に正規化

# 前回の方法
#（0度から180度まで1度刻みで最大分散の方向に全探索）
angles = np.linspace(0, 180, 181)
variances = []
for angle in angles:
    rad = np.radians(angle)
    w = np.array([np.cos(rad), np.sin(rad)])
    projections = X_centered @ w
    var = np.var(projections, ddof=1)
    variances.append(var)

angle_search = angles[np.argmax(variances)]

print(f"固有値分解で求めた角度: {angle_eigen:.1f}度")
print(f"全探索で求めた角度: {angle_search:.1f}度")
print(f"差: {abs(angle_eigen - angle_search):.1f}度")

以下、実行結果です。

固有値分解で求めた角度: 33.0度
全探索で求めた角度: 33.0度
差: 0.0度

このコードを実行すると、2つの方法で求めた角度がほぼ一致することが確認できます。

固有値分解を使えば、全探索をしなくても最大分散の方向が正確に求まることがわかりました。

固有値 = その方向の分散

もう一つ重要な確認をしましょう。固有値は「その方向に射影したときの分散」です。そのことを検証します。

# 第1主成分方向への射影
v1 = eigenvectors_sorted[:, 0]
projection1 = X_centered @ v1
variance1 = np.var(projection1, ddof=1)

# 第2主成分方向への射影
v2 = eigenvectors_sorted[:, 1]
projection2 = X_centered @ v2
variance2 = np.var(projection2, ddof=1)

print(f"第1主成分:")
print(f"  固有値: {eigenvalues_sorted[0]:.3f}")
print(f"  射影後の分散: {variance1:.3f}")
print()
print(f"第2主成分:")
print(f"  固有値: {eigenvalues_sorted[1]:.3f}")
print(f"  射影後の分散: {variance2:.3f}")

以下、実行結果です。

第1主成分:
  固有値: 12.118
  射影後の分散: 12.118

第2主成分:
  固有値: 2.124
  射影後の分散: 2.124

固有値と射影後の分散がぴったり一致することが確認できます。

固有値分解という一つの操作で、「最適な方向」と「その方向での分散」の両方が同時に求まるのです。

2つの主成分は直交している

最後に、第1主成分と第2主成分が互いに直交（90度で交わる）していることを確認しましょう。

# 2つの固有ベクトルの内積を計算
v1 = eigenvectors_sorted[:, 0]
v2 = eigenvectors_sorted[:, 1]
inner_product = np.dot(v1, v2)

print(
    "第1主成分と第2主成分の内積:"
    f" {inner_product:.10f}"
)

以下、実行結果です。

第1主成分と第2主成分の内積: 0.0000000000

内積がほぼ0になっています。これは、2つの主成分が互いに直交していることを意味します。

直交しているということは、第1主成分と第2主成分が表す情報に重複がないということです。

これがPCAの重要な性質の一つです。

まとめ

この第2回では、PCAの数学的な仕組みを学びました。

分散は、1つの変数のばらつきを測る指標です。データが平均からどれくらい散らばっているかを表します。

共分散は、2つの変数の連動性を測る指標です。正の共分散は「一緒に増減する」関係、負の共分散は「逆に動く」関係を表します。

共分散行列は、すべての変数の分散と共分散を1つの表にまとめたものです。対角成分が分散、非対角成分が共分散になります。

固有値分解を共分散行列に適用すると、次のことがわかります。

固有ベクトル = 主成分の方向（データが広がっている方向）
固有値 = その方向での分散（どれくらい広がっているか）

固有ベクトルは互いに直交しており、情報の重複がありません。固有値が大きい順に第1主成分、第2主成分…と呼びます。

Pythonで体感する次元削減入門 – PCAと因子分析の基礎のキソ— 第3回 —次元はいくつ残す？寄与率とスクリープロットの読み方