Pythonで体感する次元削減入門 – PCAと因子分析の基礎のキソ
— 第5回 —
PCAと因子分析、何が違う？

40
Pythonで体感する次元削減入門 – PCAと因子分析の基礎のキソ— 第5回 —PCAと因子分析、何が違う？

ここまで4回にわたって、主成分分析（PCA）を学んできました。

— 第1回 —
なぜ「次元を減らす」のか？ 情報の海で溺れないために
https://www.salesanalytics.co.jp/datascience/datascience286/
— 第2回 —
PCAのしくみを分散・共分散・固有値分解で理解する
https://www.salesanalytics.co.jp/datascience/datascience288/
— 第3回 —
次元はいくつ残す？ 寄与率とスクリープロットの読み方
https://www.salesanalytics.co.jp/datascience/datascience289/
— 第4回 —
scikit-learnでさくっとPCAを実施する
https://www.salesanalytics.co.jp/datascience/datascience290/

共分散行列の固有値分解によって「データが最も広がる方向」を見つけ、次元を削減する手法でしたね。

ところで、PCAと似た手法に因子分析（Factor Analysis）があります。

どちらも「多くの変数を少数にまとめる」という目的で使われますが、実は根本的な考え方が異なります。

「PCAと因子分析って何が違うの？」
「どう使い分ければいいの？」

今回は、この疑問にしっかり答えていきます。

両者の違いを理解することで、分析の目的に応じて適切な手法を選べるようになります。

身近な例で考える

高校生の5教科（国語、数学、英語、物理、化学）のテスト結果があるとします。これらの成績の「背後」には何があるでしょうか？

　PCAの考え方

PCAは、5教科の点数をできるだけ情報を失わずに少ない変数にまとめたいという発想です。

「第1主成分は総合学力、第2主成分は文理の傾向を表している」などと解釈することはありますが、それはあくまで結果の解釈であり、最初から「総合学力」を想定しているわけではありません。

PCAは「データ → 要約」という方向で考えます。

 

　因子分析の考え方

一方、因子分析は、観測できない「潜在的な能力」が各科目の点数を生み出していると考えます。

たとえば、「言語能力」という見えない因子が国語と英語の点数に影響し、「数理能力」という因子が数学、物理、化学の点数に影響している、というモデルを想定します。

因子分析は「潜在因子 → データ」という方向で考えます。

この「矢印の向き」の違いが、両者の本質的な違いです。

 

数学的な違いを理解する

　PCAのモデル

PCAは、厳密には統計モデルではありません。

単に共分散行列を固有値分解して、分散が最大になる方向を見つけているだけです。

主成分得点は次のように計算されます。

$$
\mathbf{z} = W^T \mathbf{x}
$$
ここで、\mathbf{x}は観測データ、Wは固有ベクトルを並べた行列、\mathbf{z}は主成分得点です。

データ\mathbf{x}から主成分得点\mathbf{z}への変換は一意に決まります。

 

　因子分析のモデル

因子分析は、データがどのように生成されたかを仮定する統計モデルです。

$$
\mathbf{x} = \Lambda \mathbf{F} + \boldsymbol{\varepsilon}
$$

  • x（観測変数）は、実際に測定できる変数（テストの点数など）です。
  • F（因子）は、直接観測できない潜在的な変数（言語能力、数理能力など）です。
  • Λ（因子負荷量）は、因子が観測変数にどれだけ影響するかを表す係数です。
  • ε（独自因子・誤差）は、因子では説明できない各変数固有の成分です。

因子分析では、「因子\mathbf{F}があって、それが各科目の点数\mathbf{x}を生み出している」と考えます。

因子得点は観測データから推定する必要があり、一意には決まりません。

 

準備

　ライブラリの準備

今回は因子分析のためにfactor_analyzerライブラリを使います。インストールされていない場合はpip install factor_analyzerでインストールしてください。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib

# PCA用
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

# 因子分析用
from factor_analyzer import FactorAnalyzer

# 乱数のシードを固定
np.random.seed(42)

 

このコードを実行すると、PCAと因子分析の両方を実行する準備が整います。

 

　サンプルデータの生成

実際にデータを使って、PCAと因子分析の違いを確認してみましょう。

まず、「言語能力」と「数理能力」という2つの潜在因子から5教科の成績が生成される、というシナリオでデータを作成します。

以下のコードでは、2つの潜在因子（言語能力、数理能力）から5教科の成績データを生成します。これは因子分析のモデル\mathbf{x} = \Lambda \mathbf{F} + \boldsymbol{\varepsilon}に従ったデータの生成です。

# サンプル数
n = 200

# 2つの潜在因子を生成（これは通常観測できない）
F_language_ability = np.random.normal(0, 1, n)
F_math_ability = np.random.normal(0, 1, n)

# 因子負荷量の設定（どの因子がどの科目に影響するか）
# 国語・英語 ← 言語能力が強く影響
# 数学・物理・化学 ← 数理能力が強く影響

# 国語の成績を生成
japanese = (
    0.8 * F_language_ability + 
    0.1 * F_math_ability + 
    np.random.normal(0, 0.3, n)
)
# 英語の成績を生成
english = (
    0.7 * F_language_ability + 
    0.2 * F_math_ability + 
    np.random.normal(0, 0.3, n)
)
# 数学の成績を生成
math = (
    0.2 * F_language_ability + 
    0.8 * F_math_ability + 
    np.random.normal(0, 0.3, n)
)
# 物理の成績を生成
physics = (
    0.1 * F_language_ability + 
    0.7 * F_math_ability + 
    np.random.normal(0, 0.3, n)
)
# 化学の成績を生成
chemistry = (
    0.2 * F_language_ability + 
    0.6 * F_math_ability + 
    np.random.normal(0, 0.3, n)
)

# DataFrameにまとめる
grades_data = pd.DataFrame({
    'Japanese': japanese, 
    'English': english, 
    'Math': math, 
    'Physics': physics, 
    'Chemistry': chemistry
})

print("成績データの基本統計量:")
print(grades_data.describe().round(2))

 

以下、実行結果です。

成績データの基本統計量:
       Japanese  English    Math  Physics  Chemistry
count    200.00   200.00  200.00   200.00     200.00
mean      -0.12    -0.08   -0.03    -0.03      -0.04
std        0.86     0.78    0.79     0.74       0.67
min       -2.18    -2.04   -2.44    -2.09      -2.16
25%       -0.73    -0.61   -0.54    -0.60      -0.46
50%       -0.05    -0.05    0.04    -0.01      -0.01
75%        0.43     0.47    0.50     0.56       0.46
max        2.18     1.83    1.88     1.62       1.71

 

このデータは「言語能力」と「数理能力」という2つの因子から生成されています。

生成したデータの相関行列を確認してみましょう。因子構造が反映されているはずです。

# 相関行列を計算
corr_matrix = grades_data .corr()

# ヒートマップで可視化
plt.figure(figsize=(8, 6))
sns.heatmap(
    corr_matrix, annot=True, fmt='.2f', 
    cmap='coolwarm', center=0, linewidths=1, 
    vmin=-1, vmax=1
)

plt.title('5教科の相関行列')
plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

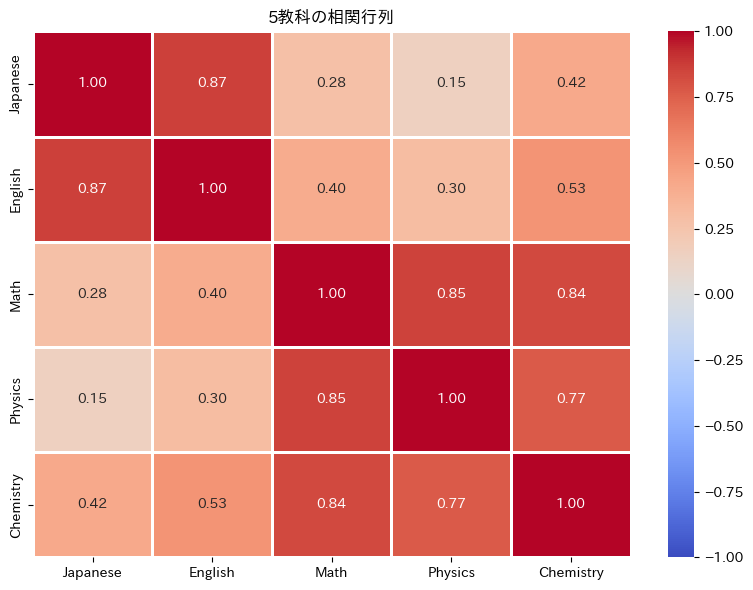
このヒートマップを見ると、「国語・英語」のグループと「数学・物理・化学」のグループ内で相関が高く、グループ間の相関は低いことがわかります。

これは、2つの異なる因子がそれぞれのグループに影響しているためです。

 

PCA（主成分分析）

　PCAを実施

まず、このデータにPCAを適用してみましょう。

# データを標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(grades_data)

# PCAを実行（2成分を抽出）
pca = PCA(n_components=2)
pca_scores = pca.fit_transform(X_scaled)

# 寄与率を表示
print("=== PCAの結果 ===")
print(f"第1主成分の寄与率: {pca.explained_variance_ratio_[0]*100:.1f}%")
print(f"第2主成分の寄与率: {pca.explained_variance_ratio_[1]*100:.1f}%")
print(f"累積寄与率: {sum(pca.explained_variance_ratio_)*100:.1f}%")

 

以下、実行結果です。

=== PCAの結果 ===
第1主成分の寄与率: 66.6%
第2主成分の寄与率: 24.8%
累積寄与率: 91.5%

 

2つの主成分で全体の分散の大部分を説明できることがわかります。

主成分と元の変数の関係を確認してみましょう。主成分負荷量は、固有ベクトルに固有値の平方根を掛けたものです。

# 主成分負荷量を計算（固有ベクトル × √固有値）
pca_loadings = (
    pca.components_.T * 
    np.sqrt(pca.explained_variance_)
)

# 主成分負荷量をデータフレームに変換
pca_loadings_df = pd.DataFrame(
    pca_loadings,
    index=grades_data.columns,
    columns=['PC1', 'PC2']
)

print("=== PCA：主成分負荷量 ===")
print(pca_loadings_df.round(3))

 

以下、実行結果です。

=== PCA：主成分負荷量 ===
             PC1    PC2
Japanese   0.682  0.691
English    0.749  0.610
Math       0.904 -0.323
Physics    0.834 -0.469
Chemistry  0.900 -0.272

 

各科目が主成分にどれだけ寄与しているかがわかります。

PC1にはすべての科目がプラスに寄与していて「総合学力」のように見え、PC2は文系（プラス方向）と理系（マイナス方向）を区別する軸になっています。

 

　主成分得点で散布図を作成

plt.figure(figsize=(10, 8))

# 散布図を描画
plt.scatter(
    pca_scores[:, 0], # PC1の得点
    pca_scores[:, 1], # PC2の得点
    c='b', s=80, alpha=0.7
)

plt.xlabel(f'PC1 ({pca.explained_variance_ratio_[0]*100:.1f}%)')
plt.ylabel(f'PC2 ({pca.explained_variance_ratio_[1]*100:.1f}%)')
plt.title('PCA: 主成分得点の散布図')
plt.grid(True, alpha=0.3)
plt.axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
plt.axvline(x=0, color='gray', linestyle='-', linewidth=0.5)
plt.show()

 

以下、実行結果です。

 

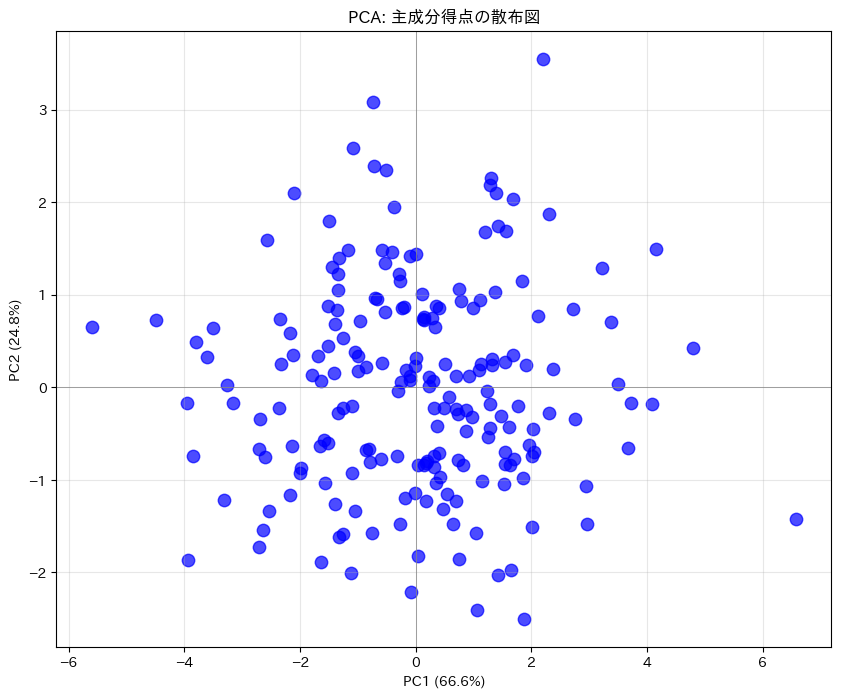
　バイプロットを作成

plt.figure(figsize=(10, 8))

# 主成分得点をプロット
plt.scatter(
    pca_scores[:, 0], # PC1の得点
    pca_scores[:, 1], # PC2の得点
    c='b', s=80, alpha=0.7,
)

# 主成分負荷量をプロット
scale_factor = 5  # 矢印の長さを調整するためのスケールファクター
pca_loadings_corrected = pca_loadings_df * scale_factor
for i in range(pca_loadings_corrected.shape[0]):
    plt.arrow(
        0, 0, 
        pca_loadings_corrected.iloc[i, 0], 
        pca_loadings_corrected.iloc[i, 1],
        color='red', alpha=0.5, head_width=0.05
    )
    plt.text(
        pca_loadings_corrected.iloc[i, 0] * 1.05, 
        pca_loadings_corrected.iloc[i, 1] * 1.05,
        pca_loadings_corrected.index[i], 
        color='red'
    )

plt.xlabel(f'PC1 ({pca.explained_variance_ratio_[0]*100:.1f}%)')
plt.ylabel(f'PC2 ({pca.explained_variance_ratio_[1]*100:.1f}%)')
plt.title('PCA: 主成分分析バイプロット')
plt.grid(True, alpha=0.3)
plt.axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
plt.axvline(x=0, color='gray', linestyle='-', linewidth=0.5)
plt.show()

 

以下、実行結果です。

 

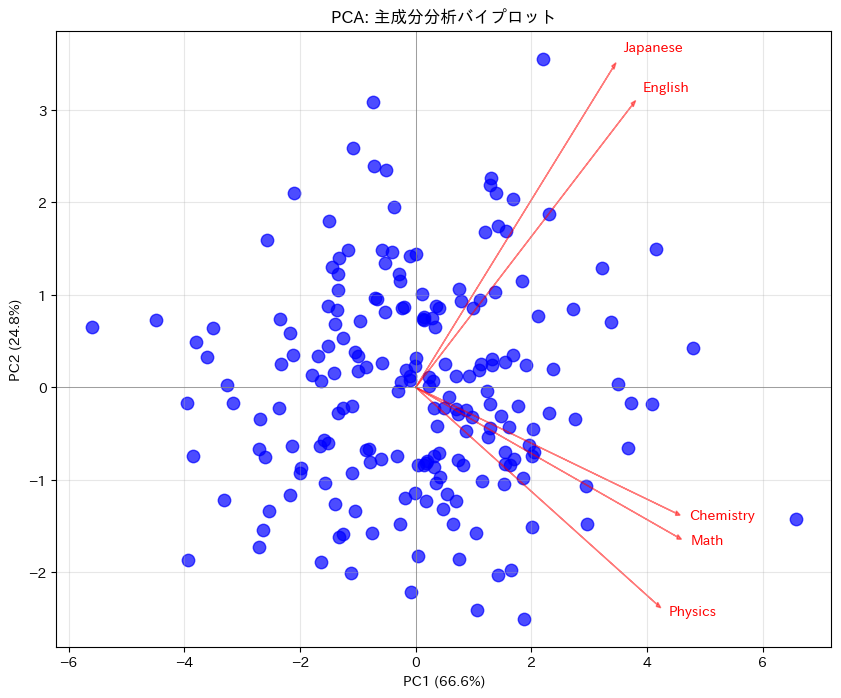
因子分析

　因子分析（回転なし）を実施

次に、同じデータに因子分析を適用してみましょう。

# 因子分析を実行（2因子を抽出、回転なし）
fa = FactorAnalyzer(
    n_factors=2,        # 抽出する因子数
    rotation=None,      # 回転なし
    method='principal', # 主成分法
)
fa.fit(X_scaled)

# 因子負荷量を取得
fa_loadings = fa.loadings_

# 因子負荷量をデータフレームに変換
fa_loadings_df = pd.DataFrame(
    fa_loadings,
    index=grades_data.columns,
    columns=['因子1', '因子2']
)

print("=== 因子分析：因子負荷量（回転なし） ===")
print(fa_loadings_df.round(3))

 

以下、実行結果です。

=== 因子分析：因子負荷量（回転なし） ===
             因子1    因子2
Japanese   0.680  0.689
English    0.747  0.609
Math       0.902 -0.322
Physics    0.832 -0.468
Chemistry  0.897 -0.271

 

回転なしの状態では、PCAの主成分負荷量と似た結果になることが多いです。

ここで使用したmethod='principal'は主成分法と呼ばれる推定方法です。

主成分法は、まず共分散行列（または相関行列）の固有値分解を行い、そこから因子負荷量を推定します。

PCAと似た手順ですが、因子分析では「共通因子」と「独自因子」を区別する点が異なります。「共通因子」と「独自因子」については後で説明します。

 

FactorAnalyzerでは、他にも様々な推定方法を選択できます。

method 推定方法 説明
'principal' 主成分法 共分散行列の固有値分解に基づく方法。計算が速く安定しているため、探索的な分析でよく使われます。
'minres' 最小残差法 残差（観測された相関と再現された相関の差）を最小化する方法。収束しやすく、多くの場面で推奨されます。
'ml' 最尤法 データが多変量正規分布に従うと仮定し、尤度を最大化する方法。モデルの適合度検定が可能ですが、分布の仮定が必要です。
'uls' 重み無し最小二乗法 残差の二乗和を最小化する方法。最小残差法と同様のアプローチです。
'gls' 一般化最小二乗法 残差に重み付けをして最小化する方法。変数間の関係を考慮した推定ができます。

初学者の方は、まず'principal'（主成分法）または'minres'（最小残差法）から始めることをおすすめします。どちらも安定した結果が得られやすく、多くの実務で使われています。

 

　因子分析（回転あり）を実施

因子分析の大きな特徴の一つが回転です。

因子分析で得られた因子負荷量は、そのままでは解釈しづらいことがあります。

たとえば、回転前の結果では「因子1にすべての変数が中程度に寄与している」という状態になりがちです。これでは「因子1は何を表すのか」を説明するのが難しくなります。

回転は、因子の解釈をしやすくするための操作です。因子空間内で軸を回転させることで、各変数がどれか一つの因子に強く関係する（他の因子への負荷が小さくなる）パターンを目指します。

回転しても、因子が説明する分散の合計は変わりません。つまり、情報を失うことなく解釈しやすくなるのです。

# バリマックス回転を適用した因子分析を実行
fa_rotated = FactorAnalyzer(
    n_factors=2,        # 抽出する因子数
    rotation='varimax', # バリマックス回転
    method='principal', # 主成分法
)
fa_rotated.fit(X_scaled)

# 因子負荷量を取得
fa_rotated_loadings = fa_rotated.loadings_

# 因子負荷量をデータフレームに変換
fa_rotated_loadings_df = pd.DataFrame(
    fa_rotated.loadings_,
    index=grades_data.columns,
    columns=['因子1', '因子2']
)

print("=== 因子分析：因子負荷量（バリマックス回転後） ===")
print(fa_rotated_loadings_df.round(3))

 

以下、実行結果です。

=== 因子分析：因子負荷量（バリマックス回転後） ===
             因子1    因子2
Japanese   0.165  0.954
English    0.266  0.926
Math       0.925  0.250
Physics    0.950  0.090
Chemistry  0.892  0.289

 

rotation='varimax'で指定するバリマックス回転は、最もよく使われる回転方法です。

バリマックス回転は、因子負荷量の二乗の分散を最大化します。これにより、各変数が「高い負荷を持つ因子」と「低い負荷を持つ因子」にはっきり分かれ、「この変数はこの因子に属する」という解釈がしやすくなります。

また、バリマックス回転は直交回転の一種で、回転後も因子同士は互いに無相関を保ちます。

 

FactorAnalyzerでは、他にも様々な回転方法を選択できます。

rotation 回転方法 種類 説明
None 回転なし – 回転を適用しません。因子の解釈が難しいことがあります。
'varimax' バリマックス回転 直交 因子負荷量の分散を最大化。最も一般的で、因子が無相関と仮定できる場合に使用します。
'quartimax' クォーティマックス回転 直交 各変数が少数の因子で説明されるようにします。一般因子が現れやすい特徴があります。
'equamax' イクアマックス回転 直交 バリマックスとクォーティマックスの中間的な手法です。
'promax' プロマックス回転 斜交 因子間の相関を許容する斜交回転。心理学などで因子の相関が想定される場合に使用します。
'oblimin' オブリミン回転 斜交 斜交回転の一種。因子間の相関を柔軟に許容します。

直交回転と斜交回転の違いは、回転後の因子同士が相関するかどうかです。

直交回転（varimax、quartimaxなど）では因子間は無相関を保つため解釈がシンプルですが、現実には因子間に相関があることも多いです。

斜交回転（promax、obliminなど）では因子間の相関を許すため、より柔軟なモデルになります。ただし、解釈はやや複雑になります。

初学者の方は、まず'varimax'から始め、因子間に相関があると考えられる場合に'promax'を試してみるとよいでしょう。

 

　負荷量の比較（ヒートマップ）

PCAと因子分析の結果を、ヒートマップで並べて比較してみましょう。

fig, axes = plt.subplots(3, 1, figsize=(8, 15))

# PCA
ax = axes[0]
sns.heatmap(
    pca_loadings_df, 
    annot=True, fmt='.2f', cmap='coolwarm',
    center=0, linewidths=1, vmin=-1, vmax=1, 
    ax=ax
)
ax.set_title('PCA\n（主成分負荷量）')

# 因子分析（回転なし）
ax = axes[1]
sns.heatmap(
    fa_loadings_df, 
    annot=True, fmt='.2f', cmap='coolwarm',
    center=0, linewidths=1, vmin=-1, vmax=1, 
    ax=ax
)
ax.set_title('因子分析\n（回転なし）')

# 因子分析（回転後）
ax = axes[2]
sns.heatmap(
    fa_rotated_loadings_df, 
    annot=True, fmt='.2f', cmap='coolwarm',
    center=0, linewidths=1, vmin=-1, vmax=1, 
    ax=ax
)
ax.set_title('因子分析\n（バリマックス回転後）')

plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

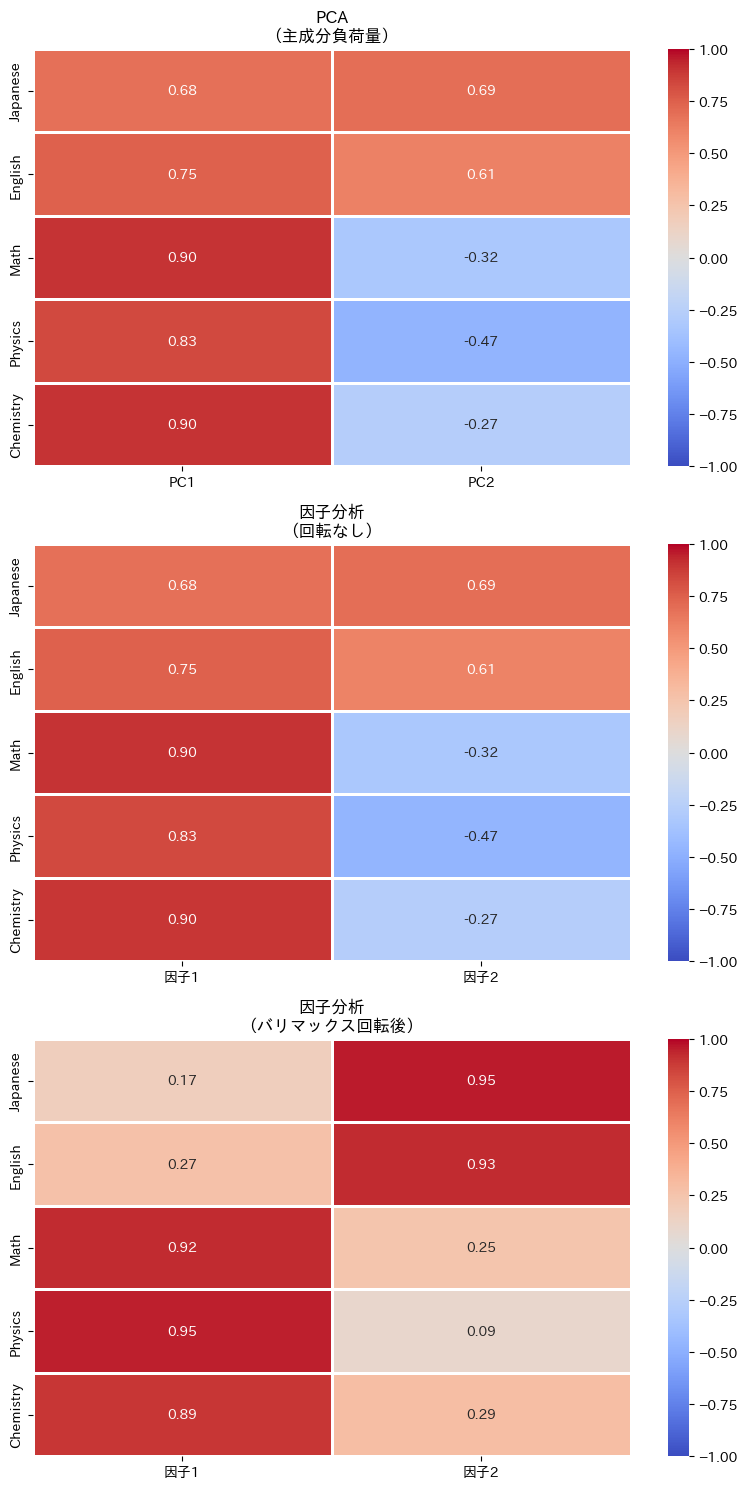
この3つのヒートマップを比較すると、因子分析（回転後）では「国語・英語が因子1に」「数学・物理・化学が因子2に」というように、元の因子構造がより明確に復元されていることがわかります。

 

　因子得点を計算する

因子得点とは、各サンプル（今回の例では各生徒）が各因子をどれくらい持っているかを表す数値です。

PCAの主成分得点は一意に計算できましたが、因子分析の因子得点は推定値です。因子は直接観測できない潜在変数なので、データから「おそらくこれくらいだろう」と推定するのです。

FactorAnalyzerでは、transformメソッドを使って因子得点を計算できます。

 

まず、回転なしの因子得点です。

# 因子得点を計算（回転なし）
factor_scores_no_rotation = fa.transform(X_scaled)

# 因子得点をデータフレームに変換（回転なし）
factor_scores_no_rotation_df = pd.DataFrame(
    factor_scores_no_rotation,
    columns=['因子1', '因子2']
)

print("=== 因子得点（回転なし、最初の5サンプル） ===")
print(factor_scores_no_rotation_df.head().round(3))

 

以下、実行結果です。

=== 因子得点（回転なし、最初の5サンプル） ===
因子1 因子2
0 0.702 -0.164
1 0.170 -0.667
2 1.297 0.181
3 1.760 1.155
4 -1.284 0.660

 

次に、回転ありの因子得点です。

# 因子得点を計算（回転なし）
factor_scores_no_rotation = fa.transform(X_scaled)

# 因子得点をデータフレームに変換（回転なし）
factor_scores_no_rotation_df = pd.DataFrame(
    factor_scores_no_rotation,
    columns=['因子1', '因子2']
)

print("=== 因子得点（回転あり、最初の5サンプル） ===")
print(factor_scores_rotated_df.head().round(3))

 

以下、実行結果です。

=== 因子得点（回転あり、最初の5サンプル） ===
     因子1    因子2
0  0.670  0.266
1  0.520 -0.451
2  0.962  0.889
3  0.786  1.953
4 -1.431 -0.190

 

この結果は、最初の5人の生徒がそれぞれの因子をどれくらい持っているかを示しています。

たとえば、4番目の生徒（インデックス3）は因子1（数理能力）が0.786、因子2（言語能力）が1.953と高く、両方の能力が平均より高いことがわかります。

因子得点は、元の5変数を2つの因子に要約したものです。これにより、各生徒の「言語能力タイプ」「数理能力タイプ」といった特徴を把握しやすくなります。

 

　因子得点で散布図を作成

因子得点で散布図を描いてみます。横軸が因子1、縦軸が因子2です。

fig, axes = plt.subplots(2, 1, figsize=(10, 16))

# 因子分析（回転なし）の因子得点をプロット
axes[0].scatter(
    fa.transform(X_scaled)[:, 0], # 因子1の得点
    fa.transform(X_scaled)[:, 1], # 因子2の得点
    c='b', s=80, alpha=0.7
)
axes[0].set_xlabel('因子1')
axes[0].set_ylabel('因子2')
axes[0].set_title('因子分析: 因子得点の散布図（回転なし）')
axes[0].grid(True, alpha=0.3)
axes[0].axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
axes[0].axvline(x=0, color='gray', linestyle='-', linewidth=0.5)

# 因子分析（バリマックス回転後）の因子得点をプロット
axes[1].scatter(
    fa_rotated.transform(X_scaled)[:, 0], # 因子1の得点
    fa_rotated.transform(X_scaled)[:, 1], # 因子2の得点
    c='b', s=80, alpha=0.7
)
axes[1].set_xlabel('因子1')
axes[1].set_ylabel('因子2')
axes[1].set_title('因子分析: 因子得点の散布図（バリマックス回転後）')
axes[1].grid(True, alpha=0.3)
axes[1].axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
axes[1].axvline(x=0, color='gray', linestyle='-', linewidth=0.5)

plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

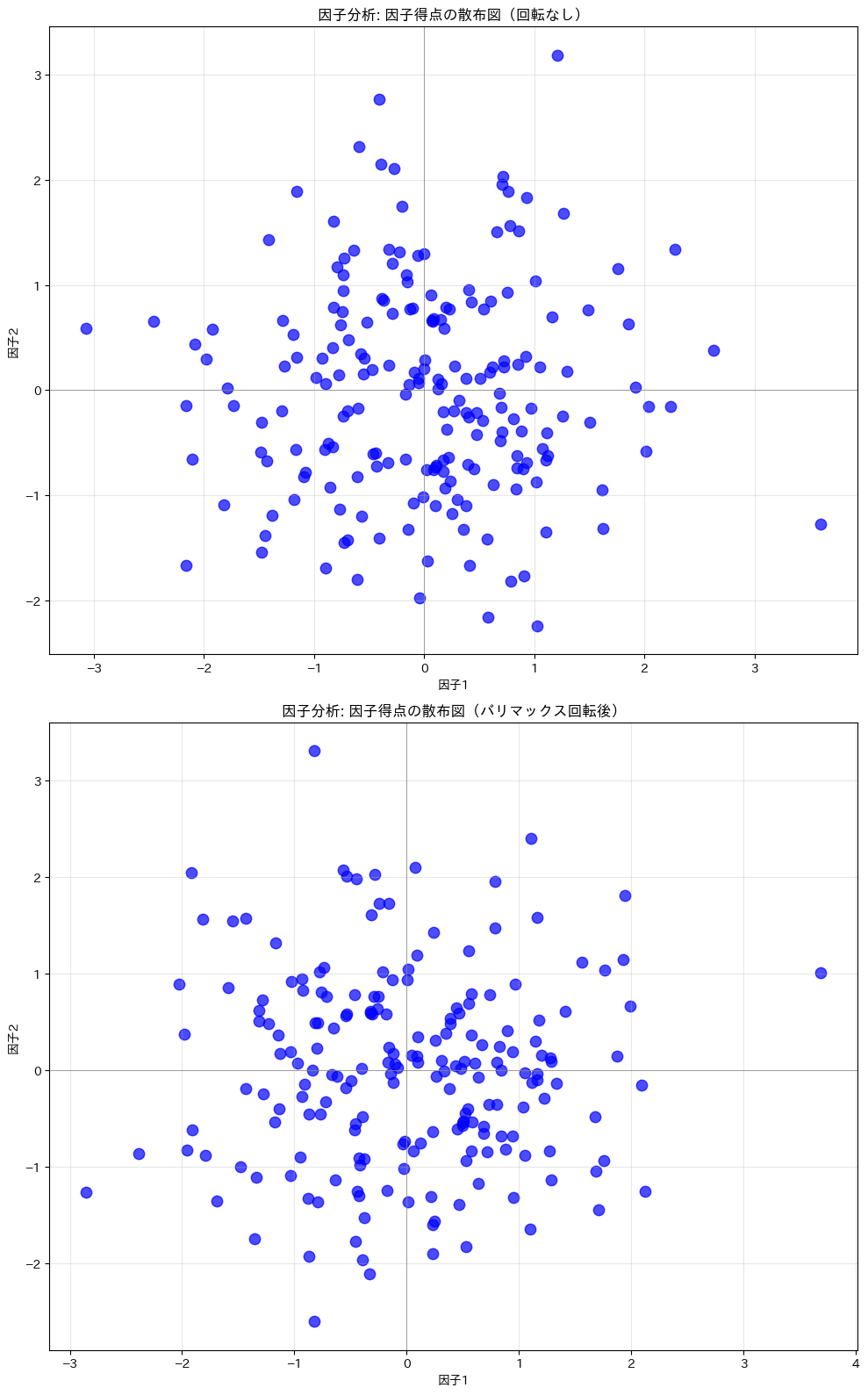
　バイプロットを作成

因子負荷量もともにプロットします。

fig, axes = plt.subplots(2, 1, figsize=(10, 16))

# 矢印の長さを調整するためのスケールファクター
scale_factor = 3

# 因子分析（回転なし）の因子得点をプロット
axes[0].scatter(
    fa.transform(X_scaled)[:, 0], # 因子1の得点
    fa.transform(X_scaled)[:, 1], # 因子2の得点
    c='b', s=80, alpha=0.7
)
axes[0].set_xlabel('因子1')
axes[0].set_ylabel('因子2')
axes[0].set_title('因子分析: 因子得点のバイプロット（回転なし）')
axes[0].grid(True, alpha=0.3)
axes[0].axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
axes[0].axvline(x=0, color='gray', linestyle='-', linewidth=0.5)

# 因子負荷量をプロット
fa_loadings_corrected = fa_loadings_df * scale_factor
for i in range(fa_loadings_corrected.shape[0]):
    axes[0].arrow(
        0, 0, 
        fa_loadings_corrected.iloc[i, 0], 
        fa_loadings_corrected.iloc[i, 1],
        color='red', alpha=0.5, head_width=0.05
    )
    axes[0].text(
        fa_loadings_corrected.iloc[i, 0] * 1.05, 
        fa_loadings_corrected.iloc[i, 1] * 1.05,
        fa_loadings_corrected.index[i], 
        color='red'
    )

# 因子分析（バリマックス回転後）の因子得点をプロット
axes[1].scatter(
    fa_rotated.transform(X_scaled)[:, 0], # 因子1の得点
    fa_rotated.transform(X_scaled)[:, 1], # 因子2の得点
    c='b', s=80, alpha=0.7
)
axes[1].set_xlabel('因子1')
axes[1].set_ylabel('因子2')
axes[1].set_title('因子分析: 因子得点のバイプロット（バリマックス回転後）')
axes[1].grid(True, alpha=0.3)
axes[1].axhline(y=0, color='gray', linestyle='-', linewidth=0.5)
axes[1].axvline(x=0, color='gray', linestyle='-', linewidth=0.5)

# 因子負荷量をプロット（バリマックス回転後）
fa_rotated_loadings_corrected = fa_rotated_loadings_df * scale_factor
for i in range(fa_rotated_loadings_corrected.shape[0]):
    axes[1].arrow(
        0, 0, 
        fa_rotated_loadings_corrected.iloc[i, 0], 
        fa_rotated_loadings_corrected.iloc[i, 1],
        color='red', alpha=0.5, head_width=0.05
    )
    axes[1].text(
        fa_rotated_loadings_corrected.iloc[i, 0] * 1.05, 
        fa_rotated_loadings_corrected.iloc[i, 1] * 1.05,
        fa_rotated_loadings_corrected.index[i], 
        color='red'
    )

plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

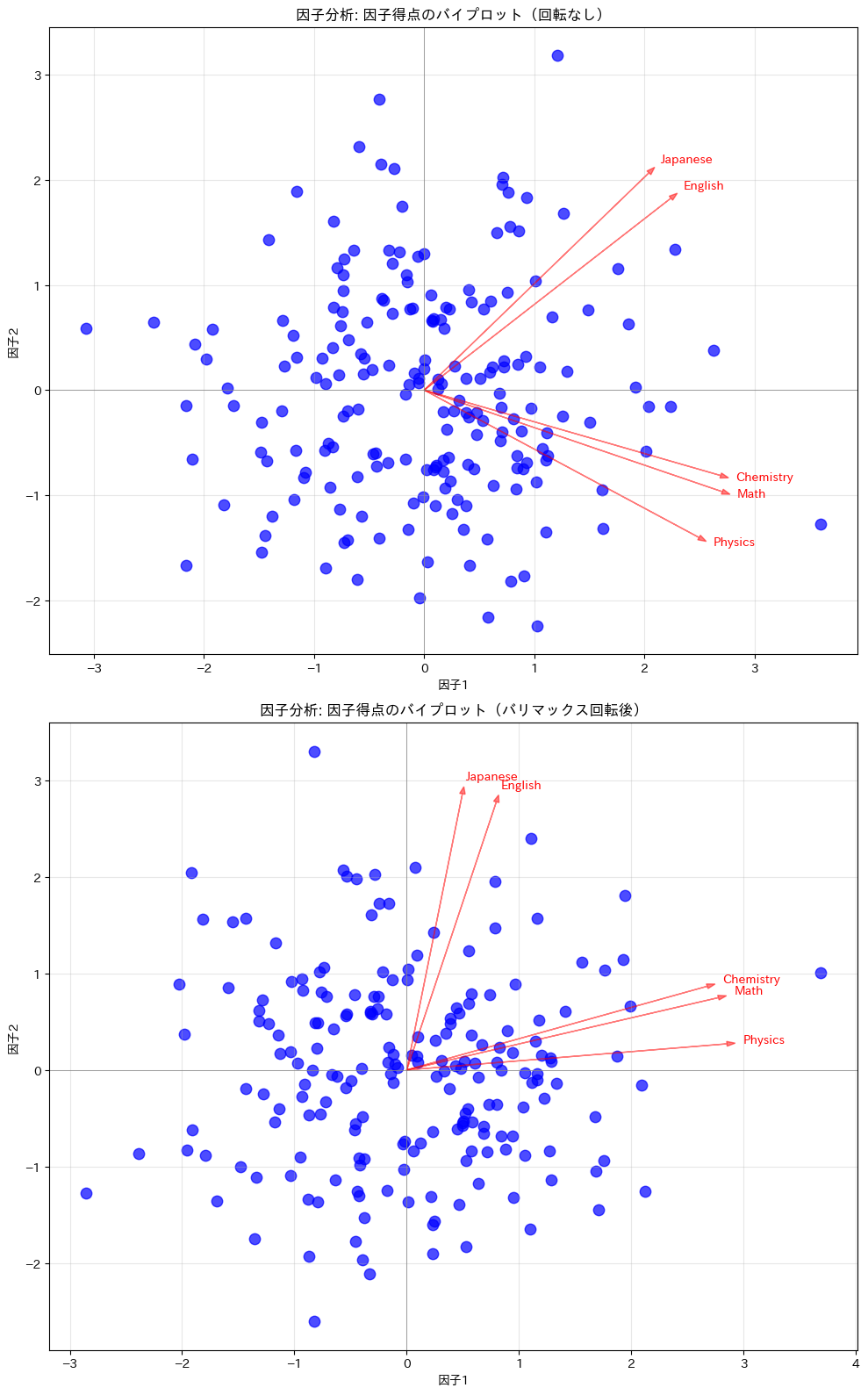
　独自性（uniqueness）

因子分析にあってPCAにない重要な概念が独自性（uniqueness）です。

因子分析のモデル\mathbf{x} = \Lambda \mathbf{F} + \boldsymbol{\varepsilon}において、\boldsymbol{\varepsilon}は因子では説明できない各変数固有の成分です。

この独自成分\boldsymbol{\varepsilon}の分散が「独自性」であり、1から独自性を引いたものが「共通性（communality）」です。

  • 共通性: 因子によって説明される分散の割合
  • 独自性: 因子では説明できない、その変数固有の分散の割合
# 共通性を計算
communalities = fa_rotated.get_communalities()
# 独自性を計算
uniquenesses = fa_rotated.get_uniquenesses()

# 共通性と独自性をデータフレームにまとめる
result_df = pd.DataFrame({
    '共通性': communalities,
    '独自性': uniquenesses
}, index=grades_data.columns)

print("=== 共通性と独自性 ===")
print(result_df.round(3))

 

以下、実行結果です。

=== 共通性と独自性 ===
             共通性    独自性
Japanese   0.938  0.062
English    0.928  0.072
Math       0.918  0.082
Physics    0.911  0.089
Chemistry  0.879  0.121

 

共通性が高い変数は因子によってよく説明され、独自性が高い変数は因子では説明しきれない固有の成分を多く持っています。

PCAでは、すべての分散を主成分で説明しようとします。

因子分析では、共通因子で説明できる部分と、説明できない独自成分を区別します。

これが両者の大きな違いの一つです。

 

　真の因子との相関を比較する

今回はデータを自分で生成したので、「真の因子」がわかっています。

推定された成分・因子が真の因子とどれだけ一致しているか確認してみましょう。

# 因子得点を計算
fa_scores = fa_rotated.transform(X_scaled)

# 真の因子との相関を計算
print("=== 推定結果と真の因子の相関 ===")
print()
print("【PCA】")
print(f"  PC1 vs 言語能力: {np.corrcoef(pca_scores[:, 0], F_言語能力)[0,1]:.3f}")
print(f"  PC1 vs 数理能力: {np.corrcoef(pca_scores[:, 0], F_数理能力)[0,1]:.3f}")
print(f"  PC2 vs 言語能力: {np.corrcoef(pca_scores[:, 1], F_言語能力)[0,1]:.3f}")
print(f"  PC2 vs 数理能力: {np.corrcoef(pca_scores[:, 1], F_数理能力)[0,1]:.3f}")
print()
print("【因子分析（回転後）】")
print(f"  因子1 vs 言語能力: {np.corrcoef(fa_scores[:, 0], F_言語能力)[0,1]:.3f}")
print(f"  因子1 vs 数理能力: {np.corrcoef(fa_scores[:, 0], F_数理能力)[0,1]:.3f}")
print(f"  因子2 vs 言語能力: {np.corrcoef(fa_scores[:, 1], F_言語能力)[0,1]:.3f}")
print(f"  因子2 vs 数理能力: {np.corrcoef(fa_scores[:, 1], F_数理能力)[0,1]:.3f}")

 

以下、実行結果です。

=== 推定結果と真の因子の相関 ===

【PCA】
  PC1 vs 言語能力: 0.602
  PC1 vs 数理能力: 0.818
  PC2 vs 言語能力: 0.732
  PC2 vs 数理能力: -0.511

【因子分析（回転後）】
  因子1 vs 言語能力: 0.077
  因子1 vs 数理能力: 0.963
  因子2 vs 言語能力: 0.945
  因子2 vs 数理能力: 0.047

 

因子分析（回転後）の因子が真の因子とより高い相関を示すことがわかるはずです。

これは、因子分析が「潜在因子を復元する」という目的に適していることを示しています。

 

　スクリープロットを作成

特定の主成分数を指定せずに、すべての主成分を抽出することもできます。

すべての主成分を抽出しスクリープロットを作成します。

# 全因子を抽出する因子分析を実行
fa_full = FactorAnalyzer(
    n_factors=5, 
    rotation=None, 
    method='principal'
)
fa_full.fit(X_scaled)

# 固有値を取得
fa_eigenvalues, _ = fa_full.get_eigenvalues()

# スクリープロットを作成
fig, axes = plt.subplots(2, 1, figsize=(10, 10)) 

# 上: 固有値
ax = axes[0]
x = np.arange(1, len(fa_eigenvalues) + 1)
ax.bar(x, fa_eigenvalues)
ax.set_xlabel('因子')
ax.set_ylabel('固有値（分散）')
ax.set_title('スクリープロット（因子分析）')
ax.set_xticks(x)

# 下: 累積寄与率
ax = axes[1]
cumsum = np.cumsum(fa_eigenvalues) / np.sum(fa_eigenvalues) * 100
ax.bar(
    x, fa_eigenvalues / np.sum(fa_eigenvalues) * 100, 
    label='寄与率'
)
ax.plot(
    x, cumsum, 
    'ro-', markersize=10, linewidth=2, 
    label='累積寄与率'
)
ax.axhline(y=80, color='green', linestyle='--', label='80%ライン')
ax.set_xlabel('因子')
ax.set_ylabel('寄与率 (%)')
ax.set_title('寄与率と累積寄与率（因子分析）')
ax.set_xticks(x)
ax.legend(loc='center right')

plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

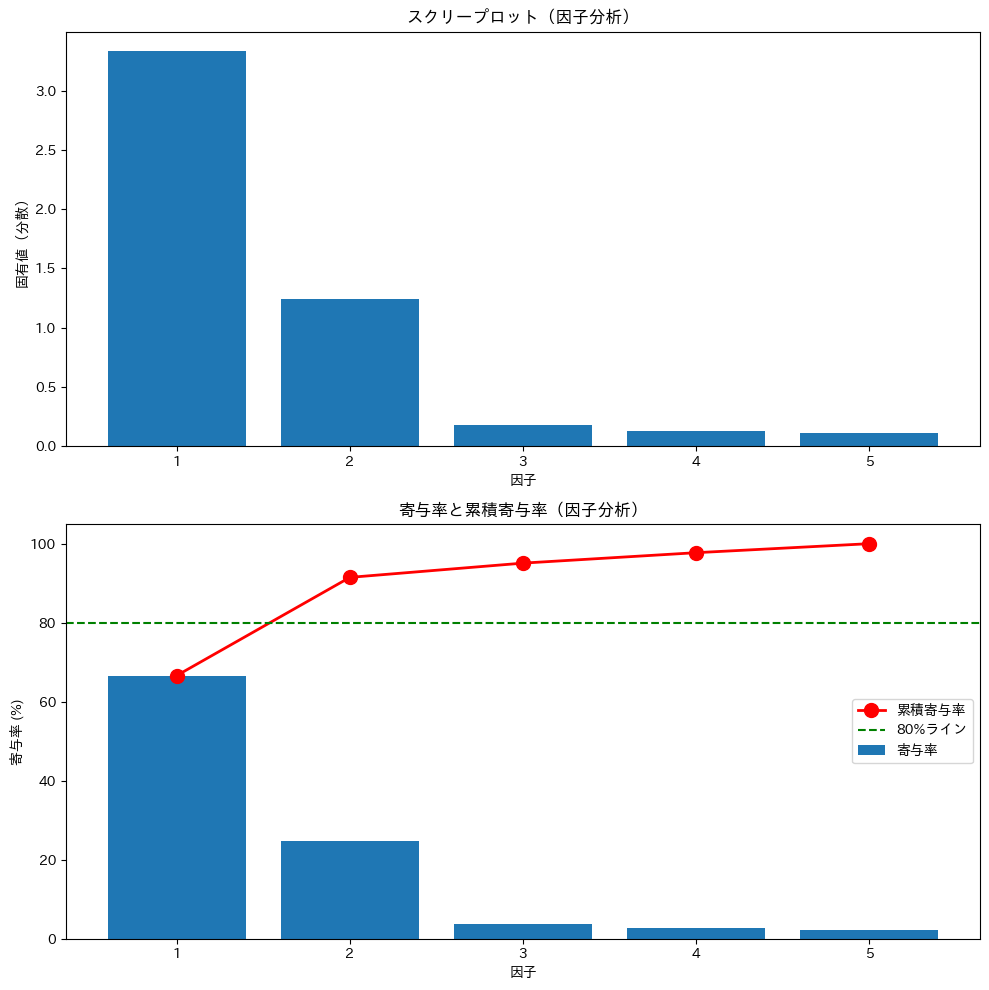
このグラフを使って、適切な因子分析数を判断できます。

 

　因子数の決め方と因子分析の流れ

実際の分析では、最初から因子数がわかっているわけではありません。

今回はデータを自分で生成したので「2因子」とわかっていましたが、実務では因子数も探索的に決める必要があります。

因子分析の典型的な流れは次のようになります。

 

　　ステップ1：まず全因子を抽出してスクリープロットを作成する

最初に、変数と同じ数の因子を抽出します。今回の例では5変数なので、n_factors=5として因子分析を実行し、すべての固有値を確認します。

この段階では回転は適用しません（rotation=None）。固有値は回転の前に計算されるため、スクリープロットを作成するだけなら回転は不要です。

 

　　ステップ2：因子数を決定する

スクリープロットと以下の基準を総合的に見て、因子数を決めます。

カイザー基準では、固有値が1以上の因子のみを採用します。固有値が1未満の因子は、元の変数1個分の情報も持たないと考えるためです。ただし、この基準はやや厳しくなりがちなので、他の基準と併用するのが一般的です。

肘法（エルボー法）では、スクリープロットで固有値が急に小さくなる「肘」の位置で打ち切ります。今回のグラフでは、第2因子と第3因子の間で傾きが急に緩やかになっているため、2因子が適切と判断できます。

累積寄与率では、抽出した因子で全体の分散の何%を説明できるかを見ます。70〜80%程度を目安にすることが多いですが、分析の目的によって変わります。

また、理論的な根拠も重要です。今回のように「言語能力と数理能力という2つの潜在的な能力があるはずだ」という仮説があれば、それも因子数の決定に影響します。

 

　　ステップ3：決定した因子数で因子分析を再実行する

因子数が決まったら、その数をn_factorsに指定して因子分析を実行します。このとき、回転（通常はバリマックス回転）も適用します。

 

　　ステップ4：因子負荷量を確認して因子を解釈・命名する

回転後の因子負荷量を見て、各因子がどのような変数と強く関係しているかを確認します。一般的に、負荷量の絶対値が0.4以上（厳密には0.5以上とすることも）の変数に注目すると、因子の意味を解釈しやすくなります。

今回の結果では、因子1は数学・物理・化学に高い負荷を持ち、因子2は国語・英語に高い負荷を持っていました。これにより「因子1＝数理能力」「因子2＝言語能力」と命名できます。

 

　　ステップ5：因子得点を計算して活用する

必要に応じて因子得点を計算します。因子得点は、各サンプルがそれぞれの因子をどれくらい持っているかを表す数値です。

因子得点は、サンプルの特徴を把握したり、クラスタリングや回帰分析など後続の分析に利用したりできます。たとえば、「この生徒は数理能力が高く言語能力は平均的」といった個人の特徴を数値で表現できるようになります。

因子分析は探索的な手法なので、一発で最適な解が得られるとは限りません。因子数や回転方法を変えながら、解釈しやすく意味のある結果を探っていくことも重要です。

 

PCAと因子分析の使い分け方

　PCAを選ぶべき場面

PCAは、データの次元を減らして可視化したい場合に適しています。

また、機械学習の前処理として特徴量を圧縮したい場合や、多重共線性を解消したい場合にもPCAが有効です。

PCAは、潜在的な構造よりも「データの分散をできるだけ保存する」ことを重視する手法です。

 

　因子分析を選ぶべき場面

因子分析は、観測変数の背後にある潜在的な構造を理解したい場合に適しています。

心理学のアンケート調査で「性格特性」を抽出したい場合や、社会科学で「潜在的な態度」を測定したい場合など、理論的に意味のある因子を想定できる場面で力を発揮します。

 

　判断のポイント

判断に迷ったときは、「因子の解釈が重要か」を考えてみてください。

潜在的な概念（能力、態度、特性など）の存在を仮定し、それを測定したいなら因子分析が適しています。

単にデータを圧縮・可視化したいだけなら、PCAで十分です。

 

まとめ

この第5回では、PCAと因子分析の違いを学びました。

PCAの特徴として、統計モデルを仮定しない記述的手法であること、データの分散を最大限保存する方向を見つけること、主成分得点は一意に計算できること、そして次元削減・可視化・前処理に適していることが挙げられます。

因子分析の特徴として、データの生成過程を仮定する統計モデル（\mathbf{x} = \Lambda \mathbf{F} + \boldsymbol{\varepsilon}）であること、潜在因子が観測変数を生み出すと考えること、因子得点は推定値であり一意でないこと、回転によって解釈しやすい解が得られること、独自性の概念があること、そして潜在構造の理解・心理測定に適していることが挙げられます。

矢印の向きの違いを覚えておくと、両者の違いを理解しやすくなります。PCAは「データ → 要約」、因子分析は「潜在因子 → データ」という向きで考えます。