前回は「似ている」を距離で測る方法を学びました。
今回は、その距離を使って実際にデータをグループ分けしていきます。
ここで、あなたの友人関係を思い浮かべてみてください。
高校時代の友人、大学時代の友人、職場の同僚、趣味のサークル仲間…。これらは自然といくつかのグループに分かれているでしょう。
さらに細かく見ると、高校時代の友人の中にも「部活仲間」と「クラスメイト」がいるかもしれません。
職場の同僚も「同じプロジェクトのメンバー」と「別部署の知り合い」に分かれるでしょう。
このように、大きなグループの中に小さなグループがあり、その中にさらに小さなグループがあるという構造を「階層構造」と呼びます。
生物の分類(界→門→綱→目→科→属→種)や、会社の組織図を思い浮かべるとわかりやすいかもしれません。
今回学ぶ階層的クラスタリングは、まさにこのような階層構造を発見する手法です。
そして、その構造を美しく表現するのが樹形図(デンドログラム)です。
Contents
- 階層的クラスタリングの考え方
- 「最も似た2つをまとめる」を繰り返す
- シンプルな例で理解しよう
- まずはPythonの準備
- 5つの都市データを用意する
- 標準化を忘れずに
- 階層的クラスタリングを実行する
- デンドログラムを描いてみよう
- 基本のデンドログラム
- デンドログラムの読み方
- クラスタラベルを取得する
- クラスタの特徴を数値で確認
- 散布図で視覚的に確認
- 結合方法(リンケージ法)を理解しよう
- なぜ結合方法が重要なのか
- 代表的な結合方法
- ウォード法(Ward’s method)
- 最短距離法(Single linkage)
- 最長距離法(Complete linkage)
- 群平均法(Average linkage)
- 結合方法の違いを視覚的に比較する
- どの結合方法を選ぶべきか
- 階層的クラスタリングの長所と短所
- まとめ
階層的クラスタリングの考え方
「最も似た2つをまとめる」を繰り返す
階層的クラスタリングのアイデアは驚くほどシンプルです。
- STEP 1 – 最初は、すべてのデータが個別のグループ(1人1グループ)
- STEP 2 – 最も距離が近い2つを見つけて、1つのグループにまとめる
- STEP 3 – グループ間の距離を再計算する
- 以後 2〜3 を繰り返し、最終的にすべてが1つのグループになるまで続ける
たとえば、5人の友人A、B、C、D、Eがいるとします。
AとBが最も仲が良い(距離が近い)なら、まずAとBを1つのグループにまとめます。
次に、「A-Bグループ」「C」「D」「E」の中で最も近い組み合わせを探し、またまとめる…… という作業を繰り返すのです。
この過程を逆さまの木のような図で表現したものがデンドログラムです。
シンプルな例で理解しよう
まずはPythonの準備
今回は、scipy の階層的クラスタリング機能を使います。dendrogramは樹形図を描く関数、linkageはクラスタリングを実行する関数です。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import japanize_matplotlib # 階層的クラスタリングのためのライブラリ from scipy.cluster.hierarchy import dendrogram, linkage, fcluster from scipy.spatial.distance import pdist # 標準化のためのライブラリ from sklearn.preprocessing import StandardScaler
5つの都市データを用意する
まずは小さなデータで階層的クラスタリングの動きを確認しましょう。
5つの都市の「年間平均気温」と「年間降水量」のデータを使います。これはあくまでも仮のデータです。
# 10都市の気候データ(気象庁のデータを簡略化)
cities = pd.DataFrame({
'都市': ['札幌', '仙台', '東京', '名古屋', '大阪',
'広島', '高松', '福岡', '鹿児島', '那覇'],
'平均気温': [9.2, 13.0, 16.3, 16.5, 17.1,
16.8, 16.8, 17.5, 19.2, 23.5],
'年間降水量': [1110, 1250, 1530, 1535, 1280,
1540, 1080, 1690, 2270, 2040],
'日照時間': [1740, 1850, 1920, 2120, 2050,
2040, 2100, 1900, 1970, 1800]
})
print(cities)
以下、実行結果です。
都市 平均気温 年間降水量 日照時間 0 札幌 9.2 1110 1740 1 仙台 13.0 1250 1850 2 東京 16.3 1530 1920 3 名古屋 16.5 1535 2120 4 大阪 17.1 1280 2050 5 広島 16.8 1540 2040 6 高松 16.8 1080 2100 7 福岡 17.5 1690 1900 8 鹿児島 19.2 2270 1970 9 那覇 23.5 2040 1800
東京・大阪・福岡は気温が似ていて、札幌は寒く、那覇は暑いことがわかります。
階層的クラスタリングでこの「似ている構造」を発見できるか試してみましょう。
標準化を忘れずに
前回学んだように、スケールの異なる変数を扱う場合は標準化が必要です。
気温は10〜25℃程度、降水量は1000〜2000mm程度とスケールが大きく異なるので、まず標準化します。
# 数値データを抽出
X = cities[['平均気温', '年間降水量']].values
# 標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print("標準化後のデータ:")
print(
pd.DataFrame(
X_scaled,
columns=['平均気温(標準化)', '年間降水量(標準化)'],
index=cities['都市']
)
)
以下、実行結果です。
標準化後のデータ:
平均気温(標準化) 年間降水量(標準化)
都市
札幌 -2.104320 -1.148555
仙台 -1.022261 -0.767969
東京 -0.082578 -0.006796
名古屋 -0.025628 0.006796
大阪 0.145224 -0.686414
広島 0.059798 0.020389
高松 0.059798 -1.230109
福岡 0.259125 0.428159
鹿児島 0.743204 2.004874
那覇 1.967639 1.379625
標準化後は、両方の変数が同じくらいの範囲(およそ-2〜+2)に収まっています。これで公平に距離を計算できます。
階層的クラスタリングを実行する
いよいよ階層的クラスタリングを実行します。linkage関数がその処理を行います。
# 階層的クラスタリングを実行(ウォード法を使用)
Z = linkage(X_scaled, method='ward')
print("クラスタリング結果(linkage matrix):")
print(Z)
以下、実行結果です。
クラスタリング結果(linkage matrix): [[ 2. 3. 0.05855006 2. ] [ 5. 10. 0.13361198 3. ] [ 4. 6. 0.55036476 2. ] [ 7. 11. 0.61641967 4. ] [ 0. 1. 1.14703872 2. ] [ 8. 9. 1.37483741 2. ] [12. 13. 1.74984697 6. ] [14. 16. 3.08603757 8. ] [15. 17. 4.8481313 10. ]]
linkage関数の戻り値Zは、クラスタリングの過程を記録した行列です。
各行は「どの2つのクラスタが、どの距離で、何個のデータを含むグループに結合されたか」を表しています。
この数値を見ても直感的にはわかりにくいですよね。そこで登場するのがデンドログラムです。
デンドログラムを描いてみよう
基本のデンドログラム
デンドログラムは、クラスタリングの過程を視覚化した図です。
縦軸は「距離」を表し、下から上に向かってクラスタが結合していく様子を表現しています。
# デンドログラムを描画
plt.figure(figsize=(10, 6))
dendrogram(
Z,
labels=cities['都市'].values,
leaf_font_size=12
)
plt.title('City Climate Dendrogram')
plt.xlabel('City')
plt.ylabel('Distance')
plt.tight_layout()
plt.show()
以下、実行結果です。
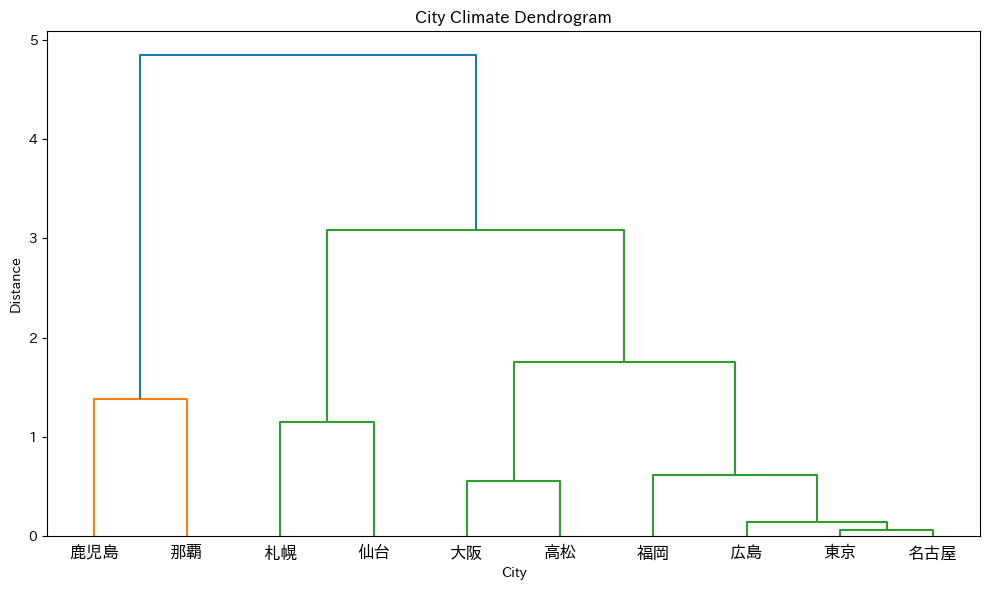
このグラフを見ると、クラスタリングの過程が一目でわかります。
下の方で結合しているペアほど「似ている」ということです。
東京・大阪・福岡が近い位置で結合し、札幌と那覇はそれぞれ離れた位置で合流しています。
デンドログラムの読み方
デンドログラムを正しく読み解くためのポイントを整理しましょう。
縦軸(高さ)は距離を表す
- 下の方で結合している=距離が近い=似ている
- 上の方で結合している=距離が遠い=あまり似ていない
横軸は順番に意味がない
横軸の並び順は見やすさのために調整されているだけで、「左にあるから似ている」というわけではありません。重要なのは「どこで枝分かれしているか」です。
水平線を引いてクラスタを決める
任意の高さで水平線を引くと、その線と交差する枝の数がクラスタ数になります。
線を引く位置を変えることで、細かい分類から大まかな分類まで自由に調整できます。
では、線を引いてみます。
# 水平線を引いてクラスタ数を確認
plt.figure(figsize=(10, 6))
dendrogram(Z, labels=cities['都市'].values, leaf_font_size=12)
plt.axhline(y=2.5, color='r', linestyle='--', label='3 clusters')
plt.axhline(y=4, color='g', linestyle='--', label='2 clusters')
plt.title('Dendrogram with Cluster Thresholds')
plt.xlabel('City')
plt.ylabel('Distance')
plt.legend()
plt.tight_layout()
plt.show()
以下、実行結果です。
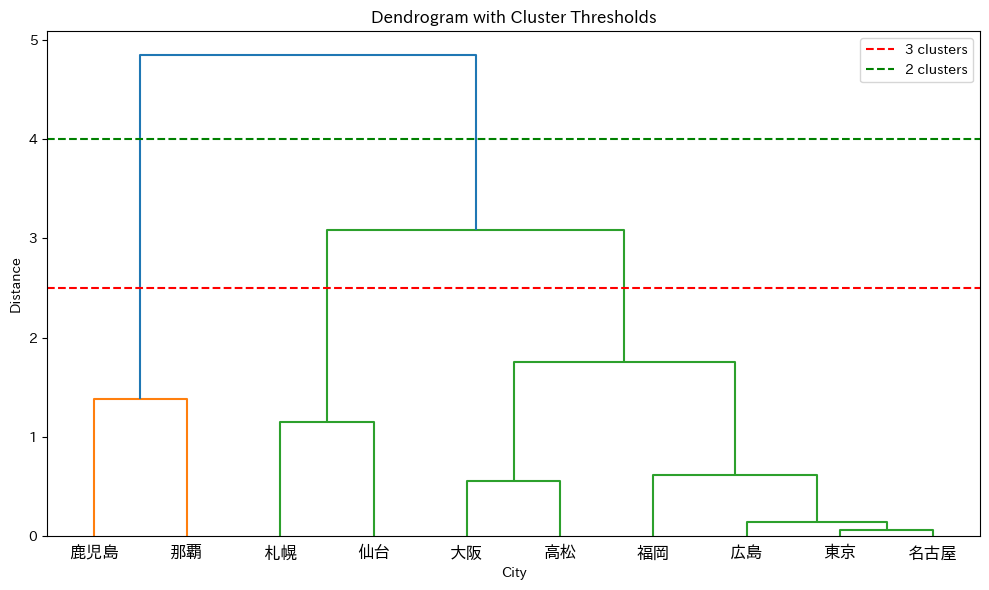
赤い線(距離2)で切ると3つのクラスタ、緑の線(距離3)で切ると2つのクラスタができることがわかります。
クラスタラベルを取得する
デンドログラムを見てクラスタ数を決めたら、各データがどのクラスタに属するかを取得しましょう。fcluster関数を使います。
# 距離2.5で切って、クラスタラベルを取得 clusters = fcluster(Z, t=2.5, criterion='distance') # 結果を確認 cities['クラスタ'] = clusters print(cities)
以下、実行結果です。
都市 平均気温 年間降水量 日照時間 クラスタ 0 札幌 9.2 1110 1740 2 1 仙台 13.0 1250 1850 2 2 東京 16.3 1530 1920 3 3 名古屋 16.5 1535 2120 3 4 大阪 17.1 1280 2050 3 5 広島 16.8 1540 2040 3 6 高松 16.8 1080 2100 3 7 福岡 17.5 1690 1900 3 8 鹿児島 19.2 2270 1970 1 9 那覇 23.5 2040 1800 1
クラスタごとに都市をまとめます。
# クラスタごとに都市を表示
print("=== クラスタリング結果 ===")
for cluster_id in sorted(cities['クラスタ'].unique()):
members = cities[cities['クラスタ'] == cluster_id]['都市'].tolist()
print(f"クラスタ {cluster_id}: {', '.join(members)}")
以下、実行結果です。
=== クラスタリング結果 === クラスタ 1: 鹿児島, 那覇 クラスタ 2: 札幌, 仙台 クラスタ 3: 東京, 名古屋, 大阪, 広島, 高松, 福岡
どのような都市がグループ化されたでしょうか?
地理的に近い都市、または気候が似ている都市が同じクラスタに入っています。
クラスタの特徴を数値で確認
各クラスタの平均値を計算して、グループの特徴を把握しましょう。
# クラスタごとの平均値を計算
cluster_means = cities.groupby('クラスタ')[[
'平均気温', '年間降水量', '日照時間'
]].mean()
print("=== クラスタごとの平均値 ===")
print(cluster_means.round(1))
以下、実行結果です。
=== クラスタごとの平均値 ===
平均気温 年間降水量 日照時間
クラスタ
1 21.4 2155.0 1885.0
2 11.1 1180.0 1795.0
3 16.8 1442.5 2021.7
この結果から、各クラスタがどのような気候的特徴を持つか解釈できます。
たとえば「平均気温が低いグループ」「降水量が多いグループ」などの特徴が見えてきます。
散布図で視覚的に確認
2つの変数を選んで散布図を描き、クラスタリングの結果を視覚的に確認しましょう。
plt.figure(figsize=(10, 7))
# クラスタごとに色を変えてプロット
colors = ['#e74c3c', '#3498db', '#2ecc71', '#9b59b6', '#f39c12']
for cluster_id in sorted(cities['クラスタ'].unique()):
mask = cities['クラスタ'] == cluster_id
plt.scatter(
cities.loc[mask, '平均気温'],
cities.loc[mask, '年間降水量'],
c=colors[cluster_id-1],
s=150,
label=f'Cluster {cluster_id}',
alpha=0.7
)
# 都市名をラベル表示
for _, row in cities[mask].iterrows():
plt.annotate(
row['都市'],
(row['平均気温'], row['年間降水量']),
fontsize=10, ha='left', va='bottom'
)
plt.xlabel('Average Temperature (°C)')
plt.ylabel('Annual Precipitation (mm)')
plt.title('Japanese Cities Clustered by Climate')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
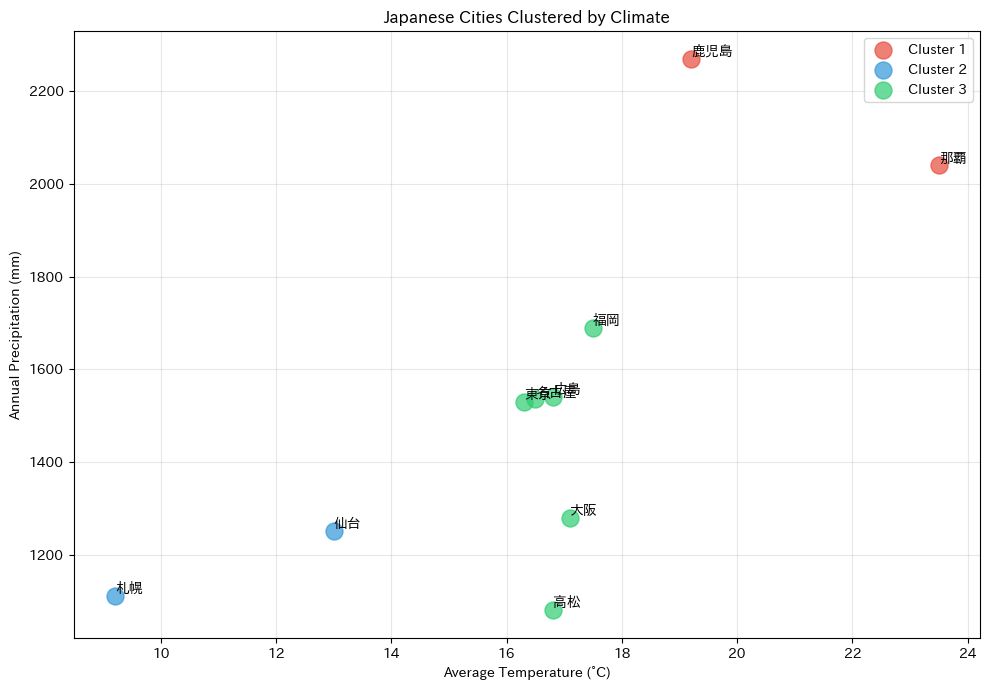
散布図を見ると、同じ色(同じクラスタ)の都市が近くに集まっていることがわかります。
階層的クラスタリングが「似たもの」を正しくグループ化できていることが視覚的に確認できます。
結合方法(リンケージ法)を理解しよう
なぜ結合方法が重要なのか
階層的クラスタリングでは、「最も近い2つのクラスタを順に結合していく」と説明されることが多いですが、ここで重要なのが「クラスタ間の距離をどのように定義するか」という点です。
この距離の定義方法を 結合方法(リンケージ法) と呼びます。
データ点同士の距離であれば、ユークリッド距離などを用いて容易に計算できます。しかし、複数の点からなるクラスタ同士の距離は、一意には定まりません。
なぜなら、クラスタ内には複数の点が存在し、どの点同士を基準にするかによって、距離の値が変わるからです。
たとえば、次のような選択肢が考えられます。
- 最も近い点同士の距離を見るのか
- 最も遠い点同士の距離を見るのか
- すべての点の距離を平均するのか
このように、クラスタ間距離の定義の違いが、結合の順序や最終的なクラスタ構造に大きな影響を与えるため、結合方法の選択は階層的クラスタリングにおいて非常に重要なのです。
代表的な結合方法
階層的クラスタリングでは、「どのクラスタ同士を結合するか」を決める結合方法(linkage)が結果に大きく影響します。
ここでは代表的な4つの結合方法を紹介します。
ウォード法(Ward’s method)
2つのクラスタを結合したときに、クラスタ内分散(平方和)がどれだけ増加するかを基準にします。その増加量が最小になるクラスタの組み合わせを順に結合していきます。
Z_ward = linkage(X_scaled, method='ward')
- クラスタ内のばらつきを抑える方向で結合される
- 比較的サイズが均等で、コンパクトなクラスタができやすい
- 実務・教材ともに最もよく使われる方法の一つ
ウォード法は ユークリッド距離が前提となる点に注意が必要です(距離を変更すると理論的な意味が崩れます)。
最短距離法(Single linkage)
2つのクラスタ間で、最も近い点同士の距離をクラスタ間距離として採用します。
Z_single = linkage(X_scaled, method='single')
- 点と点が「鎖(チェーン)」のようにつながっていく
- 鎖状(チェーン状)のクラスタができやすい
- ノイズや外れ値の影響を受けやすい
「どこか1点でも近ければ結合される」ため、直感的には分かりやすい一方、形の整ったクラスタにはなりにくいことがあります。
最長距離法(Complete linkage)
2つのクラスタ間で、最も遠い点同士の距離をクラスタ間距離として採用します。
Z_complete = linkage(X_scaled, method='complete')
- クラスタ内の最大距離を抑える方向で結合される
- コンパクトで引き締まったクラスタができやすい
- 外れ値に比較的強い
「クラスタの中で一番離れた点同士でも、あまり離れすぎない」ことを重視する方法です。
群平均法(Average linkage)
2つのクラスタ間の、すべての点ペアの距離の平均をクラスタ間距離として採用します。
Z_average = linkage(X_scaled, method='average')
- 最短距離法と最長距離法の中間的な考え方
- 極端な鎖状・極端な分断を避けやすい
- バランスの取れたクラスタになりやすい
どの方法を使うか迷った場合の「無難な選択肢」として使われることも多い結合方法です。
結合方法の違いを視覚的に比較する
4つの結合方法でデンドログラムがどう変わるか、並べて比較してみましょう。
fig, axes = plt.subplots(4, 1, figsize=(10, 16))
# 階層的クラスタリングの方法
methods = [
'ward',
'single',
'complete',
'average'
]
# 樹形図のタイトル
titles = [
'ウォード法 (Ward Method)',
'最短距離法 (Single Linkage)',
'最長距離法 (Complete Linkage)',
'群平均法 (Average Linkage)'
]
# 樹形図を描画
for ax, method, title in zip(axes, methods, titles):
Z_temp = linkage(X_scaled, method=method)
dendrogram(Z_temp, labels=cities['都市'].values, ax=ax, leaf_font_size=10)
ax.set_title(title)
ax.set_xlabel('City')
ax.set_ylabel('Distance')
plt.tight_layout()
plt.show()
以下、実行結果です。
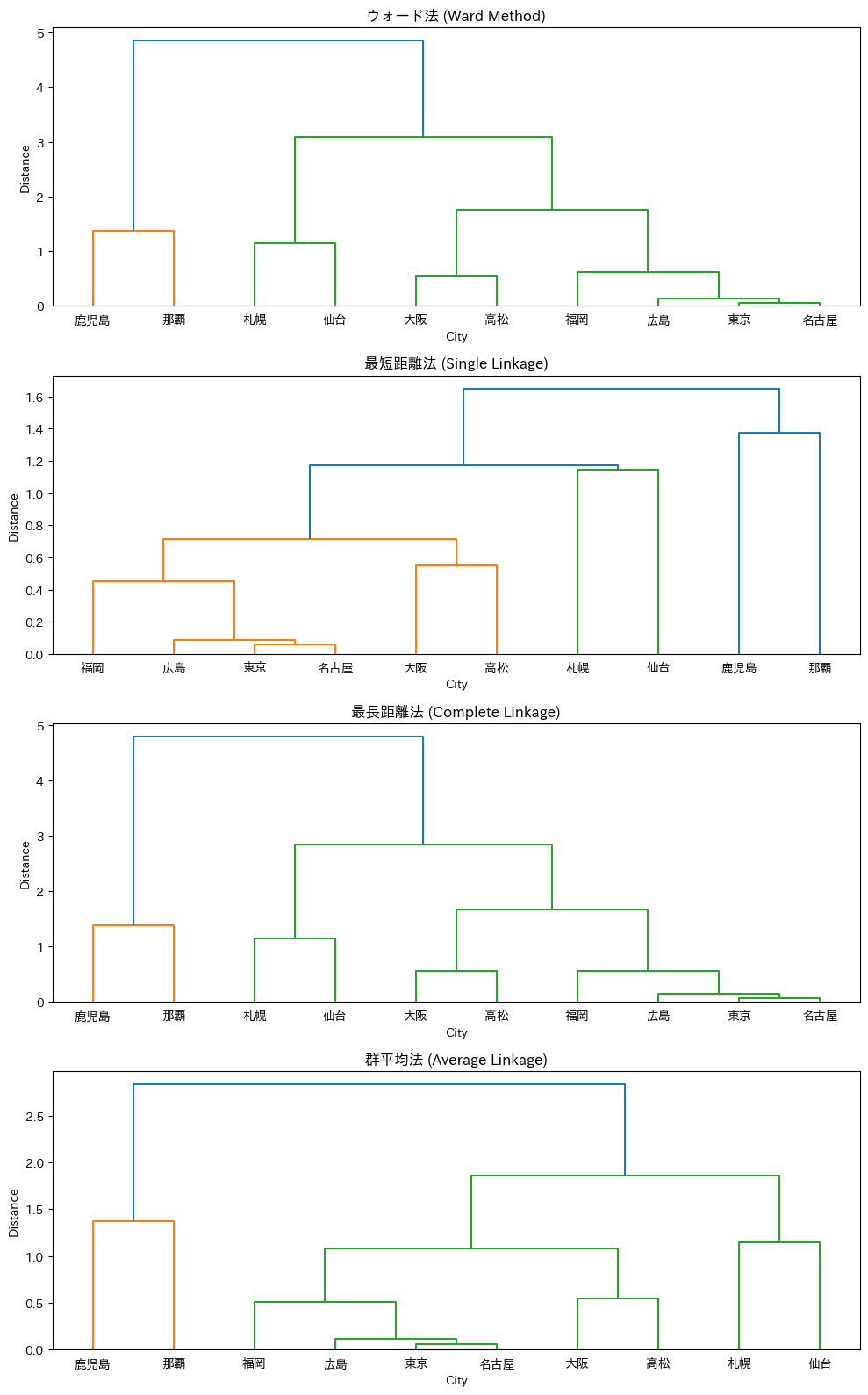
同じデータでも、結合方法によって樹形図の形がかなり異なることがわかります。
特にシングルリンケージ(最短距離法)は、他の方法とは明らかに違う形状になることが多いです。
どの結合方法を選ぶべきか
実務では、ウォード法を最初に試すのがおすすめです。
ウォード法は比較的均等なサイズのクラスタを作りやすく、解釈しやすい結果が得られることが多いためです。
ただし、データの性質や分析の目的によっては、他の方法が適している場合もあります。
- まず試すなら:ウォード法
- 形状を重視・ノイズに強く:最長距離法
- 極端な性質を避けたい:群平均法
- 連結構造を見たい特殊用途:最短距離法
迷ったときは、複数の方法を試して結果を比較し、ビジネス的に解釈しやすいものを選ぶというアプローチも有効です。
階層的クラスタリングの長所と短所
階層的クラスタリングは、データを段階的にまとめていくことで、クラスタ数の決定とデータ構造の理解を同時に行える手法です。
| 区分 | 観点 | 内容 |
|---|---|---|
| 長所 |
クラスタ数を事前に決めなくてよい | デンドログラムを見てから、適切な高さで切ることでクラスタ数を後から決定できる |
| 階層構造が可視化できる | 大きなグループの中に小さなグループが含まれる入れ子構造を直感的に把握できる | |
| 結果の解釈がしやすい | デンドログラムにより、クラスタがどの順で結合されたかを視覚的に説明できる | |
| 短所 |
計算量が多い | データ点間の距離を広範に扱うため、データ数が増えると計算時間・メモリ消費が増大する |
| 一度結合すると戻せない | 凝集型では、一度結合したクラスタを後から分割することはできない | |
| 外れ値に敏感 |
このように、階層的クラスタリングは 「クラスタ数が分からない段階でデータの全体像を把握したい場合」や 「分析結果を可視化し、構造を説明したい場合」に非常に有効です。
一方で、計算量や外れ値への感度といった制約があるため、大規模データや高速処理が求められる場面では、K-means 法などの非階層的クラスタリング手法と使い分けることが重要になります。
まとめ
今回は、「最も近い2つをまとめる」を繰り返すシンプルなアルゴリズムである、階層型クラスター分析を紹介しました。
その過程をデンドログラム(樹形図)で可視化できるため、非常に分かりやすいのが特徴です。縦軸は距離を表し、下で結合しているほど「似ている」。水平線を引く位置でクラスタ数を調整できます。
ただし、幾つかのクラスターの結合方法(リンケージ法)があり、適切なものを選ぶ必要があるます。その中で、ウォード法が最も一般的でおすすめ。最短距離法、最長距離法、群平均法など、データの性質に応じて使い分けます。
次回は、大規模データにも対応できるK-means法(非階層的クラスタリング手法)を紹介します。

