友人から「最近のテストどうだった?」と聞かれたとき、あなたはどう答えますか?
「数学85点、英語72点、物理78点、化学80点だったよ」と全科目を列挙する人は少ないでしょう。
多くの人は「だいたい80点くらいかな」と答えるはずです。
この「だいたい80点くらい」という答え方、実はすでに統計学をやっています。
複数のデータを一つの数字で代表させる。これが統計学の出発点です。
今回は、データを代表する値(代表値)の中でも最も基本的な「平均」「中央値」「最頻値」の3つを、Pythonで手を動かしながら学んでいきます。
Contents
平均(Mean):すべてを足して、個数で割る
平均の直感的な意味
5人の学生のテストの点数が以下だったとします。
- Aさん:72点
- Bさん:85点
- Cさん:68点
- Dさん:90点
- Eさん:75点
この5人の「典型的な成績」を一つの数字で表すとしたら?
全員の点数を合計して、人数で割ればいいですね。これが平均です。
まずはPythonで計算してみよう
5人のテストの点数データを作成し、中身を確認します。len() はデータの個数を返す関数です。
以下、コードです。
import numpy as np
# 5人のテストの点数
scores = np.array([72, 85, 68, 90, 75])
print("テストの点数:", scores)
print(f"人数: {len(scores)}人")
以下、実行結果です。
テストの点数: [72 85 68 90 75] 人数: 5人
平均を「手計算」の手順で求めます。まず合計を出し、次に人数で割ります。
以下、コードです。
# ステップ1:すべてのデータを合計する
合計 = np.sum(scores)
print(f"合計: {合計}点")
# ステップ2:データの個数で割る
平均 = 合計 / len(scores)
print(f"平均: {平均}点")
以下、実行結果です。
合計: 390点 平均: 78.0点
合計が390点、平均が78点と計算されます。
「5人の成績を代表する値は78点程度」という意味になります。
78点より上の人もいれば下の人もいますが、全体の「重心」が78点ということです。
平均の数式
数式で書くと、n 個のデータ x_1, x_2, \ldots, x_n の平均 \bar{x}(エックスバーと読みます)は、次のようになります。
$$
\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i = \frac{x_1 + x_2 + \cdots + x_n}{n}
$$
NumPyの便利な関数を使う
実務では、NumPyの mean() 関数を使って一行で平均を計算します。
以下、コードです。
# NumPyの関数で一発計算
平均_numpy = np.mean(scores)
print(f"NumPyで計算した平均: {平均_numpy}点")
以下、実行結果です。
NumPyで計算した平均: 78.0点
手計算と同じ78点が得られます。
平均の落とし穴:外れ値に弱い
平均には大きな弱点があります。外れ値(極端に大きい・小さい値)の影響を強く受けるのです。
1人だけ極端に高い点数(200点、満点超えのボーナス問題があったとしましょう)がいた場合、平均がどう変わるか確認します。
以下、コードです。
# 通常のデータ
scores_normal = np.array([72, 85, 68, 90, 75])
# 1人だけ極端に高い点数がいる場合
scores_outlier = np.array([72, 85, 68, 90, 200])
print(f"通常データの平均: {np.mean(scores_normal):.1f}点")
print(f"外れ値ありの平均: {np.mean(scores_outlier):.1f}点")
print(f"差: {np.mean(scores_outlier) - np.mean(scores_normal):.1f}点")
以下、実行結果です。
通常データの平均: 78.0点 外れ値ありの平均: 103.0点 差: 25.0点
1人の点数が75点→200点に変わっただけで、平均が78点→103点へと25点も上昇しました。
これでは「典型的な成績」を表しているとは言えません。
平均は「すべてのデータを足す」ため、一つでも極端な値があると、それに引っ張られてしまいます。
日常でも同じことが起きます。「日本人の平均年収」を考えると、一部の超高所得者が平均を押し上げてしまい、多くの人が感じる「普通の年収」とズレが生じます。
中央値(Median):外れ値に強い味方
中央値は、データを小さい順に並べたときの「真ん中の値」です。
- データ数が奇数なら:ちょうど真ん中の値
- データ数が偶数なら:真ん中2つの平均
先ほどの外れ値ありデータで、平均と中央値を比較します。
以下、コードです。
# 外れ値ありデータ
scores_outlier = np.array([72, 85, 68, 90, 200])
# ソートして確認
print("小さい順に並べると:", np.sort(scores_outlier))
print(f"平均: {np.mean(scores_outlier):.1f}点")
print(f"中央値: {np.median(scores_outlier):.1f}点")
以下、実行結果です。
小さい順に並べると: [ 68 72 85 90 200] 平均: 103.0点 中央値: 85.0点
ソート結果は [68, 72, 85, 90, 200] となり、真ん中(3番目)の85点が中央値です。
平均は103点に引っ張られましたが、中央値は85点のまま。外れ値の影響をほとんど受けていません。
中央値は「順位」だけで決まるため、極端な値がいくら極端でも、順位さえ変わらなければ影響しません。
200点が1000点になっても、中央値は85点のまま。これが中央値の強みです。
最頻値(Mode):最も多く出現する値
最頻値は、データの中で最も頻繁に現れる値です。「モード」とも呼ばれます。
たとえば、靴屋さんで「一番売れているサイズは?」と聞かれたら、答えは最頻値です。
平均サイズが25.7cmと言われても靴は作れませんが、「26cmが一番多い」なら在庫管理に役立ちます。
アンケートで「好きな評価(1〜5)」を集めたデータから最頻値を求めます。
以下、コードです。
from scipy import stats
# 10人のアンケート結果(1〜5の5段階評価)
ratings = np.array([4, 5, 3, 4, 4, 5, 3, 4, 2, 4])
print("アンケート結果:", ratings)
print(f"平均: {np.mean(ratings):.1f}")
print(f"中央値: {np.median(ratings):.1f}")
# 最頻値を求める
mode_result = stats.mode(ratings, keepdims=True)
print(
f"最頻値: {mode_result.mode[0]}"
f"({mode_result.count[0]}回出現)"
)
以下、実行結果です。
アンケート結果: [4 5 3 4 4 5 3 4 2 4] 平均: 3.8 中央値: 4.0 最頻値: 4(5回出現)
「4」が5回出現しており、最頻値は4です。
平均3.8、中央値4と近い値ですが、「最も多くの人が選んだのは4」という情報は、平均や中央値からは直接読み取れません。
最頻値は、特にカテゴリデータや離散的なデータで威力を発揮します。
最頻値には気をつけるべき点があります。最頻値が複数ある場合や、存在しない場合です。
たとえば、すべての値が1回ずつしか出現しない場合、最頻値は代表値として機能しません。
そのため、連続データ(身長や体重など)では、最頻値はあまり使われません。
3つの代表値の使い分け
| 特徴 | 向いているデータ | |
|---|---|---|
| 平均 | すべてのデータを反映 / 外れ値に弱い | 外れ値が少ない連続データ |
| 中央値 | 外れ値に強い / 順位だけで決まる | 年収・不動産価格など歪んだ分布 |
| 最頻値 | 最も多い値 / カテゴリに使える |
実務では、データの性質を見て使い分けることが大切です。
そして、迷ったら複数の代表値を並べて比較することで、データの特徴が見えてきます。
可視化で直感をつかむ
数字だけでなく、グラフで見ると理解が深まります。
ヒストグラムを描いて、3つの代表値の位置を視覚的に確認します。
以下、コードです。
import matplotlib.pyplot as plt
import japanize_matplotlib
# 外れ値のあるデータ(80点が最頻値)
data = np.array([
72, 80, 68, 80, 75, 80, 78, 82, 200,
92, 100, 178, 120, 85, 140, 158, 162,
])
# 代表値を計算
mean_val = np.mean(data)
median_val = np.median(data)
mode_val = stats.mode(data, keepdims=True).mode[0]
# ヒストグラムを描く
plt.figure(figsize=(10, 5))
plt.hist(
data,
bins=20, edgecolor='black', alpha=0.7
)
plt.axvline(
mean_val,
color='red', linestyle='--', linewidth=2,
label=f'平均: {mean_val:.1f}'
)
plt.axvline(
median_val,
color='blue', linestyle='-', linewidth=2,
label=f'中央値: {median_val:.1f}'
)
plt.axvline(
mode_val,
color='green', linestyle=':', linewidth=2,
label=f'最頻値: {mode_val}'
)
plt.xlabel('点数')
plt.ylabel('人数')
plt.title('テストの点数分布と3つの代表値')
plt.legend()
plt.show()
以下、実行結果です。
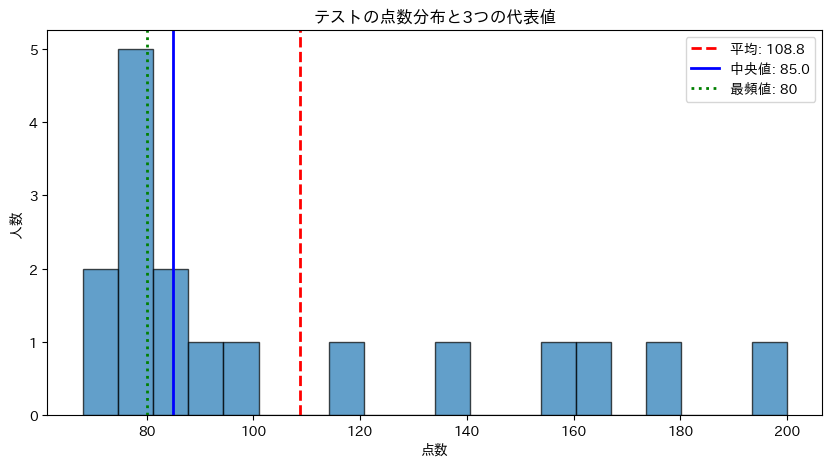
- 赤い破線(平均):外れ値に引っ張られて右にズレている
- 青い実線(中央値):データの「塊」の中心付近にある
- 緑の点線(最頻値):最も多い値(80点)を指している
3つの代表値がそれぞれ異なる情報を伝えていることがわかります。
まとめ
今回は、データを一つの数字で代表させる「代表値」として、平均・中央値・最頻値の3つを紹介しました。
平均は、すべてのデータを足して個数で割ることで求められ、データ全体の「重心」を表します。ただし、外れ値があると大きく引っ張られてしまうという弱点があります。
中央値は、データを小さい順に並べたときの真ん中の値です。順位だけで決まるため、外れ値の影響をほとんど受けません。年収や不動産価格のように分布が歪みやすいデータでは、平均よりも中央値のほうが「普通の値」を表すことが多いです。
最頻値は、データの中で最も頻繁に現れる値です。洋服のサイズやアンケートの評価など、カテゴリデータに対しても使えるのが特徴です。ただし、すべての値が1回ずつしか出現しない場合は意味をなさず、複数の値が同じ回数出現することもあります。
実務では、これら3つの代表値を並べて比較することで、データの特徴が見えてきます。
平均と中央値が大きくズレていれば外れ値の存在を疑い、カテゴリデータを扱うときは最頻値を確認する、このように、データの性質に応じて代表値を使い分けることが大切です。

