ここまでの4回で、コレスポンデンス分析(CA)と多重コレスポンデンス分析(MCA)の仕組みと実行方法を学んできました。
しかし、マップを描いただけでは分析は完了していません。
たとえば、あなたが上司やクライアントにCA/MCAの結果を報告するとします。
マップを見せたとき、こんな質問が飛んでくるかもしれません。
- この軸は何を表しているの?
- この点の位置は信頼できるの?
- 2つの点が近いって言うけど、どれくらい近いと意味があるの?
これらの質問に根拠を持って答えるためには、定量的な指標が必要です。
今回は、CA/MCAの結果を正しく解釈するための3つの柱を学びます。
- 寄与度(Contribution):その点がその軸をどれだけ「作っている」か
- cos²(表現の質):その点がそのマップにどれだけ「うまく表現されている」か
- 距離の解釈:点どうしの「近さ」をどう読むか
この3つを使いこなせば、マップを「なんとなく眺める」段階から「根拠を持って報告する」段階へステップアップできます。
Contents
- ライブラリとデータ
- ステップ1:イナーシャと寄与率の復習
- 総イナーシャ
- 各次元の寄与率
- ステップ2:寄与度 ― 「この軸を作っているのは誰?」
- 寄与度とは
- Pythonで寄与度を計算する
- 寄与度の活用:軸に名前をつける
- ステップ3:cos² ― 「この点の表現は信頼できる?」
- cos²とは
- Pythonで cos² を計算する
- ステップ4:寄与度とcos²をマップに反映する
- ステップ5:距離の解釈 ― 「近さ」の正しい読み方
- 距離の意味
- 原点からの距離:特徴の強さ
- カテゴリ間の距離を計算する
- ステップ6:解釈のチェックリスト
- ステップ7:軸に名前をつける実践
- よくある誤解と注意点
- 点が近いことは「相関が高い」ことを意味しない
- 原点から遠い点が必ずしも重要とは限らない
- 2次元の図は情報の一部を表しているにすぎない
- 行と列の点の距離は直接比べない
- シリーズ全体のまとめ
ライブラリとデータ
第1回で使った「学部 × メニュー」のクロス集計表を再び使います。
以下、コードです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
import prince
from scipy import stats
# おなじみのクロス集計表
data = {
'カレー': [45, 30, 25, 35],
'ラーメン': [40, 25, 20, 30],
'パスタ': [20, 35, 40, 25],
'定食': [35, 30, 25, 40],
'サラダ': [10, 30, 40, 20]
}
index = ['工学部', '経済学部', '文学部', '理学部']
cross_table = pd.DataFrame(data, index=index)
print("【クロス集計表】")
print(cross_table)
以下、実行結果です。
【クロス集計表】
カレー ラーメン パスタ 定食 サラダ
工学部 45 40 20 35 10
経済学部 30 25 35 30 30
文学部 25 20 40 25 40
理学部 35 30 25 40 20
コレスポンデンス分析を実行し、基本的な座標を取得しておきます。
以下、コードです。
ca = prince.CA(n_components=2, random_state=42)
ca = ca.fit(cross_table)
row_coords = ca.row_coordinates(cross_table)
col_coords = ca.column_coordinates(cross_table)
print("【行座標(学部)】")
print(row_coords.round(4))
print("\n【列座標(メニュー)】")
print(col_coords.round(4))
以下、実行結果です。
【行座標(学部)】
0 1
工学部 0.3665 -0.0595
経済学部 -0.1385 -0.0050
文学部 -0.3547 -0.0269
理学部 0.1267 0.0914
【列座標(メニュー)】
0 1
カレー 0.2155 -0.0397
ラーメン 0.2529 -0.0466
パスタ -0.2618 -0.0231
定食 0.1379 0.1027
サラダ -0.4469 0.0013
ステップ1:イナーシャと寄与率の復習
解釈指標を学ぶ前に、第2〜3回で登場したイナーシャと寄与率を復習しておきましょう。これらは以降の指標の土台になります。
総イナーシャ
総イナーシャ(Total Inertia)は、クロス集計表における「独立からのズレの総量」を表す値です。第2回で学んだカイ二乗統計量 \chi^2 を総度数 n で割ったものと一致します。
$$
\text{総イナーシャ} = \frac{\chi^2}{n} = \sum_{k=1}^{K} \lambda_k
$$
ここで \lambda_k は第 k 次元の固有値(=第3回で学んだ特異値 \sigma_k の二乗)、K は次元の数(= \min(I-1, J-1)、I は行数、J は列数)です。
以下、コードです。
# カイ二乗検定で総イナーシャを計算
chi2, p_value, dof, _ = stats.chi2_contingency(cross_table)
n = cross_table.values.sum()
total_inertia = chi2 / n
print(f"カイ二乗統計量: {chi2:.4f}")
print(f"総度数: {n}")
print(f"総イナーシャ: {total_inertia:.4f}")
print(f"p値: {p_value:.6f}")
以下、実行結果です。
カイ二乗統計量: 46.2697 総度数: 600 総イナーシャ: 0.0771 p値: 0.000006
p値が0.05未満のため、学部とメニューに有意な関連があることを意味します。そのため、コレスポンデンス分析の結果を解釈する意味があります。
各次元の寄与率
寄与率(Percentage of Variance / Explained Inertia)は、各次元が総イナーシャのうち何%を説明しているかを表します。第 k 次元の寄与率は次の式で計算されます。
$$
\text{第 } k \text{ 次元の寄与率} = \frac{\lambda_k}{\sum_{k’} \lambda_{k’}} \times 100\%
$$
以下、コードです。
# 固有値(各次元のイナーシャ)
eigenvalues = ca.eigenvalues_
print("【各次元の固有値と寄与率】")
cumulative = 0
for i, ev in enumerate(eigenvalues):
pct = ca.percentage_of_variance_[i]
cumulative += pct
print(
f" 第{i+1}次元: "
f"λ={ev:.4f}, "
f"寄与率={pct:.1f}%, "
f"累積={cumulative:.1f}%"
)
以下、実行結果です。
【各次元の固有値と寄与率】 第1次元: λ=0.0738, 寄与率=95.7%, 累積=95.7% 第2次元: λ=0.0032, 寄与率=4.1%, 累積=99.8%
累積寄与率が70%以上あれば、2次元マップでデータの変動を十分に捉えていると判断できます。逆に低い場合は、3次元目以降の情報も重要であることを意味します。
ステップ2:寄与度 ― 「この軸を作っているのは誰?」
寄与度とは
寄与度(Contribution)は、各カテゴリが各次元のイナーシャにどれだけ「貢献」しているかを表す指標です。言い換えれば、「その軸の形成にどれだけ影響を与えているか」を数値化したものです。
第 k 次元における行 i(学部)の寄与度 \text{ctr}_{ik} は次の式で定義されます。
$$
\text{ctr}_{ik} = \frac{r_i \cdot \phi_{ik}^2}{\lambda_k}
$$
ここで、r_i は行 i の周辺確率(その学部の回答者が全体に占める割合)、\phi_{ik} は行 i の第 k 次元における座標、\lambda_k は第 k 次元の固有値です。
同様に、列 j(メニュー)の寄与度 \text{ctr}_{jk} は次のように定義されます。
$$
\text{ctr}_{jk} = \frac{c_j \cdot \gamma_{jk}^2}{\lambda_k}
$$
ここで c_j は列 j の周辺確率、\gamma_{jk} は列 j の第 k 次元における座標です。
寄与度は0から1の値をとり、すべての行(または列)の寄与度を足すと1(= 100%)になります。寄与度が高いカテゴリほど、その次元の「主役」です。
Pythonで寄与度を計算する
prince ライブラリでは、寄与度を直接取得するメソッドはありませんが、座標と周辺確率から計算できます。
以下、コードです。
# 周辺確率の計算
P = cross_table / cross_table.values.sum()
r = P.sum(axis=1).values # 行の周辺確率
c = P.sum(axis=0).values # 列の周辺確率
# 固有値
eigenvalues = ca.eigenvalues_
# 行の寄与度
row_contrib = pd.DataFrame(index=cross_table.index, columns=['次元1', '次元2'])
for k in range(2):
row_contrib.iloc[:, k] = (r * row_coords.iloc[:, k].values**2) / eigenvalues[k]
print("【行の寄与度(%表示)】")
print((row_contrib * 100).round(2))
print(f"\n各次元の合計: {(row_contrib.sum() * 100).round(2).tolist()}")
print("\n","="*50,"\n")
# 列の寄与度
col_contrib = pd.DataFrame(index=cross_table.columns, columns=['次元1', '次元2'])
for k in range(2):
col_contrib.iloc[:, k] = (c * col_coords.iloc[:, k].values**2) / eigenvalues[k]
print("【列の寄与度(%表示)】")
print((col_contrib * 100).round(2))
print(f"\n各次元の合計: {(col_contrib.sum() * 100).round(2).tolist()}")
以下、実行結果です。
【行の寄与度(%表示)】
次元1 次元2
工学部 45.476243 28.010115
経済学部 6.495844 0.19809
文学部 42.592559 5.717311
理学部 5.435354 66.074484
各次元の合計: [100.0, 100.0]
==================================================
【列の寄与度(%表示)】
次元1 次元2
カレー 14.149074 11.199494
ラーメン 16.609783 13.147233
パスタ 18.571503 3.370232
定食 5.584262 72.274083
サラダ 45.085378 0.008958
各次元の合計: [100.0, 100.0]
各次元の寄与度の合計が100%(小数点誤差を除く)になることを確認してください。
寄与度の活用:軸に名前をつける
寄与度が高いカテゴリは、その軸を「定義している」と言えます。たとえば、第1次元に対して「工学部」と「文学部」の寄与度が高ければ、第1次元は「工学部的 ↔ 文学部的」という対立軸を表していると解釈できます。
寄与度を可視化して、どのカテゴリが各軸の主役かを確認しましょう。
以下、コードです。
fig, axes = plt.subplots(2, 1, figsize=(10, 6))
# 行の寄与度
(row_contrib * 100).plot(
kind='bar', ax=axes[0], colormap='viridis')
axes[0].set_title('行(学部)の寄与度')
axes[0].set_ylabel('寄与度 (%)')
axes[0].set_xlabel('')
axes[0].legend(title='次元')
axes[0].tick_params(axis='x', rotation=0)
# 列の寄与度
(col_contrib * 100).plot(
kind='bar', ax=axes[1], colormap='viridis')
axes[1].set_title('列(メニュー)の寄与度')
axes[1].set_ylabel('寄与度 (%)')
axes[1].set_xlabel('')
axes[1].legend(title='次元')
axes[1].tick_params(axis='x', rotation=45)
plt.tight_layout()
plt.show()
以下、実行結果です。
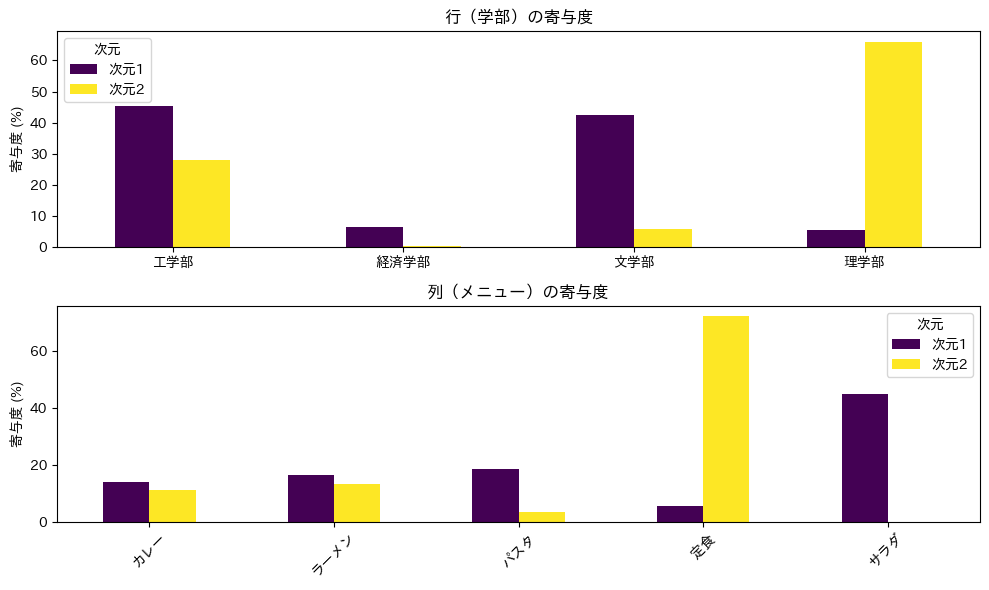
棒グラフを見て、各次元でどのカテゴリの寄与度が突出しているかを確認してください。寄与度が高いカテゴリに注目して軸を解釈するのが、正しいアプローチです。
一般に、寄与度が平均を上回るカテゴリに注目します。平均寄与度は 1/I(行の場合)または 1/J(列の場合)です。今回のデータでは、行の平均は 1/4 = 25\%、列の平均は 1/5 = 20\% です。
ステップ3:cos² ― 「この点の表現は信頼できる?」
cos²とは
cos²(コサイン二乗、Squared Cosine)は、各カテゴリがその次元にどれだけ「うまく表現されている」かを表す指標です。別名「表現の質(Quality of Representation)」とも呼ばれます。
cos²は、そのカテゴリの原点からの距離のうち、特定の次元がどれだけの割合を占めているかを測ります。行 i の第 k 次元における cos² は次の式で定義されます。
$$
\cos^2_{ik} = \frac{\phi_{ik}^2}{\sum_{k’=1}^{K} \phi_{ik’}^2}
$$
分母はその点の原点からの総距離の二乗(すべての次元での座標の二乗和)、分子は第 k 次元の座標の二乗です。つまり、cos² は「原点からのズレのうち、どれだけがこの次元で捉えられているか」を表しています。
cos²は0から1の値をとり、すべての次元の cos² を足すと1になります。2次元マップでの累積 cos²(第1次元 + 第2次元)が高いほど、その点はマップ上でうまく表現されています。逆に低い場合、その点のマップ上の位置は「本来の位置」からズレている可能性があり、解釈に注意が必要です。
Pythonで cos² を計算する
以下、コードです。
# 行のcos²
row_coords_all = ca.row_coordinates(cross_table)
row_dist_sq = (row_coords_all ** 2).sum(axis=1)
row_cos2 = pd.DataFrame(
index=cross_table.index,
columns=['次元1', '次元2']
)
for k in range(2):
row_cos2.iloc[:, k] = (row_coords_all.iloc[:, k] ** 2) / row_dist_sq
row_cos2['累積'] = row_cos2['次元1'] + row_cos2['次元2']
print("【行のcos²】")
print(row_cos2.round(4))
print("\n","="*50,"\n")
# 列のcos²
col_coords_all = ca.column_coordinates(cross_table)
col_dist_sq = (col_coords_all ** 2).sum(axis=1)
col_cos2 = pd.DataFrame(
index=cross_table.columns,
columns=['次元1', '次元2']
)
for k in range(2):
col_cos2.iloc[:, k] = (col_coords_all.iloc[:, k] ** 2) / col_dist_sq
col_cos2['累積'] = col_cos2['次元1'] + col_cos2['次元2']
print("【列のcos²】")
print(col_cos2.round(4))
以下、実行結果です。
【行のcos²】
次元1 次元2 累積
工学部 0.974281 0.025719 1.0
経済学部 0.998695 0.001305 1.0
文学部 0.99428 0.00572 1.0
理学部 0.657459 0.342541 1.0
==================================================
【列のcos²】
次元1 次元2 累積
カレー 0.967189 0.032811 1.0
ラーメン 0.967189 0.032811 1.0
パスタ 0.992282 0.007718 1.0
定食 0.643213 0.356787 1.0
サラダ 0.999991 0.000009 1.0
ステップ4:寄与度とcos²をマップに反映する
寄与度と cos² の情報をマップに反映させると、どの点に注目すべきかが一目でわかります。点のサイズを寄与度に、色の濃さを cos² に連動させてプロットしてみましょう。
以下、コードです。
fig, ax = plt.subplots(figsize=(10, 8))
# 行(学部)をプロット
for i, faculty in enumerate(cross_table.index):
x, y = row_coords.iloc[i]
# 寄与度の平均でサイズを決定
contrib = (row_contrib.iloc[i, 0] + row_contrib.iloc[i, 1]) / 2
cos2_val = row_cos2.loc[faculty, '累積']
size = 50 + contrib * 5000 # 寄与度に応じたサイズ
alpha = 0.3 + cos2_val * 0.5 # cos²に応じた透明度
ax.scatter(
x, y, s=size, c='#2E86AB', alpha=alpha,
edgecolors='white', linewidths=2
)
ax.annotate(
faculty, (x, y),
fontsize=12, fontweight='bold',
xytext=(10, 10), textcoords='offset points',
color='#2E86AB'
)
# 列(メニュー)をプロット
for j, menu in enumerate(cross_table.columns):
x, y = col_coords.iloc[j]
contrib = (col_contrib.iloc[j, 0] + col_contrib.iloc[j, 1]) / 2
cos2_val = col_cos2.loc[menu, '累積']
size = 50 + contrib * 5000
alpha = 0.3 + cos2_val * 0.5
ax.scatter(
x, y, s=size, c='#E94F37', alpha=alpha, marker='^',
edgecolors='white', linewidths=2
)
ax.annotate(
menu, (x, y), fontweight='bold',
xytext=(10, 10), textcoords='offset points',
color='#E94F37'
)
ax.axhline(y=0, color='gray', linestyle='--', linewidth=0.8)
ax.axvline(x=0, color='gray', linestyle='--', linewidth=0.8)
ax.set_xlabel(f'次元1(寄与率: {ca.percentage_of_variance_[0]:.1f}%)')
ax.set_ylabel(f'次元2(寄与率: {ca.percentage_of_variance_[1]:.1f}%)')
ax.set_title('CAマップ(サイズ:寄与度、濃さ:cos²)')
from matplotlib.lines import Line2D
legend_elements = [
Line2D(
[0], [0],
marker='o', color='w',
markerfacecolor='#2E86AB',
markersize=12, label='学部'
),
Line2D(
[0], [0],
marker='^', color='w',
markerfacecolor='#E94F37',
markersize=12, label='メニュー'
)
]
ax.legend(handles=legend_elements, loc='best')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
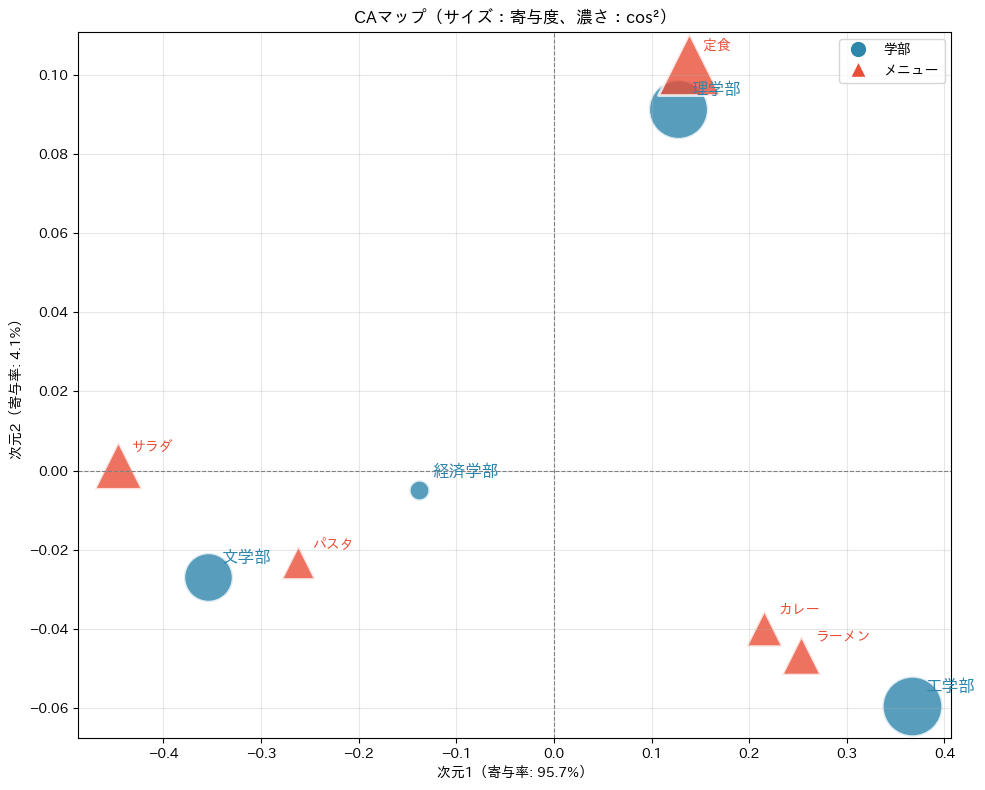
このマップでは、大きくて濃い点ほど「その次元を形作っており、かつマップ上でうまく表現されている」ことを意味します。解釈の際は、まずこれらの点に注目しましょう。
ステップ5:距離の解釈 ― 「近さ」の正しい読み方
距離の意味
CAマップでは「近い点どうしは関連が強い」と解釈しますが、これをより正確に理解しておく必要があります。
同じ種類のカテゴリ間の距離(行どうし、または列どうし)は、プロファイルの類似性を表します。2つの学部が近ければ、メニューの選び方のパターンが似ているということです。この距離はカイ二乗距離と呼ばれ、第3回で学んだ標準化残差から導かれます。
異なる種類のカテゴリ間の距離(行と列の間)は、直接比較することに注意が必要です。行と列は異なる「空間」から同じマップに射影されているため、厳密な意味での「距離」ではありません。ただし、同じ方向にある行と列は正の関連(その組み合わせが期待より多い)、反対方向にある行と列は負の関連(その組み合わせが期待より少ない)と解釈できます。
原点からの距離:特徴の強さ
原点は「平均的なプロファイル」を表します。原点からの距離が大きいカテゴリほど、平均から離れた特徴的なパターンを持っています。
以下、コードです。
# 原点からの距離
row_dist_from_origin = np.sqrt(
(row_coords.iloc[:, :2] ** 2).sum(axis=1))
col_dist_from_origin = np.sqrt(
(col_coords.iloc[:, :2] ** 2).sum(axis=1))
print("【原点からの距離(2次元)】")
print("\n行(学部):")
for faculty, dist in row_dist_from_origin.items():
trait = "特徴的" if dist > row_dist_from_origin.median() else "平均的"
print(f" {faculty}: {dist:.4f} ({trait})")
print("\n列(メニュー):")
for menu, dist in col_dist_from_origin.items():
trait = "特徴的" if dist > col_dist_from_origin.median() else "平均的"
print(f" {menu}: {dist:.4f} ({trait})")
以下、実行結果です。
【原点からの距離(2次元)】 行(学部): 工学部: 0.3713 (特徴的) 経済学部: 0.1386 (平均的) 文学部: 0.3557 (特徴的) 理学部: 0.1563 (平均的) 列(メニュー): カレー: 0.2191 (平均的) ラーメン: 0.2572 (平均的) パスタ: 0.2628 (特徴的) 定食: 0.1720 (平均的) サラダ: 0.4469 (特徴的)
カテゴリ間の距離を計算する
同じ種類のカテゴリ間の距離を計算し、最も近いペアと最も遠いペアを確認してみましょう。
以下、コードです。行(学部)間の距離です。
from itertools import combinations
# 行(学部)間の距離
print("【学部間の距離】")
row_distances = {}
for (f1, f2) in combinations(cross_table.index, 2):
d = np.sqrt(
(
(row_coords.loc[f1] - row_coords.loc[f2]) ** 2
).sum()
)
row_distances[(f1, f2)] = d
print(f" {f1} ↔ {f2}: {d:.4f}")
closest = min(row_distances, key=row_distances.get)
farthest = max(row_distances, key=row_distances.get)
print(f"\n 最も近いペア: {closest[0]} ↔ {closest[1]}")
print(f" 最も遠いペア: {farthest[0]} ↔ {farthest[1]}")
以下、実行結果です。
【学部間の距離】 工学部 ↔ 経済学部: 0.5079 工学部 ↔ 文学部: 0.7219 工学部 ↔ 理学部: 0.2834 経済学部 ↔ 文学部: 0.2173 経済学部 ↔ 理学部: 0.2822 文学部 ↔ 理学部: 0.4957 最も近いペア: 経済学部 ↔ 文学部 最も遠いペア: 工学部 ↔ 文学部
以下、コードです。列(メニュー)間の距離です。
# 列(メニュー)間の距離
print("【メニュー間の距離】")
col_distances = {}
for (m1, m2) in combinations(cross_table.columns, 2):
d = np.sqrt(
(
(col_coords.loc[m1] - col_coords.loc[m2]) ** 2
).sum()
)
col_distances[(m1, m2)] = d
# 上位3ペアと下位3ペアを表示
sorted_dists = sorted(
col_distances.items(),
key=lambda x: x[1]
)
print(" 近いペア(Top 3):")
for (m1, m2), d in sorted_dists[:3]:
print(f" {m1} ↔ {m2}: {d:.4f}")
print(" 遠いペア(Top 3):")
for (m1, m2), d in sorted_dists[-3:]:
print(f" {m1} ↔ {m2}: {d:.4f}")
以下、実行結果です。
【メニュー間の距離】
近いペア(Top 3):
カレー ↔ ラーメン: 0.0381
カレー ↔ 定食: 0.1622
パスタ ↔ サラダ: 0.1867
遠いペア(Top 3):
定食 ↔ サラダ: 0.5936
カレー ↔ サラダ: 0.6636
ラーメン ↔ サラダ: 0.7015
近いペアは「選ばれ方のパターンが似ている」ことを意味します。たとえば「カレー」と「ラーメン」は、同じ学部の学生に好まれる傾向があると解釈できます。
ステップ6:解釈のチェックリスト
ここまで学んだ指標を活用して、CAの結果を報告する際に確認すべきポイントをチェックリストにまとめます。
以下、コードです。
# チェックリストの結果を計算
check_items = []
# 1. 関連性の有意性
check_items.append({
'項目': '① 関連性の検定',
'基準': 'p値 < 0.05',
'結果': f'p = {p_value:.4f}',
'判定': '✓' if p_value < 0.05 else '×'
})
# 2. 累積寄与率
cum_var = sum(ca.percentage_of_variance_[:2])
check_items.append({
'項目': '② 累積寄与率',
'基準': '70%以上',
'結果': f'{cum_var:.1f}%',
'判定': '✓' if cum_var >= 70 else '△'
})
# 3. 主要カテゴリのcos²
min_row_cos2 = row_cos2['累積'].min()
min_col_cos2 = col_cos2['累積'].min()
min_cos2 = min(min_row_cos2, min_col_cos2)
check_items.append({
'項目': '③ 最小cos²(累積)',
'基準': '50%以上',
'結果': f'{min_cos2*100:.1f}%',
'判定': '✓' if min_cos2 >= 0.5 else '△'
})
check_df = pd.DataFrame(check_items)
print("【CA結果の解釈チェックリスト】")
print(check_df.to_string(index=False))
以下、実行結果です。
【CA結果の解釈チェックリスト】
項目 基準 結果 判定
① 関連性の検定 p値 < 0.05 p = 0.0000 ✓
② 累積寄与率 70%以上 99.8% ✓
③ 最小cos²(累積) 50%以上 100.0% ✓
ステップ7:軸に名前をつける実践
寄与度を活用して、各軸に解釈可能な「名前」をつける実践をしてみましょう。
以下、コードです。
print("【軸の解釈】")
print("--- 第1次元 ---")
# コピーを作成
row_contrib_num = row_contrib.copy()
col_contrib_num = col_contrib.copy()
# 列を数値化
row_contrib_num['次元1'] = pd.to_numeric(
row_contrib_num['次元1'],
errors='coerce'
)
col_contrib_num['次元1'] = pd.to_numeric(
col_contrib_num['次元1'],
errors='coerce'
)
# 行で寄与度が高いカテゴリ(第1次元)
row_top_dim1 = row_contrib_num['次元1'].nlargest(4)
print(f"行の主要寄与者: {list(row_top_dim1.index)}")
# 列で寄与度が高いカテゴリ(第1次元)
col_top_dim1 = col_contrib_num['次元1'].nlargest(4)
print(f"列の主要寄与者: {list(col_top_dim1.index)}")
# 座標の正負で対立を確認
print("\n座標による対立構造:")
# 行(学部)
for cat in row_top_dim1.index:
coord = row_coords.loc[cat, 0]
side = "正(右)" if coord > 0 else "負(左)"
print(f" [行] {cat}: {side}")
# 列(メニュー)
for cat in col_top_dim1.index:
coord = col_coords.loc[cat, 0]
side = "正(右)" if coord > 0 else "負(左)"
print(f" [列] {cat}: {side}")
以下、実行結果です。
【軸の解釈】 --- 第1次元 --- 行の主要寄与者: ['工学部', '文学部', '経済学部', '理学部'] 列の主要寄与者: ['サラダ', 'パスタ', 'ラーメン', 'カレー'] 座標による対立構造: [行] 工学部: 正(右) [行] 文学部: 負(左) [行] 経済学部: 負(左) [行] 理学部: 正(右) [列] サラダ: 負(左) [列] パスタ: 負(左) [列] ラーメン: 正(右) [列] カレー: 正(右)
カレー・ラーメンが正方向、サラダ・パスタが負方向にあるので、第1次元は「ガッツリ系 ↔ ヘルシー系」と名付けられるかもしれません。
よくある誤解と注意点
最後に、CAの解釈でよくある誤解をまとめておきます。
点が近いことは「相関が高い」ことを意味しない
コレスポンデンス分析(CA)の図を見ると、点どうしの距離に目が行きがちです。
そのため、「点が近いほど相関が高い」と考えてしまうことがあります。しかし、この解釈は正しくありません。
CAの図で点が近いというのは、数学で学ぶ相関係数が大きいことを意味するのではなく、そのカテゴリどうしの特徴が似ている、あるいは偶然よりも一緒に現れやすい関係にあることを表しています。
したがって、CAの距離は「強さ」ではなく、「性質の似かより方」を示していると理解することが大切です。
原点から遠い点が必ずしも重要とは限らない
次によくある誤解が、「原点から遠くにある点ほど重要である」という考え方です。
図の外側にある点は目立つため、つい重要だと感じてしまいますが、それだけでは判断できません。その点が、横軸や縦軸の意味をどれだけ説明しているかは、寄与度によって決まります。
たとえ原点から離れていても、寄与度が小さければ、その点はその軸の解釈にほとんど貢献していない場合があります。
見た目だけでなく、数値もあわせて確認する必要があります。
2次元の図は情報の一部を表しているにすぎない
CAの結果は、たくさんの情報を少ない次元にまとめて図にしたものです。
そのため、「この2次元の図を見ればすべてが分かる」と考えるのは危険です。この図が、データ全体のどれくらいを説明できているかは、累積寄与率で確認します。
また、それぞれのカテゴリが図の中でどれくらい正確に表現されているかは、cos²という指標で判断します。
累積寄与率が低い場合や、cos²が小さいカテゴリが多い場合、この図は全体の一部しか表していないことになります。
行と列の点の距離は直接比べない
最後に注意したいのが、行と列の点どうしの距離の扱い方です。
行どうし、あるいは列どうしの距離を比べることには意味がありますが、行と列の点の距離をそのまま比べることはできません。
行と列の関係を見るときは、距離の近さではなく、同じ方向に位置しているか、反対方向に位置しているかに注目します。
同じ方向にあれば関連が強く、反対方向にあれば関連が弱い、あるいは逆の関係にあると判断します。
シリーズ全体のまとめ
全5回にわたるシリーズ「Pythonで学ぶコレスポンデンス分析入門」を完走いただき、ありがとうございました。最後に、シリーズ全体の学びを振り返っておきましょう。
第1回では、クロス集計表とヒートマップの限界を確認し、コレスポンデンス分析(CA)がカテゴリ間の関係を2次元マップで可視化する手法であることを学びました。「近い点は関連が強い」という直感的な読み方を体験しました。
第2回では、「期待度数」と「独立からのズレ(残差)」がCAの出発点であることを理解しました。カイ二乗検定で「分析のゴーサイン」を確認する習慣も身につけました。
第3回では、CAの心臓部である特異値分解(SVD)を学びました。対応行列 P、標準化残差行列 S、そして S = U\Sigma V^T という分解から座標が生まれるプロセスを、数式とコードで追いかけました。
第4回では、3つ以上のカテゴリ変数を扱う多重コレスポンデンス分析(MCA)を学びました。指示行列 Z とBurt行列 B = Z^T Z の概念を理解し、顧客セグメンテーションへの応用も体験しました。
第5回(今回)では、結果を正しく解釈するための3つの柱を学びました。寄与度で軸に名前をつけ、cos²で信頼できる点を見抜き、距離の正しい読み方を身につけました。
これらの知識を武器に、ぜひ実際のデータでCA/MCAを試してみてください。マーケティング調査、社会調査、テキスト分析など、カテゴリカルデータが登場するあらゆる場面で、コレスポンデンス分析は強力な洞察をもたらしてくれるはずです。

