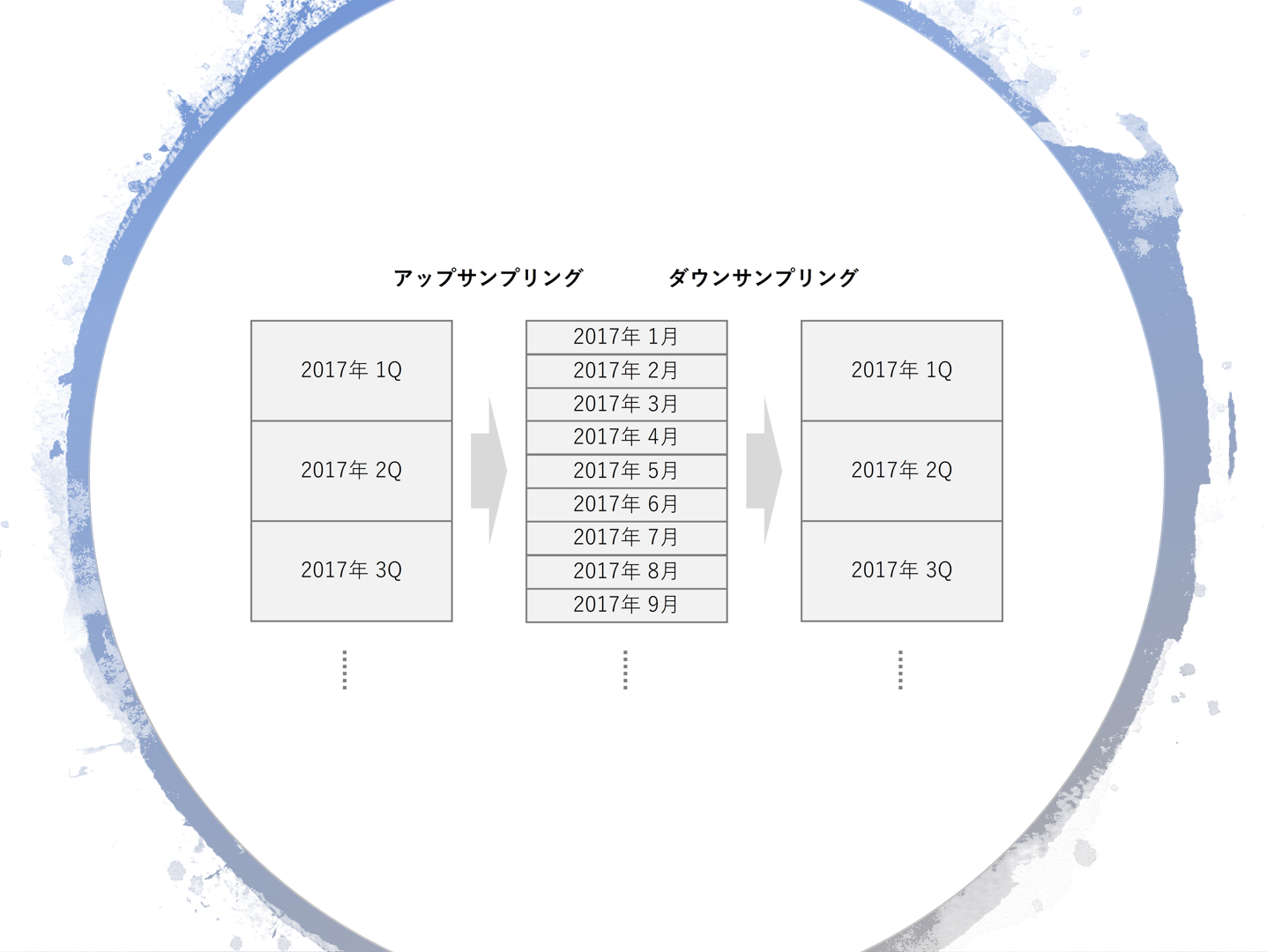
時系列データを扱っていると、時間間隔の異なる複数の時系列データを扱うことがあります。
1カ月単位の時系列データもあれば、四半期単位の時系列データもあります。
1時間単位の時系列データもあれば、1日単位の時系列データもあります。
ちょっとした時間間隔であれば、時間間隔を揃えるデータサイエンス技術があります。
時系列リサンプリングです。
今回は、「時間間隔の異なる時系列データの時間間隔を揃える『時系列リサンプリング』」というお話しをします。
Contents
時系列リサンプリングとは?
時系列リサンプリングは、時間間隔を一定にするために使用されます。
異なる時間間隔で取得された時系列データは、一定の時間間隔でリサンプリングすることで均一な時間間隔のデータに変換できます。
リサンプリングには主に2つのタイプがあります。
アップサンプリング
データの時間間隔を短くするプロセス。例えば、1時間ごとのデータを30分ごとのデータに変換することなどが含まれます。アップサンプリングでは、新たに作成されるデータポイントの値をどのように決定するかという問題が生じます。これは通常、隣接するデータポイントの値から補間により決定されます。
ダウンサンプリング
データの時間間隔を長くするプロセス。例えば、1分ごとのデータを1時間ごとのデータに変換することなどが含まれます。ダウンサンプリングでは、多数のデータポイントを一つのデータポイントにまとめる必要があります。これは通常、平均、中央値、最大値、最小値などの要約統計量により決定されます。
要は、アップサンプリングは時期列欠測補完技術が求められ、ダウンサンプリングはデータの集約技術(平均値など)が求められます。
そのため、元の時系列データの時間間隔から大きく乖離すると、あまりよろしくありません。
Pythonでどうやるの?
Pythonで時系列リサンプリングする方法は主に2つです。
- 基本となるPythonライブラリーの機能を使う
- 時系列データ用のPythonライブラリーの機能を使う
基本となるPythonライブラリーとは、pandasやnumpyなどのPythonユーザがほぼデフォルトで利用するライブラリーのことです。
時系列データ用のPythonライブラリーとは、時系列クラスタリングや時系列分類問題などで使われるtslearnというライブラリーのことです。今現在(2023年8月1日現在)tslearnでできる時系列リサンプリングは相当限られており柔軟性に欠けます。
そのため、pandasやnumpyなどを使った方がいいでしょう。主に使うのはpandasのresampleメソッドです。
アップリサンプリング
概要
時系列データのアップサンプリングとは、データの時間的な解像度(つまり、データポイントが取られる頻度)を高めるプロセスを指します。
例えば、四半期(Q)ごとのデータを1カ月(M)ごとのデータに変換することなどがアップサンプリングに該当します。
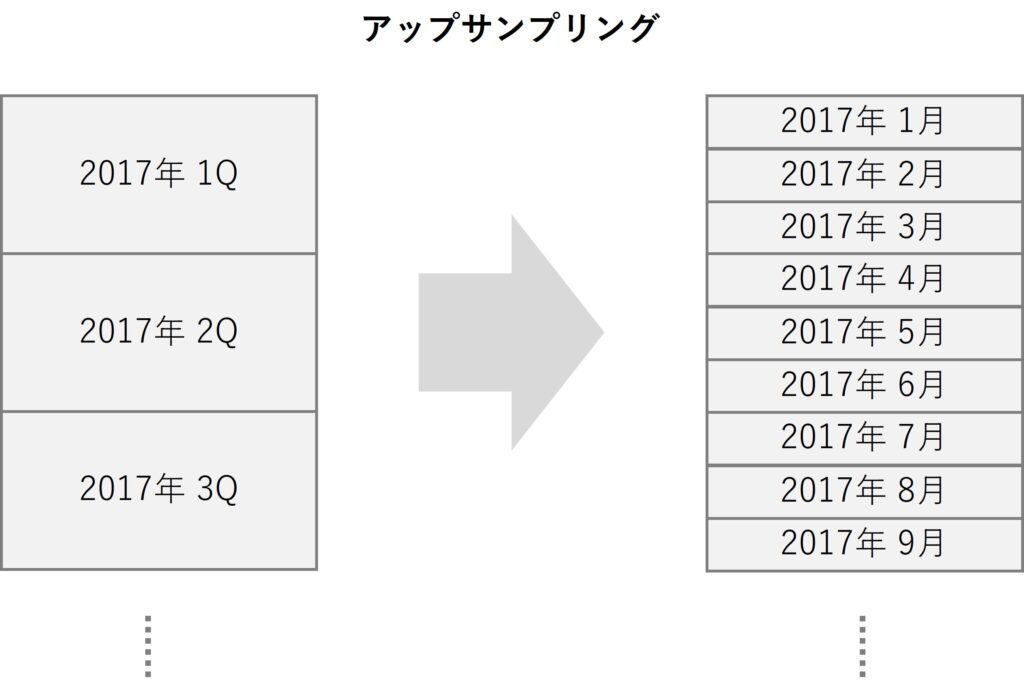
アップサンプリングは、データをより詳細に分析したり、より頻繁に更新される予測モデルを構築したりする際に有用です。
しかし、アップサンプリングにはデータが存在しない時間点の値を何らかの方法で推定する必要があります。これを欠測値補間と呼びます。
アップサンプリングにおける補間の方法は多数存在します。
一部を以下に列挙します。
- 線形補間:2つのデータポイント間の値を直線的に補間します。これは、データが直線的に変化していると仮定した場合の最も単純な補間方法です。
- 最近傍補間:欠損値の直前または直後のデータポイントの値を使用します。これは、データが一定であると仮定した場合の補間方法です。
- 多項式補間やスプライン補間:2つ以上のデータポイント間の値を補間するためのより複雑な方法で、データが非線形に変化していると仮定します。
これらの手法はすべて、pandasライブラリのresampleとinterpolateメソッドを使用して実装することができます。どの手法を選ぶべきかは、データの性質と分析の目的によります。
Python実施例
時系列のサンプルデータを生成します。
四半期(Q)単位のデータです。
以下、コードです。
import pandas as pd import numpy as np # サンプルデータの生成 index = pd.date_range(start="2017-01-01", end="2022-12-31", freq="Q") data = np.random.rand(len(index)) ts = pd.Series(data=data, index=index) ts #確認
以下、実行結果です。四半期末の日付(例:2017年1月~3月の場合は2017-03-31)になっています。
2017-03-31 0.334647 2017-06-30 0.890882 2017-09-30 0.792992 2017-12-31 0.981053 2018-03-31 0.771901 2018-06-30 0.097800 2018-09-30 0.119999 2018-12-31 0.338517 2019-03-31 0.312901 2019-06-30 0.117221 2019-09-30 0.512509 2019-12-31 0.646545 2020-03-31 0.430387 2020-06-30 0.276599 2020-09-30 0.920999 2020-12-31 0.076724 2021-03-31 0.465291 2021-06-30 0.428180 2021-09-30 0.060319 2021-12-31 0.236733 2022-03-31 0.420085 2022-06-30 0.123170 2022-09-30 0.586810 2022-12-31 0.802111 Freq: Q-DEC, dtype: float64
では、アップサンプリングします。
四半期(Q)から月単位(M)にします。欠測値の値補は、線形補間(linear)で行います。
以下、コードです。
# アップサンプリング(四半期単位→1か月単位)
ts_upsampled = ts.resample("M").asfreq()
# 線形補完
ts_up_interpolated = ts_upsampled.interpolate(method="linear")
# 確認
ts_up_interpolated
以下、実行結果です。月末の日付(例:2017年3月の場合は2017-03-31)になっています。
2017-03-31 0.231589
2017-04-30 0.335207
2017-05-31 0.438825
2017-06-30 0.542443
2017-07-31 0.537510
...
2022-08-31 0.167728
2022-09-30 0.031605
2022-10-31 0.240842
2022-11-30 0.450079
2022-12-31 0.659316
Freq: M, Length: 70, dtype: float64
欠測値補完手法(pandasのinterpolate)
時系列データをアップサンプリングするときに使える、pandasのinterpolate関数で実施できる主な欠測値補完手法の一覧です。
| 手法 | 説明 | メリット | デメリット |
|---|---|---|---|
| 線形補間(linear) | データを直線で補間する | 単純で高速。データが線形に変化する場合にはよく機能する | データが線形に変化しない場合にはうまく機能しない可能性がある |
| 時間補間(time) | 時間間隔を考慮してデータを直線で補間する(datetime型のインデックスのみに適用可能) | データポイント間の実際の時間間隔を考慮する | datetime型のインデックスにのみ適用可能 |
| インデックスに基づく補間(index) | インデックスの実数値を考慮してデータを直線で補間する | データポイント間の実際の数値間隔を考慮する | データが線形に変化しない場合にはうまく機能しない可能性がある |
| 値に基づく補間(values) | 値の実数値を考慮してデータを直線で補間する | データポイント間の実際の数値間隔を考慮する | データが線形に変化しない場合にはうまく機能しない可能性がある |
| 前方補填(pad/ffill) | 欠損値を前の値で補填する | 単純で高速。データが欠損値の間で一定である場合には理にかなっている | データの実際のパターンを反映していない可能性がある |
| 後方補填(backfill/bfill) | 欠損値を次の値で補填する | 単純で高速。データが欠損値の間で一定である場合には理にかなっている | データの実際のパターンを反映していない可能性がある |
| 最近傍補間(nearest) | 欠損値を最も近い値で補填する | 単純で高速。最も近い値が最良の推定値である場合には理にかなっている | データの実際のパターンを反映していない可能性がある |
| 多項式補間(polynomial) | 多項式関数を使用してデータを補間する | より複雑なパターンをフィットできる。多項式の次数を調整可能 | 計算量が多い。過学習または学習不足になりやすい |
| スプライン補間(spline) | スプライン関数を使用してデータを補間する | より複雑なパターンをフィットできる。スプラインの次数を調整可能 | 計算量が多い。過学習または学習不足になりやすい |
ダウンサンプリング
概要
時系列データのダウンサンプリングとは、データの時間的な解像度(つまり、データポイントが取られる頻度)を下げるプロセスを指します。
例えば、1カ月(M)ごとのデータを四半期(Q)ごとのデータに変換することなどがダウンサンプリングに該当します。
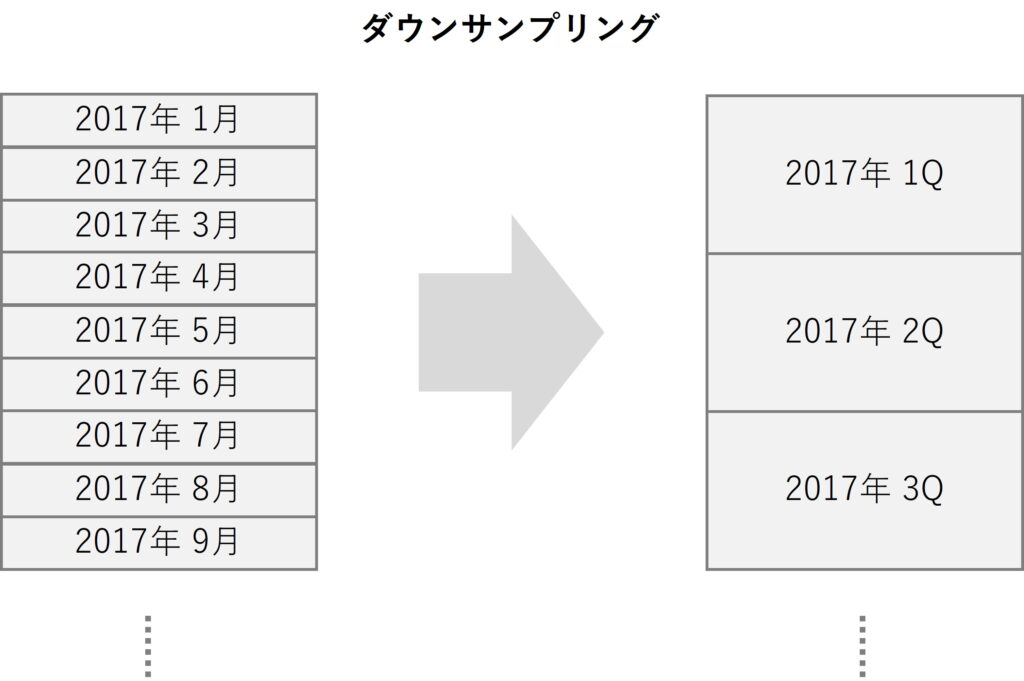
ダウンサンプリングは、大量の高頻度データを扱う場合や、長期的なトレンドを調査する場合などに有用です。
ダウンサンプリングすると、データの量が減少し、計算量やストレージの要件を削減できます。また、ノイズの影響を抑えることができるため、データの本質的なパターンやトレンドをより明確に見ることができます。
ダウンサンプリングの際には、より低い頻度でデータをどのように集約するかを決める必要があります。
一部の主な集約手法を以下に列挙します。
- 平均(Mean):各時間間隔のデータポイントの平均値を計算します。これは、データがその間隔にわたって一様に分布しているという仮定に基づいています。
- 中央値(Median):各時間間隔のデータポイントの中央値を計算します。これは、データがその間隔にわたって一様に分布しているという仮定に基づいていますが、平均よりも外れ値の影響を受けにくいです。
- 最大値(Max)や最小値(Min):各時間間隔のデータポイントの最大値や最小値を採用します。これは、データの範囲を維持することが重要な場合に有用です。
- 最初(First)や最後(Last):各時間間隔の最初や最後のデータポイントを採用します。これは、データが基本的に定常的で、時間間隔の始めや終わりのデータがその間隔全体を代表するという仮定に基づいています。
これらの手法はすべて、pandasライブラリのresampleメソッドを使用して実装することができます。どの手法を選ぶべきかは、データの性質と分析の目的によります。
Python実施例
時系列のサンプルデータを生成します。
日(D)単位のデータです。
以下、コードです。
import pandas as pd import numpy as np # サンプルデータの生成 index = pd.date_range(start="2018-01-01", end="2022-12-31", freq="D") data = np.random.rand(len(index)) ts = pd.Series(data=data, index=index) ts #確認
以下、実行結果です。
2018-01-01 0.414745
2018-01-02 0.166138
2018-01-03 0.908514
2018-01-04 0.812799
2018-01-05 0.748413
...
2022-12-27 0.347672
2022-12-28 0.606249
2022-12-29 0.701003
2022-12-30 0.488414
2022-12-31 0.440597
Freq: D, Length: 1826, dtype: float64
では、ダウンサンプリングします。
日(D)から週単位(W)にします。平均で集約します。
以下、コードです。
# ダウンサンプリング(1日単位→1週間単位、平均値で集約)
ts_downsampled = ts.resample("W").mean()
# 確認
ts_downsampled
以下、実行結果です。
2018-01-07 0.564914
2018-01-14 0.387317
2018-01-21 0.496218
2018-01-28 0.526550
2018-02-04 0.567396
...
2022-12-04 0.619027
2022-12-11 0.423468
2022-12-18 0.282629
2022-12-25 0.396464
2023-01-01 0.470388
Freq: W-SUN, Length: 261, dtype: float64
集約手法(pandasのresample)
時系列データをダウンサンプリングするときに使える、pandasのresampleメソッドで実施できる主な集約手法です。
| 集約法 | 説明 | メリット | デメリット |
|---|---|---|---|
| mean() | データの平均値を取得します。 | データの全体的な傾向をつかむことができます。 | データに外れ値があると、平均値はそれに引きずられる傾向があります。 |
| sum() | データの合計値を取得します。 | 合計が重要な場合に便利です(例:売上高)。 | データの数が異なる場合、それぞれの期間を直接比較するのが難しい場合があります。 |
| median() | データの中央値を取得します。 | 外れ値の影響を受けにくいです。 | データが二項分布など、特定の形状をしていないと、中央値が真の傾向を反映しないことがあります。 |
| max() | データの最大値を取得します。 | データの最大値を把握でき、特にピークや異常値の検出に役立ちます。 | データの平均的な傾向や分散を捉えられません。また、単独の最大値は外れ値に敏感です。 |
| min() | データの最小値を取得します。 | データの最小値を把握でき、特に最低点や異常値の検出に役立ちます。 | データの平均的な傾向や分散を捉えられません。また、単独の最小値は外れ値に敏感です。 |
| std() | データの標準偏差を取得します。 | データのばらつき具合を把握するのに役立ちます。 | 平均値を中心とした偏差を示すため、データが正規分布に従っていない場合、意味をなさないことがあります。 |
| first() | データの最初の値を取得します。 | データの開始値を直接把握するのに役立ちます。また、時系列データにおける初期状態を把握するのに便利です。 | 間のデータを無視するため、全体的な傾向を把握するのには不適です。 |
| last() | データの最後の値を取得します。 | データの終了値を直接把握するのに役立ちます。また、時系列データにおける最終状態を把握するのに便利です。 | 間のデータを無視するため、全体的な傾向を把握するのには不適です。 |
まとめ
今回は、「時間間隔の異なる時系列データの時間間隔を揃える『時系列リサンプリング』」というお話しをしました。
簡単にできるので、どうしても時間間隔の異なる時系列データの時間間隔を揃える必要がある場合、試しに実施して頂ければと思います。