次の Python コードの出力はどれでしょうか？

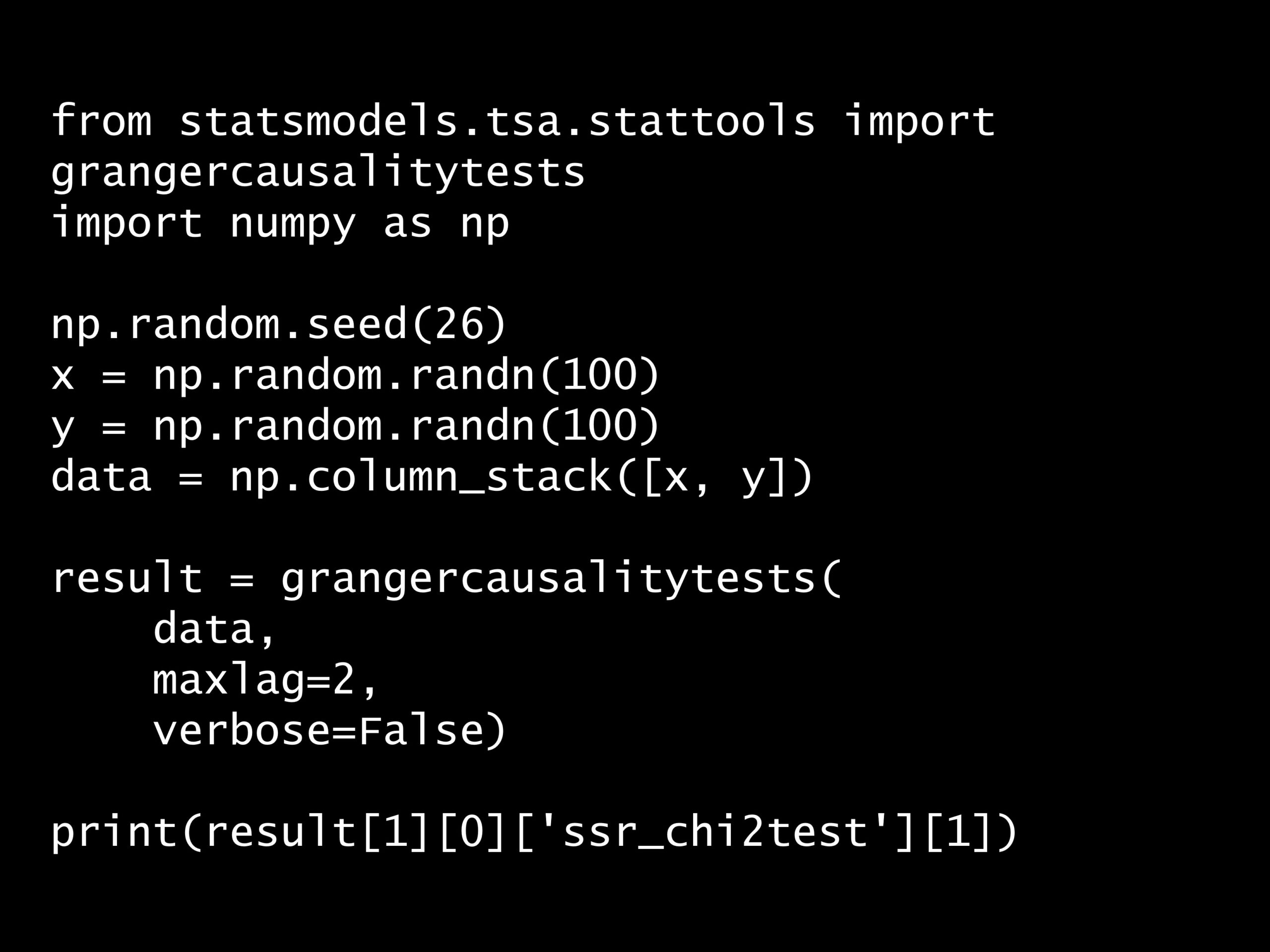
Python コード:

from statsmodels.tsa.stattools import grangercausalitytests
import numpy as np

np.random.seed(26)
x = np.random.randn(100)
y = np.random.randn(100)
data = np.column_stack([x, y])

result = grangercausalitytests(
    data,
    maxlag=2,
    verbose=False)

print(result[1][0]['ssr_chi2test'][1])

 

回答の選択肢:

(A) 1次ラグにおけるGranger因果関係検定のp値
(B) 1次ラグにおけるGranger因果関係検定の統計量
(C) 2次ラグにおけるGranger因果関係検定のp値
(D) 2次ラグにおけるGranger因果関係検定の統計量

出力例:

0.1830303232298846

 

正解: (A)

 

回答の選択肢:

(A) 1次ラグにおけるGranger因果関係検定のp値
(B) 1次ラグにおけるGranger因果関係検定の統計量
(C) 2次ラグにおけるGranger因果関係検定のp値
(D) 2次ラグにおけるGranger因果関係検定の統計量

このPythonコードは、Granger因果関係検定を実行しています。

from statsmodels.tsa.stattools import grangercausalitytests
import numpy as np

np.random.seed(26)
x = np.random.randn(100)
y = np.random.randn(100)
data = np.column_stack([x, y])

result = grangercausalitytests(
    data,
    maxlag=2,
    verbose=False)

print(result[1][0]['ssr_chi2test'][1])

Granger因果関係検定は、二つの時系列データ間に因果関係が存在するかどうかを判断する方法です。具体的には、ある時系列が他の時系列よりも先行する情報を提供し、その予測に役立つかどうかを評価します。

 

詳しく説明します。

numpyの乱数生成器を使って2つの時系列データxとyを生成します。

np.random.seed(26)
x = np.random.randn(100)
y = np.random.randn(100)

 

そして、これらのデータを列方向に結合(np.column_stack)し、2列の時系列データセットdataを作成します。

data = np.column_stack([x, y])

dataに格納されているデータは次のようになっています。

[[ 1.95993212e-01  9.07173602e-02]
 [-1.94123640e+00 -6.72845486e-01]
 [ 7.13785479e-01 -9.20565055e-01]
 [ 6.62148149e-01 -3.28195949e-02]
 [-2.28862121e-01 -1.97196051e+00]
 [ 2.71750826e-01  1.69214375e+00]
 [-2.90689504e-02 -5.37080021e-02]
 [-1.75958211e+00 -1.73726180e+00]
 [-7.94280551e-01 -1.15880839e+00]
 [ 6.22622499e-01 -4.83777994e-01]
 [ 1.59340300e-01 -3.99459879e-01]
 [-1.31430353e+00  3.40905705e-01]
 [ 9.56256542e-01 -4.01524708e-01]
 [-7.96090732e-01  7.14468462e-01]
 [-9.25213316e-01  9.64861296e-02]
 [-1.03197719e+00 -6.27284590e-01]
 [-5.84334464e-01 -5.74909944e-01]
 [ 2.74592527e+00 -5.01122693e-01]
 [ 4.97619216e-01  1.62542504e-01]
 [ 2.08811096e+00 -2.04107769e-04]
 [ 6.88251040e-02 -2.08268732e+00]
 [ 2.73637745e-01 -3.93544307e-01]
 [-9.69933933e-01 -1.33704537e+00]
 [ 1.04352875e+00  1.91428133e+00]
 [ 1.45835748e+00  2.37468545e-01]
 [ 5.82631820e-01  8.71153908e-02]
 [ 6.39545181e-01 -1.63542160e+00]
 [ 2.13584151e-01 -1.61476184e+00]
 [ 3.01550069e-01  5.83621625e-01]
 [ 8.10261527e-01  4.34745262e-01]
 [ 1.03332172e+00 -9.14807651e-01]
 [-1.15648635e+00 -5.58999136e-01]
 [-6.40492598e-01  8.58518571e-01]
 [-3.82342216e-01 -1.71366819e-01]
 [-1.92382178e+00 -1.20015138e+00]
 [ 1.47908095e+00 -9.22095140e-01]
 [ 1.13260577e+00 -5.03948141e-01]
 [ 1.93076023e-01 -2.78546591e-01]
 [-2.66327917e-01 -1.22518003e-01]
 [-7.37382499e-01 -1.15755911e+00]
 [ 2.91028985e-01  1.99776738e-01]
 [ 4.13467943e-01  8.47669970e-01]
 [-3.85524816e-01  6.36343303e-01]
 [-2.53378221e-01 -7.52399447e-01]
 [ 5.83240090e-01  1.98819715e-01]
 [-7.23978261e-01 -9.75327388e-01]
 [ 5.24672103e-02  1.45702275e+00]
 [-1.36488942e+00 -1.98587971e-01]
 [ 4.65516359e-02  3.68559622e-02]
 [-8.38400124e-01 -9.43215448e-01]
 [-2.92428351e-01  2.03886931e+00]
 [-3.55270994e-01  7.04554087e-01]
 [ 2.79357763e-01 -1.83580558e-01]
 [-8.24663746e-01 -6.78076260e-01]
 [ 3.67186609e-02  1.08176421e+00]
 [ 6.29512139e-01 -6.21394615e-01]
 [ 1.07545897e-01 -7.36907683e-01]
 [-2.11239336e+00 -4.50591321e-01]
 [ 2.00727322e-01  1.43941517e+00]
 [-5.70801566e-02 -6.96048035e-01]
 [-9.48707226e-01 -6.85551943e-01]
 [-1.13142731e+00  7.09979440e-01]
 [-2.09542156e-01 -1.08548811e+00]
 [ 2.24178410e+00  1.61714380e+00]
 [-1.55589878e+00 -3.93678729e-01]
 [-6.04401849e-01  7.20029570e-01]
 [-1.18523238e-01  7.94985812e-01]
 [ 1.11371333e+00 -4.54129348e-01]
 [-4.21940417e-01 -1.32447487e+00]
 [ 1.83638722e+00  1.19456735e-01]
 [-1.77447941e-01 -8.16020009e-01]
 [-3.77583064e-01  1.16481988e-02]
 [-7.04872264e-02  1.06773006e+00]
 [ 1.62604455e-02 -7.63572742e-01]
 [ 1.53763806e+00  1.19371324e+00]
 [-1.00789500e+00  5.08379436e-01]
 [-2.06666891e-01 -1.53198760e+00]
 [ 3.51736288e-01  1.15006486e+00]
 [-1.23884666e-01  5.92984682e-01]
 [ 1.38993730e-02 -2.08303590e-01]
 [ 1.27103222e+00  1.88031442e-01]
 [-6.38279171e-01  2.31429941e+00]
 [-9.52772753e-01 -4.01615408e-01]
 [-1.03013820e+00  2.97361115e-01]
 [ 7.98126130e-01  1.75934637e+00]
 [-1.30663210e+00 -2.12272615e-01]
 [ 7.93855475e-02 -2.66623069e-01]
 [-1.55265114e+00  2.06621958e-01]
 [ 7.15824598e-01 -5.88234584e-01]
 [ 3.69779596e-01 -1.21800533e-01]
 [-1.94384628e-01 -5.77568802e-02]
 [ 1.11630433e+00  8.98752978e-01]
 [ 1.36934624e+00  5.01490962e-01]
 [ 4.28145327e-01 -5.78221393e-01]
 [ 2.10569564e+00  3.87823891e-03]
 [ 9.39023436e-01  1.14677722e+00]
 [ 1.60153634e+00  1.41145276e+00]
 [ 4.98698144e-01  1.25459613e+00]
 [ 3.42390417e-01 -7.59373001e-01]
 [-6.56491526e-01 -1.31581325e+00]]

 

このデータセットに対してGranger因果関係検定を行います。

result = grangercausalitytests(
    data,
    maxlag=2,
    verbose=False)

 

このgrangercausalitytests関数は、Granger因果関係検定を行うための関数であり、以下のパラメータを取ります。

• 第一引数は検定を行う2つの時系列データで、列ごとに時系列データが格納された2次元配列（この例ではdata）を入力します。
• maxlagパラメータは検定に用いるラグ数を指定します。ラグは過去の情報が現在に及ぼす影響を表す時間的なズレのことを指します。
• verboseパラメータは、検定の結果を詳細に表示するかどうかを指定します。Falseに設定すると、検定の結果は表示されず、結果は代わりにresult変数に保存されます。

 

ラグ1の時のGranger因果関係検定のp値を表示します。

print(result[1][0]['ssr_chi2test'][1])

0.1830303232298846

p値が0.05以下であれば、帰無仮説（この場合、xがyの予測に役立たない）を棄却することが一般的です。

 

resultに格納されているGranger因果関係検定の結果を、もう少し詳しく説明します。

resultには、各ラグ値（この場合は1と2）ごとのGranger因果関係検定の結果が格納されています。これは辞書（dictionary）形式で格納されており、検定結果はそのラグ値と検定方法をキーとしてアクセスすることができます。

以下は4つの検定方法のキーです。

• ssr_ftest：F検定による検定統計量とp値
• ssr_chi2test：χ^2（カイ二乗）検定による検定統計量とp値
• lrtest：尤度比検定による検定統計量とp値
• params_ftest：別形式のF検定による検定統計量とp値

以上のそれぞれのキーを直接使用することで、特定の検定結計の検定統計量とp値にアクセスすることができます。

たとえば、result[1][0]['ssr_chi2test'][1]により、ラグ1におけるχ二乗検定のp値にアクセスできます（`[1]`がp値を指しています。検定統計量にアクセスする場合は`[0]`を使用します）。

その他のラグ値（この場合は2）でも同様にアクセス可能で、例えばresult[2][0]['ssr_ftest'][0]とすれば、ラグ2におけるF検定の検定統計量にアクセスできます。

タブ「4つのGranger因果関係検定」で、さらに詳しく説明します。

Granger因果関係は、ある時系列が別の時系列の予測に有意に寄与している場合、前者は後者の「Granger原因」であると定義します。具体的には、ある時系列Xが別の時系列Yの未来の値を予測するのに有用な情報を提供するとき、XはYのGranger原因とされます。

Granger因果は、時系列データの分析でよく用いられる概念で、一つの時系列（原因）が別の時系列（結果）に影響を及ぼしているかどうかを明らかにすることができます。

Granger因果関係を識別する主な手段は統計的な手法で、具体的にはGranger因果関係検定を使います。この検定は、ある時系列（説明変数）が別の時系列（被説明変数）の予測に有意に寄与しているかを評価します。

あくまでも統計的な概念であり、真の（実際の）因果関係を示すものではないことに注意が必要です。因果関係の存在を確認するためには、追加の実証的なエビデンスや理論的な支持が必要となります。

Granger因果関係が存在すると主張するためには、Granger因果検定の結果で、帰無仮説（ある時系列が他の時系列の予測に役立たない）を棄却することが必要です。これは、帰無仮説が真である確率を示すp値が一定の有意水準（たとえば0.05）より小さい場合に可能です。

一般的な手順

Granger因果関係検定を行う一般的な手順は以下のようになります。

1. データの準備
検定を行うための時系列データを準備します。一般に、2つ以上の時系列データが必要です。

2. モデルの指定
Granger因果関係検定を行うためのモデル（通常はベクトル自己回帰モデル等）と使用するラグ数を指定します。このラグ数は、過去の情報が現在に及ぼす影響を表す時間的なズレのことを指します。例えば、1ラグのモデルでは、各時系列は1期前の自己の値と他の時系列の値との関係が調べられます。

3. Granger因果検定の適用
Granger因果検定は、ある時系列が他の時系列よりも先行する情報を提供し、その予測に役立つかどうかを評価します。Pythonでは、statsmodels.tsa.stattoolsモジュールのgrangercausalitytests関数を使ってGranger因果関係を検定することができます。

4. 結果の解釈
検定の結果は、F検定、χ二乗検定、尤度比検定などの形で提供されます。これらのp値が一定の有意水準（通常は0.05）以下であれば、帰無仮説（ある時系列が他の時系列の予測に役立たない）を棄却します。

grangercausalitytests関数とは？

grangercausalitytests関数はPythonの統計モデルパッケージStatsmodelsに含まれている関数で、時系列データに対するGranger因果関係の検定を行うことができます。

grangercausalitytests関数には、次のような引数があります。

• x：2つ以上の時系列データを列方向（axis=1）に結合した多次元配列（NumPy array）またはデータフレーム（Pandas DataFrame）。
• maxlag：検定に使用する最大ラグ数。この数値に基づいて、1からmaxlagまでの各ラグ数についてGranger因果関係が検定されます。
• addconst（オプション）：定数（切片）をモデルに追加するかどうかを決定します。デフォルトはTrueです。
• verbose（オプション）：検定の結果を出力するかどうかを決定します。デフォルトはTrueです。

そして、関数は指定したmaxlagまでの各ラグについて4つの統計的検定（ssr_ftest、ssr_chi2test、lrtest、params_ftest）の結果を返します。

• ssr_ftest：F検定による検定統計量とp値
• ssr_chi2test：χ^2（カイ二乗）検定による検定統計量とp値
• lrtest：尤度比検定による検定統計量とp値
• params_ftest：別形式のF検定による検定統計量とp値

Granger因果関係が存在すると主張するためには、Granger因果検定の結果で、帰無仮説（ある時系列が他の時系列の予測に役立たない）を棄却することが必要です。

これは、帰無仮説が真である確率を示すp値が一定の有意水準（たとえば0.05）より小さい場合に可能です。

この4つの統計的検定（ssr_ftest、ssr_chi2test、lrtest、params_ftest）の帰無仮説と対立仮説などを含めた簡単な説明をします。

F検定（ssr_ftestおよびparams_ftest）
モデル内の全ての説明変数の係数はゼロであるという帰無仮説に対して、一つでも説明変数の係数が0ではないという対立仮説を支持する（p値＜0.05）ことが必要です。これは、モデルにおいて一つ以上の予測変数が有意に目的変数に影響を与えることを示すためです。

• 帰無仮説（Null hypothesis）：モデル内の全ての説明変数の係数はゼロである（すなわち、各説明変数は目的変数に対して有意な影響を及ぼさない）。
• 対立仮説（Alternative hypothesis）：少なくとも一つの説明変数の係数はゼロではない（すなわち、少なくとも一つの説明変数が目的変数に有意な影響を及ぼす）。

χ^2（カイ二乗）検定（ssr_chi2test）
観測データは期待頻度に従うという帰無仮説に対して、観測データは期待頻度に従わないという対立仮説を支持する（p値＜0.05）ことが必要です。これは、ある変数が他の変数の予測に寄与することを示すためです。

• 帰無仮説（Null hypothesis）：観測データは期待頻度に従う（すなわち、ある変数が他の変数の予測に寄与しない）。
• 対立仮説（Alternative Hypothesis）：観測データは期待頻度に従わない（すなわち、ある変数が他の変数の予測に寄与する）。

尤度比検定（lrtest）
定数モデルがフルモデルと同じくらい良く、データを説明できるという帰無仮説に対して、フルモデルが定数モデルよりもデータをより良く説明するという対立仮説を支持する（p値＜0.05）ことが必要です。これは、制約がモデルの適合度を低下させることを示すためです。

• 帰無仮説（Null Hypothesis）：制約モデルがフルモデルと同じくらい良く、データを説明できる（すなわち、制約がモデルの適合度を低下させない）。
• 対立仮説（Alternative Hypothesis）：フルモデルが制約モデルよりもデータをより良く説明する（すなわち、制約がモデルの適合度を低下させる）。

以上のいずれか（またはすべて）のp値が有意水準（たとえば0.05）未満であれば、説明変数が目的変数の予測に有意に役立つ、つまりGranger因果関係が存在すると主張できます。ただし、Granger因果関係があるか否かの判断は、これらの統計的検定だけに依存するものではなく、調査の文脈や他の情報も考慮に入れるべきです。

grangercausalitytests関数の結果の見方

今回の以下のコードの結果（result）の中を見ていきます。

from statsmodels.tsa.stattools import grangercausalitytests
import numpy as np

np.random.seed(26)
x = np.random.randn(100)
y = np.random.randn(100)
data = np.column_stack([x, y])

result = grangercausalitytests(
    data,
    maxlag=2,
    verbose=False)

 

ラグ1におけるGranger因果関係検定の結果を見てみます。

以下、コードです。

result[1][0]

 

以下、実行結果です。

{'ssr_ftest': (1.7191228657128637, 0.19293353272637032, 96.0, 1),
 'ssr_chi2test': (1.7728454552663904, 0.1830303232298846, 1),
 'lrtest': (1.7571588096990354, 0.18497929539158597, 1),
 'params_ftest': (1.7191228657128874, 0.19293353272636418, 96.0, 1.0)}

 

これはラグ1におけるGranger因果関係検定の結果を表しており、複数の異なる統計的検定の統計量とp値を含んでいます。

具体的には、以下の通りです。

• ssr_ftest: F検定による統計量とp値。ここでは(1.7191228657128637, 0.19293353272637032, 96.0, 1)という値が得られており、F検定の統計量は約1.719、p値は約0.193です。
• ssr_chi2test: χ二乗検定による統計量とp値。ここでは(1.7728454552663904, 0.1830303232298846, 1)という値が得られており、χ二乗検定の統計量は約1.773、p値は約0.183です。
• lrtest: 尤度比検定による統計量とp値。ここでは(1.7571588096990354, 0.18497929539158597, 1)という値が得られており、尤度比検定の統計量は約1.757、p値は約0.185です。
• params_ftest: 別の形式のF検定（パラメーターF検定）による統計量とp値。ここでは(1.7191228657128874, 0.19293353272636418, 96.0, 1.0)という値が得られており、このF検定の統計量は約1.719、p値は約0.193です。

これらの値は、帰無仮説（つまり、ある時系列（x）が他の時系列（y）の予測に役立たない）が真である場合に、観測された統計量（またはそれ以上の統計量）が得られる確率を表しています。

p値が一般的な有意水準（例えば、0.05）以下であれば、帰無仮説を棄却し、因果関係が存在すると結論付けます。この場合、p値は全て0.05以上なので、xがyの予測に役立たないという帰無仮説は棄却できません。

 

次に、ラグ2におけるGranger因果関係検定です。

ここで注意点があります。

ラグ2におけるGranger因果関係検定の結果とは、2つ前の時点までのデータに基づくGranger因果検定結果になります。

つまり、各ラグに対するGranger因果関係検定とは、そのラグ値までの過去のデータを考慮しています。

繰り返しになりますが、ラグ2におけるGranger因果関係検定の結果は、ラグ1とラグ2の両方のデータが統計的検定に利用されています。

これは、時間的に遡るほどの影響をどの程度現在のデータに持っているかを評価するためです。

では、ラグ2におけるGranger因果関係検定の結果を見てみます。

以下、コードです。

result[2][0]

 

以下、実行結果です。

{'ssr_ftest': (1.012039829790555, 0.3674441686189348, 93.0, 2),
 'ssr_chi2test': (2.1329011466553633, 0.34422816424227887, 2),
 'lrtest': (2.110021970141929, 0.34818860240868266, 2),
 'params_ftest': (1.0120398297905457, 0.3674441686189384, 93.0, 2.0)}

 

これはラグ2におけるGranger因果関係検定の結果を表示しています。この結果も複数の統計的検定の統計量とp値を含んでいます。

具体的には以下の通りです。

• ssr_ftest: F検定による検定統計量とp値、自由度。ここでは(1.012039829790555, 0.3674441686189348, 93.0, 2)という値が得られています。これは、F検定統計量が約1.012で、対応するp値が約0.367、観測値の自由度が93、予測値の自由度が2を意味します。
• ssr_chi2test: χ二乗検定による検定統計量とp値、自由度。この結果は(2.1329011466553633, 0.34422816424227887, 2)となっており、χ二乗統計量は約2.133、対応するp値が約0.344、自由度が2です。
• lrtest: 尤度比検定による検定統計量とp値、自由度。ここでは(2.110021970141929, 0.34818860240868266, 2)という値が得られ、尤度比統計量は約2.110、対応するp値が約0.348、自由度が2です。
• params_ftest: 別の形式のF検定（パラメーターF検定）による検定統計量とp値、自由度。ここでは (1.0120398297905457, 0.3674441686189384, 93.0, 2.0)が得られており、F検定の統計量は約1.012、p値は約0.367、観測値の自由度が93、予測値の自由度が2です。

これらのp値がすべて0.05以上であることから、ラグ2においてはxがyの予測に寄与していないという帰無仮説を棄却できないことになります。