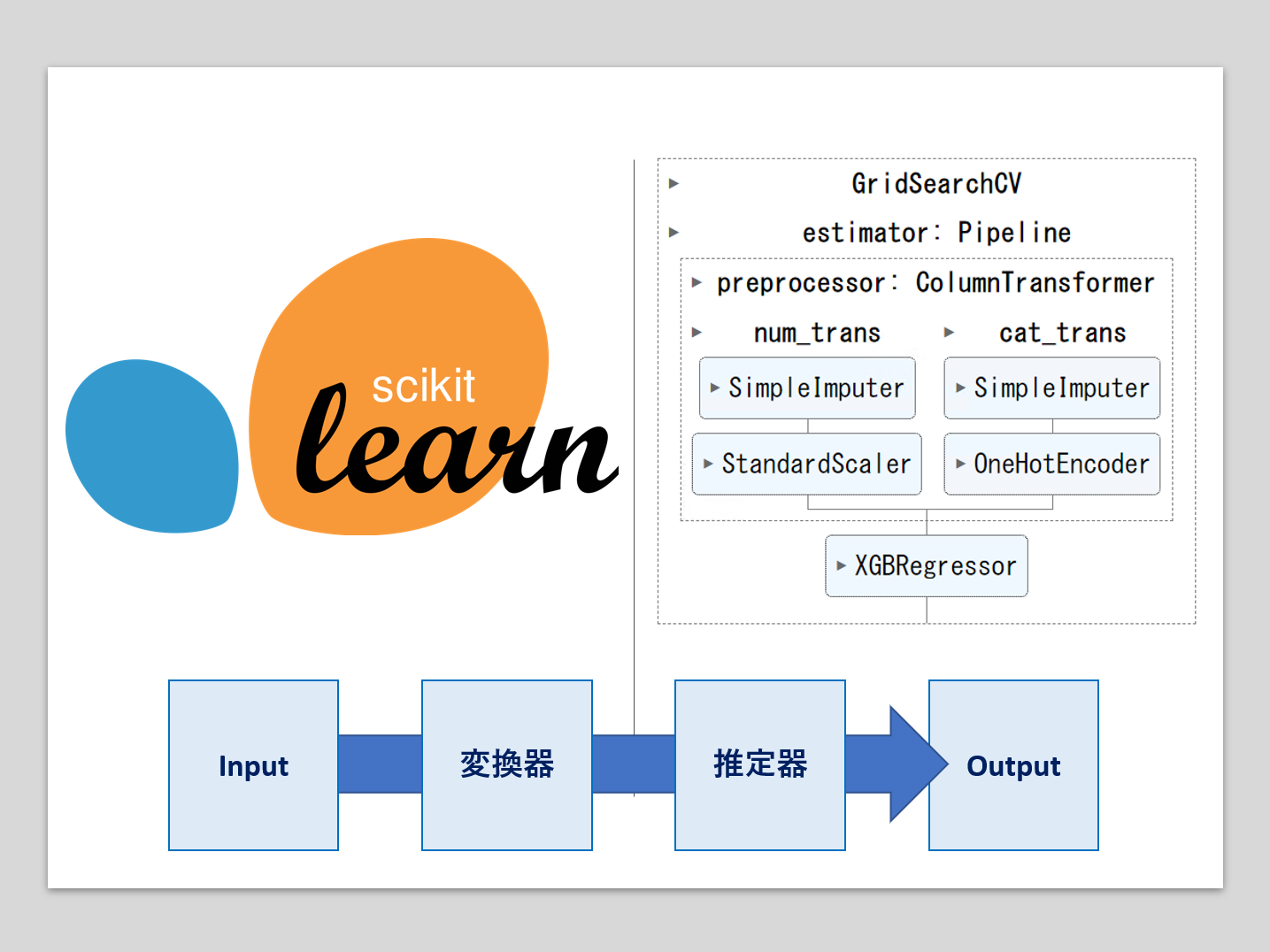
機械学習のパイプラインとは、複数の処理を直列に連結したものです。
最小構成は、1つの変換器と1つの推定器(予測器)を連結したものです。

- 変換器:特徴量X(説明変数)などの欠測値処理や変数変換などの、特徴量変換(Transformor)
- 推定器:線形回帰モデルやXGBoostなどの数理モデルを使い、目的変数yの予測を実施(Estimator)
多くの場合、Inputは特徴量(説明変数)Xで、Outputは目的変数yの予測値です。
全ての変数に対し同じ変換を施すこともあるでしょうが、いつも全ての変数に対し同じ変換を施すわけでもありません。
前回は、変数ごとに変数変換を実施する関数の自動選択について説明しました。
変数変換に利用する関数には、ハイパーパラメータが存在することがあります。
今回は、さらに一歩話を進め、変数ごとに利用する関数を自動選択し、さらにその関数ごとにハイパーパラメータをチューニングする方法についてお話しします。
前回同様に、ベイズ最適化ライブラリーであるOptunaを利用したいと思います。
Contents
利用する関数(変数変換用の関数)
今回は、話しを分かりやすくするために、以下の3つのS字曲線の関数を利用します。
- 一般化ロジスティック関数
- 一般化ハイパボリックタンジェント関数
- ゴンペルツ関数
それぞれ、ハイパーパラメータが存在します。
それぞれを数式を使い紹介します。
一般化ロジスティック関数
以下は、一般化ロジスティック関数の数式です。
\displaystyle f(x) =\frac{L}{(1 + e^{-k \times (x - x_0)})}- xは入力変数
- Lはカーブの最大値
- kはカーブの急峻さを決定するパラメニータ
- x_0はxの値がL / 2になる点
一般化ハイパボリックタンジェント関数
以下は、一般化ハイボリックタンジェント関数の数式です。
\displaystyle f(x) = A \times tanh(B \times x + C) + D- xは入力変数
- A,B,C,Dは形状パラメニータ
ゴンペルツ関数
以下は、Gompertz関数の数式です。
\displaystyle f(x) = a \times e^{-b \times e^{-c \times x}}- xは入力変数
- a,b,cは形状パラメニータ
変換器の関数とクラス
変換器の関数の定義
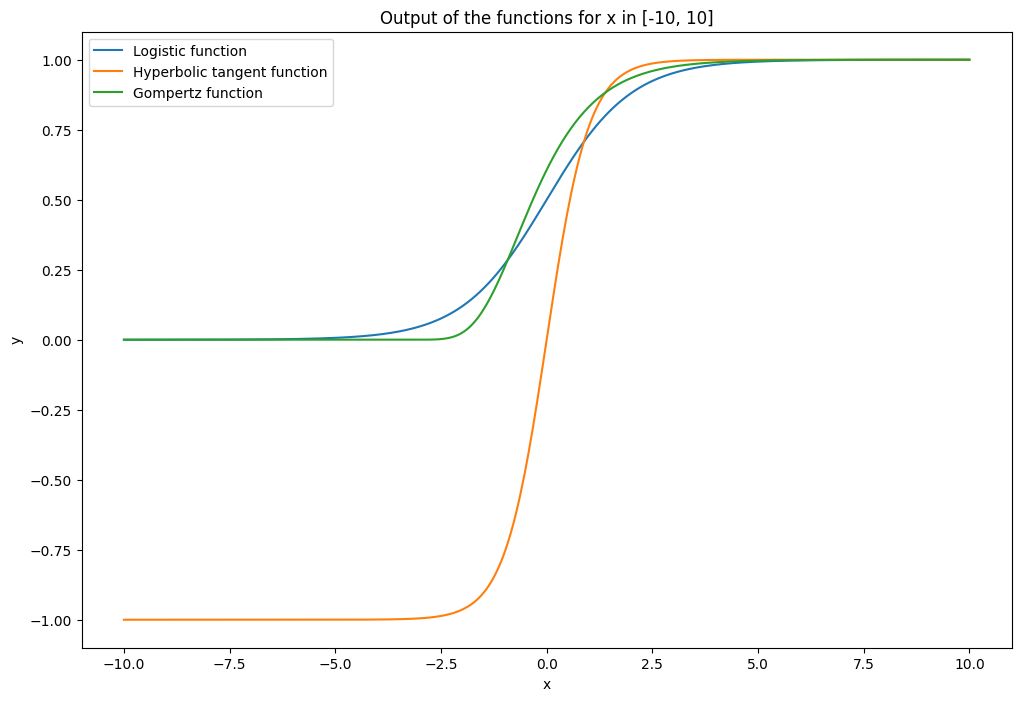
今紹介した以下の3つのS字曲線の関数を、Pythonで定義しプロットしてみます。
- 一般化ロジスティック関数
- 一般化ハイパボリックタンジェント関数
- ゴンペルツ関数
以下、コードです。
# モジュールの読み込み
import numpy as np
import matplotlib.pyplot as plt
# 関数定義
def logistic_function(x, L, k, x0):
return L / (1 + np.exp(-k * (x - x0)))
def hyperbolic_tangent_function(x, A, B, C, D):
return A * np.tanh(B * x + C) + D
def gompertz_function(x, a, b, c):
return a * np.exp(-b * np.exp(-c * x))
# xの生成
x = np.linspace(-10, 10, 400)
# 各関数に任意のパラメーターを設定しxの値を求める
logistic_y = logistic_function(x, L=1, k=1, x0=0)
hyperbolic_tangent_y = hyperbolic_tangent_function(x, A=1, B=1, C=0, D=0)
gompertz_y = gompertz_function(x, a=1, b=0.5, c=1)
# 関数の出力をプロットする
plt.figure(figsize=(12, 8))
plt.plot(x, logistic_y, label='Logistic function')
plt.plot(x, hyperbolic_tangent_y, label='Hyperbolic tangent function')
plt.plot(x, gompertz_y, label='Gompertz function')
plt.title('Output of the functions for x in [-10, 10]')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
このコードは、3つの関数(一般化ロジスティック関数、一般化ハイパボリックタンジェント関数、およびゴンペルツ関数)を使用してグラフを描画します。
まず、必要なモジュール(numpyとmatplotlib)をインポートし、次に各関数を定義します。関数は、指定されたパラメータを使用してxの値に基づいてyの値を計算します。
次に、xの値は、np.linspaceを使用して-10から10までの範囲で均等に分割された400の値を生成します。そして、各関数にそれぞれ特定のパラメータセットを適用し、yの値(出力)を計算します。
最後に、plt.plotを使用して各関数の出力をプロットし、関数ごとに異なるラベルを設定します。x軸とy軸へのラベル付け、グラフのタイトルの設定、凡例の表示を行い、最後にグラフを表示します。
以下、実行結果です。
変換器のクラス化
あとでこれらの関数をパイプラインで利用するため、以下のようにクラス化します。
以下、コードです。
# モジュールの読み込み
from sklearn.base import BaseEstimator, TransformerMixin
# S字曲線を適用するカスタム変換器クラス
class CustomSigmoidTransformer(BaseEstimator, TransformerMixin):
def __init__(self, curve_params=None):
self.curve_params = curve_params if curve_params is not None else []
def fit(self, X, y=None):
return self
def transform(self, X):
transformed_X = np.copy(X)
for i, params in enumerate(self.curve_params):
curve_type = params.pop('curve_type')
if curve_type == 'logistic':
transformed_X[:, i] = logistic_function(X[:, i], **params)
elif curve_type == 'hyperbolic_tangent':
transformed_X[:, i] = hyperbolic_tangent_function(X[:, i], **params)
elif curve_type == 'gompertz':
transformed_X[:, i] = gompertz_function(X[:, i], **params)
params['curve_type'] = curve_type
return transformed_X
このコードは、定義した3つの関数(一般化ロジスティック関数、一般化ハイパボリックタンジェント関数、およびゴンペルツ関数)をデータに適用するためのカスタムscikit-learn変換器(`BaseEstimator` および `TransformerMixin` クラスを継承)を定義しています。
- `
__init__` メソッドは、変換器の初期化を行います。オプションのパラメータ `curve_params` は、各機能がどのタイプのS字形を使用するか及びその対応するパラメータを指定するための辞書のリストです。`curve_params` は `None` がデフォルトで、その場合空リストが割り当てられます。 - `
fit` メソッドは、トランスフォーマーが学習する特別な動作はないため、自身 (`self`) を返すだけです。 - `
transform` メソッドは、説明変数(特徴量) `X` を受け取ります。まず、`np.copy(X)` を使用して入力データのコピーを作成します。次に、各 `curve_params` のリストを反復処理し、各S字形関数を対応する特徴に適用します。それぞれのS字形関数のパラメータは、 `curve_params` から取得します。最後に、変換された新しいデータセットを返します。
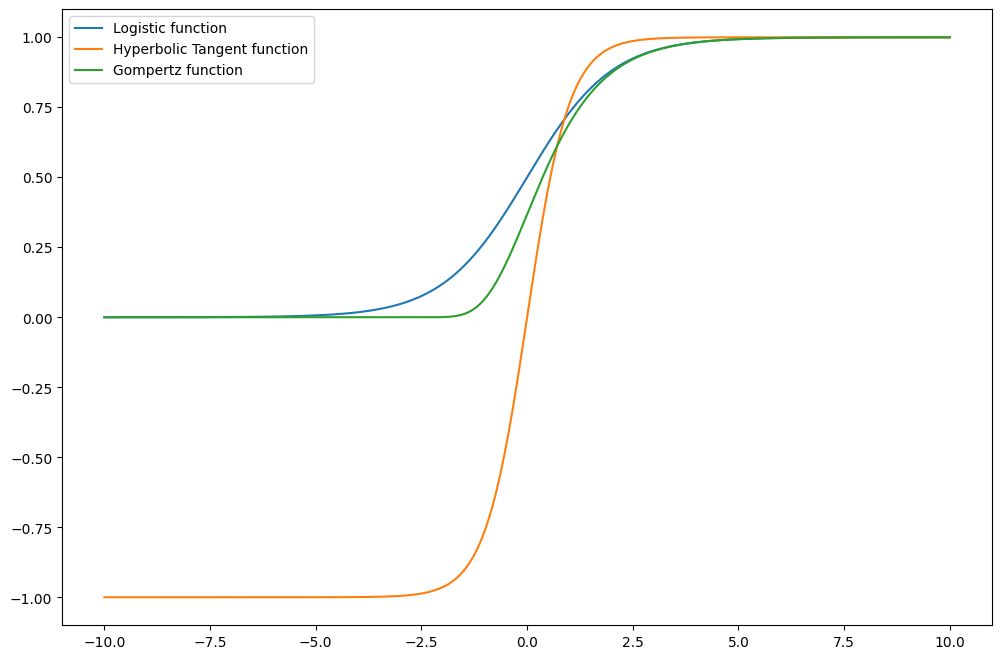
この変換器クラスを使い、S字曲線を描いてみます。
以下、コードです。
# 3変量のxの値を作成する
x = np.transpose([np.linspace(-10, 10, 400) for _ in range(3)])
# 各変数のハイパーパラメータの設定
params = [
{'curve_type': 'logistic', 'L': 1, 'k': 1, 'x0': 0},
{'curve_type': 'hyperbolic_tangent', 'A': 1, 'B': 1, 'C': 0, 'D': 0},
{'curve_type': 'gompertz', 'a': 1, 'b': 1, 'c': 1}
]
# 変換器のインスタンスの生成
transformer = CustomSigmoidTransformer(curve_params=params)
# xに対し変換器を適用する
transformed_X = transformer.transform(x)
# 変換された関数の出力をプロットする
plt.figure(figsize=(12, 8))
plt.plot(x[:, 0], transformed_X[:, 0], label='Logistic function')
plt.plot(x[:, 1], transformed_X[:, 1], label='Hyperbolic Tangent function')
plt.plot(x[:, 2], transformed_X[:, 2], label='Gompertz function')
plt.legend()
plt.show()
以下、実行結果です。
パイプラインの学習と予測
今定義した関数や変換器クラスを使い、パイプラインを構築していきます。変換器はXGBoostを使います。
準備
まず、必要なモジュールを読み込みます。
以下、コードです。
import pandas as pd
import numpy as np
import xgboost as xgb
import optuna
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import (
mean_absolute_error,
mean_absolute_percentage_error,
r2_score)
import matplotlib.pyplot as plt
pandas: このライブラリは、データ分析と操作のための高度なデータ構造と操作を提供します。具体的には、データフレームを扱うために使われます。numpy: Numpyは、数値計算を効率的に行うためのライブラリです。ベクトルや行列等の配列に対する演算が提供されます。xgboost:XGBoostは、決定木ベースのアンサンブル学習を行う勾配ブースティングライブラリの一つです。精度が高く、並列計算に対応しているため計算速度が速い特徴があります。optuna: Optunaは、ハイパーパラメータの自動最適化(ハイパーパラメータチューニング)を支援するライブラリです。sklearn.base.BaseEstimator, sklearn.base.TransformerMixin: Scikit-learnライブラリを使用してカスタムエスティメータまたは変換器を作成するためのクラスです。sklearn.pipeline.Pipeline: ワークフローを定義するためのユーティリティクラスで、特に前処理ステップとモデル訓練ステップを一緒に実行するときに有用です。sklearn.model_selection.train_test_split: これにより、データセットを訓練データとテストデータに分割することができます。sklearn.metrics (mean_absolute_error, mean_absolute_percentage_error, r2_score): これらはモデルの予測の品質を評価するための異なるメトリクス(評価指標)です。matplotlib.pyplot: データを視覚化するためのライブラリで、このモジュールを使ってグラフを作成したり、作成したグラフをカスタマイズしたりすることができます。
次に、サンプルデータを読み込み、学習データとテストデータに分割します。目的変数yは1つで、特徴量(説明変数)は5変数です。
以下からダウンロードできます。
sample_data.csv
https://www.salesanalytics.co.jp/913d
以下、コードです。
# データを読み込む
data = pd.read_csv('sample_data.csv')
# 特徴量Xと目標変数yを定義
X = data.drop('Target', axis=1)
y = data['Target']
# 学習データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
test_size=0.2,
random_state=42)
- X_train: 学習データの特徴量
- X_test: テストデータの特徴量
- y_tarin: 学習データの目的変数
- y_test: テストデータの目的変数
ハイパーパラメータチューニング
では、以下の手順で、変数ごとの関数選択、その各関数や推定器のハイパーパラメータのチューニングを実施します。
- 関数と変換器クラスの定義
- Optunaの目的関数の定義
- ハイパーパラメータチューニングの実施
その結果、パイプラインにとって最適と思われるハイパーパラメータの値(関数選択含む)を出力します。
関数と変換器クラスの定義
以下、コードです。先ほどのものと同じです。
# 一般化ロジスティック関数
def logistic_function(x, L, k, x0):
return L / (1 + np.exp(-k * (x - x0)))
# 一般化ハイパボリックタンジェント関数
def hyperbolic_tangent_function(x, A, B, C, D):
return A * np.tanh(B * x + C) + D
# Gompertz関数
def gompertz_function(x, a, b, c):
return a * np.exp(-b * np.exp(-c * x))
# S字曲線を適用するカスタム変換器クラス
class CustomSigmoidTransformer(BaseEstimator, TransformerMixin):
def __init__(self, curve_params=None):
self.curve_params = curve_params if curve_params is not None else []
def fit(self, X, y=None):
return self
def transform(self, X):
transformed_X = np.copy(X)
for i, params in enumerate(self.curve_params):
curve_type = params.pop('curve_type')
if curve_type == 'logistic':
transformed_X[:, i] = logistic_function(X[:, i], **params)
elif curve_type == 'hyperbolic_tangent':
transformed_X[:, i] = hyperbolic_tangent_function(X[:, i], **params)
elif curve_type == 'gompertz':
transformed_X[:, i] = gompertz_function(X[:, i], **params)
params['curve_type'] = curve_type
return transformed_X
Optunaの目的関数の定義
機械学習モデルのハイパーパラメータチューニングに使用されるOptunaの目的関数を定義します。
以下、コードです。特徴量(説明変数)の変数の数は可変にしています。
# Optunaによるハイパーパラメータチューニングの関数
def objective(trial):
# S字曲線のパラメータチューニング
curves = []
transformed_X = np.empty_like(X_data)
for i in range(X_data.shape[1]):
# 各説明変数に対してS字曲線のタイプを選択
curve_type = trial.suggest_categorical(f"curve_type_{i}", ["logistic", "hyperbolic_tangent", "gompertz"])
# 関連するパラメータを選択
if curve_type == 'logistic':
params = {
'L': trial.suggest_float(f"L_{i}", 0.1, 10),
'k': trial.suggest_float(f"k_{i}", 0.1, 10),
'x0': trial.suggest_float(f"x0_{i}", -10, 10)
}
elif curve_type == 'hyperbolic_tangent':
params = {
'A': trial.suggest_float(f"A_{i}", 0.1, 10),
'B': trial.suggest_float(f"B_{i}", 0.1, 10),
'C': trial.suggest_float(f"C_{i}", -10, 10),
'D': trial.suggest_float(f"D_{i}", -10, 10)
}
elif curve_type == 'gompertz':
params = {
'a': trial.suggest_float(f"a_{i}", 0.1, 10),
'b': trial.suggest_float(f"b_{i}", 0.1, 10),
'c': trial.suggest_float(f"c_{i}", -10, 10)
}
else:
raise ValueError("Invalid curve type")
# Append curve params
curves.append({'curve_type': curve_type, **params})
# XGBoostのハイパーパラメータチューニング
xgb_params = {
'learning_rate': trial.suggest_loguniform('learning_rate', 0.01, 0.5),
'max_depth': trial.suggest_int('max_depth', 3, 9),
'subsample': trial.suggest_uniform('subsample', 0.5, 1.0),
'colsample_bytree': trial.suggest_uniform('colsample_bytree', 0.5, 1.0),
'n_estimators': trial.suggest_int('n_estimators', 50, 300)
}
# パイプラインの構築
pipeline = Pipeline([
('transformer', CustomSigmoidTransformer(curve_params=curves)),
('regressor', xgb.XGBRegressor(**xgb_params))
])
pipeline.fit(X_data, y_data)
# モデルの評価
predictions = pipeline.predict(X_data)
return np.mean((y_data - predictions) ** 2)
コードの各部分を簡単に順に説明します。
- Optunaの目的関数の定義:
objective(trial)という関数を定義。この関数は試行を意味するトライアル(trial)を引数に取ります。この関数内で、モデルのハイパーパラメータを選択し、最終的なモデルの性能を評価します。- S字曲線のパラメータチューニングの設定: 入力データ
X_dataの各特徴量に対して、S字曲線(sigmoid curve)のタイプ(一般化ロジスティック関数、一般化ハイパボリックタンジェント関数、およびゴンペルツ関数)の選択(タイプそのものがハイパーパラメータ)し、それぞれのタイプに応じたハイパーパラメータ(例えば、ロジスティック曲線の場合はL,k,x0)を設定。ハイパーパラメータの探索範囲が定義されています。 - XGBoostのハイパーパラメータチューニングの設定: XGBoostモデルのいくつかの重要なハイパーパラメータ(学習率、最大深度、サブサンプル率、カラムサンプルバイトゥリー、推定器の数)を設定。ハイパーパラメータの探索範囲が定義されています。
- パイプラインの構築:
Pipelineを使用して、データ変換器(CustomSigmoidTransformer)とXGBoost回帰モデルを組み合わせたパイプラインを構築しています。これにより、データの前処理とモデルの訓練を一連のステップとして扱うことができます。 - モデルの訓練: 構築したパイプラインを
X_dataとy_dataに適用して、モデルを訓練します。 - モデルの評価: 訓練されたモデルを使用して
X_dataの予測を行い、実際の値y_dataとの平均二乗誤差を計算しています。この値がOptunaによる最適化の目的関数として使用されます。
- S字曲線のパラメータチューニングの設定: 入力データ
ハイパーパラメータチューニングの実施
Optunaを用いて機械学習モデルのハイパーパラメータを、学習データを使いチューニング(設定した試行回数の中で最もいいハイパーパラメータの探索)をしていきます。
以下、コードです。
# 学習データの設定
X_data = X_train.values
y_data = y_train.values
# Optunaによるハイパーパラメータ探索実行
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=100)
# 最適なパラメータの出力
print("Best trial:")
trial = study.best_trial
print(f" Value: {trial.value}")
print(" Params: ")
for key, value in trial.params.items():
print(f" {key}: {value}")
コードの各部分を簡単に順に説明します。
- 学習データの設定
X_data = X_train: 学習用の特徴量(X_train)をX_dataに代入しています。y_data = y_train: 学習用の目的変数(y_train)をy_dataに代入しています。
- Optunaのスタディ作成
study = optuna.create_study(direction="minimize"): Optunaにおいて新しいスタディ(実験)を作成します。ここでのdirection="minimize"は、目的関数の最小化(例えば、誤差の最小化)を目指すことを示します。study.optimize(objective, n_trials=100): 先に定義したobjective関数を使用して、100回の試行(n_trials=100)を通じてハイパーパラメータを最適化します。
- 最適なパラメータの出力
- スタディで最も良い結果を得た試行(
best_trial)を出力します。 print(f" Value: {trial.value}"): 最適な試行の目的関数の値を出力します。- 以下のループで、最適な試行の各ハイパーパラメータの値を出力します。
for key, value in trial.params.items(): print(f" {key}: {value}")
- スタディで最も良い結果を得た試行(
以下、実行結果です。
Best trial:
Value: 1.9942332161051506e-07
Params:
curve_type_0: logistic
L_0: 1.1216606915075427
k_0: 3.861648155317229
x0_0: 3.4238921296298095
curve_type_1: logistic
L_1: 7.173175758269514
k_1: 0.8030255037499656
x0_1: 9.894391149451344
curve_type_2: hyperbolic_tangent
A_2: 9.312350403256
B_2: 1.5018123822666092
C_2: 8.314736969768592
D_2: -0.34898906137010577
curve_type_3: logistic
L_3: 5.9729340374498525
k_3: 8.28305342491419
x0_3: 1.9165879140109334
curve_type_4: logistic
L_4: 2.894581980180275
k_4: 6.482531519447111
x0_4: 5.7057642117282175
learning_rate: 0.4563521600861446
max_depth: 9
subsample: 0.5347061773401943
colsample_bytree: 0.9621577212699071
n_estimators: 299
これはOptunaによるハイパーパラメータチューニング、つまりベストトライアル(設定した試行回数の中で最もいいハイパーパラメータ)の結果です。
目標関数(objective function)が最小の値1.9942332161051506e-07を返しています。
最適なモデルのハイパーパラメータは次の通りです。
- 0番目の特徴量に対するS字曲線
- 一般化ロジスティック関数
- L=1.1216606915075427、k=3.861648155317229、x0=3.4238921296298095
- 1番目の特徴量に対するS字曲線
- 一般化ロジスティック関数
- L=7.173175758269514、k=0.8030255037499656、x0=9.894391149451344
- 2番目の特徴量に対するS字曲線
- 一般化ハイパーボリックタンジェント関数
- A=9.312350403256、B=1.5018123822666092、C=8.314736969768592、D=-0.34898906137010577
- 3番目の特徴量に対するS字曲線
- 一般化ロジスティック関数
- L=5.9729340374498525、k=8.28305342491419、x0=1.9165879140109334
- 4番目の特徴量に対するS字曲線
- 一般化ロジスティック関数
- L=2.894581980180275、k=6.482531519447111、x0=5.7057642117282175
- 推定器XGboostのパラメータ
- learning_rate = 0.4563521600861446
- max_depth = 9 (決定木の最大の深さ)
- subsample = 0.5347061773401943
- colsample_bytree = 0.9621577212699071
- n_estimators = 299 (作成される弱学習器(決定木)の数)
パイプラインを構築し検証
Optunaによるハイパーパラメータの最適化後、最適なパラメータを使用してモデルを訓練し、テストデータでその性能を評価しています。
最適ハイパーパラメータでパイプラインを構築
先ずは、先ほど見つけたベストなハイパーパラメータを使い、学習データでパイプラインを構築します。
以下、コードです。
# トライアルから最良のパラメータを取得
optimal_params = trial.params
# 各特徴量の使用する曲線とそのハイパーパラメータを設定
curves = []
for i in range(X_data.shape[1]):
curve_type = optimal_params.get(f"curve_type_{i}")
if curve_type == 'logistic':
params = {
'L': optimal_params.get(f"L_{i}"),
'k': optimal_params.get(f"k_{i}"),
'x0': optimal_params.get(f"x0_{i}")
}
elif curve_type == 'hyperbolic_tangent':
params = {
'A': optimal_params.get(f"A_{i}"),
'B': optimal_params.get(f"B_{i}"),
'C': optimal_params.get(f"C_{i}"),
'D': optimal_params.get(f"D_{i}")
}
elif curve_type == 'gompertz':
params = {
'a': optimal_params.get(f"a_{i}"),
'b': optimal_params.get(f"b_{i}"),
'c': optimal_params.get(f"c_{i}")
}
else:
raise ValueError("無効な曲線タイプ")
curves.append({'curve_type': curve_type, **params})
# XGBoostに対しハイパーパラメータを設定
xgb_params = {
'learning_rate': optimal_params.get('learning_rate'),
'max_depth': optimal_params.get('max_depth'),
'subsample': optimal_params.get('subsample'),
'colsample_bytree': optimal_params.get('colsample_bytree'),
'n_estimators': optimal_params.get('n_estimators')
}
# パイプラインの構築(変換器+推定器)
optimal_pipeline = Pipeline([
('transformer', CustomSigmoidTransformer(curve_params=curves)),
('regressor', xgb.XGBRegressor(**xgb_params))
])
# パイプラインを学習
optimal_pipeline.fit(X_train.values, y_train.values)
コードの各部分を簡単に順に説明します。
- トライアルから最良のパラメータを取得:
optimal_params = trial.params:で、Optunaによる最適化プロセスで見つかった最良のパラメータセットを取得します。 - 各特徴量の使用する曲線とそのハイパーパラメータを設定:各特徴量に対して、最適な曲線タイプ(一般化ロジスティック関数、一般化ハイパボリックタンジェント関数、およびゴンペルツ関数)とそのハイパーパラメータを設定します。
- XGBoostに対しハイパーパラメータを設定:Optunaの最適化により得られたXGBoostモデルのハイパーパラメータを設定しています。
- パイプラインの構築(変換器+推定器):
Pipelineを使用して、データ変換器(CustomSigmoidTransformer、ここで曲線パラメータが使用されます)とXGBoost回帰モデルを組み合わせます。 - パイプラインを学習:構築したパイプラインを学習データ(
X_train,y_train)に適用し訓練します。
最適なパイプラインで予測し検証
以下、コードです。
# 最適なパイプラインを使って予測を生成
predicted_y = optimal_pipeline.predict(X_test.values)
# 評価指標を計算
mae = mean_absolute_error(y_test, predicted_y)
mape = mean_absolute_percentage_error(y_test, predicted_y)
r2 = r2_score(y_test, predicted_y)
print('MAE:',mae)
print('MAPE:',mape,'%')
print('R2:',r2)
コードの各部分を簡単に順に説明します。
- 予測の生成:訓練済みのパイプラインを使用してテストデータ(
X_test)に対する予測を生成します。 - 評価指標の計算と出力:生成された予測と実際のテストデータのターゲット値(
y_test)を比較して、平均絶対誤差(MAE)、平均絶対パーセント誤差(MAPE)、決定係数(R2スコア)を計算し、それらを出力しています。
以下、実行結果です。
MAE: 0.26494686183086763 MAPE: 1.015784392839631 % R2: 0.9565935186404735
これらの値は、機械学習モデル(この場合はカスタムパイプライン)の予測の質を評価するためのメトリクスです。
- MAE (Mean Absolute Error)
- 絶対誤差の平均です。つまり、各予測とその対応する真の値の間の絶対値を取った誤差の平均を表します。
- MAEが0に近いほどモデルの予測精度が高いと言えます。
- このケースでは、MAEは0.26です。
- MAPE (Mean Absolute Percentage Error)
- 平均絶対パーセンテージエラーで、予測誤差の平均値をパーセンテージで表したものです。
- MAPEも0に近いほどよく、完全な予測ではMAPEは0になります。
- このケースでは、MAPEは約1.02%です。
- R2 (R-squared)
- 決定係数とも呼ばれ、予測値が目標値をどれだけ説明しているかを示します。
- R2の範囲は通常0から1で、1に近いほどモデルがデータをよく説明していることを示します。
- このケースでは、R2は0.96です。
以上のことから、予測の精度が高く、実際のデータを非常によく説明していることを示しています。
散布図(実測×予測)
テストデータの、実際の値と予測された値の関係を視覚的に示す散布図を作成しています。
以下、コードです。
plt.figure(figsize=(10,8))
plt.scatter(y_test, predicted_y, alpha=0.7)
plt.plot([y_test.min(), y_test.max()], [predicted_y.min(), predicted_y.max()], color='red')
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.title('Actual vs Predicted')
plt.show()
コードの各部分を簡単に順に説明します。
- グラフの初期設定:
plt.figure(figsize=(10,8)):で、グラフのサイズを幅10インチ、高さ8インチに設定します。 - 散布図の描画:
plt.scatter(y_test, predicted_y, alpha=0.7)で、実際の値(y_test)と予測値(predicted_y)の散布図を描画します。alpha=0.7は点の透明度を設定しており、0(完全に透明)から1(完全に不透明)の範囲で値を設定できます。 - 対角線の描画:
plt.plot([y_test.min(), y_test.max()], [predicted_y.min(), predicted_y.max()], color='red')で、実際の値の最小値と最大値を基にした直線(赤色)を描画します。この直線は、完全な予測精度(実際の値と予測値が完全に一致する場合)を示す基準線として機能します。 - ラベルとタイトルの設定:
plt.xlabel('Actual')とplt.ylabel('Predicted'):で、x軸に「Actual」(実際の値)、y軸に「Predicted」(予測値)というラベルを設定します。plt.title('Actual vs Predicted'):で、グラフのタイトルを「Actual vs Predicted」(実際の値と予測値の比較)として設定します。 - グラフの表示:
plt.show()で、上記の設定に基づいたグラフを表示します。
以下、実行結果です。
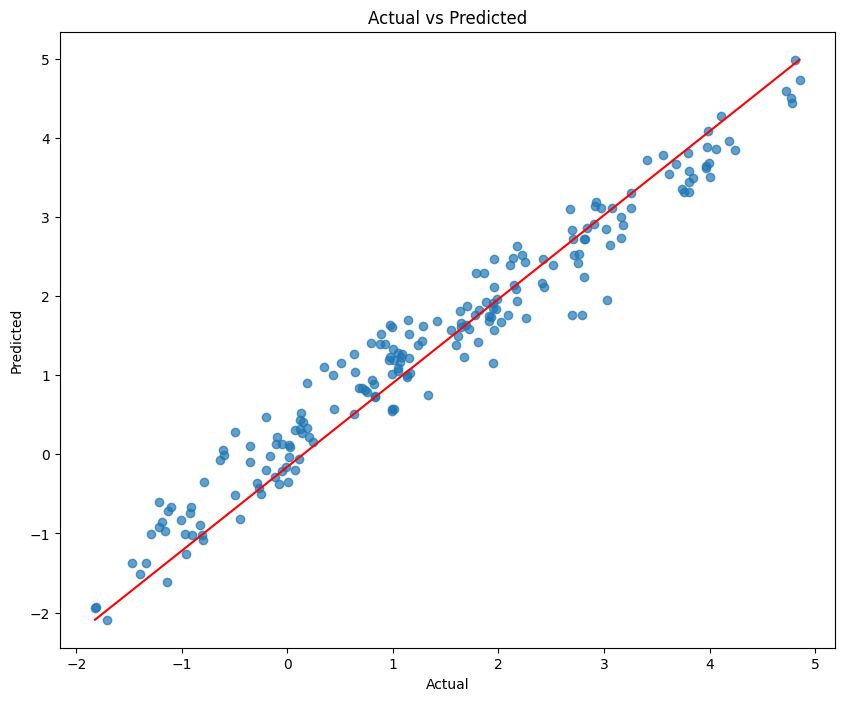
予測精度が高い場合、実測値(Actual)と予測値(Predicted)の散布図を描くと、このように赤い対角線近辺にプロットされます。
まとめ
今回は、変数ごとに利用する関数を自動選択し、さらにその関数ごとにハイパーパラメータをチューニングする方法についてお話ししました。
全ての特徴量(説明変数)に対し、同じ変数変換をせず、変数ごとに実施する変数変換やそのハイパーパラメータを設定した方がいいでしょう。
今回の方法は、AutoMLのように、予測精度を最適化するようにハイパーパラメータチューニングをしたため、もしかしたら可笑しな設定をしている可能性があります。
そのため、最終的には人が判断した方がいいでしょう。
次回は、変換器のアルゴリズム(回帰モデルや分類モデルなど)も複数用意し、その中から最適な変換器とそのハイパーパラメータをチューニングする方法について説明します。
このあたりまでくると、自作AutoMLになります。