データ分析の世界で最も難しく、そして最も重要な問いの一つが「原因と結果を正しく見極める」ことです。

健康食品を飲んだら体調が良くなった、新しい教育プログラムを導入したら成績が上がった、マーケティング施策を実施したら売上が伸びた。

これらは本当に因果関係があるのでしょうか、それとも単なる偶然の一致なのでしょうか。

私たちは日常的に、観察したデータから因果関係を推測しています。

しかし、その推測はしばしば間違っています。

なぜなら、単純な比較では見落としてしまう「隠れた要因」が存在するからです。

統計的因果推論は、このような落とし穴を避けて、観察データから正しい因果関係を導き出すための科学的な方法論です。

今回は、実験ができない現実世界のデータから、いかにして「りんごとりんご」の公平な比較を実現し、信頼できる結論を導くかを簡単に解説します。

なぜ「公平な比較」が重要なのか

　栄養指導プログラムの例で考える比較の難しさ

ある病院で、糖尿病患者向けの栄養指導プログラムの効果を評価したいという場面を想像してみてください。

プログラムを受けた患者さんの血糖値が改善したというデータが得られたとします。

これで「プログラムは効果的だ」と結論づけてよいでしょうか。

実は、そう単純ではありません。

なぜなら、栄養指導を受けた患者さんと受けなかった患者さんには、プログラムへの参加以外にも様々な違いがある可能性が高いからです。

例えば、プログラムに参加した患者さんは、もともと健康意識が高く、医師のアドバイスを積極的に聞く傾向があるかもしれません。

あるいは、病状が深刻で医師から強く勧められた人かもしれません。

時間的・経済的な余裕がある人だけが参加できた可能性もあります。これらの要因自体が、血糖値の改善に影響している可能性があるのです。

　単純比較が導く間違った結論

単純な比較の危険性を、もう一つの例で見てみましょう。

ある企業で、在宅勤務制度を利用している社員の生産性を調査したところ、オフィス勤務の社員よりも高いという結果が出ました。

これを見て「在宅勤務は生産性を向上させる」と結論づけるのは早計です。

よく調べてみると、在宅勤務を選択した社員には特定の傾向がありました。

子育て中の社員が多く、通勤時間を削減できることで仕事に集中できる時間が増えていました。

また、自己管理能力の高い社員が在宅勤務を選ぶ傾向もありました。

さらに、在宅勤務が許可されるのは、すでに一定の成果を上げている信頼できる社員に限られていたのです。

つまり、生産性の違いは在宅勤務そのものの効果ではなく、在宅勤務を選択した（あるいは選択できた）社員の特性によるものかもしれません。

このような状況で単純に比較しても、在宅勤務の真の効果は分からないのです。

　ランダム化試験ができない現実世界での課題

理想的な因果関係の検証方法は、ランダム化比較試験（RCT）です。

くじ引きのようにランダムに人を振り分けることで、グループ間の違いを偶然のレベルまで小さくできます。

しかし、現実世界ではRCTを実施できない場面が多々あります。

倫理的な理由で、必要な治療をランダムに拒否することはできません。

実務的な理由で、教育プログラムや経営施策をランダムに適用することが困難な場合もあります。

さらに、すでに実施された施策の効果を後から評価したい場合は、時間を巻き戻してRCTを行うことは不可能です。

そこで必要になるのが、観察データから因果関係を推論する技術です。

「もしこの人が違う選択をしていたら、どうなっていたか」という反事実を、データから推測する必要があります。

これが統計的因果推論の核心であり、今回紹介する様々な手法の目的なのです。

「似た人同士」を見つける魔法の数字「傾向スコア」

　傾向スコアとは何か：山田さんと佐藤さんの例

傾向スコアという概念を理解するために、具体的な例から始めましょう。

山田さんという55歳の男性患者がいます。

彼はBMI28で肥満気味、糖尿病と診断されており、フルタイムで働いています。

一方、佐藤さんという別の患者は、54歳の男性で、BMI27、同じく糖尿病患者で、フルタイムの仕事をしています。

この二人は非常に似た特徴を持っていますが、山田さんは栄養指導プログラムに参加し、佐藤さんは参加しませんでした。

もし二人の血糖値の変化を比較すれば、栄養指導の効果をかなり正確に推定できそうです。

なぜなら、二人の違いはほぼ「プログラムに参加したかどうか」だけだからです。

しかし、実際のデータには何百人、何千人もの患者がいて、それぞれが年齢、性別、BMI、病歴、生活習慣など、多くの特徴を持っています。

この中から「似た人同士」を見つけるのは、まるで巨大な迷路を解くような作業です。

ここで登場するのが傾向スコアです。

傾向スコアとは、「ある人が介入（この場合は栄養指導）を受ける確率」を一つの数値にまとめたものです。

年齢、BMI、病歴など、すべての情報を統計モデルに入力し、「この特徴を持つ人が栄養指導を受ける確率は何％か」を計算します。

　傾向スコアの計算方法と解釈

傾向スコアの計算は、通常ロジスティック回帰という統計手法を使います。

これは「YES/NO」の結果（栄養指導を受けるか受けないか）を予測するのに適した方法です。

例えば、山田さんの情報をモデルに入力すると、「栄養指導を受ける確率70％」という結果が出たとします。

これが山田さんの傾向スコアです。同様に、佐藤さんの傾向スコアが72％だったとしましょう。

ここで重要なのは、二人の傾向スコアがほぼ同じ（70％と72％）にもかかわらず、実際には一人は指導を受け、一人は受けなかったという点です。

傾向スコアが近い人同士は、「介入を受ける可能性」という観点から見て似ています。

つまり、測定されたすべての特徴を一つの数値に要約することで、多次元の複雑な比較を一次元のシンプルな比較に変換できるのです。

　実務での活用シーンと注意点

傾向スコアは様々な分野で活用されています。

医療分野では新しい治療法の効果評価、教育分野では教育プログラムの効果測定、ビジネス分野ではマーケティング施策の効果分析などに使われています。

例えば、ECサイトでプレミアム会員制度の効果を評価したいとします。

プレミアム会員は一般会員より購買額が多いですが、これは会員制度の効果でしょうか、それとももともと購買意欲の高い人がプレミアム会員になっただけでしょうか。

過去の購買履歴、サイト訪問頻度、登録期間などから傾向スコアを計算し、「プレミアム会員になる確率」が同じくらいの人同士で比較することで、会員制度の真の効果を推定できます。

ただし、傾向スコアには重要な限界があります。

最大の問題は、測定されていない要因は考慮できないことです。

例えば、「やる気」や「家族のサポート」といった測定困難な要因が結果に大きく影響する場合、傾向スコアを使っても正しい因果効果は推定できません。

また、傾向スコアが極端な値（0に近いまたは1に近い）の場合は注意が必要です。

傾向スコアが0.01の人は「ほぼ確実に介入を受けない」特徴を持っているのに実際は受けているため、比較対象を見つけることが困難です。

データの偏りを見抜く！ 視覚化テクニック

　ヒストグラムで分布の違いを発見

数字の羅列を眺めていても、データの偏りはなかなか見えてきません。

視覚化することで、一瞬で問題を発見できることがあります。

最も基本的で効果的な方法が、ヒストグラムによる分布の比較です。

例えば、運動プログラムの効果を評価する研究で、参加者と非参加者の年齢分布を見てみましょう。

参加者グループの年齢が40〜60歳に山なりに分布しているのに対し、非参加者グループが20〜40歳に集中していたとします。

この場合、単純に両グループを比較すると、年齢の違いによる影響と運動プログラムの効果を区別できません。

理想的には、両グループのヒストグラムがほぼ同じ形になることです。

山の位置、広がり、高さが似ていれば、少なくとも年齢という観点では公平な比較ができていることになります。

複数の変数について同時に確認することも重要です。年齢は揃っていても、健康状態や生活習慣が大きく異なっていては意味がありません。

そこで、重要な変数すべてについてヒストグラムを並べて表示し、総合的にバランスを確認します。

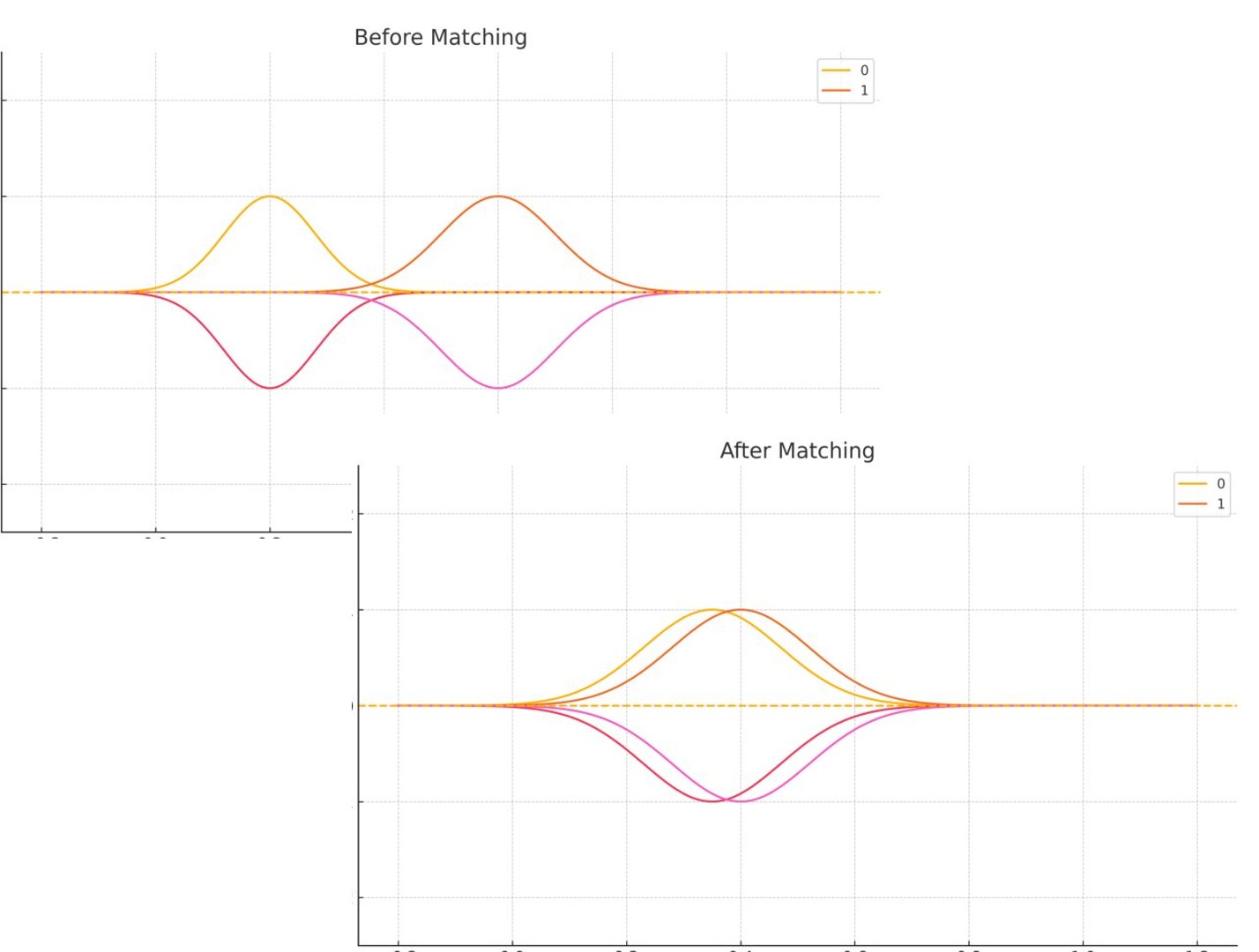
　傾向スコアの重なりをチェックする方法

傾向スコアを計算したら、必ず両グループの分布を確認しましょう。

よく使われるのは「ミラーヒストグラム」という表示方法です。

介入群のヒストグラムを上向きに、対照群を下向きに描くことで、分布の重なりが一目で分かります。

理想的な状況では、両グループの傾向スコアが広い範囲で重なっています。

これは「共通サポート」と呼ばれ、どちらのグループにも似た特徴の人がいることを示します。

逆に、重なりが少ない場合は要注意です。

例えば、介入群の傾向スコアが0.6〜0.9に集中し、対照群が0.1〜0.4に集中している場合、両グループはそもそも比較可能ではない可能性があります。

無理に比較しても、推定結果は信頼できません。

箱ひげ図も有効な可視化方法です。

中央値、四分位範囲、外れ値が一目で分かるため、分布の中心と広がりを素早く把握できます。

両グループの箱が大きく重なっていれば、比較可能性が高いと判断できます。

　バランスプロットの読み方と作り方

マッチングや重み付けを行った後、本当にバランスが改善したか確認する必要があります。

ここで威力を発揮するのがバランスプロットです。

バランスプロットは、横軸に標準化差、縦軸に変数名を取った散布図です。

標準化差とは、両グループの平均の差を標準偏差で割った値で、変数間でスケールが異なっても比較可能になります。

例えば、年齢の平均が介入群55歳、対照群45歳で、標準偏差が10歳だった場合、標準化差は(55-45)/10 = 1.0となります。一般的に、標準化差が0.1以下であれば十分にバランスが取れていると判断されます。

バランスプロットの優れた点は、調整前後の変化を一つの図で表現できることです。

調整前は多くの変数で大きな標準化差があっても、適切な調整後はほとんどの点が0付近に集まるはずです。

もし調整後も大きな差が残る変数があれば、その変数についてさらなる対処が必要かもしれません。

実践的なコツとして、重要な変数ほど上に配置すると読みやすくなります。

また、臨床的・実務的に意味のある差の基準線を追加すると、統計的な基準だけでなく実質的な意味でのバランスも評価できます。

よくある統計的アプローチ

　回帰分析による調整（共変量調整）

傾向スコアが開発される以前から、研究者たちは「回帰分析による調整」という方法を使ってきました。

この伝統的な手法は、今でも多くの場面で有効です。

回帰分析の基本的な考え方は、「他の条件を一定に保った上で、介入の効果を推定する」というものです。

例えば、ウォーキングプログラムが血圧に与える影響を調べる際、年齢、性別、BMI、喫煙習慣などをモデルに組み込むことで、これらの影響を統計的に「取り除いた」プログラムの効果を推定します。

ある企業の健康診断データを使った具体例を見てみましょう。

ウォーキングプログラム参加者の血圧は非参加者より平均5mmHg低いという結果が得られました。

しかし、詳しく調べると、参加者は非参加者より平均年齢が若く、BMIも低い傾向がありました。

そこで重回帰分析を使い、血圧を目的変数、プログラム参加を説明変数、年齢・性別・BMI・喫煙・飲酒を調整変数として分析します。

その結果、調整後のプログラム効果は3mmHgに減少しました。

つまり、単純比較で見られた5mmHgの差のうち、2mmHgは参加者の特性の違いによるものだったのです。

回帰分析の強みは、その解釈のしやすさにあります。

「他の条件が同じなら、プログラム参加により血圧が3mmHg下がる」という結果は、医師にも患者にも理解しやすいでしょう。

また、連続変数をそのまま扱えるため、年齢を「若い・高齢」と分類する必要がなく、情報の損失を防げます。

しかし、回帰分析には重要な限界もあります。

最大の問題は、変数間の関係が直線的であることを仮定している点です。

現実では、BMIと血圧の関係は低BMI領域と高BMI領域で異なるかもしれません。

このような非線形な関係を見落とすと、誤った結論に至る可能性があります。

　マッチング法の種類と使い分け

マッチング法にも様々な種類があり、それぞれに特徴があります。

データの性質と研究目的に応じて、適切な方法を選ぶことが重要です。

また、傾向スコアを使ったマッチングでは、傾向スコアの値が近いかどうかでマッチングします。

　　完全マッチング

完全マッチングは最も単純な方法で、すべての特徴が完全に一致する人同士をペアにします。

「45歳・男性・非喫煙者・BMI25」の介入群の人には、全く同じ特徴を持つ対照群の人をマッチングします。

この方法の利点は、マッチングされたペアが本当に「同じ」であることです。

しかし、変数が増えると完全に一致する人を見つけることが困難になり、多くのデータが分析から除外されてしまいます。

この問題を解決するのが粗いマッチング（Coarsened Exact Matching）です。

　　粗いマッチング

連続変数をカテゴリー化してからマッチングを行います。

年齢を5歳刻み、BMIを3段階に分類することで、マッチング可能な人数が大幅に増えます。

ただし、カテゴリー化により細かな情報は失われます。

最近傍マッチングは、何らかの距離指標で最も「近い」人をマッチング相手とする方法です。

例えば、年齢とBMIでマッチングする場合、「年齢の差の2乗＋BMIの差の2乗」の平方根を距離として計算します。

この方法は柔軟性が高く、多くの変数を同時に考慮できます。

　　カーネルマッチング

カーネルマッチングは、一対一ではなく、対照群の複数の人を重み付けして使う方法です。

介入群の人に近い対照群の人ほど大きな重みを与えることで、情報を無駄なく活用できます。

サンプルサイズが限られている場合に特に有効です。

　逆確率重み付け（IPW）

マッチング法の欠点は、マッチング相手が見つからない人のデータを捨ててしまうことです。

重み付け法は、この問題を解決する優れたアプローチです。

の基本的な考え方は、「珍しい人ほど重視する」というものです。

健康プログラムに若い人が参加しやすい傾向がある場合、60歳の参加者は珍しいので重要です。

逆に、25歳の参加者はたくさんいるので、一人一人の重要性は相対的に低くなります。

具体的には、介入群の人には「1/傾向スコア」、対照群の人には「1/(1-傾向スコア)」の重みを与えます。

傾向スコアが0.2（参加確率20％）なのに実際に参加した人は、1/0.2=5倍の重みを持つことになります。

ただし、単純なIPWには極端な重みが生じるという問題があります。

傾向スコアが0.01の人が介入を受けた場合、重みは100になってしまい、この一人が結果を大きく左右してしまいます。

そこで、安定化重みという改良版を使うことで、重みの変動を抑えることができます。

　複数手法の組み合わせで信頼性を高める

実践的な研究では、一つの方法だけに頼るのではなく、複数の方法で分析を行うことが推奨されます。

これを「感度分析」と呼びます。

例えば、教育プログラムの効果を評価する際、傾向スコアマッチング、回帰分析による調整、逆確率重み付けの3つの方法で分析を行います。

もしすべての方法で似た結果が得られれば、推定された効果の信頼性は高いと言えます。逆

に、方法によって結果が大きく異なる場合は、なぜそうなるのかを詳しく調べる必要があります。

また、手法を組み合わせることで、それぞれの弱点を補うこともできます。

例えば、傾向スコアで大まかなバランスを取った後、残った不均衡を回帰分析で調整する「二重にロバストな推定」という方法があります。

この方法は、どちらか一方のモデルが正しければ、正しい推定値が得られるという優れた性質を持っています。

手法選択のフローチャート

　データ特性から最適な手法を選ぶ

統計的因果推論の手法選択は、料理のレシピ選びに似ています。

材料（データ）の特性と、作りたい料理（研究目的）に応じて、最適なレシピ（手法）を選ぶ必要があります。

まず確認すべきは、介入群と対照群のサンプルサイズです。

　　サンプルサイズ

両群のサイズが大きく異なる場合、マッチング法では多くのデータが無駄になってしまいます。

例えば、介入群100人に対して対照群1000人いる場合、900人分のデータが活用されません。

このような場合は、重み付け法や回帰分析が適しています。

　　共変量の数

次に、共変量（調整したい変数）の数と性質を確認します。

共変量が少ない（5個以下）場合は、どの手法でも問題ありません。

しかし、20個、30個と増えてくると、完全マッチングは現実的でなくなり、傾向スコアや回帰分析が有力な選択肢になります。

　　共変量の性質

変数の性質も重要です。

カテゴリカル変数（性別、地域など）が多い場合は、完全マッチングや粗いマッチングが使いやすいでしょう。

連続変数（年齢、収入など）が多い場合は、回帰分析や傾向スコアが情報を無駄にしません。

　結果の頑健性チェックの方法

分析結果が得られたら、それで終わりではありません。

結果の頑健性（ロバストネス）を確認することが、信頼できる因果推論には不可欠です。

　　異なる手法での再分析

まず行うべきは、異なる手法での再分析です。

傾向スコアマッチングで効果ありという結果が得られたら、回帰分析や逆確率重み付け（IPW）でも同様の結果が得られるか確認します。

結果が大きく異なる場合は、その理由を探る必要があります。

　　分析に含める変数を変える

次に、分析に含める変数を変えてみます。

重要だと思われる変数を追加したり、逆に削除したりして、結果がどう変わるか確認します。

結果が大きく変わらなければ、推定は安定していると言えます。

　　極端な値を持つ観測値を除外し再分析

外れ値の影響も確認しましょう。

極端な値を持つ観測値を除外して再分析し、結果が大きく変わらないか確認します。

特に重み付け法では、極端な重みを持つ観測値が結果を左右することがあります。

　　サブグループ分析

最後に、サブグループ分析も有効です。

男女別、年齢層別、地域別などで分析を行い、効果が一貫しているか確認します。

特定のグループでのみ効果が見られる場合は、そのメカニズムを考察する必要があります。

よくある失敗と対処法

　交絡因子の見落とし

因果推論で最も深刻な失敗は、重要な交絡因子を見落とすことです。

交絡因子とは、原因と結果の両方に影響を与える第三の要因のことです。

これを見落とすと、誤った因果関係を「発見」してしまいます。

典型的な例として、アイスクリームの売上と水難事故の関係があります。

データを見ると強い正の相関がありますが、アイスクリームが水難事故を引き起こすわけではありません。

気温という交絡因子が両方に影響しているのです。

交絡因子の見落としを防ぐには、体系的なチェックリストが有効です。

まず、先行研究で指摘されている要因をリストアップします。

次に、理論的に考えられる要因を追加します。

さらに、現場の専門家（医師、教師、マネージャーなど）の意見を聞くことも重要です。

データ収集の段階で、「念のため」測定しておくことも大切です。

後から「あの変数も測っておけばよかった」と後悔しても手遅れです。

ただし、むやみに変数を増やすと、今度は過剰適合の問題が生じるので、バランスが重要です。

　極端な傾向スコアへの対処

傾向スコアが0に近い、または1に近い人は、分析上の問題を引き起こします。

傾向スコアが0.01の人は「ほぼ確実に介入を受けない」特徴を持っているのに実際は受けているため、この人に似た対照群を見つけることは困難です。

実践的な対処法として、まず傾向スコアの分布を確認し、極端な値がどの程度存在するか把握します。

少数であれば、これらの観測値を分析から除外することを検討します。

ただし、除外により結果の一般化可能性が制限されることに注意が必要です。

別の方法として、傾向スコアの推定モデルを見直すことも有効です。

交互作用項や非線形項を追加することで、より柔軟なモデルになり、極端な予測値が減ることがあります。

また、マッチングの際に「キャリパー」を設定する方法もあります。

これは、マッチングを許可する傾向スコアの最大差を決めることです。

例えば、キャリパーを0.2標準偏差に設定すると、それ以上離れたペアは作られません。

　結果の過度な一般化を避ける

統計的因果推論で得られた結果を解釈する際、過度な一般化は避けなければなりません。

分析に使用したサンプルの特性を超えて、結果を適用することには慎重になるべきです。

例えば、都市部の病院で実施した栄養指導プログラムの効果を、そのまま農村部に適用できるとは限りません。

患者の特性、利用可能な食材、生活習慣などが異なる可能性があるからです。

外的妥当性（結果の一般化可能性）を評価するには、まず分析対象となった集団の特性を明確に記述することが重要です。

年齢分布、性別比、地域特性、時期などを詳しく報告し、読者が自分の状況と比較できるようにします。

また、サブグループ分析の結果も参考になります。

様々な特性を持つグループで一貫した効果が見られれば、結果の一般化可能性は高いと考えられます。

逆に、特定のグループでのみ効果が見られる場合は、その理由を考察し、適用範囲を限定する必要があります。

今回のまとめ

今回紹介した様々な手法は、いずれも観察データから因果関係を推論するための優れたツールです。

しかし、どんなに洗練された手法を使っても、観察研究には本質的な限界があることを忘れてはいけません。

最大の限界は、測定されていない交絡因子の存在です。

どんなに注意深くデータを集めても、すべての関連要因を測定することは不可能です。

「やる気」「家族のサポート」「遺伝的要因」など、測定困難または不可能な要因が結果を左右している可能性は常に残ります。

また、因果の方向性の問題もあります。

健康な人ほど運動するのか、運動するから健康なのか、観察データだけでは完全には区別できません。

時間的前後関係である程度推測できますが、確実ではありません。

これらの限界を認識することは、悲観的になることではありません。

むしろ、結果を適切に解釈し、意思決定に活用するために不可欠です。

「この分析には○○という限界があるが、利用可能な最善の証拠として、△△という結論が得られた」という形で、限界と結論をセットで提示することが重要です。

何よりも信頼できる因果推論のためには、分析プロセスの透明性が欠かせません。

どのような仮定を置いたか、なぜその手法を選んだか、どのような感度分析を行ったか、すべてを明確に記録し報告する必要があります。

また、否定的な結果も正直に報告することが大切です。

「効果がなかった」という結果も、重要な知見です。

効果があった研究だけが公表される出版バイアスは、全体として誤った結論を導く危険があります。

今回は、統計的因果推論の基本的な考え方と主要な手法を紹介しました。

しかし、これは氷山の一角に過ぎません。因果推論の世界は広く深く、常に新しい手法が開発されています。

次のステップとして、まず実際のデータで手法を試してみることをお勧めします。

公開されているサンプルデータなどを使って、傾向スコアマッチングや重み付け法を実践してみましょう。

理論を学ぶだけでなく、実際に手を動かすことで、各手法の特性や限界がより深く理解できます。

専門書での学習も有効です。

計量経済学、疫学、統計学など、異なる分野の統計的因果推論の教科書を読み比べると、同じ手法でも異なる視点や応用例が学べます。

特に、自分の専門分野以外の本を読むことで、新しい発見があるかもしれません。

最新の研究動向を追うことも重要です。

機械学習を使った因果推論、時系列データでの因果推論、ネットワークデータでの因果推論など、新しい領域が次々と開拓されています。

学会やセミナーに参加し、最前線の研究者から直接学ぶ機会を作りましょう。

最後に、因果推論は単なる統計技術ではなく、世界を理解するための思考法であることを忘れないでください。

日常生活でも、ニュースを見るときも、ビジネスの意思決定でも、「これは本当に因果関係か？」と問い続ける習慣を持つことが、真実に近づく第一歩なのです。